环面蜗轮滚刀螺旋槽前刀面设计及修正方法<sup>*</sup> - 北京航空航天大学论文文献

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

环面蜗轮滚刀螺旋槽前刀面设计及修正方法^*

本站小编 Free考研考试/2021-12-25

与圆柱蜗杆传动相比，环面蜗杆传动具有承载能力强、体积小、传动效率高和使用寿命长等优点^[1-3]。环面蜗杆传动中的蜗轮通常由蜗轮滚刀滚切而成，滚刀的切削性能影响蜗轮的生产效率和齿面精度^[4-5]。对于同一头数的环面蜗轮滚刀，容屑槽的类型决定刀齿刃口线的几何形状和刀齿两侧前角的大小，进而影响滚刀的切削性能^[6]。
环面蜗轮滚刀头数较多时，如果容屑槽采用直槽^[7-8]，滚刀刀齿分度环面上的前角一侧为正值另一侧为负值，且前角的绝对值较大。负前角一侧引起主切削力增大^[9]，导致切削条件恶劣甚至无法加工^{[4, 10-11]}。因此，多头、大模数滚刀通常采用零前角螺旋槽^[4]。但是，由于环面蜗轮滚刀的每个刀齿形状不同，每个刀齿在同一环面螺旋线上的螺旋升角也不相同，其螺旋槽无法采用圆柱滚刀^[12]和齿轮滚刀^[13]一样的设计方法，而且不易保证每个刀齿的左右两侧前角都为0°，只能近似地控制在0°附近。
本文提出一种由圆柱产形面变传动比展成环面蜗轮滚刀螺旋槽前刀面的方法。首先，建立平面二次包络环面蜗轮滚刀前刀面的数学模型，求解刀齿两侧前角，得到每个刀齿从齿顶到齿根左右两侧前角的变化规律。然后，进一步对前刀面进行修正，将修正后的滚刀模型导入VERICUT软件中，测量其前角，验证设计方法的正确性。
1 前刀面展成原理及数学模型以平面为产形面Σ_d，一次包络展成螺旋面为Σ₁的环面蜗杆，称为平面包络环面蜗杆^[1]；以Σ₁作为滚刀产形面，二次包络展成蜗轮齿面Σ₂。上述环面蜗杆与蜗轮相配组成平面二次包络环面蜗杆副^[1](见图 1)。其中，作为滚刀产形面Σ₁的环面蜗杆称为滚刀基本蜗杆，以圆柱面为产形面Σ_qd，将滚刀基本蜗杆包络出螺旋槽，形成螺旋槽前刀面Σ₃。滚刀产形面Σ₁和螺旋槽前刀面Σ₃的交线即为刀齿的刃口线^[1]，前刀面Σ₃的成形方法决定刀齿刃口线的几何形状和刀齿两侧前角的大小，进而影响滚刀的切削性能。

图 1 环面蜗杆传动及蜗轮滚刀 Fig. 1 Hourglass worm driving and worm gear hob

图选项

1.1 由平面产形面Σ_d包络展成滚刀基本蜗杆螺旋面Σ₁ 如图 2所示，取静坐标系σ_oi(O_oi；i_oi，j_oi，k_oi)(i=1，2)与机架固连^[1]。下标“1”表示环面蜗杆，下标“2”表示蜗轮，

是环面蜗杆副的中心距。

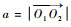
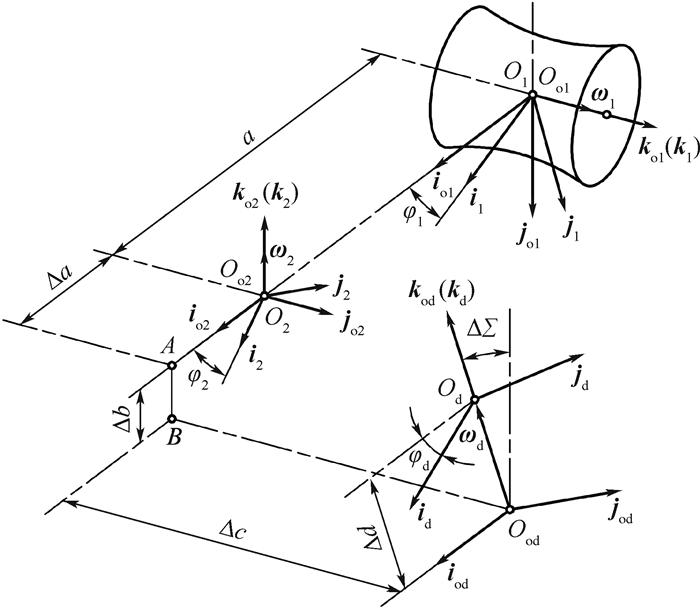图 2 刀座的位置和坐标系^[1] Fig. 2 Position and coordinate systems of grinding head^[1]

图选项

取动坐标系σ_i(O_i；i_i，j_i，k_i)(i=1，2)分别与蜗杆1和蜗轮2固连^[1]；蜗杆瞬时转角为φ₁，蜗轮瞬时转角为φ₂=i₂₁φ₁，i₂₁为蜗轮和蜗杆的传动比，初始位置φ₁=φ₂=0°。
取静坐标系σ_od(O_od；i_od，j_od，k_od)与机架固连^[1]，取动坐标系σ_d(O_d；i_d，j_d，k_d)与刀座固连^[1]，加工滚刀基本蜗杆螺旋面时，蜗杆毛坯绕回转轴k_o1的转速为ω₁，瞬时转角为φ₁=|ω₁|Δt，刀座绕回转轴k_od的转速为ω_d，转角为φ_d=|ω_d|Δt，初始位置：φ₁=φ_d=0°。
蜗杆毛坯瞬时转角φ₁和刀座瞬时转角φ_d成正比，即φ₁=i_1dφ_d，i_1d为蜗杆毛坯和刀座的速比。
通过改变刀座与蜗杆毛坯的相对位置和相对运动来实现滚刀基本蜗杆螺旋面的修形，本文中的修形参数：Δb=Δc=Δd=0，ΔΣ=0，Δa＞0，Δi=i_1d-i₁₂，i₁₂为蜗杆副的传动比^[1]。
如图 3所示，产形面Σ_d与半径为r_b的蜗轮主基圆相切；与刀座回转轴线呈β角。u和v为产形面Σ_d的参数，u直线与i_d平行，v直线与u直线垂直；n为产形面上任一点处的法向量；Q为产形面上的任一个点。由平面产形面Σ_d包络展成右旋的滚刀基本蜗杆螺旋面Σ₁。由齿轮啮合原理^[14-17]得到滚刀基本蜗杆螺旋面Σ₁在σ₁中的方程为

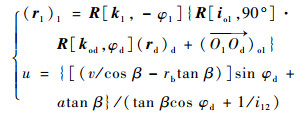(1)

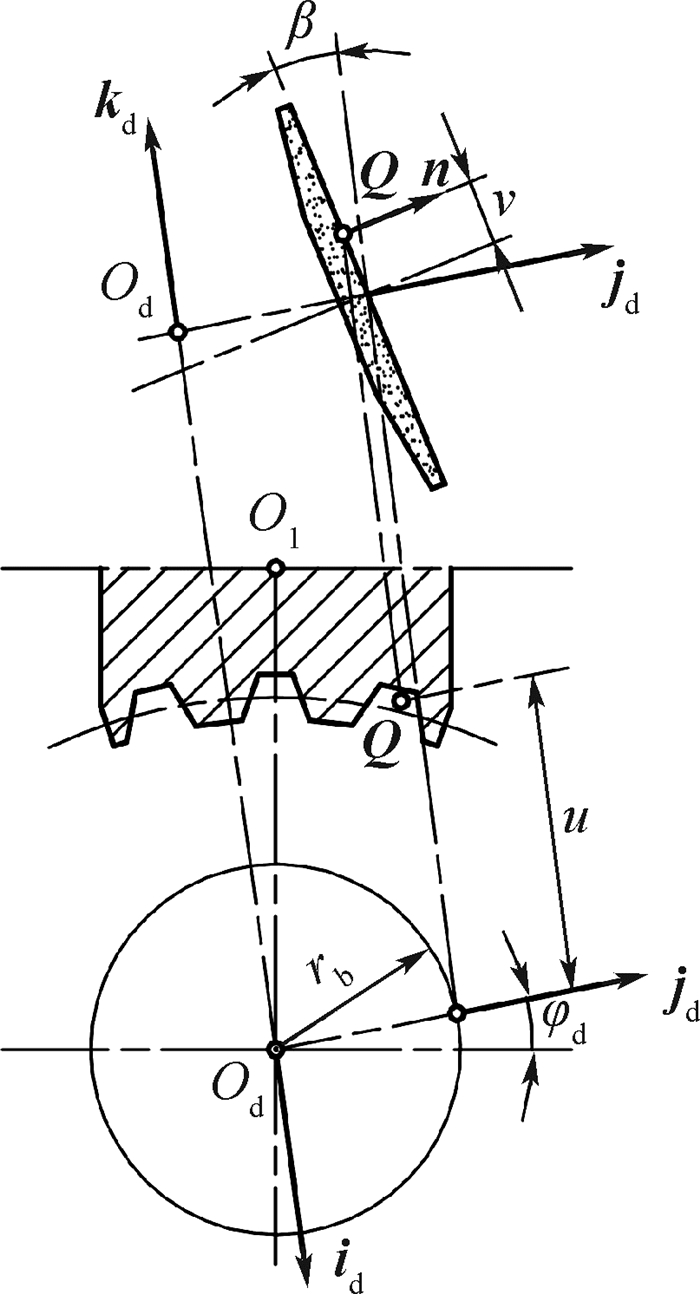图 3 由平面产形面Σ_d包络展成滚刀基本蜗杆螺旋面Σ₁^[1] Fig. 3 Grinding spiral surface Σ₁ of basic hob worm using a plane generating surface Σ_d^[1]

图选项

式中：

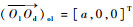
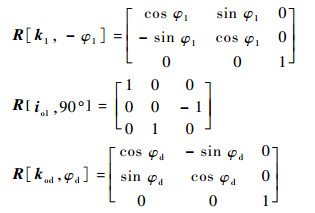；(r_d)_d为产形面Σ_d在坐标系σ_d中的表达式，且(r_d)_d=[-u, r_b-vsin β, vcos β]^T；坐标变换矩阵分别为

1.2 由圆柱产形面Σ_qd包络展成螺旋槽前刀面Σ₃ 建立如图 4所示的右旋直角坐标系，取静坐标系σ_qo1(O_qo1；i_qo1，j_qo1，k_qo1)与机架固连，动坐标系为σ_q1(O_q1；i_q1，j_q1，k_q1)与滚刀基本蜗杆固连，O_q1为坐标原点，O_qo1和O_q1重合，k_qo1=k_q1与滚刀基本蜗杆回转轴线重合。

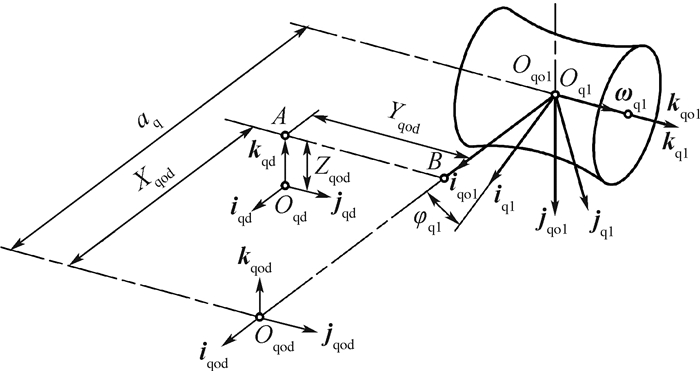图 4 加工前刀面的坐标系 Fig. 4 Coordinate systems of rake face machining

图选项

取静坐标系σ_qod(O_qod；i_qod，j_qod，k_qod)与机架固连，i_qod=i_qo1，k_qod=-j_qo1。取动坐标系σ_qd(O_qd；i_qd，j_qd，k_qd)与刀座固连，i_qd=i_qod，k_qd与刀座轴线重合，刀座轴心O_qd到A点的距离为Z_qod，a_q=

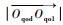
是两静坐标系的中心距。设定O_qod和滚刀基本蜗杆回转轴线确定平面S。
圆柱产形面的轴线与

平行，其前端面的圆心与O_qd重合，以速度v_x和v_y分别沿着i_qod轴和j_qod轴做平移运动，其合速度是v_qd。本文中定义：滚刀基本蜗杆绕回转轴k_qo1的瞬时转速ω_q1的绝对值与圆柱产形面沿j_qod轴移动的瞬时速度v_y的绝对值的比值为加工前刀面时的传动比，后文中统一记为传动比i_qd1，即i_qd1=-|ω_q1|/|v_y|，负号表示加工出的前刀面为右旋，与滚刀基本蜗杆螺旋面的旋向相反。
图 5为圆柱产形面的示意图，θ和h为产形柱面Σ_qd的参数，θ≥0，h≥0。

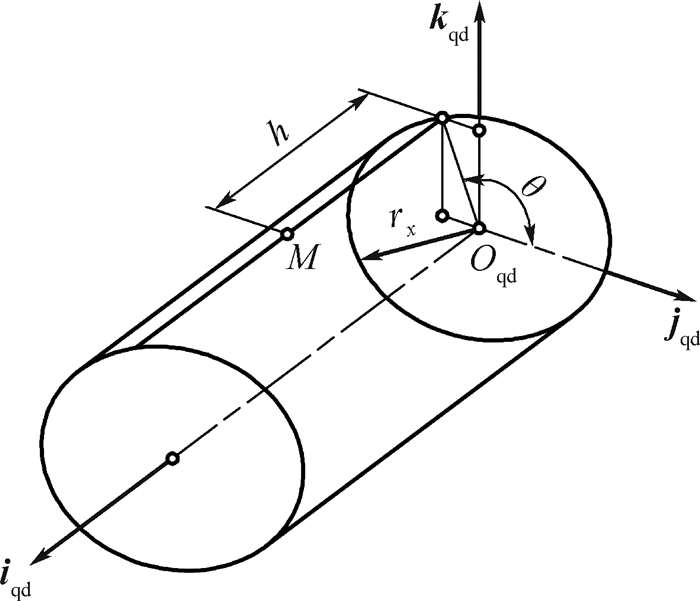图 5 圆柱产形面 Fig. 5 Cylindrical generating surface

图选项

如图 6所示，由圆柱产形面Σ_qd展成螺旋槽前刀面Σ₃。刀座沿i_qod轴和j_qod轴移动的瞬时速度分别为v_x和v_y，v_x=v_ytan δ；圆柱产形面的前端面的运动轨迹为以R_f1为半径，以O_qod为圆心的圆弧，且在σ_qod中的坐标为

，并且满足：

；坐标的增量分别为dX_qod=|v_x|dt，dY_qod=|v_y|dt。

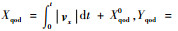
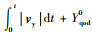
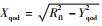
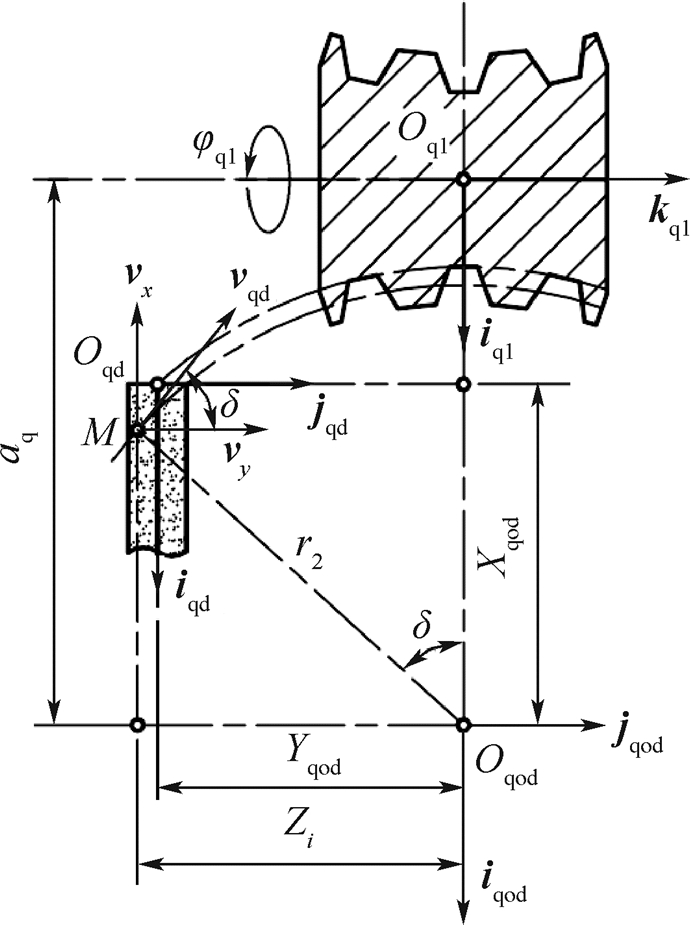图 6 展成螺旋槽原理图 Fig. 6 Schematic diagram of spiral flute machining

图选项

滚刀基本蜗杆绕回转轴k_qo1的瞬时转速为ω_q1，转角为

，转角变化量为dφ_q1=|ω_q1|dt。X_qod⁰和Y_qod⁰为圆柱产形面在初始位置时的坐标，φ_q1⁰为滚刀基本蜗杆在初始位置时的转角。当圆柱产形面运动到其轴线与

重合时，其前端面在σ_qod中的坐标X_qod=R_f1，Y_qod=0，此时滚刀基本蜗杆的转角φ_q1=φ_h。其中：r₂为蜗杆分度圆弧半径，R_f1为蜗杆齿根圆弧半径，φ_h为滚刀基本蜗杆的喉部转到S平面时对应蜗杆毛坯的转角。由齿轮啮合原理^[14-17]得到滚刀前刀面Σ₃在σ_q1中的数学模型，表示如下：

(2)

式中：

=X_qodi_qod+Y_qodJ_qod+Z_qodk_qod；h=-X_qod-a_q-1/(i_qd1tan θ)为圆柱产形面加工前刀面的共轭条件方程；

；(r_qd)_qd为产形柱面Σ_qd在坐标系σ_qd中的表达式，且(r_qd)_qd=[h, r_xcos θ, r_xsin θ]^T，坐标变换矩阵分别为

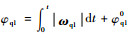
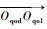
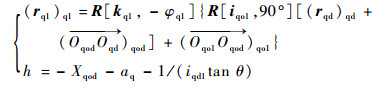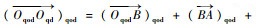
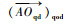
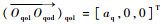
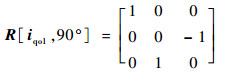2 传动比i_qd1的求解方法设定：滚刀基本蜗杆分度环面螺旋线的导程角为γ，前刀面曲线的导程角为γ_q。在滚刀基本蜗杆的各径向截面Y_qod=Z_i(-0.5L_w≤Z_i≤0.5L_w，L_w为滚刀基本蜗杆的工作长度)处，令导程角满足关系式：

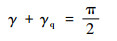(3)

即

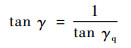(4)

2.1 滚刀基本蜗杆分度环面螺旋线导程角γ 在滚刀基本蜗杆的各径向截面Y_qod=Z_i处，蜗杆毛坯v₁与平面砂轮的线速度v_d分别为

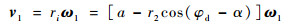(5)

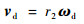(6)

滚刀基本蜗杆分度环面螺旋线的导程角γ(螺旋面右旋时为正)由式(7)求得^{[1, 18]}：

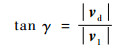(7)

将式(5)和式(6)代入式(7)得

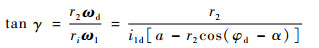(8)

式中：r_i为滚刀基本蜗杆在轴向坐标Z_i(-0.5L_w≤Z_i≤0.5L_w)处的分度圆半径；α为蜗轮分度圆压力角；φ_d为加工滚刀基本蜗杆螺旋面时刀座的瞬时转角；i_1d=ω₁/ω_d为蜗杆毛坯和刀座的速比。
2.2 前刀面曲线的导程角γ_q 如图 6所示，在滚刀基本蜗杆的各径向截面Y_qod=Z_i处，滚刀基本蜗杆和刀座的线速度表达式分别为

(9)

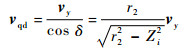(10)

前刀面曲线(左旋)的导程角γ_q(左旋为负)由式(11)求得：

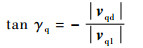(11)

将式(9)和式(10)代入式(11)得

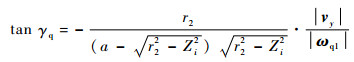(12)

2.3 i_qd1的表达式将式(8)和式(12)代入式(4)式求得传动比i_qd1的表达式为

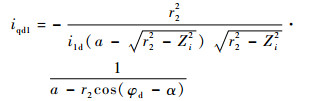(13)

当r_i=r₁时，由式(8)求得滚刀基本蜗杆喉部分度圆导程角γ_m的表达式为

(14)

由式(12)求得前刀面曲线的导程角γ_q为

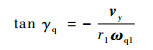(15)

将式(14)和式(15)代入式(4)求得定传动比i′_qd1的表达式为

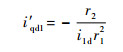(16)

式中：r₁=0.5d₁，d₁为蜗杆分度圆直径。
3 实例本文针对表 1提供的算例，首先求解导程角和传动比i_qd1。由于本算例是4头环面蜗轮滚刀，将滚刀设计为4排刀齿可以保证每排刀齿具有相同的前角变化规律，便于讨论。因此，在滚刀圆周方向上加工不同螺旋槽前刀面时传动比一致。
表 1 平面二次包络环面蜗轮滚刀基本参数 Table 1 Basic parameters of plane double enveloping hourglass worm gear hob

参数	数值
中心距a/mm	160
传动比i₁₂	10
滚刀头数z₁	4
蜗轮分度圆压力角α/(°)	21.866 7
蜗轮分度圆直径d₂/mm	255
蜗杆分度圆直径d₁/mm	65
滚刀齿顶圆弧半径R_a1/mm	122.24
滚刀齿根圆弧半径R_f1/mm	133.24
滚刀工作长度L_w/mm	90
滚刀喉部分度圆导程角γ_m/(°)	21.420 5
产形平面轴线倾角β/(°)	22.5
主基圆直径d_b/mm	95

表选项

由式(8)求得左侧齿面分度环面螺旋线的导程角在17.1°~21.4°之间，滚刀基本蜗杆喉部分度圆导程角最大，为γ_m=21.420 5°；环面蜗轮滚刀左侧齿面螺旋线的导程角和右侧齿面螺旋线的导程角关于Z_i=0对称，为照顾左右两侧刀齿的前角都能近似为0°，取分度环面上左右两侧齿面螺旋线导程角的平均值来求解传动比，其导程角的变化规律如图 7所示。

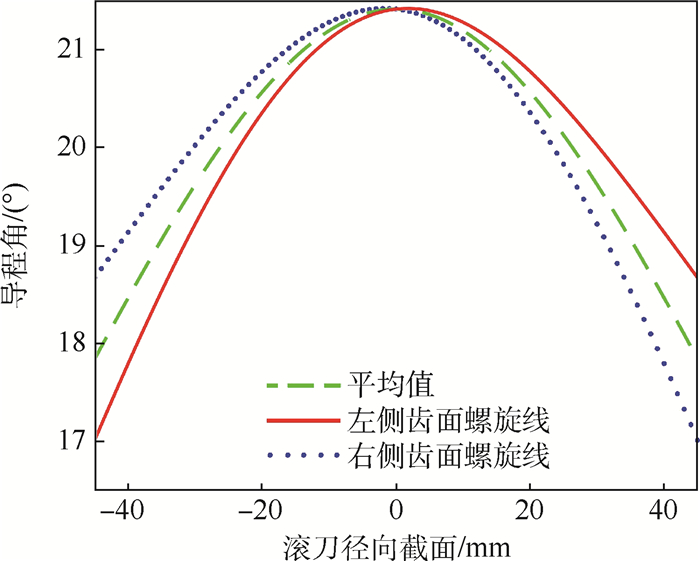图 7 分度环面处螺旋线导程角变化 Fig. 7 Variation of helix lead angle of indexing torus

图选项

由式(16)求得定传动比i′_qd1=-0.012 1，由式(13)求得传动比i_qd1的平均值在-0.008 6~-0.012 1之间，其变化规律如图 8所示。

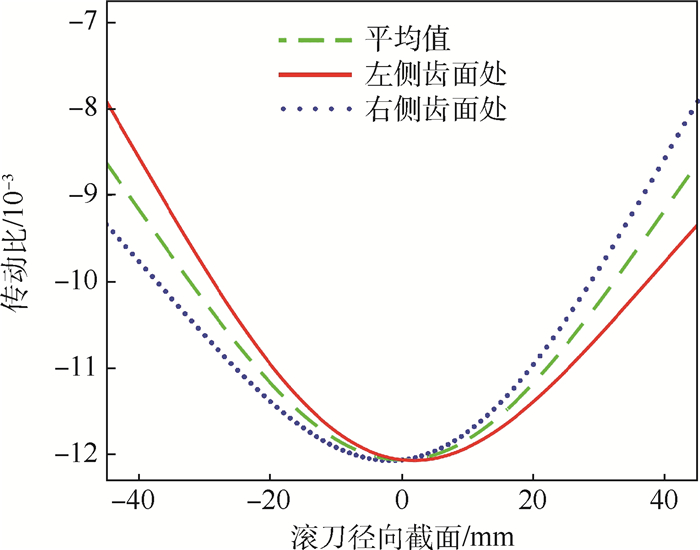图 8 分度环面处传动比变化 Fig. 8 Variation of transmission ratio at indexing torus

图选项

滚刀基本蜗杆和刀座按照求得的传动比运动，形成如图 9所示的螺旋槽前刀面Σ₃，其中：L_3-1、L_3-2和L_3-3分别为螺旋槽前刀面Σ₃与滚刀基本蜗杆齿顶环面、分度环面和齿根环面的交线。将滚刀基本蜗杆螺旋面Σ₁的方程式(1)和螺旋槽前刀面Σ₃的方程式(2)联立，即可求得滚刀刀齿的刃口线。设定：滚刀基本蜗杆左侧螺旋面和前刀面的交线为左侧刃口线，左侧刃口线上任一点处的前角为左侧前角，同理，右侧刃口线上任一点处的前角为右侧前角，其中，L_3-1、L_3-2和L_3-3与刃口线交点处的前角依次记为V_q(R_i=122.24 mm)、V_q(R_i=127.5 mm)、V_q(R_i=132.24 mm)。

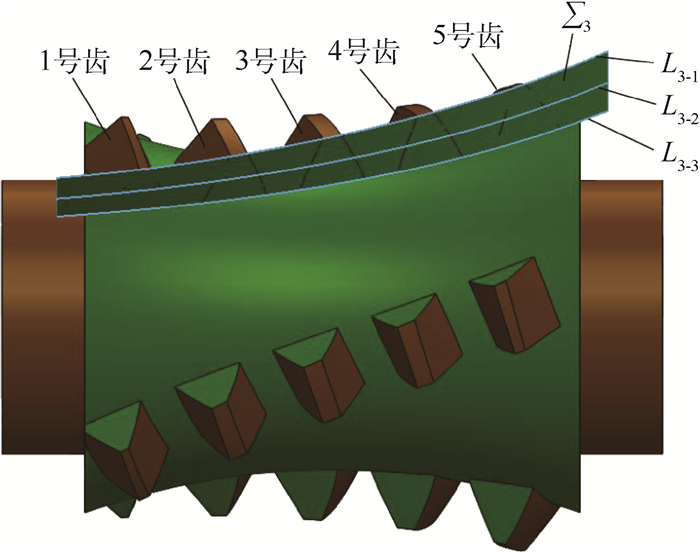图 9 螺旋槽滚刀三维模型 Fig. 9 Three-dimensional model of spiral flute hob

图选项

在σ₁坐标系中，由刃口线上任一点在前刀面的法向量(n_q1)₁和在螺旋面的法向量(n₁)₁求得该点处的前角V_q表达式为^{[16, 19]}

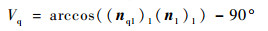(17)

式中：arccos((n_q1)₁(n₁)₁)记为该点处的夹角W_q，(n_q1)₁表达式为

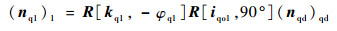(18)

其中：(n_qd)_qd表示在刀座动坐标系σ_qd中Σ_qd上任一点的单位法矢量，表达式为

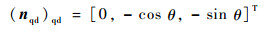(19)

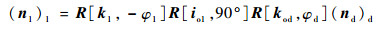(20)

式中：(n_d)_d表示在刀座动坐标系σ_d中Σ_d上任一点的单位法矢量，表达式为

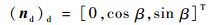(21)

由式(17)分别求得采用?6 mm的圆柱产形面定传动比和变传动比加工滚刀的螺旋槽前刀面时，L_3-2与刀齿刃口线交点处的前角，结果如表 2和表 3所示。
表 2 定传动比加工螺旋槽前刀面对应分度环面上各刀齿左右两侧的前角 Table 2 Rake angles on both sides of cutting teeth on indexing torus of spiral flute rake face processed by fixed transmission ratio

齿序号	左侧		右侧
齿序号	前角/(°)	轴向位置Z_i/mm	前角/(°)	轴向位置Z_i/mm
1号齿	1.708 83	-38.171 39	-5.341 03	-30.950 36
2号齿	-0.060 04	-21.520 36	-1.637 29	-13.517 04
3号齿	-0.501 66	-4.226 86	-0.085 59	3.920 86
4号齿	1.129 17	13.246 70	-0.667 29	21.148 44
5号齿	4.830 84	30.652 93	-2.642 67	37.881 56

表选项

表 3 变传动比加工螺旋槽前刀面对应分度环面上各刀齿左右两侧的前角 Table 3 Rake angles on both sides of cutting teeth on indexing torus of spiral flute rake face processed by variable transmission ratio

齿序号	左侧		右侧
齿序号	前角/(°)	轴向位置Z_i/mm	前角/(°)	轴向位置Z_i/mm
1号齿	0.445 06	-38	-0.378 63	-31
2号齿	0.067 97	-21	-0.116 36	-13
3号齿	-0.036 67	-4	0.087 35	4
4号齿	0.131 01	13	-0.062 32	21
5号齿	0.411 12	31	-0.511 75	38

表选项

由表 2和表 3可知：采用定传动比加工前刀面时，分度环面上左右两侧前角都在±5°左右，而采用变传动比加工前刀面时，刀齿分度环面上左右两侧前角都在±0.5°左右；变传动比有效减小了刀齿两侧前角的绝对值，使得分度环面上刀齿左右两侧的前角近似为0°。
再由式(17)求得采用变传动比加工滚刀的螺旋槽前刀面时，各个刀齿从齿顶到齿根左右两侧前角的大小，结果如表 4所示。
表 4 变传动比加工螺旋槽滚刀对应的前角 Table 4 Rake angles of spiral flute hob processed by variable transmission ratio

(°)
齿序号	前角类型	不同环面的R_i值
齿序号	前角类型	122.24 mm	124 mm	126 mm	127.5 mm	129 mm	131 mm	132.24 mm
1号齿	左侧前角	7.025 7	5.088 7	2.614 5	0.445 1	-2.024 5	-6.025 4	-8.589 3
1号齿	右侧前角	-5.082 5	-3.736 9	-1.985 1	-0.378 6	1.405 1	4.081 5	5.744 1
2号齿	左侧前角	5.978 7	4.364 7	2.052 5	0.068 0	-2.140 9	-5.414 3	-7.523 2
2号齿	右侧前角	-4.134 5	-3.016 4	-1.422 3	-0.116 4	1.066 4	2.958 2	4.167 5
3号齿	左侧前角	4.879 0	3.545 8	1.613 1	-0.036 7	-1.965 0	-4.761 3	-6.593 1
3号齿	右侧前角	-6.584 7	-4.642 2	-2.027 5	0.087 4	2.166 4	5.054 4	6.760 8
4号齿	左侧前角	4.178 1	3.022 8	1.435 6	0.131 0	-1.413 2	-3.730 5	-5.314 0
4号齿	右侧前角	-6.183 8	-4.516 3	-2.106 9	-0.062 3	2.159 2	5.557 6	7.692 8
5号齿	左侧前角	5.360 6	3.935 0	2.047 6	0.411 1	-1.593 7	-4.552 7	-6.391 6
5号齿	右侧前角	-6.899 1	-4.953 6	-2.504 0	-0.511 8	1.900 8	5.554 3	7.985 6

表选项

根据表 4的数据，绘制螺旋槽前刀面对应各刀齿从齿顶到齿根左右两侧的前角，其变化规律如图 10所示。

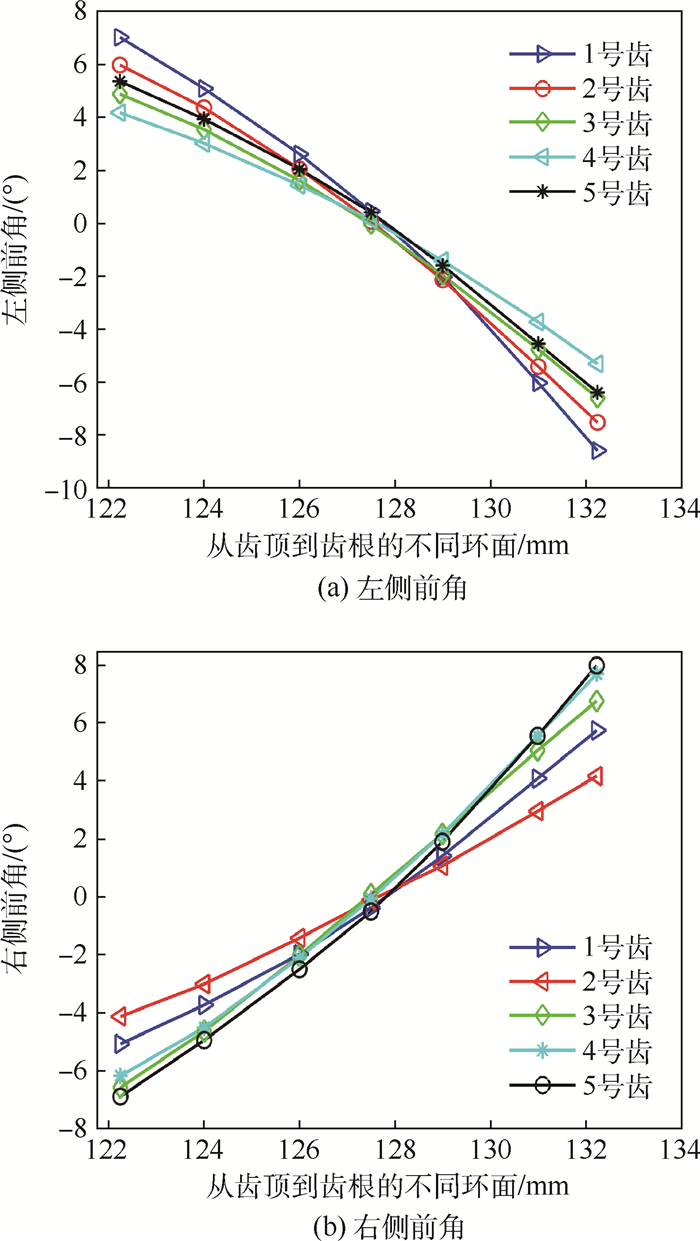图 10 两侧前角变化规律 Fig. 10 Variation of rake angles on both sides

图选项

由图 10可知，滚刀分度环面处的前角近似为0°，而刀齿左侧的前角从齿顶到齿根由正变负，右侧的前角从齿顶到齿根由负变正，并且正前角和负前角的绝对值较大。因此，需要对滚刀前刀面进行修正。
4 前刀面的修正滚刀基本蜗杆各环面螺旋线的导程角都不相同，式(8)中，代入不同环面处的分度圆半径和对应的刀座转角φ_d，求得齿顶环面螺旋线导程角和齿根环面螺旋线导程角。其变化规律如图 11所示。

图 11 不同环面处螺旋线导程角变化 Fig. 11 Variation of lead angles on different torus

图选项

分别取左右两侧齿面螺旋线导程角的平均值求得传动比的变化规律如图 12所示。

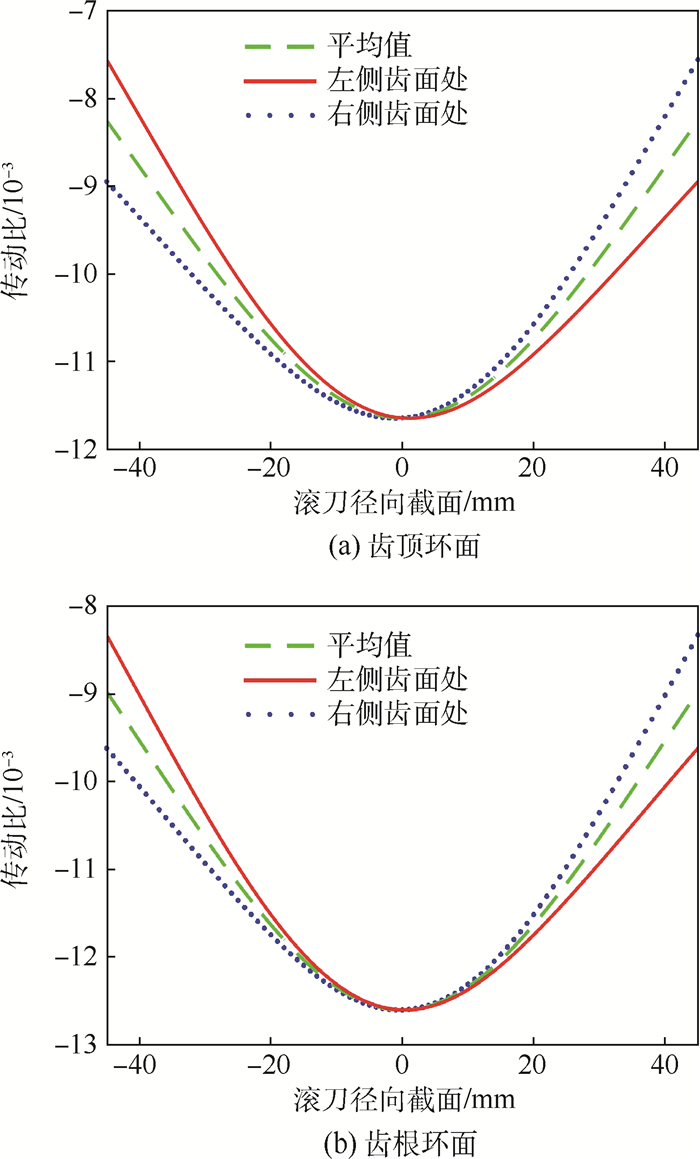图 12 不同环面处传动比变化 Fig. 12 Variation of transmission ratio on different torus

图选项

采用不同的传动比会形成不同的前刀面，图 13分别表示由分度环面螺旋线、齿顶环面螺旋线和齿根环面螺旋线的导程角对应的铣削传动比加工出的不同螺旋槽前刀面Σ₃、Σ4和Σ5，其中：L_4-1、L_4-2和L_4-3分别为螺旋槽前刀面Σ4与滚刀基本蜗杆齿顶环面、分度环面和齿根环面的交线；L_5-1、L_5-2和L_5-3分别为螺旋槽前刀面Σ5与滚刀基本蜗杆齿顶环面、分度环面和齿根环面的交线。

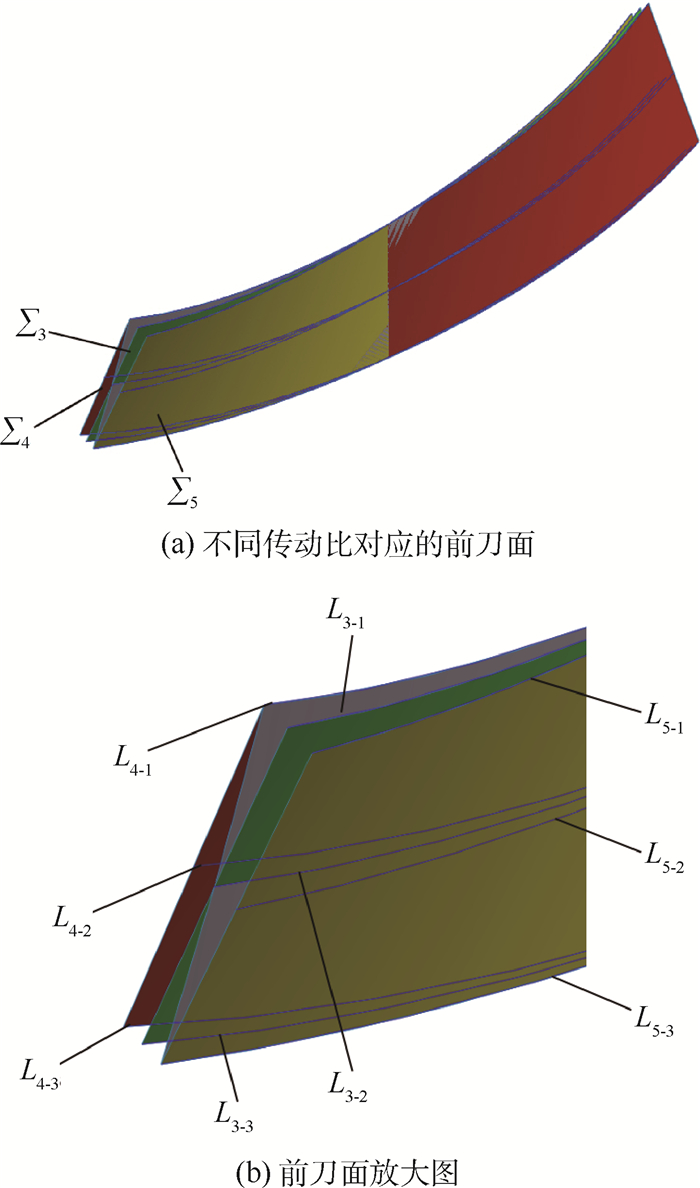图 13 前刀面示意图 Fig. 13 Schematic of rake faces

图选项

分别求解L_4-1和L_5-3与刃口线交点处的前角，结果如表 5和表 6所示。以齿顶环面处的传动比加工螺旋槽前刀面对应各刀齿两侧的前角在±0.5°左右，以齿根环面处传动比加工螺旋槽前刀面对应各刀齿两侧的前角在±0.6°左右。因此，采用L_4-1和L_5-3这两条曲线来修正前刀面Σ₃，使得齿顶环面和齿根环面上刀齿左右两侧的前角也近似为0°。
表 5 以齿顶环面处传动比加工螺旋槽前刀面对应各刀齿左右两侧的前角 Table 5 Rake angles on both sides of cutting teeth corresponding to spiral flute rake face processed by transmission ratio on tooth top torus

齿序号	左侧		右侧
齿序号	前角/(°)	轴向位置Z_i/mm	前角/(°)	轴向位置Z_i/mm
1号齿	0.462 56	-38	-0.483 52	-31
2号齿	-0.038 43	-21	0.131 94	-13
3号齿	-0.114 90	-4	0.176 31	4
4号齿	0.267 71	13	-0.204 22	21
5号齿	0.333 19	31	-0.430 43	38

表选项

表 6 以齿根环面处传动比加工螺旋槽前刀面对应各刀齿左右两侧的前角 Table 6 Rake angles on both sides of cutting teeth corresponding to spiral flute rake face processed by transmission ratio on tooth root torus

齿序号	左侧		右侧
齿序号	前角/(°)	轴向位置Z_i/mm	前角/(°)	轴向位置Z_i/mm
1号齿	0.511 02	-38	-0.420 14	-31
2号齿	0.239 34	-21	-0.135 27	-13
3号齿	-0.068 67	-4	0.170 25	4
4号齿	0.125 45	13	0.076 51	21
5号齿	0.395 23	31	-0.558 03	38

表选项

由曲线L_4-1、L_3-2和L_5-3拟合出一个新的曲面作为滚刀的螺旋槽前刀面。图 14为最终拟合出的螺旋槽环面蜗轮滚刀三维模型。

图 14 最终拟合出的滚刀模型 Fig. 14 Final fitted hob model

图选项

如图 15所示，将滚刀模型导入VERICUT软件中，测量刃口线上任一点处两法向量的夹角W_q，再由V_q=W_q-90°计算出刀齿两侧的前角V_q，如表 7所示，结果表明：1~5号刀齿从齿顶到齿根左右两侧的前角在-0.6°~0.5°之间。

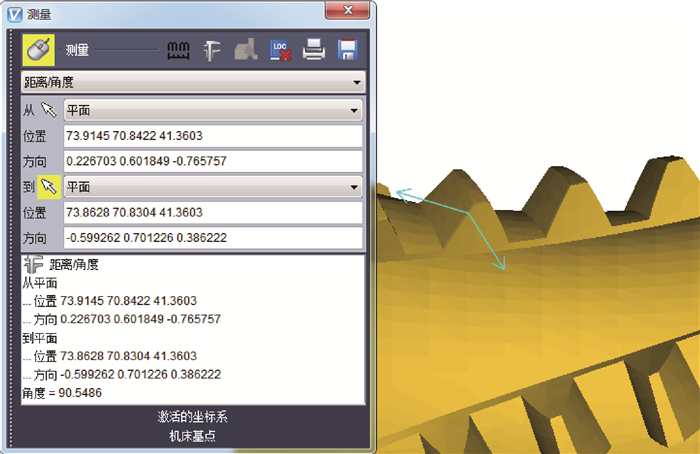图 15 测量两法向量的夹角W_q Fig. 15 Measurement of angle W_q between two normal vectors

图选项

表 7 测量螺旋槽滚刀对应的前角 Table 7 Measurement of rake angles of hob with spiral flute

(°)
齿序号	前角类型	不同环面的R_i值
齿序号	前角类型	122.24 mm	125 mm	127.5 mm	130 mm	132.24 mm
1号齿	左侧前角	0.227 9	0.405 1	0.315 2	-0.376 6	-0.144 6
1号齿	右侧前角	0.031 3	-0.188 5	-0.502 7	0.125 0	0.076 3
2号齿	左侧前角	0.276 0	0.147 4	0.091 1	0.041 9	0.153 8
2号齿	右侧前角	-0.222 8	0.095 6	0.184 8	-0.081 8	0.260 1
3号齿	左侧前角	-0.098 1	-0.073 3	0.132 2	-0.137 1	-0.190 1
3号齿	右侧前角	0.171 5	-0.130 6	-0.210 7	0.195 5	-0.061 2
4号齿	左侧前角	0.305 6	0.233 4	-0.086 0	-0.122 4	0.382 8
4号齿	右侧前角	-0.150 8	0.082 1	-0.254 3	0.265 3	0.115 5
5号齿	左侧前角	0.418 4	0.166 6	0.320 1	-0.177 6	-0.160 4
5号齿	右侧前角	-0.185 2	-0.332 7	-0.267 3	0.289 1	0.256 2

表选项

5 结论 1) 本文提出一种由圆柱产形面变传动比展成环面蜗轮滚刀螺旋槽前刀面的方法。建立了平面二次包络环面蜗轮滚刀螺旋槽前刀面的数学模型；分别求解采用定传动比加工螺旋槽和变传动比加工螺旋槽时，滚刀左右两侧前角的变化规律；对比分析了变传动比对滚刀前角的改善效果；得出变传动比可以控制刀齿左右两侧的前角近似为0°。
2) 计算出每个刀齿从齿顶到齿根左右两侧前角的变化规律，进一步提出前刀面的修正方法，将修正后的滚刀模型导入VERICUT软件中，测量其前角。结果表明，1~5号刀齿从齿顶到齿根左右两侧的前角在-0.6°~0.5°之间，解决了滚刀两侧前角绝对值较大的问题，具有实用价值。
3) 由于此设计方法采用圆柱产形面来包络前刀面，并且在计算传动比时采用数值计算方法，难以保证刀齿两侧的前角绝对0°。
致谢
感谢中南大学高性能复杂制造国家重点实验室对VERICUT软件提供的技术支持。
参考文献

[1]	董学朱. 环面蜗杆传动设计和修形[M].北京: 机械工业出版社, 2004: 14-15. DONG X Z. Design and modification of enveloping worm gearing[M].Beijing: Machine Industry Press, 2004: 14-15.(in Chinese)

[2]	李海涛, 董李扬.二次包络环面蜗轮滚刀侧后角面的设计方法: 201310172562.X[P].2013-05-10. LI H T, DONG L Y.Design method of the relief surfaces of double enveloping hourglass worm gear hob: 201310172562.X[P].2013-05-10(in Chinese).

[3]	李海涛, 柳冠伊.平面二次包络环面蜗轮滚刀侧后角面的数控磨削加工方法: 201410613061.5[P].2015-03-25. LI H T, LIU G Y.CNC grinding method of the relief surfaces of plane double enveloping hourglass worm gear hob: 201410613061.5[P].2015-03-25(in Chinese).

[4]	唐建生. 金属切削与刀具[M].武汉: 武汉理工大学出版社, 2009: 188-189. TANG J S. Cutting and cutting tools[M].Wuhan: Wuhan University of Technology Press, 2009: 188-189.(in Chinese)

[5]	ZHAO Y P, SU D Z, ZHANG Z. Meshing analysis and technological parameters selection of dual tori double-enveloping toroidal worm drive[J].Mechanism and Machine Theory, 2010, 45(9): 1269–1285.DOI:10.1016/j.mechmachtheory.2010.04.004

[6]	周良墉. 环面蜗杆修型原理及制造技术[M].长沙: 国防科技大学出版社, 2005: 558-559. ZHOU L Y. The modification principle and manufacturing technology of hourglass worm[M].Changsha: National University of Defense Technology Press, 2005: 558-559.(in Chinese)

[7]	董李扬.包络环面蜗杆副蜗轮滚刀数控加工技术的研究[D].北京: 中国农业大学, 2013: 15-20. DONG L Y.Research on NC machining technology of enveloping worm gear hob[D].Beijing: China Agricultural University, 2013: 15-20(in Chinese).

[8]	柳冠伊.包络环面蜗轮滚刀数控成形理论及技术研究[D].北京: 中国农业大学, 2016: 13-14. LIU G Y.Research on CNC relief grinding technology of enveloping worm gear hob[D].Beijing: China Agricultural University, 2016: 13-14(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10019-1016085319.htm

[9]	GUNAY M. Investigation of the effect of rake angle on main cutting force[J].International Journal of Machine Tools & Manufacture, 2004, 44(9): 953–959.

[10]	GUNAY M. Experimental investigation of the effect of cutting tool rake angle on main cutting force[J].Journal of Materials Processing Technology, 2005, 166(1): 44–49.DOI:10.1016/j.jmatprotec.2004.07.092

[11]	SAGLAM H, UNSACAR F, YALDIZ S. Investigation of the effect of rake angle and approaching angle on main cutting force and tool tip temperature[J].International Journal of Machine Tools and Manufacture, 2006, 46(2): 132–141.DOI:10.1016/j.ijmachtools.2005.05.002

[12]	CHANG S L. Helix gash of hob cutter manufactured by milling[J].Journal of Materials Processing Technology, 2003, 142(2): 569–575.DOI:10.1016/S0924-0136(03)00661-7

[13]	陈就, 刘丰林, 康权. 一种滚刀径向铲磨优化方法[J].中国机械工程, 2014, 25(14): 1883–1887. CHEN J, LIU F L, KANG Q. An optimization method for hob relief grinding[J].China Mechanical Engineering, 2014, 25(14): 1883–1887.DOI:10.3969/j.issn.1004-132X.2014.14.008(in Chinese)

[14]	DONG L Y, WANG J Y, LIU P Y, et al. An NC rough turning method of an enveloping toroidal worm[J].International Journal of Production Engineering, 2012, 6(2): 129–135.DOI:10.1007/s11740-012-0368-8

[15]	LIU G Y, WEI W J, DONG X Z, et al. Relief grinding of planar double-enveloping worm gear hob using a four-axis CNC grinding machine[J].International Journal of Advanced Manufacturing Technology, 2016, 89(9-12): 1–10.

[16]	YANG J, LI H T, RUI C J, et al.Research on a generating method of spiral flutes of hourglass worm gear hob[C]//Proceedings of the ASME Design Engineering Technical Conference.New York: ASME Press, 2017: V010T11A023.http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=2662593

[17]	RUI C J, LI H T, YANG J, et al.Research on incomplete design and generating theory of the relief surfaces of dual-cone double enveloping hourglass worm gear hob[C]//Proceedings of the ASME Design Engineering Technical Conference.New York: ASME Press, 2017: V010T11A022.http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleID=2662592

[18]	舒勤业.双锥面二次包络环面蜗杆副及其关键制造装备的设计与研究[D].杭州: 浙江大学, 2015: 21-30. SHU Q Y.Design and research of dual-cone doublehourglass worm gear pair and its key manufacturing equipment[D].Hangzhou: Zhejiang University, 2015: 21-30(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10335-1015630213.htm

[19]	姜正健, 张伟, 李铸宇. 微钻的前角计算及其钻削试验[J].大连工业大学学报, 2011, 30(2): 145–147. JIANG Z J, ZHANG W, LI Z Y. Calculation of the rake angle of micro drill and drilling test[J].Journal of Dalian Institute of Light Industry, 2011, 30(2): 145–147.DOI:10.3969/j.issn.1674-1404.2011.02.019(in Chinese)