飞行器在外太空姿态机动的过程中通常可看作为刚体。描述六自由度刚体姿态的系统通常是具有强耦合特性的多输入多输出(MIMO)非线性系统,因此飞行器能量最优姿态机动控制问题实质上是有限时域内非线性系统最优控制问题的一个特例。针对此问题,Bharadwaj等提出了逆最优控制(inverse optimal control)的方法[3],通过构造李雅普诺夫函数和求解HJB(Hamilton-Jacobi-Bellman)方程获得反馈控制量,实现满足性能指标最优的动力学系统控制,并被广泛用于飞行器能量最优姿态机动和控制当中,如文献[4-7]。然而,逆最优控制方法满足的是终端精度与能量消耗的加权和在无穷时域上的最优,并非有限时间内满足终端条件的能量最优控制。同时,逆最优控制姿态机动的终端精度、机动时间和消耗能量取决于若干控制参数的调节,在实际使用中有所不便。
为此,本文提出了一种基于模型预测控制(Model Predictive Control, MPC)和线性伪谱的能量最优姿态机动控制方法。
模型预测控制是一种基于滚动优化的在线控制策略,具有对模型要求低、抗干扰性好、鲁棒性强等优点,能够在优化性能指标的同时处理各种约束条件,得到了工程技术人员和理论研究者的重视,并被应用到飞行器姿态控制问题的研究当中[1, 8-9]。近年来,快速MPC逐渐引起关注。模型预测控制通常涉及到当前状态线性化后的局部最优控制问题,一般地,求解该最优控制问题可转化为求解一个两点边值问题(Two-Point Boundary Value Problem, TPBVP),专家****为提高控制指令求解速率和控制精度做了大量工作[10],针对具有强终端约束以及二次性能指标的控制问题,提出了模型预测静态规划(Model Predictive Static Programming, MPSP)非线性最优控制方法[11],并将其成功运用在飞行器再入制导领域[12]。尽管MPSP方法能获得全局最优解,但其在计算过程中需要采用大量离散节点以保证积分精度,导致计算效率较低。针对该问题,Yang等[13]提出了线性高斯伪谱模型预测控制(Linear Gauss Pseudo-spectral Model Predictive Control, LGPMPC)方法,该方法综合了非线性近似模型预测控制、线性二次最优控制以及高斯伪谱法,采用较MPSP更少的离散节点达到更高的计算效率及精度,被应用于大气层外制导[14]。针对多段问题,Yang等[15]又在LGPMPC的基础上提出了多段线性伪谱模型预测控制(Multi-segment Linear Pseudo-spectral Model Predictive Control, MLPMPC)方法,并被成功应用于飞行器再入段制导。
本文在LGPMPC和MLPMPC方法的基础上,针对飞行器姿态机动问题,利用KKT (Karush-Kuhn-Tucher)条件和线性伪谱推导了能量最优控制指令修正量的解析表达式,从而得到基于线性伪谱模型预测控制的能量最优姿态机动控制方法。该方法能够同时满足多个终端约束,并保证修正后的控制指令仍然满足能量最优。基于线性伪谱模型预测控制的能量最优姿态机动控制方法的基本策略为:根据飞行任务离线优化出初始姿态机动轨迹,实际飞行过程中在线修正标称控制以保证姿态机动终端精度,同时迭代更新姿态机动标称轨迹。数值仿真结果表明,该方法能够在限定时间内实现能量最优大角度姿态机动,在近似精度的前提下,相比于传统线性二次型调节器(Linear Quadratic Regulator, LQR)跟踪节省约10%的能量消耗。
1 飞行器模型及姿态机动问题 本文采用修正罗德里格斯参数(Modified Rodrigues Parameters, MRPs)描述飞行器姿态。考虑一般的刚体飞行器,其姿态运动学和动力学方程可描述为
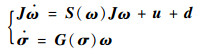 | (1) |
式中:J=diag(J1, J2, J3)为飞行器转动惯量矩阵;ω=[ω1??ω2??ω3]T为飞行器本体系相对于惯性系的姿态角速度矢量;u=[u1??u2??u3]T为飞行器的控制力矩矢量;d=[d1??d2??d3]T为飞行器受到的干扰力矩矢量;σ=[σ1??σ2??σ3]T为MRPs,描述了飞行器的本体系相对于惯性系的姿态;S(·)算子为3×3的反对称矩阵,对于任意一个向量a=[a1??a2??a3]T,有
 | (2) |
G(σ)∈R3×3为飞行器姿态运动学矩阵,定义为
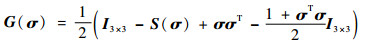 | (3) |
式中:I3×3为3×3单位矩阵。飞行器姿态机动过程中,控制力矩存在如式(4)幅值约束:
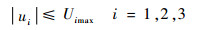 | (4) |
式中:Uimax>0为每个姿态控制通道上的最大力矩幅值。
设状态量x=[σ1??σ2??σ3??ω1??ω2??ω3]T,则飞行器姿态运动系统可采用状态空间的形式描述为
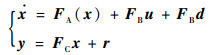 | (5) |
式中:FA(x)∈R6×6为状态转移矩阵,可由式(1)~式(3)推出;FB=[03×3??J-1]T为控制转移矩阵;此处假设飞行器的姿态和姿态角速度均可被测量,故FC=I6×6;r=[r1??r2??r3]T为测量误差;d=[d1??d2??d3]T为干扰力矩。
综上,飞行器能量最优姿态机动问题可描述为:寻找时变控制指令u(t)∈R3,使得满足状态空间方程式(5)的系统的状态量x在有限时间tf≤T(T为当前姿态机动时间)内从初始状态x0tar转变为终端状态xftar,同时满足过程约束和控制消耗的能量最优,即
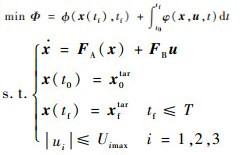 | (6) |
式中:t0和tf分别为飞行器姿态机动的起始时刻和终端时刻;?为末值型项指标;φ为积分型项指标。此处性能指标Φ只考虑能量最优,故只与控制量相关,一般地,取
 | (7) |
2 线性伪谱能量最优姿态机动控制 线性伪谱模型预测控制方法的主要思想为:将非线性动力学方程在标称状态量附近进行拟线性化,建立一个以偏差为自变量的线性微分方程,通过拉格朗日插值多项式对该线性微分方程的状态量进行逼近,将微分动力学约束通过正交配点转化为一组多变量代数约束,最终将非线性方程的积分问题转化为一个连续求解线性代数方程组的问题,从而得到非线性动力学过程的终端状态与状态偏差、控制偏差的等式关系,以实现偏差修正[13-14]。
基于线性伪谱模型预测控制的能量最优姿态机动控制策略需要基于一条标称机动轨迹,因此须先求解最优控制问题,规划得到标称机动轨迹。本文采用高斯伪谱法将能量最优姿态机动问题离散为非线性规划问题,采用SNOPT工具包求解该非线性规划问题。标称机动轨迹的具体求解及优化过程,并非本文研究重点,此处不再赘述。
线性伪谱模型预测能量最优姿态机动控制方法可以分为终端状态解析预测和控制指令修正两部分。
2.1 线性伪谱姿态机动终端状态解析预测 一般地,考虑具有终端约束的姿态机动非线性动力学方程如下:
 | (8) |
假设已存在一条能量最优姿态机动标称轨迹,则标称轨迹中每一时刻的状态量
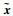
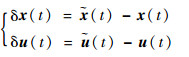 | (9) |
标称轨迹的终端状态量
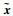
 | (10) |
称δx(t)为状态偏差,δu(t)为控制修正。将动力学方程在标称状态量
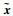
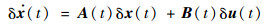 | (11) |
式中:A(t)∈R6×6为状态误差传播矩阵,B(t)∈R6×3为控制误差传播矩阵。对式(1)~式(3)描述的飞行器姿态动力学系统而言,状态误差传播矩阵和控制误差传播矩阵的具体形式为
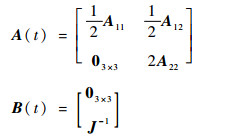 | (12) |
其中:A11∈R3×3,A12∈R3×3,A22∈R3×3,具体表达式分别为
 | (13) |
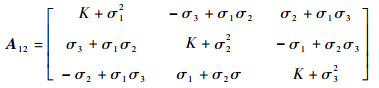 | (14) |
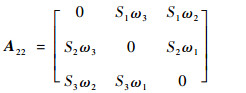 | (15) |
式中:K、S1、S2和S3为中间变量,其表达式分别为
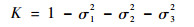 | (16) |
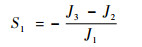 | (17) |
 | (18) |
 | (19) |
对状态量和控制量进行伪谱离散时,通常有3种高斯正交节点可供选择:LG(Legendre Gauss)节点、LGR(Legendre Gauss Radau)节点、LGL(Legendre Gauss Lobatto)节点。其中,LG节点不含终端点,LGR节点含有一个终端点(通常为左端归一化时间τ=-1),LGL节点含有2个终端点,如图 1所示。考虑到工程实际中的控制连续性,此处选取LGR节点对状态量和控制量进行离散。
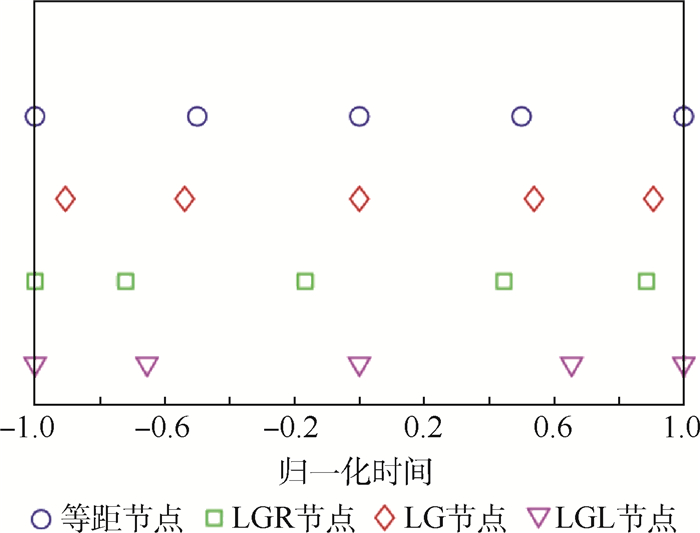 |
| 图 1 高斯正交节点示意图 Fig. 1 Schematic diagram of Gauss quadrature points |
| 图选项 |
首先,将实际机动时间t∈[t0, tf]映射到归一化时间τ∈[-1, 1]上:
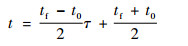 | (20) |
则归一化后的误差传播动力学方程为
 | (21) |
式中:p为归一化转换变量,其表达式为
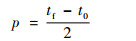 | (22) |
定义Ll(τ)为N阶拉格朗日插值多项式的第l项,τi为N阶拉格朗日多项式的根(N阶拉格朗日插值多项式有N+1个根),则可将误差传播动力学方程中的状态偏差δx用一组由LGR节点τi为支撑点所形成的拉格朗日插值多项式基的线性组合
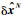
 | (23) |
同样地,本文得到控制量的插值拟合:
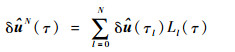 | (24) |
拉格朗日插值多项式满足以下性质:
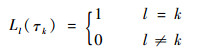 | (25) |
故有
 | (26) |
通过对状态量求导可得
 | (27) |
式中:微分逼近矩阵D∈RN×(N+1)是通过对拉格朗日插值多项式的各个元素分别求导获得的,其具体表达式为
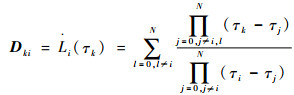 | (28) |
记
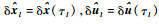
 | (29) |
式中:k=1, 2, …, N。
为保证控制指令的连续性,令δ?0=[0??0??0]T,但
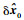
除了τ0时刻以外,其他节点时刻τi的预测状态偏差
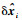
 | (30) |
重新组合微分逼近矩阵D,可得到预测状态偏差序列和控制修正序列表示的关系式如下:
 | (31) |
其中:
 | (32) |
 | (33) |
 | (34) |
矩阵A*和B*的表达式分别为
 | (35) |
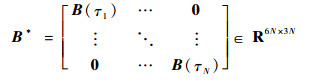 | (36) |
则其他LGR节点上的各个状态量可表示为
 | (37) |
在伪谱离散过程中,LGR节点并不包括最右侧的终端节点(τ=1),但终端状态偏差预测

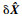
 | (38) |
式中:wi为高斯型积分的权函数,可通过数值计算获得,则终端状态偏差预测

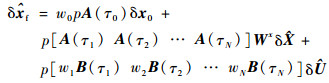 | (39) |
其中:Wx为高斯型积分公式的权函数矩阵,可表示为
 | (40) |
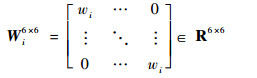 | (41) |
最终,可得预测终端状态偏差

 | (42) |
式中:Kx∈R6×6,Ku∈R6×3N,具体表达式分别为
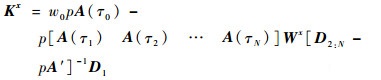 | (43) |
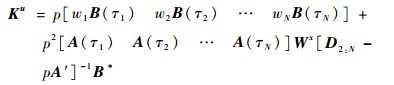 | (44) |
至此,本文获得了预测终端状态偏差关于初始状态偏差和控制修正的解析等式关系。
2.2 线性伪谱能量最优姿态机动控制指令修正 在求得预测终端状态偏差关于初始状态偏差和控制修正的解析等式关系后,可以根据最优控制理论反推控制指令修正量。
设当前时刻为t0,已知标称状态量
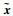

1) 求当前状态量与标称状态量的初始偏差δx0=
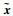

2) 以当前状态作为初始状态,保持控制为标称控制,进行数值积分,从而预测终端状态偏差

本文采用方法1)预测终端状态偏差,采用方法2)修正标称控制量及标称状态量。其原因如下:对于终端偏差的预测而言,方法1)和方法2)的精度相当,且由于方法1)无需积分,计算速度更快。然而,方法1)成立的前提是基于一条准确的标称轨迹,如果采用方法1)进行标称轨迹的更新,将会导致标称轨迹与实际轨迹的误差不断累计。因此,尽管方法2)涉及数值积分,速度较慢,但对于标称轨迹的准确获取仍是必要的。
采用方法2)得到新的标称轨迹以及积分预测终端偏差
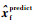
 | (45) |
控制修正的目的在于消除当前的积分预测终端偏差δ
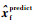
 | (46) |
由于δ?∈R3N×1,δ

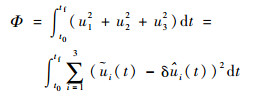 | (47) |
注意,能量最优是指修正后的控制消耗的能量最小,而非控制修正量本身消耗能量最小,即并非

将Φ展开,有
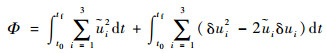 | (48) |
由于?i为标称控制量,故有
 | (49) |
设tk(k=1, 2, …, N)为[t0, tf]上LGR节点所在的时间点,?ik为第i通道在tk时刻的标称控制,δ?ik为第i通道在tk时刻的控制修正,则可用LGR节点上的离散值δ?ik对全时域积分Φ*进行拟合:
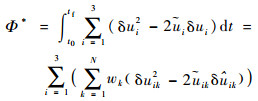 | (50) |
式中:wk为高斯型积分的权函数。
故求解δ?min的问题可描述为一个二次规划问题:
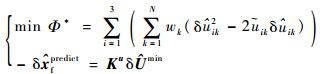 | (51) |
此二次规划问题可利用成熟算法迭代求得数值解,此处给出其解析解的求解过程。定义拉格朗日函数L为
 | (52) |
式中:kiu为矩阵Ku的第i行;
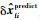
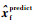
 | (53) |
经代数运算,可得
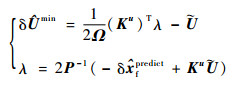 | (54) |
式中:?∈R3N×1为LGR节点上的标称控制,λ=[λ1??λ2…λ6]T,Ω∈R3N×3N,其表达式为
 | (55) |
P∈R6×6,设其第i行j列的元素为pij,则有
 | (56) |
式中:kimu为矩阵Ku第i行m列的元素;Ωmm为矩阵Ω第m行m列的元素。
根据式(54)~式(56)即可求出能量最优的LGR节点控制修正量δ?min,从而根据式(24)插值得到每一时刻的控制修正δ?min(t),得到既满足终端约束又保证能量最优的姿态机动控制umin(t)为
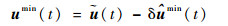 | (57) |
需要注意的是,为简单起见,本文在推导线性伪谱模型预测控制修正时定义了状态量偏差
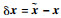
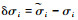
任何的3个参数姿态表示方法都不可能是全局非奇异的。设采用σ代表的姿态机动等价于绕单位固定轴ê旋转角度?,对应的姿态四元数为Q=[q0??q1?? q2 ??q3]T,当?→360°时(或q0→-1时),|σ|→∞,MRPs参数发生奇异,无法表示飞行器姿态,同时当?接近360°时,微小的偏差δ?将带来巨大的偏差δσ,推导线性伪谱模型预测控制修正时的线性化前提便不再成立。
由于四元数±Q代表的是同一姿态变换,因此本文在进行线性伪谱模型预测控制修正时有以下特殊规定:规定姿态四元数Q的第1项q0≥0,若q0 < 0,取Q=-Q。作上述人为规定后,能够避免MRPs在表示姿态时的奇异性,即当实际姿态偏差为小值时,MRPs参数偏差δσ也为小值,从而保证线性伪谱模型预测控制修正方法中的线性化前提成立。
2.3 能量最优姿态机动控制方法实施步骤 线性伪谱模型预测能量最优姿态机动控制方法的具体实施步骤如下:
步骤1??机动任务初始化:设置姿态机动的任务参数,包括姿态机动时间限制T,初始姿态角[γ0??θ0??ψ0],初始姿态角速度[ω10??ω20??ω30],终端姿态角[γf??θf??ψf],终端姿态角速度[ω1f??ω2f??ω3f],控制幅值约束[U1max??U2max??U3max]等。
步骤2??获得姿态机动能量最优标称控制轨迹:利用高斯伪谱法将飞行器能量最优姿态机动最优控制问题转化为非线性规划问题,再利用SNOPT求解该非线性规划问题,从而获得飞行器能量最优姿态机动标称轨迹
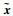
步骤3??修正参数设置:设置线性伪谱模型预测控制修正方法的节点数N,数值积分步长,控制修正更新检查间隔τcheck,控制修正阈值δxfTH(注:δxfTH为矢量,以便于针对各个通道的姿态角和角速度分别设定阈值)。
步骤4??基准控制段:飞行器将按照标称控制轨迹进行姿态机动控制,同时记录当前的时间;若当前时间距上次更新检查时间到达τcheck时,进入步骤5;若当前时间到达姿态机动限定时间T时,停止控制,完成姿态机动。
步骤5??控制更新检查:根据当前状态与标称状态的差别,求出δx0,利用式(42),估算出积分预测终端偏差


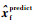
步骤6??控制指令修正:基于线性伪谱、最优控制理论、变分原理等获取终端状态量与高斯节点的状态量、控制量之间的关系,根据步骤5得到的终端状态预测偏差δ
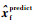
3 能量最优姿态机动控制仿真 3.1 飞行器模型参数与控制参数设定 能量最优姿态机动控制仿真中使用的飞行器模型参数如表 1所示。
表 1 飞行器模型参数 Table 1 Model parameters of spacecraft
| 参数 | J/(kg·m2) | Umax/(N·m) |
| 数值 | diag(5, 70, 70) | [5??10??10] |
表选项
姿态机动任务的初始姿态角为
 |
姿态机动的初始角速度为
 |
机动目标终端姿态角为
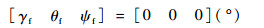 |
机动目标终端角速度为
 |
机动时间限制为
 |
其中:γ为绕飞行器本体系OXbZ轴转动的滚转角;θ为绕飞行器本体系OYb轴转动的俯仰角;ψ为绕飞行器本体系OZb轴转动的偏航角。飞行器采用Z-Y-X的旋转顺序进行姿态变换。
取干扰力矩di~N(0, 0.05),欧拉角测量误差riangle~N(0, 0.05)(实际中,从陀螺仪上获取的姿态信息通常为欧拉角形式,故此处设定的测量误差ri为欧拉角及角速度测量误差,仿真中再通过参数变换得到MRPs的测量误差),角速度测量误差riangvel~N(0, 0.01)。
取线性伪谱模型预测控制中的拉格朗日插值多项式的阶数N=8。
指令更新间隔时间设为τcheck=2 s。
姿态角控制修正阈值设为0.01(单位:1),角速度控制修正阈值设为0.005(°)/s。
为对比控制效果,本文同时进行了4组的LQR姿态机动控制的仿真,分别为
1) Q=100×I6×6, R=0.01×I3×3,采用LQR方法跟踪标称轨迹。
2) Q=100×I6×6, R=0.01×I3×3,采用LQR方法直接进行机动。
3) Q=100×I6×6, R=0.1×I3×3,采用LQR方法跟踪标称轨迹。
4) Q=100×I6×6, R=0.1×I3×3,采用LQR方法直接进行机动。
本文采用的仿真环境为:Intel Core i5-4200M处理器,4 G内存,Windows 7 32位操作系统以及MATLAB R2013a。
3.2 能量最优姿态机动单次仿真 设初始姿态角偏差为
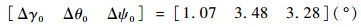 |
初始角速度偏差为
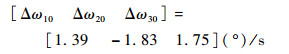 |
仿真结果如表 2和图 2~图 4所示。
表 2 姿态机动单次仿真结果 Table 2 Single simulation results of attitude maneuvers
| 控制方法 | [γf??θf??ψf]/(°) | [ω1f??ω2f??ω3f]/((°)·s-1) | Φ/(N2·m2·s) |
| 线性伪谱模型预测控制 | [0.15??-0.19??0.07] | [0.008 1??0.94??-0.48] | 247.98 |
| LQR跟踪标称轨迹-参数1 | [0.26??-0.16??0.35] | [-0.097??1.04??-0.56] | 260.54 |
| LQR直接控制-参数1 | [7.76??17.7??-9.78] | [2.21??1.43??-3.28] | 489.22 |
| LQR跟踪标称轨迹-参数2 | [1.14??0.7??0.62] | [-0.13??0.75??-0.75] | 240.58 |
| LQR直接控制-参数2 | [8.7??23.4??-12.1] | [1.93??4.09??-2.76] | 249.75 |
表选项
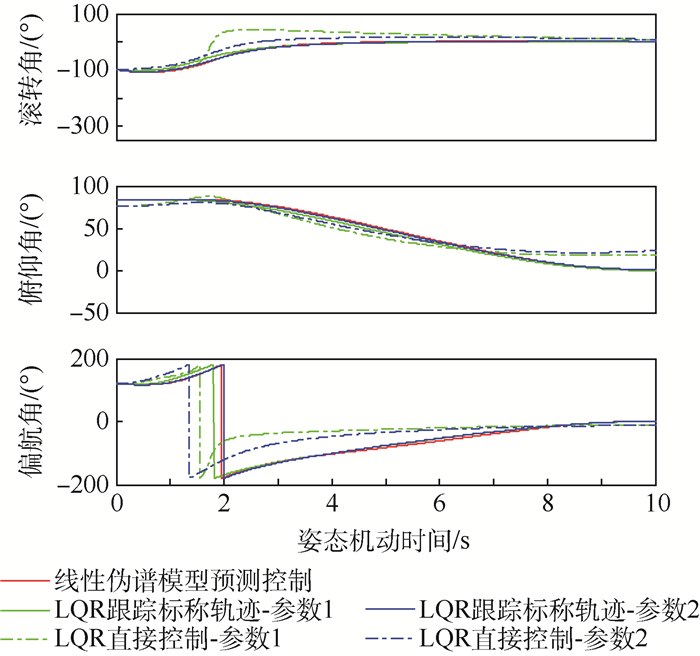 |
| 图 2 能量最优姿态机动姿态角仿真曲线 Fig. 2 Simulation curves of attitude angles of fuel-optimal attitude maneuvers |
| 图选项 |
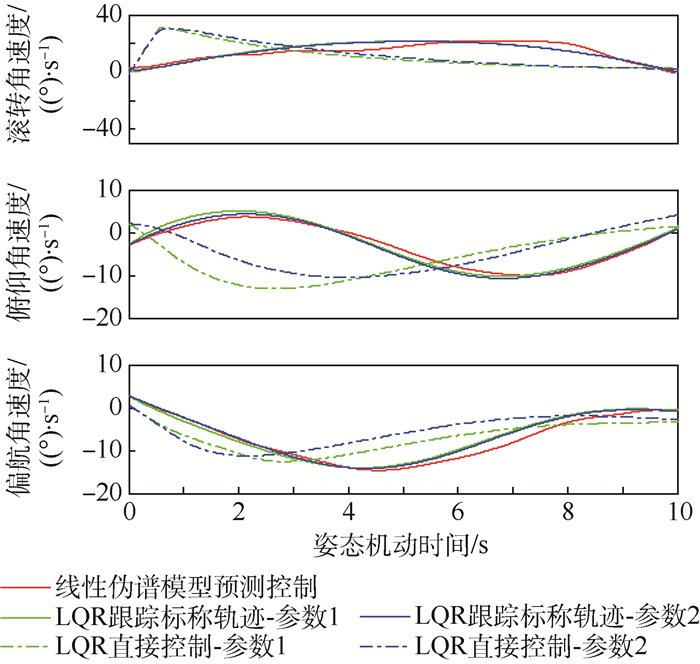 |
| 图 3 能量最优姿态机动角速度仿真曲线 Fig. 3 Simulation curves of angular velocities of fuel-optimal attitude maneuvers |
| 图选项 |
 |
| 图 4 能量最优姿态机动控制力矩仿真曲线 Fig. 4 Simulation curves of control moment of fuel-optimal attitude maneuvers |
| 图选项 |
从仿真结果能够看出,线性伪谱能量最优姿态机动控制能够达到较高的控制精度,实现飞行器有限时间内的大角度姿态机动,并且相比于LQR控制消耗更少的能量,同时其控制指令更加平滑。
同时能够看出,采用LQR跟踪标称轨迹的控制精度要优于直接控制。对于LQR控制而言,面临着终端精度和消耗能量之间的权衡,若仿真参数R选取较大,尽管消耗能量变小,控制平滑,但终端精度下降;若仿真参数Q选取较大,终端状态精度将提高,但消耗能量增大,同时控制量将发生振荡。仿真表明,采用参数1的LQR跟踪标称轨迹的控制方法获得的姿态机动终端精度与线性伪谱模型预测方法最为相近。
通过蒙特卡罗仿真,可以统计与比较这几种方法在计算精度、计算时间、消耗能量之间的差别。
3.3 能量最优姿态机动蒙特卡罗仿真 为了在终端精度相当的前提下比较能量消耗,此处采用LQR跟踪标称轨迹(参数1)的方法与线性伪谱模型预测控制方法作蒙特卡罗仿真对比。设初始姿态角偏差满足正态分布N(0, 10),初始角速度偏差满足正态分布N(0, 5),做200次蒙特卡罗仿真,结果如表 3和表 4、图 5~图 8所示。
表 3 姿态机动蒙特卡罗仿真终端精度 Table 3 Terminal accuracy of attitude maneuvers using Monte Carlo simulation
| 终端项 | 线性伪谱模型 预测控制 | LQR跟踪 标称轨迹-参数1 | |||
| 均值 | 标准差 | 均值 | 标准差 | ||
| γf/(°) | 0.004 7 | 0.004 7 | -0.046 | 0.222 3 | |
| θf/(°) | -0.056 5 | 0.056 5 | -0.050 | 0.118 3 | |
| ψf/(°) | 0.028 4 | 0.028 4 | 0.020 | 0.198 0 | |
| ω1f/((°)·s-1) | 0.004 6 | 0.004 6 | -0.008 3 | 0.076 8 | |
| ω2f/((°)·s-1) | 0.994 6 | 0.994 6 | 1.014 8 | 0.031 6 | |
| ω3f/((°)·s-1) | -0.496 2 | 0.496 2 | -0.489 7 | 0.055 7 | |
表选项
表 4 姿态机动蒙特卡罗仿真仿真时间 Table 4 Simulation time of attitude maneuvers using Monte Carlo simulation
| 仿真时间 | LQR跟踪 标称轨迹- 参数1 | 线性伪谱模型预测控制 | ||
| 8个节点 | 10个节点 | 12个节点 | ||
| 指令生成时间/ms | 14.6 | 59 | 70 | 78 |
| 全过程仿真时间/s | 4.286 | 4.143 | 4.352 | 4.704 |
表选项
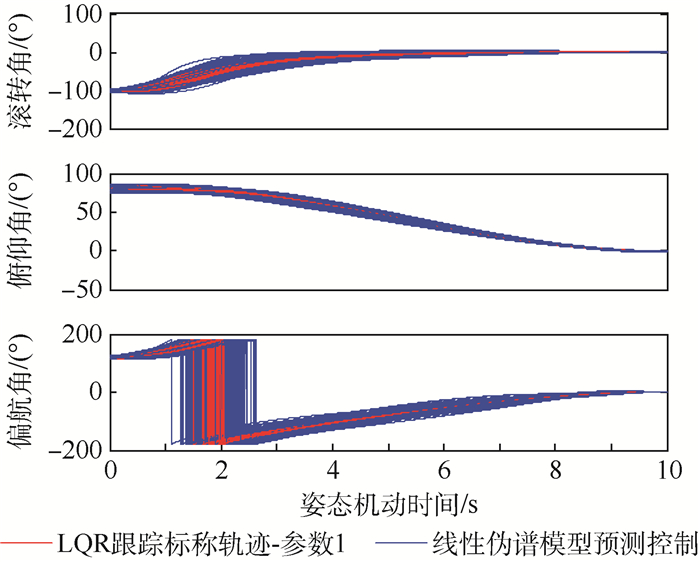 |
| 图 5 姿态机动蒙特卡罗仿真姿态角曲线 Fig. 5 Curves of attitude angle maneuvers using Monte Carlo simulation |
| 图选项 |
 |
| 图 6 姿态机动蒙特卡罗仿真角速度曲线 Fig. 6 Curves of angular velocities of attitude maneuvers using Monte Carlo simulation |
| 图选项 |
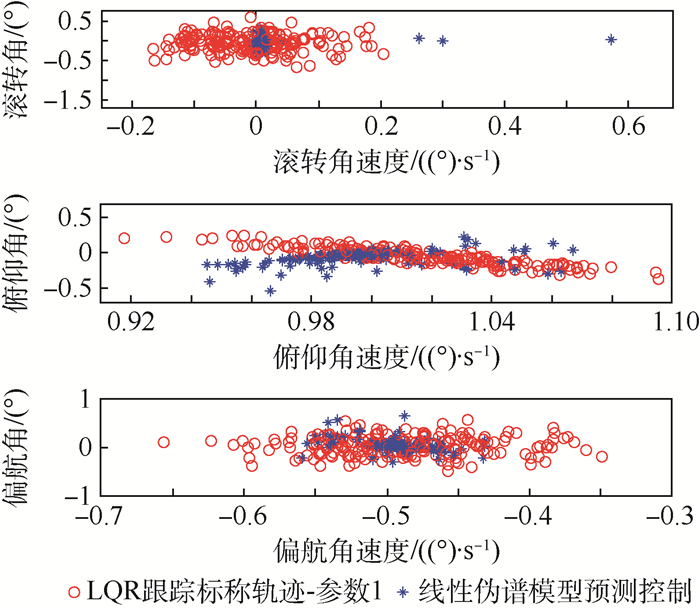 |
| 图 7 姿态机动蒙特卡罗仿真终端精度散布图 Fig. 7 Scatter diagram of terminal accuracy of attitude maneuvers using Monte Carlo simulation |
| 图选项 |
 |
| 图 8 姿态机动蒙特卡罗仿真能量消耗对比图 Fig. 8 Comparison of energy consumption of attitude maneuvers using Monte Carlo simulation |
| 图选项 |
仿真中,线性伪谱能量最优姿态机动控制方法(节点数为8)进行一次指令修正更新的计算时间约为59 ms;LQR控制指令更新一次的计算时间约为14.6 ms。尽管线性伪谱控制指令修正的计算时间大于LQR控制,但该方法不需要每一时刻都计算更新指令,只有在预测偏差大于设定阈值的情况下才更新,在仿真中,指令更新数基本在1~3次的范围内,故全过程仿真花费的时间两者相差不大。因此,线性伪谱能量最优姿态机动控制方法能够满足飞行器上计算的实时性要求。
从仿真结果可以看出,线性伪谱能量最优姿态机动控制方法和LQR跟踪方法都能满足终端约束,能够实现对初始偏差的修正,对干扰力矩以及测量误差都有一定的抗干扰作用。然而,2种方法的姿态机动轨迹并不相同,LQR跟踪方法趋向于尽快将当前状态修正到标称状态,而线性伪谱能量最优姿态机动控制方法只关心终端状态是否修正到目标状态,对中间过程并不关心。实际上,当只关心终端约束时,并不需要立即将当前状态修正到标称状态,而这种不必要的立即修正带来了额外的能量消耗。
从控制的角度来看,线性伪谱能量最优姿态机动控制方法更具有优势,因为其控制更加平稳,而LQR跟踪的控制显得更加振荡。在考虑控制器的动态特性后,LQR的控制效果将会下降。
从图 8可以看出,线性伪谱能量最优姿态机动控制方法能量消耗小于LQR跟踪控制,前者平均约能节省10%的能量。
4 结论 本文基于线性伪谱模型预测控制,设计了线性伪谱能量最优姿态机动控制方法,该控制方法具有以下优势:
1) 能够实现限定时间内飞行器能量最优大角度姿态机动,相比于LQR跟踪规划轨迹的方法能够节省约10%的能量消耗。
2) 该方法能够得到的平滑且连续的控制量。
3) 该方法能够快速地进行控制修正,满足在线使用的要求。
4) 该方法的设计思路能推广到更为一般的具有终端约束的微分动力学系统跟踪问题上。
该方法目前还存在着以下缺陷:
1) 实际使用中,需根据飞行器的计算能力进行节点数、积分步长和控制精度之间的权衡。
2) 修正得到的控制量无法保证一定满足过程约束,若直接在得到的修正控制量上增加限幅模块,则得到的修正控制无法保证能量最优。同时可能导致额外的控制更新。
3) 本文提出的方法只适用于连续控制,不适用于Bang-Bang控制(开关式控制)。
第2)、3)点缺陷,将是未来的研究重点。
参考文献
| [1] | 盖俊峰, 赵国荣, 周大旺. 刚体飞行器姿态机动的模型预测控制方法[J]. 弹箭与制导学报, 2015, 35(2): 5-9. GAI J F, ZHAO G R, ZHOU D W. A model predictive control method for rigid aircraft attitude maneuver[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2015, 35(2): 5-9. (in Chinese) |
| [2] | 赵健康, 尹秋岩, 戴金海. 空间飞行器姿态机动预测跟踪控制技术[J]. 系统仿真学报, 2004, 16(4): 711-713. ZHAO J K, YIN Q Y, DAI J H. Forecast-tracking control of attitude maneuver of spacecraft based on tracking-filter[J]. Journal of System Simulation, 2004, 16(4): 711-713. DOI:10.3969/j.issn.1004-731X.2004.04.030 (in Chinese) |
| [3] | BHARADWAJ S, OSIPCHUK M, MEASE K D, et al. Geometry and inverse optimality in global attitude stabilization[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(6): 930-939. DOI:10.2514/2.4327 |
| [4] | TEWARI A. Optimal nonlinear spacecraft attitude control through Hamilton-Jacobi formulation[J]. The Journal of the Astronautical Sciences, 2002, 50(1): 99-112. |
| [5] | SHARMA R, TEWARI A. Optimal nonlinear tracking of spacecraft attitude maneuvers[J]. IEEE Transactions on control systems technology, 2004, 12(5): 677-682. DOI:10.1109/TCST.2004.825060 |
| [6] | LUO W, CHU Y C, LING K V. Inverse optimal adaptive control for attitude tracking of spacecraft[J]. IEEE Transactions on Automatic Control, 2005, 50(11): 1639-1654. DOI:10.1109/TAC.2005.858694 |
| [7] | YONMOOK P. Inverse optimal and robust nonlinear attitude control of rigid spacecraft[J]. Aerospace Science and Technology, 2013, 28(1): 257-265. DOI:10.1016/j.ast.2012.11.006 |
| [8] | ALEXIS K, NIKOLAKOPOULOS G, TZES A. Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances[J]. Control Engineering Practice, 2011, 19(10): 1195-1207. DOI:10.1016/j.conengprac.2011.06.010 |
| [9] | GAVILAN F, VAZQUEZ R, CAMACHO E F. Chance-constrained model predictive control for spacecraft rendezvous with disturbance estimation[J]. Control Engineering Practice, 2012, 20(2): 111-122. DOI:10.1016/j.conengprac.2011.09.006 |
| [10] | OHTSUKA T, FUJⅡ H A. Real-time optimization algorithm for nonlinear receding horizon control[J]. Automatica, 1997, 33(6): 11471154. |
| [11] | PADHI R, KOTHARI M. Model predictive static programming:A computationally efficient technique for suboptimal control design[J]. International Journal of Innovative Computing, Information and Control, 2009, 5(2): 399-411. |
| [12] | OZA H B, PADHI R. Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 153-164. DOI:10.2514/1.53647 |
| [13] | YANG L, ZHOU H, CHEN W C. Application of linear gauss pseudospectral method in model predictive control[J]. Acta Astronautica, 2014, 96(1): 175-187. |
| [14] | RAHMAN T, ZHOU H, YANG L, et al. Pseudospectral model predictive control for exo-atmospheric guidance[J]. International Journal of Aeronautical and Space Sciences, 2015, 16(1): 64-76. DOI:10.5139/IJASS.2015.16.1.64 |
| [15] | YANG L, CHEN W C, LIU X M, et al. Robust entry guidance using multi-segment linear pseudospectral model predictive control[J]. Journal of Systems Engineering and Electronics, 2017, 28(1): 103-125. DOI:10.21629/JSEE.2017.01.13 |
