文献[1-2]提出了构型空间, 即C空间的概念, 将机械臂的工作空间分为自由空间和障碍空间, 并在自由空间内利用启发式搜索算法寻找机械臂的运动路径。在众多启发式算法中, 快速扩展随机树(RRT)算法[3]特别适合多自由度机器人的运动规划问题。Bertram等[4]提出了一种新的在路径规划过程中的目标选择方法, 该方法保证了新生长的节点不断向着目标点生长。Stilman[5]对RRT算法进行了改进, 使得末端轨迹能够满足特定的约束条件。但是RRT算法搜索效率较低, 不具有实时性。
在机器人运动轨迹规划时, 还需要综合考虑各种约束条件。一些****利用基于多项式的伪逆路径规划算法对路径进行规划[6-7]。Haddad等[8]在用机械臂拦截快速飞行的物体时, 对机械臂的运动轨迹施加关节速度约束和力矩约束。Shimizu等[9]推导出了具有特殊关节配置的7R机械臂的解析逆解, 并且使所有的关节满足其关节角度限制。Tian等[10]将工作空间划分成一个个小格, 得到每个小格内拟人的关节角度, 建立查找表, 根据要求的末端位置, 在查找表中找到冗余角q3, 根据解析逆解求出其他关节角。Tran等[11]利用运动元的方式实现拟人运动。然而, 此类方法没有将躲避障碍物考虑在内。
文献[12]采用的是关节角优化控制方法, 在关节角的速度层面下, 建立回避障碍物的指标函数, 将指标函数的梯度加入到运动学逆解过程中进行求解。贠超等[13]利用二次规划技术替代雅可比矩阵伪逆的方法, 描述机械臂受到的约束, 并建立单层RBF (Radical Basis Function)神经网络模型, 通过调整其输出权值, 使得机械臂达到最佳构型, 同时避开关节极限和障碍物。然而, 此类方法精度不高, 稳定性较差, 不适用于精度要求较高的场合。王俊龙等[14]采用改进人工势场法, 当局部极小值产生时, 添加一个虚拟障碍以使机械臂逃离局部极小点。汪首坤等[15]利用三维空间投影求出碰撞临界值, 然后采用导航势函数法逃离局部极小值, 进而实现冗余机械臂避障。此种方法未将机械臂运动的平稳性的因素考虑其中。
针对以上问题, 本文采用构形平面方法, 对冗余机械臂在空间的运动轨迹以机械臂构形的方式进行规划, 能够极大提高规划的效率。
1 机械臂的构形平面 1.1 构形平面的划分 构形平面的示意图如图 1所示。构形平面内的第1个关节是回转关节, 最后一个关节是摆动关节或者移动关节。第1个构形平面的第1个关节可以不是回转关节。假如串联机器人的最后一个关节是回转关节, 则把此关节单独看作一个构形平面。
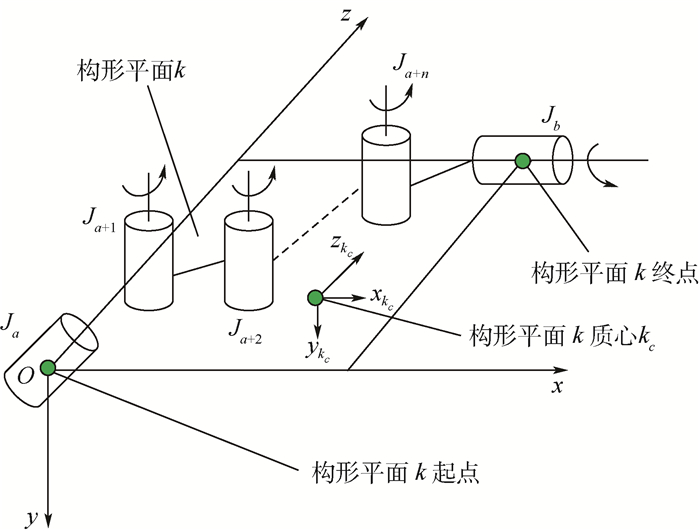 |
| 图 1 构形平面示意图 Fig. 1 Schematic diagram of configuration plane |
| 图选项 |
平面构形中回转关节对构形末端和构形中心之间的距离关系无影响, 与连杆作用相同, 只有摇摆关节和移动关节会改变构形末端和构形中心位置关系, 因此, 摇摆关节和移动关节的数量是构形平面中的自由度数目。
1.2 构形平面的运动学表达形式 为便于构形平面匹配, 需简化其运动学模型。构形平面以角度连杆和回转关节进行区分, 其中角度连杆的连接角度为固定角度, 可通过虚拟构形平面的方式处理, 使构形平面都变成统一的形式, 便于进行匹配。
一个通用形式构形平面如图 2所示, O为该构形平面的中心; P为工作构形通过虚拟构形平面处理后第1个回转关节的起始点, 若无需进行虚拟构形平面处理, O与P重合; 该构形平面由n个关节组成, Ji(i=1, 2, …, n)为第i个关节的旋转轴线。
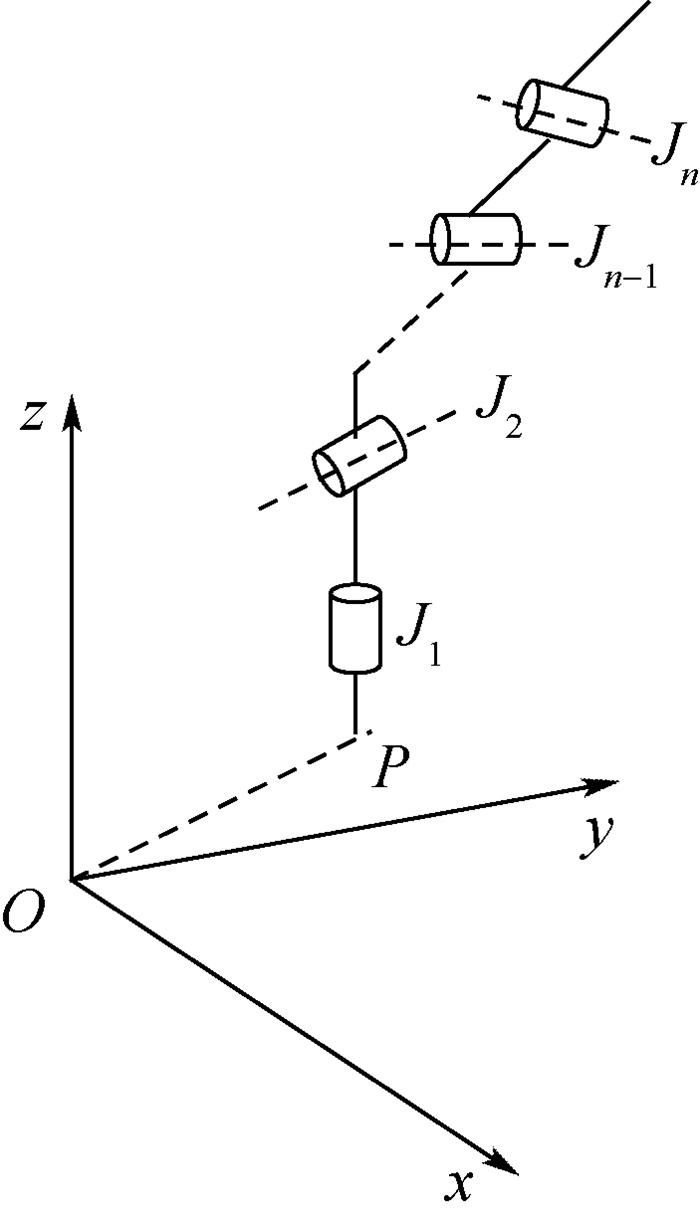 |
| 图 2 构形平面的运动学模型 Fig. 2 Kinematic model of configuration plane |
| 图选项 |
图 2中J2为摇摆关节, 与y轴平行, J1为回转关节, 与z轴平行。构形平面末端点在二维空间运动学简化模型表达为
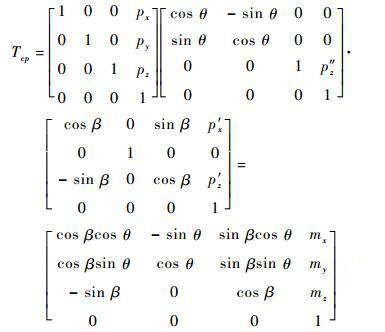 | (1) |
式中:等式右边第1个转换矩阵为通过简化和平面化处理后的附加矩阵, px、py和pz分别为构形平面化处理后的构形平面中心补偿的三维空间坐标值; 第2个矩阵中, θ为构形平面中包含的回转关节转动角度, p″z为回转关节的结构参数; 第3个转换矩阵为构形平面中依次相连摇摆关节和移动关节转换矩阵, β=β2+β3+…+βn-1, βi(i=2, 3, …, n-1)为第i个摇摆关节转动角度, 若第i个关节是移动关节, 则βi为零, p′x和p′z为转换矩阵相乘后的参数; 得到的构形平面转换矩阵中mx、my和mz为连乘后的简化。
2 冗余机械臂轨迹规划 2.1 问题提出 冗余机械臂通过在轨迹规划中增加系统的优化目标, 可以使得冗余机械臂满足更多的要求, 如:空间避障、能量优化等。轨迹规划的基本要求如下:
1) 空间避障要求:空间避障常用的方法是对空间障碍物用简单三维图形进行包覆, 避免空间机械臂本体发生干涉和碰撞。
2) 运动轨迹:按照任务要求进行机械臂末端运动, 同时运动要求平稳快速, 常用的方法是在关节空间内对机械臂关节进行多次样条曲线插补, 实现运动轨迹平滑和运动平稳。
3) 能量优化:在众多的运动规划中, 通常要求机械臂各关节的运动角度、运动速度和运动加速度的指标最优, 常用的方法是通过对机械臂各关节的运动量(角度、速度和加速度)进行叠加统计, 在这样的方法中往往容易忽略各关节在相同运动角度和速度条件下消耗的能量不同, 靠近基座的关节消耗的能量相对靠近机械臂末端的关节消耗的能量要大很多。
基于上述问题本文采用构形平面的方法, 并采用构形平面的动力学方法评价规划的成效。
为了更加详细介绍这种规划方法, 本文以空间7自由度的冗余机械臂为例进行介绍。
2.2 空间障碍物检测方法 为了进行空间避障检测, 首先需要检测机械臂在进行空间运动时是否与空间物体发生运动干涉。通常空间机械臂与障碍物的碰撞检测是通过三维空间的方式, 采用物体空间的碰撞和图形学的碰撞检测作为空间域内碰撞检测的2种主要方法。一般将空间障碍物用常用空间规范几何体进行表示。几何体的表示是否得当决定了在有空间障碍物的条件下能否求得机械臂的运动空间。
本文研究的空间障碍物的描述方法是基于构形平面方法进行的。基于构形平面的空间障碍物的碰撞检测是在冗余机械臂完成机械臂末端轨迹规划后进行的, 组成机械臂的构形平面的空间位置和表达式已经确定, 需要进行该构形平面的位形和障碍物之间的干涉检测。
构形平面内的机械臂关节与障碍物之间不干涉有2种情况:一种是机械臂关节所在的构形平面与障碍物不相交; 另一种是机械臂关节所在的构形平面与障碍物相交, 但机械臂关节本身不与障碍物干涉。由于第1种情况较为简单, 不做讨论, 本节重点讨论第2种情况。
这种情况下的构形平面的中心和末端点的位置是已知的, 如图 3所示的O点和P点, 构形平面与机械臂基坐标系的相互关系, 可以用式(1)表示。
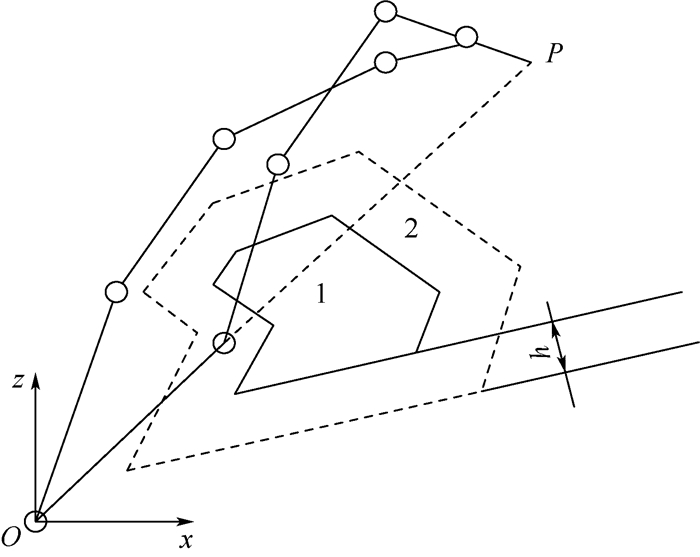 |
| 图 3 构形平面内的障碍物干涉检测 Fig. 3 Interference detection of obstacles within configuration planes |
| 图选项 |
如图 3所示, 三维空间障碍物被构形平面所在二维平面横切成截面图形, 这个截面图形可能很不规则, 采用较为简单的依次相连的直线段进行包覆。考虑到机器人连杆具有的外形尺寸和安全距离, 因此在障碍物区域1外扩距离h, 这样障碍物的实际区域就变为区域2的状态。
设安全避障区域由m段线段组成, 则第i段线段可由式(2)表示:
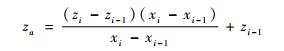 | (2) |
机器人构形由n段线段组成, 则第j段线段由式(3)表示:
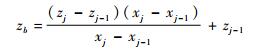 | (3) |
在平面几何中, 2条直线要么平行要么相交。因此, 为了提高判断过程的效率, 首先比较式(2)和式(3)所表示的2个线段的斜率是否相等, 不等则需求解2条线段所在直线的交点, 那么这交点是否在这2条线段之间就容易判断了。
按照冗余机械臂轨迹规划的过程, 构形平面的中心和末端不能够在障碍区域内, 否则冗余机械臂就不能完成工作了。因此, 机器人关节部分与组成安全障碍区域的边界线段存在干涉状况。为了提高整体机器人规划计算效率, 也无须将所有的机器人关节和组成安全障碍区域的所有线段之间都进行判断, 只需对在该构形平面中的干涉关节进行重新调整, 对干涉关节与安全障碍区域在靠近机器人基座一侧的边界线段之间进行判断。
2.3 机械臂关节约束 基于构形平面的轨迹规划过程力求快速简洁, 避免复杂计算过程。在已知机械臂关节约束、机械臂末端轨迹和空间障碍物位置的条件下, 通过组成冗余机械臂的构形平面规划机械臂的空间轨迹。
空间关节约束如式(4)所示:
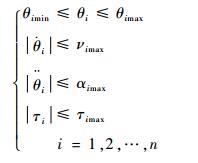 | (4) |
式中:θi为机械臂的第i个关节角度; θimin为第i个关节角度的最小值; θimax为第i个关节角度的最大值; n为机械臂中的关节数量;
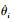

2.4 冗余机械臂的构形平面空间位置确定 机械臂末端轨迹在很多情况下是由所承担的任务决定的, 其空间轨迹是已知的, 如点焊机器人末端轨迹通常是由焊接件的焊缝位置决定, 或直线, 或圆弧; 喷涂机器人也要根据喷涂面的空间角度进行喷涂。对于一些如直线、圆弧等确定的轨迹, 通过给定起始点和末端点的位置和姿态矩阵, 采用插补的方式即可确定每一轨迹上空间点的位姿。
构形平面空间位置的确定采用加权空间矢量法, 如图 4所示, 图中Pi为机械臂末端轨迹规划中的第i点, 连接Pi和O0, kj(j=1, 2, …, n)为构形平面j的起点到末端点的连线。
 |
| 图 4 空间构形平面位置确定 Fig. 4 Determining space position of configuration planes |
| 图选项 |
以
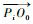
在空间障碍物对机械臂工作空间占用不多的情况下, 机械臂的构形平面空间位置有了更多的选择。如图 5所示, 左侧图和右侧图分别是在相同的轨迹条件下的2种状态, 由于运动轨迹的要求, 机械臂最后关节所在的构形平面CPn是确定的, 故2种状态下的构形平面CPn是相同的。
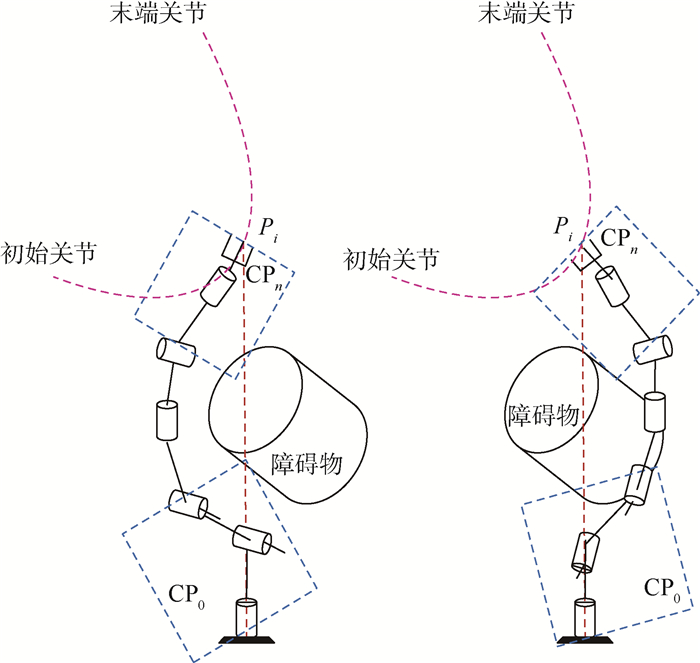 |
| 图 5 已知轨迹点的构形平面规划 Fig. 5 Configuration plane planning based on known trajectory points |
| 图选项 |
这种情况下, 要对机械臂的空间轨迹规划进行整体考虑。以上一个轨迹点的工作构形为参考, 建立评价函数:
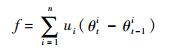 | (5) |
式中:下标t表示当前时刻; θti为当前t时刻第i个关节角度; ui(i=1, 2, …, n)为加权值, 该加权值与第i关节的功率和位置有关, 功率越大和靠近基座越近的关节, 该加权值越大。在多种选择条件下, 通过该加权值可使得功率大的关节运动幅度增大, 提高机械臂的动力学功能; f用来评价当前轨迹点与上一个轨迹点的工作构形的差别, 在多种选择条件下力求最小。
为保证机械末端运动平稳, 采用B样条曲线进行轨迹规划。使用B样条曲线的方法, 使得机器人的速度、加速度、加加速度以及机器人的起始点和终止点的位置能够稳定且符合要求。
3 仿真实例 以7自由度冗余机械臂为例进行仿真, 介绍冗余机械臂的轨迹规划方法。
3.1 7自由度机械臂建模 冗余机械臂的关节参数如表 1所示, 冗余机械臂的运动学模型如图 6所示。
表 1 关节参数 Table 1 Joint parameters
| 关节名称 | 运动范围/(°) | 关节参数尺寸/mm |
| 关节1 | -180≤θ1≤180 | d1=350 |
| 关节2 | -190≤θ2≤10 | d2=450 |
| 关节3 | -100≤θ3≤100 | d3=350 |
| 关节4 | -100≤θ4≤100 | d4=150 |
| 关节5 | -150≤θ5≤150 | d5=145 |
| 关节6 | -100≤θ6≤100 | d6=150 |
| 关节7 | -180≤θ7≤180 | d7=160 |
表选项
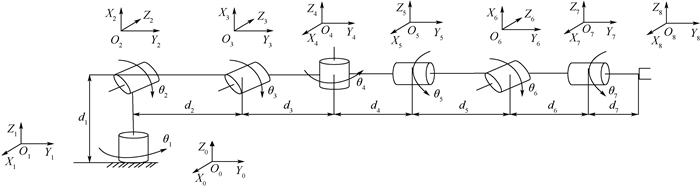 |
| 图 6 7自由度冗余机械臂运动模型 Fig. 6 Kinematic model of a 7-DOF redundant manipulator |
| 图选项 |
3.2 构形平面划分 按照构形平面定义, 如图 7所示, 将该冗余机械臂划分为3个构形平面:关节1为回转关节, 关节2和关节3为非偏置型的摇摆关节, 无论3个关节如何运动, 关节1的回转中心轴线、连接关节2的2个连杆中心轴线和连接关节3的2个连杆中心轴线始终在同一个几何平面上, 并将其定义为构形平面1;关节6为非偏置型的摇摆关节, 关节5为回转关节, 连接关节6的2个连杆中心轴线和关节5的回转中心轴线组成构形平面2;关节7为回转关节, 需要满足机械臂手爪抓取物体的姿态要求, 关节7的回转中心轴线与垂直手爪开合方向组合为构形平面3。而关节4为非偏置型的摇摆关节, 其旋转轴线与关节3的关节轴线垂直, 构形平面1和构形平面2相交于关节4的旋转轴线上, 连接关节4两个连杆的中心轴线分别在构形平面1和构形平面2内。
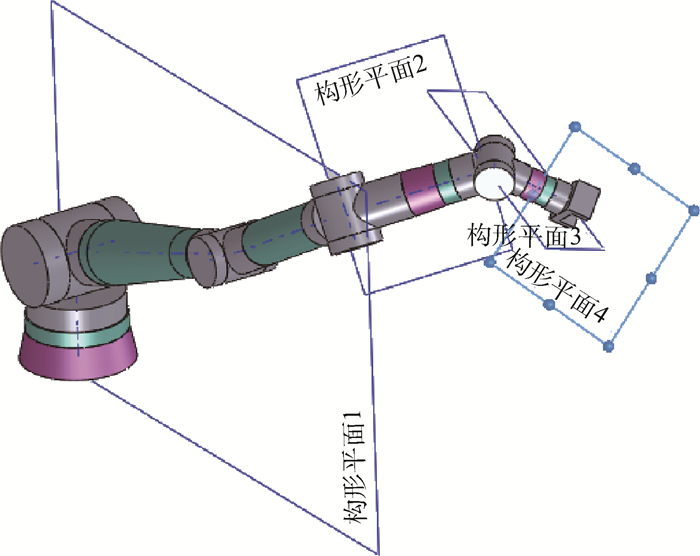 |
| 图 7 冗余机械臂构形平面划分 Fig. 7 Division of configuration plane of a redundant manipulator |
| 图选项 |
3.3 规划任务 本例中的机械臂轨迹规划任务要求机械臂末端点轨迹为一条直线段, 机械臂运动过程中, 手爪夹持面垂直该直线轨迹, 且在机械臂工作空间中存在空间障碍物。运动过程为加速—匀速—减速。
线段起始点位姿矩阵为
 |
线段终点位姿矩阵为
 |
根据任务轨迹的起点和终点的空间位置, 进行空间轨迹插补计算, 整体分成10段, 共11个空间轨迹点, 轨迹点的空间坐标如图 8所示。
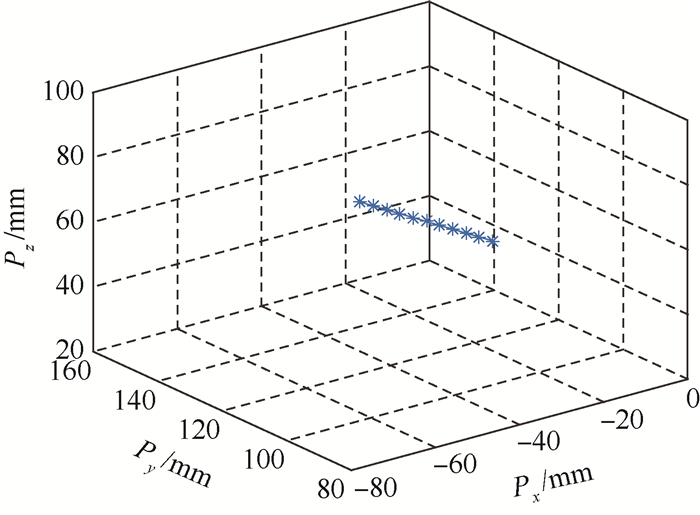 |
| 图 8 机械臂插补轨迹点的坐标 Fig. 8 Coordinates of trajectory interpolation points of manipulator |
| 图选项 |
根据图 8所示的空间轨迹点的坐标, 按照构形平面轨迹规划方法, 通过构形平面的匹配, 同时计算机械臂和空间障碍物的干涉检测, 从起点起始, 确定冗余机械各关节角在各插补点的关节角度数值曲线, 如图 9所示。
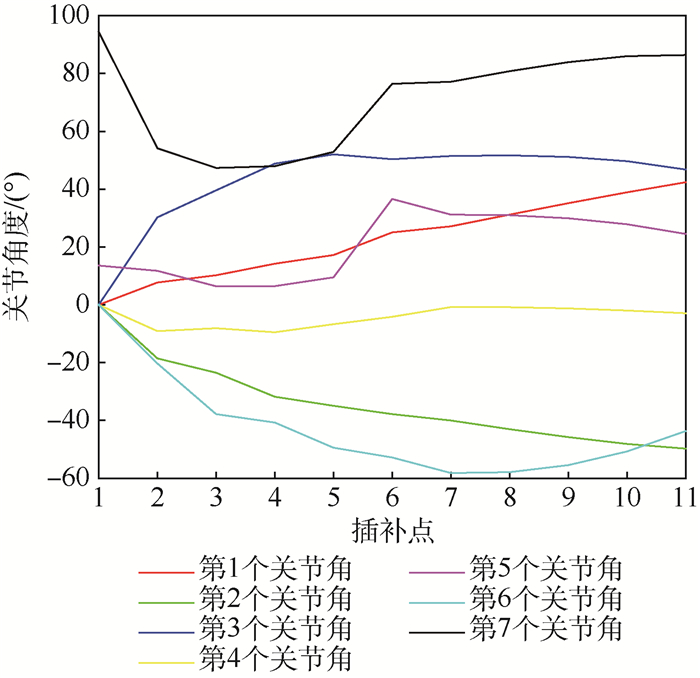 |
| 图 9 机械臂各关节在插补点的角度 Fig. 9 Joint angles of manipulator when end-effector is located in trajectory points |
| 图选项 |
4 结论 本文介绍了一种新颖的冗余机械臂轨迹规划方法, 利用构形平面的方法实现空间避障、关节约束和轨迹优化的多目标冗余机械臂空间轨迹规划, 得到如下结论:
1) 总结串联形式的机器人结构特点和工作方式, 引出构形平面概念, 建立了构形平面表达式。该方法能够分解复杂的冗余机械臂拓扑结构, 为运动学求解、轨迹规划、空间避障工作奠定基础。
2) 以构形平面为基础, 通过空间矢量引导的方式对构形平面进行空间位置确定, 进而确定较为合理的冗余机械臂空间位形。该方法避免了采用传统解析方法即依赖机器人构形形式和自由度, 也避免了数值方法中求解精度和求解速度问题, 具有实用性和通用性。
参考文献
| [1] | LOZANO-PEREZ T. Automatic planning of manipulator transfer movements[J].IEEE Transaction on Systems Man and Cybermetics, 1980, 11(10): 681–698. |
| [2] | LOZANO-PEREZ T. Spatial planning:A configuration space approach[J].IEEE Transactions on Computers, 2006, 32(2): 108–120. |
| [3] | LAVALLE S.Rapidly-exploring random trees: Progress and prospects[C]//Procceedings of the 2000 Fourth International Workshop on Algorithmic Foundations on Robotics.Piscataway, NJ: IEEE Press, 2000: 1-19. |
| [4] | BERTRAM D, KUFFNER J, DILLMANN R, et al.An integrated approach to inverse kinematics and path planning for redundant manipulators[C]//Proceedings of the 2006 IEEE International Conference on Robotics and Automation.Piscataway, NJ: IEEE Press, 2006: 1874-1879. |
| [5] | STILMAN M. Global manipulation planning in robot joint space with task constraints[J].IEEE Transactions on Robotics, 2010, 26(3): 576–584.DOI:10.1109/TRO.2010.2044949 |
| [6] | 陈撼, 裴甲瑞, 陆智俊, 等. 空间冗余机械臂的路径规划算法研究[J].上海航天, 2017, 34(5): 30–39. CHEN H, PEI J R, LU Z J, et al. Research on path planning algorithm for spatially redundant manipulator[J].Shanghai Aerospace, 2017, 34(5): 30–39.(in Chinese) |
| [7] | 高涵, 张明路, 张小俊. 冗余机械臂空间轨迹规划综述[J].机械传动, 2016, 40(10): 176–180. GAO H, ZHANG M L, ZHANG X J. A survey of space trajectory planning for redundant manipulators[J].Mechanical Transmission, 2016, 40(10): 176–180.(in Chinese) |
| [8] | HADDAD M, KHALIL W, LEHTIHET H E. Trajectory planning of unicycle mobile robots with a trapezoidal-velocity constraint[J].IEEE Transactions on Robotics, 2010, 26(5): 954–962.DOI:10.1109/TRO.2010.2062090 |
| [9] | SHIMIZU M, KAKUYA H, YOON W K, et al. Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and Its application to redundancy Resolution[J].IEEE Transactions on Robotics, 2008, 24(5): 1131–1142.DOI:10.1109/TRO.2008.2003266 |
| [10] | TIAN Y, CHEN X, HUANG Q, et al.Kinematic analysis and solution of the natural posture of a 7-DOF humanoid manipulator[C]//Proceedings of the 2010 IEEE International Conference on Automation and Logistics.Piscataway, NJ: IEEE Press, 2010: 156-162. |
| [11] | TRAN M T, SOUERES P, TAIX M, et al.Humanoid human-like reaching control based on movement primitives[C]//Proceedings of the 201019th IEEE International Symposium on Robot and Human Interactive Communication. Piscataway, NJ: IEEE Press, 2010: 546-551. |
| [12] | MARTIN D P, BAILLIEUL J, HOLLERBACH J M. Resolution of kinematic redundancy using optimization techniques[J].IEEE Transactions on Robotics and Automation, 1989, 5(4): 529–533.DOI:10.1109/70.88067 |
| [13] | 贠超, 刘刚, 王刚, 等. 基于RBF神经网络和二次规划的冗余机械臂避障问题研究[J].机电工程, 2016, 33(1): 1–7. YUN C, LIU G, WANG G, et al. Research on obstacle avoidance of redundant manipulator based on RBF neural network and quadratic programming[J].Electrical and Mechanical Engineering, 2016, 33(1): 1–7.DOI:10.3969/j.issn.1009-9492.2016.01.001(in Chinese) |
| [14] | 王俊龙, 张国良, 羊帆, 等. 改进人工势场法的机械臂避障路径规划[J].计算机工程与应用, 2013, 49(21): 266–270. WANG J L, ZHANG G L, YANG F, et al. Improved artificial potential field method for manipulator obstacle avoidance path planning[J].Computer Engineering and Applications, 2013, 49(21): 266–270.DOI:10.3778/j.issn.1002-8331.1201-0360(in Chinese) |
| [15] | 汪首坤, 朱磊, 王军政. 基于导航势函数法的六自由度机械臂避障路径规划[J].北京理工大学学报, 2015, 35(2): 186–191. WANG S K, ZHU L, WANG J Z. Obstacle avoidance path planning based on navigation potential function method for six degrees of freedom manipulator[J].Journal of Beijing Institute of Technology, 2015, 35(2): 186–191.(in Chinese) |
