近年来,随着各行业从业人员和产品的开发应用,数据挖掘技术得到了长足的发展。例如:金融证券行业利用大数据预测股票价格的波动和走势,分析用户投资习惯;电力行业利用大数据进行电力负载情况的统计,加强分时分流管理;互联网行业利用大数据挖掘上网用户的使用习惯,为用户推荐相应优质内容。而在航天领域,国内外也有相当多的****进行了深入研究。
Chen等[3]站在数据库研究人员的角度,对数据挖掘技术做出了综合性阐述,调查各类数据挖掘新技术,包括挖掘关联规则的Apriori算法、数据立方体方法、基于决策树(Decision Tree,DT)的数据分类方法等内容。Tanner等[4]提出了星上数据挖掘的概念,将传感器数据进行星上处理,可以提升网络通信能力,并降低成本,可适用于无人自主航天器、火星表面测绘卫星、生物识别系统等。Sánchez-Sánchez等[5]通过大数据和神经网络(Neural Network, NN)学习连续确定非线性系统的状态反馈最优控制问题,利用深度神经网络对最优控制问题生成的轨道进行有监督学习。最终利用得到的神经网络求解Hamilton-Jacobi-Belman方程,借此直接在星上实时生成近优控制行为。Hennes等[6]考虑航天器在主带小行星间的小推力最优转移问题,针对相位值、最大初始质量和最大最终质量,采用计算智能技术(包括分解框架的多目标进化算法、超体积指标和机器学习回归),分别对3个目标函数进行最优设计。
李德仁等[7]分析了空间数据挖掘和知识发现(Spatial Data Mining and Knowledge Discovery,SDMKD)的内涵和外延,利用SDMKD从空间数据库中自动或半自动地挖掘事先未知却潜在有用的空间模式。宫辉力等[8]针对国内缺乏对海量卫星遥感数据的有效数据挖掘和知识发现技术,设计了一种面向地学应用的卫星多源遥感图像数据挖掘系统框架和原型。Peng和Bai[9]针对空间目标编录中通常缺失的面质比信息,利用随机森林(Random Forest,RF)方法学习一致性误差和面质比间的关系,从而确定空间目标的面质比类型。
异常检测与模式挖掘作为数据挖掘的一个重要分支,也逐渐成为研究热点方向。胡小平等[10]分析了液体火箭发动机的工作和故障特点,提出利用数据挖掘方法从数据仓库的角度对液体火箭发动机进行故障检测和诊断的策略。徐宇航和皮德常[11]为了及时发现卫星故障情况并提取异常模式,提出一种基于PrefixSpan算法,对卫星异常数据集进行模式挖掘。肇刚和李言俊[12]研究时间序列数据挖掘技术现状,提出一种基于时间序列数据挖掘的航天器故障诊断方法,包括7个步骤:确定诊断对象、遥测数据选取、数据再处理、时间序列特征表示、数据挖掘方法执行、挖掘结果的解释与评估、软件系统开发。对促进航天器故障诊断技术的发展和完善有重要意义。
某型号卫星是一颗典型的低轨卫星,在其轨道预报和实际运行中,大气阻力是最主要的非保守力。本文基于以上现状,将利用基于决策树的随机森林方法、神经网络、支持向量机(Support Vector Machine,SVM)这3类数据挖掘的方法,学习大气阻力在不同误差情况下导致的轨道预报的偏差,借此对所使用的大气模型进行修正,并评估3种方法的修正性能,以及给出方法间的对比。本文的创新点如下:1)针对有监督学习方法需要先验类标签的问题,利用2种不同精度的轨道预报模型作为仿真环境,产生训练数据和测试数据。2)采用了大数据处理技巧中的3种数据挖掘方法与传统数理统计方法相比,具有快速处理大数据集(本文中数据点达到18万左右,甚至更多)、能够挖掘隐藏在轨道预报微小误差中的潜在信息等优势,验证了数据挖掘方法的应用可行性,为未来在实际运行环境下进一步修正大气模型提供参考。
1 轨道动力学模型 高精度轨道预报需要对空间环境进行精确建模,轨道预报的主要摄动因素包括地球引力、太阳引力、太阳光压和大气阻力。首先,对各摄动因素进行了精确的数学建模;然后,提出2种轨道动力学模型,作为轨道预报和产生训练数据的基础。
1.1 高阶地球引力场 根据参考文献[13]给出的相关内容,地球引力势可以写成
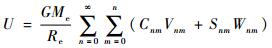 | (1) |
式中:
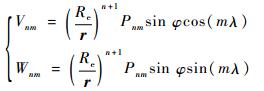 | (2) |
GMe为地球引力常数,G为万有引力常数,Me为地球质量;r为地心固连坐标系中的航天器位置矢量;φ和λ分别为航天器的地心纬度和地心经度;Re为地球的赤道半径;Pnm为n阶m次缔合勒让德多项式;Cnm和Snm分别为相应的重力势系数。
这种形式的引力场模型可以扩展至任意阶次,而不仅仅限制在带谐项,因此可以用以精确描述地球引力场。
因此,地心引力加速度
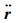
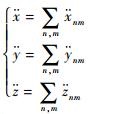 | (3) |
式中:
 | (4) |
式(1)~式(4)得到的是地心固连坐标系中的加速度,为统一各摄动加速度,后文所有其他加速度也将转换到地心固连坐标系下,如式(5)所示:
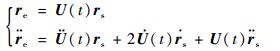 | (5) |
式中:U(t)为坐标转换矩阵,用以刻画地球自转,实际计算中还需考虑岁差和章动效应;r为航天器位置矢量,下标e和s分别表示地心固连坐标系和空间固定坐标系。
1.2 非地球引力摄动 太阳引力引起的摄动加速度可在地心惯性坐标系下表示为
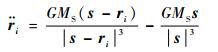 | (6) |
式中:ri和s分别为航天器和太阳的地心坐标;MS为太阳的质量。
由于太阳辐射光压导致的摄动加速度可以表示为
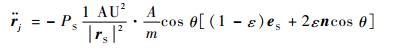 | (7) |
式中:PS为太阳辐射压;1 AU为一个天文单位,1 AU=1.496×108 km;|rS|为太阳地心矢量;n为航天器表面的单位法线矢量,A为航天器的迎风面积;eS为太阳方向单位矢量;θ为矢量n和矢量eS间的夹角;ε为航天器所用材料的反射率。卫星在运行过程中,由于存在太阳光遮挡的问题,本文在进行轨道预报的过程中,将采用参考文献[14]中的地影预报算法,计算卫星当前是否处于地影区,从而判断当前状态是否存在太阳光压摄动。
对于低轨卫星而言,大气阻力是最主要的非保守力。大气阻力引起的摄动加速度可表示为
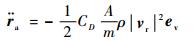 | (8) |
式中:CD为阻力系数;m为航天器质量;ρ为航天器所处位置的大气密度,本文采用MSISE86大气密度模型[15];|vr|为航天器相对于大气的速度;ev为相对速度的单位矢量,即ev=vr/|vr|。
1.3 精确模型和误差简化模型 1.1节和1.2节已经给出了航天器轨道动力学模型,该模型可以用于航天器轨道预报。为产生分类器的训练数据和测试数据,本节将给出2种模型,精确模型将作为航天器轨道预报的基准,模拟航天器在轨“真实”情况;不同的误差模型将人为对大气模型施加误差,从工程实践角度出发,CD(A/m)ρ可以被视作一个阻力系数CS,因此本文实际上是对CS进行修正,因此式(8)在误差简化模型中可写成如下形式:
 | (9) |
通过精确模型产生的轨道,与误差简化模型产生的轨道的各项数据差值,即可作为分类器的训练数据和测试数据。2种模型具体的参数设置由表 1所示。
表 1 精确模型与误差简化模型参数 Table 1 Parameters of accurate model and error simplified model
| 参数 | 精确模型 | 误差简化模型 |
| 地球形状 | WGS84 | WGS84 |
| 阶数 | 50×50 | 5×5 |
| 第三体引力摄动 | 太阳 | |
| 太阳光压 | 精确地影预报 | |
| 大气阻力 | MSIS | MSIS+(-100%~100%)误差 |
表选项
2 数据挖掘方法 数据挖掘能够从大量杂乱的数据中挖掘出有价值的信息,但是其过程是相当复杂的。针对本文的研究内容及数据的特性,本节将介绍3种分类方法,利用这3种分类方法就能够学习第1节得到的训练数据,并通过测试数据对3种分类方法进行准确度检验。
2.1 决策树与随机森林 决策树又称分类树,是应用最为广泛的分类方法之一。如图 1所示,决策树是一种监督学习方法,通过不断地划分数据,使依赖变量的差别最大,最终目的是将数据分类到不同的组织或不同的分枝,在依赖变量的基础上建立最强的归类,其训练结果是类似流程图的树结构。
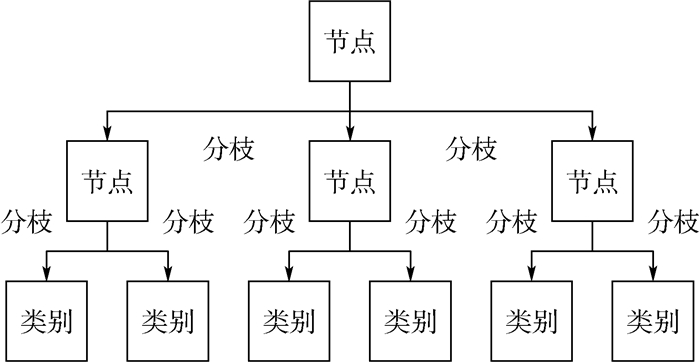 |
| 图 1 决策树 Fig. 1 Decision tree |
| 图选项 |
但是决策树是一种“贪心算法”,在应用过程中,每一步的判断,仅是针对当前测试做出最优选择,并不考虑全局结果。如果将多棵树以某种关系结合起来,对数据进行分类,以解决单一决策树泛化能力弱的缺点,这就是随机森林。
随机森林实际上是套袋法与决策树的结合,如图 2所示,随机森林的随机性体现在:
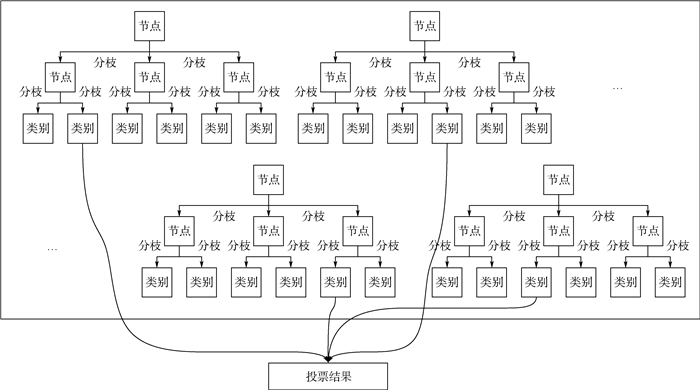 |
| 图 2 随机森林 Fig. 2 Random forest |
| 图选项 |
1) 从样本中随机选择n个样本。
2) 从所有属性中随机选择k个属性。
3) 选择最佳分割属性作为节点建立决策树;
4) 以上步骤重复j次,即得到j棵决策树,进而完成随机森林训练。
5) 分类问题中,通过投票决定数据的类别。回归问题中,由j棵决策树预测结果的均值作为最后的预测结果。
随机森林的优点很多,对于多种数据,随机森林可以产生高精度的分类器;建造森林时,随机森林可以在内部对于一般化后的误差产生不偏差的估计;在决定类别时,可以评估变数的重要性等等。当然随机森林的缺点也是显而易见的,因为要训练m棵决策树,其训练过程会是训练单棵决策树的数倍。
2.2 神经网络 神经网络是应用类似于人脑神经突触连接的结构进行信息处理的数学模型。在早期对人脑的理解中,人脑主要由称为神经元的神经细胞组成,神经元通过轴突的纤维丝连接在一起,当一个神经元受到刺激时,神经脉冲通过轴突从一个神经元传递到另一个神经元。一个神经元通过树突连接到其他神经元的轴突,树突是神经元的延伸物。树突与轴突之间的连接点叫做神经键。人脑通过在同一脉冲反复刺激下改变神经元之间的神经键连接强度来进行学习。类似于人脑的结构,神经网络也是由一组相互连接的节点和有向链构成。
图 3为神经网络最简单的模型——感知器,包含多个输入节点、一个输出节点,节点即是神经元。在感知器中,每个输入节点通过一个加权的链连接到输出节点,该加权链用以模拟神经元之间神经键的连接强度,如人脑一样,训练一个感知器就是不断调整链的权值,直到能拟合出输入输出间的关系为止。
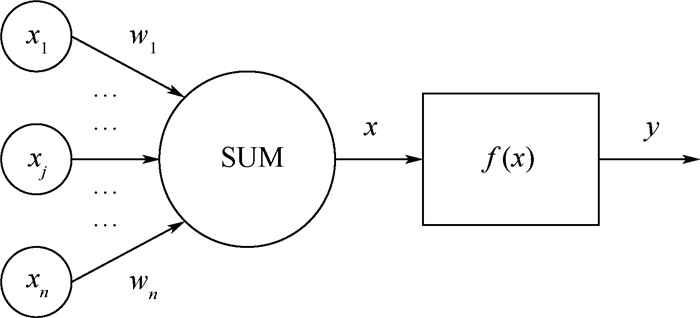 |
| 图 3 神经网络感知器 Fig. 3 Neural network perceptron |
| 图选项 |
本文将采用前馈负向传播神经网络,前馈是指:每一层的神经元仅与前一层连接,且输出给下一层,各层之间没有反馈,不对网络的参数进行调整。负向传播是指:误差会进行方向传播,用以调整权值和阈值。至少含有一个隐藏层的多层神经网络可以用来拟合任何目标函数,且可以处理冗余特征,但是神经网络对于噪声十分敏感,训练过程也很耗时。
2.3 支持向量机 支持向量机是建立在统计学习理论基础上的机器学习方法。支持向量机通过构建分割多类的超平面,在构建过程中,会试图将多类之间的分割达到最大化(如图 4所示)。
 |
| 图 4 支持向量机分类方法示意图 Fig. 4 Schematic diagram of classification method of SVM |
| 图选项 |
支持向量机的理论包括3个要点:最大化间距、对偶理论和核函数。“最大化间距”实际上是一个优化问题,该优化问题,可以利用拉格朗日对偶理论变换到对偶变量的优化问题。然而在输入空间中,数据可能是不可分的,支持向量机就需要通过非线性映射,将数据映射到某个其他点积空间。本文所使用的支持向量机将采用高斯核函数:
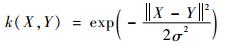 | (10) |
式中:X为空间中任一点; Y为核函数中心; σ为函数的宽度参数。高斯核函数对于噪声有着较好的抗干扰能力,但是其参数决定了函数作用范围,超过了这个范围,数据的作用就“基本消失”。
3 分类器训练与评估 首先,将利用第1节提出的2种轨道动力学模型进行轨道预报,并生成训练数据;然后,将训练数据导入第2节中介绍的各分类方法,进行适当参数调整后完成训练。
某型号卫星是中国第一代传输型立体测绘卫星,于2010年8月24日发射成功,其轨道高度为500 km左右,运行过程中,大气阻力对其造成较大的轨道衰减。因此本节将以该卫星在轨实际状态作为轨道预报起点,从而生成一系列训练数据。
3.1 训练数据生成 仿真起始时刻为2016年5月31日21:07:05,卫星真实在轨状态如表 2所示,其中:a为半长轴;e为偏心率;i为轨道倾角;Ω为升交点赤经;ω为近地点幅角;M为平近点角; rx、ry、rz为卫星在惯性系下的位置三轴分量;vx、vy、vz为卫星在惯性系下的速度三轴分量。
表 2 仿真初始状态 Table 2 Initial state of simulation
| 参数 | 数值 |
| a/km | 6 871.209 3 |
| e | 0.002 5 |
| i/(°) | 97.560 4 |
| Ω/(°) | -74.218 7 |
| ω/(°) | 95.295 7 |
| M/(°) | 21.168 3 |
| rx/km | -1 611.425 2 |
| ry/km | 2 731.717 4 |
| rz/km | 6 081.641 7 |
| vx/(km·s-1) | -1.426 1 |
| vy/(km·s-1) | 6.690 5 |
| vz/(km·s-1) | -3.372 2 |
表选项
向后进行1 d轨道预报可以得到多条卫星轨道,预报间隔为10 s,每一个点都对应一定时间后由25个变量组成的卫星在轨状态Xi:
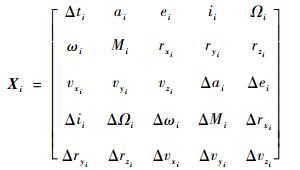 | (11) |
式中:Δt为该点的预报时长;前标Δ表示误差简化模型与精确模型间的差值;下标i表示该组状态的编号。
因此可以得到181 440组卫星的在轨状态,且每一组状态都对应一个人为施加在大气模型上的误差值εi,即可以得到181440个样本数据及其类别属性的组合[Xi εi]作为训练数据,训练数据的如表 3所示。
表 3 部分训练数据 Table 3 Partial training data
| εi/% | Δt/d | a/km | e | i/(°) | Ω/(°) | ω/(°) | M/(°) |
| -50 | 0.301 | 6 871.102 | 0.002 5 | 97.565 | -73.712 | 94.707 | 229.007 |
| -40 | 0.600 | 6 871.051 | 0.002 5 | 97.563 | -73.605 | 93.301 | 72.578 |
| -30 | 0.300 | 6 871.102 | 0.002 5 | 97.565 | -73.912 | 94.701 | 227.745 |
| -20 | 0.600 | 6 871.048 | 0.002 5 | 97.563 | -73.605 | 93.299 | 73.216 |
| -10 | 0.500 | 6 871.142 | 0.002 5 | 97.561 | -73.707 | 94.098 | 243.763 |
| 0 | 0.900 | 6 871.174 | 0.002 5 | 97.563 | -73.301 | 93.709 | 278.117 |
| 10 | 0.800 | 6 871.061 | 0.002 5 | 97.565 | -73.403 | 93.410 | 87.899 |
| 20 | 0.200 | 6 871.072 | 0.002 5 | 97.564 | -74.014 | 95.067 | 39.982 |
| 30 | 0.300 | 6 871.096 | 0.0025 | 97.565 | -73.912 | 94.703 | 228.378 |
| 40 | 0.500 | 6 871.135 | 0.002 5 | 97.561 | -73.707 | 94.097 | 243.766 |
| 50 | 0.600 | 6 871.036 | 0.002 5 | 97.563 | -73.605 | 93.298 | 73.220 |
表选项
由表 3可以看出,不同误差值的模型进行轨道预报,得到的在轨状态数据相差很小,无法用传统方法得到这些值与误差值间的关系,更无法通过这些值准确得到误差值大小,因此本文采用数据挖掘的技巧,对以上数据进行处理、分类,这也是本文的创新点之一。
3.2 分类器训练 将3.1节得到的训练数据导入各分类模型,并适当设置参数,即可完成分类器训练的初始化。各分类模型的训练参数设置如表 4~表 6所示。
表 4 随机森林训练参数设置 Table 4 Training parameter setting of random forest
| 分类模型 | 决策树数量 |
| 随机森林 | 50 |
表选项
表 5 神经网络训练参数设置 Table 5 Training parameter setting of neural network
| 分类模型 | 神经网络层数 | 隐藏层神经元数 | 训练函数 | 适应性学习函数 | 最大验证失败次数 | 最小性能梯度 | 性能 |
| 神经网络 | 8 | 10 | 列文伯格算法 | LEARNDM | 10 | 1×10-9 | 均方差 |
表选项
表 6 支持向量机训练参数设置 Table 6 Training parameter setting of SVM
| 分类模型 | 核函数 | 核尺度 | 特征选择 |
| 支持向量机 | 高斯 | 1.3 | 主成分分析法 |
表选项
3.3 训练结果与评估 随机森林方法分类结果如图 5所示,横坐标为181 440组状态的编号,纵坐标为该组状态对应的大气模型误差值。因为随机森林的训练和预测中采用投票机制决定最终结果,所以图 5(b)的结果是通过选择图 5(a)的最大概率取值得到的。可以看到,5(a)中颜色越接近红色,表示概率越大,因为随机性和投票机制,最终的精确度高达99.99%。
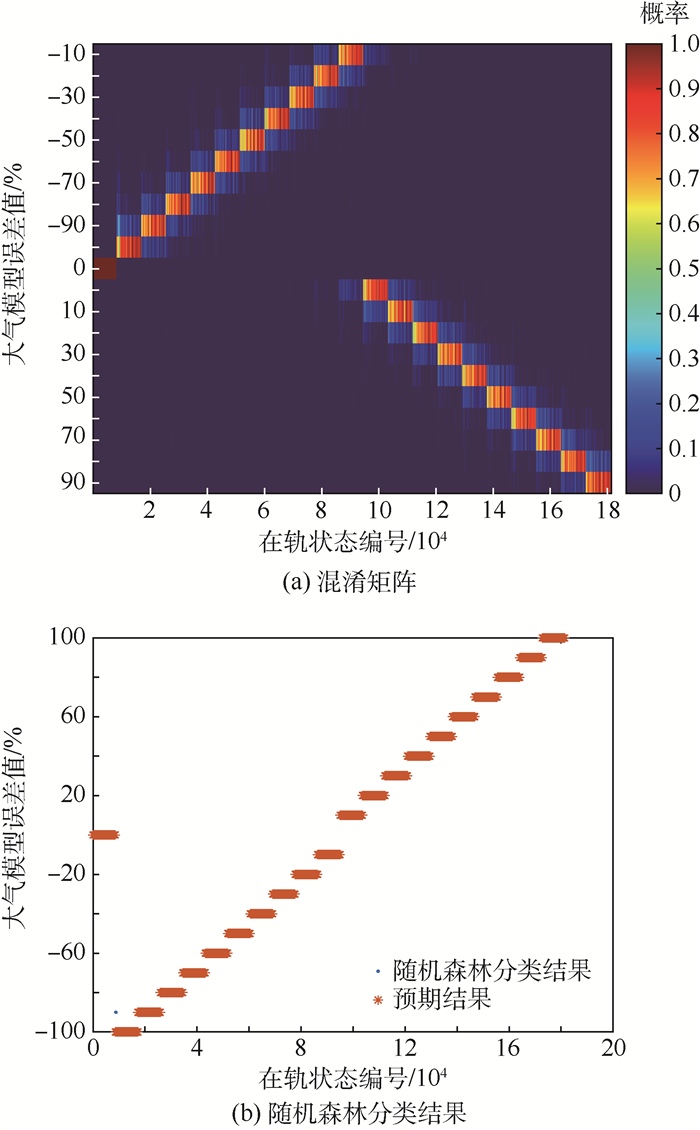 |
| 图 5 混淆矩阵和随机森林分类结果 Fig. 5 Classification results of confusion matrix and random forest |
| 图选项 |
神经网络训练结果如图 6所示,图 6(a)为在5 461次循环中,神经网络通过不断调整神经键上的权值,逐步减小性能函数的取值,于5 451次循环时达到最小值0.014 55,并在第5 461次循环后达到最大验证数据失败的次数,停止循环;图 6(b)为在5 461次循环中,性能梯度、动量和验证数据失败次数的变化,性能梯度于5461次循环时达到最小值0.022 783,动量于5 461次循环时达到最小值1×10-7,验证数据失败次数于5 461次循环时达到最大值10次。
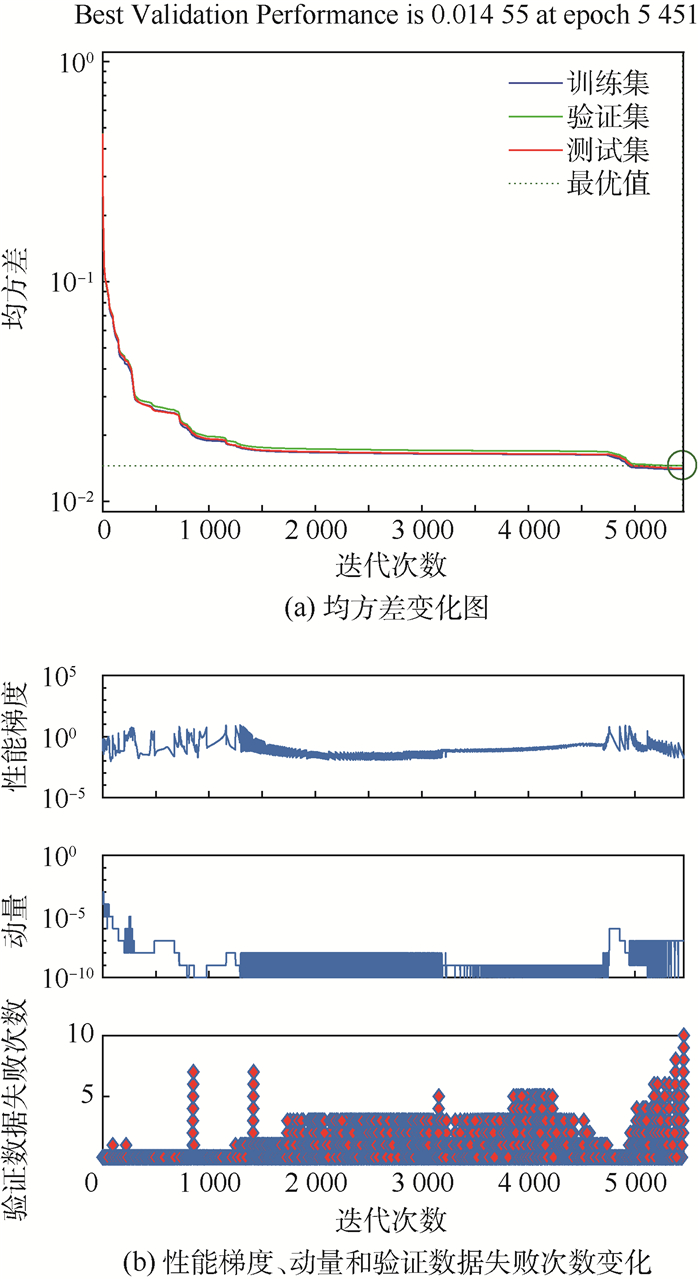 |
| 图 6 神经网络训练过程 Fig. 6 Training process of neural network |
| 图选项 |
图 7横坐标为181 440组状态的编号,纵坐标为该组状态对应的大气模型误差值,可以看到训练结果相比随机森林已经有了较大的降幅,精确率仅有0.011 6%。而且通过图 8可以看出,在预报时长较小时,因为不同模型得到的在轨状态差值很小,这一段内的结果误差尤其剧烈,甚至超过了100%,随着预报时长的增加,误差将会逐步减小。支持向量机分类结果如图 9所示,结果误差较大,其精确度仅为50.7%。对比图 7,神经网络分类结果仅在一定范围内波动,而支持向量机的结果可能在全域内离散波动。
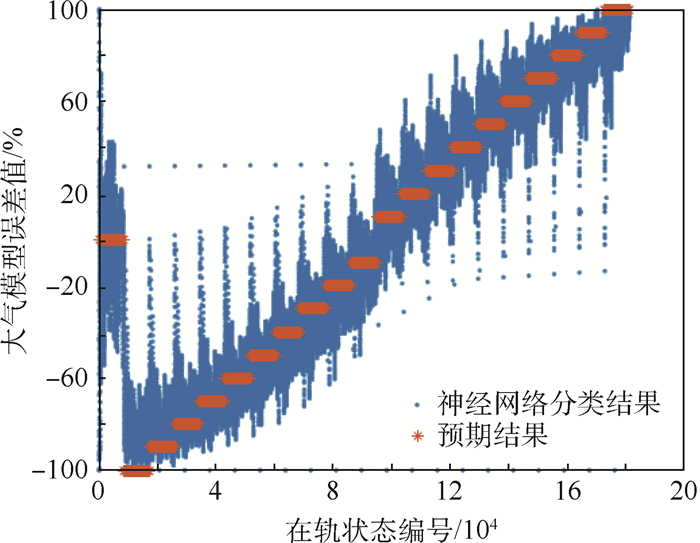 |
| 图 7 神经网络分类结果 Fig. 7 Classification results of neural network |
| 图选项 |
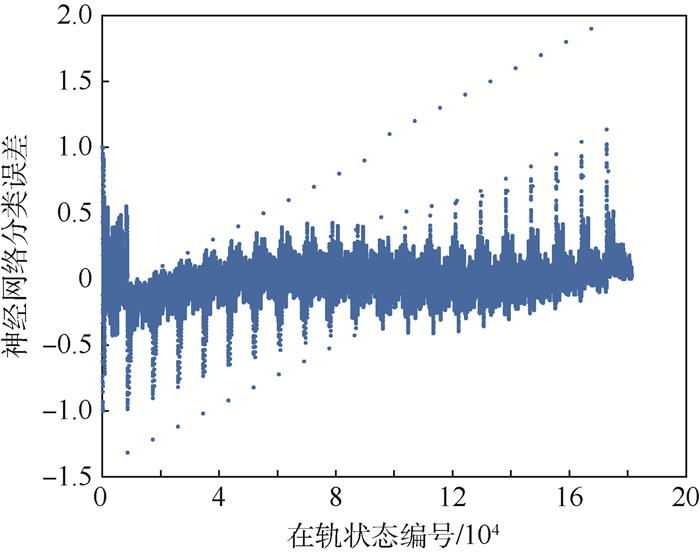 |
| 图 8 神经网络分类误差变化 Fig. 8 Classification error variation of neural network |
| 图选项 |
 |
| 图 9 支持向量机分类结果 Fig. 9 Classification results of SVM |
| 图选项 |
对比3种方法的性能(见表 7),随机森林训练时长最短,精确度最高,因此该方法的性能最佳,考虑到森林中包含决策树的数量为50棵,减少决策树的数会进一步缩短训练时长。而神经网络和支持向量机的应用结果都不理想,原因在于本文中使用的在轨状态和大气模型误差值的训练数据,对于这2种方法来说学习较为困难,尤其是神经网络,容易出现过拟合以及不学习,即过早达到最大验证失败次数的情况。
表 7 3种分类方法性能对比 Table 7 Performance comparison of three classification methods
| 分类模型 | 训练时长/s | 精确度/% |
| 随机森林 | 241.434 2 | 99.99 |
| 神经网络 | 2 102 | 0.011 6 |
| 支持向量机 | 29 167.627 4 | 50.7 |
表选项
4 结论 本文以某型号卫星的轨道预报及数据挖掘方法作为切入点,完成了以下内容的研究分析:
1) 对卫星在轨的空间环境进行数学建模,基于各个摄动力因素,提出了2种轨道动力学模型,精确模型用于模拟卫星在轨真实情况,误差简化模型通过人为对大气模型施加-100%~100%的误差,作为生成训练数据的基础。
2) 对本文利用到的支持向量机、神经网络、随机森林3种分类方法进行了概述和总结,阐明了3种方法的原理及特点。
3) 利用2种模型向后进行1 d的轨道预报,预报结果作差,由此产生181 440组训练数据,并导入3种分类模型训练。
4) 从训练结果可以看出,数据挖掘方法能够对大气模型的误差进行较好的反演,尤其是随机森林的方法,反演的结果高达99.99%。
本文的结果为卫星轨道预报以及大气模型的建立提供了新思路,结合时下热门的大数据概念,将数据挖掘方法应用至传统的航天领域, 具有良好的参考意义,为航天领域应用人工智能、大数据等技术奠定了基础。
参考文献
| [1] | 周英, 卓金武, 卞月青. 大数据挖掘:系统方法与实例分析[M]. 北京: 机械工业出版社, 2016: 4-7. ZHOU Y, ZHUO J W, BIAN Y Q. Big data mining:System method and instance analysis[M]. Beijing: China Machine Press, 2016: 4-7. (in Chinese) |
| [2] | 韩家炜, KAMBER M. 数据挖掘:概念与技术[M]. 北京: 机械工业出版社, 2012: 1-9. HAN J W, KAMBER M. Data mining:Concepts and techniques[M]. Beijing: China Machine Press, 2012: 1-9. (in Chinese) |
| [3] | CHEN M S, HAN J, YU P S. Data mining:An overview from a database perspective[J]. IEEE Transactions on Knowledge and data Engineering, 1996, 8(6): 866-883. DOI:10.1109/69.553155 |
| [4] | TANNER S, STEIN C, GRAVES S J.On-board data mining[M]//GABER M M.Scientific Data Mining and Knowledge Discovery.Berlin: Springer, 2009: 345-376. |
| [5] | SáNCHEZ-SáNCHEZ C, IZZO D, HENNES D.Learning the optimal state-feedback using deep networks[C]//2016 IEEE Symposium Series on Computational Intelligence (SSCI).Piscataway, NJ: IEEE Press, 2016: 1-8. http://www.researchgate.net/publication/313802801_Learning_the_optimal_state-feedback_using_deep_networks |
| [6] | HENNES D, IZZO D, LANDAU D.Fast approximators for optimal low-thrust hops between main belt asteroids[C]//2016 IEEE Symposium Series on Computational Intelligence (SSCI).Piscataway, NJ: IEEE Press, 2016: 1-7. http://ieeexplore.ieee.org/abstract/document/7850107/ |
| [7] | 李德仁, 王树良, 李德毅, 等. 论空间数据挖掘和知识发现的理论与方法[J]. 武汉大学学报(信息科学版), 2002, 27(3): 221-233. LI D R, WANG S L, LI D Y, et al. Theories and technologies of spatial data mining and knowledge discovery[J]. Geometrics and Information Science of Wuhan University, 2002, 27(3): 221-233. (in Chinese) |
| [8] | 宫辉力, 赵文吉, 李京. 多源遥感数据挖掘系统技术框架[J]. 中国图象图形学报, 2005, 10(5): 620-623. GONG H L, ZHAO W J, LI J. The technological framework of data mining from the polygenetic remotely sensed data[J]. Journal of Image and Graphics, 2005, 10(5): 620-623. DOI:10.3969/j.issn.1006-8961.2005.05.014 (in Chinese) |
| [9] | PENG H, BAI X. Recovering area-to-mass ratio of resident space objects through data mining[J]. Acta Astronautica, 2018, 142: 75-86. DOI:10.1016/j.actaastro.2017.09.030 |
| [10] | 胡小平, 张丽娟, 王艳梅, 等. 液体火箭发动机故障检测和诊断中数据挖掘策略的分析[J]. 国防科技大学学报, 2005, 27(3): 1-5. HU X P, ZHANG L J, WANG Y M, et al. The analysis of data mining strategy in fault detection and diagnosis of the liquid rocket engine[J]. Journal of National University of Defense Technology, 2005, 27(3): 1-5. DOI:10.3969/j.issn.1001-2486.2005.03.001 (in Chinese) |
| [11] | 徐宇航, 皮德常. 卫星异常模式挖掘方法[J]. 小型微型计算机系统, 2015, 36(9): 1988-1992. XU Y H, PI D C. Method to mine satellite abnormal patterns[J]. Journal of Chinese Computer Systems, 2015, 36(9): 1988-1992. DOI:10.3969/j.issn.1000-1220.2015.09.014 (in Chinese) |
| [12] | 肇刚, 李言俊. 基于时间序列数据挖掘的航天器故障诊断方法[J]. 飞行器测控学报, 2010, 29(3): 1-5. ZHAO G, LI Y J. Spacecraft fault diagnosis method based on time series data mining[J]. Journal of Spacecraft TT & C Technology, 2010, 29(3): 1-5. (in Chinese) |
| [13] | MONTENBRUCK O, GILL E. Satellite orbits:Models, methods and applications[M]. Berlin: Springer Science & Business Media, 2012. |
| [14] | JIA X H, XU M, PAN X, et al. Eclipse prediction spaceborne algorithms for low-earth-orbiting satellites[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2963-2975. DOI:10.1109/TAES.2017.2722518 |
| [15] | HDEIN A E. MSIS-86 thermospheric model[J]. Journal of Geophysical Research:Space Physics, 1987, 92(A5): 4649-4662. DOI:10.1029/JA092iA05p04649 |
