碳钢因其优良的力学性能和较低的成本等特点，作为国民领域中最基本的结构材料，被广泛用于金属结构件和设备中^[1-2]。然而金属构件设施多在大气环境下服役，大气腐蚀是造成这些构件损坏失效的重要原因^[3]。碳钢的大气腐蚀失效造成了巨大的经济损失，引起了人们的广泛关注。影响碳钢大气腐蚀速率的外部因素主要包括暴露时间、气候因素和环境因素^[4]。目前针对具体的气候和环境因素对碳钢大气腐蚀速率的影响，科研人员已经做了很多相关工作。Cole等^[5]研究了碳钢表面湿度对碳钢腐蚀速率的影响；林翠和刘月娥^[6]探讨了温度对碳钢腐蚀行为的影响；Song和Chen^[7]研究了日照紫外线对Q235碳钢大气腐蚀的影响；Ma等^[8]研究了Cl离子对碳钢的腐蚀率的影响；Wang等^[9]分析了碳钢在含SO₂大气中腐蚀产物的演变；闫松涛等^[10]研究了大气沉积颗粒物对碳钢腐蚀行为的影响；Singh等^[11]研究表明，暴露地点的气候条件对钢的腐蚀速率有很大的影响；汪川等^[12]论证了碳钢和耐候钢大气腐蚀的差异是由不同地区大气腐蚀特征因子不同导致的。然而，目前包括以上研究在内的大多数研究只是针对一种、几种影响因素或典型气候类型地点对影响碳钢腐蚀速率影响，而对各具体的碳钢腐蚀速率影响因子(暴露时间、平均相对湿度、平均温度、SO₂、降尘量等)对碳钢腐蚀速率影响的相对权重大小却没有展开相关分析和研究。而这方面的研究对碳钢腐蚀的预测和预防具有重要的意义。因此，本文将以BP神经网络为基础的平均影响值(Mean Impact Value，MIV)算法应用于碳钢腐蚀数据解析，分析覆盖多种影响因素的15种具体的碳钢腐蚀影响因子(暴露时间、平均温度、平均相对湿度、日照时数、降水量、平均风速、海盐粒子浓度、SO₂、HCl、NO₂、H₂S、硫酸盐化速率、NH₃、降尘量-非水溶性、降尘量-水溶性)对碳钢腐蚀速率的影响，定量地说明各碳钢腐蚀影响因子对腐蚀速率影响的相对权重大小。
1 因子选取及数据预处理 1.1 腐蚀速率的影响因子及评价因子选取 影响碳钢大气腐蚀速率的因素包括材料性质、暴露时间、气候因素和环境因素4个方面。材料性质属于影响腐蚀速率的内因，而另外3个因素属于影响腐蚀因素的外因。其中，随着暴露时间的增加，不断地形成腐蚀产物，进而影响腐蚀速率^[13]。气候因素和环境因素的多样性和复杂性对碳钢腐蚀速率影响最为显著。气候因素主要包括平均温度、平均相对湿度、日照时数、降水量、平均风速和海盐粒子浓度等因子。环境因素主要包括SO₂、HCl、NO₂、H₂S、硫酸盐化速率、NH₃、降尘量-非水溶性、降尘量-水溶性等因子^[14-15]。本文将通过MIV影响因子权重分析算法，分别对影响Q235、Ste355、St12和Q450这4种碳钢的腐蚀速率的暴露时间、气候因素和环境因素的相对权重进行分析，具体影响因子包括暴露时间、平均温度、平均相对湿度、日照时数、降水量、平均风速、海盐粒子浓度、SO₂、HCl、NO₂、H₂S、硫酸盐化速率、NH₃、降尘量-非水溶性、降尘量-水溶性。
常见的腐蚀评价方法有点蚀深度、点蚀密度、平均腐蚀深度等。碳钢的腐蚀主要以均匀腐蚀为主，因而平均腐蚀深度(即金属材料在单位时间内的平均腐蚀深度)能更为准确地反映出碳钢均匀腐蚀的速率，因此，本文选取碳钢的平均腐蚀深度作为腐蚀速率评价因子，且本文中碳钢的平均腐蚀深度数据来源于多个数据站最终的汇总结果，数据对误差具有更高的抗性。
1.2 数据来源及预处理 本文数据来源于国家材料环境腐蚀平台——中国腐蚀与防护网，包括上述4种碳钢8个典型气候环境地点(库尔勒、武汉、沈阳、西双版纳、北京、广州、青岛、琼海)在2006—2014年间的1、2、5和8 a腐蚀数据，月均气候和环境影响因子数据。使用剔除法和多重估算法^[16]，剔除、填充月均气候和环境因子数据中的缺陷值和缺失值，整理得数据共计5 376个，其中剔除和填充数据323个。并计算气候和环境因子数据与碳钢腐蚀速率时间为1、2、5和8 a均值，上述数据整理结果中一组如表 1所示，共128组, 数据代号为Ste-1, 材料名称为Ste355, 试验地点为北京，开始日期为2006年11月，测试日期为2007年11月，平均腐蚀深度为40.000 μm/a。
表 1 腐蚀速率影响及评价因子数据 Table 1 Impact and evaluation factor data of corrosion rate

评价因子	数值
实验时间/a	1
平均温度/℃	12.750
平均相对湿度/%	50.151
日照时数/h	85.642
降水量/mm	50.879
平均风速/(m·s-1)	2.025
瞬时法SO2/(mg·cm-3)	0.001
瞬时法HCl/(mg·cm-3)	0.052
连续法NO2/(mg·(100 m2·d)-1)	0.106
连续法H2S/(mg·(100 m2·d)-1)	0.056
连续法硫酸盐化速率/(mg·(100 m2·d)-1)	0.320
连续法NH3 /(mg·(100 m2·d)-1)	0.054
连续法海盐粒子浓度/(mg·(100 m2·d)-1)	0.010
自然降尘量-非水溶性/(g·(cm2·mol·L-1)-1)	4.371
自然降尘量-水溶性/(g·(cm2·mol·L-1)-1)	1.496

表选项






2 方法与结果 2.1 MIV算法 MIV算法建立的基础是BP神经网络，其被认为是神经网络评价中评价变量相关性最好的指标之一^[17]。BP神经网络结构如图 1(a)所示，其是一种具有3层或3层以上的神经网络，包括输入层、隐含层和输出层。各层神经元仅与相邻层神经元之间相互全连接，同层内神经元之间无连接，各层神经元之间无反馈连接，构成具有层次结构的前馈型神经网络系统。当实际输出与期望输出不符时，进入误差的反向传播阶段。误差通过输出层，按误差梯度下降的方式修正各层权值，向隐含层、输入层逐层反传^[18]。MIV能够反映出各变量在神经网络中的权重矩阵变化，可定量评价各自变量对于因变量影响的重要性大小。

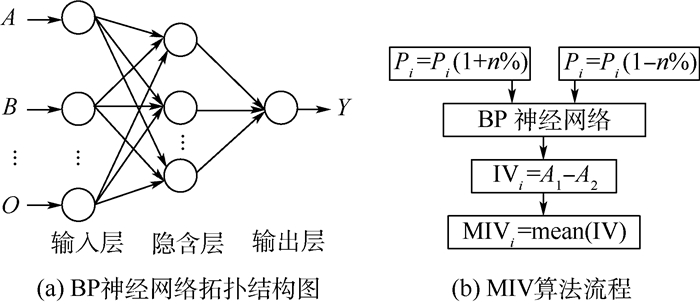图 1 MIV算法原理 Fig. 1 Principle of MIV algorithm

图选项

MIV作为确定输入神经元对输出神经元影响大小的一个指标，其绝对值大小代表影响的相对权重。MIV算法的实现过程如下^[19-20]:
1) 在BP神经网络训练完成后，将训练样本P中每一自变量特征在其原值的基础上分别增加或者减少一定比例，构成2组新的训练样本P_i。
2) 将2组新的训练样本P_i作为仿真样本，利用已建成的网络进行模拟计算，可以得到2个仿真结果A₁和A₂。
3) A₁和A₂的差值，即为变动该自变量后对输出产生的影响变化值IV_i。
4) 变化值IV_i按观测样本数求平均值，得到该自变量对于因变量网络输出的MIV_i值。
按照上述步骤，如图 1(b)所示，即可依次算出各个自变量的MIV_i值，判断出各输入参数对网络输出结果影响的相对重要性，即输入参数对预测结果影响的权重。
2.2 MIV实验及输出结果 本文通过MATLAB软件创建MIV算法程序。算法程序将暴露时间、气候因素和环境因素的15个因子作为输入变量，4种碳钢的平均腐蚀深度作为输出变量，训练并优化神经网络模型，设定MIV的调节率(变量改变的幅度)分别为5%、10%、15%、20%、25%，其中调节率为变量改变的幅度。对每种碳钢进行多次测试实验，将每组实验各变量的MIV值组内加权，并分别计算多次实验输出各变量值加权后的绝对值的平均值。持续增加测试实验数至平均值保持稳定。由于不同输入变量对输出变量的作用有正面和负面之分，表现为MIV值有正负数之分，为便于对比不同输入变量的影响权重，本实验将所有MIV值取绝对值，记为|MIV|。不同调节率下的Q235、Q450、St12和Ste355的不同输入变量的|MIV|实验计算结果如表 2~表 5所示。
表 2 不同调节率下Q235的各影响因子|MIV|值 Table 2 |MIV| values of impact factors of Q235 with different regulation rates

MIV调节率/%	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
5	0.228	0.407	0.646	0.634	0.477	0.085	0.023	0.114	0.044	0.069	0.054	0.042	0.053	0.230	0.152
10	0.220	0.451	0.670	0.571	0.402	0.123	0.041	0.118	0.070	0.090	0.088	0.056	0.078	0.253	0.157
15	0.243	0.455	0.669	0.626	0.419	0.121	0.029	0.125	0.055	0.074	0.073	0.045	0.046	0.264	0.168
20	0.230	0.462	0.698	0.627	0.434	0.108	0.040	0.143	0.059	0.081	0.077	0.037	0.059	0.251	0.167
25	0.202	0.385	0.708	0.622	0.411	0.096	0.035	0.151	0.058	0.085	0.079	0.039	0.058	0.256	0.128
注: A为暴露时间; B为平均温度; C为平均相对湿度; D为日照时数; E为降水量; F为平均风速; G为连续法海盐粒子浓度; H为瞬时法SO2; I为瞬时法HCl; J为连续法NO2; K为连续法H2S; L为连续法硫酸盐化速率; M为连续法NH3; N为自然降尘量-非水溶性; O为自然降尘量-水溶性。

表选项






表 3 不同调节率下Q450的各影响因子|MIV|值 Table 3 |MIV| values of impact factors of Q450 with different regulation rates

MIV调节率/%	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
5	0.279	0.534	0.685	0.487	0.427	0.140	0.044	0.122	0.078	0.113	0.080	0.043	0.032	0.189	0.231
10	0.340	0.558	0.712	0.528	0.427	0.172	0.043	0.128	0.073	0.120	0.066	0.064	0.045	0.211	0.222
15	0.285	0.514	0.663	0.570	0.442	0.159	0.039	0.130	0.070	0.113	0.068	0.053	0.034	0.204	0.210
20	0.306	0.510	0.714	0.552	0.403	0.137	0.035	0.142	0.078	0.113	0.072	0.042	0.037	0.236	0.209
25	0.297	0.552	0.702	0.516	0.439	0.186	0.044	0.149	0.085	0.131	0.088	0.068	0.037	0.243	0.197

表选项






表 4 不同调节率下St12的各影响因子|MIV|值 Table 4 |MIV| values of impact factors of St12 with different regulation rates

MIV调节率/%	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
5	0.228	0.448	0.755	0.560	0.427	0.124	0.050	0.112	0.057	0.102	0.065	0.031	0.026	0.162	0.174
10	0.244	0.477	0.749	0.540	0.441	0.128	0.058	0.118	0.061	0.107	0.091	0.034	0.029	0.170	0.188
15	0.228	0.552	0.719	0.550	0.397	0.134	0.047	0.120	0.068	0.113	0.085	0.030	0.024	0.179	0.184
20	0.216	0.457	0.758	0.546	0.336	0.126	0.045	0.124	0.064	0.108	0.076	0.017	0.039	0.180	0.153
25	0.224	0.474	0.731	0.538	0.437	0.120	0.029	0.130	0.045	0.096	0.070	0.042	0.029	0.183	0.191

表选项






表 5 不同调节率下Ste355各影响因子|MIV|值 Table 5 |MIV| values of impact factors of Ste355 with different regulation rates

MIV调节率/%	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
5	0.286	0.476	0.681	0.523	0.497	0.153	0.032	0.121	0.058	0.100	0.062	0.040	0.030	0.157	0.148
10	0.304	0.473	0.692	0.551	0.425	0.139	0.031	0.128	0.063	0.121	0.073	0.049	0.028	0.190	0.181
15	0.361	0.495	0.720	0.535	0.460	0.183	0.045	0.135	0.091	0.120	0.076	0.059	0.036	0.206	0.186
20	0.304	0.549	0.732	0.562	0.417	0.152	0.042	0.131	0.082	0.121	0.080	0.038	0.030	0.191	0.199
25	0.334	0.598	0.760	0.530	0.421	0.177	0.047	0.150	0.104	0.105	0.083	0.070	0.039	0.193	0.234

表选项






3 分析与讨论 3.1 腐蚀影响因子敏感度分析 根据不同调节率下针对碳钢Q235、Q450、St12和Ste355的不同输入变量的|MIV|值实验计算结果，绘制了4种碳钢在不同调节率下影响因子的|MIV|值的变化曲线及其标准差柱状图如图 2~图 5所示。

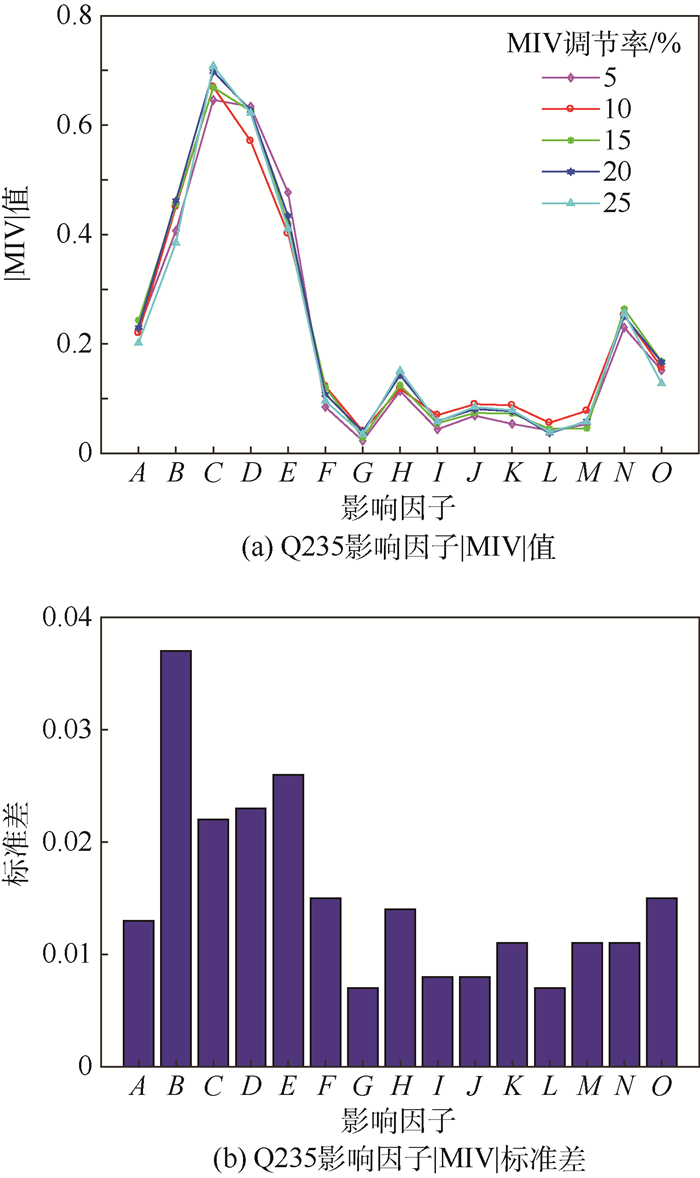图 2 不同调节率下Q235影响因子|MIV|值的变化曲线及标准差柱状图 Fig. 2 |MIV| values variation curves and standard deviation histogram of impact factors of Q235 with different regulation rates

图选项

图 3 不同调节率下Q450腐蚀影响因子|MIV|值的变化曲线及标准差柱状图 Fig. 3 |MIV| values variation curves and standard deviation histogram of corrosion impact factors of Q450 with different regulation rates

图选项

图 4 不同调节率下St12腐蚀影响因子|MIV|值的变化曲线及标准差柱状图 Fig. 4 |MIV| values variation curves and standard deviation histogram of corrosion impact factors of St12 with different regulation rates

图选项

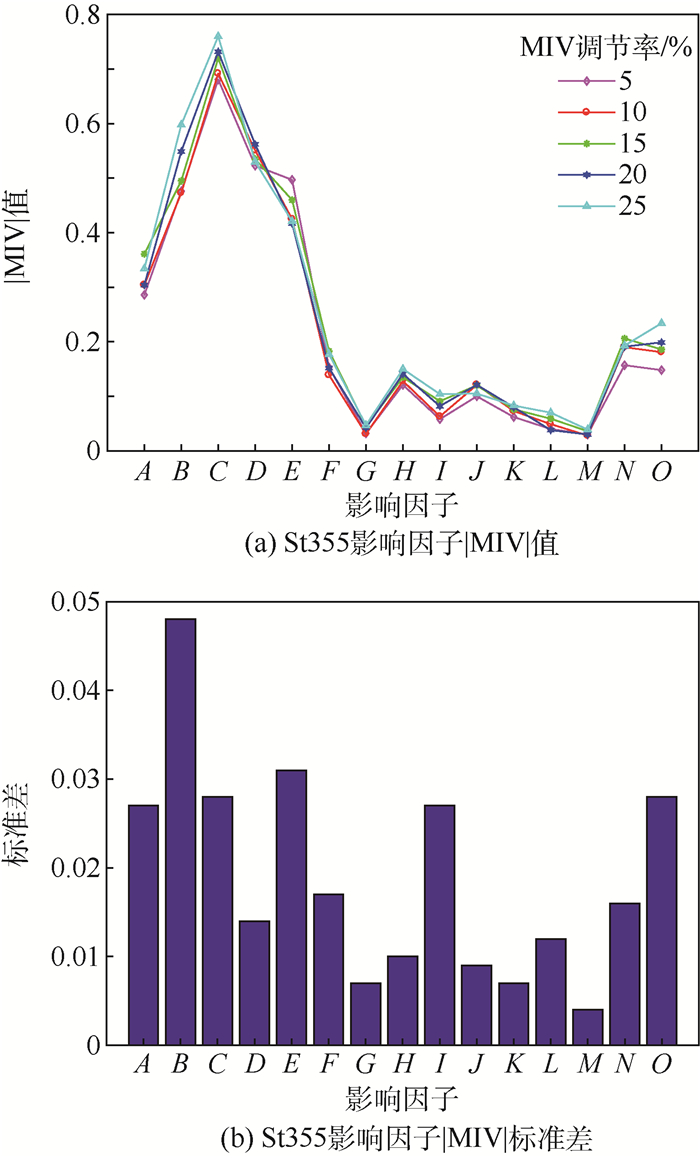图 5 不同调节率下Ste355腐蚀影响因子|MIV|值的变化曲线及标准差柱状图 Fig. 5 |MIV| values variation curves and standard deviation histogram of corrosion impact factors of Ste355 with different regulation rates

图选项

经过200次实验，4种碳钢的|MIV|值均趋于平稳，不同调节率下，同种碳钢的|MIV|值基本保持一致。尽管权重变化曲线的走势基本保持一致，但随着调节率的变化，各输入变量对腐蚀速率的影响程度略有不同。
不同调节率下Q235腐蚀的影响因子|MIV|值及其标准差如图 2所示，当调节率发生变化时，影响因子B、C、D、E、F的|MIV|值变化较为活跃，其中B最为活跃，可知Q235的腐蚀速率对影响因子B的敏感度较高。影响因子C、H的|MIV|值随着调节率的增加而增加，可见当影响因子C、H的|MIV|值增加时，其在影响腐蚀速率中的权重也会增加。而调节率变化时其他活跃因素并没有出现类似的正相关现象，是由于腐蚀是由多方面因素协同造成的，但单一影响因子的改变不一定存在着明显的趋势。
不同调节率下Q450腐蚀的影响因子|MIV|值及标准差如图 3所示，当调节率发生变化时，影响因子A、D、H、N的|MIV|值变化较为活跃，其中H最为活跃，其含量发生改变时，可知Q450的腐蚀速率对影响因子H的敏感度较高。影响因子H、N的|MIV|值随着调节率的增加而增加，可见当影响因子H、N的|MIV|值增加时，其在影响腐蚀速率中的权重也会增加。
不同调节率下St12腐蚀的影响因子|MIV|值及标准差如图 4所示，当调节率发生变化时，影响因子B、E的|MIV|值变化较为活跃，其含量发生改变时，可知St12的腐蚀速率对影响因子H的敏感度较高。影响因子H的|MIV|值随着调节率的增加而增加，可见当影响因子H的|MIV|值增加时，其在影响腐蚀速率中的权重也会增加。整体而言，St12调节率变化时|MIV|值最为稳定，当影响因素改变时，其影响腐蚀速率权重变化最小。
不同调节率下Ste355腐蚀影响因子|MIV|值及标准差如图 5所示，当调节率发生变化时，影响因子A、B、C、E、I、O的|MIV|值变化较为活跃，其中B最为活跃，其含量发生改变时，可知Ste355的腐蚀速率对影响因子H的敏感度较高。影响因子C、H、O的|MIV|值随着调节率的增加而增加，可见当影响因子C、H的|MIV|值增加时，其在影响腐蚀速率中的权重也会增加。整体而言，Ste355调节率变化时|MIV|值最为不稳定，当影响因素改变时，其影响腐蚀速率权重变化最大。
3.2 腐蚀影响因子权重分析 由MIV实验结果可以看出，4种碳钢在各调节率下的影响因子对腐蚀速率影响的权重分布规律基本保持一致，各影响因子|MIV|值仅在较小范围内波动。说明MIV调节率的变化对影响因子的权重影响不大。因此，选取任一调节率下的各影响因子的权重均具有代表性。本文选取调节率为15%，分析各影响因子对腐蚀速率影响的权重情况。根据图 6(a)可知影响因子对4种碳钢的影响基本一致，因此，可取4种碳钢的各影响因子权重的平均值作为各影响因子对腐蚀速率影响的权重，记为|MIV|_M15%，如图 6(b)所示。求得的腐蚀速率影响因子权重大小依次为: 平均相对湿度(0.693)>日照时数(0.570)>平均温度(0.504)>降水量(0.430)>暴露时间(0.279)>自然降尘量-非水溶性(0.213)>自然降尘量-水溶性(0.187)>平均风速(0.150)>瞬时法SO₂(0.128)>连续法NO₂(0.105)>连续法H₂S(0.076)>瞬时法HCl(0.071)>连续法硫酸盐化速率(0.047)>连续法海盐粒子浓度(0.040)>连续法NH₃(0.035)。

图 6 调节率为15%时碳钢影响因子|MIV|值变化曲线及误差棒图 Fig. 6 |MIV| values variation curves and error bar chart of carbon steel impact factors with 15% regulation rate

图选项

根据图 6和上述排序可以看出，对腐蚀速率影响最大的是气候因素，除连续法海盐粒子浓度和平均风速外，其他气候影响因子的|MIV|_M15%值均为0.400~0.700。其次是暴露时间，|MIV|_M15%值为0.279。环境因素对腐蚀速率的影响最小，|MIV|_M15%均为0.035~0.213。排除一些对腐蚀速率影响极小的影响因子，气候因素|MIV|_M15%值是暴露时间|MIV|_M15%值的2倍左右，是环境因素|MIV|_M15%值的5倍左右。因此，对碳钢腐蚀速率的影响，气候因素大于暴露时间，大于环境因素。
气候因素中平均相对湿度在腐蚀速率影响因素中权重最大，|MIV|_M15%值为0.700左右，平均相对湿度是影响腐蚀速率的最显著因素；其次是日照时数、平均温度和降水量，|MIV|_M15%值均在0.500左右；日照时数直接影响材料在大气环境中暴露的润湿时间，日照时间长，润湿时间短，材料表面液膜存在时间短，腐蚀速率降低。反之，日照时数短，润湿时间长，增加材料的腐蚀速率。比较|MIV|值，其大小反应影响因子的权重，包括正影响和负影响，日照时数属于负影响。平均风速|MIV|_M15%值为0.150，远小于其他气候因子，但和环境因子|MIV|_M15%值相当；连续法海盐粒子浓度的|MIV|_M15%值为0.040，远小于气候影响因子，甚至小于环境影响因子，这是由于所使用的数据点连续法海盐粒子浓度较低，没有达到显著影响腐蚀速率的数量级。
环境因素中自然降尘量在腐蚀速率影响因素中权重最大，|MIV|_M15%值为0.200左右；其次是瞬时法SO₂和连续法NO₂|MIV|_M15%值为0.120左右；连续法H₂S、瞬时法HCl、连续法硫酸盐化速率和连续法NH₃的|MIV|_M15%值均小于0.080，对腐蚀速率影响的权重很小。
3.3 不同类型碳钢影响因子|MIV|值对比分析 不同类型的碳钢，影响因子对腐蚀速率的影响存在着差异，根据图 6(b)可知，在对Q235、Q450、St12和Ste355的腐蚀速率影响权重上存在着显著差异的影响因子是暴露时间、平均温度、日照时数、自然降尘量-非水溶性，因此着重对这4种影响因子进行分析，结果如图 7所示。

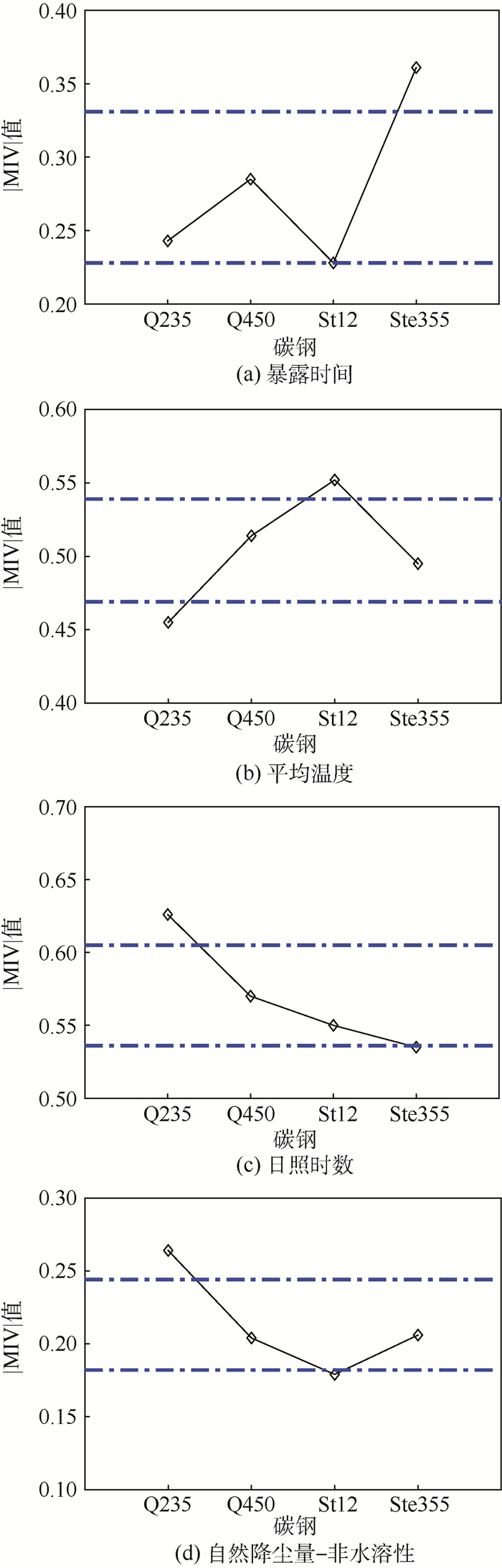图 7 不同碳钢各影响因子|MIV|值对比 Fig. 7 Comparison of impact factor |MIV| values among different carbon steels

图选项

从暴露时间的影响上看，Ste355对应的|MIV|值明显大于另外3种碳钢，说明Ste355较其他3种碳钢受暴露时间的影响更大；从平均温度的影响上看，St12对应的|MIV|值最大，且明显大于Q235，差值接近0.100，说明4种碳钢中St12最易受温度影响；从日照时数的影响上看，Q235对应的|MIV|值最大，更易受日照时数影响，而Ste355对应的|MIV|值最小，受到的日照时数影响相对较小；从自然降尘量-非水溶性的影响上看，Q235对应的|MIV|值最大，更易受自然降尘量-非水溶性影响，而St12对应的|MIV|值最小，受到的自然降尘-非水溶性影响相对较小。
4 结论 本文应用MIV算法对影响碳钢腐蚀速率的因子权重进行了分析和研究。选用不同的调节率进行数值实验，定量地给出了各环境因素对腐蚀速率影响的权重。并对不同碳钢的腐蚀因素进行了对比研究。
1) 当MIV调节率从5%依次递增至25%时，同种碳钢影响因子的|MIV|值基本保持一致，即对腐蚀速率的影响权重变化不大。
2) 当调节率变化时，Q235的平均温度、平均相对湿度、日照时数、降水量、平均风速对应的|MIV|值较为活跃，平均相对湿度、瞬时法SO₂随着调节率的增加其在影响腐蚀速率中的权重也会增加；Q450的暴露时间、日照时数、瞬时法SO₂、自然降尘量-非水溶性对应的|MIV|值变化较为活跃，瞬时法SO₂、自然降尘量-非水溶性随着调节率的增加其在影响腐蚀速率中的权重也会增加；St12的平均温度、降水量对应的|MIV|值变化得最为活跃，瞬时法SO₂随着调节率的增加其在影响腐蚀速率中的权重也会增加，对比另外3种碳钢影响因子变化时，其权重变化最小；Ste355的暴露时间、平均温度、平均相对湿度、降水量、瞬时法HCl、自然降尘量-水溶性的|MIV|值变化得较为活跃，瞬时法SO₂随着调节率的增加其在影响腐蚀速率中的权重也会增加，对比另外3种碳钢影响因子变化时，其权重变化最大。
3) 腐蚀速率影响因子权重大小依次为: 平均相对湿度(0.693)>日照时数(0.570)>平均温度(0.504)>降水量(0.430)>暴露时间(0.279)>自然降尘量-非水溶性(0.213)>自然降尘量-水溶性(0.187)>平均风速(0.150)>瞬时法SO₂(0.128)>连续法NO₂(0.105)>连续法H₂S(0.076)>瞬时法HCl(0.071)>连续法硫酸盐化速率(0.047)>连续法海盐粒子浓度(0.040)>连续法NH₃(0.035)。
4) 除|MIV|值极小的影响因子，气候因素|MIV|值是暴露时间|MIV|值的2倍左右，是环境因素|MIV|值的5倍左右。平均相对湿度和自然降尘量分别是气候因素和环境因素中对腐蚀速率影响权重最大的因子。
5) 对于4种不同类型碳钢，在暴露时间、平均温度、日照时数、自然降尘量-非水溶性差异最大。4种碳钢中，暴露时间对Ste355影响最显著，平均温度对St12影响最显著，日照时数和自然降尘量-非水溶性均对Q235影响最为显著。

参考文献

[1]	王振尧, 于国才, 韩薇. 我国自然环境大气腐蚀性调查[J].腐蚀与防护, 2003, 24(8): 323–326. WANG Z Y, YU G C, HAN W. A survey of the atmospheric corrosiveness of nature environments in China[J].Corrosion & Protection, 2003, 24(8): 323–326.DOI:10.3969/j.issn.1005-748X.2003.08.001(in Chinese)
[2]	柯伟. 中国腐蚀调查报告[M].北京: 化学工业出版社, 2003: 13. KE W. Chinese corrosion survey report[M].Beijing: Chemical Industry Press, 2003: 13.(in Chinese)
[3]	柯伟, 王振尧, 韩薇. 大气腐蚀与装备环境工程[J].装备环境工程, 2004, 1(4): 1–6. KE W, WANG Z Y, HAN W. Atmospheric corrosion and materiel environmental engineering[J].Equipment Environmental Engineering, 2004, 1(4): 1–6.DOI:10.3969/j.issn.1672-9242.2004.04.001(in Chinese)
[4]	梁彩凤. 钢在中国大陆的大气腐蚀研究[J].电化学, 2001, 7(2): 215–219. LIANG C F. Atmospheric corrosion of steels in China[J].Electrochemistry, 2001, 7(2): 215–219.DOI:10.3969/j.issn.1006-3471.2001.02.012(in Chinese)
[5]	COLE I S, GANTHER W D, SINCLAIR J D, et al. A study of the wetting of metal surfaces in order to understand the processes controlling atmospheric corrosion[J].Journal of the Electrochemical Society, 2004, 151(12): B627–B635.DOI:10.1149/1.1809596
[6]	林翠, 刘月娥. 高湿度无污染大气中温度对碳钢腐蚀的影响[J].腐蚀与防护, 2009, 30(12): 874–878. LIN C, LIU Y E. Effect of temperature on corrosion behavior of carbon steel in pollution-free atmosphere with high relative humidity[J].Corrosion & Protection, 2009, 30(12): 874–878.(in Chinese)
[7]	SONG L, CHEN Z. The role of UV illumination on the NaCl-induced atmospheric corrosion of Q235 carbon steel[J].Corrosion Science, 2014, 86(9): 318–325.
[8]	MA Y, LI Y, WANG F. Corrosion of low carbon steel in atmospheric environments of different chloride content[J].Corrosion Science, 2009, 51(5): 997–1006.DOI:10.1016/j.corsci.2009.02.009
[9]	WANG C, WANG Z, KE W. Initial corrosion behavior of carbon steel Q235 in the atmosphere with SO2[J].Acta Metallurgica Sinica, 2008, 44(6): 729–734.
[10]	闫松涛, 文磊, 金莹. 大气沉积颗粒物对碳钢腐蚀行为的影响[J/OL]. 中国科技论文在线(2016-06-20)[2017-08-01]. http://www.paper.edu.cn/releasepaper/content/201606-759. YAN S T, WEN L, JIN Y. The influence of the deposited atmospheric particulates on the corrosion behavior of carbon steel[J/OL]. Sciencepaper Online(2016-06-20)[2017-08-01]. http://www.paper.edu.cn/releasepaper/content/201606-759 (in Chinese).
[11]	SINGH D D N, YADAV S, SAHA J K. Role of climatic conditions on corrosion characteristics of structural steels[J].Corrosion Science, 2008, 50(1): 93–110.DOI:10.1016/j.corsci.2007.06.026
[12]	汪川, 曹公旺, 潘辰, 等. 碳钢、耐候钢在3种典型大气环境中的腐蚀规律研究[J].中国腐蚀与防护学报, 2016, 36(1): 39–46. WANG C, CAO G W, PAN C, et al. Atmospheric corrosion of carbon steel and weathering steel in three environments[J].Journal of Chinese Society for Corrosion and Protection, 2016, 36(1): 39–46.(in Chinese)
[13]	朱世东, 尹志福, 白真权, 等. 温度对P110钢腐蚀行为的影响[J].中国腐蚀与防护学报, 2009, 29(6): 493–498. ZHU S D, YANG Z F, BAI Z Q, et al. Influences of temperature on corrosion behaviour of P110 steel[J].Journal of Chinese Society for Corrosion and Protection, 2009, 29(6): 493–498.(in Chinese)
[14]	李牧铮, 张军, 祁凤玉. 环境因子与大气腐蚀关系的数学模型和大气腐蚀预测[J].中国腐蚀与防护学报, 1993, 13(1): 10–18. LI M Z, ZHANG J, QI F Y. Mathematical models for dependence of atmospheric corrosion on environment factors and prediction of atmospheric corrosion[J].Journal of Chinese Society for Corrosion and Protection, 1993, 13(1): 10–18.(in Chinese)
[15]	崔梦晨, 穆志纯, 付冬梅, 等. 大气环境中碳钢腐蚀速率推测方法[J].腐蚀与防护, 2016, 37(6): 503–507. CUI M C, MU Z C, FU D M, et al. Speculation of carbon steel corrosion rate in atmospheric environment[J].Corrosion & Protection, 2016, 37(6): 503–507.(in Chinese)
[16]	冯志兰, 刘桂芬, 刘力生, 等. 缺失数据的多重估算[J].中国卫生统计, 2005, 22(5): 274–277. FENG Z L, LIU G F, LIU L S, et al. Multiple estimates of missing data[J].Chinese Journal of Health Statistics, 2005, 22(5): 274–277.DOI:10.3969/j.issn.1002-3674.2005.05.001(in Chinese)
[17]	孙文彬, 刘希亮, 王洪斌, 等. 基于MIV的抛掷爆破影响因子权重分析[J].中国矿业大学学报, 2012, 41(6): 993–998. SUN W B, LIU X L, WANG H B, et al. Weight analysis of cast blasting effective factors based on MIV method[J].Journal of China University of Mining & Technology, 2012, 41(6): 993–998.(in Chinese)
[18]	武田艳, 占建军, 严韦. 基于MIV-BP型网络实验的房地产价格影响因素研究[J].数学的实践与认识, 2015, 45(18): 43–50. WU T Y, ZHAN J J, YAN W. Research on influence factors of real estate price based on MIV-BP neural network test[J].Journal of Mathematics in Practice and Theory, 2015, 45(18): 43–50.(in Chinese)
[19]	周莹. 基于MIV特征筛选和BP神经网络的滚动轴承故障诊断技术研究[D]. 北京: 北京交通大学, 2011: 25. ZHOU Y. Research on ball fault diagnosis technology based on MIV algorithm selection and BP neural network[D]. Beijing: Beijing Jiaotong University, 2011: 25(in Chinese).http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1963354
[20]	聂铭, 周冀衡, 杨荣生, 等. 基于MIV-SVM的烤烟评吸质量预测模型[J].中国烟草学报, 2014, 20(6): 56–62. NIE M, ZHOU J H, YANG R S, et al. MIV-SVM-based prediction model for smoking quality of flue-cured tobacco[J].Acta Tabacaria Sinica, 2014, 20(6): 56–62.(in Chinese)