基于深度学习和强化学习算法已经成功地解决了很多具有挑战性的问题,如围棋程序和机器人学习[4]。AlphaZero[5]作为基于深度强化学习的围棋程序新版本,在棋类游戏的离散状态空间下已经体现出了其在没有棋谱等先验知识的情况下学会多种棋类游戏并且超越人类的能力。引导策略搜索(Guided Policy Search,GPS)[4]作为一种基于模型(model-based)的算法,可以在机器人控制这种高维连续状态空间下重复实验中不断优化控制效果,完成机器人拾取物体等动作。而深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)算法[6]作为一种非基于模型(model-free)的算法,也在OpenAI Gym[7]仿真平台上实现了多种控制任务的自主学习,完成传统控制算法难以完成的复杂控制目标,如自主学习双足行走等。这些实验结果表明深度强化学习(Deep Reinforcement Learning, DRL)算法可以达到软件定义卫星姿态控制系统对自主性、智能性、适应性的要求。
然而机器学习算法普遍对计算平台的计算能力和存储能力有较高的要求,卫星姿态控制系统往往使用的是PID控制[8-9]、滑模控制[10]、模糊控制[11-12]等传统控制算法。PID控制算法易于理解和实现,需要的计算资源少,仍然是目前卫星姿态控制使用的主流基础控制算法,然而该算法需要针对不同的硬件系统和软件进行调节,无法快速适应空间环境的变化和空间任务的变化。滑模控制的主要目的是处理控制系统的非线性,和PID控制一样,有自适应能力的问题。智能控制算法如模糊控制,提升了系统的适应能力,然而模糊控制系统需要专家知识进行系统设计,而不是根据实时生成的数据进行调节。软件定义卫星搭载的超算平台大大提升了卫星的计算能力,因此使得基于机器学习的控制算法成为可能,从而进一步提升控制算法的自适应能力和自主性。
本文使用了基于模型的深度强化学习算法来建立姿态控制系统。该算法主要由3部分构成:动力学模型网络、控制策略网络以及基于启发式搜索的优化方法。其中,动力学模型网络使用深度学习网络、可以根据地面仿真和在线生成数据的学习生成动力学模型,使用基于模型的算法比非基于模型的算法收敛速度更快,可以更快的速度找到优化策略。控制策略网络同样使用深度学习网络,可以根据地面仿真和启发式搜索优化的效果来学习控制策略,同时为启发式搜索的优化提供具有一定效果的初始策略,加速算法的收敛。启发式搜索根据动力学模型和强化学习原理进行策略迭代,在每一步实际执行控制策略时寻找更优的策略。通过这种深度强化学习算法,姿态控制系统可以在卫星物理参数未知、执行机构和传感器不同、卫星轨道不同的情况下根据在线生成的数据不断优化姿态控制的效果。
1 基本理论 背景分为3个部分,包括姿态仿真系统、传统控制算法和强化学习算法。首先介绍姿态仿真系统,由于卫星发射成本较高,在进行姿态控制算法实验时,需要在仿真环境下进行仿真实验,仿真系统主要考虑到卫星姿态动力学、运动学模型和空间干扰力矩。卫星的姿态动力学介绍卫星角速度随执行机构控制力矩的变化规律,运动学模型介绍卫星姿态四元数随角速度的变化规律。卫星姿态动力学和运动学模型是进行卫星姿态控制的基础模型。然后介绍传统控制算法,PID控制算法仍然是卫星姿态控制的主流算法,因此主要介绍基于PID的卫星姿态控制算法相关研究进展。最后介绍强化学习算法的基础,主要介绍应用较为广泛的Q学习算法,以及在Q学习基础上结合深度学习发展起来的深度强化学习。
1.1 卫星姿态动力学和运动学模型 如图 1所示,卫星姿态动力学模型的输入为卫星所受的空间环境力矩,输出为卫星姿态角速度,动力学模型主要依赖于卫星的动力学方程。
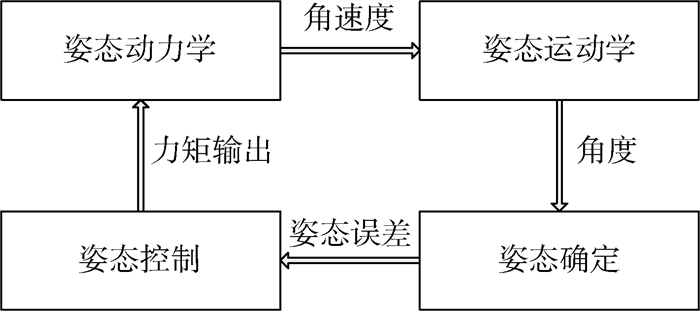 |
| 图 1 卫星姿态控制系统过程图 Fig. 1 Procedure chart of satellite attitude control system |
| 图选项 |
如果假设卫星为刚体,那么卫星姿态的动力学模型表达式为
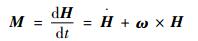 | (1) |
式中:M为卫星的控制力矩,为3维空间矢量;H为卫星的角动量;ω为卫星的角速度;t为时间。式(1)表示了卫星的角速度和控制力矩根据转动惯量变化的关系。
以四元数表示卫星的姿态,那么卫星姿态运动学表达式为
 | (2) |
式中:q为卫星的姿态四元数;
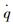
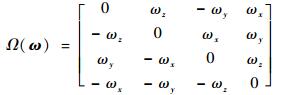 | (3) |
式中:ωx、ωy和ωz分别为卫星姿态角速度在三维坐标轴的分量。
此外,卫星的姿态还会受到空间干扰力矩的影响,主要包括重力梯度力矩、空气阻力力矩、太阳光压力矩和潮汐力矩等。
根据文献[13]的摄动力数据,结合经验公式推算出干扰力矩如表 1所示,可见在不同的轨道高度下,不同类型的干扰力矩对姿态的影响也有所不同。在低轨状态下,地球重力梯度力矩和空气阻力力矩是主要的干扰力矩;在中轨状态下,地球重力梯度力矩依旧是主要的干扰力矩,而空气阻力力矩已经大幅下降,太阳光压力矩、月球和太阳重力梯度力矩影响增大;而在地球同步轨道状态下,地球重力梯度力矩也大幅下降,空气阻力力矩则可以忽略不计。
表 1 3种经典轨道状态下的干扰力矩 Table 1 Disturbance torque under three classic orbit states
| N·m | |||
| 干扰力矩 | 低轨(200 km) | 中轨(1 000 km) | 地球同步轨道(35 800 km) |
| 地球重力梯度 | 10-3 | 10-3 | 10-7 |
| 空气阻力 | 0.4×10-5 | 10-9 | 0 |
| 太阳光压 | 0.2×10-8 | 10-9 | 0.4×10-9 |
| 太阳重力梯度 | 0.3×10-7 | 0.5×10-7 | 0.2×10-6 |
| 月球重力梯度 | 0.6×10-7 | 0.1×10-6 | 0.5×10-6 |
| 太阳潮汐 | 0.4×10-7 | 0.4×10-7 | 10-11 |
| 月球潮汐 | 0.5×10-7 | 0.3×10-7 | 0.8×10-11 |
表选项
主要考虑了3种干扰力矩的影响:地球重力梯度力矩、空气阻力力矩和太阳光压力矩。每种干扰力矩的影响主要依据文献中使用的经验公式进行仿真计算。
地球重力梯度力矩计算式为[14]
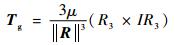 | (4) |
式中:μ为地球重力参数;||R||为卫星到地球中心的距离;I为卫星的转动惯量;R3为卫星轨道参数。
空气阻力力矩计算式为[14]
 | (5) |
式中:CD为空气阻力参数;ρ为大气密度参数,由标准大气模型计算得到;Vr为卫星相对于大气的速度;A为卫星的迎风面积;Cp为压力中心相对于卫星中心距离的向量;v为风速的单位方向向量。这些参数可以根据经验进行初始化。
太阳光压力矩计算式为[15]
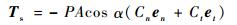 | (6) |
式中:P为距离1 AU的太阳辐射压力常数,1 AU≈1.496×1 011 m;en和et分别为卫星的法向和切向向量;α为太阳角度;Cn和Ct表达式分别为
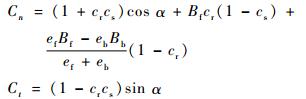 |
其中:cr为表面反射率;cs为镜面反射系数;ef和eb分别为前向和后向辐射系数;Bf和Bb分别为前向和后向的非朗伯系数。
将3种干扰力矩和控制力矩Tc相叠加,可以给出卫星所受的合力矩的影响,即本节所述的卫星姿态动力学方程中的M值:
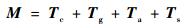 | (7) |
1.2 基于PID的卫星姿态控制算法 虽然PID控制有前面所述的缺点,但因为其实现简单,计算资源要求较低,仍然被大量卫星姿态控制系统所使用。PID控制算法的定义如下[16]:
 | (8) |
式中:Kp、Ki和Kd是非负参数,分别为比例、积分和微分系数;e(t)为当前状态和目标状态的误差值;τ为积分中间变量。PID控制算法的原理如图 2所示,反馈环节通过对3种误差的调节实验控制过程,y(t)表示当前状态,r(t)表示目标状态。
 |
| 图 2 PID控制算法原理图 Fig. 2 Schematic diagram of PID control algorithm |
| 图选项 |
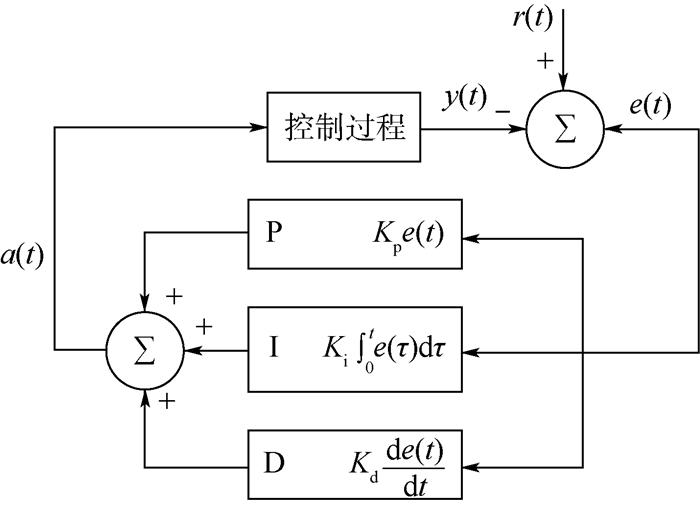
通常使用比例(P)和微分(D)环节设计卫星姿态控制算法,用式(9)表示:
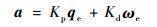 | (9) |
式中:qe为卫星姿态四元数的误差;ωe为卫星角速度的误差;a为执行机构的控制力矩输出。忽略积分环节可以增加控制算法对误差的反应速度,但可能会导致控制的稳定度下降。
PID控制算法的性能会受到传感器误差和空间环境的干扰力矩的影响,导致卫星的姿态确定系统稳定性降低。因此一种平滑角速度观测器[9]的方法被提出以提升卫星姿态的估计精度:
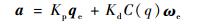 | (10) |
式中:C(q)为根据卫星姿态对角速度的补偿矩阵。这类改进方法提升了控制算法输入的精度和稳定度,从而提升了算法的性能。
PID控制算法的性能同样会受到执行机构误差的影响,导致卫星的姿态控制稳定性下降。因此一种非线性模型[2]被提出,用来处理执行机构饱和,死区非线性和动量轮速度限制的问题。一种基于最优控制的方法[8]被提出,使用磁力矩器帮助动量轮进行动量卸载,防止其到达速度上限。这一类改进可以提升控制系统输出的性能。
为了提升控制系统的整体性能,一种基于量化控制的方法[17]被提出用来改进PID控制的反馈机制。此外,一种使用线性二次型控制算法的方法被提出,能够比传统PID控制降低8%的能量消耗[18]。在能量有限的太空环境中,节约能源可以让卫星整体的运行更加稳定。
这些在传统PID控制基础上改进的方法需要对不同问题分别建模分析并且加以改进,然而基于机器学习的深度强化学习姿态控制算法可以根据实时生成的数据利用神经网络的泛化能力对这些问题进行整体优化。例如在输入不稳定的情况下,状态观测器的补偿矩阵可以通过深度强化学习中的模型网络进行学习优化,同时执行机构的非线性误差也可以通过深度强化学习中的策略网络进行自适应的学习改进;此外,能量消耗也可以通过强化学习的价值函数给出,让强化学习算法在优化控制效果的同时尽量降低系统的能量消耗。
1.3 强化学习算法 PID控制仍可作为智能控制算法的基础策略,为强化学习控制提供初始化功能。强化学习包含以下几个部分:智能体、智能体所处的环境和所执行的动作。在每个离散时间步长t内智能体会观测其所处的环境得到t时刻的状态st,根据该状态执行动作at,并且获得此时的奖励值rt以及达到下一时刻的状态st+1。在一个具有随机性的环境中,包含一个初始状态分布p(s0),状态转移模型p(st+1|st, at)和奖励函数r。
Q学习[19]作为强化学习里的一类基本算法,使用:
 | (11) |
式中:Q(st, at)为智能体在时间t时的状态st下执行动作at所产生的效用;γ∈(0, 1)为对未来奖励函数的折扣因子,防止时序过长时奖励函数过大。Q学习生成的策略需要最大化Q值μ(s)=
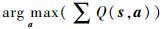
随着深度学习技术的发展,神经网络对高维度且高度非线性的函数拟合能力越来越强,神经网络对复杂Q值的表示能力也越来越强,因此在DDPG算法中,使用了神经网络拟合Q值,加强了强化学习算法对高维空间内复杂任务的学习能力。假设拟合函数为θQ,那么损失函数的定义如下:
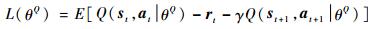 | (12) |
式中:Q(st, at|θQ)为t时刻网络对Q值的估计;最后两项为t时刻执行动作之后的效果。DDPG算法通过最小化损失函数来拟合Q值。该算法同时使用神经网络来拟合策略函数μ(s|θμ),该函数会根据当前状态和网络中的参数确定执行的策略,因此网络同时需要对策略网络进行学习,更新算法定义如下:
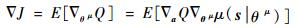 | (13) |
式中:?J为策略的变化引起的Q值变化。该公式的含义是根据策略的变化引起的Q值变化来确定参数θμ的更新。策略函数使用高斯白噪声进行改变,定义如下:
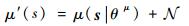 | (14) |
式中:
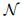
机器学习算法通常使用梯度下降算法进行算法收敛的计算,但在模型梯度不可靠的时候,也会采取其他方案进行优化计算。对应于梯度下降算法,启发式搜索类的算法是另一种对神经网络等机器学习算法进行优化的方案。梯度下降算法的优点是收敛速度快,缺点是容易陷入局部最优。而启发式搜索类的算法收敛速度较慢,但是一种全局性的优化算法。因此,在很多实际应用中,也会采用基于启发式搜索的优化方法进行机器学习算法收敛过程的计算。
常用的启发式搜索算法有很多种,如粒子群优化、人工蜂群算法、蚁群算法、萤火虫算法、模拟退火算法和进化策略等。每种算法的优缺点和应用场景都有所不同。本文对启发式搜索算法的具体选取在2.3节中介绍。
2 深度强化学习姿态控制算法 基于模型的深度强化学习算法由以下3个部分组成:模型网络、策略网络和启发式搜索。如图 3所示,模型网络为启发式搜索提供动力学模型,并且从实际执行的数据中学习,提高模型的精度。策略网络为模型预测控制提供根据经验优化的初始策略,并且从实际执行的数据中学习,优化初始策略。模型策略根据模型网络提供的动力学模型和策略网络提供的初始策略进行优化,通过强化学习寻优,进一步优化策略,并且实际执行控制输出。此外,本文算法在初始化时可用PID控制等对策略网络和模型网络进行初始化。
 |
| 图 3 基于模型的深度强化学习算法原理图 Fig. 3 Schematic diagram of model based deep reinforcement learning algorithm |
| 图选项 |
本文算法的运行过程如下:
步骤1??随机初始化模型网络和策略网络,或者通过迁移学习等进行预初始化。
步骤2??由策略网络根据当前状态计算出当前策略,然后使用模型网络预测下一状态并给出Q值,交给启发式搜索进行下一步优化。
步骤3??使用启发式搜索在当前策略的邻域进行搜索,以找到具有更高Q值的策略。
步骤4??执行启发式搜索给出的优化后的策略,并且获取真实的状态输出和Q值,计算出模型预测误差。
步骤5??如果得到的Q值比初始化策略更好,则将此次结果作为策略网络的训练集。
步骤6??如果到达的状态空间超出了安全阈值,则使用如PID控制等引导策略使其回归到安全区域。
步骤7??每一次执行的结果都可以作为模型网络的训练集。
步骤8??如果状态达到且稳定在控制目标,则训练结束,否则返回步骤2。
2.1 模型网络 机器学习算法已经被应用于卫星姿态动力学构建。本文使用深度学习神经网络构建动力学模型。模型网络st+1=fθs(st, at)使用前一时间点的动作-状态对作为输入,下一时间点的状态作为输出,θs为网络中的参数。系统状态st包括四元数q和三维角速度ω,策略输出at为三维力矩。参数可以随机初始化,也可以通过地面仿真或事先获取的数据进行初始化,使用迁移学习等方法进行应用。使用经过预训练的网络可以提高算法的在线性能。
模型网络的损失函数为L(θs)=||s′t-st2||,s′t为模型网络的输出,st为下一时间点的实际状态,L(θs)为二者的均方误差,作用是最小化误差值,从而使得预测更加准确。网络的激励函数可以使用sigmoid函数、relu函数或者tanh函数,并且通过实验筛选出性能最好的使用。
为了提高模型网络的精度,本文算法从DDPG算法中引入了目标网络(target network),将非基于模型的优化应用在基于模型的算法之中,优化了算法的收敛精度。目标网络s′t+1=fθ′s(st, at)与原网络定义基本相同,但不随着原网络的优化算法优化,每次原网络参数优化之后使用θ′=τ′θ+(1-τ′)θ′对网络参数进行优化,其中0 < τ′?1,可理解为参数更新权重。在DDPG中目标网络是为了减缓网络的优化速度,从而解决Q学习无法收敛的问题。将此方法应用在模型网络中也可以提高模型的精度。
加入模型网络的算法比非基于模型的算法可以更快地收敛,因为模型网络可以根据每次得到的数据进行优化,而非基于模型的算法在找到合理的解之前会进行漫长的探索,从而收敛得更慢。而且模型网络在使用其他控制算法时也可以进行优化,让算法的适应性更强。
2.2 策略网络 策略网络同样使用深度网络构建网络模型:at=gθa(st),当前状态st为模型的输入,θa为网络参数,生成的策略at为模型的输出。类似地,模型参数可以随机初始化,也可以通过PID控制等引导策略进行初始化,从而加快算法的收敛速度,并且降低算法进入发散不可控区域的可能性。
策略网络的损失函数为L(θa)=||a′t-at||2,a′t为策略网络根据当前状态得到的输出,at为数据中实际执行的策略,L(θa)是二者的均方误差,作用是最小化误差值,从而可以使策略网络尽可能模仿实际执行的策略,并且根据神经网络的泛化能力使策略网络可以给出合理的初始化策略。网络的激励函数同样可以使用结合了目标网络的sigmoid、relu和tanh函数。
与模型网络不同的是,数据中的策略并不是一个“正确的策略”,实际执行的策略也是在不断优化中生成的,无法保证每次学习都让策略得到优化。因此,需要使用模型预测控制作为优化方法使得生成的数据可以保证不断优化,从而让策略网络的学习进一步优化。策略网络的输出也并不直接给出控制输出,而是作为模型预测控制的输入给出合理的初始策略。
和GPS算法不同的是,基于深度学习的策略网络可以给出一个全局的初始化策略,和任务路径无关,并且可以根据不同的任务学习模仿新的引导策略,提升在线适应的能力。
2.3 启发式搜索 启发式搜索包括多种性能优异的算法,如:模拟退火算法[20]、粒子群算法[21]和进化策略[22]算法等。它们使用策略网络的输出作为输入,输出奖励值最高的动作作为最优策略。每个时间点内的奖励函数为
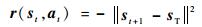 |
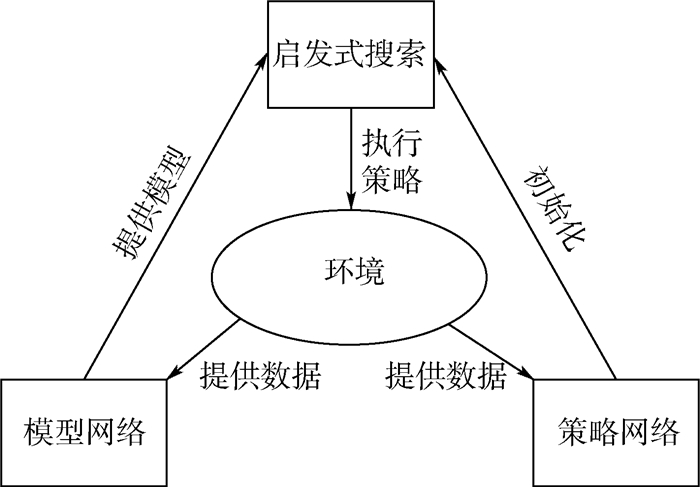
t时刻的奖励函数为状态st下执行动作at导致的状态st+1和目标sT之间的二次差值。负号代表二者距离越近奖励值越高。
模拟退火算法和AlphaGo中使用的蒙特卡罗搜索树同属于蒙特卡罗-马尔可夫链(Monte Carlo-Markov Chain,MCMC)方法,较适合于应用在多维连续空间的控制算法中。然而该算法的随机游走过程不利于并行化实现,因此本文使用易于并行化且同样在强化学习中被证明有效的自然进化策略算法来进行优化,以提高算法的收敛速度。
自然进化策略计算式为
 |
式中:左边为参数的更新梯度;右边为计算方法;θa为策略网络的参数,也可以直接对动作输出进行直接优化;N(0, I)为标准差为0,方差为单位矩阵的正态分布矩阵,目的是生成一个与θ维度相同的随机变量;σ为该随机变量的标准差;?为一个小量的正数;F函数是强化学习的价值函数,该更新公式可以使得θ参数朝F值最大的方向移动。
通过并行化执行该过程,同时生成n个随机正态分布,并且统一对θ参数执行更新过程:
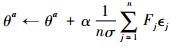 |
该并行化更新算法可以大幅降低运行时间。
算法1??基于模型的深度强化学习算法
初始化:θa和θs。
while未到控制目标do
??生成初始策略ain←gθa(st)和最优策略aopt
??while启发式搜索do
????在范围内搜索:aout←ain+rand()
????状态预测:st+1←fθs(st, aout)
????Q(st, aout)←||st+1-st||2·ωs
????进化策略更新:aopt
??end while
??执行aopt并得到数据
??根据数据优化θa和θs
end while
3 实验结果 本文使用基于STK(Satellite Tool Kit)开发的卫星姿态控制仿真系统进行仿真实验,仿真系统结构如图 4所示,卫星轨道和空间环境参数由STK生成,并且传递给仿真系统。控制器会根据当前姿态,控制指令和控制目标确定当前策略输出给执行器执行,执行器会输出控制力拒,卫星的姿态动力学会根据控制力矩和空间干扰力矩得到新的姿态信息,传感器会将带有测量误差的姿态信息交给姿态确定系统,并且返回给控制器,进行下一次控制循环。
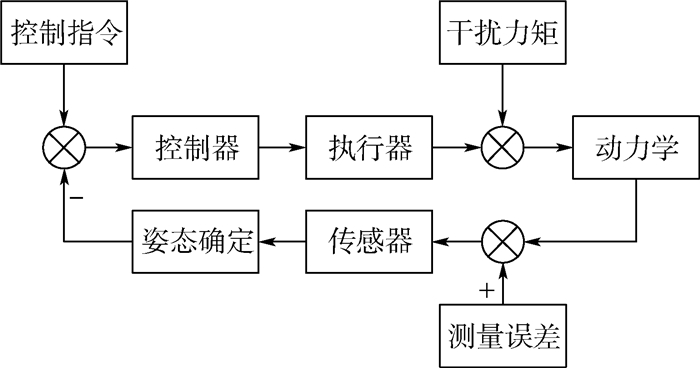 |
| 图 4 卫星姿态控制仿真系统结构 Fig. 4 Satellite attitude control simulation system structure |
| 图选项 |
基于强化学习的算法计算过程如图 5所示。纵轴的均方误差为卫星姿态四元数的误差与卫星角速度的误差之和,用于衡量模型网络的学习效果,因此不含单位。图 5(a)展示了当PID参数调节出问题,或卫星受到干扰力矩影响等因素导致控制算法无法稳定达到控制目标。图 5 (b)引入强化学习控制,算法在一开始仍使用PID控制作为引导策略使姿态控制系统进入可控范围内,而后交给强化学习控制算法进行控制学习,由于强化学习算法初期无法很快收敛,为防止控制系统失控,算法在均方误差增大时会继续切换回引导策略,保证算法始终可控。实际执行切换操作时,可以认为状态空间st中的四元数q对控制系统的稳定性影响较小,而角速度ω会对控制系统稳定性产生更大的影响,因此算法会根据角速度的大小进行切换。当||ω||>A1时,会从强化学习策略切换到引导策略,而当||ω|| < A2时,会从引导策略切换回强化学习策略,一般取A1>A2,以让控制系统更平滑地运行,防止过于频繁的切换影响姿态的稳定度,仿真实验中选取了A1=1.0,A2=0.5,也可根据系统的实际运行情况选取合适的切换区间。如图 5所示,在经过若干次的迭代之后,本文算法最终会收敛到较小的误差值。
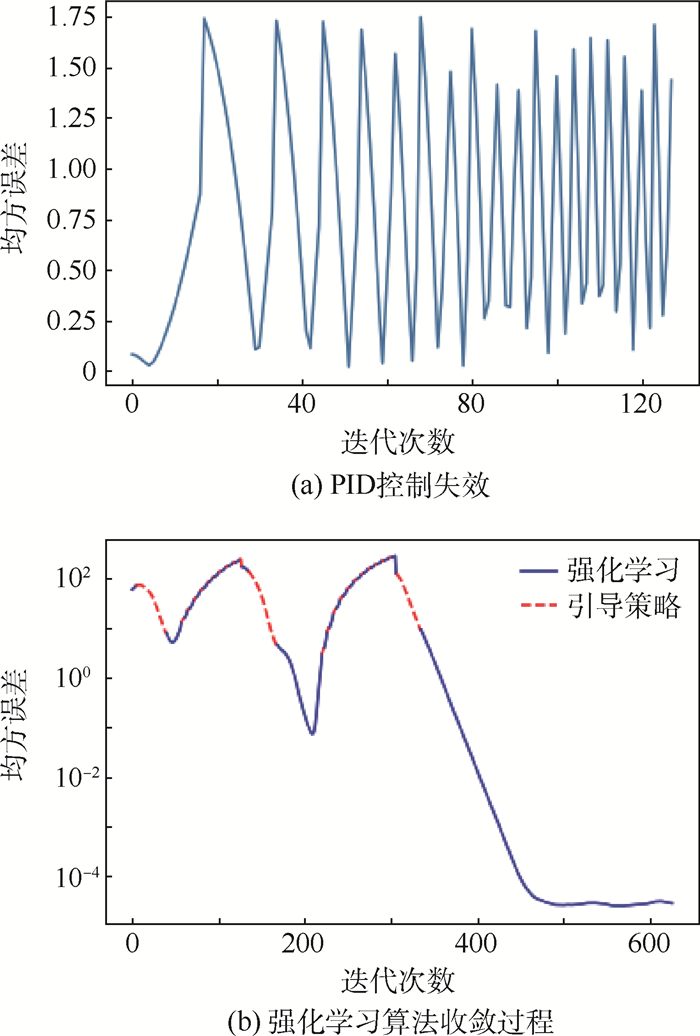 |
| 图 5 控制算法比较 Fig. 5 Comparison of control algorithms |
| 图选项 |
姿态仿真实验对比了全连接网络和基于目标网络的模型网络精度,同时对比了并行化前后算法的执行时间。使用tanh作为激活函数,3层全连接网络神经元个数分别为64、128和64,5层全连接网络神经元个数分别为32、128、512、128和32,目标网络使用的神经网络设置与3层全连接网络相同,学习速率设置为0.000 1。此外,进化策略使用1 024个线程同时进行策略计算,学习速率设置为0.01,为了提高搜索精度,算法的搜索范围会随着迭代过程而减小。
实验结果如图 6所示,分别对比了3层全连接网络,5层全连接网络和目标网络的模型网络收敛精度。每组实验进行了20次,图中圆点代表均值,直线的两端分别为模型收敛之后的最后100次模型预测误差的最大值和最小值。图 6(a)为3层全连接网络的实验结果,可见均值基本在1.0以上,其中可见多次均值贴近最小值,因为模型最后基本稳定在最小值处,但仍然有小概率会出现模型效果变差的情况出现。图 6 (b)为5层全连接网络的实验结果,均值已经能达到1.0以下,相比于3层网络有小幅改进,同样出现了均值贴近最小值的情况。图 6 (c)为目标网络的实验结果,可见均值已经可以达到0.5左右,而最小值已经可以接近于0,相比于全连接网络有了明显的提高。而最大值接近2.0,说明网络的稳定程度还需要改进。
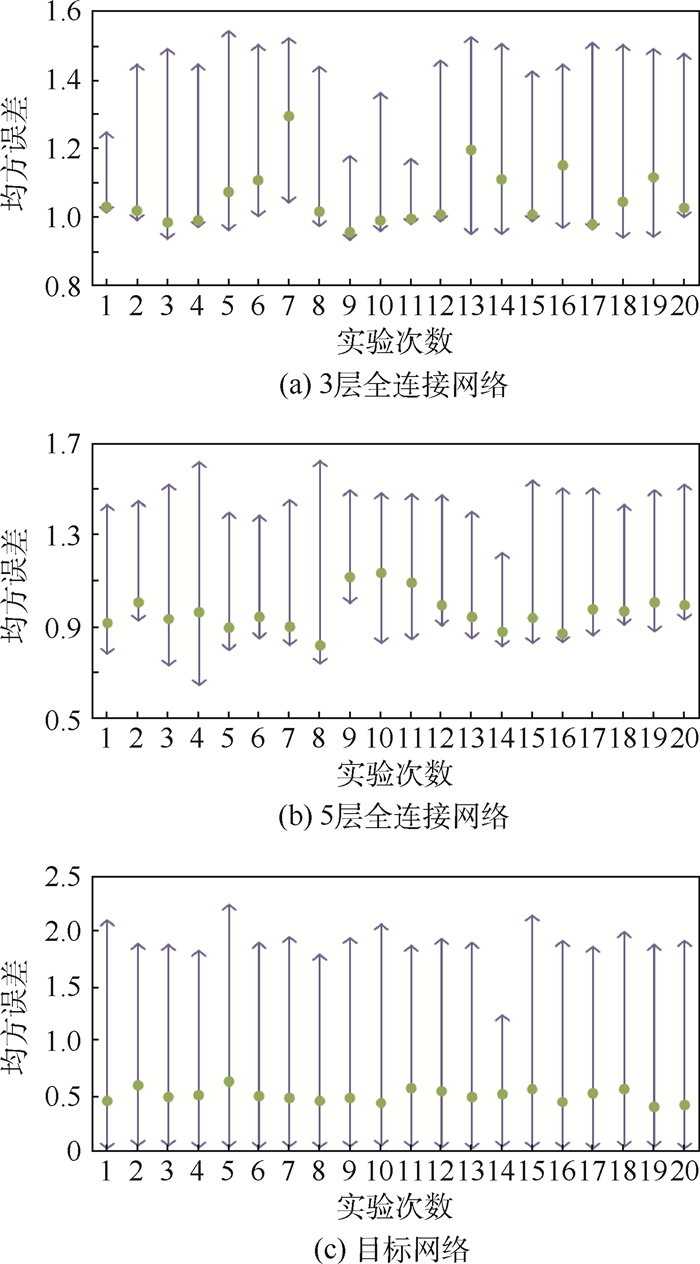 |
| 图 6 不同网络设置下的均方误差 Fig. 6 Mean square error with different networks |
| 图选项 |
对比图 6(a)~(c)可知,全连接网络可以相对稳定地收敛,然而网络的最小值和均值无法降低,证明了不带目标网络的算法的理论精度要低于目标网络。而带目标网络的算法收敛的稳定程度有所不足,最小值和均值之间的间距偏大,但这一段距离都在全连接网络的收敛精度之下,可见整体的收敛性能明显高于全连接网络,在实际应用时使用目标网络会取得更好的预测结果。
总体统计结果如表 2所示,结果表明,仅使用更深层的网络对于动力学模型精度提升有限,且增加了系统的计算量。而使用基于目标网络的算法能够显著提高动力学网络的平均收敛精度,尤其是均值和最小值,均值平均收精度从0.913提升到0.448,最小值平均收精度从0.745提升到0.014。此外,经过并行化的进化策略也使得收敛速度提高了10倍左右,大大提升了算法的在线运行能力。
表 2 不同算法收敛精度及速度对比 Table 2 Comparison of convergence accuracy and speed among different algorithms
| 网络设置 | 均方误差 | 收敛耗时/s | ||
| 最小值 | 最大值 | 均值 | ||
| 3层全连接 | 0.931 | 1.515 | 1.047 | 301.05 |
| 5层全连接 | 0.745 | 1.510 | 0.913 | 440.15 |
| 目标网络 | 0.014 | 1.908 | 0.448 | 28.10 |
表选项
4 结论 本文使用深度强化学习算法学习动力学模型和全局策略,并且使用模型预测控制优化控制策略。该算法框架下,可以使用不同的神经网络模型和策略优化方法。得益于软件定义卫星的发展,机器学习的算法可以在轨运行甚至于在轨学习,卫星姿态控制算法可以脱离传统姿态控制算法使用机器学习算法,从而为整星提供更好的姿态控制服务。本文算法可以在卫星物理参数未知的情况下学习得到优化的控制策略,并且在引导策略效果变差时通过学习生成优化的控制策略,使得卫星姿态控制系统更加智能化、自主化,对环境的适应性也有所提高。
实验结果表明,基于目标网络的动力学模型网络可以明显提升算法的收敛精度,而基于进化策略的启发式搜索并行化算法可以大大提升算法的收敛速度,从而提高强化学习姿态控制系统在轨运行在线计算的能力。
本文所使用的强化学习算法为贪心算法,在面对可能具有多个局部最优解的复杂控制问题如路径跟踪、目标追踪等问题时较容易陷入局部最优解。因此需要使用动态规划或模型预测控制等全局优化算法进一步提升算法的性能。神经网络目前使用的是全连接网络,泛化能力有限,在较为简单的仿真环境中可以取得不错的效果,然而实际空间环境更为复杂,需要使用泛化能力更强的卷积神经网络构建学习算法,并且可以使用递归神经网络拟合实际控制系统中的时间滞后效应。
参考文献
| [1] | WILLIAMS T W, SHULMAN S, SEDLAK J, et al.Magnetospheric multiscale mission attitude dynamics: Observations from flight data[C]//AIAA/AAS Astrodynamics Specialist Conference.Reston: AIAA, 2016. |
| [2] | HU Q, LI L, FRISWELL M I. Spacecraft anti-unwinding attitude control with actuator nonlinearities and velocity limit[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(10): 1-8. |
| [3] | MAZMANYAN L, AYOUBI M A.Takagi-Sugeno fuzzy model-based attitude control of spacecraft with partially-filled fuel tank[C]//AIAA/AAS Astrodynamics Specialist Conference.Reston: AIAA, 2014. |
| [4] | LEVINE S, FINN C, DARRELL T, et al. End-to-end training of deep visuomotor policies[J]. Journal of Machine Learning Research, 2016, 17(1): 1334-1373. |
| [5] | SILVER D, HUBERT T, SCHRITTWIESER J, et al.Mastering chess and shogi by self-play with a general reinforcement learning algorithm[EB/OL].(2017-12-05)[2018-06-13].http://cn.arxiv.org/abs/1712.01815. |
| [6] | LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[J]. Computer Science, 2015, 8(6): A187. |
| [7] | BROCKMAN G, CHEUNG V, PETTERSSON L, et al.OpenAI Gym[EB/OL].(2016-01-05)[2018-06-13].http://cn.arxiv.org/abs/1606.01540. |
| [8] | GROSS K, SWENSON E, AGTE J S.Optimal attitude control of a 6u cubesat with a four-wheel pyramid reaction wheel array and magnetic torque coils[C]//AIAA Modeling and Simulation Technologies Conference.Reston: AIAA, 2015. https://www.researchgate.net/publication/306357094_Optimal_Attitude_Control_of_a_6U_CubeSat_with_a_Four-Wheel_Pyramid_Reaction_Wheel_Array_and_Magnetic_Torque_Coils |
| [9] | AKELLA M R, THAKUR D, MAZENC F.Partial Lyapunov strictification: Smooth angular velocity observers for attitude tracking control[C]//AIAA/AAS Astrodynamics Specialist Conference.Reston: AIAA: 2015: 442-451. https://www.researchgate.net/publication/269163652_Partial_Lyapunov_Strictification_Smooth_Angular_Velocity_Observers_for_Attitude_Tracking_Control |
| [10] | XIAO B, HU Q, ZHANG Y, et al. Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 838-849. DOI:10.2514/1.61369 |
| [11] | WALKER A R, PUTMAN P T, COHEN K. Solely magnetic genetic/fuzzy-attitude-control algorithm for a CubeSat[J]. Journal of Spacecraft & Rockets, 2015, 52(6): 1627-1639. |
| [12] | GHADIRI H, SADEGHI M, ABASPOUR A, et al.Optimized fuzzy-quaternion attitude control of satellite in large maneuver[C]//International Conference on Space Operations.Reston: AIAA, 2015. http://www.researchgate.net/publication/303098915_Optimized_Fuzzy-Quaternion_Attitude_control_of_Satellite_in_Large_maneuver |
| [13] | 卢伟.基于阻力参数估计的低轨卫星轨道确定与预报[D].哈尔滨: 哈尔滨工业大学, 2008. LU W.Orbit determination and prediction of low earth orbit satellites based on estimating drag parameters[D]. Harbin: Harbin Institute of Technology, 2008(in Chiense). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D254198 |
| [14] | WANG P, ZHENG W, ZHANG H B, et al.Attitude control of low-orbit micro-satellite with active magnetic torque and aerodynamic torque[C]//20103rd In International Symposium on Systems and Control in Aeronautics and Astronautics.Reston: AIAA, 2010: 1460-1464. https://www.researchgate.net/publication/251967428_Attitude_control_of_low-orbit_micro-satellite_with_active_magnetic_torque_and_aerodynamic_torque |
| [15] | YOO Y, KOO S, KIM G, et al.Attitude control system of a cube satellite with small solar sail[C]//AIAA Aerospace Sciences Meeting.Reston: AIAA, 2013. http://www.researchgate.net/publication/273135427_attitude_control_system_of_a_cube_satellite_with_small_solar_sail |
| [16] | FRANKLIN G F. Feedback control of dynamic systems[M]. Beijign: Posts and Telecom Press, 2007. |
| [17] | WU B L. Spacecraft attitude control with input quantization[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 176-181. DOI:10.2514/1.G001427 |
| [18] | TURKOGLU K, GONG A.Preliminary design and prototyping of a low-cost spacecraft attitude determination and control setup[C]//AIAA Guidance, Navigation, and Control Conference.Reston: AIAA, 2015. http://gateway.proquest.com/openurl?res_dat=xri:pqm&ctx_ver=Z39.88-2004&rfr_id=info:xri/sid:baidu&rft_val_fmt=info:ofi/fmt:kev:mtx:article&genre=article&jtitle=Aiaa%20Journal&atitle=Preliminary%20Design%20and%20Prototyping%20of%20a%20Low-Cost%20Spacecraft%20Attitude%20Determination%20and%20Control%20Setup |
| [19] | WATKINS C J C H, DAYAN P. Q-learning[J]. Machine Learning, 1992, 8(3-4): 279-292. DOI:10.1007/BF00992698 |
| [20] | KIRKPATRICK S, VECCHI M P.Optimization by simulated annealing[M]//MEZARO M, PARISI G, VIRASORO M.Spin glass theory and beyond: An introduction to the replica method and its applications.Singapore: World Scientific Press, 1987: 339-348. |
| [21] | KENNEDY J, EBERHART R.Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks.Piscataway, NJ: IEEE Press, 2002: 1942-1948. |
| [22] | SALIMANS T, HO J, CHEN X, et al.Evolution strategies as a scalable alternative to reinforcement learning[EB/OL].(2017-12-07).[2018-06-13].https://arxiv.org/abs/1703.03864. |
