宾夕法尼亚大学的Kumar等[4-6]借助微分平坦理论、几何控制方法和混合整数优化等工具,在微分平坦空间内来解决无人机吊挂系统的路径生成和跟踪控制问题。苏黎世联邦理工学院(ETH)的研究人员[7]采用迭代线性二次型控制器(iLQR),使得该系统能够在状态空间内,通过不断迭代学习的方式实现复杂约束条件下的最优控制。近年来,也有国内的研究人员将各种不同的控制方法应用在该系统中。鲜斌等[8]对此系统设计了基于能量分析的非线性控制器,并与LQR控制器进行了对比。李伟荣等[9]针对带悬挂负载的八旋翼无人机设计了一个PID串级控制器,并通过实验实现了稳定飞行。Yi等[10]设计了一个滑模控制器,以提高系统的鲁棒性和跟踪性能。Guo等[11]设计了一个带有约束的H2/H∞混合控制器,实现系统暂态性能与鲁棒性能的综合。
上述研究都是针对只有一个无人机的情况,当负载较重时,就有必要使用多个无人机,因此,本文将研究有2个无人机的吊挂飞行系统。文献[12-13]将单个的情况推广到了多个无人机,并针对吊挂载荷为质点和刚体这2种情况,分别设计几何控制器,再根据微分平坦理论进行参考轨迹设计和路径跟踪。
现有的应用大多都将该问题考虑为只有一个目标函数的控制系统。但是在实际应用中,因为性能配置的差异或者所处空间位置的不同,2个无人机可能有着不一样的控制需求。比如,第1架无人机只需要负责跟踪参考轨迹,第2架无人机则主要负责保持队形并稳定吊挂负载。在这种情况下,如果只设计一个目标函数,或者是简单的性能加权而不考虑两者之间互动的影响,可能无法充分发挥系统的潜力。
博弈论就是这样一个有助于理解不同决策主体相互作用的工具[14]。一般说来,博弈有2类模型:非合作型和合作型。其中,前者是以单个参与人的可能行动为基本元素,而后者以参与人群的可能联合行动集合为基本元素。目前,博弈论已经广泛应用于多智能体领域。文献[15]将多个无人小车的编队运动看成是一个非合作的博弈问题,并在图论的基础上为不同的无人车设计目标函数,用微分博弈方法来求解。类似的,文献[16]研究了有1个领导者和N个跟随者的多智能体系统,领导者负责跟踪目标,跟随者负责保持队形。
本文首先建立受控系统的动力学模型并线性化,然后将2个无人机看成是具有不同目标函数的决策主体,并在非合作二人博弈的框架下进行控制器设计,最后通过数值仿真进行验证。
1 动力学模型 类似文献[8],为了简化分析,本文做如下合理假设:
1) 四旋翼无人机是几何中心与质心重合的刚体。
2) 吊挂负载认为是质点,通过2根质量不计的无弹性绳子吊挂在无人机的质心处。
3) 2根绳子的张力始终大于0,所有的空气阻力都忽略不计。
1.1 考虑外界扰动的非线性模型 如图 1所示,{G:xgygzg}为地面惯性坐标系,{Bi:xbiybizbi}为机体坐标系,{S:xyz}为与吊挂负载固连,方向与{G}相同的过渡坐标系。Q′i为Qi在xgyg平面上的投影, i=1, 2,分别表示第1架和第2架无人机。
 |
| 图 1 带吊挂负载的2个四旋翼无人机 Fig. 1 Two quadrotor UAVs carrying cable-suspended payload |
| 图选项 |
αi, βi为2根绳子在{S}内的角度,因为吊挂负载始终在2个无人机之间,因此有0°<βi<90°,定义从吊挂负载到无人机的单位方向向量为
 |
无人机的控制输入为各自作用在{Bi}内的力FQi和力矩MQi分别为
 | (1) |
考虑有一个作用在吊挂负载上的扰动力FP,其在{G}中可以表示为FPG=[FxP, FyP, FzP]T。
根据几何关系,给定无人机1的位置后,可以依次确定吊挂负载和无人机2的位置:
 | (2) |
式中:ξQ1G、ξQ2G和ξPG分别为无人机1、无人机2和吊挂负载的位置;Lr为2根绳子长度。
记{Bi}到{G}的坐标变换矩阵为TBiG,即FQiG=TBiGFQiBi。记角速率Jacobian矩阵为Ji,即ΩiBi=Ji

分析易得,该受控系统共有13个自由度,本文选择无人机1的位置ξQ1G,2个无人机的欧拉角ηi和αi, βi作为系统的广义坐标,即q=[xQ1, yQ1, zQ1, ?1, θ1, ψ1, α1, β1, α2, β2, ?2, θ2, ψ2]T。
根据D’Alembert原理,与广义坐标相对应的广义力为
 | (3) |
式中:MQiηi=JiTMQiBi,由MQη·



因此,系统的动能和势能分别表示为
 | (4) |
式中:mP、mQ1和mQ2分别为吊挂负载、无人机1和无人机2的质量;IQ1和IQ2分别为无人机1和无人机2的转动惯量; g为重力加速度矢量。
Euler-Lagrange方程为
 | (5) |
将式(3)和式(4)代入式(5),可得
 | (6) |
式中:G=GT∈R13×13;g(F, q,
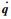
进一步,状态向量x∈R26可定义为[xQ1,



 | (7) |
1.2 平衡点分析和参数化线性模型 为了进行线性控制器设计,需要分析系统(无干扰项)的平衡点并建立对应的线性模型。
图 2为该系统的俯视图。当系统处于非平衡状态时,吊挂负载为P′;而当系统处于平衡状态时,无人机(Q1, Q2)和吊挂负载(P)将处于同一垂直平面内。同时,为了控制两无人机之间的相对位置关系保持不变,默认系统平衡时β1=β2=45°,定义αF为无人机队形方向角。
 |
| 图 2 带吊挂负载的四旋翼无人机(俯视) Fig. 2 Quadrotor UAVs carrying a cable-suspended payload (Top) |
| 图选项 |
给定系统的平衡点(xeq, ueq)之后,利用Taylor级数展开公式,可以得到依赖于队形方向角形αF的参数化线性模型为
 | (8) |
为了充分考虑不同无人机的性能差异,并能够在非合作博弈的框架下讨论,式(8)中的控制输入项可以拆成式(9)的形式:
 | (9) |
式中:Bu(αF)=[Bu1(αF), Bu2(αF)];uδ=[u1δT, u2δT]T。
2 有限时间开环纳什博弈 2.1 纳什博弈模型 在数字控制系统中,若控制器的工作频率为fs, 则动力学微分方程式(9)(不表示干扰输入项)可以改写成如式(10)差分形式:
 | (10) |
根据文献[17],可以将式(10)看成是有2个参与者的非合作动态博弈模型。根据参与者掌握的信息情况,该模型可以有不同的类型,比如斯塔伯格模型和纳什模型。本文采用纳什模型,即假定每个参与者同时知道自己和对方的目标函数。换言之,每个决策主体都希望从其可能的控制策略ui中,找出一个使其目标函数Γi最小的策略。很显然,当各决策主体的目标函数相同时,该问题就是一般的最优控制问题,而当目标函数不同时,则无法利用一般的最优控制来求解,此时,需要求出系统的纳什均衡。
所谓二人博弈的纳什均衡策略[18-19]是每个参与者对其他参与者的最优反应策略的集合,并且任一参与者单方面改变决策之后必然导致其目标函数变差,即
 | (11) |
式中:(u1, u2)为二人博弈的纳什均衡策略。
为了求出上述纳什均衡策略,需要事先确定参与者对过去状态信息的掌握情况。一般说来,在求解动态博弈模型第k步的控制策略时,存在如下3种情况[17]:
1) 完全信息结构:参与者知道系统过去的所有状态信息。
2) 反馈信息结构:参与者仅知道系统初始状态x[0]和当前状态x[j]。
3) 开环信息结构:参与者仅知道系统初始状态x[0]。
与完全信息结构相比,开环信息结构不需要存储过去所有的状态信息;与反馈信息结构相比,其问题的复杂程度较低[15]。因此,本文采用开环信息结构来求解纳什均衡,并进一步将其与滚动优化相结合使其仍然具有状态反馈的形式。
2.2 线性二次型开环纳什均衡解 考虑一个如式(10)的动态系统,其初始状态为x[0],2个决策主体的控制序列分别为u1[k]和u2[k],(0≤k≤N-1),当该控制序列作用于系统之后,可以为每个决策主体设计一个线性二次型目标函数:
 | (12) |
 | (13) |
此时,纳什均衡就是求出一系列控制序列组合(u1[k], u2[k]),使得各自的目标函数满足式(11)。根据文献[17],可以通过增广矩阵的形式将动态问题看成是静态博弈问题来求解,但是当增广矩阵的维度较高时会导致过多的存储需求,因此,本文采用如下迭代的方式来求解纳什均衡解。
给定任意初始值x[0],开环纳什均衡解:
 | (14) |
式中:u1, 2(k, x[0])为给定初始状态x[0]时,接下来N个时刻的纳什均衡控制策略;Hu1[k]和Hu2[k]由式(15)~式(18)逆序求出;ψ[k]在前者基础上,根据式(19)顺序求出:
 | (15) |
 | (16) |
 | (17) |
 | (18) |
式中:P1[N]=S1;P2[N]=S2。
 | (19) |
式中:ψ[0]=I。
纳什均衡解的存在性必要条件为,对所有的k、G1[k]、G2[k]、G1[k]-E1[k]G2-1[k]E2[k]和G2[k]-E2[k]G1-1[k]E1[k]都可逆。
3 控制器设计 3.1 滚动纳什控制器结构 为了将开环信息结构的纳什均衡解应用于动态系统中,本文借鉴模型预测控制中的滚动优化方法,设计一种状态反馈滚动纳什控制器。
假设当前时刻为j,此时系统的状态量为x[j],将x[j]看成是式(14)中的初始状态x[0] (当用于跟踪控制时,x[j]应为当前时刻状态与参考状态的差),求出从当前时刻j起接下来N步开环纳什均衡解,记作u1, 2[k, x[j]], 0≤j≤N-1,并将第一个值作为当前j时刻的控制量,即u1, 2*[x[j]]=u1, 2[0, x[j]]。
3.2 算法流程 若纳什控制器的滚动优化时长为TN,那么该控制器解的序列总长度为N=TNfs。类似的,若仿真总时长为TM,则仿真序列的总长度为M=TMfs。
因此,滚动纳什控制的算法流程如下:
仿真过程0≤k≤M,滚动周期0≤i≤N。
1) 读取当前时刻状态信息x[k]。
2) 将x[k]作为开环纳什均的初始状态信息,求出均衡解ui[i, x[k]]和相应的状态轨迹x[i, x[k]]。
3) 将开环纳什均衡解的第一个值ui[0, x[k]]用于[k, k+1]控制周期。
4) 令k←k+1,重复步骤1),直至k=M。
4 数值仿真 本节设计2个仿真实例来验证滚动纳什控制器的效果:第1个实例是无人机在有外部干扰的情况下控制系统保持平衡;第2个实例是在有外部扰动的情况下,无人机1跟踪参考轨迹,无人机2保持队形和稳定吊挂负载,并将该控制器与LQR进行了对比。这2个仿真实例的3D动画视频可参见相关链接(https://youtu.be/-0Nkp26EPGs)。
4.1 仿真设置 无人机吊挂系统的部分物理参数设定如下:
 |
为方便起见,本文不考虑队形变化的情况,即αF始终等于0°,因此可得系统平衡时的非零状态如下:α1=0°, β1=45°, θ1=8.74°, α2=180°, β2=45°, θ2=-8.74°, Fz1=Fz2=6.44 N。
目标函数中的权值矩阵类似于LQR控制器,需要根据各无人机控制目的进行设计。本文设定无人机1的任务主要是跟踪参考轨迹,而无人机2的任务主要是保持队形同时稳定吊挂负载。同时设定式(12)和式(13)中的相关权值矩阵均时不变,具体如下:
 |
其中:S1=Q1;S2=Q2;ρw1和ρw2用来调节状态/控制平衡。
为了与LQR控制器进行对比,需要将2个目标函数转变为一个目标函数,本文采用直接相加的方式,即Q=Q1+Q2, R=diag([R11, R22])。
本文仿真中,控制器的控制频率fs=50 Hz,纳什控制器的滚动优化时长TN=2 s,即N=100。
4.2 悬停抗干扰(情形1) 当2个四旋翼无人机与吊挂负载处于悬停平衡状态时,考虑外部有一个沿着y方向的干扰如图 3所示,该干扰由方波和白噪声叠加构成,沿着y方向作用在吊挂负载上。仿真时长TM=8 s,即M=400。
 |
| 图 3 作用在吊挂负载上的外部干扰 Fig. 3 Exogenous disturbances acting on cable-suspended payload |
| 图选项 |
应用滚动纳什控制器后,2个无人机会沿着y方向来回移动以稳定吊挂负载。无人机和吊挂负载的平面运动轨迹如图 4所示,各自y方向的位置误差如图 5所示。
 |
| 图 4 外部干扰下的运动轨迹(俯视) Fig. 4 Motion trajectories with exogenous disturbances (Top) |
| 图选项 |
 |
| 图 5 外部干扰下的y方向位置 Fig. 5 Position errors in y direction with exogenous disturbances |
| 图选项 |
由图 4和图 5可知,吊挂负载受到y轴方向的外部干扰后偏离平衡位置。因为无人机1的主要任务是稳定自身的位置,因此仍然保持较小的位置误差。而无人机2的任务是保持队形和稳定吊挂负载,因此它会沿着y轴方向快速移动来使系统尽快恢复平衡。
4.3 路径跟踪(情形2) 第2个仿真实例中,系统仍然存在一个外部扰动作用在吊挂负载上(仿真时间为30 s),但是此时无人机1的任务为跟踪一个“★”形参考轨迹,而无人机2负责跟踪无人机1以保持队形和稳定吊挂负载。仿真时长TM=30 s,即M=1 500。
在跟踪参考轨迹的过程中,当吊挂负载受到外部干扰时,其产生的摇摆运动必然会对无人机的性能产生负面影响。应用LQR控制器和滚动纳什控制器后,2个四旋翼无人机和吊挂负载的平面运动轨迹分别如图 6所示。
 |
| 图 6 跟踪参考轨迹(俯视) Fig. 6 Tracking a given trajectory (Top) |
| 图选项 |
由图 6可知,因为LQR控制器只是简单地将各目标函数相加,而未考虑无人机之间的互相影响,因此其效果比应用纳什控制器要差一些。而对于纳什控制器,通过合理地设置目标函数J1和J2之后,无人机1仍然能够较好地跟踪参考轨迹,与此同时,无人机2则能够通过不断调整自身位置的方式,一方面让吊挂负载可以从外部干扰的作用下重新恢复平衡,另一方面还能够跟踪无人机1并尽可能保持队形。
5 结论 1) 本文在非合作博弈的框架下对有2个四旋翼无人机的吊挂飞行系统进行研究,设计了一个基于状态反馈的滚动纳什控制器。
2) 该方法允许用户通过调节无人机的目标函数来设定不同的任务,比如,用户可以让一架无人机主要负责路径跟踪,另一架则负责保持队形和稳定吊挂负载。
3) 与只有一个目标函数的控制器相比,这种分布式的方法充分考虑无人机的差异性,因而使得系统有了更大的调节空间。
4) 本文主要针对线性时不变模型进行了仿真验证,在后续的工作中,将进一步应用于线性时变模型以及更多无人机的情况。
参考文献
| [1] | MATHEW N, SMITH S L, WASLANDER S L. Planning paths for package delivery in heterogeneous multirobot teams[J]. IEEE Transactions on Automation Science and Engineering, 2015, 12(4): 1298-1308. DOI:10.1109/TASE.2015.2461213 |
| [2] | ZHAN P, YU K, SWINDLEHURST A L. Wireless relay communications with unmanned aerial vehicles:Performance and optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 2068-2085. DOI:10.1109/TAES.2011.5937283 |
| [3] | DEBUSK W M.Unmanned aerial vehicle systems for disaster relief: Tornado alley[C]//Infotech@Aerospace Conferences.Reston: AIAA, 2010: 3506. https://www.researchgate.net/publication/264885840_Unmanned_Aerial_Vehicle_Systems_for_Disaster_Relief_Tornado_Alley |
| [4] | TANG S, SREENATH K, KUMAR V.Aggressive maneuvering of a quadrotor with a cable-suspended payload[C]//Robotics: Science and Systems, Workshop on Women in Robotics, 2014. |
| [5] | SREENATH K, LEE T, KUMAR V.Geometric control and differential flatness of a quadrotor UAV with a cablesuspended load[C]//52nd IEEE Conference on Decision and Control.Piscataway, NJ: IEEE Press, 2013: 2269-2274. https://www.researchgate.net/publication/271549811_Geometric_control_and_differential_flatness_of_a_quadrotor_UAV_with_a_cable-suspended_load |
| [6] | TANG S, KUMAR V.Mixed integer quadratic program trajectory generation for a quadrotor with a cable-suspended payload[C]//IEEE International Conference on Robotics and Automation (ICRA).Piscataway, NJ: IEEE Press, 2015: 2216-2222. https://www.researchgate.net/publication/283231367_Mixed_Integer_Quadratic_Program_trajectory_generation_for_a_quadrotor_with_a_cable-suspended_payload |
| [7] | DE C, FARSHIDIAN F, BUCHLI J.Aggressive optimal control for agile flight with a slung load[C]//IROS 2014 Workshop on Machine Learning in Planning and Control of Robot Motion.Piscataway, NJ: IEEE Press, 2014. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.713.9357 |
| [8] | 鲜斌, 张旭, 杨森. 无人机吊挂飞行的非线性控制方法设计[J]. 控制理论与应用, 2016, 33(3): 273-279. XIAN B, ZHANG X, YANG S. Nonlinear controller design for an unmanned aerial vehicle with a slung-load[J]. Control Theory & Application, 2016, 33(3): 273-279. (in Chinese) |
| [9] | 李伟荣, 方舟, 李诚龙. 带悬挂负载的八旋翼无人机建模与控制[J]. 计算机应用, 2015, 35(S2): 138-142. LI W R, FANG Z, LI C L. Modeling and control of unmanned octocopter with slung load[J]. Journal of Computer Applications, 2015, 35(S2): 138-142. (in Chinese) |
| [10] | YI K, GU F, YANG L.Sliding mode control for a quadrotor slung load system[C]//Proceedings of the 36th Chinese Control Conference.Piscataway, NJ: IEEE Press, 2017: 3967-3703. https://www.researchgate.net/publication/320114768_Sliding_mode_control_for_a_quadrotor_slung_load_system |
| [11] | GUO M, SU Y, GU D.Mixed H2/H∞ tracking control with constraints for single quadcopter carrying a cable-suspended payload[C]//IFAC-PapersOnLine.Toulous: Elsevier, 2017, 50(1): 4869-4874. https://www.sciencedirect.com/science/article/pii/S2405896317314490 |
| [12] | SREENATH K, KUMAR V.Dynamics, control and planning for cooperative manipulation of payloads suspended by cables from multiple quadrotor robots[C]//Robotics: Science and Systems, 2013. https://core.ac.uk/display/22717635 |
| [13] | LEE T. Geometric control of quadrotor UAVs transporting a cablesuspended rigid body[J]. IEEE Transactions on Control Systems Technology, 2018, 26(1): 255-264. DOI:10.1109/TCST.2017.2656060 |
| [14] | MARTIN J O, ARIEL R.博弈论教程[M].魏玉根, 译.北京: 中国社会科学出版社, 2000: 1-2. MARTIN J O, ARIEL R.A course in game theory[M].WEI Y G, translated.Beijing: China Social Sciences Press, 2000: 1-2(in Chinese). |
| [15] | GU D. A differential game approach to formation control[J]. IEEE Transactions on Control Systems Technology, 2008, 16(1): 85-93. DOI:10.1109/TCST.2007.899732 |
| [16] | MYLVAGNAM T, ASTOLFI A.A differential game approach to formation control for a team of agents with one leader[C]//American Control Conference (ACC).Piscataway, NJ: IEEE Press, 2015: 1469-1474. https://www.researchgate.net/publication/282937833_A_differential_game_approach_to_formation_control_for_a_team_of_agents_with_one_leader |
| [17] | RAIMO P H. Nash and Stackelberg solutions to general linearquadratic two player difference games.Ⅰ.Open-loop and feedback strategies[J]. Kybernetika, 1978, 14(1): 38-56. |
| [18] | BASAR T, OLSDER G J. Dynamic noncooperative game theory[M]. 2nd ed. Philadelphia: SIAM, 1998: 97-100. |
| [19] | ENGWERDA J. LQ dynamic optimization and differential games[M]. New York: Wiley, 2005: 261-263. |
