UMAC对精密伺服运动轴的控制主要采用传统的PID控制,这种控制方法原理比较简单,使用起来相对方便;同时它具有一定的自适应性和鲁棒性,常常被应用于各类工业环境[3-4]。然而,精密伺服运动控制场合对控制品质要求高,传统的PID控制很难适应由运动结构变化引起参数摄动、蠕变等,再加上运动系统负载的变化和干扰的存在,使获取高的控制品质变得更加困难[5-6]。针对这一问题,目前主要采用的方法是将模糊理论引入到UMAC的PID参数调节上,优化原传统的PID控制器,提高伺服系统控制品质。如白晶、王克选等将模糊控制与传统的PID控制相结合,设计了一种模糊PID控制器,基于被控对象的实时状态来动态调节PID控制器的参数[7-9]。模糊PID控制在一定程度上加强了系统的自适应性和鲁棒性,提高了被控系统的动静态性能,然而该方法在隶属度函数的选取方面需要经验,其使用规则比较复杂。
为了解决目前控制方法下系统自适应性和鲁棒性不强,动静态性能不理想的问题,本文提出了将径向基函数(RBF)神经网络引入到UMAC中PID控制器的参数调节上。RBF神经网络是一种高效的前馈式神经网络,其具有强大的非线性映射能力,同时能够自主学习、调整自适应于环境变化。在对模型进行训练的过程中,它能最佳地逼近于实际(线性/非线性)模型并获取全局最优解。同时,相较于模糊理论,不需要隶属度函数调节经验并且使用规则简便,因此被广泛应用于模型预测[10-12]。
在利用RBF神经网络PID进行控制的过程中,本文首先利用RBF神经网络对被控对象模型进行实时动态预测,然后根据预测结果对UMAC的PID控制器的3个参数Kp(比例增益Ixn30)、Ki(积分增益Ixn33)、Kd(微分增益Ixn31)进行动态调整,实现了伺服系统的自适应性和鲁棒性加强,以及动静态性能的提高。
1 系统描述 1.1 基于UMAC的伺服系统 图 1为基于UMAC的伺服系统结构。在该系统中,工控机负责向UMAC发送位置控制指令,UMAC负责接收伺服电机实际位置和指令位置,做差值比较并向伺服驱动器发送伺服电机转动方向和脉冲信息,驱动设备则根据脉冲和方向信息对信号进行SVPWM调制,驱动伺服电机转动。
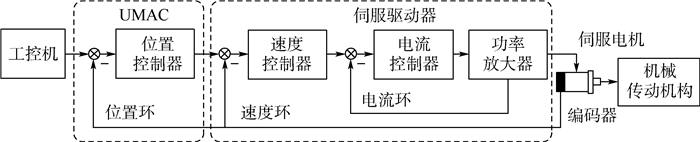 |
| 图 1 基于UMAC的伺服系统结构 Fig. 1 Structure of servosystem based on UMAC |
| 图选项 |
1.2 PMSM数学模型及仿真模型的建立 PMSM数学模型是在不影响控制性能前提下,忽略电机铁心的饱和,永磁材料导磁率为零,不计涡流和磁滞损耗,三相绕组是对称均匀的,绕组中感应电势波形是正弦波的条件下建立的[13-15]。
在假设条件下,PMSM的转子为圆筒形(Ld=Lq=L),Ld、Lq为d-q轴定子电感,得到d-q旋转坐标系下PMSM的状态方程为
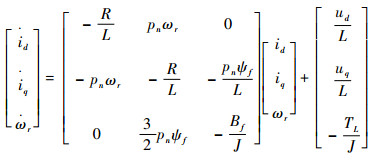 | (1) |
式中:R为电枢绕组电阻;ud、uq为d-q轴定子电压;id、iq为d-q轴定子电流;ψf为转子磁场等效磁链;J为转动惯量;Bf为黏滞摩擦系数;ωr为转子角速度;ω=pnωr为转子电角速度,pn为极对数;TL为负载扰动。
采用id≡0的控制方式得PMSM的解耦线性状态方程为
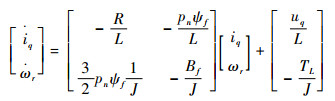 | (2) |
根据式(2)建立PMSM传递模型,如图 2所示。
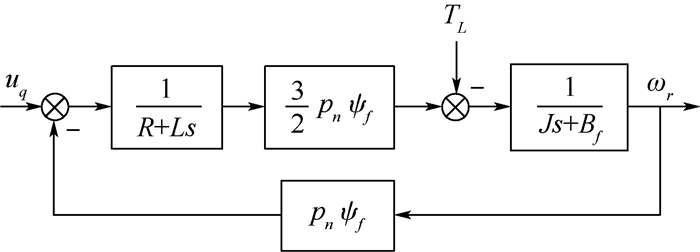 |
| 图 2 PMSM传递模型 Fig. 2 Transfer model of PMSM |
| 图选项 |
2 仿真分析 2.1 RBF神经网络PID控制原理 RBF神经网络是由Moody和Darken[16]在20世纪80年代末提出的一种神经网络,其是具有单隐层的三层前馈网络。由于模拟了人脑中局部调整、相互覆盖接受域的神经网络结构,因此,RBF神经网络是一种局部逼近网络,已证明它能以任意精度逼近任意连续函数[17]。
2.1.1 网络结构 RBF神经网络是一种三层前向网络,如图 3所示,由输入到输出的映射是非线性的,而隐含层到输出空间的映射是线性的,从而大大加快了学习速度并避免局部极小问题。
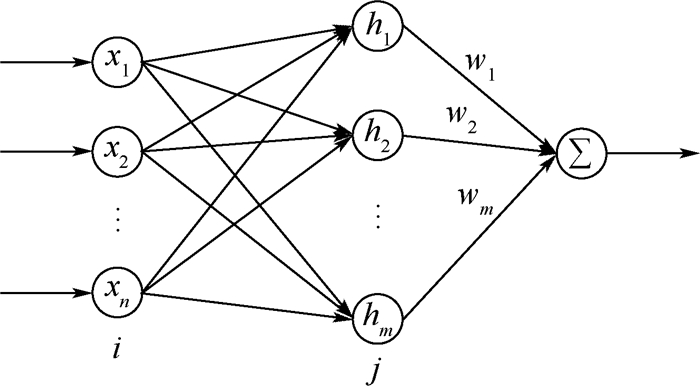 |
| 图 3 RBF神经网络结构 Fig. 3 Structure of RBF neural network |
| 图选项 |
2.1.2 被控对象Jacobin信息的辨识算法 在RBF神经网络结构中,x=[x1, x2, …, xn]T为网络的输入向量。设RBF神经网络的径向基向量h=[h1, h2, …, hm]T,hj为高斯基函数。
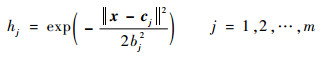 | (3) |
式中:cj=[cj1, cj2, …, cji, …, cjn]T(i=1, 2, …, n)为网络的第j个节点的中心矢量;bj为节点j的基宽度参数,且为大于零的数。
设神经网络的基宽向量为
 | (4) |
神经网络的权向量为
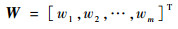 | (5) |
辨识神经网络的输出为
 | (6) |
辨识器的性能指标函数为
 | (7) |
根据梯度下降法,输出权、节点中心及节点基宽度参数的迭代算法如下:
 | (8) |
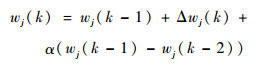 | (9) |
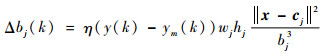 | (10) |
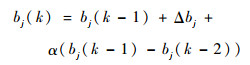 | (11) |
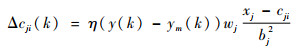 | (12) |
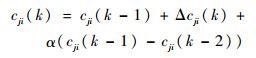 | (13) |
式中:η为学习速率;α为动量因子。
Jacobin阵(即为对象的输出对控制输入变化的灵敏度信息)算法为
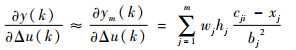 | (14) |
式中:xj=Δu(k)。
控制器的输入误差为
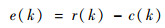 | (15) |
式中:r(k)为系统输入;c(k)为系统输出。
RBF神经网络的整定指标为
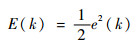 | (16) |
比例增益Kp、积分增益Ki、微分增益Kd采用梯度下降法进行调整:
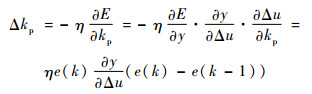 | (17) |
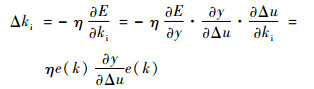 | (18) |
 | (19) |
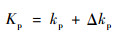 | (20) |
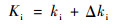 | (21) |
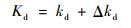 | (22) |
式中:kp、ki、kd为PID整定的初值;
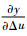
在MATLAB/Simulink下,利用S-函数对RBF神经网络PID控制算法进行编程实现,并将其引入到对PMSM的控制中得到基于RBF神经网络PID控制的PMSM伺服仿真模型,如图 4所示。图中:Kω为速度放大器的增益;Kpf、Kωf分别为位置、速度反馈增益。
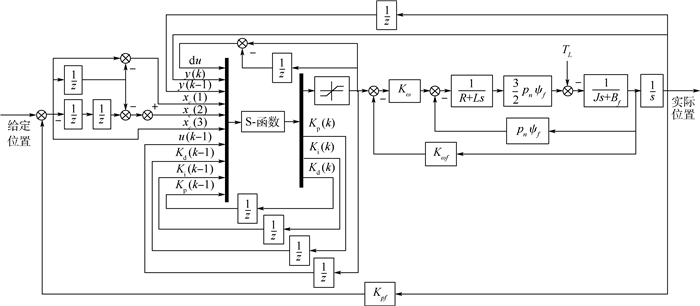 |
| 图 4 RBF神经网络PID控制的PMSM伺服仿真模型 Fig. 4 Servo simulation model of PMSM based on RBF neural network tuning PID control |
| 图选项 |
2.2 仿真实验及结果分析 根据某型PMSM电机,设置仿真参数R=0.012 07 Ω,L=2.79 mH,pn=4,ψf=0.076 45 Wb,Bf=0.000 1 N/(m/s)。给定幅值为1 000 counts的阶跃位置信号,并在t=1 s处给定负载扰动信号TL=0.2 N·m,得到传统PID控制、模糊PID控制和RBF神经网络PID控制下的位置阶跃响应曲线如图 5所示。图中:tr1、tr2、tr3分别为传统PID控制、模糊PID控制和RBF神经网络PID控制下的位置阶跃响应上升时间;ts1、ts2、ts3分别为传统PID控制、模糊PID控制和RBF神经网络PID控制下的位置阶跃响应调节时间(2%)。
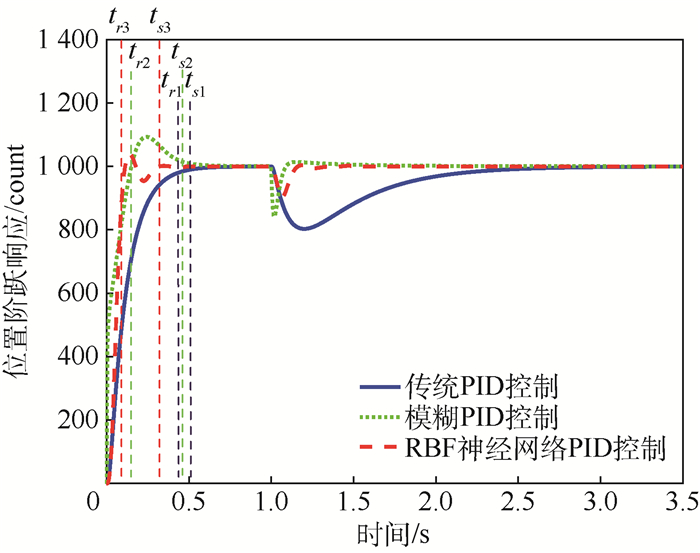 |
| 图 5 传统PID控制、模糊PID控制、RBF神经网络PID控制下位置阶跃响应曲线 Fig. 5 Step response of position by traditional PID control, fuzzy PID control and RBF neural network tuning PID control |
| 图选项 |
通过仿真结果对比可知,相较于传统的PID控制和模糊PID控制,RBF神经网络PID控制响应时间快,调节时间短;在外加扰动情况下,RBF神经网络PID控制仍能很好地对输入信号进行跟随,具有较强的自适应性和鲁棒性。
利用RBF神经网络对PID控制器参数进行调节可以解决现有UMAC中自适应性和鲁棒性差、系统动静态性能不理想的问题,因此将RBF神经网络方法引入UMAC的PID参数调节中,下面将基于嵌入式PLC对该算法进行实现。
3 控制实现 3.1 UMAC的PID控制器 UMAC提供了带有速度和加速度前馈的PID+陷波滤波控制器,使用者可以针对被控对象的要求直接对相应的参数进行调节,从而达到控制系统所需要的性能[18]。UMAC的PID控制器原理如图 6所示。
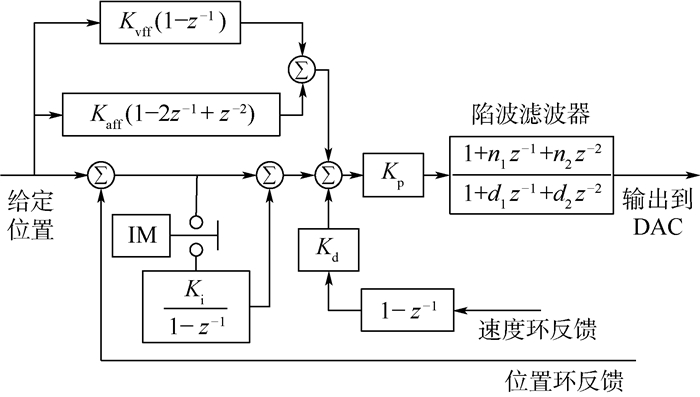 |
| 图 6 UMAC的PID算法原理图 Fig. 6 PID algorithm schematic diagram of UMAC |
| 图选项 |
图 6中:IM为积分模式(Ixn34);Kvff为速度前馈增益(Ixn32);Kaff为加速度前馈增益(Ixn35)。陷波滤波器的系数分别为:n1为Ixn36;n2为Ixn37;d1为Ixn38;d2为Ixn39(I为UMAC的设置变量,xn为对应的电机编号)。由图 6可以推出控制器的输出为
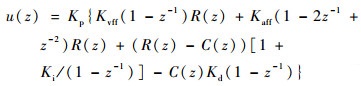 | (23) |
式中:R(z)为给定位置;C(z)为实际反馈位置。
在此,忽略陷波滤波器对UMAC的影响,可以得出UMAC主要由常规的PID控制器部分和速度、加速度部分组成。
3.2 PLC程序的设计与实现 在利用RBF神经网络实现对UMAC的PID参数的调整上,主要通过UMAC的嵌入式PLC程序实现。UMAC的嵌入式PLC程序可以通过反馈通道实时地获取位置反馈,再与给定位置进行比较获取位置误差,根据位置误差再相应地对UMAC的3个PID参数比例增益Kp、积分增益Ki、微分增益Kd进行调整,其具体实现步骤如下:
步骤1?首先,根据手动整定信息,设置kp、ki、kd的初值;然后,设置RBF神经网络的输入层节点数n、隐含层节点数m、学习速率η、动量因子α。
步骤2?采样获取r(k)、c(k)的值,计算e(k)=r(k)-c(k)。
步骤3?对RBF神经网络的输入层参数进行归一化处理,包括u(k)-u(k-1),c(k),c(k-1),e(k)-e(k-1),e(k),e(k)-2e(k-1)+e(k-2),u(k-1),Kp(k-1),Ki(k-1),Kd(k-1)。
步骤4?根据梯度下降法,对输出权wj(k)、节点中心cji(k)及节点基宽度参数bj(k)进行迭代计算。
步骤5?计算待预测模型的Jacobian信息。
步骤6?采用梯度下降法计算Δkp、Δki、Δkd及Kv(k)、Ki(k)、Kd(k),返回步骤2。
以上步骤可由图 7来表示。
 |
| 图 7 RBF神经网络PID控制PLC程序流程图 Fig. 7 PLC program flowchart of RBF neural network tuning PID control |
| 图选项 |
4 实验验证 图 8为精密装配系统,其主要由多轴协同运动精密装配平台和以UMAC为核心的控制系统组成。
 |
| 图 8 精密装配系统 Fig. 8 Precise assembly system |
| 图选项 |
图 9为精密装配系统下基于UMAC的单轴伺服运动实验子系统。该实验子系统主要由PC、UMAC、某型伺服电机、24 V开关电源和中间继电器等部分组成。
 |
| 图 9 基于UMAC的伺服系统 Fig. 9 Servosystem based on UMAC |
| 图选项 |
在实验子系统下,分别进行了传统PID控制、模糊PID控制和RBF神经网络PID控制下的伺服系统位置阶跃响应实验和正弦跟踪实验,并对伺服电机期望转动位置、实际转动位置和跟随误差进行了实时采集。
1) 给定的阶跃位置信号为
 | (24) |
式中:A1为阶跃信号幅值,取1 000 counts;T1为阶跃信号保持时间,取500 ms。
由图 10可知,RBF神经网络PID控制下的伺服电机位置阶跃响应上升时间由传统PID控制下的0.164 s和模糊PID控制下的0.118 s减小到了0.017 s,峰值时间由传统PID控制下的0.196 s和模糊PID控制下的0.131 s减小到了0.023 s,调节时间由传统PID控制下的0.216 s和模糊PID控制下的0.142 s减小到了0.025 s(1%),电机响应速度变快。
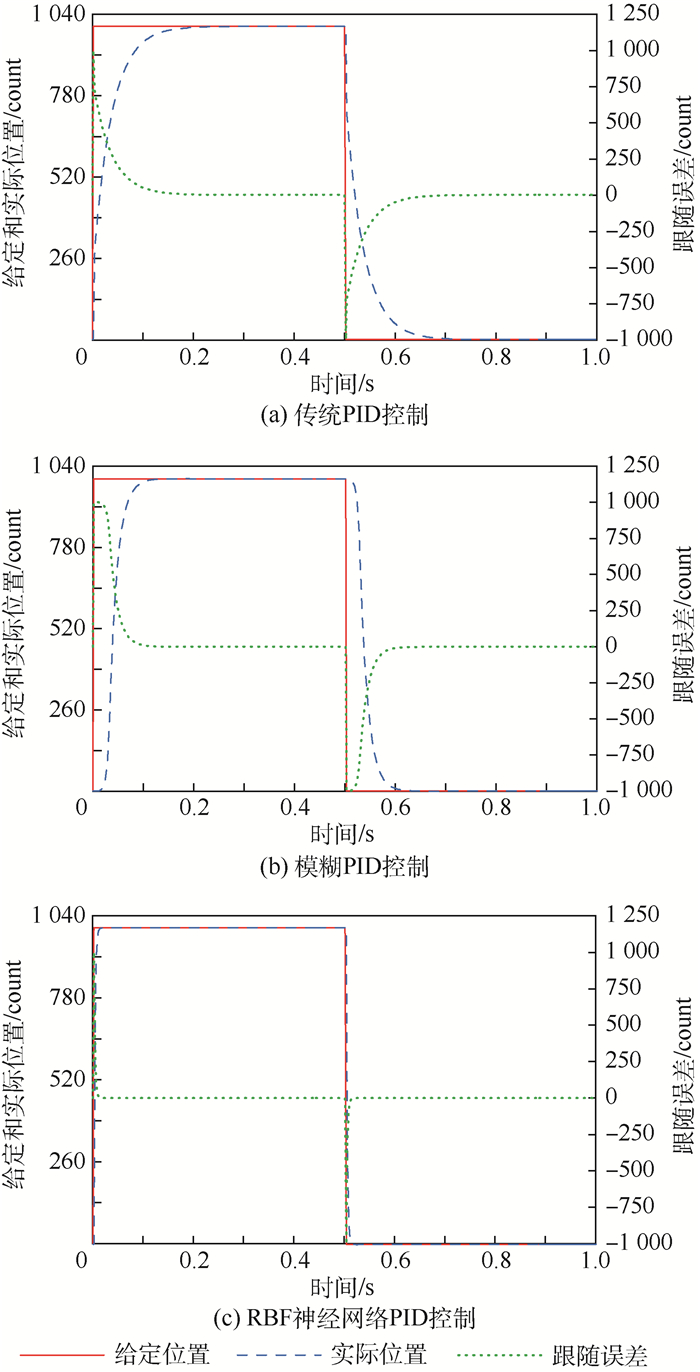 |
| 图 10 给定位置条件下位置阶跃响应曲线 Fig. 10 Position step response curves under given position condition |
| 图选项 |
2) 给定的正弦位置信号为
 | (25) |
式中:A2为正弦信号幅值,取1 000 counts;f为正弦信号频率,取1 Hz。正弦信号重复周期数为2。
通过对比传统PID控制、模糊PID控制、RBF神经网络PID控制下伺服电机位置正弦响应曲线(见图 11),RBF神经网络PID控制下的位置动态跟随最大误差由传统PID控制下的188 counts和模糊PID控制下的120 counts减小到了39 counts,且误差波动较小,平稳性更好,电机动态跟随性能显著提高。
 |
| 图 11 给定位置条件下位置正弦响应曲线 Fig. 11 Position sinusoidal response curves under given position condition |
| 图选项 |
根据位置阶跃响应实验和正弦跟踪实验结果可知,与传统的PID控制和模糊PID控制相比,RBF神经网络PID控制可以有效地提高被控伺服电机的动静态性能,提升控制品质。
5 结论 本文基于UMAC,将RBF神经网络引入到了PID控制器的参数调节上,对伺服电机进行了控制。
1) 通过仿真实验对比可知,相较于传统的PID控制和模糊PID控制,RBF神经网络PID控制响应时间快,调节时间短;在外加扰动情况下,RBF神经网络PID控制仍能很好地对输入信号进行跟随,具有较强的自适应性和鲁棒性。
2) 通过位置阶跃响应实验可知,RBF神经网络PID控制下的伺服电机位置阶跃响应上升时间由传统PID控制下的0.164 s和模糊PID控制下的0.118 s减小到了0.017 s, 峰值时间由传统PID控制下的0.196 s和模糊PID控制下的0.131 s减小到了0.023 s,调节时间由传统PID控制下的0.216 s和模糊PID控制下的0.142 s减小到了0.025 s(1%),电机响应速度变快。
3) 通过正弦跟踪实验可知,RBF神经网络PID控制下的位置动态跟随最大误差由传统PID控制下的188 counts和模糊PID控制下的120 counts减小到了39 counts,且误差波动较小,平稳性更好,电机动态跟随性能显著提高。
RBF神经网络PID控制有效地提高了基于UMAC的电机伺服系统的动静态性能,提升了系统的控制品质。
参考文献
| [1] | 夏链, 俞晓慧, 韩江, 等. 基于UMAC的工业机器人运动控制系统设计[J]. 合肥工业大学学报(自然科学版), 2015, 38(8): 1009-1012. XIA L, YU X H, HAN J, et al. Design of motion control system of industrial robot based on UMAC[J]. Journal of Hefei University of Technology(Natural Science), 2015, 38(8): 1009-1012. DOI:10.3969/j.issn.1003-5060.2015.08.001 (in Chinese) |
| [2] | SPIESER A, IVANOV A. Design of an electrochemical micromachining machine[J]. International Journal of Advanced Manufacturing Technology, 2015, 78(5-8): 737-752. DOI:10.1007/s00170-014-6332-3 |
| [3] | 刘金琨. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2011: 301-319. LIU J K. MATLAB simulmion of advanced PID control[M]. Beijing: Electronic Industry Press, 2011: 301-319. (in Chinese) |
| [4] | 赵凤姣, 厉虹. PID控制器改进方法研究[J]. 控制工程, 2015, 22(3): 425-431. ZHAO F J, LI H. Research on improved methods of PID controller[J]. Control Engineering of China, 2015, 22(3): 425-431. (in Chinese) |
| [5] | 廖洪波, 范世珣, 黑墨, 等. 光电稳定平台伺服系统动力学建模与参数辨识[J]. 光学精密工程, 2015, 23(2): 477-484. LIAO H B, FAN S X, HEI M, et al. Modeling and parameter identification for electro-optical stabilized platform servo systems[J]. Optics and Precision Engineering, 2015, 23(2): 477-484. (in Chinese) |
| [6] | HUANG W L, KUO F C, CHOU S C, et al. High-performance and high-precision servo control of a single-deck dual-axis PMLSM stage[J]. International Journal of Advanced Manufacturing Technology, 2017, 90(1-4): 865-874. DOI:10.1007/s00170-016-9355-0 |
| [7] | 王克选, 李新国. 基于PMAC的模糊自整定PID算法设计[J]. 计算机仿真, 2013, 30(9): 331-334. WANG K X, LI X G. Design of fuzzy self-regulation PID algorithm based on PMAC[J]. Computer Simulation, 2013, 30(9): 331-334. DOI:10.3969/j.issn.1006-9348.2013.09.077 (in Chinese) |
| [8] | 白晶, 于喜红, 秦现生. 基于PMAC的码垛机器人模糊PID算法研究[J]. 机械设计与制造工程, 2016, 45(3): 46-49. BAI J, YU X H, QIN X S. Study on fuzzy PID algorithm for palletizing robot based on PMAC[J]. Machine Design and Manufacturing Engineering, 2016, 45(3): 46-49. DOI:10.3969/j.issn.2095-509X.2016.03.010 (in Chinese) |
| [9] | TIAN C X, LI X W, HU Z. The study of fuzzy self-regulation PID algorithm based on PMAC[J]. Machinery & Electronics, 2010, 57(10): 60-63. |
| [10] | SONG Y, LIU Y, ZHU H. A PMSM speed controller based on RBF neural network and single neuron PID[J]. Electronics World, 2017, 38(2): 122-126. |
| [11] | 江维, 吴功平, 曹琪, 等. 输电线路带电作业机器人机械手RBF神经网络控制[J]. 东北大学学报(自然科学版), 2017, 38(10): 1388-1393. JIANG W, WU G P, CAO Q, et al. RBF neural network control of live operation robot manipulator for high voltage transmission line[J]. Journal of Northeastern University(Natural Science), 2017, 38(10): 1388-1393. DOI:10.12068/j.issn.1005-3026.2017.10.005 (in Chinese) |
| [12] | 周佳, 卢少武, 周凤星. 伺服位置控制参数的RBF神经网络自整定研究[J]. 组合机床与自动化加工技术, 2016(3): 75-77. ZHOU J, LU S W, ZHOU F X. Study on position control parameters auto-tuning of servo system based on RBF neural network[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(3): 75-77. (in Chinese) |
| [13] | 舒志兵, 周玮, 李运华. 交流伺服运动控制系统[M]. 北京: 清华大学出版社, 2006: 66-82. SHU Z B, ZHOU W, LI Y H. AC servo motion control system[M]. Beijing: Tsinghua University Press, 2006: 66-82. (in Chinese) |
| [14] | ABU-RUB H, IQBAL A, GUZINSKI J. High performance control of AC drives with MATLAB/Simulink models[M]. New York: Wiley, 2012. |
| [15] | KUNG Y S, NGUYEN V Q, HUANG C C, et al.Simulink/ModelSim co-simulation of sensorless PMSM speed controller[C]//Industrial Electronics and Applications.Piscataway, NJ: IEEE Press, 2012: 1405-1410. |
| [16] | DARKEN C, MOODY J.Fast adaptive k-means clustering: Some empirical results[C]//IJCNN International Joint Conference on Neural Networks.Piscataway, NJ: IEEE Press, 1990: 233-238. |
| [17] | 李文鹏.基于UMAC的超精密机床数控系统设计及参数自整定研究[D].哈尔滨: 哈尔滨工业大学, 2016: 45-57. LI W P.Design of ultra-precision machine tool numerical control system and auto-tuning for parameter based on UMAC[D].Harbin: Harbin Institute of Technology, 2016: 45-57(in Chinese). |
| [18] | 吴晓明, 马立廷, 郑协, 等. 改进的RBF神经网络PID算法在电液伺服系统中应用[J]. 机床与液压, 2015, 43(11): 63-66. WU X M, MA L T, ZHENG X, et al. Improved RBF neural network PID control strategy used in electro-hydraulic servo system[J]. Machine Tool & Hydraulics, 2015, 43(11): 63-66. DOI:10.3969/j.issn.1001-3881.2015.11.018 (in Chinese) |
