因此,本文设计了基于负载转矩变化率自适应估计的二阶终端滑模转速控制器,相比于普通滑模控制,实现了快速响应,改善了状态渐近收敛的特性,能够在有限时间内进行收敛,提高了控制精度,增强了系统鲁棒性,同时无需知道负载扰动界限,实现了负载扰动的鲁棒性。在增强系统鲁棒性的同时,考虑到在电机换相时转矩脉动较大的缺点,将传统的6个扇区进行细分,增加了电压矢量,在一定程度上减少了换相过程中产生的转矩脉动。本文从鲁棒性和转矩脉动2个角度提升SRM-DTC的性能,仿真和实验结果表明,改进的DTC系统可以实现高精度、快响应的控制效果,可进一步减少转矩脉动,增强系统鲁棒性。
1 SRM-DTC系统 SRM-DTC系统框图如图 1所示[11],主要由SRM、电压矢量开关表模块、区间判断模块、功率变换器等组成,采用双闭环控制结构,外环是速度环,通过调节得到系统参考转矩,内环是转矩环,将转矩误差、磁链误差和区间信号通过DTC原理转换为控制功率变换器的通断信号,实现对电机的控制。
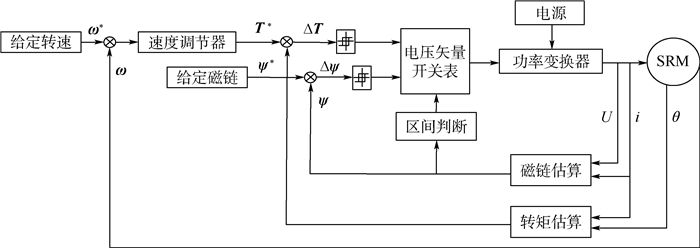 |
| 图 1 SRM-DTC系统框图 Fig. 1 Block diagram of SRM-DTC system |
| 图选项 |
根据文献[12]的公式,有
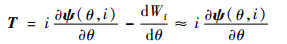 | (1) |
式中:T为瞬时转矩;Wf为磁场储能;θ为转子位置角;ψ为定子磁链;i为绕组电流。
由式(1)可知,在保持ψ幅值恒定的基础上,通过控制磁链的加速或者减速,来控制转矩的变化。SRM的电压方程为[12]
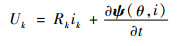 | (2) |
式中:Uk、Rk和ik分别为k相绕组的电压、电阻和电流。
忽略绕组电阻压降,并进行离散化处理,得
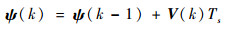 | (3) |
式中:V(k)为电压矢量。
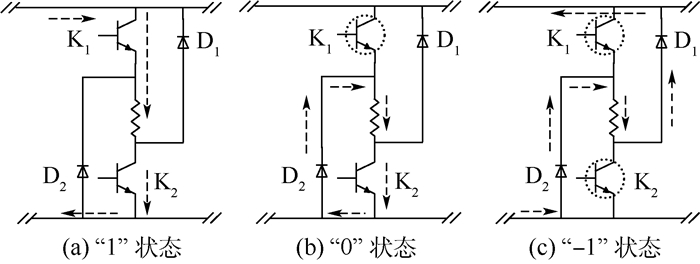
由式(3)可知,通过选择电压矢量来控制ψ幅值增加或者减小,从而实现直接控制转矩。定子绕组有3种通电状态,即正电压(用“1”状态表示)、负电压(用“-1”状态表示)和零电压(用“0”状态表示),如图 2所示。
 |
| 图 2 相绕组功率管开关状态设定 Fig. 2 Switch state setting of phase winding power tube |
| 图选项 |
当电机处于“1”状态时,K1、K2导通,相绕组承受正向电压。当电机处于“0”状态时,K1、K2只有一个导通,相绕组承受零电压,在回路中电流缓慢下降。当电机处于“-1”状态时,相绕组承受负电压,绕组上的电流迅速下降为零。每相绕组电压矢量可选择3种状态,三相绕组总共可以选择27种状态,可选取适当电压矢量控制电机磁链和转矩增量变化。SRM直接转矩控制电压矢量选取原则如表 1所示。
表 1 电压矢量选取规则 Table 1 Voltage vector selection principle
| 转矩和磁链变化 | 电压矢量 |
| T↑, ψ↑ | VN+1 |
| T↑, ψ↓ | VN+2 |
| T↓, ψ↑ | VN-1 |
| T↓, ψ↓ | VN-2 |
表选项
空间上各相磁链夹角相差120°,因此将其转换到α-β坐标。
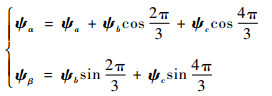 | (4) |
因此定子磁链为
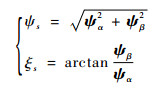 | (5) |
式中:ψs和ξs分别为磁链幅值和相角。
通过ξs对磁链所在的相位进行判断,从而选定电压矢量所在的扇区。给定转速,通过转速调节器得到的参考转矩和实际转矩作差,经过滞环控制得到转矩变换信号,参考磁链与实际磁链作差,经过滞环控制得到磁链变换信号,与ξs一起进行逻辑综合,得到功率变换器各开通角的开关信息,实现对SRM的控制。
2 基于负载转矩变化率自适应估计的二阶终端滑模转速控制器设计 传统的SRM-DTC系统采用PI控制器对转速进行精确跟踪,但是由于PI控制器存在鲁棒性差、不适合应用于非线性系统等缺点。在非线性控制方法中,由于滑模变结构控制对非线性扰动具有很好的鲁棒性[13-14],本文设计了二阶终端滑模转速控制器,提高了控制精度,增加了系统的鲁棒性,实现了转矩快速响应,使得在有限时间内系统可以迅速收敛到平衡点。
在设计SRM-DTC系统时,要充分考虑到系统中非线性扰动对控制性能的影响。SRM是一个多变量耦合的高度非线性系统,建模时存在误差,同时其绕组电阻也会随着温度变化而变化。由此导致的非线性扰动表现为慢变性,可以通过对模型参数依赖不高的二阶终端滑模转速控制器进行消除。
负载转矩的变化对系统控制性能造成很大的影响,其变化具有非线性和不确定性,在设计控制器时要充分考虑负载扰动的因素。因此增加负载转矩变化率自适应估计,在保持系统鲁棒性的基础上,实现了无需知道负载转矩扰动界限,同时减小了切换增益,对负载扰动进行抑制。
控制目标是对转速的精确跟踪,使得输出平滑的给定转矩,同时对负载扰动具有抗干扰能力。由SRM机械方程可得[15]
 | (6) |
经变换后
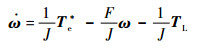 | (7) |
式中:ω为电机转速;F为阻尼系数;J为转动惯量;Te为电机的电磁转矩;TL为负载转矩。
设给定转速为ω*,该转速具有二阶连续导数,而且足够平滑,Te*为给定转矩。定义转速误差为
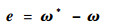 | (8) |
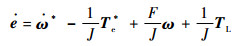 | (9) |
设计系统的滑模面为
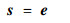 | (10) |
选取终端滑模函数为
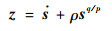 | (11) |
式中:ρ>0;p、q为正奇数,且0 < q/p < 1。
则由终端滑模面z=0可知:
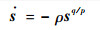 | (12) |
求解式(12)可得
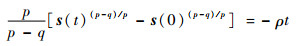 | (13) |
进一步求解式(13),可得系统从s(0)≠0到s(0)=0的时间ts为
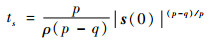 | (14) |
式中:ts为从系统到达滑模面开始一直到到达平衡点的时间。有限时间包括两部分:一个是ts,另一个是任意初始状态到达滑模面的时间tr。通过设计合适的滑模控制律使终端滑模面在有限时间收敛为零,从而使得误差状态e、?和?到达平衡点。
控制器采用指数趋近律,考虑到符号函数在工程中难以实现和避免在滑模面的附近出现高频切换从而引起系统出现抖振,符号函数sgn(z)用|z|βsgn(z)来代替,0 < β < 1,以减小系统抖振,提高控制性能。
当|z|>1时,系统会以较快的速度趋近滑模面,|z|βsgn(z)的控制作用更加明显;而当0 < |z| < 1时,

 | (15) |
对式(9)进行求导
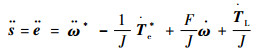 | (16) |
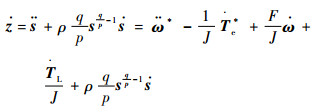 | (17) |
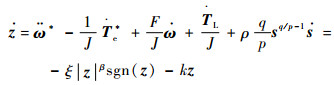 | (18) |
由式(18)设计滑模控制律Te*=Tem+Ten。
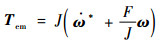 | (19) |
Ten由积分获得
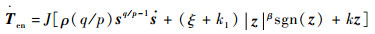 | (20) |
式中:ξ、k、k1、β为设计参数,k1为符号函数增益,取决于负载扰动的大小,满足k1>J-1(?L)。
由式(20)可得,若要求该控制器对负载扰动有足够的鲁棒性,必须满足k1>J-1(?L)。因此设计时必须知道负载转矩扰动界限的条件,而且该控制器使用大的切换增益才使得系统稳定,这会影响控制量平稳无抖振的控制效果。因此,本文在控制器的基础上增加负载转矩变化率自适应估计,在保持系统鲁棒性的基础上,无需知道负载转矩扰动界限,同时减小了切换增益。
由于负载扰动具有低频特性,Ten经过低通滤波并结合式(18)可以得到
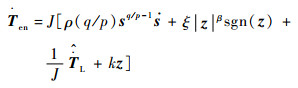 | (21) |
设计负载转矩扰动估计量为:
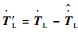

通过对负载扰动进行估计,不必知道负载扰动的上界,减小了切换函数的增益,通过终端滑模控制方式能准确输出平滑的给定转矩,提高了SRM-DTC系统的鲁棒性和抗干扰能力。
证明?选取Lyapunov函数为
 | (22) |
对时间求导得到
 | (23) |
相对于设计的负载转矩估计值而言,实际的负载转矩变化比较慢,可以认为实际的负载转矩是慢变信号,即满足
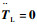
 | (24) |
由式(24)可知,当?=0时,
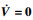
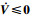
3 基于扇区细分优化的电压矢量选取方式 由式(3)得磁链幅值的变化量为
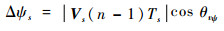 | (25) |
式中:θvψ为合成磁链与电压矢量夹角。
由表 1可知,VN+1电压矢量可使合成磁链幅值增加,VN+2则可使之减小。合成磁链幅值增加减小量分别为
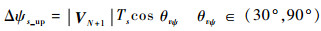 | (26) |
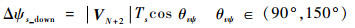 | (27) |
如图 3所示,当处于N=1区域时,即θ∈(0°, 60°),设|VN|·Ts=x, N=1, 2, …, 6,x为常数,一个扇区内合成磁链矢量幅值变化如表 2所示。
 |
| 图 3 传统的电压矢量选取方式 Fig. 3 Traditional voltage vector selection method |
| 图选项 |
表 2 合成磁链幅值变化 Table 2 Change of synthetic flux-linkage amplitude
| θ/(°) | θvψ1/(°) | θvψ2/(°) | 加V2后磁链幅值变化量/Wb | 加V3后磁链幅值变化量/Wb |
| 0 | 90 | 150 | 0 | -0.866x |
| 10 | 80 | 140 | 0.174x | -0.766x |
| 20 | 70 | 130 | 0.342x | -0.643x |
| 30 | 60 | 120 | 0.5x | -0.5x |
| 40 | 50 | 110 | 0.643x | -0.342x |
| 50 | 40 | 100 | 0.766x | -0.174x |
| 60 | 30 | 90 | 0.866x | 0 |
| 注:θvψ1为电压矢量V2与磁链的夹角; θvψ2为电压矢量V3与磁链的夹角。 | ||||
表选项
从表 2可清晰看出,θ从0°增加到20°时,加V2后磁链幅值从0 Wb增加到0.342x Wb,加V3后磁链幅值从-0.866x Wb增加到-0.643x Wb,但是V2和V3这2个电压矢量的施加使得磁链的变化程度不同,可以看出,一个周期加V3使得磁链的减小值需要加几个周期的V2才能使得磁链保持不变。θ从20°增加到40°时,磁链的增加值和减小值大致相等。θ从40°增加到60°时,一个周期加V2使得磁链的增加值需要加几个周期的V3才能使得磁链保持不变。这种不对称性会引起磁链的变化,从而在换相区产生转矩脉动。
图 3所示的电压矢量是按照相同的规则进行选取,但是经过上述分析发现,特别是在扇区的边沿处存在磁链波动的现象,造成换相时转矩脉动较大,因此将图 3的扇区进行细分,如图 4所示。
 |
| 图 4 扇区细分方法 Fig. 4 Sector segmentation method |
| 图选项 |
在图 3的基础上,将每个扇区进行细分成三等分,3个小区域分别采用NA、NB和NC表示,为了简洁表示只画出第1扇区,共18个小扇区。通过细分扇区优化选取电压矢量,如表 3所示。
表 3 基于扇区细分方法优化电压矢量选取 Table 3 Voltage vector selection optimization based on sector segmentation method
| 变化需求 | 区域N(N=1, 2, …, 6) | |||
| NA | NB | NC | ||
| ψ↑ | T↑ T↓ | VN VN-1 | VN+1 VN-1 | VN+1 VN |
| ψ↓ | T↑ T↓ | VN+2 VN+3 | VN+2 VN+4 | VN+3 VN+4 |
表选项
由表 3可知,θ从0°增加到20°时,选择V1增加磁链和转矩,选择V3和V6分别减小磁链和转矩;θ从20°增加到40°时,选择V2增加磁链和转矩,选择V3和V6分别减小磁链和转矩;θ从40°增加到60°时,选择V2增加磁链和转矩,选择V4和V5分别减小磁链和转矩。
4 系统仿真与实验分析 4.1 系统仿真 本文使用MATLAB/Simulink进行系统仿真,其中电机采用三相6/4极结构,额定电压为270 V, 额定功率为3 kW,额定转速为2 000 r/min。在速度调节器中,采用自适应二阶终端滑模控制器替代传统的PI控制器,并依据扇区细分规则设计全新的开关表。通过Ansoft进行有限元分析,建立磁链特性ψ-θ-i曲线簇和矩角特性T-θ-i曲线簇,如图 5所示。
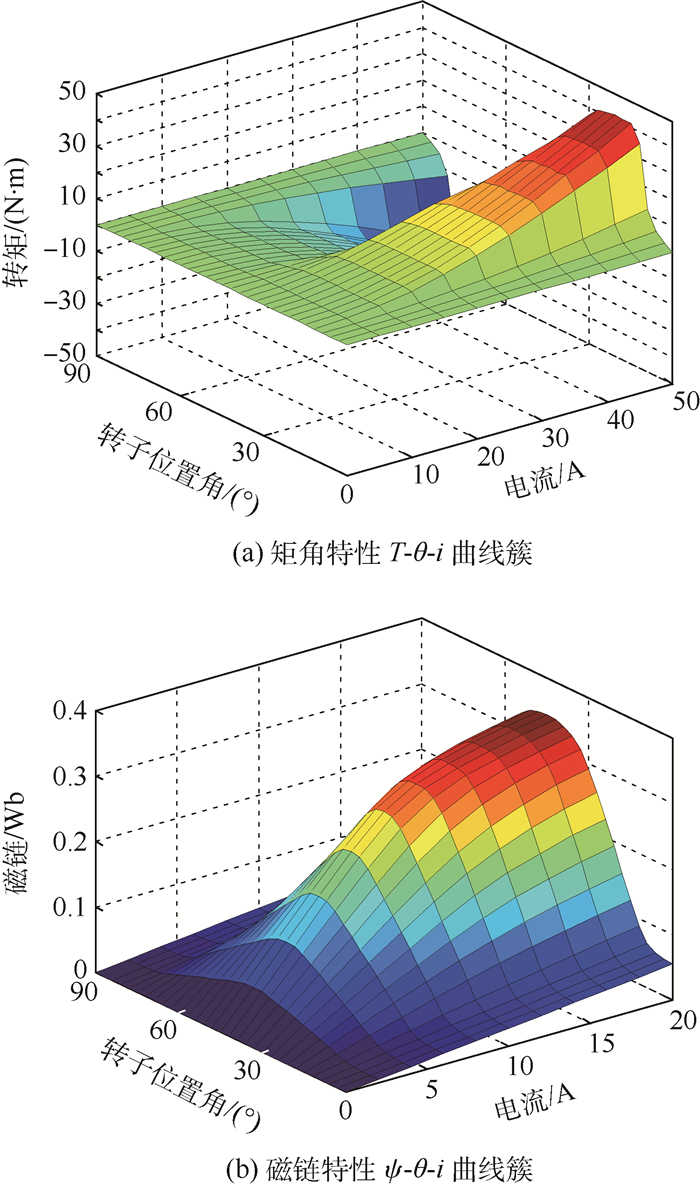 |
| 图 5 矩角特性和磁链特性 Fig. 5 Torque-angle and flux-linkage characteristics |
| 图选项 |
将图 5所示的电机非线性特性在Simulink中构造电机本体模型,搭建DTC控制系统。为了进行对比,系统转速控制器的建立分别采用了传统的PI控制、滑模变结构控制和自适应二阶终端滑模控制,分析转速精确跟踪的控制效果。给定转速为500 r/min,负载转矩为6 N·m时,其转速曲线如图 6(a)所示,转矩曲线如图 6(b)所示。
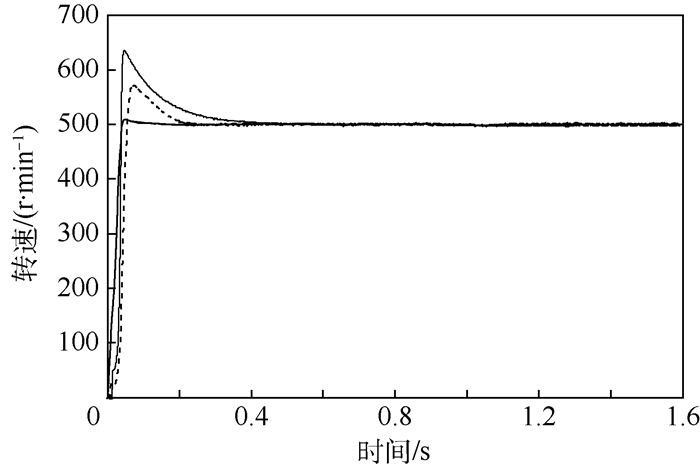 |
| 图 6 3种控制方式转速和输出转矩曲线对比 Fig. 6 Comparison of curves of speed and output torque of three control modes |
| 图选项 |
由图 6可知,基于自适应二阶终端滑模的DTC系统的转速和转矩控制效果较好,其中相较于传统的PI控制和滑模变结构控制而言,改进后的系统响应更快,超调更小,具有较好的动态特性和静态特性。起动时的转矩较为平稳迅速,稳定后转矩脉动更小,能够明显提升开关磁阻电机调速系统动态特性和静态特性,实现了良好的控制效果。
由图 7可知,合成磁链幅值基本恒定,磁链幅值变化很小,磁链幅值变化可以影响输出转矩,说明改进后的DTC系统对转矩脉动控制较好。当稳态运行时,改进后的DTC系统的合成磁链幅值变化进一步减小,合成磁链幅值基本上稳定在0.36 Wb左右,控制效果更好。
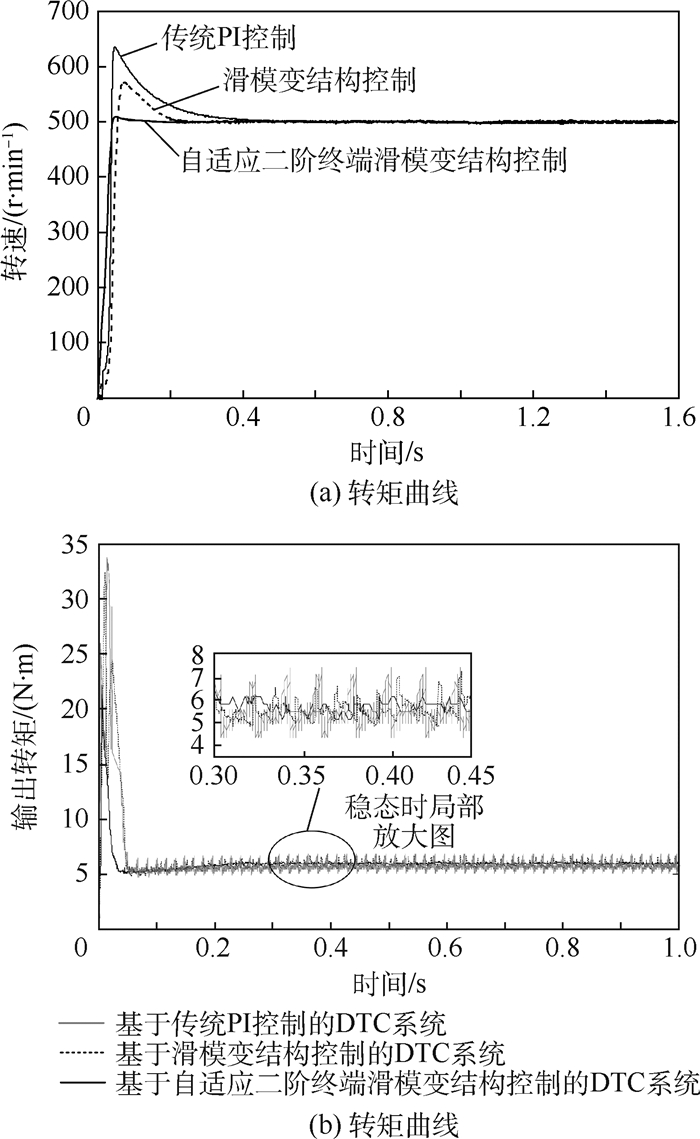 |
| 图 7 磁链轨迹 Fig. 7 Flux-linkage track |
| 图选项 |
采用改进后的转速滑模控制器,给定转速为500 r/min,负载转矩为6 N·m时,分别采用传统的扇区和细分扇区选取电压矢量,其输出转矩如图 8所示。
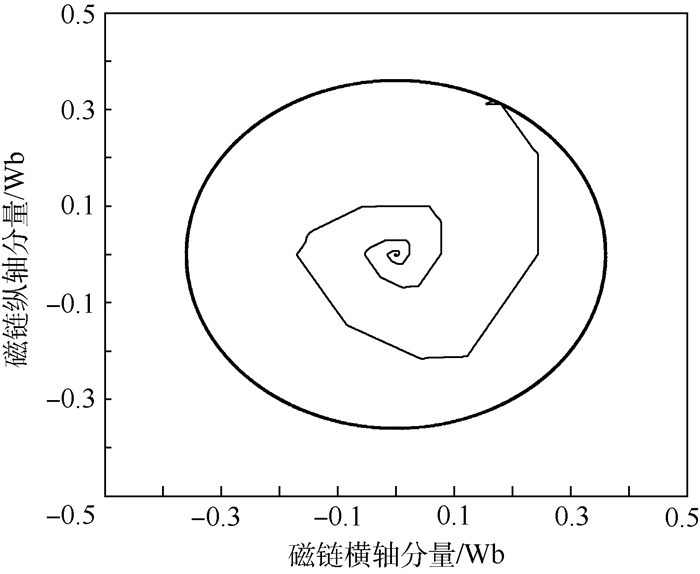 |
| 图 8 输出转矩波形 Fig. 8 Output torque waveform |
| 图选项 |
图 8(a)为采用传统的扇区,转矩在5.5~6.5N·m波动,转矩脉动为16.7%。图 8(b)采用细分扇区可以优化电压矢量的选取,转矩在5.8~6.3 N·m之间波动,转矩脉动为8.3%,相比于传统的扇区转矩脉动减小了8.4%。因此,细分扇区可以进一步减小由于电机换相带来的转矩脉动。
4.2 实验分析 搭建三相6/4极SRM平台进行实验验证。硬件平台主要由电机、功率变换器、控制系统和检测电路组成,电机本体额定功率为3 kW,控制系统中DSP芯片为TMS320F28335,CPLD芯片采用EPM1270T144C5,利用DSP将待实现的自适应二阶终端滑模控制方法进行实现,并且将信息传递给CPLD。利用CPLD将按照控制量实现电机的换相逻辑,判断换相实现系统运行。检测电路采用检测位置旋转变压器和电压、电流传感器,功率变换器电路采用不对称半桥结构。电机的结构参数如下:三相6/4极,定子外径为128 mm,定子极弧系数为0.5,定子轭高为11.94 mm,转子外径为77 mm,转子内径为33 mm,转子极弧系数为0.355。滑模面参数p=9,q=7,β=0.3,μ=1.8。将得到的实验数据输入到MATLAB中进行实验结果的数据处理。
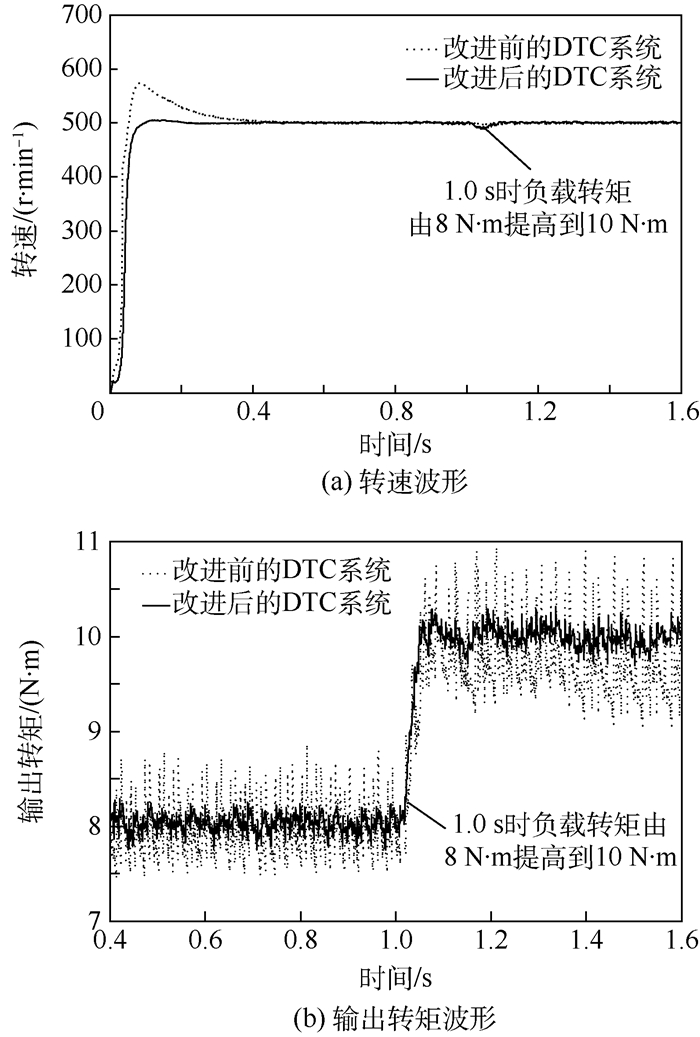
设转速为500 r/min,负载转矩为8 N·m,在1.0 s突加负载到10 N·m。实验波形如图 9所示。
 |
| 图 9 转速为500 r/min时转速和输出转矩波形 Fig. 9 Speed and output torque waveform at 500 r/min |
| 图选项 |
从图 9可知,改进后的DTC转速响应快,超调量小,当在1.0 s突加负载时,改进前的DTC转速存在一定程度的下降,而改进后的DTC转速基本上保持500 r/min左右,具有一定的抗干扰性和鲁棒性。而且其转矩脉动明显减小,稳定时转矩在7.7~8.3 N·m范围波动,转矩脉动为7.5%。
为了验证中速时的控制效果,设转速为1 500 r/min,负载转矩为22 N·m,在1.0 s突卸负载到18 N·m。实验波形如图 10所示。可以看出,随着转速的增加,DTC系统控制的效果减弱,转速超调增大,转矩脉动增大。但是改进后的DTC系统稳定时仍将转矩控制在21.5~22.5 N·m,稳定在22 N·m附近,而传统DTC系统转矩在20.3~24.1N·m范围内波动,说明改进后的DTC系统在中速范围内有较好的控制效果。
 |
| 图 10 转速为1 500 r/min时转速和输出转矩波形 Fig. 10 Speed and output torque waveform at 1 500 r/min |
| 图选项 |
5 结论 为了改善SRM-DTC系统的控制效果,进一步减少转矩脉动,提高抗干扰能力,增强系统鲁棒性,本文设计了一种负载扰动自适应估计的二阶终端滑模变结构控制器,并且对传统规则的扇区进行细分优化电压矢量选取,通过系统仿真和实验分析,得出以下结论:
1) 相比于传统PI控制和滑模变结构控制,本文设计的转速控制器超调量小,响应速度快,具有较好的动态和静态特性,系统的鲁棒性明显增强,显著提高了抗负载干扰能力。
2) 对基本空间电压矢量空间划分的6个均匀扇区进行细分,理论分析和仿真表明细分扇区可以减少换相时的转矩脉动。
3) 设计的转速滑模控制器可对负载扰动进行自适应估计,减少了控制器设计的限制条件。
4) DTC对低速的控制效果较好,转速增加时控制效果会变差。改进后的DTC系统提高了中速时的控制效果,适用于航空电气工程领域。
参考文献
| [1] | 刘勇智, 周政, 盛增津, 等. 开关磁阻电机起动/发电状态切换控制策略研究[J]. 电机与控制学报, 2015, 19(10): 57-63. LIU Y Z, ZHOU Z, SHENG Z J, et al. Study of control strategy for status switching of switched reluctance starter/generator[J]. Electric Machines and Control, 2015, 19(10): 57-63. (in Chinese) |
| [2] | 赵旭升, 邓智泉, 汪波. 一种磁悬浮开关磁阻电机用轴向径向磁轴承[J]. 北京航空航天大学学报, 2011, 37(8): 973-978. ZHAO X S, DENG Z Q, WANG B. Axial radial magnetic bearing in magnetic suspending switched reluctance motor application[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(8): 973-978. (in Chinese) |
| [3] | 昝小舒, 陈昊. 开关磁阻起动/发电系统起动性能研究[J]. 电工技术学报, 2015, 30(20): 21-29. ZAN X S, CHEN H. Study on starting performance of switched reluctance starter/generator system[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 21-29. DOI:10.3969/j.issn.1000-6753.2015.20.003 (in Chinese) |
| [4] | SONG S J, LIU W G, DIETER P, et al. Detailed design of a high speed switched reluctance starter/generator[J]. Chinese Journal of Aeronautics, 2010, 23(2): 216-226. DOI:10.1016/S1000-9361(09)60208-9 |
| [5] | 宋受俊, 葛乐飞, 刘虎成, 等. 开关磁阻电机设计及多目标优化方法[J]. 电工技术学报, 2014, 29(5): 197-204. SONG S J, GE L F, LIU H C, et al. Design and multi-objective optimization method of switched reluctance machines[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 197-204. DOI:10.3969/j.issn.1000-6753.2014.05.025 (in Chinese) |
| [6] | ANNEGRET K, ANDREAS H, RIK W. Direct instantaneous torque and force control:A control approach for switched reluctance machines[J]. IET Electric Power Applications, 2017, 11(5): 935-943. DOI:10.1049/iet-epa.2016.0515 |
| [7] | 朱叶盛, 章国宝, 黄永明. 基于PWM的开关磁阻电机直接转矩控制[J]. 电工技术学报, 2017, 32(7): 31-39. ZHU Y S, ZHANG G B, HUANG Y M. PWM-based direct instantaneous torque control of switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 31-39. (in Chinese) |
| [8] | 王玉林.开关磁阻电机直接转矩控制的研究[D].杭州: 浙江大学, 2016. WANG Y L.Research on direct instantaneous torque control of switched reluctance motor[D].Hangzhou: Zhejiang University, 2016(in Chinese). |
| [9] | 王勉华, 梁媛媛. 开关磁阻电机直接转矩模糊PI控制器的设计[J]. 电气传动, 2010, 40(1): 51-54. WANG M H, LIANG Y Y. Fuzzy-PI controller for direct torque control drives system of SRM[J]. Electric Drive, 2010, 40(1): 51-54. (in Chinese) |
| [10] | 刘勇智, 王宇, 朱晨承. 采用模糊逻辑修正的SRM滑模控制器设计[J]. 计算机测量与控制, 2014, 22(7): 2059-2062. LIU Y Z, WANG Y, ZHU C C. Sliding mode controller of SRM combined with fuzzy logic correction[J]. Computer Measurement & Control, 2014, 22(7): 2059-2062. DOI:10.3969/j.issn.1671-4598.2014.07.019 (in Chinese) |
| [11] | 刘慧武.开关磁阻电机直接转矩控制系统的研究[D].哈尔滨: 哈尔滨理工大学, 2014. LIU H W.Research on switched reluctance motor direct torque control system[D].Harbin: Harbin University of Science and Technology, 2014(in Chinese). |
| [12] | 赵洋.开关磁阻电机直接转矩控制技术研究[D].成都: 西南交通大学, 2016. ZHAO Y.Research on DTC of switched reluctance motor[D].Chengdu: Southwest Jiaotong University, 2016(in Chinese). |
| [13] | 王冕华, 邢幸. 开关磁阻电机直接转矩滑模变结构控制[J]. 电机与控制应用, 2017, 44(6): 35-39. WANG M H, XING X. Sliding mode variable structure controller for direct torque control drive system of switched reluctance motor[J]. Electric Machines & Control Application, 2017, 44(6): 35-39. DOI:10.3969/j.issn.1673-6540.2017.06.007 (in Chinese) |
| [14] | 喻晓军.基于SMO的矿用电机车调速系统设计[D].淮南: 安徽理工大学, 2015. YU X J.Research of mining accumulator locomotive speed control system based on SMO[D].Huainan: Anhui University of Science and Technology, 2015(in Chinese). |
| [15] | 吴红星. 开关磁阻电机系统理论与控制技术[M]. 北京: 中国电力出版社, 2010. WU H X. Theory and control technology of switched reluctance motor system[M]. Beijing: China Electric Power Press, 2010. (in Chinese) |
