自从1944年德军的V-2型“复仇武器”登上战场以来,弹道导弹突防与拦截技术,一直是一个经久不衰的热门话题。而多层次、多阶段和多模式的导弹防御系统极大地挤压了弹道导弹的生存空间,随着反导体系的日趋成熟,弹道导弹的突防难度也在加大。关于大气层外远程拦截导引的方法,国内外许多****以及研究机构已经多有建树。其中预测制导方案是将拦截器对来袭目标的零控脱靶量(Zero Effort Miss, ZEM)作为控制指标进行设计。Zarchan[1]在此方面做出突出工作,其在平面拦截问题过程将预测制导与比例导引以及扩展比例导引进行比较;考虑到大气层外拦截中具有较长的滑行阶段,Zes[2]对两飞行器间的重力差进行校正并将改进的比例导引应用于拦截任务;此外Zes[3]利用Kepler/Lagrange轨道方程对拦截器与目标间的ZEM进行预报;Phillips和Malyevac[4-5]利用任务图表分析的方法为带有2次脉冲控制的推进器选择发动机性能参数;Gutman和Rubinsky[6]研究了大气层外拦截中段制导,以及中末制导交班的条件,不过暂未考虑目标变轨等非理想运动状态的影响。
关于大气层外动能战斗部(Exo-atmospheric Kill Vehicle, EKV)的控制设计,重点在于保持快速响应,而且需要将连续的制导指令离散化,以适应轨控发动机的需求。Hablani[7]分析了测量信息处理的延迟对EKV脉冲导引法的影响,并通过脱靶量误差分析来设计EKV的各项参数[8]。Guo等[9]设计了一种准滑动模态导引律,而Shima和Golan[10]运用滑动模态方法研究了一种能够执行轴向加速指令的拦截器。
从进攻方的角度来看,弹道导弹防御系统是复杂的大系统,因此针对其各环节采取相应措施,分情况考虑系统的效能是有必要的[11]。吴钰飞等[12]分析了诱饵对突防效能的影响及反导系统的拦截方式和拦截策略;在单枚弹头被发现、跟踪、识别及单发拦截成功率的基础上,建立了诱饵影响下多枚弹道导弹的突防效能模型。Yao等[13]基于网络分析的方法来评估导弹防御系统的作战效能;杨晓凌和邱涤珊[14]则对导弹防御作战中威胁识别结果、落点预报以及拦截器拦截成功率的不确定性进行了分析和建模,构建了不确定条件下拦截器对来袭目标分配的规划模型。而要从宏观的角度上评估一定数量的拦截弹对抗一定数量的弹道导弹所能实现的防御效能,通常是由概率的形式来表达的[15];Glaser和Fetter[16]借用建立的概率模型分析了国际间导弹攻防战略的现实意义,从微观角度的型号建模,攻防措施,效能分析,最终上升到宏观视野下的国家战略,也是当前许多研究者努力推进的一个方向。
本文在针对当前的某型大气层外拦截弹进行调研、分析、建模的基础上,按照一定的作战想定场景,通过计算机仿真试验来对比不同突防措施的效能,以期合理地规划中远程弹道导弹与反导拦截系统之间的攻防对抗手段,为其实际应用提供有价值的参考。
1 拦截弹动力学模型 拦截弹总长度6.58 m,发射质量2 313.2 kg,采用垂直发射方式,弹体部分由三级火箭助推器以及载荷舱组成,在大气层内飞行段采用推力矢量控制(第1级)以及气动面控制(第2级),跨大气层飞行段采用推力矢量控制(第3级),最终燃尽后释放出EKV,执行碰撞拦截任务。拦截弹的主要尺寸如图 1所示。
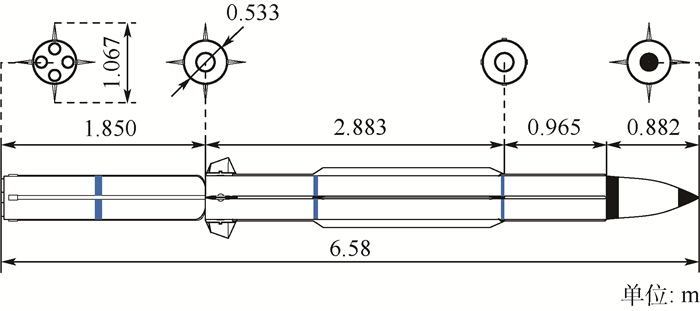 |
| 图 1 拦截弹主要尺寸 Fig. 1 Main dimensions of interceptor |
| 图选项 |
引入地面系(北-天-东)记为Od-xdydzd,弹体系记为Ob-xbybzb。依照经典的六自由度建模方法,拦截弹质心运动的动力学方程写为
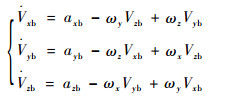 | (1) |
式中:速度分量Vxb、Vyb、Vzb,加速度分量axb、ayb、azb和旋转角速度分量ωx、ωy、ωz均表示在弹体系下。
其中主动段飞行的加速度表达式为
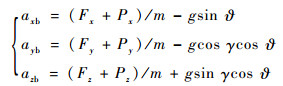 | (2) |
式中:m为导弹质量;g为重力加速度;Fx、Fy、Fz为导弹所受到的外力;Px、Py、Pz为导弹的推力分量,尤其考虑的是推力矢量控制情形;
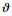
表 1 火箭助推器的基本参数 Table 1 Basic parameters of rocket booster
| 级数 | 总质量/kg | 燃料质量/kg | 推力/kN | 工作时间/s |
| 1 | 725.7 | 577.8 | 62.55×4 | 6 |
| 2 | 1 134.0 | 398.6 508.6 | 139.246 40.611 | 8 35 |
| 3 | 453.5 | 150.0 150.0 | 42.0 42.0 | 10 10 |
表选项
对于轴对称导弹,横向转动惯量Jy和Jz可以认为是相等的。设Jy=Jz=J,则绕质心转动的动力学方程可以写成
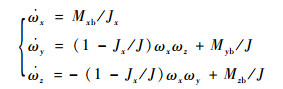 | (3) |
式中:Mxb、Myb、Mzb为弹体系下的力矩; Jx为轴向转动惯量。式(3)表明,如果能够控制导弹的滚转运动,令ωx≈0,在控制系统的设计上会带来许多方便。而对于依靠轨控发动机来制导的动能战斗部,这一点则几乎是必需的。
令拦截弹从垂直发射状态转弯至10°~90°弹道倾角,并飞行至主动段结束,如图 2所示。图中:虚线等速度线是指拦截弹加速到这个水平所处的弹道位置(由高度和横程表示),实线一端的速度是指拦截弹飞完主动段(实线末端)时刻的关机速度。可以看出关机速度随弹道高低角而变化,大致分布范围为4 900~5 500 m/s。拦截弹经历的加速过程中,达到1 000 m/s的水平较快,主要是由第1级助推器完成;1 500~2 500 m/s段跨度较大,是由第2级助推器的第2工作段所致;之后从2 500 m/s至关机,速度提升较大,体现了第3级助推器在剩余结构质量较小时有很强的加速能力。而且从飞行高度来看,第3级工作期间拦截弹基本处于跨大气层段,因此考虑把导向PIP的修正工作交给第3级助推器进行。
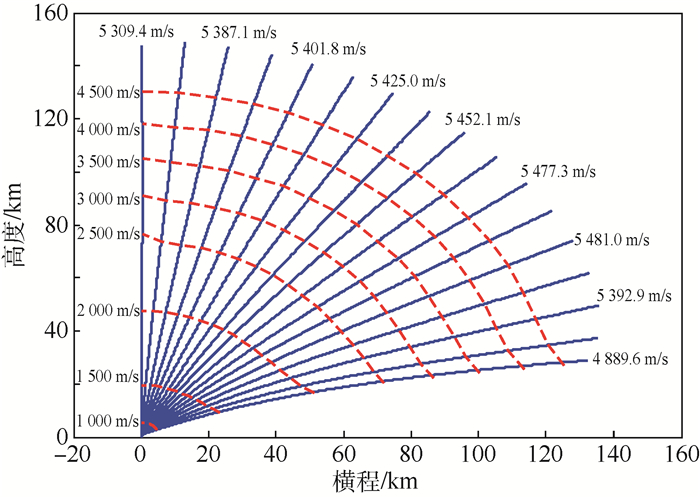 |
| 图 2 拦截弹速度分布 Fig. 2 Velocity distribution of interceptor |
| 图选项 |
2 跨大气层拦截制导策略 2.1 大气层内转弯段 将弹体绕质心的运动学方程采用Euler角(姿态角)表达为
 | (4) |
由于拦截弹垂直发射,在垂直起飞阶段会出现奇异性,具体表现为滚转角γ与偏航角ψ定义的失效。采用四元数法能够予以克服,但会使拦截弹的姿态表达得不够直观。本文提出了一种在俯仰角θ≈π/2的情况下,临时改变姿态描述来避免运动方程奇异的方法。弹体垂直姿态下的变量见图 3。
 |
| 图 3 弹体垂直姿态下的变量 Fig. 3 Variables in vertical attitude of missile body |
| 图选项 |
首先,根据式(4),只要
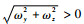
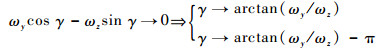 | (5) |
其次,认为完全垂直状态下的飞行器,姿态仅由俯仰角θ和滚转角γ0来定义。在进入垂直状态的瞬时,滚转角γ1=arctan(ωy/ωz),而当弹体轴xb与地面系yd轴重合的瞬间,定义新的滚转角为γ0=γ1+ψ1,相当于把之前的偏航角与滚转角“合并”。
当弹体由于转动角速度ω的作用离开垂直状态的瞬时,记iyd为yd轴向的单位向量,弹体轴xb在zdOdxd平面内的投影与向量iyd×ω共线反向。因此按照非垂直状态下的Euler角定义,则滚转角γ2为ω-ωxixb转向-zb所掠过的角度,亦即γ2=arctan(ωy/ωz)-π;而偏航角与滚转角解除“合并”的瞬时,可得ψ2=γ0-γ2。
具体到执行程序,见图 4。为了替代无限趋近垂直的过程,需要设置一个小量10-4rad,作为进入垂直姿态“附近”的界限。需要说明的是arctan(ωy/ωz)是在ybObzb平面四象限中取值的反正切函数。
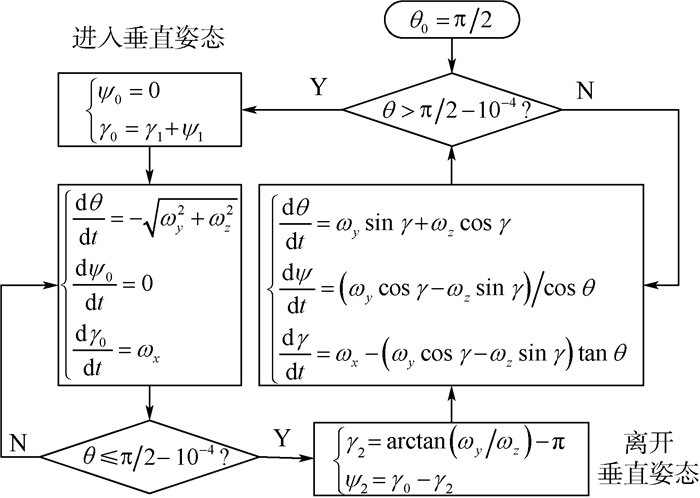 |
| 图 4 初始转弯段运动学方程 Fig. 4 Kinematic equation of initial turning phase |
| 图选项 |
令PIP为(0, 100, -140) km,在地面系中的投影位于-zd轴。观察拦截弹初始转弯过程中姿态角变化。
由于拦截弹是轴对称的,在0 s时刻取弹体轴yb与PIP在地面上的投影共线反向,以期拦截弹仅控制ωz就可使俯仰方向对准空间的PIP,因此γ0=90°;假设为了避免碰撞,拦截弹在高于100 m开始允许弹体绕zb轴转动,使得俯仰角θ < 90°;而当拦截弹离开垂直状态时,弹体在地面的投影需要与PIP投影共向,即期望的偏航角ψ2=90°;且俯仰角θ期望值为arctan(100/140),约35.6°;滚转角γ期望值为0°。从图 5可以看出,弹体在第1级结束时刻姿态角能够分别达到期望值,从而使得xb轴指向PIP,完成初始转弯任务。
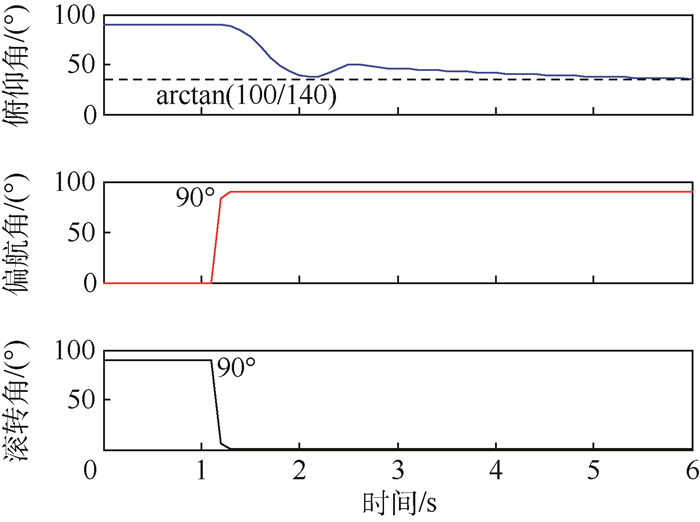 |
| 图 5 第1级助推段的姿态角曲线 Fig. 5 Curves of attitude angle during the first boosting stage |
| 图选项 |
2.2 大气层外制导段 当拦截弹离开大气层以后,由于在导引头捕获目标前需要经历较长的无动力飞行阶段,所以应在助推器燃尽时将零控脱靶量消除掉,这就要求应用Lambert原理以及“能量管理控制[1]”了。
在发动机关机时刻,拦截弹要确保能够从关机点位置按指定时间飞抵PIP,因此准确地解算关机点速度向量V0至为重要。在地心引力场的环境下,假设关机点位置对应的地心向量为r0,PIP位置对应的地心向量为rF,要求的飞行时间为tF,则所需要的关机时刻速度为[1]
 | (6) |
式中:G为地心引力常数;?为拦截弹相对于地心的角行程,即r0和rF之间的夹角
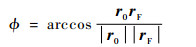 | (7) |
如图 6所示,RE为地球半径,坐标轴xr和yr由地心Oe出发,均在拦截弹射面内,因此速度向量的2个分量表示为
 | (8) |
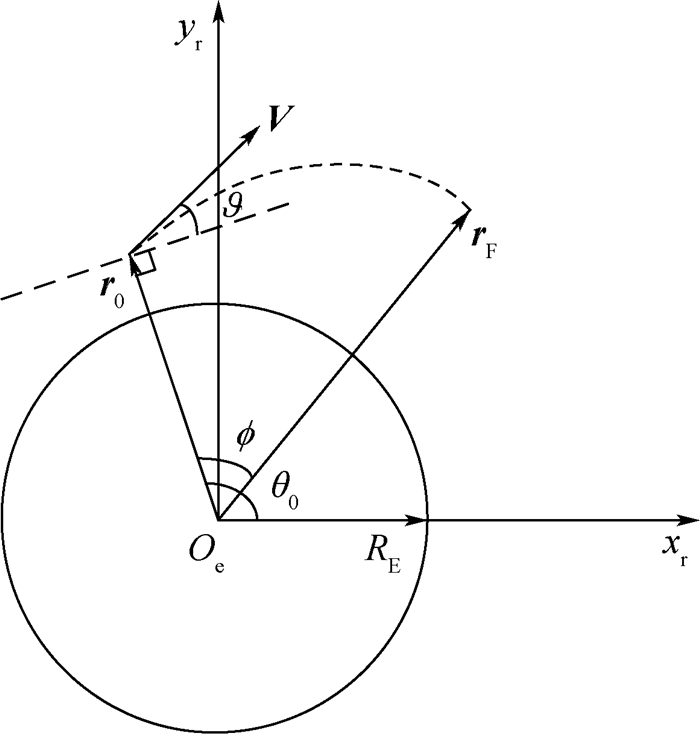 |
| 图 6 地心系下的飞行示意图 Fig. 6 Schematic diagram of travelling in earth-center frame |
| 图选项 |
当然,为了方便可以把xr轴直接取到与关机点向量r0共线,这样就有θ0=0。
一般情况下弹头需要再入大气层,因此拦截弹和目标弹头都运行在偏心率
 | (9) |
的圆锥曲线轨道(即椭圆弹道)上,那么从关机点到拦截点需要的飞行时间为[1]
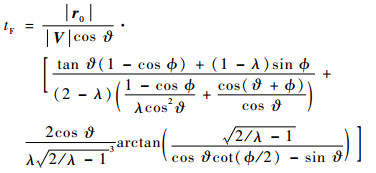 | (10) |
综上所述,可以得到一组方程
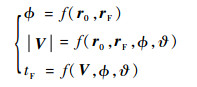 | (11) |
式中:r0和rF已知,?可以算出,那么接下来的工作就是给出期望的飞行时间tDES,就可以通过分割法迭代
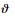

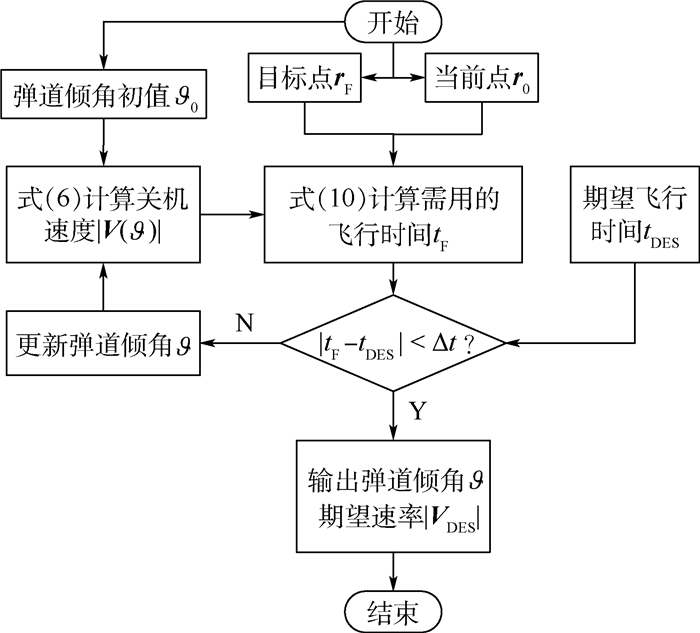 |
| 图 7 期望速度的解算流程 Fig. 7 Calculation procedure of desired velocity |
| 图选项 |
2.3 动能战斗部建模 拦截弹的有效载荷为EKV,在末制导阶段主要依靠红外导引头获取目标视线角信息,并由姿轨控系统(Divert and Attitude Control System, DACS)执行跟踪变轨指令。由于红外导引头视界很窄,通常为±1°,因此假定姿控系统能确保弹体轴xb指向目标。姿轨控系统的布局方式为:4个大推力的轨控发动机(D)沿轴向对称布置,与质心共面;6个小推力的姿控发动机(A)置于尾部。EKV的主要结构如图 8所示。
 |
| 图 8 EKV姿轨控系统结构 Fig. 8 Structure of DACS of EKV |
| 图选项 |
假设轨控发动机有10 ms的开关机延迟,且D1~D4在开启状态下的恒定推力均为Fmax。EKV的各项基本参数如表 2所示。
表 2 EKV的基本参数 Table 2 Basic parameters of EKV
| 参数 | 数值 |
| 红外导引头视距/km | 700 |
| 长度/m | 0.68 |
| 直径/m | 0.19 |
| 总质量/kg | 60.0 |
| 燃料质量/kg | 20.0 |
| 秒流量/(kg·s-1) | 1.0 |
| 推力/kN | 2.6 |
表选项
根据比例导引律,制导指令nc为
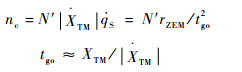 | (12) |
式中:
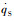
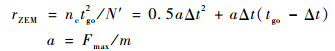 | (13) |
使得拦截弹经过Δt时间的修正后,能够确保拦截目标。由于发动机推力是固定值Fmax,只能控制工作时长Δt。而频繁开关机也是不期望的,可以等待nc增大到一定值后再执行。设轨控开机门限ION为[17]
 | (14) |
注意c < 1,且满足
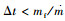
 |
| 图 9 轨控发动机开关逻辑 Fig. 9 Switching logic of divert thruster |
| 图选项 |
3 基于射表的预测拦截点选取法 使用预测导引原理拦截目标,实际上就是在飞行过程中将拦截弹向PIP导引,如果对PIP的计算是准确的,则这种导引就相当于是向空中某固定点的导引,这也是与大气层外制导阶段使用Lambert导引律的要求相呼应的。
3.1 大气层外拦截射表 文献[1]中对于瞬间达到关机速度的“脉冲”拦截弹模型,给出了利用Lambert问题数值解来获得PIP的算法。然而实际上拦截弹还包含姿态控制环节、程序转弯段以及跨大气层飞行段,多级助推的情况就更为复杂,不能仅以大气层外的飞行状态来计算PIP。一个实用的办法就是通过蒙特卡罗仿真,掌握拦截弹的性能并建立简明的数值射表。
本文中射表数据的获取,就是在完成拦截弹动力学建模的基础上,通过对地心惯性系下的一系列目标点做仿真试验。由于拦截弹采用垂直发射方式,对目标点所在的射向不敏感,因此目标位置可仅由2个参数,即当地高度h和初始弹目距离r来表征。首先按一定间隔取h∈(100, 1 500) km,r∈(300, 3 000) km范围内的点,并搜索EKV到达每个点(r, h)飞行时间tF的最大、最小可用值,分别记为tMAX(r, h)和tMIN(r, h)。然后在得到的tF取值区间[tMIN, tMAX]内找出一个使EKV燃料消耗最少的值,定义为tOPT(r, h)。图 10给出了等tOPT(r, h)曲线在射表范围内的分布,为了适应数据矩阵绘图取横程
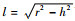
 |
| 图 10 射表中tOPT分布的示意图 Fig. 10 Schematic diagram of distribution of tOPT in firing table |
| 图选项 |
虽然按照Lambert导引理论,只要指定的tDES不太小,拦截弹总能达到理想的关机速度VDES,从而EKV无需进一步控制就可恰好在tDES时刻击中目标。但是具体到六自由度的模型中,由于自动驾驶仪存在延迟,能量管理只能保证对于一定范围内的tDES,使得关机速度误差|ΔV|接近0。由于助推段结束至EKV完成拦截的飞行时间为tF,则产生的弹道误差Δr=|tFΔV|是需要EKV消耗燃料来修正的。实际仿真中当tDES?[tMIN, tMAX]时,都会使EKV由于燃料耗尽失去控制力,从而错失拦截目标,故认为这样的tDES是“不可用的”。因此决定了tDES的选择受到限制,存在上下边界以及其间的最优值。
3.2 预测拦截点的选取 假设目标完全按照引力弹道飞行,当前时间为t0,对于目标在未来时刻t1所处的弹道上位置P1,相对于拦截阵地为(r1, h1),可以根据射表对该点的3个飞行时间tMIN、tMAX和tOPT进行插值,来判断位置P1是否能被取作PIP。
判断的标准,在于目标飞抵该点的剩余时间,是否足够拦截弹完成发射,制导,直至命中的过程。反映在射表上,即该点的(r1, h1)要满足
 | (15) |
此处暂不考虑tMAX是由于拦截弹可以待机。
如图 11所示的一段进攻弹道,这里t1-t0也就是留给拦截弹飞抵P1点的最大可用时间。通常,随着在目标弹道上搜索的时间t1不断递增,只要目标弹道的射面离拦截阵地不太远,起始时刻t0不太迟,总会遇到可用的拦截点。而t0取决于防御方探测系统首次捕获目标的时间,因此雷达的前出部署,天基红外对战场的覆盖也十分关键。
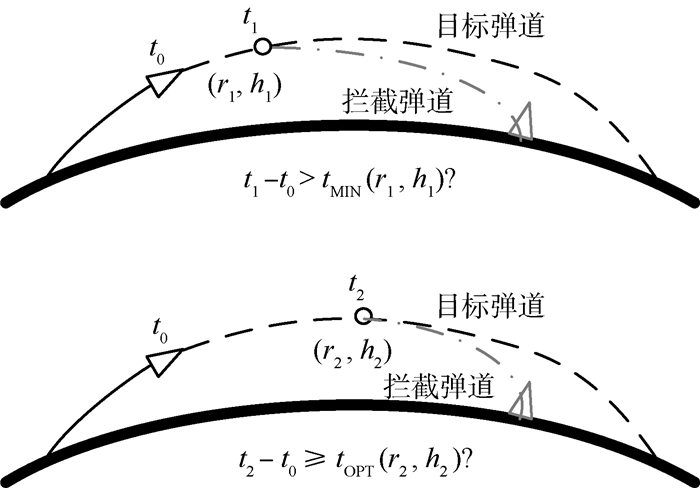 |
| 图 11 预测拦截点的搜索 Fig. 11 Search of predicted intercept point |
| 图选项 |
在此基础上,进一步寻找目标弹道上新的时间点t2和位置P2,其相对于拦截阵地的(r2, h2)满足:
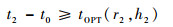 | (16) |
如果存在,意味着将该点作为PIP,并选择拦截弹的发射时间为
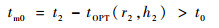 | (17) |
就可以使拦截弹在经过tOPT(r2, h2)时长的飞行后,在r2点拦截目标。根据射表中tOPT的含义,这会使得EKV消耗最少的燃料,从而比选择P1作为PIP要更加优越。
如果不存在前述时间点t2和位置P2,说明整个目标弹道上的所有位置点留给拦截弹的可用时间都不宽裕,总是有t-t0 < tOPT(r, h),那么可以选择|tMAX(r, h)-tMIN(r, h)|最大的点,发射时刻tm0就选在当前值t0,通常在这样的位置也有较好的拦截效果。
3.3 预测拦截点的更新 由于雷达探测误差、目标机动变轨等原因,自拦截弹发射时预测的目标弹道诸元需要不断更新。仍然假设大气层外目标在大部分时间内处于引力弹道附近飞行,即不认为目标具有持续的且大幅度的任意机动能力。这是预测目标弹道的前提条件,在此基础上,利用拦截弹射表来更新PIP。
图 12所示的流程从防御系统发现预报弹道误差,并完成弹道数据更新后开始,在当前时刻tNOW至弹道末时tEND之间取t1,以及对应的目标位置P1。由于拦截弹已经于tm0时刻发射,无法待机,因此需要考虑tMAX(r, h)对可用飞行时间tF的限制。所以,一方面该点相对于拦截弹发射点的(r1, h1)要满足
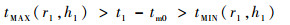 | (18) |
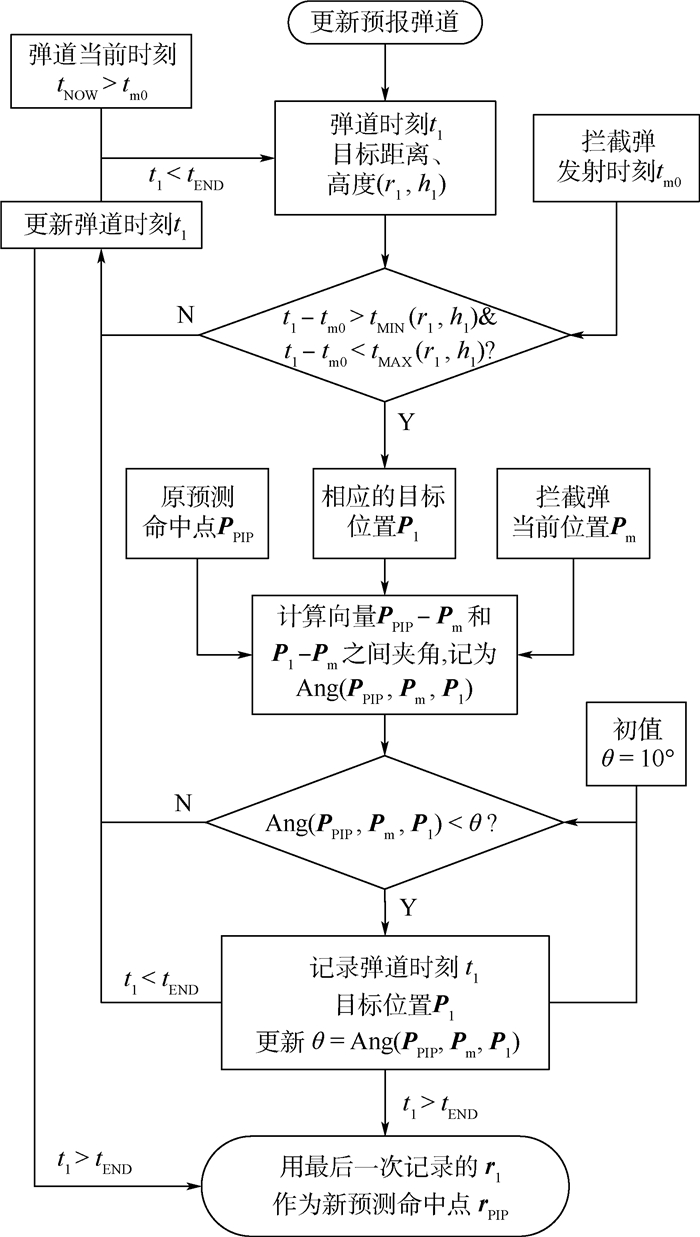 |
| 图 12 预测拦截点更新的流程 Fig. 12 Update procedure of predicted intercept point |
| 图选项 |
另一方面,考虑到拦截弹已经具有一定的飞行速率,大角度地改变速度方向会导致很高的过载。因此在满足式(18)条件的点集{P1}中应筛选出这样的点P1min,使其与原预测拦截点PPIP相对于拦截弹位置Pm张开的夹角最小,即
 | (19) |
并将此位置P1min作为新的PIP。
4 攻防仿真与效能分析 4.1 目标弹头相关设置 本文假设存在一型中远程弹道导弹,最大射程lmax=5 000 km,可以打击地面以及水面目标,并且具有大气层外变轨能力,携带电子压制干扰机以及红外诱饵。
进攻弹的弹道解算由关机时刻t0开始,图 13展示了进攻弹道在不同的飞行时间Tf下所呈现的高低形态。其中Tf=1 227.3 s是按照“最小能量弹道”的原理来取值的[1],也就是使得导弹达到最大射程时所需的最小关机速率|V0min|。而把飞行时间更短,中段高度更低、速度更快的弹道都称为压低弹道。
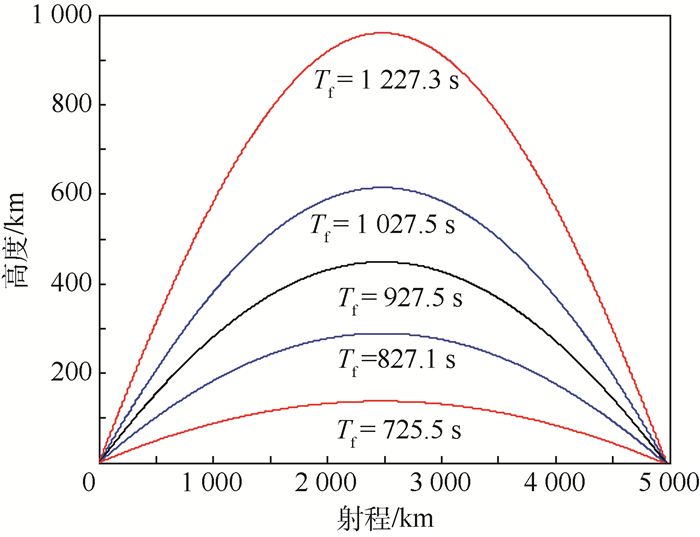 |
| 图 13 不同飞行时间以及相应的弹道 Fig. 13 Multiple flight time and corresponding trajectories |
| 图选项 |
4.2 可拦截的部署区域 按照前述进攻弹道的设计,为了简单起见将弹道导弹的发射点取在(0°, 0°),落点取在(E45°, 0°),飞行时间Tf设为1 000 s。拦截弹发射阵地按2°间隔遍历0°~E90°,S40°~N40°范围内,仿真得到可以成功拦截目标的部署阵地范围如图 14所示。
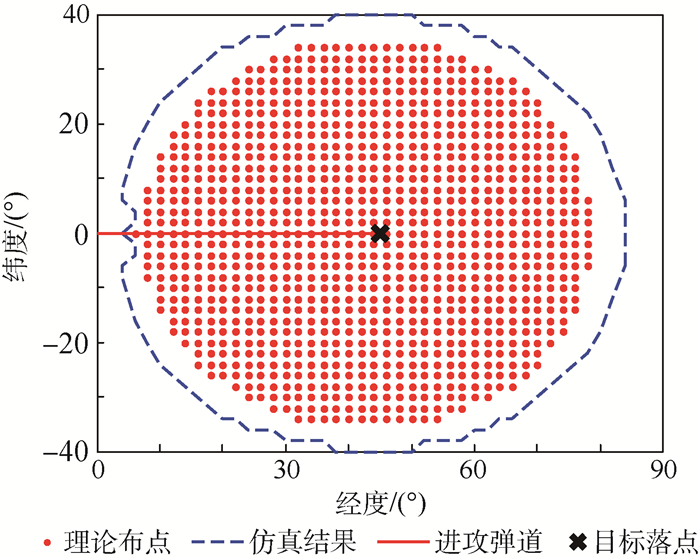 |
| 图 14 理论计算与仿真得到的布防区对比 Fig. 14 Comparison of defense deployment zone between theoretical calculation and simulation |
| 图选项 |
图 14中虚线是仿真中拦截成功的发射点集的边缘,点表示理论计算得到的可拦截布点的集合。理论计算是利用Kepler公式与Lambert迭代算法,即式(11)中加入约束|V|≤5 500 m/s得到的,相当于在该点处发射初速度不超过5 500 m/s的“脉冲”拦截弹,且不考虑大气层的作用下能够与目标弹道交会的情形。由于实际的拦截弹动力学模型考虑了助推器加速过程,所以理论模型忽略了该要素后,估算出来的可拦截防御区会比实际情况有所“缩水”。但仍可以看到虚线与点的边缘形态是相符的,体现了可拦截的部署点的分布规律,因此仍不妨用“脉冲拦截弹”的理论方法来估算大致的可用拦截布点。
关于图 14的一点补充说明,虽然部分拦截弹的发射点可能接近目标起始位置,但实际上最终的碰撞点仍然在目标弹道的外大气层段。由于拦截弹从起飞到释放EKV的时间不少于70 s,且无法在大气环境内(h≤80 km)工作,那么受3.2节中tMIN的限制,PIP将选择在弹道中段晚于tMIN时刻的位置。从而这些拦截弹的初始射向是顺着目标弹道走向,在中段较高处“截住”目标的。
根据图 14,确定起点落点后,变换不同的飞行时间会得到不同的弹道中段高度,下面考察这一变化对可拦截阵地区域的影响,仿真结果如图 15所示。
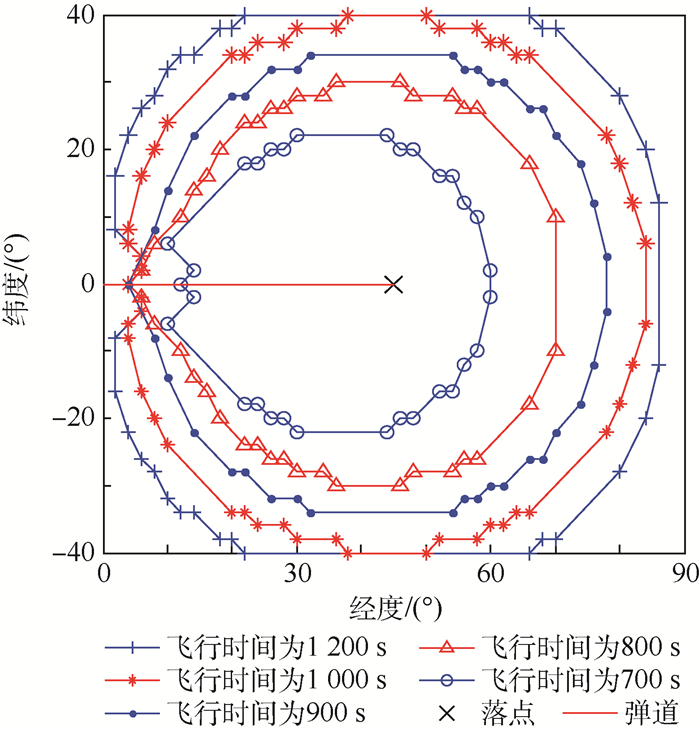 |
| 图 15 各飞行时间下弹道对应的布防区 Fig. 15 Defense deployment zones for different trajectories corresponding to each flight time |
| 图选项 |
可以看出随着目标沿着更快更低的弹道飞行,可拦截部署区域总体上是在不断缩小的。这为进攻方选择突防弹道提供了参考,在助推器性能足够的前提下,更大的关机速率和更短的飞行时间是有利于规避拦截的。而且也压缩了防御方的拦截窗口,减少可用的拦截次数,对于打击舰船、部队集结地等时敏类型的目标也很有必要。
4.3 目标弹道的拦截区段 将拦截弹的发射点固定在(E22.5°, 0°),在圆球大地模型下,设计一组近似平行的5 000 km的进攻弹道,飞行时间均为1 000 s,其在弹道中点处互相平行,且中点都投影在E22.5°经线上。通过仿真考察拦截弹在这一组弹道上的发射区段/拦截区段分布。
由图 16可以看出拦截弹部署在目标弹道正下方时,拥有最大拦截窗口,最早和最迟的拦截碰撞点仅取决于目标被发现的时间,以及再入大气层(h < 100 km)的时间。而对于远离部署点的弹道,拦截窗口逐步变窄,这是由于拦截弹需要更长的时间才能飞抵拦截段。
 |
| 图 16 针对5 000 km弹道组的发射区段与拦截区段 Fig. 16 Firing/intercept sections on a series of trajectories with range of 5 000 km |
| 图选项 |
4.4 固定部署点的保护区 假设进攻弹的发射阵地已知,设为(0°, 0°),弹道均采用“最小能量弹道”,射程从1 000~15 000 km不等。对于固定部署的拦截阵地(E45°, 0°)可以研究其能够保护的范围。当弹道导弹的落点位于这一区域,就可能在飞行过程中的某一时刻被拦截弹毁伤。
图 17中弹道导弹的落点遍历E10°~E130°,S60°~N60°的范围,其中只有圆点部分是位于(E45°, 0°)处的拦截阵地未能保护的区域。
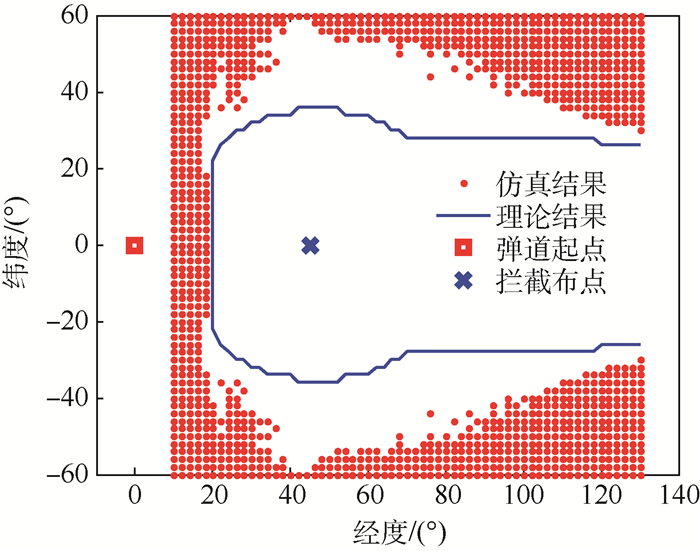 |
| 图 17 单个拦截阵地的保护区域 Fig. 17 Protective zone of single intercept position |
| 图选项 |
相同条件下考察具有5 500 m/s初速度的“脉冲”拦截弹的保护区域,如图 17中实线轮廓所示。当弹道导弹的落点进入实线内部即被拦截。与4.2节的情况相似,最大速度近似的情形下,具有三级助推加速段的拦截弹模型要比Lambert理论模型的作用范围略大。
4.5 进攻弹采用突防措施 从已有的仿真结果来看,拦截弹凭借自身较大的射程、射高以及关机速度,对于5 000~10 000 km的弹道导弹都拥有很强的拦截能力。进攻弹如果希望有效应对防御方的拦截,需要采取进一步的突防措施,具体的设计过程如下所述。
4.5.1 变轨机动策略 弹道导弹在关机时刻瞄准的是一个掩护目标点P1,弹头按照预定的时间td依靠反冲作用与附属质量体分离,同时获得所需的速度增量ΔVt而实现变轨,如图 18所示,一面摆脱拦截弹的攻击,一面使得落点变动到真正计划打击的目标P2。
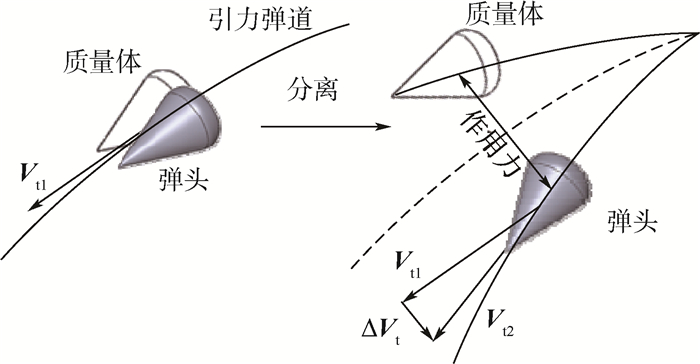 |
| 图 18 弹头机动变轨示意图 Fig. 18 Schematic diagram of warhead maneuver orbital transfer |
| 图选项 |
图 19所示情形,进攻弹在关机后200 s时调整落点,设弹头当前速度为Vt1,然后利用式(6)、式(7)并在r0处代入当前位置P0,在rF处代入落点位置P2,迭代计算不同速度倾角
 |
| 图 19 弹头变轨致使修正预测拦截点 Fig. 19 Revision of predicted intercept point due towarhead orbital transfer |
| 图选项 |
4.5.2 干扰突防措施 在变轨的同时,弹头启用电子压制干扰并释放红外诱饵。电子干扰的目的在于延迟防御方对变轨后的弹头重新进行弹道预测,具体有效的作用时间取决于防御方的抗干扰能力。
图 20展示了电子干扰的意义。当弹头(左侧)在P0处,其速度由Vt0变至Vt1时,假设拦截弹此刻位于P1处(右侧),其速度为Vm0,如能迅速响应,将速度修正至Vm1即可;而假如拦截弹一时没有响应目标的变轨机动,继续飞行到位置P2才开始修正,就需要修正速度至Vm2,当导弹速度的模|Vm|变化不大时,速度方向修正的角度越大,需要的过载也越大。因此延迟防御系统探测到变轨后的弹头,可以进一步加大拦截难度。
 |
| 图 20 电子干扰延迟拦截弹的响应 Fig. 20 Interceptor response delay due to electronic jamming |
| 图选项 |
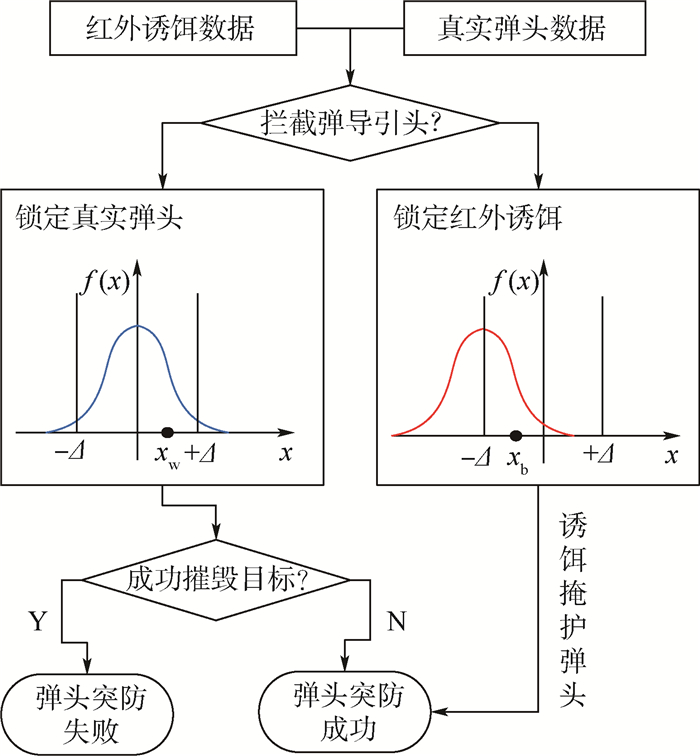
红外诱饵针对来袭的EKV红外导引头,使其有一定的概率错失真实目标。如图 21所示,假设弹头和诱饵的信号样本xw、xb均满足正态分布,则每个目标的信号值落入一个特定区间[-Δ, +Δ]的概率,是将各自的概率密度函数f(xw)和f(xb)在该区间上的积分。而导引头辨识目标的机制可以归结为一个或多个这样的区间,将信号值落在区间内部的目标认作真实弹头[18]。
 |
| 图 21 包含诱饵的拦截仿真示意图 Fig. 21 Schematic diagram of intercept simulation including baits |
| 图选项 |
文献[18]分析了红外诱饵对EKV的干扰效应,对于进入导引头视界的所有目标,EKV都将根据预设的识别机制逐个判断。其中,弹头被正确识别的概率为Pww,被判定为诱饵的概率为Pwd=1-Pww;诱饵被正确识别的概率为Pdd,被判定为弹头的概率为Pdw=1-Pdd。
当所有信号源都被识别完毕后,EKV将从自己认定的“真实目标”中,随机锁定一个并攻击。而当弹目距离接近到成像识别距离|RTM0|,如果先前锁定的是诱饵,EKV将重新搜索弹头并机动修正,直至拦截或脱靶。
4.6 突防措施的仿真检验 假设电子干扰的有效作用时间是随机的,取值范围[20, 40] s,代表防御方抗干扰能力的不确定性;红外诱饵对EKV导引头的欺骗概率为Pdw=0.7,而导引头误判弹头为诱饵的概率为Pwd=0.1。当弹目相距|RTM0|≤10 km时2种误判概率归0,即该诱饵/弹头将被EKV识别出来,其他条件见表 3。
表 3 进攻弹的仿真想定 Table 3 Scenario of ballistic missile
| 关机点 | 目标Ⅰ | 目标Ⅱ | 飞行时间/s | 诱饵数 |
| (0°, 0°) | (E45°, 0°) | (E42°, N2°) | 685.46 | 8 |
表选项
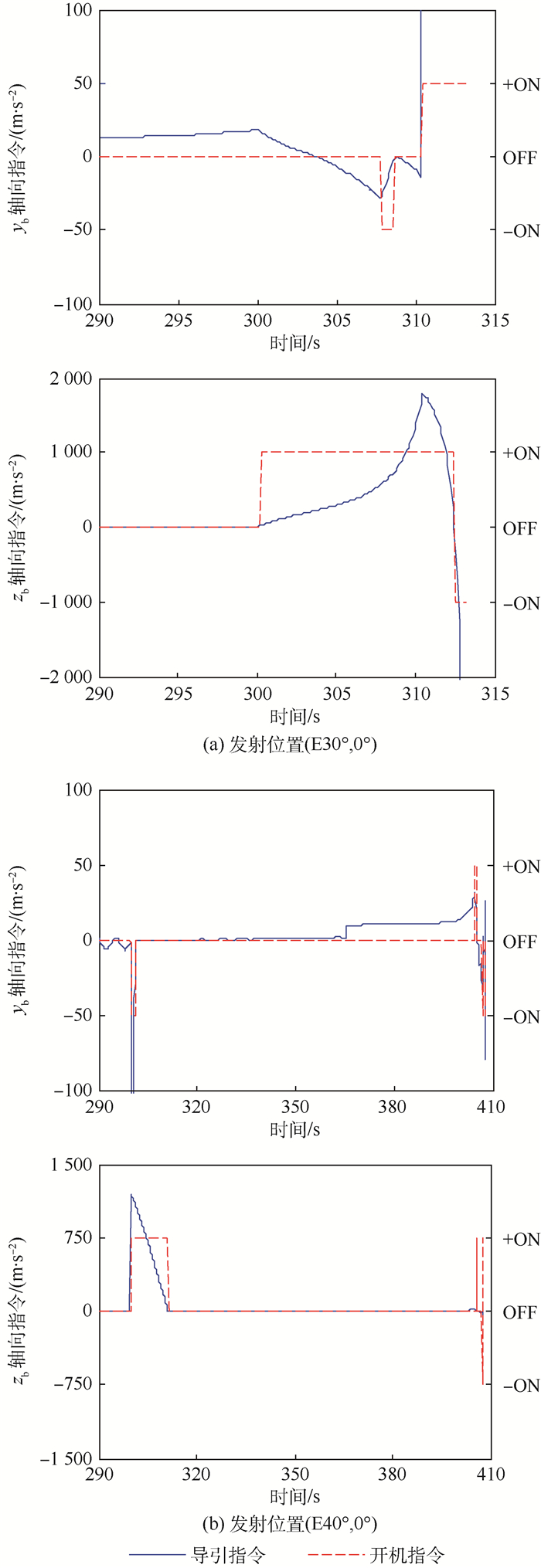
先考察弹头仅采取变轨的影响。弹头在关机300 s后与质量体分离变轨,将落点由目标Ⅰ调整至目标Ⅱ,获得速度增量604.0 m/s,完成后释放红外诱饵。防御方从(E30°, 0°)、(E40°, 0°)2处阵地同时发射拦截弹,得到的结果如图 22所示,右侧纵轴对应虚线,表示轨控发动机开关指令,只分为正向开机(+ON),反向开机(-ON)和关机(OFF) 3种情形。
 |
| 图 22 各火力单元拦截弹的末制导指令 Fig. 22 Terminal guidance commands of interceptor of each firing unit |
| 图选项 |
图 22展现了末制导过程中拦截弹的加速度导引指令和轨控发动机开关指令。自300 s开始由于目标变轨,加速度指令都产生了幅度不等的波动。比较来看当目标变轨更接近交会时刻,拦截弹的修正难度会更大。而针对同一条弹道,拦截交会时刻主要取决于拦截弹的发射位置。
从表 4中可以看出,对于(E30°, 0°)发射的拦截弹,弹头变轨的时机处在交会前13 s,且是速度突变的方式,则EKV即使全程开启轨控也难以修正,这一点在图 22左侧也有所体现;而对于(E40°, 0°)发射的拦截弹,弹头变轨的时机处在交会前110 s,因此EKV还有时间消除目标变轨产生的ZEM。
表 4 拦截仿真结果 Table 4 Intercept simulation results
| 发射阵地 | 飞行时间/s | 燃料消耗/% | 脱靶量/m |
| (E30°, 0°) | 313.22 | 72.41 | 3326.2 |
| (E40°, 0°) | 408.87 | 62.62 | 0.0393 |
表选项
图 23为弹头采用变轨措施前后可拦截阵地的对比,除目标Ⅱ方向延长线上有一片区域拦截失败以外,还有沿(E20°, N10°)→(E30°, 0°)→(E20°, S10°)形成的一个圆弧形空白区域,其中发射的拦截弹失败原因是类似的,都是由于目标变轨后留下的时间不足以修正。这提示了进攻方可以根据拦截阵地的位置选择变轨时机,使其处在这样的空白区内,从而成功突防。
 |
| 图 23 机动变轨目标及常规目标的可拦截发射点对比 Fig. 23 Comparison of launch points for intercepting maneuver orbital transfer target and general target |
| 图选项 |
以上仅为单次仿真结果。当弹头使用“变轨-干扰-诱饵”多重突防手段后,需要利用蒙特卡罗仿真来得到一些随机因素对拦截弹的影响。
从图 24中可以看到,弹头变轨前即发生交会的区域,拦截成功率普遍高于80%;而突防措施启动后的区域内,进攻弹的突防效能明显上升,拦截成功率普遍不足30%。由于对抗目标机动已经消耗大部分燃料,尽管在最后10 km范围内EKV能重新识别目标,但无余力完成弹道修正,拦截失败。这体现了多重干扰手段联合作用的效能。
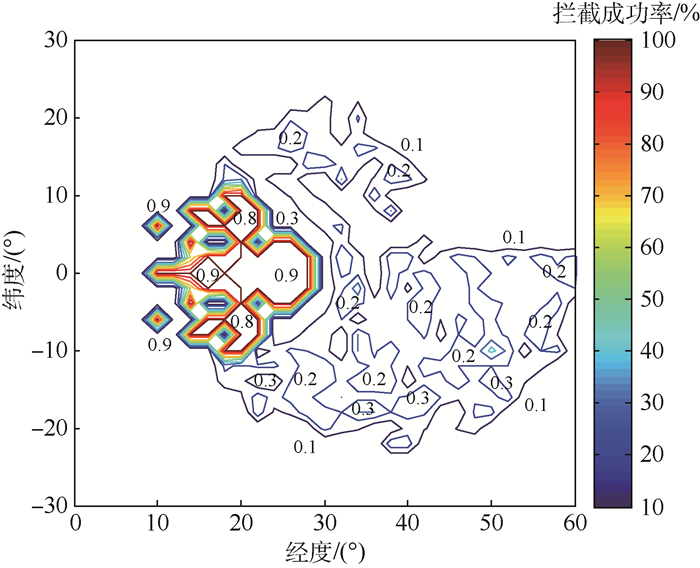 |
| 图 24 部署区域内拦截成功率的分布 Fig. 24 Successful intercept probability distribution in deployment zone |
| 图选项 |
4.7 突防措施的效能分析 本文所列举的3类突防措施,包括机动变轨、电子干扰和红外诱饵掩护。其中变轨机动和电子干扰是联合运用的,针对的是已经迫近的拦截弹,造成的影响在于预测拦截点急剧变化,从而加大拦截弹道的修正难度,即大幅消耗EKV的燃料。从4.2~4.4节的试验可以看出,防御系统针对常规弹道类目标的拦截能力较强,区域范围、时间范围都很广,说明及时、准确地预测目标弹道对于反导成功至关重要;而通过变轨、干扰雷达来打破这一环节也就成为了进攻方的选择。
相比较而言,红外诱饵掩护作用时间很长,释放后对于来袭的拦截弹普遍有效。它的作用机理主要是针对末制导,利用随机因素降低EKV的杀伤概率。从统计层面来看,拦截成功率降低和进入红外导引头视野的诱饵数目n直接相关。假设在众多目标当中只有一个真实弹头,则最终该弹头被EKV导引头选中锁定的概率为
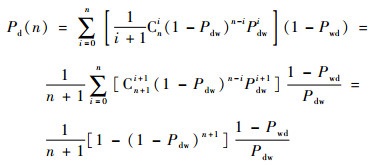 | (20) |
按照仿真条件设置,Pdw=0.7,Pwd=0.1,且诱饵总数为8(即n≤8)时,枚举各种情形可以得到表 5。
表 5 诱饵数与EKV锁定弹头的概率 Table 5 Bait number and probability of EKV locking on warhead
| n | 3 | 4 | 5 | 6 | 7 | 8 |
| Pd(n) | 0.3620 | 0.2565 | 0.2141 | 0.1836 | 0.1607 | 0.1429 |
表选项
考察弹头被诱饵成功掩护的概率1-Pd(n),与图 24中E30°以远布点的突防概率数据十分相符,说明在拦截弹有能力对抗变轨机动的情况下,弹头能否生存主要取决于末制导中EKV红外导引头捕获的诱饵数量n。由于释放后诱饵的分布与弹头速度方向相关,不同阵地发射的拦截弹沿弹目连线RTM的方向,探测到的目标个数也就有所不同。而释放8颗红外诱饵,可以确保至少在一侧方向上有4个或更多的诱饵分布,根据表 5,拦截弹锁定弹头的概率会降至25%以内。由于机动变轨已经很大程度上消耗了EKV的燃料,所以即使进入最后的识别距离|RTM0|,EKV也难以将轨迹从拦截诱饵修正到拦截真实弹头。
5 结论 本文由当前备受关注的导弹攻防对抗问题引出,探讨了某型大气层外拦截弹的反导运作机制以及弹道导弹突防作战的效能问题。
1) 基于当前装备发展信息和反导拦截各阶段的工作原理,建立了一种三级助推的大气层外拦截弹动力学模型。
2) 根据Lambert原理和射表插值思想,设计了一种大气层外远距离、长航时的拦截制导策略。
3) 研究了某中远程弹道导弹的弹道特性,通过分析拦截弹的可拦截部署区域,发射段与拦截段、指定阵地的保护区域验证了本文设计的大气层外拦截制导策略的有效性。
4) 从理论上分析了弹道导弹不同的突防措施及其所产生的效能,并与仿真结果互相印证,说明了模型、算法以及设计理论的可信度与可行性,期望能够为将来的装备规划、发展与部署提供理论支持和参考。
参考文献
| [1] | ZARCHAN P.Tactical and strategic missile guidance[M].6th ed.Reston: AIAA, 2012: 213-324, 715-862. |
| [2] | ZES D.Exo-atmospheric intercept using modified proportional guidance with gravity correction for coast phase: AIAA-94-0209[R].Reston: AIAA, 1994. |
| [3] | ZES D.Exo-atmospheric intercept with J2 correction: AIAA-98-4305[R].Reston: AIAA, 1998.https://www.sciencedirect.com/science/article/pii/S0016003211001669 |
| [4] | PHILLIPS C A, MALYEVAC D S. Pulse motor optimization via mission charts for an exoatmospheric interceptor[J].Journal of Guidance, Control, and Dynamics, 1998, 21(4): 611–617.DOI:10.2514/2.4279 |
| [5] | PHILLIPS C A, MALYEVAC D S. Exoatmospheric interceptor pulse motor optimization with discrete bias removal[J].Journal of Guidance, Control, and Dynamics, 2000, 23(2): 376–378.DOI:10.2514/2.4537 |
| [6] | GUTMAN S, RUBINSKY S.Exo-atmospheric mid-course guidance[C]//AIAA Guidance, Navigation, and Control Conference.Reston: AIAA, 2015: 1-17. |
| [7] | HABLANI H B.Pulsed guidance of exoatmospheric interceptor with image processing delays in angle measurements: AIAA-2000-4272[R] Reston: AIAA, 2000.https://www.researchgate.net/publication/269208887_Pulsed_guidance_of_exoatmospheric_interceptors_with_image_processing_delays_in_angle_measurements |
| [8] | HABLANI H B, PEARSON D W. Miss distance error analysis of exoatmospheric interceptors[J].Journal of Guidance, Control, and Dynamics, 2004, 27(2): 283–289.DOI:10.2514/1.9168 |
| [9] | GUO J G, ZHANG T B, ZHOU J, et al. The three dimensional guidance system design of terminal attack phase for exo-atmospheric kill vehicle[J].International Journal for Light and Electron Optics, 2017, 130: 1158–1167.DOI:10.1016/j.ijleo.2016.11.135 |
| [10] | SHIMA T, GOLAN O M. Exo-atmospheric guidance of anaccelerating interceptor missile[J].Journal of the Franklin Institute, 2012, 349(2): 622–637.DOI:10.1016/j.jfranklin.2011.06.024 |
| [11] | ENDER T, LEURCK R F, WEAVER B. Systems-of-systems analysis of ballistic missile defense architecture effectiveness through surrogate modeling and simulation[J].IEEE Systems Journal, 2010, 4(2): 156–166.DOI:10.1109/JSYST.2010.2045541 |
| [12] | 吴钰飞, 罗小明, 申之明, 等. 诱饵影响下多枚弹道导弹突防效能研究[J].装备学院学报, 2008, 19(3): 57–62. WU Y F, LUO X M, SHEN Z M, et al. Study on the penetration effectiveness of multiple ballistic missiles considering the effect of decoys[J].Journal of the Academy of Equipment Command & Technology, 2008, 19(3): 57–62.DOI:10.3783/j.issn.1673-0127.2008.03.013(in Chinese) |
| [13] | YAO J, HUANG Q, WANG W. Analyzing ballistic missile defense system effectiveness based on functional dependency network analysis[J].The Open Cybernetics & Systemics Journal, 2015, 9(1): 678–682. |
| [14] | 杨晓凌, 邱涤珊. 三种不确定性条件下的拦截器目标分配模型[J].弹箭与制导学报, 2012, 32(4): 4–8. YANG X L, QIU D S. Interceptor allocation models under threr types of uncertainty[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(4): 4–8.DOI:10.3969/j.issn.1673-9728.2012.04.002(in Chinese) |
| [15] | WILKENING D A. A simple model for calculating ballistic missile defense effectiveness[J].Science and Global Security, 1999, 8(2): 183–255. |
| [16] | GLASER C L, FETTER S. Should the United States reject MAD?Damage limitation and U.S.nuclear strategy toward China[J].International Security, 2016, 41(1): 49–98.DOI:10.1162/ISEC_a_00248 |
| [17] | XIE J W, CHEN W C.Switching logic design for divert and attitude control system of exoatmospheric kill vehicle[C]//8th IEEE International Conference on Cybernetics and Intelligent Systems(CIS)/IEEE Conference on Robotics, Automation and Mechatronics (RAM).Piscataway, NJ: IEEE Press, 2017: 194-200. |
| [18] | 谢经纬, 陈万春. 基于概率模型的攻防效能估算与仿真分析[J].导弹与航天运载技术, 2017(4): 1–5. XIE J W, CHEN W C. Estimation and simulation analysis based on probabilistic model for the effectiveness of penetration and defense[J].Missiles and Space Vehicles, 2017(4): 1–5.(in Chinese) |
