飞越轨道的优化设计是实施空间飞越的基础,然而因为各种不确定性因素的存在,航天器难以按照预先设计的最优轨道进行飞越,所以相对于轨道优化设计,更为关注的是在一定初始条件下发射窗口的计算方法。目前对运载火箭的发射窗口计算已较为成熟,但是对从停泊轨道出发的发射窗口研究较少。文献[6]使用遍历搜索方法,研究了嫦娥二号从环日地L2点轨道出发,飞越探测小行星的发射窗口;文献[7]提出了基于发射窗口的天基发射方案,在给定初始条件下计算了发射窗口,研究了轨道规划策略。在进行分析计算时,不同初始条件下的发射窗口不同,初始条件是一个重要的影响因素,所以有必要对此进行研究。
为研究初始条件的影响,需要对若干组不同初始条件下的发射窗口进行分析,而每一组都需要采用数值方法进行遍历搜索来计算,因此计算量大、耗时长,需要研究高效的计算方法。代理模型(surrogate models)技术是一种降低计算成本的有效方法,所谓代理模型是指计算量小、但计算结果与真实模型的结果相近似的分析模型。在研究过程中用代理模型替代真实的高精度模型,可以有效地减少计算量、提高仿真计算的效率[8-9]。代理模型技术是多学科优化领域的重要研究内容之一,但在航天器轨道设计与发射窗口计算中的应用较少。文献[10]通过构建BP神经网络(Back Propagation Neural Network,BPNN)代理模型,进行了空间飞行器可遭遇区与最小速度增量遭遇点的计算。
本文针对空间飞越问题,研究不同初始条件下发射窗口的数值计算方法和代理模型技术,对比分析不同的代理模型构造方法在解决该问题中的效果和适用性,基于代理模型快速分析初始条件对发射窗口的影响。
1 考虑初始条件的发射窗口计算 1.1 空间飞越任务流程 一次空间飞越任务如图 1所示。
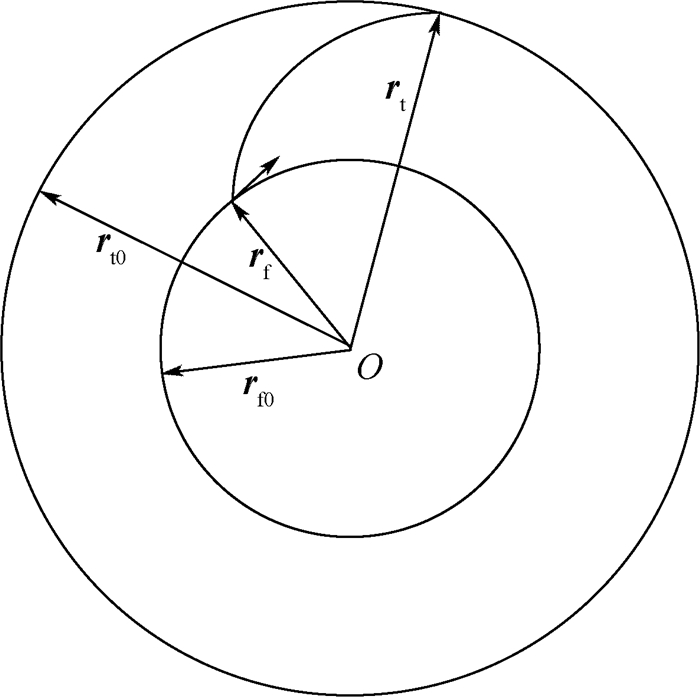 |
| 图 1 空间飞越任务示意图 Fig. 1 Schematic diagram of space fly-by mission |
| 图选项 |
从接收飞越任务指令到完成飞越任务的具体流程如下:
1) t0时刻接收指令,此时飞越航天器和目标航天器的位置分别为rf0、rt0。
2) 接收飞越任务后,飞越航天器和目标航天器继续飞行Δt0时间,到达t1时刻,t1=t0+Δt0。此时飞越航天器的位置为rf,目标航天器的位置为r ′t。
3) 在t1时刻,飞越航天器施加脉冲进行变轨。
4) 飞越航天器变轨后,飞行Δt时间,到达t2时刻,t2=t1+Δt。此时飞越航天器到达飞越点,实现飞越。因为飞越点与目标航天器的距离和该点与地心的距离相比极小,可以忽略,所以假定此时飞越航天器和目标航天器的位置均为rt。
完整的飞越任务时序如图 2所示。定义从接收指令到施加脉冲前的时间Δt0为等待时间,从施加脉冲到完成飞越的时间Δt为转移时间,总时间为飞越时间Δts= Δt0+Δt。
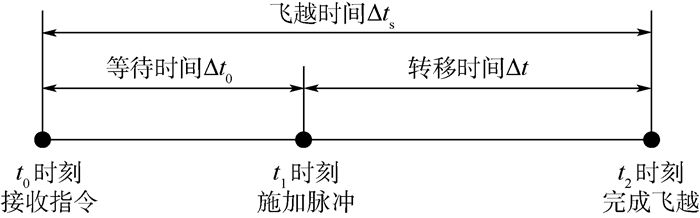 |
| 图 2 空间飞越任务时序 Fig. 2 Timing sequence of space fly-by mission |
| 图选项 |
1.2 不同初始条件下发射窗口计算方法 空间飞越发射窗口的计算需要考虑多个约束条件,包括变轨速度增量、飞越时间、飞越点状态、飞越过程燃料等。其中飞越点状态约束包括飞越点位置和速度约束、飞越点光照条件约束等;飞越过程燃料约束是为了保证飞越点精度,进行中途修正所需的燃料约束。
因为本文研究的是空间飞越而非空间交会,所以飞越点速度约束暂不考虑;本文采用二体动力学模型下的Lambert变轨,不考虑摄动因素,因而可以保证飞越点位置约束满足要求,且无需考虑中途修正及其燃料约束;在飞越点附近对目标航天器进行观测时要求日光、月光、地气光等不能进入观测设备的视场影响观测效果,仿真结果表明,光照条件在短时间内变化极小,因此本文假设在任务期间飞越点光照条件不变且满足约束。而变轨速度增量和飞越时间是最重要、最基本的2个约束,如文献[7, 10-11]均在只考虑这2个约束的条件下来计算发射窗口。综上,本文重点考虑变轨速度增量约束和飞越时间约束。
将所有满足约束的t1时刻的集合作为发射窗口,发射窗口随t0时刻初始条件的变化而变化。假设不考虑摄动力的影响,飞越航天器和目标航天器的轨道在空间固定不变,则t0时刻两者的初始位置rf0和rt0只与其平近点角mf0和mt0有关。所以,研究初始条件对发射窗口的影响即研究平近点角的影响,具体步骤如下:
步骤1??初始化飞越航天器平近点角mf0=0°。
步骤2??初始化目标航天器平近点角mt0=0°。
步骤3??初始化等待时间Δt0=Δt0 min,Δt0min为最小等待时间。
步骤4??初始化转移时间Δt=Δtmin,Δtmin为最小转移时间。
步骤5??根据mf0和mt0计算飞越航天器和目标航天器的初始位置rf0、rt0,然后根据Δt0和Δt计算出rf、rt,使用普适变量法求解Lambert问题得到速度增量Δv;计算飞越时间Δts=Δt0+Δt;如果Δv < Δvmax且Δts < Δtsmax,则t1时刻属于初始条件为mf0和mt0时的发射窗口,其中Δvmax和Δtsmax分别为变轨速度增量和飞越时间的最大允许值。
步骤6??更新Δt=Δt+Δtstep,Δtstep为转移时间的步长;如果Δt < Δtmax,则返回步骤5,否则进行步骤7,其中Δtmax为最大转移时间。
步骤7??更新Δt0=Δt0+Δt0step,Δt0step为等待时间的步长;如果Δt0 < Δt0max,则返回步骤4,否则进行步骤8,其中Δt0max为最大等待时间。
步骤8??更新mt0=mt0+mtstep,mtstep为目标航天器平近点角的步长;如果mt0 < 360°,则返回步骤3,否则进行步骤9。
步骤9??更新mf0=mf0+mfstep,mfstep为飞越航天器平近点角的步长;如果mf0 < 360°,则返回步骤2,否则结束。
计算过程如图 3所示。
 |
| 图 3 发射窗口计算过程 Fig. 3 Calculation process of launch window |
| 图选项 |
可以看出,研究初始条件对发射窗口的影响,需要对mf0、mt0、Δt0和Δt 4个变量进行循环计算,计算量极大。
文献[11]研究了一种特殊的情况:飞越航天器和目标航天器的轨道为共面圆轨道时,初始条件对发射窗口的影响。定义初始相位角θ0为t0时刻飞越航天器与目标航天器的地心角,即两者纬度幅角之差,则在共面圆轨道的假设下,初始条件的变化只与初始相位角θ0的变化有关。因此,只需研究初始相位角的变化对发射窗口的影响,即在计算过程中只需θ0、Δt0和Δt 3个变量的循环。研究结果显示,在共面圆轨道情况下计算耗时约为10 min。而对于一般情况,初始条件与平近点角mf0和mt0有关,相比于共面圆轨道,计算过程多了一重循环,假设以1°为步长,则计算量为原来的360倍,预计耗时约60 h,计算时间过长,因此需要研究提高计算效率的方法。
2 代理模型技术 代理模型是根据真实模型的输入/输出样本数据来构造的一个替代模型。构造代理模型一般需要3个步骤:首先, 选取样本点,通过真实模型计算出对应的输出值,生成输入/输出样本数据;然后, 根据样本数据构造出代理模型;最后, 对代理模型的精度进行校验,评估其可信度[12-13]。
2.1 生成样本数据 构建代理模型,首先是选取样本点并计算样本点的输出值。通常使用试验设计作为采样策略,通过科学合理的数学安排,在设计空间内生成能够反映真实计算模型的数值特征的样本点[14]。常用的试验设计方法包括:全析因设计、正交设计、中心复合设计、均匀设计、拉丁超立方设计等。
在试验设计中,输入变量被称为因素,因素所处的状态称为水平[15]。本文选用全析因设计方法,该方法将所有因素的所有水平进行组合来选取样本点,能够全面反映输入变量及其相互间的交互作用对输出值的影响。全析因设计生成的样本点数ns为
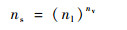 | (1) |
式中:nv为因素数,即输入变量的个数;nl为水平数。
通过试验设计得出样本点x=[x1, x2, …, xns]之后,需要计算每个样本点所对应的输出值,针对本文研究的问题来说,即为样本点所对应的发射窗口长度。发射窗口长度的计算使用1.2节的方法,只是对于每个样本点来说,mf0和mt0确定,只需计算Δt0和Δt 2个变量的循环,即步骤3~步骤7。最终得到样本点输出数据y=[y1, y2, …, yns]。
生成输入/输出样本数据后,可以进行代理模型的构造。
2.2 构造代理模型 常用的代理模型构造方法包括多项式响应面法(Response Surface Method,RSM)、移动最小二乘(Moving Least Square,MLS)、径向基函数(Radial Basis Function,RBF)、Kriging模型、BPNN和支持向量回归(Support Vector Regression,SVR)等。文献[14]从近似精度、计算成本、实现难度等方面对典型的代理模型构造方法进行了对比评估,得出RBF模型和Kriging模型的综合性能优于其他代理模型。因此,本文研究这2种代理模型在空间飞越发射窗口计算中的应用。
2.2.1 RBF模型 径向函数是以未知点与样本点之间的欧氏距离为自变量的一类函数。以径向函数为基函数,通过线性叠加构造出来的模型即为RBF模型,其基本形式为[14, 16]
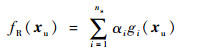 | (2) |
式中:fR(xu)为未知设计点xu处RBF模型的预测值;α=[α1, α2, …, αns]T为权重系数向量;gi(xu)为径向函数,常用的径向函数有
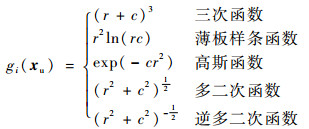 | (3) |
式中:r=||xu-xi||为两点之间的欧氏距离,xi为第i个样本点;c为形状系数,可通过经验公式或优化求得。
构建RBF模型的重点是求解权重系数α,α应满足插值条件,使样本点处的预测值与真实值相等,即
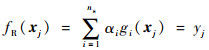 | (4) |
式中:xj为第j个样本点;yj为第j个样本点的输出。式(4)的矩阵形式为
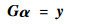 | (5) |
式中:G为径向函数矩阵
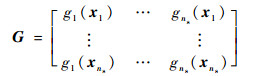 | (6) |
则权重系数
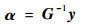 | (7) |
2.2.2 Kriging模型 Kriging模型是由南非地质****Krige提出的一种针对空间分布数据的无偏最优估计插值模型,由全局模型和局部偏差模型叠加而成,其基本形式为[14, 17]
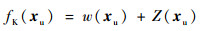 | (8) |
式中:w(xu)为多项式全局近似模型,反映近似对象在设计空间内的总体变化趋势,可取常数μ;局部偏差项Z(xu)是一个随机过程,其均值为零、方差为σ2、协方差非零。Kriging模型的近似能力主要由局部偏差项Z(xu)决定,其协方差矩阵可表示为
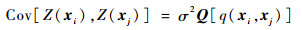 | (9) |
式中:Q为对称相关矩阵; q(xi, xj)为高斯相关函数
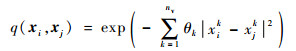 | (10) |
式中:xik为第i个样本点中的第k个变量;θk为相关参数,为了降低复杂度,通常θk可以取常值θ。
对任一设计点xu,引入相关向量p(xu)为
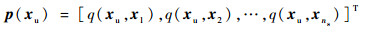 | (11) |
由此,Kriging模型可以表示为
 | (12) |
式中:d可设为元素全为1的ns维列向量。模型中存在3个未知量:μ、θ和σ2,其中μ和σ2都是θ的函数,两者的最小二乘估计可通过式(13)和式(14)求出:
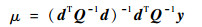 | (13) |
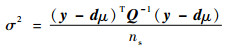 | (14) |
将μ和σ2的表达式代入式(15)所示的一维优化问题可求解得到相关参数:
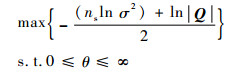 | (15) |
2.3 校验代理模型精度 代理模型构建完成之后,需要对其精度进行评估和校验。通常根据以下2个准则来判断代理模型的精度[8]:复相关系数R2和均方根误差(Root Mean Square Error,RMSE),其表达式为
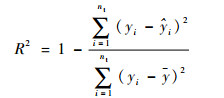 | (16) |
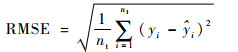 | (17) |
式中:nt为进行精度校验的测试样本点个数;?i为测试样本点通过代理模型预测得到的输出值;y为样本点真实输出值的均值。
R2越接近1,表示代理模型的全局近似程度越好,一般认为大于0.9即满足要求,此处R2为统计学符号,并非平方,其值可能为负;RMSE越接近0,表示最大的局部误差越小,一般认为小于0.2即满足要求。
3 两种代理模型方法的对比 针对本文研究的空间飞越过程中初始条件对发射窗口影响的问题,利用1.2节提出的数值计算方法,根据代理模型技术构造RBF模型和Kriging模型,对2种模型的精度进行对比分析。
设t0时刻飞越航天器和目标航天器的轨道根数如表 1所示。表中,a为半长轴,e为偏心率,i为轨道倾角,Ω为升交点赤经,ω为近地点幅角。
表 1 t0时刻轨道根数 Table 1 Orbit elements at moment t0
| 航天器 | a/km | e | i/(°) | Ω/(°) | ω/(°) |
| 飞越航天器 | 6 978 | 0.06 | 97.1 | 180 | 0 |
| 目标航天器 | 7 878 | 0.15 | 102.0 | 180 | 90 |
表选项
采用全析因试验设计方法选取样本点。本文研究的是初始条件对发射窗口的影响,因此输入变量设为飞越航天器和目标航天器的平近点角mf0和mt0,因素数为2;在设计空间[0°, 360°)内以10°为步长取值,因素数为36;因此是一个2因素36水平的试验设计问题,样本点数ns=362=1 296。
计算出每个样本点所对应的输出值,利用输入/输出样本数据x、y构建RBF模型和Kriging模型。
为校验代理模型的精度,在设计空间内随机选取200个测试样本点,计算2个代理模型的R2和RMSE。计算结果如表 2所示。
表 2 两种代理模型精度对比 Table 2 Accuracy comparison of two surrogate models
| 模型 | R2 | RMSE |
| RBF模型 | 0.993 | 0.018 |
| Kriging模型 | 0.952 | 0.049 |
表选项
从表 2可以看出,以R2和RMSE 2个准则来判断,RBF模型的精度都高于Kriging模型。测试样本点的预测值与真实值的对比如图 4所示,图中的点越靠近对角线,表示该点的预测值与真实值越接近。可以看出,相对于Kriging模型,RBF模型的点在对角线附近更集中,精度更高。
 |
| 图 4 测试样本点分布 Fig. 4 Distribution of test sample points |
| 图选项 |
因此,本文采用RBF模型研究空间飞越过程中初始条件对发射窗口影响。
4 实例验证 以表 1中的轨道根数为例,基于RBF模型进行分析。计算发射窗口时,变轨速度增量约束Δvmax=500 m/s,飞越时间约束Δtsmax= 9 000 s。
提高计算效率、减小计算耗时是本文研究代理模型的初衷和目的,因此首先检验应用代理模型后计算时间上的变化。根据第1节中的分析,在设计空间内以1°为步长使用真实模型进行计算,预计耗时约60 h,计算时间过长。因此以2°为步长使用真实模型和代理模型分别进行计算,计算时间如表 3所示。
表 3 代理模型和真实模型计算时间对比 Table 3 Comparison of calculation time between surrogate model and true model
| s | |||
| 模型 | 代理模型 构建时间 | 发射窗口 计算时间 | 总计算 时间 |
| 真实模型 | 57 688 | 57 688 | |
| RBF模型 | 3 473 | 168 | 3 641 |
表选项
从表 3可以看出,使用RBF模型计算发射窗口耗时仅为使用真实模型的0.29%,计算效率得到极大提高。使用代理模型之前需要先进行构建,因为在构建和校验精度时需要大量样本数据,而这些样本数据是通过使用真实模型计算得出的,所以需要花费一定的时间。但总计算时间也仅为使用真实模型的6.31%,相比而言效率还是较高。而且代理模型的构建是一次性的,一旦构建完成,对于相同轨道根数情况的计算就可以重复使用,无需再次构建。
代理模型除了极大地提高计算效率外,还需要满足一定的精度要求。表 2中的数据显示,RBF模型的R2>0.9,RMSE < 0.2,均满足要求。为直观显示其应用效果,绘制发射窗口长度相对于平近点角mf0和mt0的等值线图,如图 5所示。可以看出,应用RBF模型计算得到的等值线图与使用真实模型得到的结果基本相同,可以反映出初始条件对发射窗口的影响。
 |
| 图 5 真实模型和RBF模型的发射窗口长度等值线图 Fig. 5 Contour map of launch window length of true model and RBF model |
| 图选项 |
通过对等值线图分析可以看出:
1) 对于飞越航天器和目标航天器为非共面圆轨道的情况,发射窗口长度取决于初始时刻两者的平近点角,平近点角之差相同并不能保证发射窗口长度相同。图 6中的虚线为两者平近点角之差为零的点的集合,这些点对应的发射窗口长度不等,最长为2 204.4 s,最短为0 s。
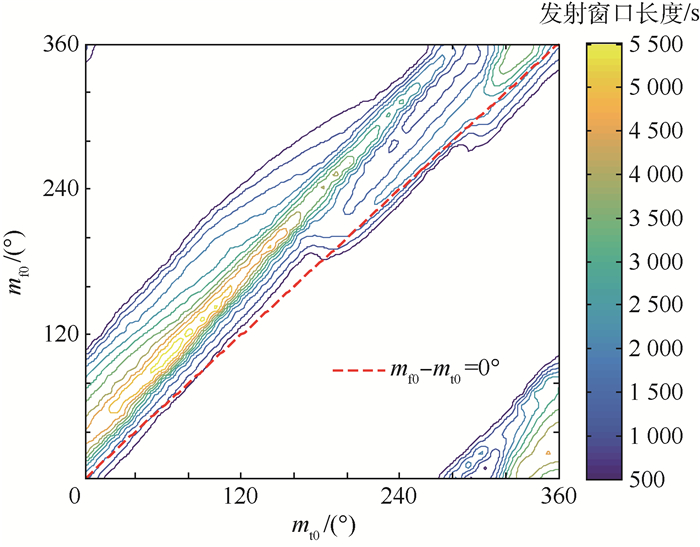 |
| 图 6 平近点角相等时的发射窗口长度 Fig. 6 Launch window length of equal mean anomalies |
| 图选项 |
2) 对于任意的mf0,都存在对应的可行mt0区间,使发射窗口存在,即当目标航天器位于该区间内时,飞越航天器在速度增量和时间约束下能够实现飞越。不同的mf0对应的mt0区间不同,区间长度108°~172°;同样,对于任意的mt0,都存在mf0区间,区间长度108°~188°。如图 7所示,当mf0=160°时,可行mt0区间为[40°, 158°],区间长度118°;当mt0=160°时,可行mf0区间为[162°, 288°],区间长度126°。
 |
| 图 7 可行的平近点角区间示意图 Fig. 7 Schematic diagram of feasible region of mean anomaly |
| 图选项 |
3) 从图 5能够直观地看出发射窗口长度的分布情况和变化趋势,可以选取发射窗口较长的点,在实施空间飞越任务时将其作为初始条件。从图 5(b)可以看出,当以mf0=112°、mt0=72°为初始条件时发射窗口最长,为5 743.1 s。而飞越航天器的轨道周期为5 801.1 s,这意味着在一个周期之内基本都可以实施飞越。
4) 对任意一点,可以根据图 5直接判断其是否具备飞越条件及其发射窗口长度;若以某点为初始条件的发射窗口为0,则可以判断出多长时间后可以具备飞越条件。如图 8所示,A点对应的mf0和mt0为(40°, 80°),以其为初始条件,发射窗口为0,根据飞越航天器和目标航天器的轨道根数,两者平均角速度n1/n2=1.2,则两者的位置随时间的变化在图上表示为以A为起点、斜率为1.2的线段,如图中的虚线所示。可以看出,经过2 526.2 s后虚线与等值线图首次相交于B点,以该点为初始点发射窗口长度为500 s;若要求发射窗口长度不少于某值,如2 000 s,则需要从A点起经过4 124.6 s后到达C点,以C点为初始条件开始飞越。以A点为起点,发射窗口长度随时间变化如图 9所示。
 |
| 图 8 任意一点的发射窗口分析 Fig. 8 Analysis of launch window of one point |
| 图选项 |
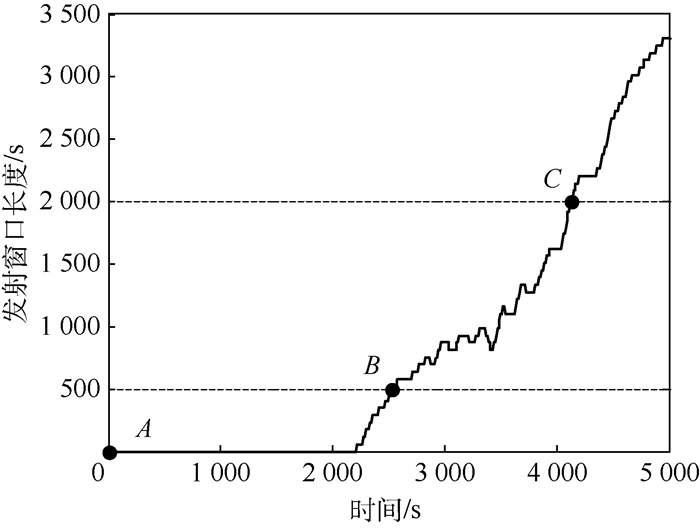 |
| 图 9 发射窗口长度随时间的变化 Fig. 9 Change of launch window length with time |
| 图选项 |
5 结论 1) 本文分析了空间飞越任务流程,建立了用于分析初始条件对发射窗口影响的数值计算模型,该模型包含4个变量的循环,计算耗时约60 h,效率较低。
2) 研究了代理模型技术,采用全析因试验设计方法生成样本数据,构建了RBF模型和Kriging模型,以R2和RMSE准则对比了2种模型的精度,结果表明RBF模型精度较高。
3) 应用RBF模型计算发射窗口长度,计算耗时仅为真实模型0.29%,而且精度校验满足要求。根据发射窗口长度的等值线图,分析了初始条件对发射窗口的影响。
4) 后续可以在2个方面进一步开展研究:一方面,提高发射窗口计算模型的精度,如采用高精度轨道动力学模型,考虑飞越点状态约束、飞越过程燃料约束等;另一方面,提高代理模型的效率和精度,如改善样本点选取方法来减少构建代理模型的成本,研究代理模型的更新和修正方法来提高模型精度等。
参考文献
| [1] | 田野.空间目标飞越式抵近观察制导方法研究[D].长沙: 国防科学技术大学, 2010: 1-2. TIAN Y.Study on guidance methods of fly-by approaching observation of space target[D].Changsha: National University of Defense Technology, 2010: 1-2(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1011280059.htm |
| [2] | 黄江川, 王晓磊, 孟林智, 等. 嫦娥二号卫星飞越4179小行星工程参数分析[J]. 中国科学:技术科学, 2013, 43(6): 596-601. HUANG J C, WANG X L, MENG L Z, et al. Analysis of engineering parameters of CE-2 fly-by 4179 asteroid[J]. Science China:Technology Science, 2013, 43(6): 596-601. (in Chinese) |
| [3] | 李广华.近旁飞越航天器末制导方法研究[D].长沙: 国防科学技术大学, 2011: 1. LI G H.Study on terminal guidance of flyby spacecraft[D].Changsha: National University of Defense Technology, 2011: 1(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1012020948.htm |
| [4] | MATSUMOTO S, DUBOWSKY S, JACOBSEN S, et al.Fly-by approach and guidance for uncontrolled rotating satellite capture[C]//AIAA Guidance Navigation and Control Conference and Exhibit.Reston: AIAA, 2003: 1-10. |
| [5] | 郝瑞, 孟云鹤, 郭胜鹏. 多约束航天器飞越式接近的两级运动规划方法[J]. 上海航天, 2015, 32(3): 16-21. HAO R, MENG Y H, GUO S P. Two-stage motion planning method for fly-by approach of spacecraft with multiple constraints[J]. Aerospace Shanghai, 2015, 32(3): 16-21. DOI:10.3969/j.issn.1006-1630.2015.03.004 (in Chinese) |
| [6] | 刘磊, 刘勇, 曹建峰, 等. "嫦娥二号"探测小行星任务转移轨道设计[J]. 宇航学报, 2014, 35(3): 262-268. LIU L, LIU Y, CAO J F, et al. Mission design of the CHANG'E-2 asteroid exploration[J]. Journal of Astronautics, 2014, 35(3): 262-268. DOI:10.3873/j.issn.1000-1328.2014.03.003 (in Chinese) |
| [7] | 闫循良, 廖守亿, 张金生, 等. 天基发射方案与规划策略仿真研究[J]. 计算机仿真, 2013, 30(9): 83-87. YAN X L, LIAO S Y, ZHANG J S, et al. Space-based launch scheme and planning strategy simulation[J]. Computer Simulation, 2013, 30(9): 83-87. DOI:10.3969/j.issn.1006-9348.2013.09.019 (in Chinese) |
| [8] | 王宇.基于不确定性的优化方法及其在飞机设计中的应用[D].南京: 南京航空航天大学, 2010: 18. WANG Y.Uncertainty-based optimization method and its application in aircraft design[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2010: 18(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291502.htm |
| [9] | 王琦, 丁运亮, 陈昊. 基于多级代理模型的优化算法[J]. 南京航空航天大学学报, 2008, 40(4): 501-506. WANG Q, DING Y L, CHEN H. Simulation optimization based on multilevel-surrogate models[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(4): 501-506. DOI:10.3969/j.issn.1005-2615.2008.04.017 (in Chinese) |
| [10] | 周须峰, 唐硕, 高小五. 空间目标可拦截区与可遭遇区确定[J]. 航天控制, 2006, 24(1): 33-38. ZHOU X F, TANG S, GAO X W. Determination of interceptable section and encounter section for space target[J]. Aerospace Control, 2006, 24(1): 33-38. DOI:10.3969/j.issn.1006-3242.2006.01.008 (in Chinese) |
| [11] | 李人杰, 陈杨, 向开恒. 考虑初始相位角影响的空间飞越发射窗口研究[J]. 现代防御技术, 2018, 46(3): 171-176. LI R J, CHEN Y, XIANG K H. Study of launch window of space fly-by under influence of initial phase angle[J]. Modern Defense Technology, 2018, 46(3): 171-176. (in Chinese) |
| [12] | 王琦.MDO优化算法研究[D].南京: 南京航空航天大学, 2008: 39. WANG Q.Research on arithmetic of MDO[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2008: 39(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1011253992.htm |
| [13] | 胡添元.飞翼布局飞机总体多学科设计优化研究[D].南京: 南京航空航天大学, 2010: 30. HU T Y.Multidisciplinary design optimization for flying wing aircraft preliminary design[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2010: 30(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291579.htm |
| [14] | 龙腾, 刘建, WANG G G, 等. 基于计算试验设计与代理模型的飞行器近似优化策略探讨[J]. 机械工程学报, 2016, 52(14): 79-105. LONG T, LIU J, WANG G G, et al. Discuss on approximate optimization strategies using design of computer experiments and metamodels for flight vehicle design[J]. Journal of Mechanical Engineering, 2016, 52(14): 79-105. (in Chinese) |
| [15] | 姚雯.不确定性MDO理论及其在卫星总体设计中的应用[D].长沙: 国防科学技术大学, 2007: 27-28. YAO W.Research on uncertainty multidisciplinary design optimization theory and application to satellite system design[D].Changsha: National University of Defense Technology, 2007: 27-28(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098123.htm |
| [16] | LIANG B. Radial basis functions for solving PDEs[J]. Mathematic Applicata, 2004, 17(2): 227-233. |
| [17] | 李靖.基于改进量子粒子群算法的运载火箭弹道优化[D].湘潭: 湘潭大学, 2014: 19-23. LI J.Launch vehicle trajectory optimization based on improved quantum particle swarm algorithm[D].Xiangtan: Xiangtan University, 2014: 19-23(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10530-1014412550.htm |
