为了解决上述问题,近年来出现了基于光学原理的空速测量传感器和测量系统。光学大气测速系统是一种基于气溶胶粒子米散射的主动式非接触测量传感器,其通过相干探测散射光的多普勒频移来实现空速测量,能够测量三维风速矢量及解算真空速、攻角和侧滑角等参数。Sonnenschein和Horrigan[4]于1971年对连续波聚焦的共轴激光和大气气溶胶后向散射的光外差方法做出了很好的阐释和设计。激光多普勒测速器于1974年被Mu?ioz等[5]首次提出并使用。1985年,Rogers[6]提出了利用激光信号的多普勒频移测量大气参数的思想。Katsibas等[7]于2008年提出了机载光学大气数据系统的架构和数据处理方法。2009—2011年,Verbeek和Jentink通过机载试验证明晴空、小雨、沙尘等不利天气环境下,光学测速系统能够实现测速功能[8]。Cézard等[9]进行了不同波长、能量级和谱分析方法下瑞利散射和米散射的性能对比,米散射在低能量级和高粒子浓度环境下更具有优势。Spuler和Richter等[10]于2011年通过机载试验成功验证了激光大气运动传感器(Laser Air Motion Sensor,LAMS)能够实现空速测量,能够提供飞机机身附近有价值的气流运动信息,且对单个机翼吊舱向外发射多角度光束的三维风速测量方法进行了设计和讨论[11]。Augere等[12]于2014年进行了三轴光学大气速度传感器的机载试验。上述研究都基于固定翼飞行器。目前,由于技术成熟度较低,光学大气速度传感器还没有能够在直升机上装机应用,国际上对直升机光学大气技术还处于研究、试飞阶段,例如美国OADS公司的原型机在休伊直升机上已进行了飞行试验[13],国内则尚无相关研究开展。
中国航空工业集团有限公司成都凯天电子股份有限公司是世界范围内仅三家能够研制直升机三轴大气数据系统的单位之一,为中国武装直升机发展做出了重大贡献[14]。为解决现有三轴大气数据系统的固有缺陷,开展了基于光学多普勒的相干空速测量方法研究[15]。本文提出了一种基于多普勒频移的直升机光学大气测速系统,并介绍了其工作原理和性能指标的验证情况。
1 系统工作原理 1.1 激光多普勒空速测量原理 飞行器在飞行时与周围大气产生相对运动,与周围大气的相对速度即为真空速。直升机光学大气测速系统的工作原理是基于多普勒频移的激光相干测速,系统对外界大气发射激光束,激光与大气气溶胶发生作用后,产生携带了多普勒频移的散射光信号,散射光信号被系统接收后得到多普勒频移变化量Δf。多普勒频移与相对空速之间的关系为
 | (1) |
式中:Δf为多普勒频移量;V为相对空速矢量;l为激光束的单位矢量;λ为发射激光的波长。
1.2 三轴空速测量原理 由于单束激光仅能测量沿激光束的一维速度分量,为了获得三维矢量空速,需要至少在一组3个正交方向上布置光学天线,分别向3个方向上发射激光,测量矢量空速在3个方向上的速度投影,并进行三维矢量合成,解算三轴空速,进而解算出真空速Vt、攻角α和侧滑角β等参数。
在直升机光学大气测速系统中,光学天线布置在系统受感器组件内部。令3束激光A、B和C的光轴交汇于同一点,则可以认为激光均从该点发射。以该点为原点建立受感器组件右手坐标系,如图 1所示。
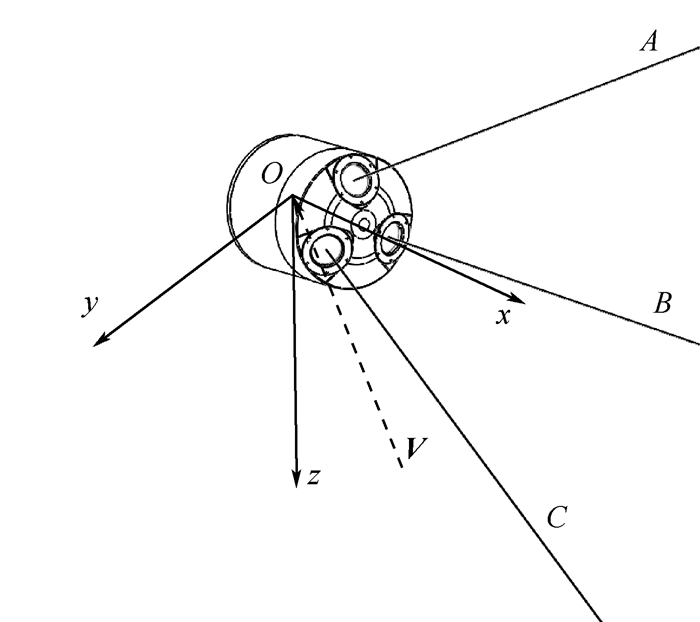 |
| 图 1 受感器组件坐标系定义 Fig. 1 Definition of sensor component coordinate system |
| 图选项 |
对单个激光光轴定义以下2个角度:①激光光轴在y-z平面上的投影沿逆时针方向转动到与+y轴重合所经过的转动角φ;②激光光轴与+x轴的夹角θ。则V在激光光轴上的速度投影V′为
 | (2) |
从而可以得到V在3束激光A、B和C上的速度投影关系为
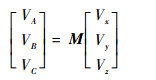 | (3) |
式中:
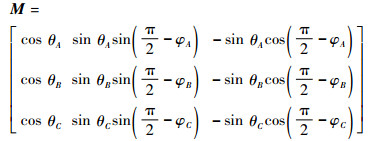 | (4) |
对式(3)求逆,即可获得由三轴激光测速解算合成得到的空速矢量公式。在实际装机时,不能完全保证受感器组件坐标系与直升机机体坐标系重合,并且为避免低空飞行时激光射向地面,受感器组件应整体向上倾斜一个角度。此时,需精确测量受感器组件的安装角度,得到机体坐标系到受感器组件坐标系的转换矩阵M1,从而得到三维矢量空速的计算公式为
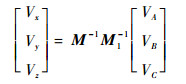 | (5) |
在三维矢量空速的基础上,进一步计算直升机大气数据参数得到
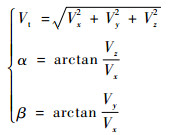 | (6) |
1.3 与三轴大气数据系统的对比分析 与传统直升机三轴大气数据系统相比,本文所提出的系统具有以下特点:
1) 传统方法根据伯努利定律测量空速,是沉浸式的被动探测系统;本文方法依据多普勒定律,是遥感式的主动探测系统。
2) 传统方法使用皮托管作为动压受感器,测量点在总、静压孔,受直升机气动外形和旋翼下洗流干扰非常大;本文方法通过发射激光遥感测量,测量点远离机身,可以最大程度避免下洗流的干扰。
3) 传统方法无法感知诸如突风、涡流环等对直升机飞行安全有影响的危险气流;本文方法可以感知到这些危险气流。
4) 传统方法中空速与动压的转换关系是非线性的,在空速较低时皮托管的测量精度和测量稳定性较低;本文方法中大气空速与频移的转换关系是线性的,在高、低速环境下都有较好的一致性,尤其是低空速测量精度远优于传统测量方法。
5) 传统方法可直接输出指示空速Vi,进一步解算后才能得到真空速Vt;本文方法则直接测量真空速,进一步解算后才能获得指示空速。
2 系统设计与实现 2.1 系统总体架构 直升机光学大气测速系统由传感器组件和受感器组件组成,组件之间使用光电缆连接。系统采用全分立式三轴光路结构,在系统内集成了三通道激光多普勒空速传感器,每一路都具有相对独立的光学天线、光纤光路、光电转换和信号采集处理模块,其结构如图 2所示。
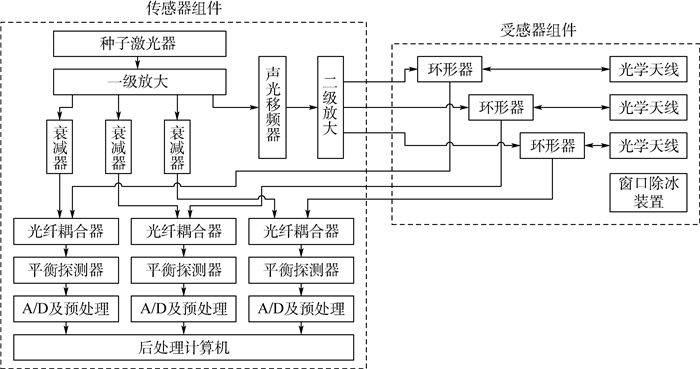 |
| 图 2 系统结构 Fig. 2 System architecture |
| 图选项 |
系统采用两级放大的光纤放大器,种子激光器产生的1 550 nm连续窄线宽激光通过一级放大输出4路激光,其中3路作为本振光,第4路经过固定频移(中频)fm为40 MHz的声光移频器后送入第二级放大,再输出3路大功率(约29 dBm)激光信号作为出射光。环形器和光学天线组成收发一体的光学系统,同时实现出射光发射和散射光接收。本振光通过衰减器实现振幅匹配后,与散射光在光纤耦合器中相干混频,输出两路具有相位差为π的光信号,经过平衡探测器转换为包含固定频移fm和多普勒频移Δf的中频信号。中频信号经过A/D信号采集和预处理,解算出3个方向的轴向风速,最终在后处理计算机中进行三轴空速的矢量合成,并进一步解算出真空速、攻角和侧滑角等参数。
2.2 受感器组件设计与实现 受感器组件设计为吊挂在直升机外部,外形为圆柱体,如图 1所示。在组件内部均匀分布3具光学天线,以实现三轴测速。光学天线的功能是将激光束发射聚焦到指定的距离,接收大气气溶胶散射的光信号并耦合进入光纤。由于载机空间有限,光学大气测速系统难以被分配理想的大口径光学窗口,因而经过性能平衡,使用口径?=30 mm,焦距f=100 mm的非球面镜片进行光学天线设计,输入光纤芯径9 μm,数值孔径NA=0.12,在30 m处的聚焦光斑直径为4.2 mm,瑞利长度为±3.7 m。光学天线结构和光斑分布仿真如图 3所示。
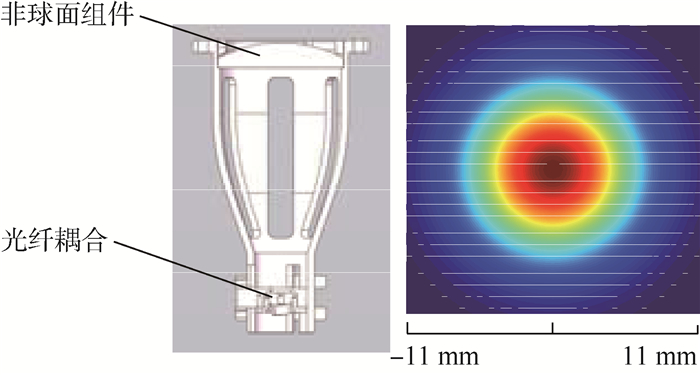 |
| 图 3 光学天线结构及仿真 Fig. 3 Optical antenna structure and simulation |
| 图选项 |
光学天线的夹角θ均设计为20°,三光轴绕x轴均布,即转动角φ设计为90°、210°和330°。考虑到冬季、高原等恶劣环境试飞需求,设计了基于电加热的窗口除冰装置。
2.3 信号采集与预处理 传统大气数据系统的量程和精度主要由压力传感器决定,而光学大气测速系统的量程主要由A/D采样带宽决定,精度主要由多普勒频移测量精度决定。由式(1)计算可得,每1 MHz多普勒频移大约对应2.8 km/h的相对速度。在中频fm为40 MHz的情况下,要满足直升机正常飞行速度约300 km/h的测速需求,最低约需要150 MHz的A/D采样带宽。本系统选择使用采样频率为400 Msample/s的A/D采样电路,理论最大轴向测速量程为-111.6~446.4 km/h。
多普勒频移的测量通过快速傅里叶变换(Fast Fourier Transform,FFT)进行,FFT点数决定了频谱分辨率,从而决定了速度测量精度。系统使用基于Xilinx XC5VSX50T的FPGA电路进行包含FFT和信噪比累积在内的预处理计算,预处理计算流程如图 4所示,其中FFT点数为2048点,对应的单轴测速精度为±0.27 km/h;信噪比累积目标值为25 dB,完成累积后在地面气溶胶浓度下频移信号的信噪比为5 dB。FPGA电路完成一次预处理的时间为4.64 ms,系统单轴测速刷新率可以达到200 Hz。
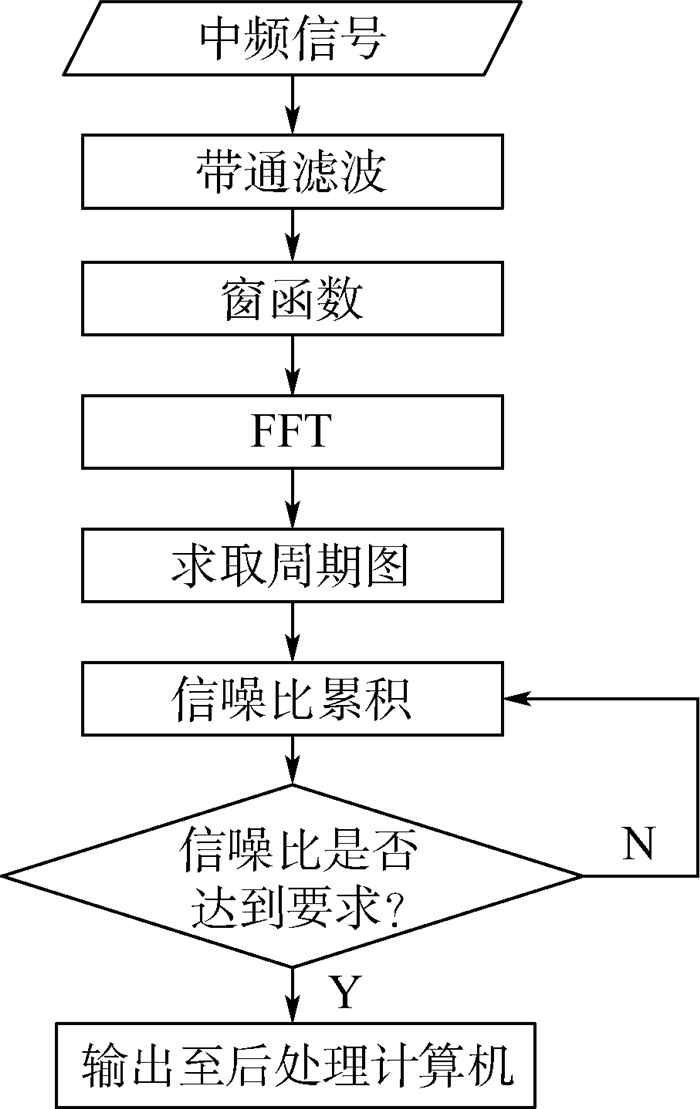 |
| 图 4 预处理计算流程 Fig. 4 Preprocessing calculation flowchart |
| 图选项 |
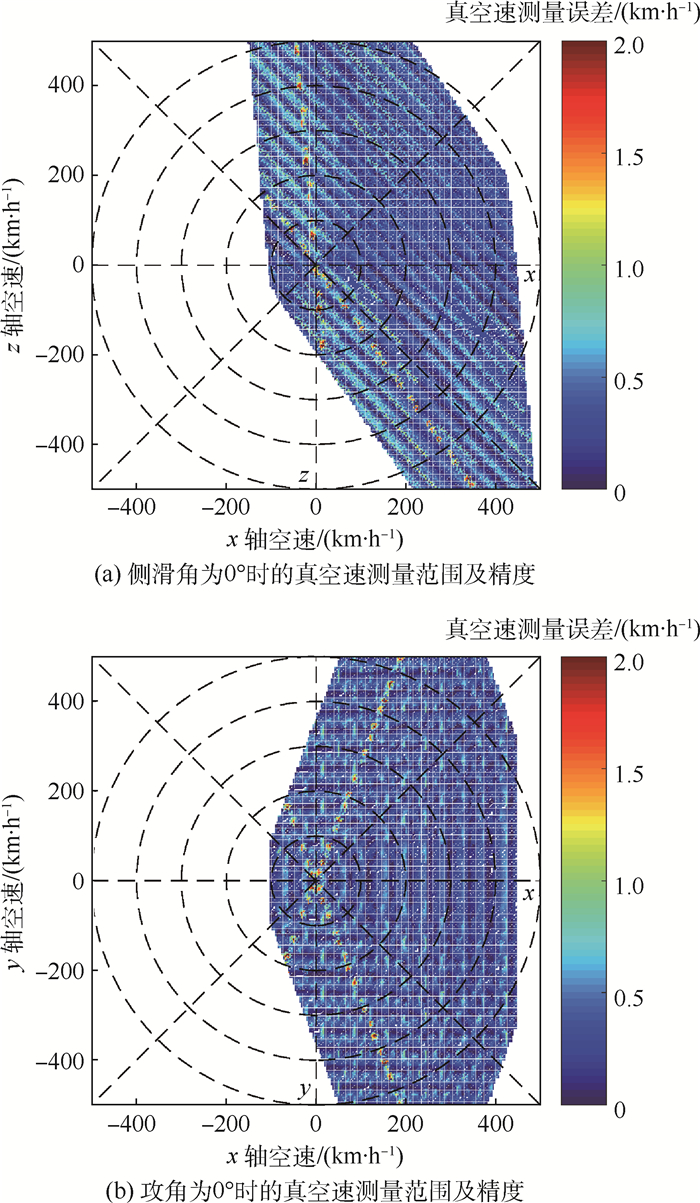
3 性能仿真与地面试验 3.1 性能仿真 光学大气测速系统的性能包线与传统大气数据系统不相同。传统大气数据系统使用皮托管测量空速,使用风标测量攻角和侧滑角,速度和角度的量程、精度是分开的;而光学大气测速系统通过三轴测速解算矢量空速,再换算为空速、攻角和侧滑角,这些参数的测量是相互关联的。为了验证光学大气测速系统的性能指标,进行了性能仿真,仿真结果如图 5所示。仿真结果给出了直升机真空速与攻角(侧滑角)的探测关系。
 |
| 图 5 系统性能仿真结果 Fig. 5 System performance simulation results |
| 图选项 |
从图 5中可以看出,在真空速不同时,传感器能测量的最大攻角和侧滑角范围是不同的。当真空速小于100 km/h时,攻角和侧滑角测量范围为-180°~180°,即直升机在任意飞行动作(正飞、倒飞和垂直升降)情况下,光学大气测速系统均能够正确测量大气数据信息;而传统直升机大气数据系统在该速度范围内,由于皮托管固有特性及旋翼下洗流影响,测量误差很大。当真空速提高时,系统后向空速探测能力逐渐丧失,但是此时的空速测量能力仍然能够完整覆盖直升机的飞行包线。系统最大前向可探测空速约为450 km/h,可覆盖大部分直升机的正常飞行包线,但这一性能尚不能满足新研制的高速直升机的要求。当直升机在传感器测量包线以外飞行时,传感器类似于丢失目标的雷达,不能正确地测量大气参数,也不能给出极限信息。为解决该问题,需要将传感器测量包线设计为能够完全覆盖直升机的飞行包线;或者需要引入其他飞行参数,提供参考极限信息。
从仿真结果可以看出,在大部分情况下,光学大气测速系统的真空速探测精度都优于±1 km/h,但是当矢量空速与某一根光轴垂直时,该光轴近似于失效,此时系统精度就会降低到±2 km/h。增加系统光轴数量能够有效地避免该问题。
3.2 地面试验 直升机光学大气测速系统样机实物如图 6所示。完成系统样机研制后,使用转台和风洞等设备对系统单光轴测速性能进行了验证。相对于传统大气数据系统而言,目前尚没有较好的能覆盖三轴光学大气测速系统性能包线的地面试验方法。为解决该问题,设计了一种基于移动平台的地面试验方法,并对研制的直升机光学大气测速系统样机进行了地面跑车试验验证。
 |
| 图 6 系统实物图 Fig. 6 Picture of system |
| 图选项 |
本文搭建的跑车试验系统通过跑车行驶带动光学大气测速系统与周围大气相对运动,从而模拟空速产生的多普勒频移。系统由电源、空速管、大气数据计算机、二维转台和光学大气测速系统样机等部分组成,其中空速管和大气数据计算机采用为某型低速无人机研制的大气数据系统,其对低空速测量进行了专门优化,空速测量精度为±3.6 km/h;二维转台能够为受感器组件提供俯仰和航向2个轴向的转动角度θR和ψR,转动精度为±0.5°,以此来模拟受感器组件运动时实际感受到的攻角和侧滑角。由于跑车试验速度相对较低,因此大气数据计算机测量得到的指示空速即视为模拟真空速Vts,模拟攻角αs和模拟侧滑角βs的计算公式为
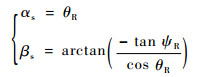 | (7) |
跑车试验地点为成温邛高速公路,试验时间为75 min。试验中最大行驶速度约为100 km/h。由于试验平台限制,为了避免激光直接指向地面,因此仅模拟了正攻角,侧滑角最大模拟到±50°。在试验过程中,A、B和C三光轴测得的轴向速度结果如图 7所示;由A、B和C三光轴测速数据解算得到的受感器组件坐标系三轴空速如图 8所示。
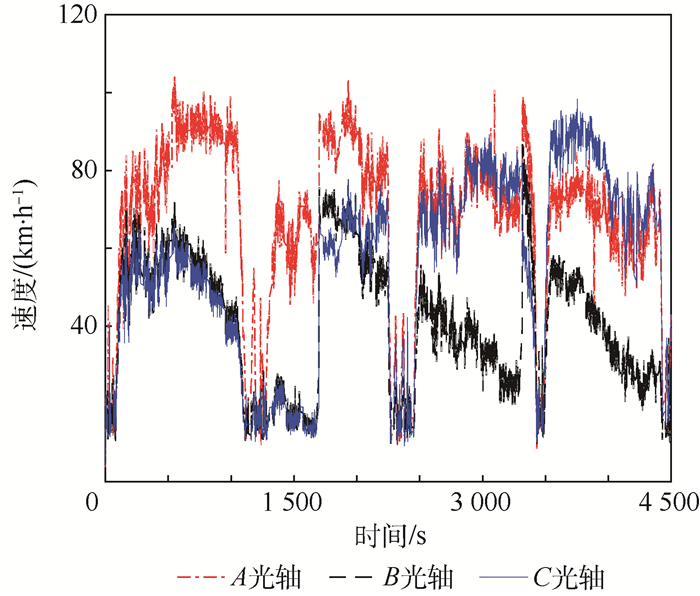 |
| 图 7 三光轴测速结果 Fig. 7 Three-optical-axis speed measurement results |
| 图选项 |
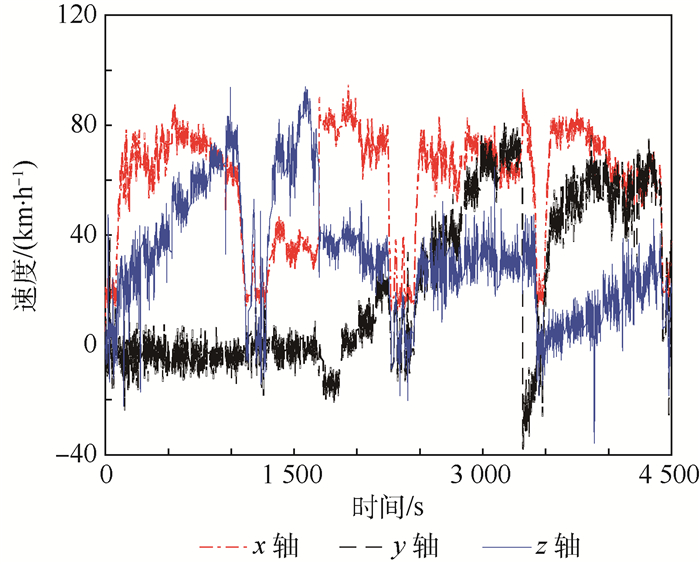 |
| 图 8 三轴空速解算结果 Fig. 8 Three-axis airspeed calculation results |
| 图选项 |
由光学大气测速系统三轴空速解算得到的真空速与试验平台大气数据计算机测量数据的对比如图 9所示。
 |
| 图 9 真空速解算结果 Fig. 9 True airspeed calculation results |
| 图选项 |
从图 9中可以看到,光学大气测速系统与基于空速管的传统大气数据系统的测量结果基本吻合,变化趋势一致,二者归一化相关系数为0.984。此外,光学大气测速系统相较大气机的测量结果超前约2~4 s,这验证了光学大气测速系统的遥感探测特性。
图 10给出由光学大气测速系统三轴空速解算得到的攻角和侧滑角与试验平台二维转台模拟角度的对比值。表 1给出攻角、侧滑角数值分析结果。
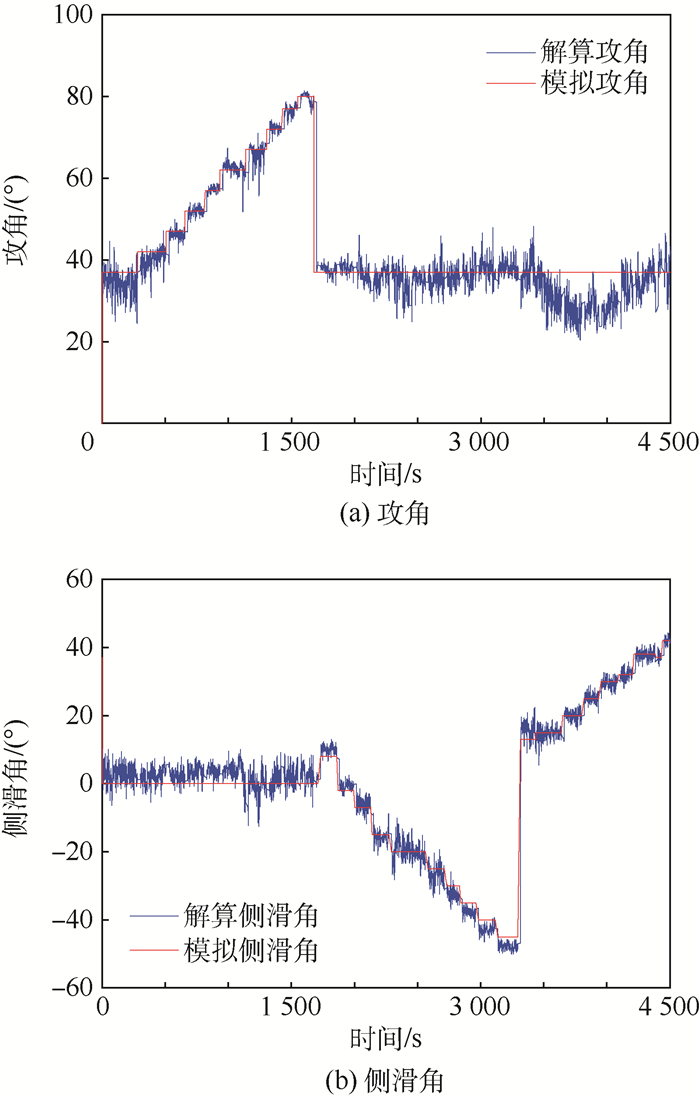 |
| 图 10 攻角、侧滑角解算结果 Fig. 10 Calculation results of angle of attack andangle of sideslip |
| 图选项 |
表 1 解算角度实测分析 Table 1 Actual measurement analysis of angle calculation
| 角度 | 时间/s | 误差/(°) | 均方误差/(°) |
| 攻角 | 0~1200 | 1.19 | 2.93 |
| 1200~2400 | 0.53 | 2.94 | |
| 2400~3600 | 0.17 | 2.84 | |
| 3600~4800 | 4.22 | 6.75 | |
| 侧滑角 | 0~1200 | 2.81 | 3.94 |
| 1200~2400 | 1.08 | 2.97 | |
| 2400~3600 | 1.11 | 3.79 | |
| 3600~4800 | 1.53 | 3.70 |
表选项
通过对图 10与表 1进行分析可知,光学大气测速系统解算得到的攻角和侧滑角与试验平台模拟角度基本一致。在试验进行到3 600 s前,光学大气测速系统能较为准确地测量矢量空速信息。系统解算攻角平均误差为0.63°,均方误差为2.90°;系统解算侧滑角平均误差为1.67°,均方误差为3.57°。在试验进行到3 600 s之后,系统攻角解算值与模拟角度出现了最大约15°的偏差,但是由于系统真空速和侧滑角测量结果均正确,因此该现象应当是由于试验环境中自然风(垂直气流)影响带来的系统误差。下一阶段的跑车试验将对平台进行改进,增加其对自然风速风向测量的能力,以进一步提高试验精度。
4 结论 本文体出了一种基于多普勒频移的光学大气测速系统。
1) 利用主动遥感探测原理探测直升机三轴矢量空速信息,可以对传统大气数据系统的固有缺陷形成良好的补充,并且能够解决旋翼飞行器在低空低速飞行时带来的测量问题。
2) 最大前向可探测空速约为450 km/h,可覆盖大部分直升机的正常飞行包线;能够测量直升机三轴空速信息、攻角、侧滑角和真空速。
3) 经过性能仿真分析和跑车试验验证证明,能够满足直升机对下一代大气数据系统的需求,特别在低速环境下能够较为准确地完成大气数据信息的采集和测量。
本文的进一步工作将完善地面试验的试验精度,并与直升机研制单位合作进行飞行试验。
参考文献
| [1] | 熊亮, 刘义明, 黄巧平. 武装直升机大气数据传感器技术研究进展[J]. 传感器与微系统, 2015, 34(2): 5-8. XIONG L, LIU Y M, HUANG Q P. Research progress in air data sensor technology for attack helicopter[J]. Transducer and Microsystem Technologies, 2015, 34(2): 5-8. (in Chinese) |
| [2] | COYLE S. The art and science of flying helicopters[M]. Ames: Iowa State University Press, 1992. |
| [3] | 梁应剑, 梅运桥, 程丽媛, 等. 基于米散射的光学大气数据系统研究[J]. 测控技术, 2015, 34(1): 32-34. LIANG Y J, MEI Y Q, CHENG L Y, et al. Research on optical air data system based on Mie scattering[J]. Measurement & Control Technology, 2015, 34(1): 32-34. DOI:10.3969/j.issn.1000-8829.2015.01.009 (in Chinese) |
| [4] | SONNENSCHEIN C M, HORRIGAN F A. Signal-to-noise relationships for coaxial systems that heterodyne backscatter from the atmosphere[J]. Applied Optics, 1971, 10(7): 1600-1604. DOI:10.1364/AO.10.001600 |
| [5] | MU?IOZ R M, MOCKER H W, KOEHLER L. Airborne laser Doppler velocimeter[J]. Applied Optics, 1974, 13(12): 2890-2898. DOI:10.1364/AO.13.002890 |
| [6] | ROGERS P L.Compact radiation fringe velocimeter for measuring in three dimensions: US4506979 A[P].1985-03-26. |
| [7] | KATSIBAS T, SEMERTZIDIS T, LACONDEMINE X, et al.Signal processing for a laser based air data system in commercial aircrafts[C]//16th European Signal Processing Conference.Piscataway, NJ: IEEE Press, 2008: 1-5. |
| [8] | VERBEEK M J, JENTINK H W.Optical air data system flight testing: NLR-TP-2012-068[R].Amsterdam: National Aerospace Laboratory NLR, 2012. |
| [9] | CéZARD N, BESSON C, DOLFI-BOUTEYRE A. Airflow characterization by Rayleigh-Mie lidars[J]. AerospaceLab, 2009, 1(1): 1-4. |
| [10] | SPULER S M, RICHTER D, SPOWART M P, et al. Optical fiber-based laser remote sensor for airborne measurement of wind velocity and turbulence[J]. Applied Optics, 2011, 50(6): 842-851. DOI:10.1364/AO.50.000842 |
| [11] | SPULER S, SPOWART M, RICHTER D.Development and application of an optical fiber-based laser remote sensor for airborne measurement of wind velocity[C]//26th International Laser Radar Conference (ILRC26), 2012: 1-4. |
| [12] | AUGERE B, BESSON B, FLEURY D, et al. 1.5μm lidar anemometer for true air speed, angle of sideslip, and angle of attack measurements on-board Piaggio P180 aircraft[J]. Measurement Science & Technology, 2016, 27(5): 0540025. |
| [13] | MOORMANR W. Life saver[J]. Vertiflite, 2012, 58(6): 18-23. |
| [14] | 刘影碧, 谭向军. 直升机三轴全向大气数据系统试飞的算法修正[J]. 航空与航天, 2000(3): 18-22. LIU Y B, TAN X J. Algorithm correction of helicopter three-axis air data system flight-test[J]. Avionics and Astronautics, 2000(3): 18-22. (in Chinese) |
| [15] | 王晓维, 梁应剑, 李翔, 等. 基于光学多普勒频移的低空速测量方法研究[J]. 激光技术, 2016, 40(5): 629-632. WANG X W, LIANG Y J, LI X, et al. Research of low-airspeed measurement based on optical Doppler frequency shift[J]. Laser Technology, 2016, 40(5): 629-632. (in Chinese) |
