当前的再入制导方法一般分为标称轨迹制导法和预测校正制导法[3]。标称轨迹制导法是指利用飞行器运动方程离线生成一条标准弹道,并在实际飞行过程中利用制导律进行在线误差修正,该方法计算量低,因而在工程上易于实现。随着飞行空域不断拓展、任务的可操作性不断增强,标称轨迹制导法的自主性与鲁棒性难以满足任务需求。与此同时,预测校正制导法以实时修正预测射程与理想射程的偏差为目标,可以达到比标称轨迹制导法更高的落点精度,且不依赖投放条件,作为近年来备受瞩目的再入制导方法而得到迅速发展。
预测校正制导法实时预测轨迹,因而自主性可达到新一代可重复运载飞行器的任务需求,但对机载芯片的计算速度和存储量要求较高。20世纪90年代以来,随着高性能计算机出现,导航手段的不断丰富,在新一代可重复使用运载飞行器的需求牵引下[2],美国启动了先进制导与控制(AG&C)计划[4],使再入制导技术的研究进入了新的阶段。在此期间,国内外****对预测校正制导法进行了较为深入的研究,并开始应用至飞行器中,其中文献[5-6]为火星探测器与Kistler K-1轨道飞行器分别设计了预测校正制导律,成功使飞行器进行轨迹在线调整,且体现了一定的抗干扰能力,但实时性难以满足当前制导需求。文献[7-9]提出了控制量参数化(CVP)模型,在此基础上研究了低升阻比飞行器的再入预测校正方法,引入了时标分离方法避免轨迹震荡,而外界干扰较大时会导致平衡滑翔条件不成立并产生约束超出现象。文献[10]引入高斯伪谱法将预测校正转化为非线性规划问题,再对轨迹进行分段优化,达到了实时最优的效果,但算法本身结构较为复杂。文献[11]基于轨迹线性化(TLC)理论设计了制导律,减少了制导指令的解算时间,提高了实时性。文献[12]基于导航信息的误差分析将轨迹设计分为轨迹跟踪段和预测校正段,目的是预防黑障区导致的轨迹跳变。文献[13]建立了基于能量的三自由度模型,并使用模糊校正器得到满足射程的倾侧角真值,满足了制导的精度要求,但是对弹道性能影响较大。文献[14]引入了禁飞区规避机制,提升了飞行器横向机动能力,且满足了制导的精度要求。
综上所述,在新一代可重复使用飞行器的发展背景下,预测校正制导法具有广阔的前景并呈现了良好的发展趋势,但是当前的预测校正算法仍然面临着挑战。具体表现为:① 求解实时性问题。算法的求解速度必须满足当前再入需求。② 算法收敛性问题。模型确定的前提下,算法具有收敛性。③ 多约束处理问题。在轨迹设计阶段要综合考虑飞行过程的各种约束,同时在实际飞行时对约束要二次保障。④ 鲁棒性。算法对飞行器参数和环境的不确定性应具有较强的抗干扰能力,并能满足制导要求。
本文针对以上问题,提出了一套适用于不同升阻比飞行器的多约束预测制导方法。研究工作主要集中于以下几点:① 满足多约束的离线轨迹优化;② 基于Gauss-Newton法的预测校正制导律设计;③ 实时约束预测限制技术。本文提出的方法创新点如下:① 离线部分生成满足过程约束与终端约束的最优轨迹,实际飞行时通过射程约束对轨迹进行预测校正,在不断修正落点误差的同时有效地保证了离线轨迹设计的弹道性能。此外,将轨迹优化部分通过离线完成,有效地减少了在线轨迹的计算量,在满足制导精度的同时提升了实时性。② 传统控制约束的建立往往依赖于平衡滑翔条件,导致实际飞行时会有约束超出现象,因此提出一种约束实时预测校正方法,基于飞行器状态反馈构建闭环控制律,可以为过程约束提供有效的保障。
1 再入问题 1.1 再入运动方程组 本文以无动力式高超声速再入飞行器为研究对象,考虑地球自转因素,运动方程如下:
 | (1) |
式中:r为飞行器与地心的距离;λ和?分别为地球经度和纬度;Se为射程角;v为相对地球速度;θ为速度倾斜角,向上为正;ψ为速度航向角,正北顺时针偏转为正;σ为飞行器倾侧角,向右偏转为正;ωe为地球自转角速度;m为飞行器质量;g为重力加速度;L和D分别为升力和阻力,具体表达式为
 | (2) |
其中:CL和CD分别为升力和阻力系数,它们为迎角和马赫数的函数;Sref为参考机翼面积;ρ为大气密度,大气模型采用指数模型。
在整个再入段,迎角预设αref幅值由以下三段式得出:
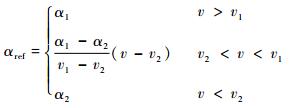 | (3) |
式中:v1=4 500 m/s;v2=3 000 m/s;α1=20°;α2=8.5°。
1.2 再入约束
1.2.1 过程约束 再入过程考虑始终满足的过程约束为热流率
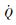
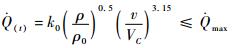 | (4) |
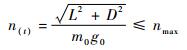 | (5) |
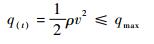 | (6) |
式中:k0为常值系数;
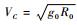
1.2.2 终端约束 终端约束为飞行器到达既定目标点的能量约束,具体包括高度、速度约束,表达式如下:
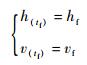 | (7) |
式中:h=r-R0为飞行器与地球表面距离。
此外,为了满足飞行任务需求与制导精度,终端约束应包括经纬度约束:
 | (8) |
1.2.3 控制约束和时间约束 考虑飞行器姿控系统能力,本文对制导指令施加限幅,具体为:倾侧角幅值0°<σ<90°,调节速度小于8 (°)/s,制导周期为0.1 s。
1.3 仿真对象和环境 本文仿真在2.50 GHz处理器下,使用MATLAB代码编译模型,采用波音公司设计锥形体再入飞行器CAV-L,气动参数详见文献[16-17],仿真条件如表 1所示。
表 1 仿真条件 Table 1 Simulation conditions
| 参数 | 数值 | |
| 初始点 | 高度/km | 100 |
| 经度/(°) | 160 | |
| 纬度/(°) | 5 | |
| 速度/(m·s-1) | 7 200 | |
| 速度倾斜角/(°) | -2 | |
| 速度航向角/(°) | 55 | |
| 终端约束 | 高度/km | 20 |
| 速度/(m·s-1) | 1 800 | |
| 目标经度/(°) | 225 | |
| 目标纬度/(°) | 25 | |
| 过程约束 | 热流率/(kW·m-2) | ≤1 200 |
| 动压/kPa | ≤200 | |
| 过载/g0 | ≤4 | |
表选项
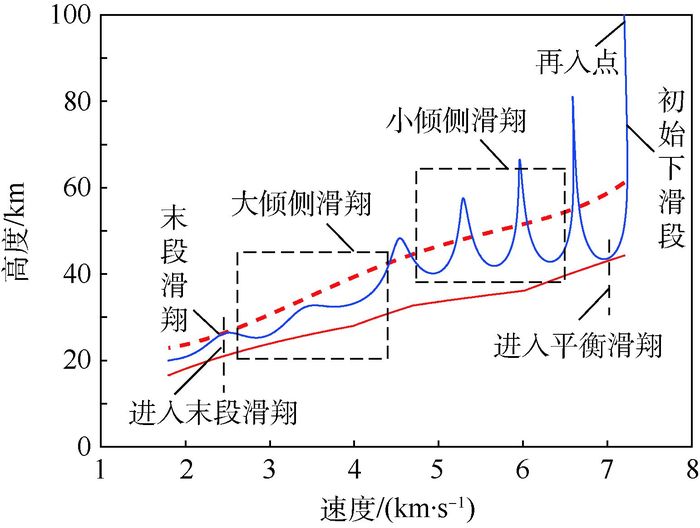
2 弹道优化设计 2.1 总体方案 按照文献[18],再入轨迹分为初始下滑段和平衡滑翔段,制导律采用纵向与横向分开设计的方法。初始下滑段由于气动力不足,倾侧角对弹道调节能力有限,一般以满足热流率约束的恒定倾侧角飞行[18],末段根据平衡滑翔条件可求得满足终端约束的倾侧角,因此,可规划区域为平衡滑翔段。
本文的预测校正制导方案如图 1所示。图中,纵向制导律的设计分为离线轨迹设计与在线预测校正2部分:离线部分对约束进行分析,建立了倾侧角走廊,在此基础上根据飞行任务进行弹道设计,采用预定迎角加倾侧角寻优的方法,对轨迹进行优化以提高弹道性能,优化结果载入控制指令生成器。在线部分通过在走廊内调整倾侧角,对轨迹进行实时校正,使预测落点与既定落点偏差最小。此外,本文提出一种约束限制方法,在不影响主体制导方法的前提下对过程约束进行二次保障。横向制导采用目标视线角横向走廊限制速度航向角与视线角偏差的方法,保证飞行器飞向目标点。
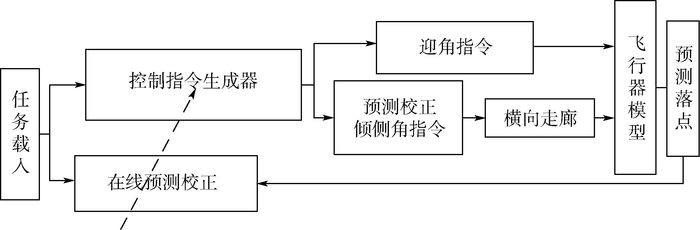 |
| 图 1 制导总体方案 Fig. 1 General guidance scheme |
| 图选项 |
2.2 再入约束分析 由式(4)~式(6) 可知,热流率、动压以及过载约束均是高度与速度的函数,参考文献[19]可求出HV走廊,如图 2所示。
 |
| 图 2 常规HV走廊[19] Fig. 2 General HV corridor[19] |
| 图选项 |
假设速度倾斜角很小,且其变化率为零,即cos θ=1且
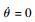
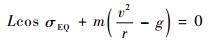 | (9) |
式中:σEQ为平衡滑翔假设下的飞行器倾侧角。
按照文献[19],可通过式(9) 将HV走廊转化为倾侧角走廊,即
 | (10) |
此外,在整个再入过程中,应始终满足:
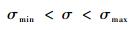 | (11) |
式中:σmin=0°。
具体走廊如图 3所示。通过式(10) 即可将代表过程约束的HV走廊(见图 2)转化为倾侧角的可行域(见图 3)。此外,滑翔要求满足高度与速度约束,因此将式(7) 代入式(10) 可得出末端的平衡滑翔倾侧角σEQ,若再入终点前满足σ equilf=σEQ,在飞行跨度一定的前提下,再入过程理论上可以满足高度与速度约束。
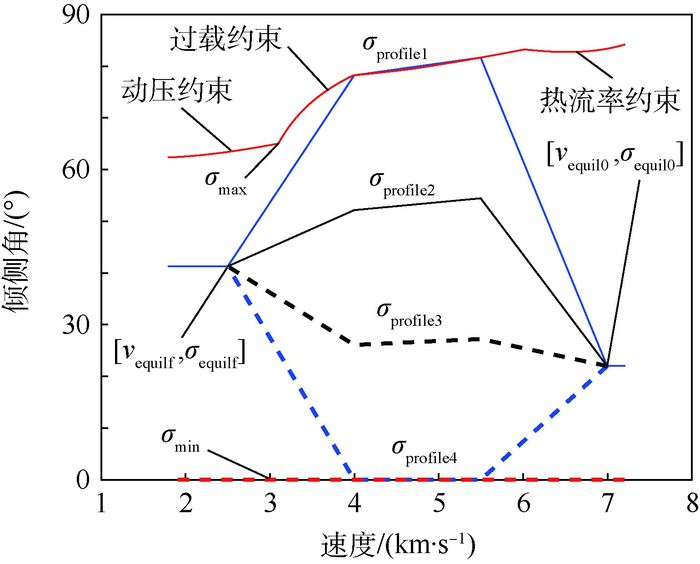 |
| 图 3 速度-倾侧角剖面 Fig. 3 Velocity-bank angle profile |
| 图选项 |
2.3 基于倾侧角剖面的多约束飞行区域包络 飞行器再入终点一般为既定目标点,设计纵向轨迹时,将经纬度转化为射程约束:
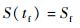 | (12) |
式中:S=Se/R0, 即射程角与射程成比例关系,因此可以用射程角对射程进行衡量。
由式(1) 可得射程角对速度的偏导数为
 | (13) |
在平衡滑翔假设下,式(13) 可以简化为
 | (14) |
式中:CD为迎角和马赫数的函数,则Se关于v的导数仅与高度有关,且随着高度的递增而递增,平衡滑翔时,飞行器纵向受升力与重力影响而作振荡运动。在平衡点处,升力的纵向分量与重力相抵消,在空域变化范围不大的前提下,重力加速度的影响可以不作考虑,此时可以认为
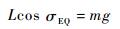 | (15) |
由式(2) 可得升力L随着h的增大而减小,同时从式(15) 可推出较大的倾侧角σEQ要求较大的总升力L以保证纵向平衡,故可得出以下结论。
在飞行器滑翔时,其稳定状态有以下规律:速度相同时,飞行器以大倾侧角飞行时对应的平衡滑翔高度较低,当以小倾侧角飞行时,则结论相反。综合式(14) 与式(15) 推论可以得出,倾侧角剖面越小,飞行器射程能力越大,即射程为倾侧角剖面的单调函数。
综上所述,在弹道规划时,若保证倾侧角剖面的单调性,则可在倾侧角走廊内规划出一条满足既定射程的倾侧角剖面以满足飞行任务需求。考虑预测校正时弹道求解的收敛性。定义倾侧角剖面的单调性如下:若在倾侧角剖面内某一段速度区间有
 | (16) |
成立,则认为倾侧角剖面2大于倾侧角剖面1。
由此可推出,以式(11) 表示的倾侧角走廊σmin与σmax参数化的倾侧角剖面应为最大与最小航程规划能力。倾侧角剖面与射程的对应关系如图 3与图 4所示。
 |
| 图 4 射程-高度曲线 Fig. 4 Range-height curves |
| 图选项 |
由式(16) 中对倾侧角剖面的定义可得,图 3中倾侧角剖面的关系为4<3<2<1。分析倾侧角剖面与图 4的射程曲线的对应关系分析得出:① 可行倾侧角剖面对应的射程介于最大射程与最小射程之间;② 倾侧角剖面越大的剖面对应射程能力越小。
2.4 控制量参数化建模 再入过程中,飞行轨迹被限制在基于过程约束的狭窄走廊内,离线轨迹设计时一般使用控制量参数化方法构建模型,引入参数优化维度N,将平衡滑翔区间[v equil0, v equilf]划分为N+1个子区间,考虑到轨迹快速规划能力,若倾侧角参数数量理想值为N=1,会大幅减小射程规划与弹道优化能力。本文以轨迹快速规划为前提,尽量保证飞行器射程,采用倾侧角参数为N=2,将最优控制问题转化为非线性规划(NLP)问题[20]。在每个子区间[v i, v i+1]内,速度对应倾侧角为
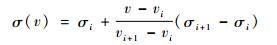 | (17) |
由式(17) 可得倾侧角参数化模型,如图 5所示。
 |
| 图 5 倾侧角参数化模型 Fig. 5 Bank angle parametric model |
| 图选项 |
图 5中:v equil0为初始下滑段与平衡滑翔段交点,参考文献[1]方法求出,v equilf为弹道优化段与末端滑翔段交点,由式(10) 与终端条件求出,优化参数为σ1、σ2。
2.5 离线弹道优化 优化性能指标一般由飞行任务需求决定,因本文重点为预测校正部分,故离线弹道优化采用常规的总气动热

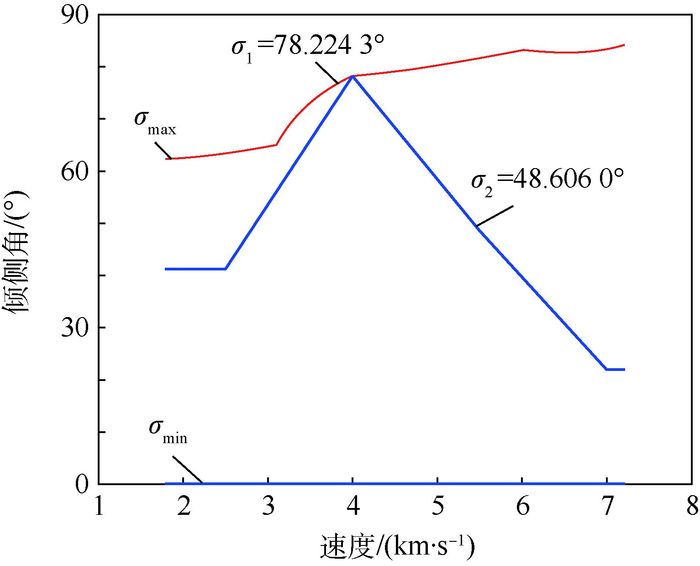 |
| 图 6 优化倾侧角剖面 Fig. 6 Optimized bank angle profile |
| 图选项 |
 |
| 图 7 纵向飞行轨迹 Fig. 7 Longitudinal flight trajectory |
| 图选项 |
参数寻优的结果为:σ1=78.224 3°,σ2=48.606 0°,J1=5.170 9×105 kJ。弹道优化采用离线设计,故不需要考虑实时性。由式(4) 可知,优化后的弹道在速度较大时,较小的倾侧角导致升力纵向分力较大,飞行器高空滑翔,气动热较小;速度较小时,飞行器低空滑翔,导致总气动热减小且满足射程,符合物理定律。
2.6 横向走廊 在纵向设计满足射程与过程约束的前提下,通过横向走廊改变倾侧角符号使飞行器朝目标点飞行。本文横向走廊采用经典的航向视线角走廊,具体反转策略如下:
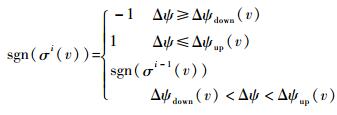 | (18) |
走廊边界如图 8所示。图 8中为保证横向制导精度且尽量减少倾侧角反转次数,设置Δψ1=10°,Δψ2=5°,Δψ3=1°,v0为初始速度,vf为终端速度,vth1=6 000 m/s和vth2=3 000 m/s为2个分段点速度。
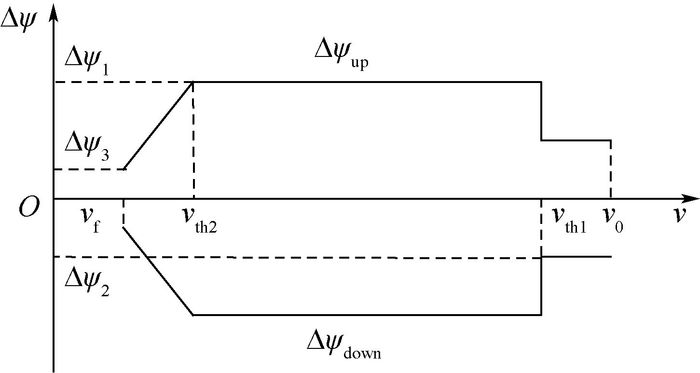 |
| 图 8 横向走廊 Fig. 8 Horizontal corridor |
| 图选项 |
3 实时预测校正 实际飞行时,计算机指令的延迟,复杂的大气环境,气动布局的不确定性,以及执行机构误差均会导致实际弹道与理论弹道存在一定的偏差。预测校正方法首先要具有一定的实时性,考虑机载芯片的计算能力,方法本身不能过于复杂,弹道校正时间要达到实际飞行需求;同时方法要具有可靠性,即在不同的飞行状态下均可规划出一条有效的弹道。因此,本文提出在倾侧角走廊内基于剩余射程对离线规划的倾侧角剖面进行调整的方法,使用Gauss-Newton法对弹道进行快速求解,具体如下:
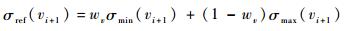 | (19) |
式中:wv为当前速度下的权重系数。
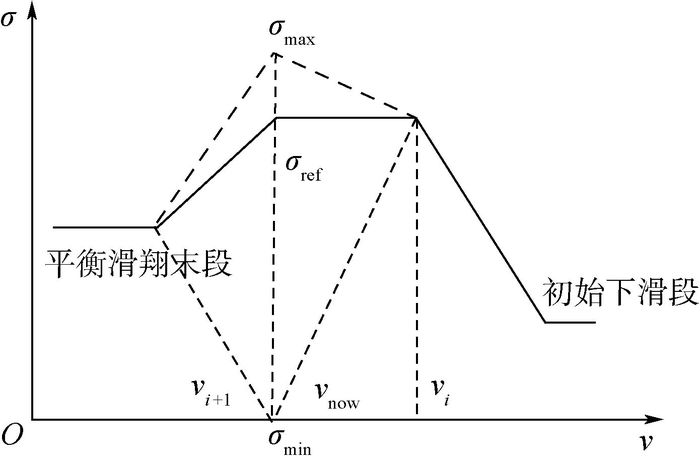
将离线控制变量模型式(17) 分割得速度调整区间,目的是增加轨迹预测校正的次数,既可以提高射程精度,也可以减小每次的调整量,满足倾侧角的调整速度约束。速度vi+1为飞行器当前速度v所在子区间[v i, v i+1]的右边界值,选取距离当前速度最近的校正速度节点可以使轨迹校正效果最快,最大程度满足方法的实时性,并减少后续的校正量。具体调整方案如图 9所示。
 |
| 图 9 倾侧角调节方案 Fig. 9 Bank angle adjustment scheme |
| 图选项 |
由图 9可知,单参数倾侧角的调节方法满足每次校正时倾侧角剖面的单调性,由2.3节结论可得,此时wv与射程是单调的。Gauss-Newton法对于单调问题的求解具有收敛速度快、精度高且方法可靠等优点,故可以快速求解出满足当前射程的倾侧角剖面,最大程度满足了实时求解弹道的需求。具体求解过程如下:
1) 将可调整的倾侧角剖面作为控制输入,则可求出当前状态下,以式(5) 作为控制输入下的剩余射程为
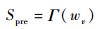 | (20) |
目标函数为
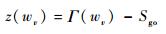 | (21) |
式中:Sgo为理想剩余射程,由当前点与终止点的经纬度求出。
2) 使用Gauss-Newton法求解目标函数z(wv)=0。第k次迭代公式为
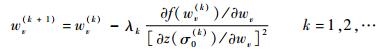 | (22) |
式中:f(wv)=z2/2为评价函数;λk=1/2i,i≥0为使得f(wv(k+1))<f(wv(k))的最小值。
3) 迭代终止条件如下,若不满足则继续第2) 步迭代:
 | (23) |
取ε=0.1 km为允许射程偏差,用以保证制导精度。此时校正结束,并更新倾侧角剖面。此外,当飞行器遇到强干扰导致迭代过程不成立时,应停止轨迹校正行为,并以最后一次成功校正后的控制指令飞行直至新的迭代过程完成。同时,应设定控制指令过渡过程:σi+1=kfσref(vi+1)+(1-kf)σi以保证轨迹的平缓性(kf为常值系数)。为验证Gauss-Newton法弹道求解的精度,以不同的剩余射程为输入,对弹道进行求解。结果如表 2所示。
表 2 弹道求解精度 Table 2 Accuracy of trajectory solvingkm
| km | ||
| 剩余射程Sgo | 求解弹道射程Spre | 射程偏差Sgo-Spre |
| 6 210.562 72 | 6 210.564 78 | -0.002 1 |
| 6 500.000 00 | 6 499.967 92 | 0.032 1 |
| 7 000.000 00 | 6 999.997 80 | 0.002 2 |
| 7 500.000 00 | 7 499.971 33 | 0.028 7 |
| 8 000.000 00 | 7 999.998 06 | 0.001 9 |
| 8 462.523 64 | 8 462.519 51 | 0.004 1 |
表选项
从表 2可以得出,参数未拉偏情况下,Gauss-Newton法求解出的弹道射程与剩余射程的偏差均在0.1 km以内,满足方法设定精度ε。同时,为验证方法的实时性,给出弹道的预测校正时间如表 3所示。
表 3 弹道求解时间 Table 3 Time of trajectory solving
| 参数 | 次数 | 最大 时间/s | 最小 时间/s | 平均 时间/s | 时间 标准差/s |
| 数值 | 27 | 0.796 4 | 0.096 1 | 0.477 1 | 0.227 1 |
表选项
由表 3可得,弹道求解速度随着射程的增加而减小,且最大求解时间在MATLAB环境下能控制在1 s以内,说明终止条件ε=0.1 km可以满足实时性要求。此外,使用Gauss-Newton法在实际飞行过程中对弹道进行校正时,应尽量减少对离线优化弹道性能的影响。为验证校正方法的这一特点,在2.3节的射程包络基础上,给出不同飞行任务下离线轨迹与实际轨迹对比效果如图 10所示。
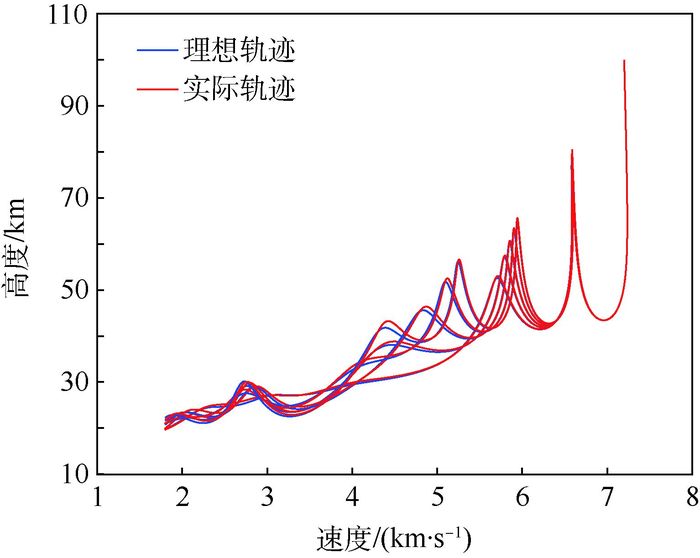 |
| 图 10 纵向轨迹对比 Fig. 10 Comparison of longitudinal trajectory |
| 图选项 |
图 10所示的离线轨迹(红色实线)与实际轨迹(蓝色实线)的偏差均较小,这是因为离线优化出的弹道已满足射程约束,最大程度地减小每次校正的目标函数值z(wv),因此可以有效地减小每次轨迹的校正量。在此基础上,可以减少Gauss-Newton法的迭代次数,提高实时性,同时轨迹小幅度的调整也会最大程度地保障弹道性能。实际弹道与离线弹道的总气动热对比情况如表 4所示。
表 4 总气动热对比 Table 4 Comparison of total aerodynamic heat
| 射程/km | 离线气动热/kJ | 在线气动热/kJ | 偏差/% |
| 5 775.8 | 419 771 | 422 666 | 0.69 |
| 6 267.9 | 439 710 | 442 212 | 0.57 |
| 6 764.7 | 459 646 | 462 756 | 0.68 |
| 7 264.8 | 476 898 | 480 360 | 0.73 |
| 7 767.2 | 493 759 | 496 492 | 0.55 |
| 8 270.9 | 505 929 | 509 214 | 0.65 |
| 8 775.2 | 524 966 | 528 531 | 0.68 |
| 9 279.5 | 545 929 | 550 088 | 0.76 |
| 9 782.9 | 560 820 | 566 370 | 0.99 |
表选项
由表 4可以得出,在线校正对弹道总气动热影响幅度均小于1%,因此可以得出结论:预测校正方法对离线设计弹道的性能影响较小,同时对于以其他优化目标建立的离线轨迹应具有同样的工程意义。
4 约束实时预测校正 再入过程中,飞行器要求满足复杂的过程约束,而代表约束的倾侧角走廊是在平衡滑翔假设下成立,而通常高升阻比飞行器的飞行轨迹振荡幅度较大,通常不能严格满足平衡滑翔假设[21]。而且实际飞行时,大气环境的不确定因素与飞行器内部的干扰使优化的轨迹的过载与热流率容易超过约束的最大边界,故需要在保证已有制导方法可靠性的前提下,对过程约束施加一个更加严格的限制以达到二次保障的效果。由式(1) 可得出高度变化率与速度倾斜角的关系如下:
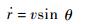 | (24) |
由式(24) 可得,轨迹振荡程度受速度倾斜角影响较大,故可基于过程约束对速度倾斜角施加一个通用有效的控制律来避免轨迹过度振荡。以动压约束为例,当动压接近最大约束值时,设计控制律如下:
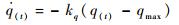 | (25) |
式中:kq=0.1为动压反馈系数,由式(6) 微分可得
 | (26) |
式中:h0=7 200为大气密度常数。
综合式(24)~式(26) 即可得速度倾斜角的反馈值如下:
 | (27) |
同理,对于热流率与动压约束也有相同的推论:
 | (28) |
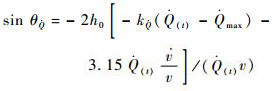 | (29) |
式中:kn=0.1和
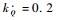

在每个制导周期中,倾侧角参考值σref决定了飞行器纵向的升力为Lcos σref,当实际速度倾斜角小于校正速度倾斜角幅值时,此时飞行器下降更快,则气动力增强并会导致约束超出,即
 | (30) |
此时弹道将超出最大约束,应进行校正。根据式(1) 可得,倾侧角变化较快而速度倾斜角变化较慢,此时基于时标分离理论[22]可得约束预测校正方法通过式(2) 的速度倾斜角对倾侧角进行反馈,具体如下:
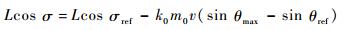 | (31) |
使sin θmax=max(sin θq,sin θn,
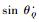
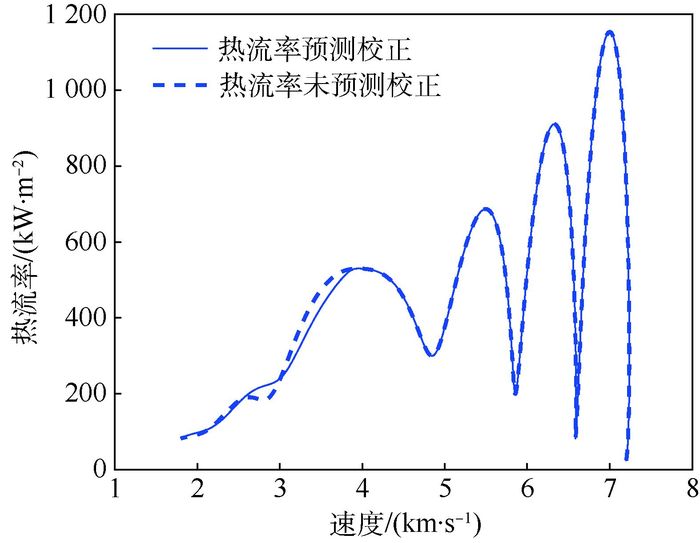 |
| 图 11 热流率曲线对比 Fig. 11 Comparison of heat flow curves |
| 图选项 |
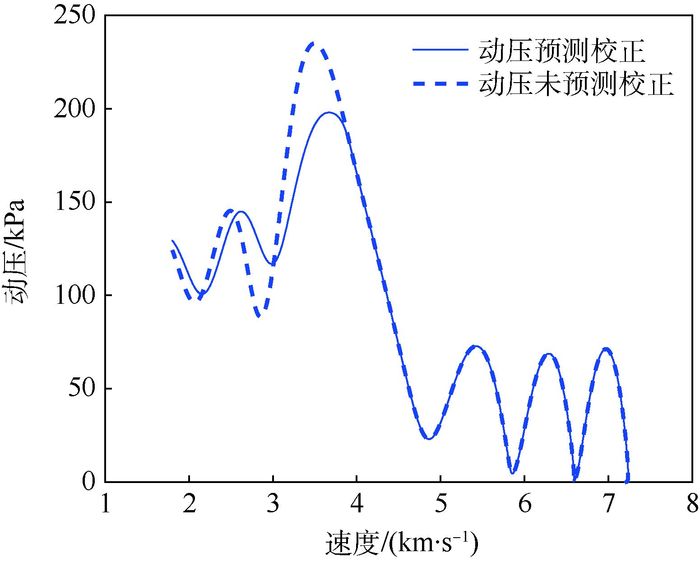 |
| 图 12 动压曲线对比 Fig. 12 Comparison of dynamic pressure curves |
| 图选项 |
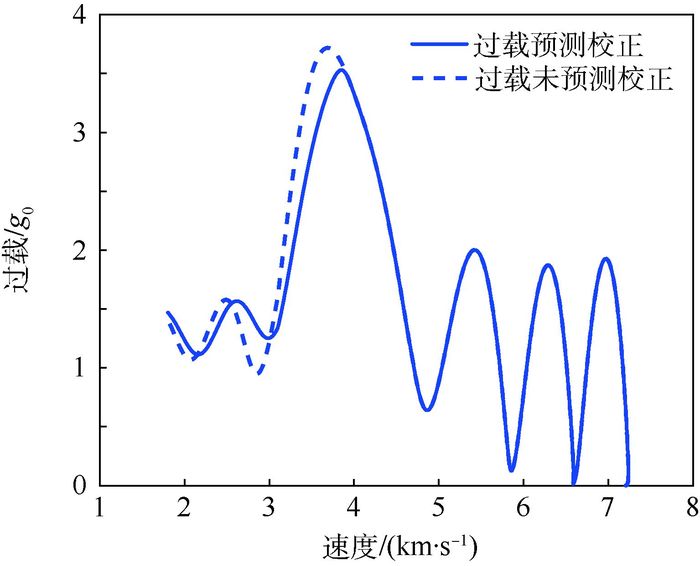 |
| 图 13 过载曲线对比 Fig. 13 Comparison of load curves |
| 图选项 |
由图 11~图 13可以看出:① 在三维飞行时,约束未经校正会超过上限值;② 未校正的约束值完全大于或等于校正后的约束值;③ 校正的效果非常明显;④ 校正后的约束均满足最大约束限制,具有良好的鲁棒性。此外,约束预测校正方法不仅要求在飞行时对过程约束进行有效的保障,且不能影响总体算法的精度与鲁棒性。
从图 14中可以看出,整个过程仅对速度倾斜角进行一次校正。结合图 7可知,在轨迹趋近HV走廊下界时,方法才会对约束产生校正效果,且校正时间远小于总体制导时间。在此分析基础上可以得出结论:对于实际飞行的不稳定因素,约束实时预测校正可以对约束产生有效的二次保障效果,同时不影响整体制导方法的性能。
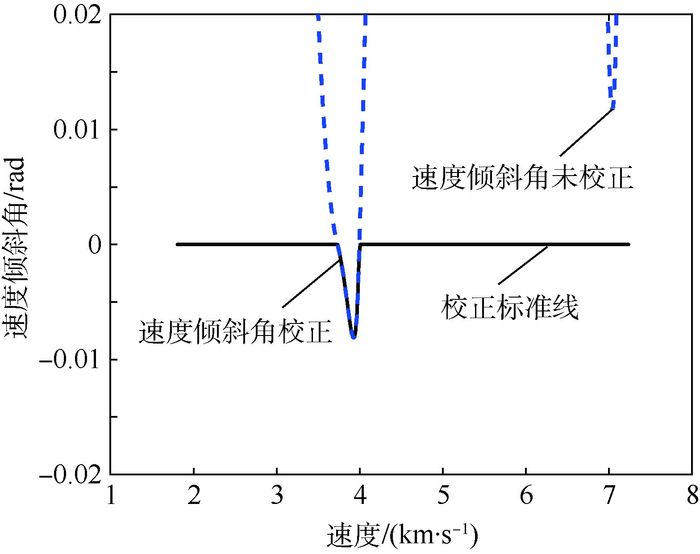 |
| 图 14 速度-倾斜角校正曲线 Fig. 14 Velocity-flight path angle corrected curves |
| 图选项 |
5 仿真验证 实际飞行时,再入轨迹的影响因素主要有:① 再入点偏差;② 气动布局的误差;③ 大气环境不确定性。针对这些影响因素,本文使用蒙特卡罗方法对其进行综合拉偏仿真,以验证制导方法的精度与鲁棒性。具体拉偏情况如表 5所示。
表 5 参数拉偏表 Table 5 Parameter deviation table
| 参数 | 拉偏值 |
| 高度/km | 5 |
| 速度/(m·s-1) | 30 |
| 速度航向角/(°) | 1 |
| 质量/% | 10 |
| 大气密度/% | 10 |
| 经度/(°) | 5 |
| 纬度/(°) | 5 |
| 速度倾斜角/(°) | 0.1 |
| 升力系数/% | 10 |
| 阻力系数/% | 10 |
表选项
表 5中所有拉偏均采用正态分布,拉偏值为正态分布的标准差。进行100次仿真,结果如图 15~图 17所示。
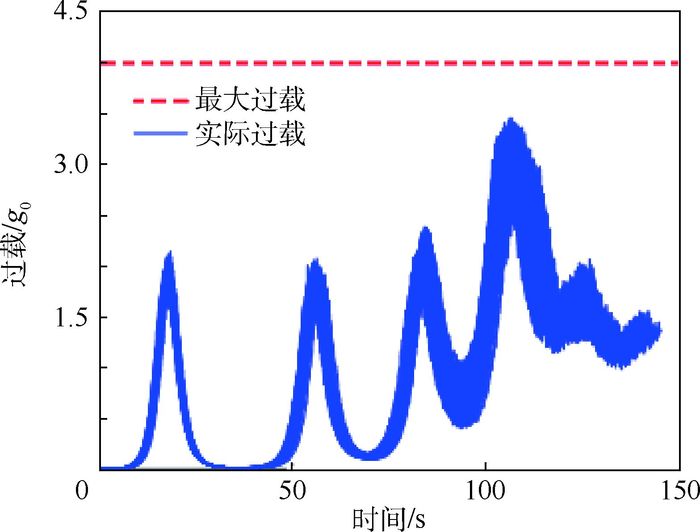 |
| 图 15 过载曲线 Fig. 15 Load curves |
| 图选项 |
 |
| 图 16 热流率曲线 Fig. 16 Heat flux curves |
| 图选项 |
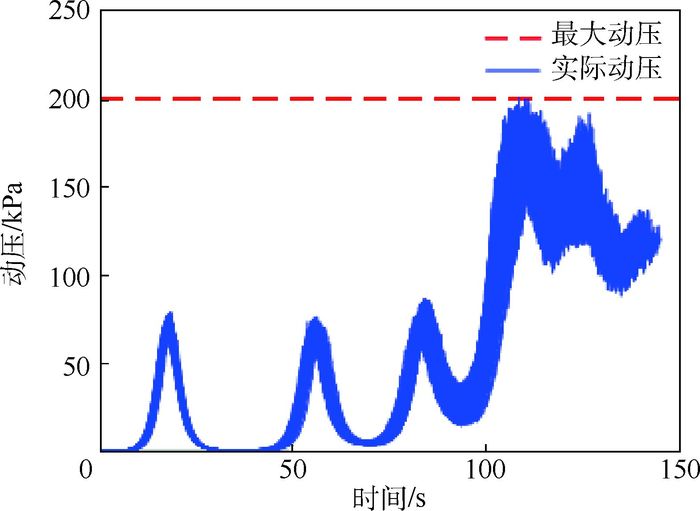 |
| 图 17 动压曲线 Fig. 17 Dynamic pressure curves |
| 图选项 |
分析图 15~图 17可得,在整个飞行过程中,约束预测校正方法始终将热流率、过载、动压限制在最大范围内,实现了对约束的限制作用,分析图 18~图 21可知,当飞行高度有超过HV走廊下界的趋势时,方法对倾侧角有校正作用,因此并不影响总体制导效果。
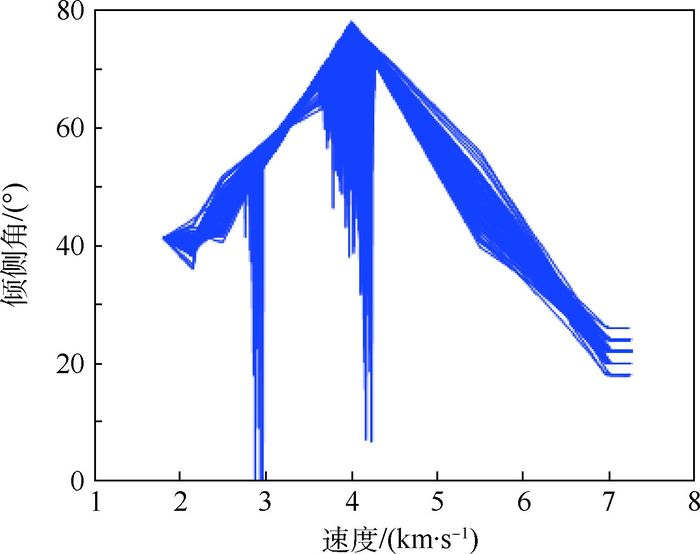 |
| 图 18 倾侧角剖面 Fig. 18 Bank angle profile |
| 图选项 |
 |
| 图 19 落点分布 Fig. 19 Droppoint distribution diagram |
| 图选项 |
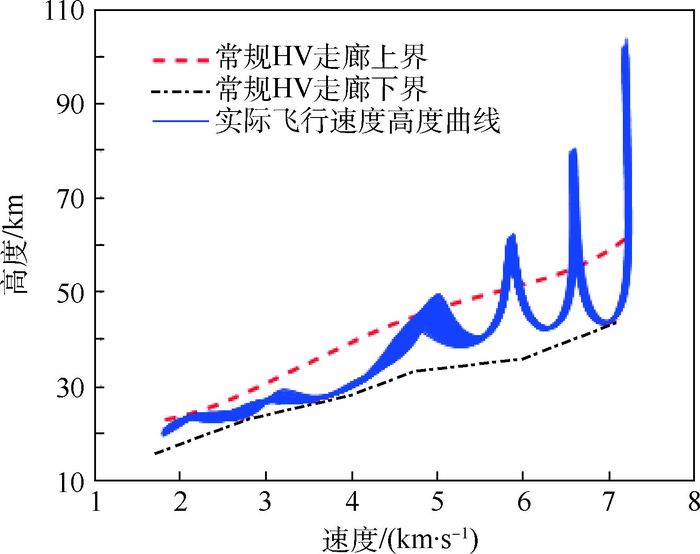 |
| 图 20 纵向轨迹分布 Fig. 20 Composition of longitudinal trajectory |
| 图选项 |
 |
| 图 21 横向轨迹分布 Fig. 21 Composition of horizontal trajectory |
| 图选项 |
分析图 15~图 21可得出以下结论:
1) 落点经纬度误差可以有效控制在0.05°以内,50%左右的落点精度达到0.01°,高度和速度均能满足要求,因此,预测校正方法能够满足再入制导的要求。速度倾斜角对于拉偏仿真的影响较为明显,故再入点应尽量保证这一参数的准确度。
2) 约束限制主要在4 000 m/s对速度倾斜角进行修正,从图 20得出末端高度分布在20 km左右,满足终端约束。结合结论1) 与过程约束图可知,在参数拉偏下经约束校正的轨迹满足再入制导要求。
3) 对于不同的投放偏差与飞行器自身参数的不确定性等因素,尤其是升阻力系数对射程的产生较大影响时,方法仍能够在满足约束的前提下保证制导的精度,故具有一定的鲁棒性。
6 结论 本文基于再入运动的特点,设计了离线弹道优化与在线预测校正相结合的制导方法,并针对使用离线优化弹道生成的控制指令进行实际飞行时,过程约束容易超出的现象,设计了基于速度倾斜角修正的约束实时校正方法。理论研究仿真验证表明:
1) 在线预测校正是对经优化的弹道进行调整,满足高度、速度、射程等终端约束,落点精度能够满足再入制导的需求,仿真表明,预测校正对弹道性能的影响不超过1%。故实际飞行弹道比一般预测校正的弹道较为经济、实用。
2) 拉偏仿真的结果表明,在初始条件、飞行器参数存在误差以及大气环境不确定时,方法都能够有效地自主调整弹道并达到较高的落点精度,能够适应飞行误差与飞行任务调整,具有良好的鲁棒性。
3) 整个方法对约束有2层保障,即以过程约束为前提的离线弹道设计与在线调整的实时约束预测校正,仿真结果表明,预测校正方法对约束具有良好的二次保障效果。
4) 本文提出的预测校正方法结构简单,对机载计算机要求不高,且计算时间随着已飞射程的增加而递减。MATLAB环境下,校正次数为27次,每次校正时间约为90~800 ms,因此,该方法具有工程运用的潜力。
综上,本文提出的制导方法能够离线对弹道进行优化,预测校正能够对约束进行有效的保障,制导精度与实时性能够满足再入制导的要求,面对复杂环境的鲁棒性较好,具有一定的工程价值。此外,本文内容重点为轨迹实时预测校正,而实际飞行任务需求多样,故离线弹道优化方法仍需改进。
参考文献
| [1] | LU P. Entry guidance:A unified method[J].Journal of Guidance, Control, and Dynamics, 2014, 37(3): 713–728.DOI:10.2514/1.62605 |
| [2] | 李惠峰, 张冉. 再入飞行器标称迎角优化设计[J].北京航空航天大学学报, 2012, 38(8): 996–1000. LI H F, ZHANG R. Optimal design of nominal attack of angle for re-entry vehicle[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8): 996–1000.(in Chinese) |
| [3] | 李惠峰. 高超声速飞行器制导与控制技术[M].北京: 中国宇航出版社, 2012: 320-325. LI H F. Guidance and control technology for hypersonic vehicle[M].Beijing: China Aerospace Publishing House, 2012: 320-325.(in Chinese) |
| [4] | HANSON J.Advanced guidance and control project for reusable launch vehicles:AIAA-2000-3957[R].Reston:AIAA, 2000. |
| [5] | POWELL R W. Six-degree-of-freedom guidance and control entry analysis of the HL-20[J].Journal of Spacecraft and Rockets, 1993, 30(5): 537–542.DOI:10.2514/3.25563 |
| [6] | FUHRY D P.Adaptive atmospheric reentry guidance for the Kistler K-1 orbital vehicle:AIAA-1999-4211[R].Reston:AIAA, 1999. |
| [7] | LU P.Regulation about time-varying trajectories:Precision entry guidance illustrated:AIAA-1999-4070[R].Reston:AIAA, 1999. |
| [8] | LU P.An integrated approach for entry mission design and flight simulations:AIAA-2004-702[R].Reston:AIAA, 2004. |
| [9] | LU P. Predictor-corrector entry guidance for low-lifting vehicles[J].Journal of Guidance, Control, and Dynamics, 2008, 31(4): 1067–1075.DOI:10.2514/1.32055 |
| [10] | 水尊师, 周军. 基于高斯伪谱方法的再入飞行器预测校正制导方法研究[J].宇航学报, 2011, 32(6): 1249–1255. SHUI Z S, ZHOU J. On-line predictor-corrector reentry guidance law based on gauss pseudospectral method[J].Journal of Astronautics, 2011, 32(6): 1249–1255.(in Chinese) |
| [11] | 朱国栋, 沈作军. 基于轨迹线性化控制的再入轨迹跟踪制导[J].北京航空航天大学学报, 2015, 41(11): 1975–1982. ZHU G D, SHEN Z J. Trajectory linearization control based tracking guidance design for entry flight[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 1975–1982.(in Chinese) |
| [12] | 赵頔, 沈作军. 基于在线轨迹迭代的自适应再入制导[J].北京航空航天大学学报, 2016, 42(7): 1526–1535. ZHAO D, SHEN Z J. Adaptive reentry guidance based on onboard trajectory iterations[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7): 1526–1535.(in Chinese) |
| [13] | 王青, 冉茂鹏. 基于预测校正法的高超声速飞行器再入制导[J].北京航空航天大学学报, 2013, 39(12): 1563–1567. WANG Q, RAN M P. Reentry guidance for hypersonic vehicle based on predictor-corrector method[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12): 1563–1567.(in Chinese) |
| [14] | 赵江, 周锐, 张超. 考虑禁飞区规避的预测校正再入制导[J].北京航空航天大学学报, 2015, 41(5): 864–870. ZHAO J, ZHOU R, ZHANG C. Predictor-corrector reentry guidance satisfying no-fly zone constraints[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 864–870.(in Chinese) |
| [15] | LU P. Entry guidance and trajectory control for reusable launch vehicle[J].Journal of Guidance, Control, and Dynamics, 1997, 20(1): 143–149.DOI:10.2514/2.4008 |
| [16] | 雍恩米, 唐国金. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D]. 长沙: 国防科学技术大学, 2008. YONG E M, TANG G J.Trajectory optimization and guidance method for hypersonic glide reentry vehicle[D].Changsha:National University of Defense Technology, 2008(in Chinese). |
| [17] | PHILLIPS T H.A common aero vehicle (CAV) model, description, and employment guide[R].Schafer Corporation for AFRL and AFSPC, 2003. |
| [18] | XUE S, LU P. Constrained predictor-corrector entry guidance[J].Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1273–1280.DOI:10.2514/1.49557 |
| [19] | SHEN Z J, LU P. Onboard generation of three-dimensional constrained entry trajectories[J].Journal of Guidance, Control, and Dynamics, 2003, 26(1): 111–121.DOI:10.2514/2.5021 |
| [20] | LZMAILOV A F, SOLODOV M V. Stabilized SQP revisited[J].Mathematical Programming, 2012, 133(1-2): 93–120.DOI:10.1007/s10107-010-0413-3 |
| [21] | LU P, FORBES S, BALDWIN M.Gliding guidance of high L/D hypersonic vehicles[C]//AIAA Guidance, Navigation, and Control Conference.Reston:AIAA, 2013:1-22. |
| [22] | LU P. Entry guidance using time-scale separation in gliding dynamics[J].Journal of Spacecraft and Rockets, 2015, 52(4): 1253–1258.DOI:10.2514/1.A33295 |
