针对无尾布局中开裂式方向舵的操纵特性,Gillard[9]对新型操纵面进行了风洞测试,指出开裂式方向舵有良好的操纵特性。Campbell和Seacord[10]进行了后掠无尾飞翼布局的全尺寸风洞试验,试验表明开裂式方向舵可以提供有效的偏航力矩。Mohamad等[11]对无尾布局开裂式方向舵的操纵性能进行了数值仿真,指出低速状态下开裂式方向舵的操纵效率随舵偏角增大而增大。张子军等[12]在不同马赫数和舵偏下, 通过实验深入研究了开裂式方向舵的作动对某无尾飞翼布局飞机气动特性的影响。王磊等[13]研究了开裂式方向舵偏转对飞机气动特性和稳定特性的影响。王旭等[14]研究了变前掠翼中平直翼和典型前掠翼布局开裂式方向舵的操纵特性,并对其操纵效率进行了比较。但是,目前对开裂式方向舵操纵特性的大多数研究均假设飞行器为刚体。
随着现代战斗机结构柔性趋于增大,飞行器的气动弹性问题显得更加突出[15]。在实际飞行过程中,机翼在气动力的作用下会发生复杂的弯扭耦合变形[16],使得安装在机翼上的开裂式方向舵的操纵特性偏离原有设计状态。因此,对弹性变形影响下的前掠翼飞行器开裂式方向舵的操纵特性进行研究十分必要。
近年来,随着计算机性能的发展,数值仿真越来越成为飞行器静气动弹性特性研究的主流方法[17-18],本文基于变前掠翼飞行器布局[6]的前掠翼构型,使用计算流体力学/计算结构力学(Computational Fluid Dynamics/Computational Structural Dynamics,CFD/CSD)松耦合静气弹数值计算方法,在亚声速条件下,对机翼刚性和弹性状态时开裂式方向舵在不同舵偏角下的操纵特性进行了研究,并对其操纵效率进行了比较。
1 计算方法 本文采用基于CFD/CSD松耦合的静气弹计算方法对全机进行数值模拟。在CFD计算收敛后将气动力传递到结构表面,结构变形后将位移传递到流场网格上,使用动网格技术对流场网格更新后进行下一次迭代,如此反复,直至结构变形收敛,CFD计算残差收敛精度为10-5,结构变形收敛精度为10-3 mm。
CFD气动力求解技术是CFD/CSD耦合计算的关键,流场计算中采用三维Navier-Stokes方程作为控制方程,在直角坐标系中,积分形式的守恒型三维Navier-Stokes方程组可表示为
 | (1) |
式中:Q为解向量; dV为体积微元;FΙ为无黏矢通量项; FV为黏性矢通量项; Ω为控制体; S为控制体表面; n为边界的外法向量。
湍流模型选择剪切应力输运(Shear-Stress Transport,SST) K-Omega模型。采用有限体积法对控制方程进行离散,流场网格采用计算效率快、收敛精度高的多面体网格[19]。
CSD计算采用有限元方法,CFD网格和CSD网格节点上的气动力和位移采用常体积转换(Constant Volume Transformation,CVT)方法进行数据传递,采用径向基函数方法[20-21]对流场网格进行变形。
使用HIRENASD气动弹性模型[22]对本文所用的数值计算方法进行验证。对流域进行多面体网格划分,对固定在机身上的HIRENASD机翼结构进行四面体网格划分,划分后的网格如图 1所示,流场网格和结构网格单元数量分别为5 797 367和195 898。
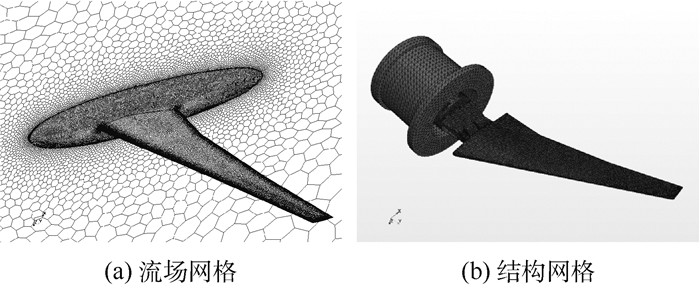 |
| 图 1 HIRENASD流场和结构网格 Fig. 1 Flow field and structure grids of HIRENASD |
| 图选项 |
计算中,流场边界条件为迎角α=2°,马赫数Ma=0.8,雷诺数Re=2.35×107,q/E=4.8×10-7,其中q为流场计算中的动压,E为结构模型的弹性模量。计算得到机翼展向y/b=0.14,0.59,0.95这3个站位处沿翼剖面弦向位置x/c的压力系数Cp如图 2所示。从图 2可以看到,y/b=0.14时,弹性翼和刚性翼压力系数差别很小,均与文献[22]实验值分布基本一致;y/b=0.59时,由于弹性翼中段变形量较翼根部大,且在气动力作用下机翼发生负扭转,使得有效迎角变小,因此弹性翼下表面压力系数较刚性翼小,弹性翼上表面压力系数较刚性翼大,翼型剖面总体升力系数下降,与实验值吻合得更好;y/b=0.95时,弹性翼变形量进一步增加,其压力分布与刚性翼差别更为明显,也更接近实验值。
 |
| 图 2 不同y/b时的压力系数 Fig. 2 Pressure coefficient of different y/b |
| 图选项 |
由上可知,本文所用数值计算方法可满足计算和分析弹性前掠翼开裂式方向舵的操纵性能。
2 计算模型 本文所使用的前掠翼计算模型由变前掠翼布局飞行器的前掠翼构型[6]转化而来,如图 3所示。机翼半展长为0.925 m,展弦比为4.65,梢根比为0.33,根弦长为0.558 m,1/4弦线处前掠角度为45°,采用NACA 0006翼型。阴影部分为开裂式方向舵,单侧舵面弦线与主机翼截面y/b=0.8段位处弦线夹角为舵偏角δ,设计舵偏角范围为0°~30°。
 |
| 图 3 前掠翼模型及舵偏角示意图 Fig. 3 Schematic of FSW model and rudder deflection angle |
| 图选项 |
根据文献[23],由于50%的空战都结束在高度H=3~5 km和Ma= 0.4~0.6的范围内,因此该前掠翼飞行器设计状态下的典型飞行状态如表 1所示。
表 1 前掠翼飞行器的典型飞行状态 Table 1 Typical flight state of FSW aircraft
| 飞行状态 | H/km | Ma |
| 起飞 | 0 | 0.2 |
| 巡航 | 10 | 0.8 |
| 空战 | 5 | 0.5 |
表选项
前掠翼模型的航向控制以开裂式方向舵为主,本文对弹性前掠翼模型开裂式方向舵的操纵特性进行数值研究,因此建立仅安装开裂式方向舵的前掠翼计算模型,如图 4所示。
 |
| 图 4 计算模型 Fig. 4 Computational model |
| 图选项 |
在空战状态下需要飞行器具有高机动性能,因此研究此工况下弹性前掠翼开裂式方向舵的操纵特性。流场计算的边界条件为:H=5 km,Ma=0.5,温度T=256 K,压力P=53 500 Pa,密度为0.610 2 kg/m3。
CFD网格近壁面第一层网格高度为10-6 m,以满足机翼表面黏性边界层的计算要求。CSD计算中,为减小计算量,将机翼根部固定在机身上,机身设为刚体,这样就只需要对机翼部分进行网格剖分。剖分后的流场和结构网格如图 5所示。
 |
| 图 5 前掠翼流场和结构网格 Fig. 5 Flow field and structure grids of FSW |
| 图选项 |
机翼主体部分采用复合材料,其材料属性为:E1=0.89GPa,E2=1.54 GPa,υ=0.31,G=2.6 GPa,ρ=0.338 g/cm3;舵面部分采用ρ=2.7 g/cm3,E=72 GPa,υ=0.34的铝合金材料。其中,E1为材料x和z方向的弹性模量,E2为y方向的弹性模量(x沿弦向,y沿展向),υ为泊松比,G为每个方向的剪切模量,ρ为机翼结构密度。
3 基本特性 仅将右侧开裂式方向舵打开,计算得到弹性翼和刚性翼的升力系数CL和升阻比K如图 6所示。
 |
| 图 6 升阻特性 Fig. 6 Lift-drag characteristics |
| 图选项 |
由图 6可以看出,随着舵偏角的增加,弹性翼和刚性翼的升力系数和升阻比都相应降低,大迎角时弹性翼和刚性翼的升阻比基本都不受舵偏角的影响;在小迎角时,弹性翼沿展向的扭转使其升力系数和升阻比大于刚性翼,大迎角时,弹性翼的升力系数和升阻比均小于刚性翼。相比刚性翼而言,弹性翼的失速迎角大约提前了2°左右,达到最大升阻比的迎角大约提前了1°左右。
图 7和图 8是在最大升阻比迎角α=6°时,弹性翼沿展向翼型剖面产生的扭转角γ和弯曲挠度w。如图 7和图 8所示,随着舵偏角的增加,机翼沿展向的扭转角变小,弯曲挠度增加。
 |
| 图 7 机翼展向扭转角 Fig. 7 Torsional angle of wing along spanwise direction |
| 图选项 |
 |
| 图 8 机翼展向弯曲挠度 Fig. 8 Bending deflection of wing along spanwise direction |
| 图选项 |
不同舵偏角下,弹性翼右侧翼梢处的扭转角响应如图 9所示。
 |
| 图 9 翼梢处扭转角响应 Fig. 9 Response of torsional angle of wing tip |
| 图选项 |
由图 9可看出,舵偏角增大,扭转角响应的幅值和收敛时间逐渐减小。因此,开裂式方向舵对弹性前掠翼的弹性振动有抑制效果,并且随着舵偏角的增大,抑制效果越好。当一个风速能够激起常规舵面的颤振时,对于具有开裂角的阻力方向舵来说,因为非定常气动力不足,而不能发生颤振[24]。因此,舵偏角对开裂式方向舵的气动弹性问题具有积极影响。
对弹性翼来说,相对于来流方向,舵面下偏部分的有效迎角较上偏部分更大,产生的压力也随之增加,如图 10所示,下翼面的压力增量明显大于上翼面的压力增量,这就会在机翼上产生低头力矩,使得机翼的扭转角度变小,舵偏角越大,方向舵提供的低头力矩越大,机翼的扭转角就越小,有效迎角减小导致升力系数也随之降低;挠度增加同样是因为下翼面压力的增加,使得机翼弯矩增大造成的。小迎角时,由于前掠机翼的弹性变形会产生正扭转,使得机翼有效迎角增大,而此时机翼的扭转没有破坏翼面的流态,机翼表面仍然保持附着流动,因此图 6中的升力系数和升阻比都增加。但随着迎角的增加,较大的挠度会减小机翼的有效展长,使升力系数减小;同时,机翼的扭转会使得气流较早与机翼表面脱离,增大飞行中的阻力,使得升阻比降低。
 |
| 图 10 压力云图 Fig. 10 Pressure contour |
| 图选项 |
计算得到的偏航力矩系数Cn如图 11所示。可以看出,刚性翼和弹性翼的偏航力矩随迎角增加均呈非线性,在迎角α < 12°时,偏航力矩的绝对值呈现缓慢增加的趋势,且弹性翼提供的力矩大于刚性翼,12°~20°之间急剧增加,20°后先减小后增加,在失速迎角附近再次降低,且弹性翼和刚性翼提供的偏航力矩几乎相同。由于舵面所在翼尖部分的扭转变形量较大,增加了舵面的有效迎角,使得弹性翼的变化幅度较刚性翼更大,且曲线的拐点较刚性翼提前。在失速迎角附近,δ=30°时弹性翼和刚性翼仍能提供大约0.034 2的偏航力矩系数。
 |
| 图 11 偏航力矩特性 Fig. 11 Yawing moment characteristics |
| 图选项 |
计算得到的滚转力矩系数Cl如图 12所示。可以看出,对于刚性前掠翼,δ=10°, 20°时,在小迎角下几乎没有滚转力矩,δ=30°时,在偏航作用的影响下,产生了较小的右滚转力矩;迎角约大于12°时,均出现了正的滚转力矩,并急剧增加,到24°左右达到最大值,然后逐渐减小至迎角30°时接近消失直至出现反向滚转效应,约34°时反向作用效果最为显著,接近失速迎角时,滚转又有所降低。在大迎角时舵偏角的增加对滚转力矩有增强的趋势。这是因为,尽管舵面的偏转使得刚性翼后缘上下翼面局部压力增大,但上下翼面的相对压差变化不大,左右两侧机翼的升力系数不会产生明显差异,因此在小迎角时,飞机的滚转力矩在0附近。
 |
| 图 12 滚转力矩特性 Fig. 12 Rolling moment characteristics |
| 图选项 |
而对于弹性前掠翼,小迎角时即出现了右滚转力矩,随着舵偏角的增加滚转效应逐渐增强,并在8°时滚转效应急剧变大,在大迎角时,弹性滚转力矩的变化趋势与刚性翼大致相同,但达到正向滚转力矩最大值的迎角提前了大约12°。这是因为对弹性翼来说,舵面的偏转会使机翼的扭转角减小,有效迎角降低,当右翼舵面偏转、左翼舵面不偏转时,两侧机翼由于有效迎角的不同会出现升力差,导致飞机发生右滚转。机翼的右滚转力矩随着舵面偏转角度的增加而增加,这是因为随着舵面偏转角度增大,机翼扭转角度减小而导致有效迎角减小,右翼升力系数就越低,由此产生的右滚转力矩就越大,对前掠翼飞机的滚转操纵通道会产生影响。因此,在弹性翼条件下,使用开裂式方向舵需要有升降副翼等其他舵面进行辅助联合控制调整飞行姿态。
滚转力矩的产生是由于左右两侧机翼的升力差造成的,舵偏角的大小会影响前掠翼的扭转变形程度。在小迎角范围内,弹性翼的滚转力矩在总体上是缓慢增加的,但在某一角度附近会产生“凹坑”现象,即δ=10°,20°,30°时,迎角α=4°,6°,8°附近的滚转力矩明显小于附近迎角下的滚转力矩。
以左翼无舵偏、右翼舵偏角δ=30°为例,其小迎角下左右两侧机翼的升力系数如图 13所示,α=8°时,右侧弹性翼的升力系数有明显的跳跃现象。这是因为在该迎角下,右翼的扭转和舵面的偏转发生耦合,使得下翼面压力的增量大于上翼面压力的增量,上下翼面压差变大,升力相对变大,右滚力矩随着左右翼升力差的减小而减小。迎角进一步增大时,耦合现象消失,右翼的升力恢复常态,滚转力矩继续增大,因此出现滚转力矩“凹坑”现象。
 |
| 图 13 升力系数 Fig. 13 Lift coefficient |
| 图选项 |
4 侧滑影响 在右翼方向舵打开,左翼方向舵闭合情况下,计算最大升阻比Kmax附近迎角α=6°、Ma=0.5、侧滑角β=-15°~15°、Δβ=5°时的刚性翼和弹性翼的侧滑特性,得到的结果如图 14所示。
 |
| 图 14 侧滑偏航特性 Fig. 14 Side slip yawing characteristics |
| 图选项 |
由图 14,刚性翼状态下,侧滑角为负(左侧滑)时,右翼舵面迎风面积变大,阻力增加,有效展长变大,阻力臂变长,产生右偏航力矩;右侧滑时,右翼舵面迎风面积减小,阻力降低,左翼有效翼展增加,相应的摩擦阻力也增加,导致偏航力矩逐渐减小直至反向。
左侧滑对偏航的影响强于右侧滑,这是因为右侧滑时右翼有效掠角增加,使得舵面产生的阻力和阻力臂都减小,偏航作用降低;左侧滑时舵面处有效掠角减小,阻力和阻力臂都增加,使偏航作用增强。
图 15给出弹性翼展向扭转角与侧滑角关系。从图中可以看出,弹性翼条件下,右侧滑时右翼有效前掠角增大,机翼扭转变形加剧,舵面处的有效迎角增加,偏航作用增强;左侧滑时右翼有效迎角减小,舵面处机翼的扭转量相对减小,偏航作用减弱。
 |
| 图 15 侧滑时的展向扭转角 Fig. 15 Torsional angle with side slip along spanwise direction |
| 图选项 |
侧滑条件下计算得到的滚转特性如图 16所示。在刚性翼条件下,左侧滑时,左翼有效前掠角变大,有效翼展减小,因此升力系数降低;右翼有效前掠角变小,有效翼展增大,升力系数增加,产生左滚转力矩,随着侧滑角的增加,滚转力矩逐渐变小,直至出现反向滚转力矩。
 |
| 图 16 侧滑滚转特性 Fig. 16 Side slip rolling characteristics |
| 图选项 |
弹性翼和刚性翼正好相反,在右侧滑时,右翼有效前掠角变大导致扭转变形更加剧烈,如图 16所示,β=15°在时,右翼的扭转角相比左翼大了1°左右,有效迎角的增加使得升力系数上升,超过了左翼有效翼展的增加带来的升力增量,因此产生向左的滚转力矩;而左侧滑时,左翼有效掠角增加,扭转变形大于右翼,且扭转角度比右翼大了1.8°左右,扭转角度差值的不同是由于右翼舵面提供了一定的低头力矩使其扭转角度相对变小的缘故,进而导致有效迎角变小,产生了右滚转力矩,且稍大于右侧滑时的左滚转力矩。
5 操纵效率比较 由于开裂式方向舵附加在前掠翼翼尖后缘上,前掠翼的扭转变形会影响阻力,从而对其操纵效率产生较大影响。弹性翼和刚性翼在α=6°、Ma=0.5时的阻力系数相对于各自无偏转构型的增加量ΔCD如表 2所示。
表 2 前掠翼阻力系数增量 Table 2 Increment of drag coefficient for FSW
| δ/(°) | ΔCD/% | |
| 刚性翼 | 弹性翼 | |
| 10 | 10.20 | 7.55 |
| 20 | 23.64 | 19.89 |
| 30 | 41.43 | 35.18 |
表选项
由以上数据可知随着舵偏角的增加,刚性翼和弹性翼开裂式方向舵的阻力系数均明显增加,但弹性翼的增加幅度要比刚性翼的小,这是因为随着舵偏角的增加,方向舵附加在翼尖处的低头力矩变大,弹性翼的扭转角度变小,方向舵的有效迎角降低,阻力增量也随之下降。
图 17为α=6°、Ma=0.5时,右侧开裂式方向舵偏转所产生的偏航力矩系数增量ΔCn[25]及偏航操纵效率Cnδ随舵偏角的变化规律。
 |
| 图 17 偏航力矩系数增量及偏航操纵效率随舵偏角的变化 Fig. 17 Variation of increment of yawing moment coefficient and yaw control efficiency with rudder deflection angle |
| 图选项 |
由图 17(a)可以看出,随着舵偏角的增加,刚性翼的偏航力矩线性较好,而弹性翼偏航力矩呈完全非线性变化,但弹性翼的偏航作用要强于刚性翼,这主要是因为方向舵所在翼尖处扭转变形较大,使得舵面处有效迎角变大所致。
根据图 17(b)可知,刚性翼和弹性翼状态下,开裂式方向舵的偏航操纵效率Cnδ均随舵偏角的增大而增大,且当20° < δ < 30°时,弹性翼操纵效率的增幅更大。舵偏角较小时,刚性翼和弹性翼偏航操纵效率均较低,且2种状态下相差不大。当舵偏角达到10°时,其偏航操纵效率分别只有0.021 49和0.024 7。舵偏角较大时,刚性翼和弹性翼的偏航操纵效率均有较大提高。当舵偏角达到30°时,其偏航操纵效率分别达到了0.037 13和0.058 78,与常规方向舵的偏航操纵效率0.05的量级[13]相比,刚性翼的偏航操纵效率较低,而弹性翼的偏航操纵效率高。因此,相对于刚性翼,弹性翼开裂式方向舵在大偏角状态下产生的偏航舵效是充足的,能满足飞机偏航操纵的要求。
阻力类偏航操纵装置在提供偏航操纵力矩的同时,与滚转力矩存在一定程度的耦合[25]。在刚性和弹性状态下,当机翼右侧开裂式方向舵打开时,产生使得机头向右的偏航力矩,同时右翼升力减小,产生向右侧的滚转力矩,因此前掠翼飞机上的开裂式方向舵也具有良好的滚转-偏航协调性。图 18为α=6°、Ma=0.5时,弹性翼和刚性翼滚转力矩系数随舵偏角的变化规律。
 |
| 图 18 滚转力矩系数随舵偏角的变化 Fig. 18 Variation of rolling moment coefficient with rudder deflection angle |
| 图选项 |
由图 18可知,舵偏角δ=10°,20°时,刚性翼的滚转力矩几乎为0,因为α=6°时,方向舵上下压差增加幅度基本相同,升力几乎没有变化,因此左右两侧机翼的升力基本相等,不会产生滚转力矩;而弹性翼的滚转力矩耦合明显,如图 18产生右滚力矩是由于方向舵附加的低头力矩使得右侧翼有效迎角减小,升力降低,左侧翼升力相对变大所致。δ=30°时,在偏航的耦合作用下,刚性翼出现右滚力矩,弹性翼的右滚作用增强。
随着舵偏角的增大,弹性翼开裂式方向舵的滚转力矩的耦合更加明显,在飞行操纵及控制律设计时应充分考虑其带来的影响。对于前掠翼飞机,以X-29A验证机为例,当副翼偏度为22.6°时副翼产生的滚转力矩量级约为0.064[23]。而即使当δ=30°时,开裂式方向舵造成的滚转力矩增量仅约为0.011 76,远小于副翼产生的滚转力矩。因此弹性翼开裂式方向舵滚转力矩耦合明显问题可通过适当偏转升降副翼产生滚转力矩来消除,对前掠翼飞机的操纵影响不大。
6 结论 1) 小迎角时,在偏航作用的影响下,刚性翼只会产生很小的、可以忽略不计的滚转力矩,而弹性翼在机翼扭转变形的影响下,会产生向开裂式方向舵一侧的滚转力矩,随着舵偏角的增加,这一现象有所增强。
2) 前掠翼的偏航力矩随迎角增加表现出非线性,在小迎角时,随着迎角的增加显现缓慢增加的趋势,大迎角时先减小后增加再减小,呈现出很强的非线性,弹性翼的变化幅度较刚性翼更大,而且变化趋势提前大约提前4°左右。
3) 左侧滑时,刚性翼产生左滚转力矩;弹性翼由于左右两侧机翼扭转变形量的不同会产生相反的右滚转力矩,随着侧滑角的增加,两者产生的滚转力矩都逐步减小直至反向。
4) 随着舵偏角的增加,刚性翼和弹性翼开裂式方向舵的阻力系数均明显增加,在方向舵附加低头力矩的作用下,弹性翼阻力的增加幅度小于刚性翼。
本文只对亚声速条件下开裂式方向舵的操纵效率进行了研究,因此研究跨声速和超声速飞行状态下的弹性翼舵面操纵效率,从而全面掌握弹性变形对前掠翼开裂式方向舵操纵效率的影响是进一步需要解决的问题。
参考文献
| [1] | SALTZMAN E J, HICKS J W.In-flight-lift drag characteristics for a forward swept wing aircraft:NASA TP-3414[R].Washington, D.C.:NASA, 1994. |
| [2] | 张彬乾, LASCHKAB. 前掠翼气动特性研究[J].西北工业大学学报, 1989, 7(3): 321–328. ZHANG B Q, LASCHKA B. On forward-swept wing's aerodynamic characteristics[J].Journal of Northwestern Poly Technical University, 1989, 7(3): 321–328.(in Chinese) |
| [3] | SPACHT G.The forward swept wing-A unique design challenge:AIAA-1980-1885[R].Reston:AIAA, 1980:1-5. |
| [4] | 吴立新, 左重, 刘平生, 等. 无尾飞翼气动布局是UCAV总体设计的最佳选择[J].洪都科技, 2003(1): 1–5. WU L X, ZUO Z, LIU P S, et al. Tailless flying wing aerodynamic configuration being optimal selection in UCAV general layout design[J].Hongdu Science and Technology, 2003(1): 1–5.(in Chinese) |
| [5] | MCMASTERS J H, CUMMINGS R M. Airplane design-past, present, and future[J].Journal of Aircraft, 2002, 39(1): 10–17.DOI:10.2514/2.2919 |
| [6] | 刘文法, 王旭, 米康. 一种新的变前掠翼无人机气动布局概念研究[J].航空学报, 2009, 30(5): 832–836. LIU W F, WANG X, MI K. A new aerodynamic configuration of UAV with variable forward-swept wing[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(5): 832–836.(in Chinese) |
| [7] | SUN J, ZHANG B, YANG G.Concept investigation of 'W' tailless configuration:AIAA-2005-4602[R].Reston:AIAA, 2005. |
| [8] | DORSETT K M, MEHL D R.Innovative control effectors (ICE):WL-TR-96-3043[R].Fort Worth:Lockheed Martin Tactical Aircraft Systems, 1996. |
| [9] | GILLARD W J.Innovative control effectors (configuration 101) dynamic wind tunnel test report.Rotary balance and forced oscillation tests:AFRL-VA-WP-TR-1998-3043[R].Wright-Patterson AFB:Air Force Research Lab, 1998. |
| [10] | CAMPBELL J P, SEACORD JR C L.Determination of the stability and control characteristics of a tailless all-wing airplane model with sweepback in the langley free-flight tunnel:NACA ACR-L5A13[R].Washington, D.C.:NACA, 1947. |
| [11] | MOHAMAD F, WISNOE W, NASIR R E M, et al.A study about the split drag flaps deflections to directional motion of UiTM's blended wing body aircraft based on computational fluid dynamics simulation[C]//The 47th International Meeting of Advances in Thermofluids.New York:AIP Publishing, 2012, 1440(1):324-329. |
| [12] | 张子军, 黎军, 李天, 等. 开裂式方向舵对某无尾飞翼布局飞机气动特性影响的实验研究[J].实验流体力学, 2010, 24(3): 63–66. ZHANG Z J, LI J, LI T, et al. Experimental investigation of split-rudder deflection on aerodynamic performance of tailless flying-wing aircraft[J].Journal of Experiments in Fluid Mechanics, 2010, 24(3): 63–66.(in Chinese) |
| [13] | 王磊, 王立新, 贾重任. 飞翼布局飞机开裂式方向舵的作用特性和使用特点[J].航空学报, 2011, 32(8): 1392–1399. WANG L, WANG L X, JIA Z R. Control features and application characteristics of split drag rudder utilized by flying wing[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1392–1399.(in Chinese) |
| [14] | 王旭, 于冲, 苏新兵, 等. 开裂式方向舵在变前掠翼布局中的操纵性能研究[J].航空学报, 2013, 34(4): 741–749. WANG X, YU C, SU X B, et al. Study of control characteristics for split rudder in variable forward swept wing configuration[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(4): 741–749.(in Chinese) |
| [15] | RODDEN W P. Theoretical and computational aeroelasticity[M].Camarillo: Crest Publishing, 2011: 1-20. |
| [16] | 张华, 马东立, 马铁林. 弹性变形对柔性机翼气动特性影响分析[J].北京航空航天大学学报, 2008, 34(5): 487–490. ZHANG H, MA D L, MA T L. Analysis of aerodynamics characteristic of flexible wing caused by deflection[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(5): 487–490.(in Chinese) |
| [17] | 陈大伟, 杨国伟. 静气动弹性计算方法研究[J].力学学报, 2009, 41(4): 469–479. CHEN D W, YANG G W. Static aeroelastic analysis of a flying-wing using different models[J].Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4): 469–479.DOI:10.6052/0459-1879-2009-4-2008-042(in Chinese) |
| [18] | CAI J, LIU F, TSAI H, et al.Static aero-elastic computation with a coupled CFD and CSD method[C]//39th Aerospace Sciences Meeting and Exhibit 2001.Reston:AIAA, 2001:1-8. |
| [19] | 许晓平, 周洲. 多面体网格在CFD中的应用[J].飞行力学, 2009, 27(6): 87–93. XU X P, ZHOU Z. Application of polyhedral mesh in CFD[J].Flight Dynamics, 2009, 27(6): 87–93.(in Chinese) |
| [20] | 张伟伟, 高传强, 叶正寅. 气动弹性计算中网格变形方法研究进展[J].航空学报, 2014, 35(2): 303–319. ZHANG W W, GAO C Q, YE Z Y. Research progress on mesh deformation method in computational aeroelasticity[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 303–319.(in Chinese) |
| [21] | GUMEROV N A, DURAISWAMI R. Fast radial basis function interpolation via preconditioned Krylov iteration[J].SIAM Journal on Scientific Computing, 2007, 29(5): 1876–1899.DOI:10.1137/060662083 |
| [22] | BALLMANN J, DAFNIS A, KORSCH H, et al.Experimental analysis of high Reynolds number aero-structural dynamics in ETW[C]//The 46th AIAA Aerospace Sciences Meeting.Reston:AIAA, 2008:7-10. |
| [23] | 方宝瑞. 飞机气动布局设计[M].北京: 航空工业出版社, 1997: 363-367. FANG B R. Aircraft aerodynamic configuration design[M].Beijing: Aviation Industry Press, 1997: 363-367.(in Chinese) |
| [24] | 韩鹏, 吴志刚, 杨超. 开裂角对阻力方向舵颤振特性的影响[J].航空科学技术, 2014, 25(10): 26–32. HAN P, WU Z G, YANG C. Effect of different split angles on flutter velocity of split drag rudder[J].Aeronautical Science & Technology, 2014, 25(10): 26–32.DOI:10.3969/j.issn.1007-5453.2014.10.007(in Chinese) |
| [25] | 李忠剑, 马东立. 飞翼布局阻力类偏航操纵装置操纵特性分析[J].北京航空航天大学学报, 2014, 40(5): 695–700. LI Z J, MA D L. Control characteristics analysis of drag yawing control devices of flying wing configuration[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(5): 695–700.(in Chinese) |
