自20世纪70年代,美国的Wolkovitch[1]提出了连翼布局飞机的概念并进行了气动及结构分析以来,国外已对菱形连翼布局飞机进行了大量的研究并进行了风洞试验[2-7],特别是在美国提出传感器飞机计划以后,菱形连翼布局的研究又出现了一个新的高潮[8-13]。在国内, 菱形连翼布局的研究范围和深度也不断提高[14-18]。李光里等[19]对菱形连翼飞机低速气动特性进行了风洞实验研究;王延奎等[20]针对菱形连翼布局俯仰力矩非线性变化特征进行了数值模拟等,但这些研究对高空长航时菱形连翼布局飞机的俯仰力矩非线性特性的产生机理缺乏深入的研究。
本文采用数值模拟的方法对高空长航时菱形连翼布局无人机的俯仰力矩非线性特性产生的原因、前后翼流动特性及布局参数变化对俯仰力矩非线性的影响进行研究,为菱形连翼布局无人机的工程设计提供理论依据。
1 数值模拟方法简述及算例 本文数值模拟采用流动雷诺平均Navier-Stokes方程(RANS)方法,采用的湍流模型为k-ω-SST模型,该模型使用间隙因子来修正K方程中的生成项、破坏项和混合函数,适合于有逆压梯度的流动计算。其耦合方程如下:
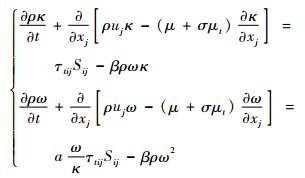 |
式中:t为时间;xj为时均距离;uj为时均速度;μ为黏性;σ为Prandtl数;β为热膨胀系数;a为声速;μt为涡黏性;Sij为平均速度应变率张量;ρ为流体密度;κ为湍动能;ω为比耗散率;τtij为雷诺应力的涡黏性。
为验证本文使用的数值模拟方法适用于亚跨声速流动的计算,结合菱形连翼布局飞机的特点和设计状态,选择变后掠AFV-D机翼作为计算模型[21],采用上述数值模拟方法,网格数为204万,并保证壁面第1层网格的y+≈1,分别选取如图 1所示2个状态作为数值模拟方法的验证算例,Y为截面距对称面的距离,b为半展长。
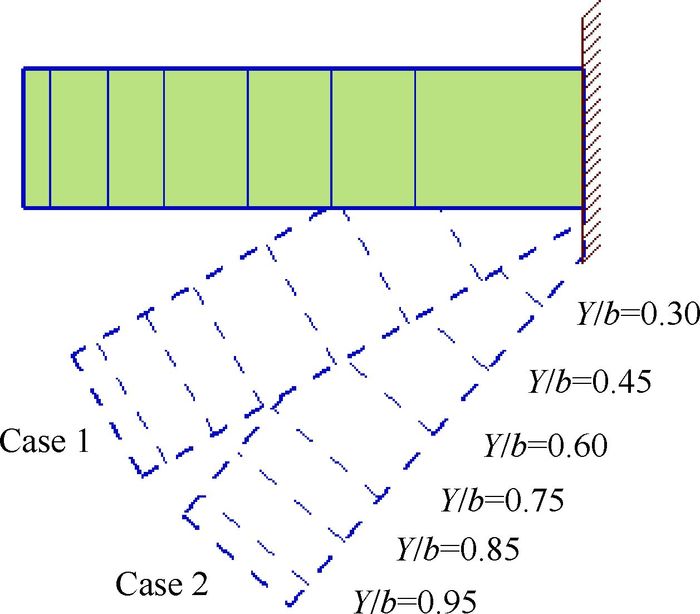 |
| 图 1 AFV-D机翼不同后掠角下展向截面位置示意图 Fig. 1 Schematic of spanwise cross-sectional position of AFV-D wing at different backswept |
| 图选项 |
1) Case 1:后掠角30°,马赫数0.7,雷诺数2.5×106,迎角α=4°。
2) Case 2:后掠角50°,马赫数0.7,雷诺数2.5×106,迎角α=6°。
计算得到表面压力系数分布与实验数据的对比图。图 2和图 3为截面数值模拟的压力系数(Cp)分布与实验数据的对比图,其中x/c为相对弦长。
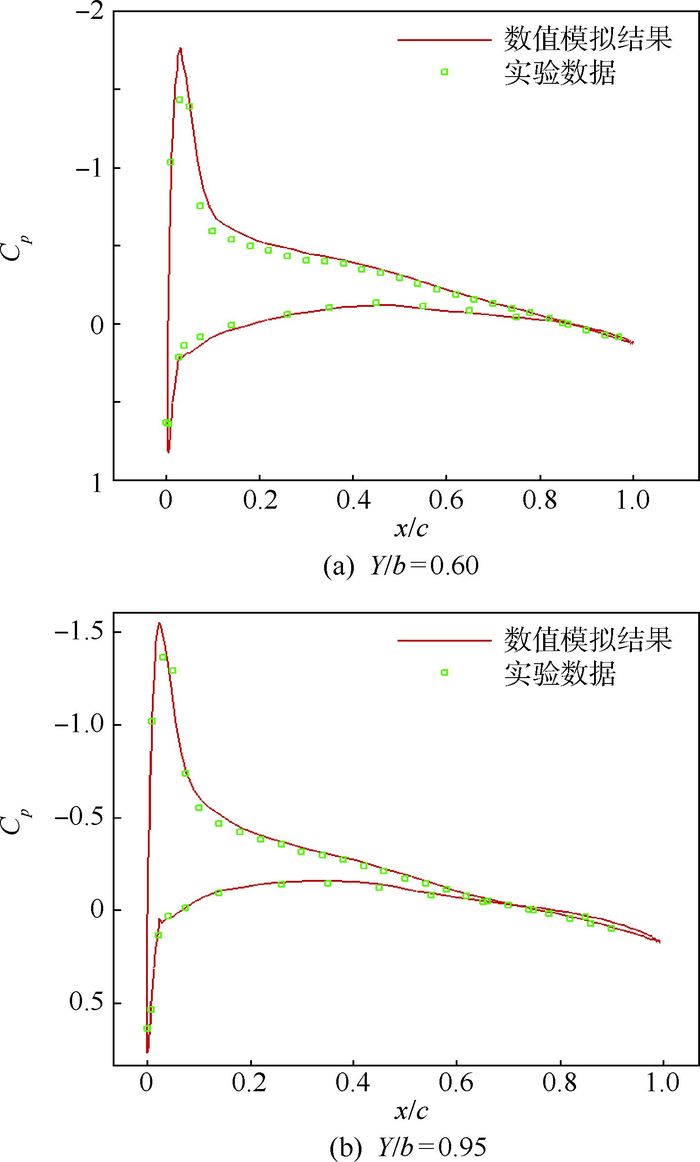 |
| 图 2 Case 1不同截面处压力系数分布与实验数据对比 Fig. 2 Case 1 pressure coefficient distribution at different sections compared with experimental data |
| 图选项 |
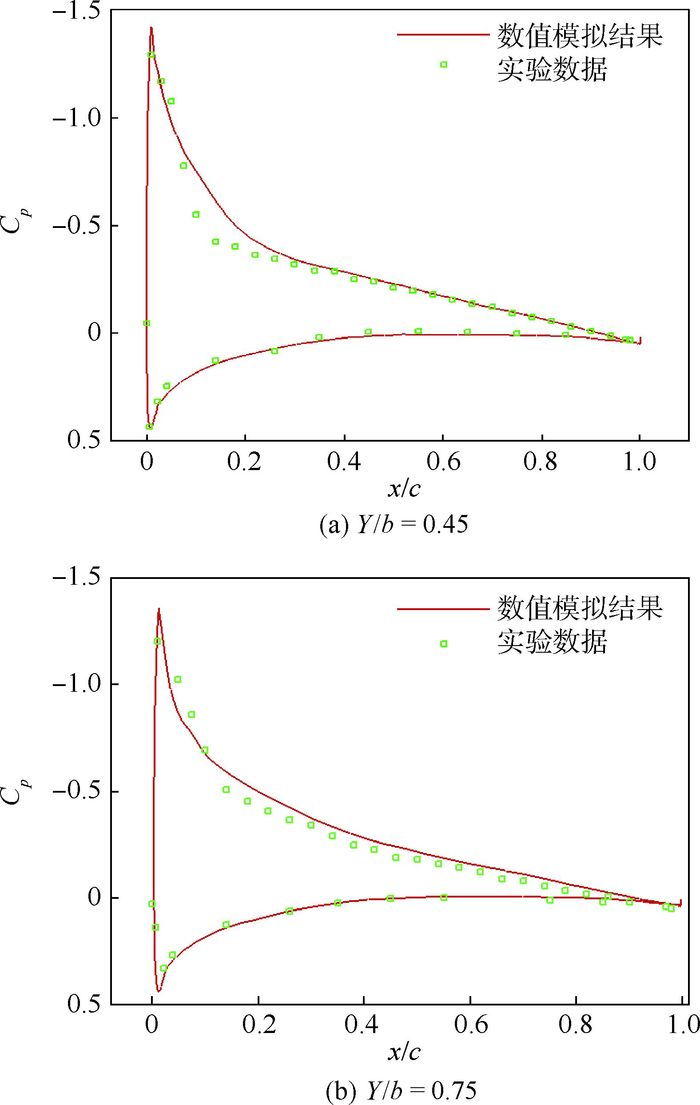 |
| 图 3 Case 2不同截面处压力系数分布与实验数据对比 Fig. 3 Case 2 pressure coefficient distribution at different sections compared with experimental data |
| 图选项 |
通过对AFV-D机翼的数值模拟计算结果与实验数据的对比可以看到,计算结果与实验值吻合良好,模拟方法可以用于对高空长航时菱形连翼布局飞机的数值计算。
2 计算模型与网格生成 菱形连翼布局无人机的初始构型Model 1由前翼和后翼组成,前翼后掠45°,后翼前掠45°,两翼在翼尖处连接,采用平列式布置,无上反角和安装角。其展长为36.21 m,机翼弦长为3.168 m,翼型使用NACA64A615层流翼型,对菱形连翼初始构型生成多块结构网格,网格数为272×145×102,保证壁面第1层网格的y+≈1,由于飞机布局为菱形连翼,存在前后2个机翼,定义的参考弦长为前后2个机翼的弦长之和,为确保计算结果的可靠性,其远场大于60倍机翼定义弦长,其半模结构网格示意图如图 4所示。
 |
| 图 4 Model 1网格示意图 Fig. 4 Schematic of grid of Model 1 |
| 图选项 |
3 高空长航时菱形连翼布局无人机俯仰力矩非线性特性分析 3.1 俯仰力矩特性的数值模拟结果 菱形连翼布局无人机设计巡航马赫数为0.6,巡航高度20 km,Model 1模型飞机俯仰力矩系数Cm的数值模拟曲线如图 5所示,下标Dia表示全机。
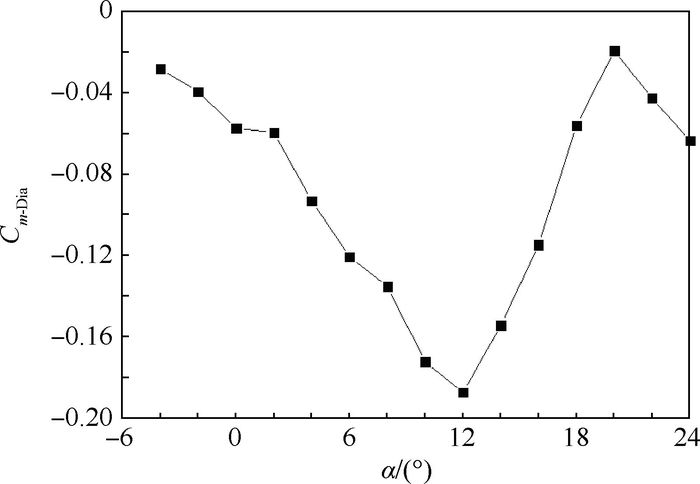 |
| 图 5 Model 1俯仰力矩特性曲线 Fig. 5 Pitching moment characteristic curve of Model 1 |
| 图选项 |
从计算结果上看在迎角α=-4°~0°范围内,随着迎角的增加俯仰力矩系数基本呈线性减少趋势,而在α=0°~4°之间时,菱形连翼布局的飞机的俯仰力矩系数呈现先上扬后下降的非线性特征,α=4°~12°范围内随着迎角的增加俯仰力矩系数基本呈线性减少的趋势,但其在α=8°附近仍出现了小幅上扬的情况。当α>12°时,俯仰力矩系数随着迎角的增大线性上仰,菱形连翼布局飞机的俯仰力矩随迎角的变化表现出很强的非线性特性。为便于区分,对俯仰力矩特性曲线中出现的先上扬后下降的现象称为“上扬”,对于曲线中出现的上仰后不再下降的现象参考后掠翼称为“上仰”。
图 6为菱形连翼布局飞机和其前后翼随迎角增大时的焦点位置变化图,下标Frt和Aft分别表示前翼和后翼。其图 6横坐标值代表参考范围,例如在α=1°时的值代表在α=0°~2°时前后翼焦点的位置。纵坐标值y代表焦点距离无人机前缘的位置。从图 6可以看到随着迎角的增大,菱形连翼布局飞机的焦点位置不断振荡但基本上在一个较小的范围内移动,但前后翼的焦点位置的移动范围在较大迎角时明显大于全机的移动范围。
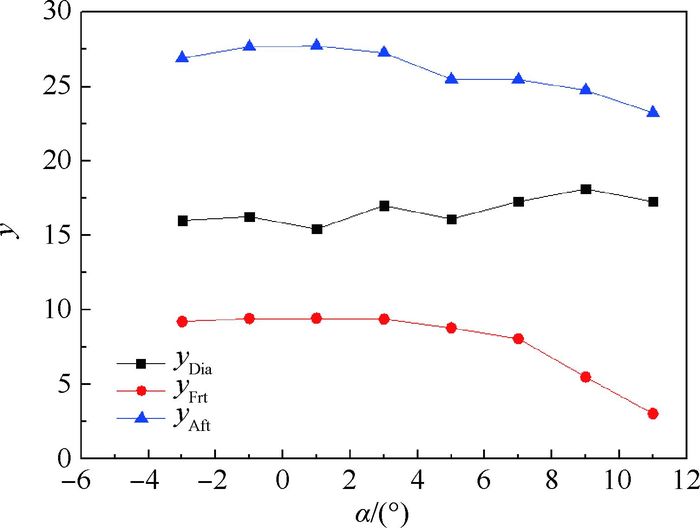 |
| 图 6 前后翼及全机焦点位置变化 Fig. 6 Change of focus positions of frt-wing, aft-wing and aircraft |
| 图选项 |
图 7为前后翼焦点的坐标位置离全机焦点坐标位置的距离,Δy为前后翼焦点距全机焦点的位置。观察图 7可以看到,在α<8°时,后翼焦点的位置距全机焦点位置的距离大于前翼焦点的位置距全机焦点位置,并在α=0°~2°范围内出现一个极大值。在α>8°以后,前翼的焦点位置距全机焦点的位置有较大的增加,前翼绕焦点的力臂开始大于后翼。
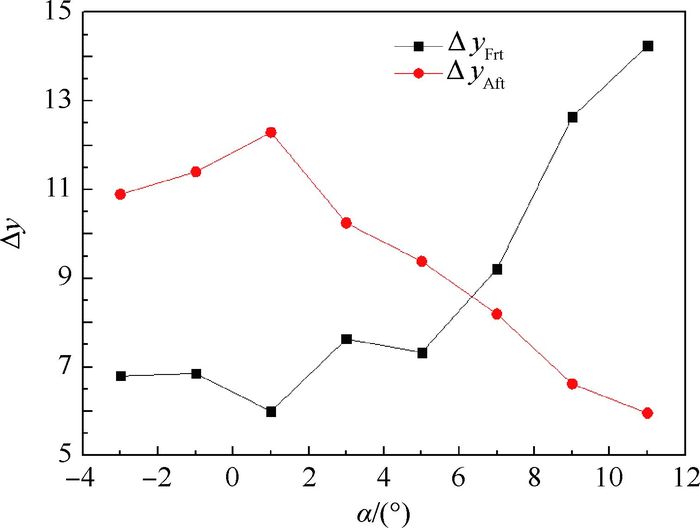 |
| 图 7 前后翼焦点位置距全机焦点距离变化 Fig. 7 Change of distance between frt-wing's and aft-wing's focus position and aircraft's focus position |
| 图选项 |
3.2 俯仰力矩非线性变化的流动机理 观察全机俯仰力矩系数非线性情况较为严重的区域,选择α=2°和α=8°附近进行流动机理分析并研究全机俯仰力矩出现上仰的原因。
3.2.1 α=2°附近出现俯仰力矩非线性现象 图 8(a)和图 8(b)分别为在α=-4°~4°时前后翼和全机俯仰力矩特性和升力特性的变化曲线, CL为升力系数。由于观察图 8不特别直观,因此分别对前后翼在α=0°和α=4°获得数值模拟数据进行线性插值获得α=2°时的差值数据与其通过数值模拟获得的数据进行对比获得表 1。
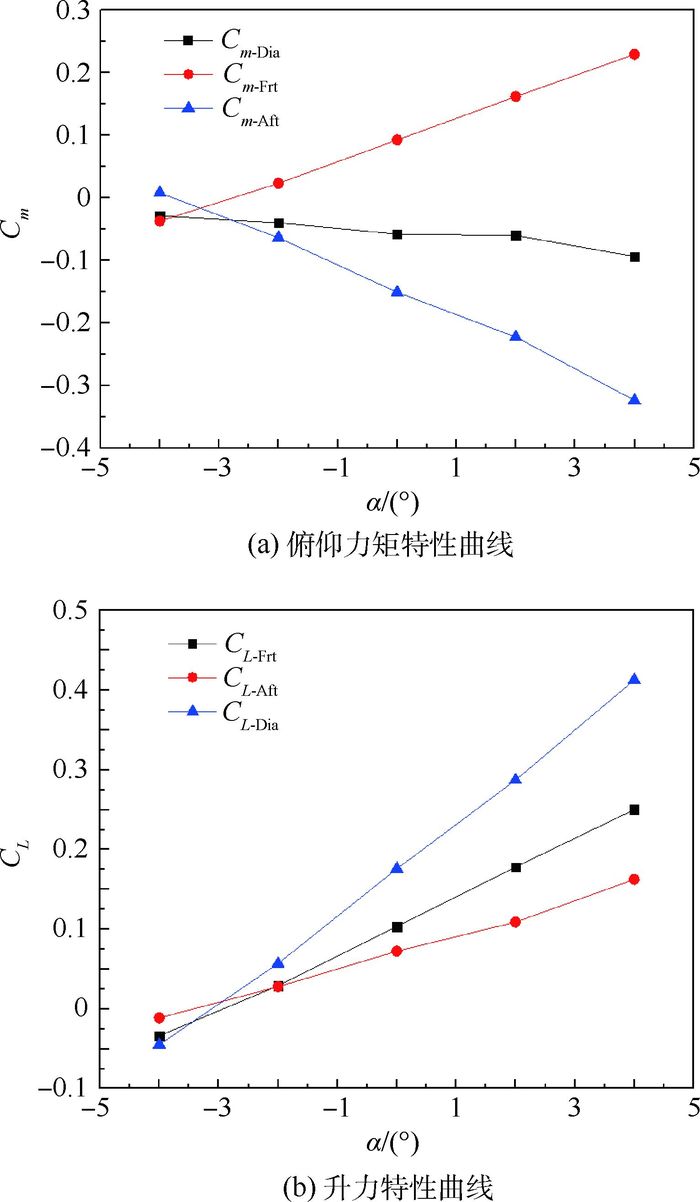 |
| 图 8 α=2°附近俯仰力矩特性曲线及升力特性曲线 Fig. 8 Pitching moment characteristic curves and lift characteristic curves near α=2° |
| 图选项 |
表 1 插值数据与数值模拟数据对比 Table 1 Comparison between interpolation data and numerical simulation data
| 位置 | 插值数据 | 数值模拟数据 | 偏差/% |
| 前翼 | 0.161 45 | 0.162 38 | 0.57 |
| 后翼 | -0.237 6 | -0.221 8 | 7.12 |
表选项
从图 8(a)和表 1中可以看出前翼的俯仰力矩特性曲线在α=-4°~4°之间呈线性增加的趋势。后翼的俯仰力矩曲线在α=2°附近线性差值数据与数值模拟数据之间的插值超过7%,出现非线性上扬特性。全机俯仰力矩系数出现非线性的原因主要是由于后翼在α=2°周围的俯仰力矩曲线的非线性所引起的。从图 8(b)中可以看出前翼的升力特性曲线在α=-4°~4°之间呈线性增加,这是导致前翼的俯仰力矩曲线在α=-4°~4°这一范围内呈线性的主要原因。后翼的升力特性曲线在α=2°附近时出现明显的气动效率降低的情况,这直接导致后翼在α=2°附近俯仰力矩曲线的非线性,由于后翼的焦点位置距离参考点的位置较远,后翼气动效率的少量降低就会导致全机俯仰力矩系数曲线产生较为严重的非线性特征。
后翼为前掠翼,其分离首先出现在翼根处。图 9为α=2°附近后翼翼根处的极限流线分布图,可以发现虽然由于较大的前掠角导致极限流线具有明显的沿展向流动的特征,但在α=2°时后翼上的极限流线仍为沿来流方向的附着流,流动分离可以忽略不计,后翼的气动效率降低并不是由于流动分离引起的。
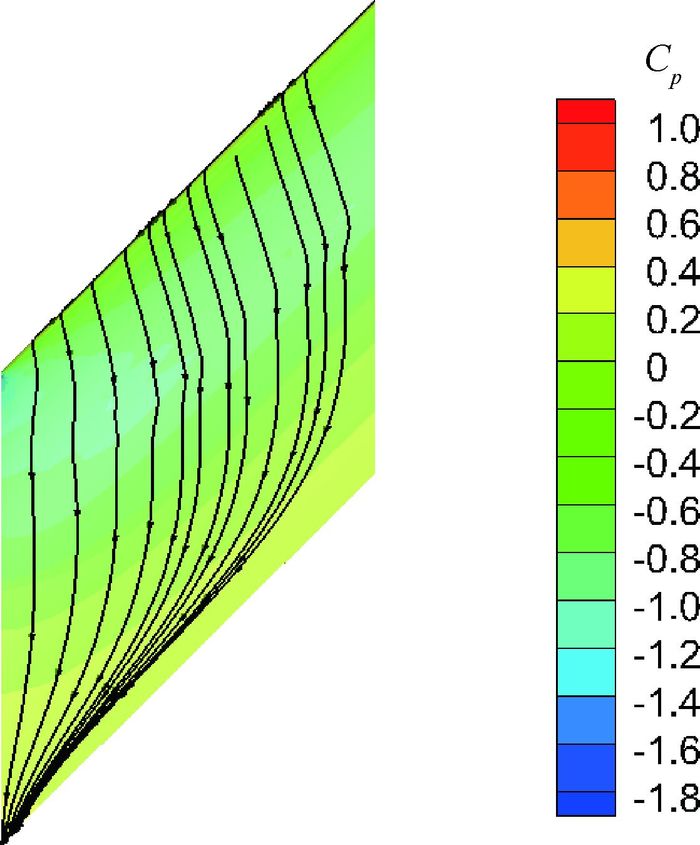 |
| 图 9 α=2°附近的后翼翼根处极限流线分布 Fig. 9 Limit streamline distribution of aft-wing root near α=2° |
| 图选项 |
选取如图 10所示位置对菱形连翼布局飞机进行切面分析,其截面的位置的展向长度为9.068 m(2Y/b=0.5), 13 m(2Y/b=0.717), 14.5 m(2Y/b=0.8)。
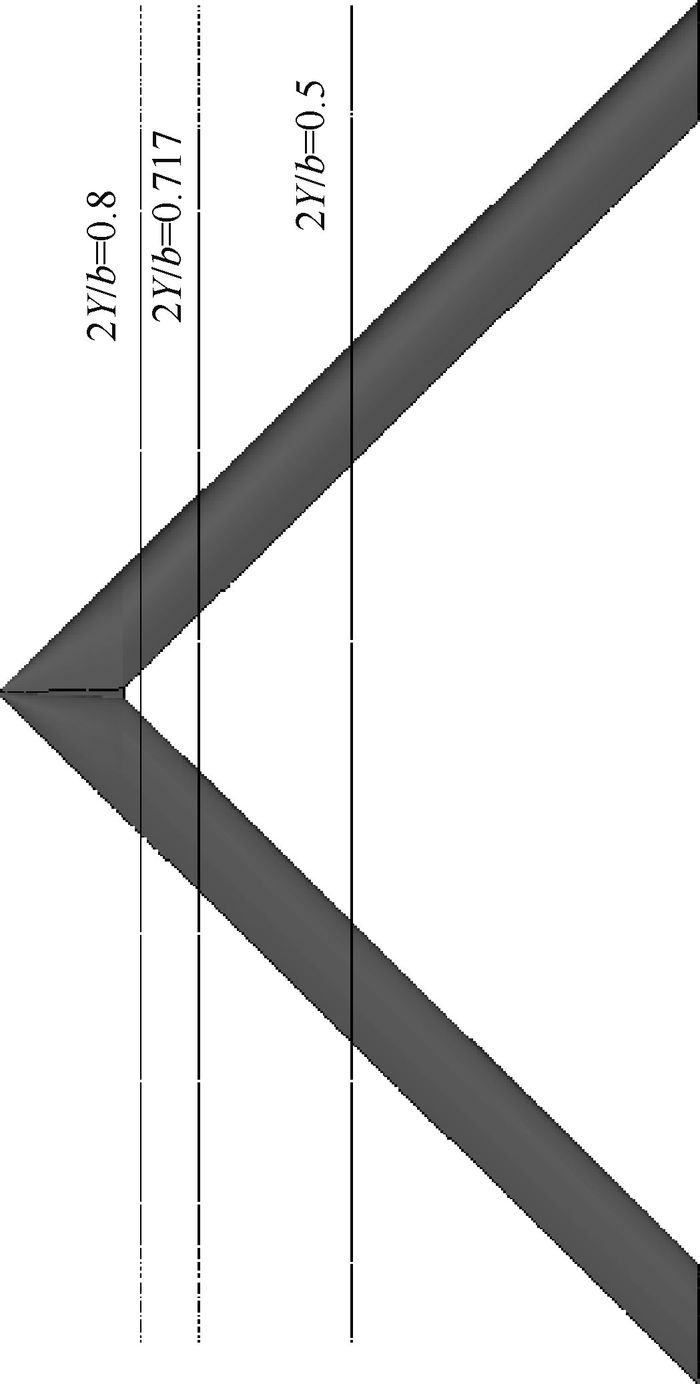 |
| 图 10 截面位置 Fig. 10 Sectional position |
| 图选项 |
参考直升机旋翼流场分析方法,图 11用湍动能κ来表示尾涡结构的强度和影响范围。湍动能可以显示流场的紊乱程度,涡量越大, 对应的湍流强度也越大, 则该区域的湍动能也越大。气流流过前翼后会产生一个含有较大湍动能的尾流区,在α=0°时,前翼的尾流从后翼的下表面流过,其尾涡的强度并不大,此时前翼对后翼的影响主要是前翼对气流的偏折导致后翼有效迎角的减少。随着迎角的增加,前翼环量增大,尾涡强度增大的同时下洗最强区向上方移动,最终在α=2°附近时前翼的尾流直接流经后翼的表面,前翼尾流与后翼边界层掺混,破坏了后翼的流场结构,同时可以看到这种流场结构变化几乎影响了后翼超过30%的展向区域,使后翼升力特性急剧减小。
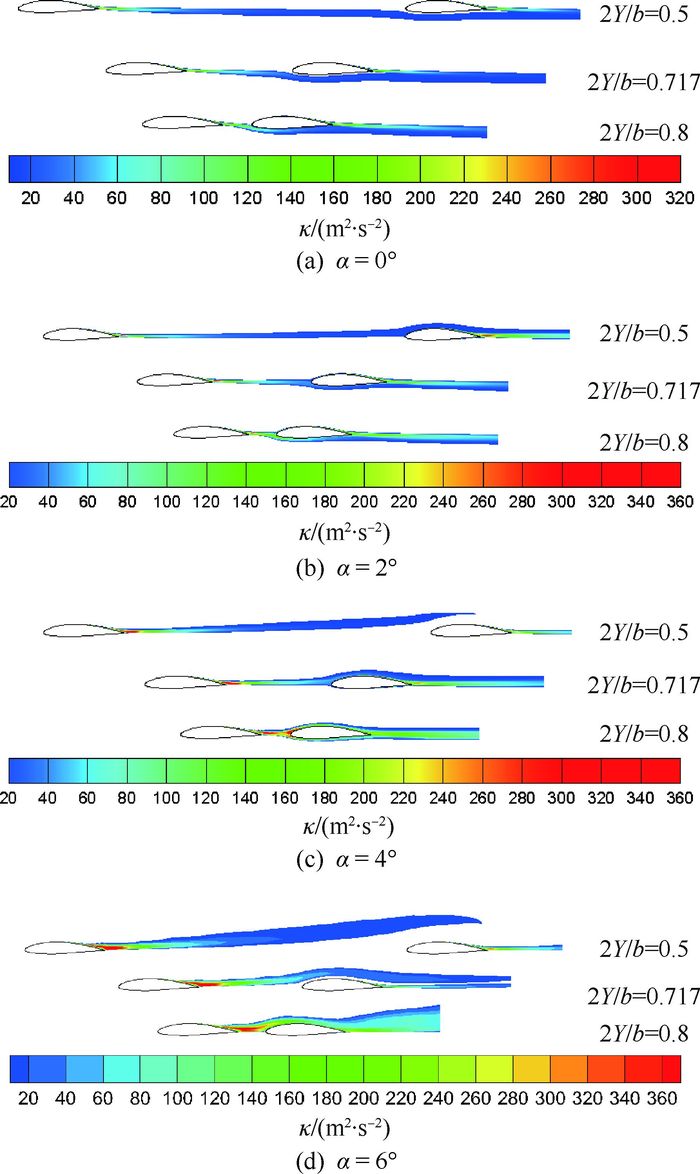 |
| 图 11 α=0°, 2°, 4°, 6°时的湍动能 Fig. 11 Turbulent kinetic energy at α=0°, 2°, 4°, 6° |
| 图选项 |
当迎角继续增大到α=4°时,虽然尾流区的强度有所增大,但其下洗最强区继续上移,在2Y/b=0.717处对后翼的表面边界层结构的影响已经较小,虽然在2Y/b=0.8处前翼产生的湍流仍然覆盖着后翼,但影响的展向区域已经大幅缩少,其升力特性得以恢复。当α增大到6°时,前翼产生的尾迹区的大部分已基本从后翼上方掠过,不再影响后翼的流场结构。
3.2.2 α=8°附近出现俯仰力矩非线性现象 在α=4°~12°范围内菱形连翼布局飞机的俯仰力矩特性曲线出现非线性变化的特征,其在α=8°附近再次出现先上扬后下降的俯仰力矩非线性特征。通过分析在这一迎角附近的俯仰力矩特性受以下4种因素的影响:
1) 前翼流动分离的影响。对比α=4°和α=8°极限流线分布图(图 12(a)和图 12(b))可以看到,在α=8°附近时,前翼外侧后缘已经开始发生分离,随着迎角的增大分离区域沿展向和弦向分别向内侧和前缘方向扩展,前翼的气动效率降低,此时的前翼外侧后缘的位置位于重心之后,失速导致全机抬头力矩少量增加。随着迎角的增大,前翼外侧后缘的分离区域扩大并越过焦点位置,前翼对全机低头力矩的增加的起主要的作用。
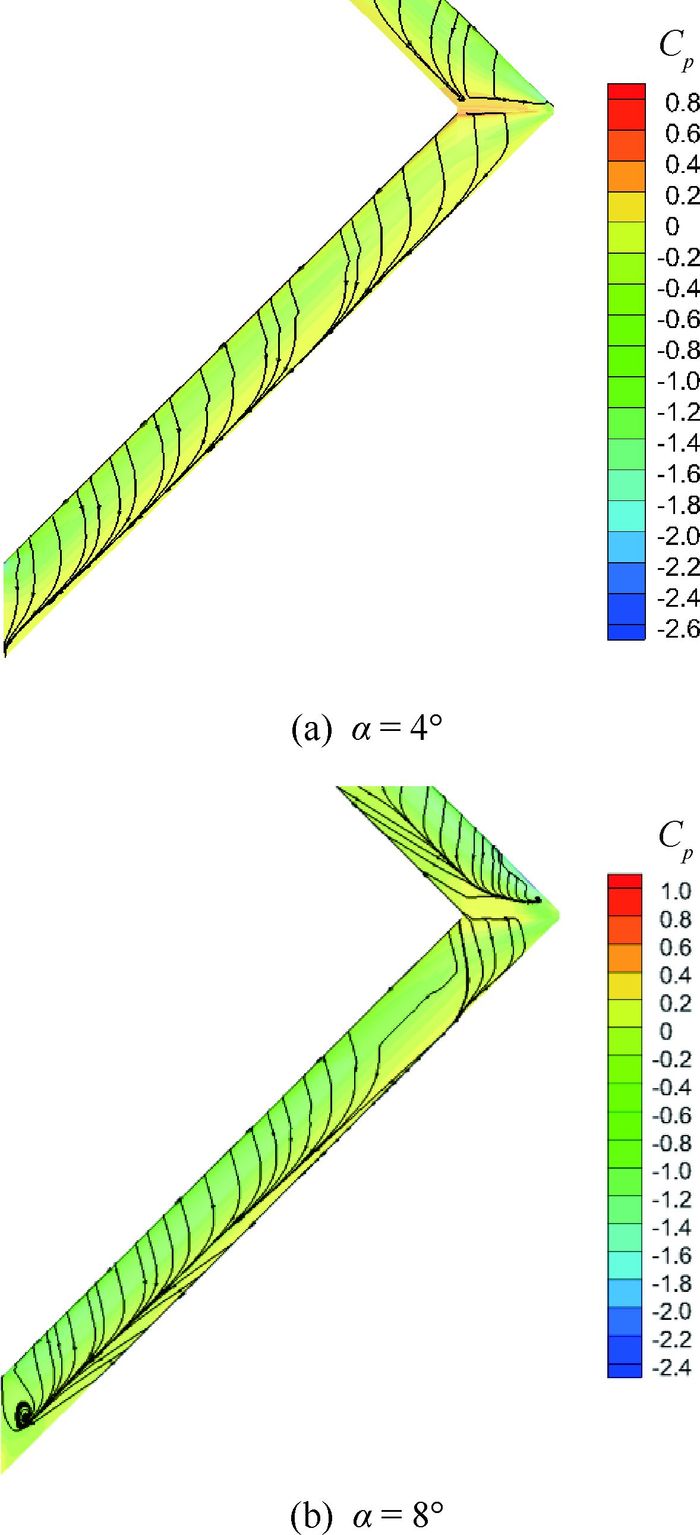 |
| 图 12 α=4°, 8°的极限流线 Fig. 12 Limit streamlines at α=4°, 8° |
| 图选项 |
2) 翼尖分离的影响。对比图 13可以看到对于单独前翼,在α=8°附近发生明显的翼尖分离,产生了翼尖分离漩涡。翼尖失速导致的升力减少会增大抬头力矩,然而对于菱形连翼布局飞机,由于后翼为前掠翼,其具有将前翼边界层向翼根输送的能力[19],因此菱形连翼翼尖分离的范围要明显小于单独前翼,且分离强度也较小,只在翼尖部分形成了一个强度较小分离螺旋点。
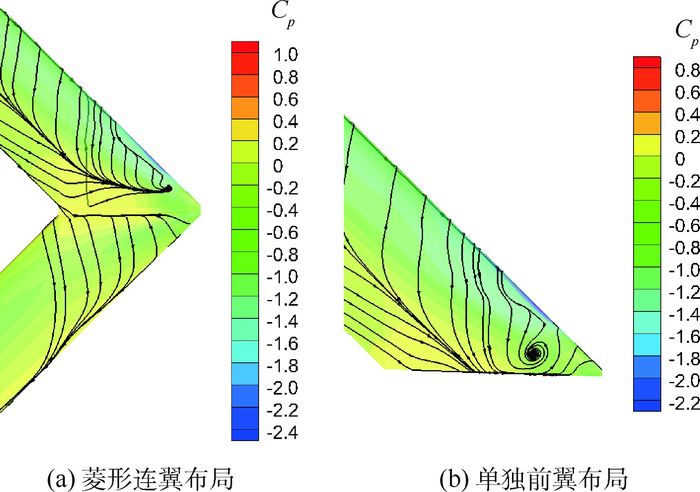 |
| 图 13 α=8°时菱形连翼布局和单独前翼布局的翼尖分离 Fig. 13 Wingtip separation of diamond joined-wing configuration and separate frt-wing configuration at α=8° |
| 图选项 |
3) 前翼尾流的影响。在α=8°附近时,前翼的尾流已经几乎不再影响后翼的表面流场结构,其对气流的偏折作用也在降低,这导致后翼的气动特性恢复,全机的低头力矩增加。
4) 后翼流动分离的影响。由于后翼的前掠角较大,虽然在其绝大部分区域的流动沿来流方向呈现附着流状态,但随着迎角的增加,前掠翼的展向流动向翼根处堆积并在后翼与机身连接处中部形成分离漩涡区。后翼分离线随着迎角的增大继续向后翼前缘和翼尖方向移动并产生一个分离旋涡并扩展到几乎整个外翼上表面。
在这4个影响因素中,由于前翼后缘分离的位置距全机焦点位置较近,前翼的流动分离导致的升力特性减小较为和缓,升力的少量损失不至于影响全机的俯仰力矩特性,翼尖分离会导致抬头力矩的增加,但由于菱形连翼布局飞机的翼尖分离强度较小且距焦点位置相对较近,因此其能提供的抬头力矩增量也相对有限。而前翼尾流的影响在α=4°时已经较小,在α=8°时其影响会进一步降低,对全机俯仰力矩变化的贡献也较小,而后翼翼根位置距全机的焦点距离较远,其后翼翼根分离导致的升力下降是这一迎角附近俯仰力矩变化的主要原因。
3.2.3 α=12°附近出现俯仰力矩上仰现象 菱形连翼布局飞机与后掠翼布局类似也存在明显的俯仰力矩“上仰”问题,当α>12°以后,俯仰力矩发生不稳定的转折,因此上仰限制了菱形连翼飞机的使用迎角,为防止产生俯仰失控情况的发生,虽然菱形连翼布局飞机具有极佳的失速性能,但仍然需要控制其使用迎角或采取其他的措施以提高菱形连翼布局飞机的大迎角使用特性。
高空长航时菱形连翼布局无人机在α=8°附近出现上扬现象后并未出现全机上仰的情况,其主要原因是由于随着迎角的增大,前翼与后翼均出现流动分离现象,且其流动分离的范围均在扩大,在这种状态下,全机的俯仰力矩由前后翼共同提供,当迎角继续增大时,前翼的失速范围扩大,并越过参考点的位置,这样前翼失速由提供少量的抬头力矩而变成提供低头力矩。而后翼在前翼下洗的影响下其流动分离的区域要小于前翼流动分离的区域,前翼先于后翼失速。这导致全机低头力矩的增加,由于前翼的气动效率较高,因此在此阶段前翼失速对全机低头力矩的贡献仍能保证全机俯仰力矩在α=8°附近小幅上扬后再次恢复纵向静稳定性,甚至可能提高菱形连翼布局的纵向静稳定裕度。随着迎角的继续增加,当迎角增大到12°以上时后翼也几乎完全失速,其所能提供的低头力矩急剧减少,全机俯仰力矩特性曲线急剧上仰。
4 高空长航时菱形连翼布局无人机总体布局参数的设计 由于高空长航时菱形连翼布局无人机的俯仰力矩特性曲线具有非线性的问题,严重影响了其实际的应用。通过研究,菱形连翼布局无人机俯仰力矩特性曲线出现非线性特征的主要原因是由前后翼流动特性耦合产生的,前后翼总体参数的变化会直接影响全机的俯仰力矩特性,因此通过改变前后翼总体参数来研究全机俯仰力矩曲线特性曲线变化的趋势可以更好地了解菱形连翼布局无人机俯仰力矩特性变化的规律。为使研究具有可比性,在对总体参数进行变化时,保持菱形连翼布局的展长和沿来流方向的弦长不变,通过在初始构型的基础上调整前后翼之间的掠角来改变菱形连翼布局翼间距,通过在初始构型的基础上调整前后翼之间的反角来改变翼夹角,并研究这些参数改变对菱形连翼布局俯仰力矩特性的影响。如图 14所示为前后翼需要进行调整的参数示意图。图中:ΛFrt和ΛAft分别为需要进行调整的前后翼的后掠角和前掠角,ΓFrt和ΓAft分别为需要进行调整的前后翼的上反角。
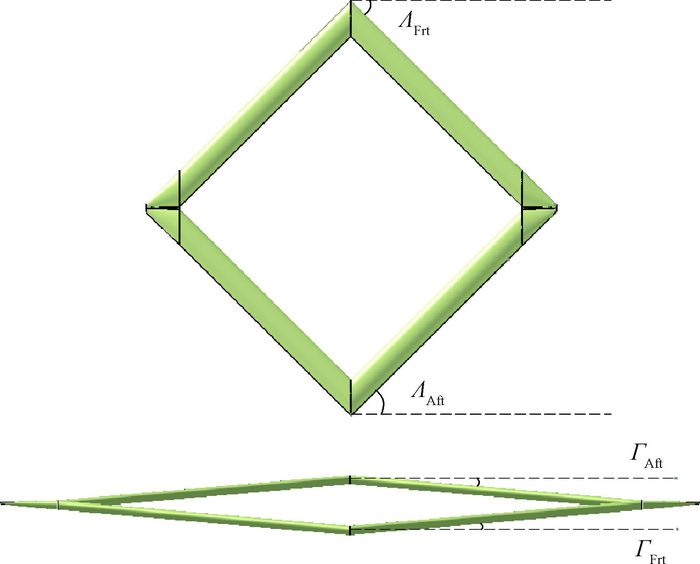 |
| 图 14 需调整参数示意图 Fig. 14 Schematic of parameters to be adjusted |
| 图选项 |
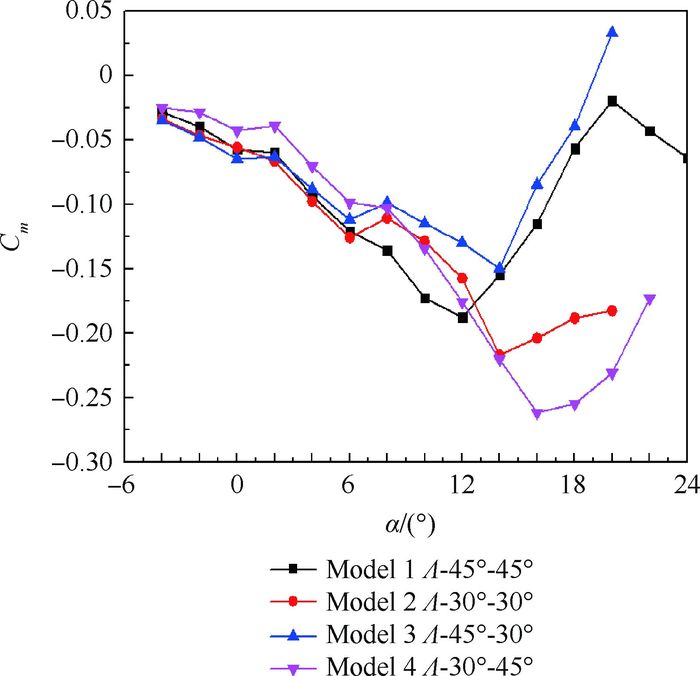
4.1 翼间距的影响 如图 15所示为改变翼间距对菱形连翼俯仰力矩特性的影响,将前后翼的掠角分别变为30°获得Model 2;保持前翼参数不变,后翼前掠角变为30°获得Model3;保持后翼不变,前翼后掠角变为30°获得Model 4。数值模拟获得俯仰力矩特性曲线如图 16所示。
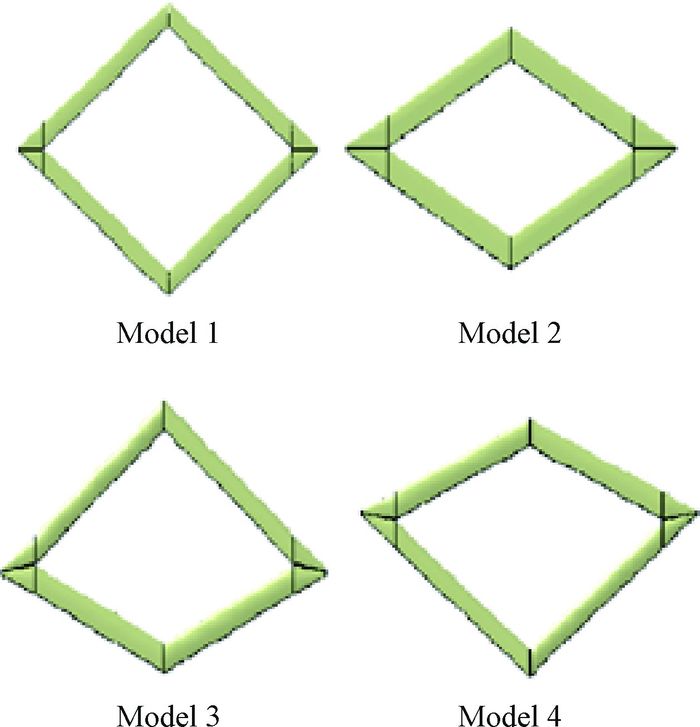 |
| 图 15 改变翼间距的菱形连翼无人机布局 Fig. 15 Diamond joined-wing UAV configuration with changing distance between wings |
| 图选项 |
 |
| 图 16 翼间距影响的俯仰力矩特性曲线 Fig. 16 Pitching moment characteristic curves influenced by distance between wings |
| 图选项 |
图 16为改变翼间距情况下的菱形连翼无人机俯仰力矩特性曲线,图中Λ-XX°-XX°前后的XX分别为模型的前翼的后掠角ΛFrt和后翼的前掠角ΛAft。对比俯仰力矩特性曲线,4个模型均在α=2°附近出现力矩上扬后恢复的阶段,说明菱形连翼布局飞机前翼尾流对后翼的直接扫掠导致的后翼升力特性的减少不可能通过改变翼间距来消除。相比于Model 1,其余3个模型的翼间距都有所减小,其耦合的气动干扰更加严重,因此在α=8°附近的俯仰力矩上扬也较Model 1要严重。Model 2和Model 3的上扬程度明显大于Model 1和Model 4的情况,这是由于Model 2和Model 3的后翼的前掠角比Model 1和Model 4的前掠角小,后翼的气动效率较高,其翼根失速导致的升力减少量更大,其导致全机的上扬更加严重。
对比Model 1和Model 4在上仰附近的俯仰力矩特性曲线可以发现Model 4的上仰时的迎角要大于Model 1,这主要是由于全机的俯仰力矩由前后翼共同提供,当前翼的后掠角减小时,其气动效率增加,其对后翼的下洗作用也在增强,这导致在同一迎角下Model 4后翼的失速范围要小于Model 1的后翼,因此力矩上仰的迎角后延且上仰幅度较小。Model 2与Model 3有相同的后翼,其后翼分离的迎角主要与后翼特性和受前翼下洗的共同作用有关,对比曲线可以看到Model 2与Model 3都在α=14°左右上仰,但Model 2的上仰幅度远小于Model 3的上仰幅度,这主要是由于模型的后翼前掠角较小,其气动效率较高,后翼的分离特性对力矩上仰的贡献较大。同时由于Model 2前翼气动效率较高且距离后翼较近,其对后翼的下洗影响较大,因此在力矩上仰后其上仰幅度小于Model 3。
4.2 翼夹角的影响 为研究翼夹角的影响,在Model 1的基础上,前翼下反5°,后翼上反5°获得翼夹角为10°的正交错布局Model 5;前翼下反10°,后翼上反10°获得翼夹角为20°正交错布局Model 6;前翼上反5°,后翼下反5°获得翼夹角为10°的负交错布局Model 7;前翼上反10°,后翼下反10°获得翼夹角为20°的负交错布局Model 8(见图 17)。数值模拟获得俯仰力矩特性曲线如图 18所示。
 |
| 图 17 改变翼夹角的菱形连翼无人机布局 Fig. 17 Diamond joined-wing UAV configuration with changing angle between wings |
| 图选项 |
 |
| 图 18 改变翼夹角情况下的菱形连翼无人机俯仰力矩特性曲线 Fig. 18 Pitching moment characteristic curves of diamond joined-wing configuration UAV with changing angle between wings |
| 图选项 |
图 18为改变翼夹情况下的菱形连翼无人机俯仰力矩特性曲线,图中Γ-XX°-XX°前后的XX分别为模型的前翼和后翼的上反角ΓFrt和ΓAft,其中下反为负。
图 19为Model 5、Model 6在α=-4°,2Y/b=0.5时湍动能分布,对于Model 5、Model 6这样正交错布局菱形连翼飞机,其前翼尾流直接流过后翼表面的迎角为负值,平飞状态下后翼就避开了前翼尾流的作用,随着迎角的增大,前翼的尾流影响越来越小,因此在α=0°到力矩上扬前正交错布局菱形连翼飞机仅有一个俯仰力矩非线区域。增大前正交错布局菱形连翼飞机前后翼之间的夹角可以使翼尾流直接扫掠后翼而导致俯仰力矩上扬的区域向较少使用的负迎角区域前移。
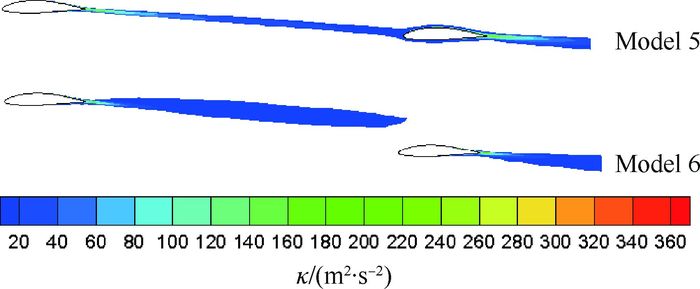 |
| 图 19 Model 5、Model 6在α=-4°, 2Y/b=0.5时湍动能分布 Fig. 19 Turbulent kinetic energy distribution of Modal 5, Model 6 at α=-4°, 2Y/b=0.5 |
| 图选项 |
图 20为Model 7在α=6°, 2Y/b=0.5时的湍动能分布,Model 8在α=10°附近也有类似的分布,对于这样正交错布局菱形连翼布局飞机,通过抬高后翼,前翼对后翼的尾流影响导致全机俯仰力矩上扬的迎角范围可以后移,并可以与后翼分离导致的力矩上扬等情况耦合使其力矩非线性的区域减少为一个,减少控制的难度。
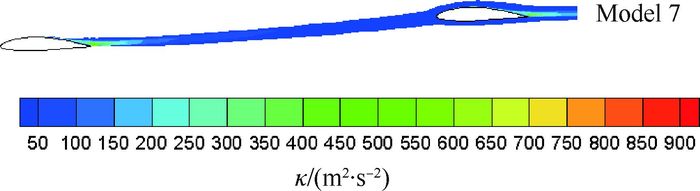 |
| 图 20 Model 7在α=6°, 2Y/b=0.5时湍动能分布 Fig. 20 Turbulent kinetic energy distribution of Model 7 at α=6°, 2Y/b=0.5 |
| 图选项 |
5 结论 1) 菱形连翼布局无人机的俯仰力矩特性曲线随着迎角的增加呈现严重的非线性,其主要由两段非线性区域组成并伴随严重的上仰。α=2°附近俯仰力矩出现非线性上扬的原因是由于前翼尾流直接扫掠后翼导致后翼流场结构改变而气动效率下降引起的。而α=8°附近的俯仰力矩非线性段形成的原因较多,但后翼分离在其中起主要的作用。而菱形连翼布局无人机俯仰力矩上仰是由于前后翼分离耦合导致的。
2) 高空长航时菱形连翼布局无人机由于后翼受前翼尾流直接扫掠影响导致后翼流场结构改变引起的俯仰力矩非线性特征无法通过改变翼间距消除,但为了不影响菱形连翼布局飞机的实际应用,选择合适的前翼翼型和菱形连翼布局的翼间距以减少尾流的强度,并选择对湍流影响敏感性较差的翼型作为后翼翼型,可以减小出现俯仰力矩曲线非线性的强度。另外通过改变前翼的安装角和前后翼之间的翼夹角可以改变出现俯仰力矩非线性特性的迎角范围以避开使用设计点。改善由于前翼尾流直接扫掠后翼导致的俯仰力矩非线性问题。
3) 通过选择翼间距,菱形连翼布局无人机可以有效地改善由于后翼分离导致的俯仰力矩非线性问题并能够将产生全机力矩上仰的迎角范围向后推迟,改善菱形连翼布局飞机的大迎角特性,通过合理选择适当的布局参数可以缓解菱形连翼布局无人机的俯仰力矩非线性的问题。但由于前后翼之间的关系高度耦合,其设计难度较大,只能提出部分设计原则供参考。
参考文献
| [1] | WOLKOVITCH J. The joined wing:An overview[J].Journal of Aircraft, 1986, 23(3): 161–178.DOI:10.2514/3.45285 |
| [2] | KROO I, SMITH S, GALLMAN J. Aerodynamic and structural studies of joined-wing aircraft[J].Journal of Aircraft, 1991, 28(1): 74–81.DOI:10.2514/3.45994 |
| [3] | LIVNE E.Aeroelasticity of joined-wing airplane configurations:Past work and future challenges-A survey[C]//Proceedings of 19th AIAA Applied Aerodynamics Conference.Reston:AIAA, 2001:16-19. |
| [4] | CRAFT R L.Drag estimates for the joined-wing sensor craft:05J02[R].Dayton:AFIT, 2005. |
| [5] | PéREZ-á LVAREZ J, CUERNO-REJADO C, MESEGUER J. Aerodynamic parametric analysis of an unconventional joined-wing aircraft configuration[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2016, 230(10): 1917–1933.DOI:10.1177/0954410015620444 |
| [6] | ANDREWS S, RUBEN P E.Stability and control effects on the design optimization of a box-wing aircraft[C]//14th AIAA Aviation Technology Integration and Operations Conference.Reston:AIAA, 2014:1-22. |
| [7] | BOND V, CANFIELD R A, MATOS M, et al.Wind tunnel testing of a twisted wing for longitudinal control in a joined-wing aircraft[C]//48th Structures Structural Dynamics and Materials Conference.Reston:AIAA, 2007:1-7. |
| [8] | RASMUSSEN C C, CANFIELD R A, BLAIR M. Joined-wing sensor-craft configuration design[J].Journal of Aircraft, 2006, 43(5): 1470–1478.DOI:10.2514/1.21951 |
| [9] | LEDOUX S, VASSBERG J, FATTA G, et al.Aerodynamic cruise design of a joined wing sensorcraft[C]//26th AIAA Applied Aerodynamics Conference.Reston:AIAA, 2008:1-13. |
| [10] | MARTINEZ J, FLICK P, PERDZOCK J, et al.An overview of sensorcraft capabilities and key enabling technologies[C]//26th AIAA Applied Aerodynamics Conference.Reston:AIAA, 2008:1-13. |
| [11] | REICHENBACH E, CASTELLUCCIO M, SEXTON B.Joined wing sensorcraft aeroservoelastic wind tunnel test program[C]//52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference.Reston:AIAA, 2011:1-30. |
| [12] | TYLER C, SCHWABACHER G, CARTER D.Comparison of computational and experimental studies for a joined-wing aircraft[C]//Proceedings of 40th AIAA Aerospace Sciences Meeting & Exhibit, Aerospace Sciences Meetings.Reston:AIAA, 2002:1-8. |
| [13] | NANGIA R K, PALMER M E, TILMANN C P.Unconventional high aspect ratio joined-wing aircraft with aft- & forward-swept wing-tips[C]//Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA, 2003:1-13. |
| [14] | 楚亮, 马东立, 张朔, 等. 一种联结翼布局气动特性的求解模型[J].航空学报, 2010, 31(5): 909–913. CHU L, MA D L, ZHANG S, et al. Solution model for aerodynamic characteristics of joined-wing configuration[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 909–913.(in Chinese) |
| [15] | 张晓萍, 曾会华, 余雄庆. CFD方法在联结翼飞机方案设计中的应用[J].南京航空航天大学学报, 2004, 36(6): 763–768. ZHANG X P, ZENG H H, YU X Q. Application of CFD in conceptual design of joined-wing aircraft[J].Journal of Nanjing University of Aeronautics & Astronautics, 2004, 36(6): 763–768.(in Chinese) |
| [16] | 刘学强, 李青, 柴建忠, 等. 盒式机翼布局气动特性研究[J].南京航空航天大学学报, 2007, 39(6): 722–725. LIU X Q, LI Q, CHAI J Z, et al. Aerodynamic characteristic research for box-wing aircraft[J].Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(6): 722–725.(in Chinese) |
| [17] | 李军, 李占科, 宋笔锋. 联翼高空长航时无人机总体布局设计研究[J].飞行力学, 2009, 27(4): 1–4. LI J, LI Z K, SONG B F. Conceptual layout design of the joined-wing high-altitude-long-endurance UAV[J].Flight Dynamics, 2009, 27(4): 1–4.(in Chinese) |
| [18] | 吉笑峰. 传感器飞行器总体设计方案研究[D]. 西安: 西北工业大学, 2008. JI X F.Research on the overall design of the sensorcraft[D].Xi'an:Northwestern Polytechnical University, 2008(in Chinese). |
| [19] | 李光里, 李国文, 黎军, 等. 连接翼布局气动特性研究[J].空气动力学学报, 2006, 24(4): 513–519. LI G L, LI G W, LI J, et al. The aerodynamics investigation of the joined-wing configuration[J].Acta Aerodynamica Sinica, 2006, 24(4): 513–519.(in Chinese) |
| [20] | 王延奎, 单继祥, 田伟, 等. 联翼布局俯仰力矩非线性变化特性的数值模拟[J].北京航空航天大学学报, 2012, 38(7): 862–866. WANG Y K, SHAN J X, TIAN W, et al. Investigation on non-linear characteristic of pitching moment of joined wing configuration aircraft[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(7): 862–866.(in Chinese) |
| [21] | MANIE F, RAYNAL J C.Transonic measurements on the ONERA AFV D variable sweep wing in the ONERA S2 MA-wind tunnel:AGARD-AR-138[R].[S.l.:s.n.], 1979. |
