由于熔接、拉锥、抛磨[7-10]等方法极易破坏二维光子晶体包层结构,从而引入大量损耗,不适宜光子带隙光纤光器件的制作,已公开报道的有关光子带隙光纤光器件均采用空间光路。基于光子带隙光纤准直器的微光学光器件采用切割工艺、空间光路,可以避免光纤拉锥、研磨等工艺对光子带隙光纤二维包层的结构破坏,对拓展光子带隙光纤的实用范围有着极其重要的意义。
本文从高斯光束通过光学系统一般模型出发,考虑光子带隙光纤的端面没有反射,且模场偏小的特点,利用矩阵光学,建立了光波在子午面和弧矢面的变化矩阵,通过仿真分析,得到了尾纤与C-lens透镜之间的间距以及透镜各参数对光子带隙光纤准直器工作距离和束腰直径的影响。
1 理论分析与建模 单模光子带隙光纤中传输的光束近似为高斯光束[11],当束腰半径为ω1高斯光束从光纤出射后,q参数表示为q1=iπω12/λ,高斯光束的单透镜成像特性如图 1所示,ω1和ω2分别为光纤出射高斯光束的束腰半径和其经透镜成像后的高斯光束束腰半径;λ为光波波长。
 |
| 图 1 高斯光束单透镜成像 Fig. 1 Single lens imaging of Gaussian-beam |
| 图选项 |
高斯光束从尾纤出射的位置即为束腰所在位置,假设尾纤与C-lens透镜斜端面之间的距离为d,对应传输矩阵M1;像方空间任意一点H到C-lens透镜球面中心的距离为S,对应传输矩阵为M2;C-lens透镜的传输矩阵为T,高斯光束从尾纤端面传播到点H对应的传输矩阵M遵循ABCD定律。
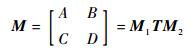 | (1) |
该光束经透镜变换后的像方光束q参数为
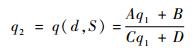 | (2) |
如图 2所示为一种光子带隙光纤,其主要光学参数主要由占空比和周期决定。光子带隙光纤包层空气孔的周期排列结构产生带隙效应,能阻碍某段频率的光在其中传播,而纤芯作为该周期性结构的一个缺陷,该段频率光波将被限制在缺陷中传播[12]。相比普通光纤, 由于其依靠带隙效应导光,光波是在纤芯的大空气孔中传输。
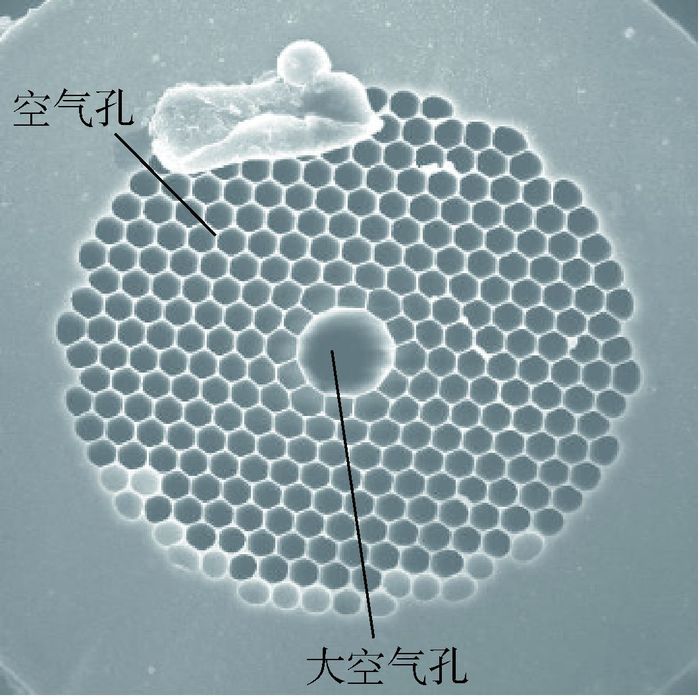 |
| 图 2 光子带隙光纤端面 Fig. 2 Photonic bandgap fiber end face |
| 图选项 |
光子带隙光纤准直器的模型如图 3所示,由光子带隙光纤的尾纤和C-lens透镜构成。不同于普通光纤准直器,在光子带隙光纤中,光束是在光纤中心的大空气孔缺陷中传播,光纤出射到空气中的光介质连续,端面没有反射和散射。
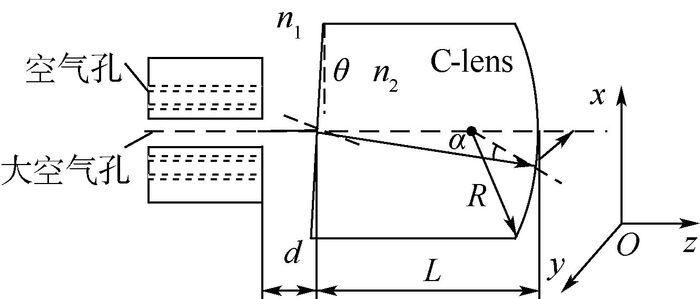 |
| 图 3 光子带隙光纤准直器结构 Fig. 3 Structure of photonic bandgap fiber collimator |
| 图选项 |
如图 3所示,因此不用像普通光纤准直器那样将尾纤研磨成斜8°,也不用在尾纤和C-lens透镜之间分别在弧矢面和子午面分开计算[13-15],其在子午面和弧矢面的传输矩阵均为
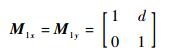 | (3) |
但是为了满足回波损耗要求[16],C-lens透镜的前端面需要一定的倾斜角θ,由于倾斜角的存在,C-lens透镜前后2个端面在子午面和弧矢面上传输矩阵T不同,假设C-lens透镜的长度为L,球面的曲率半径为R,空气的折射率为n1,透镜的折射率为n2。
在子午面内,C-lens透镜的传输矩阵TX为
 | (4) |
在弧矢面内,C-lens透镜的传输矩阵TY为
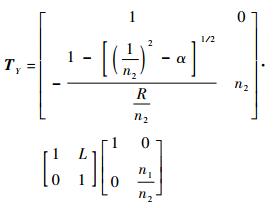 | (5) |
偏心角α可由斯涅尔公式和正弦定律求出:
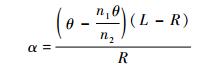 | (6) |
将式(6) 分别代入式(4) 和式(5) 可以求出C-lens在子午面和和弧矢面的传播矩阵TX和TY,将式(3)~式(5) 代入式(1) 后由式(2) 可以求出像方任意一点在子午面和弧矢面的q参数q2。
根据式(2),像方高斯光束的束腰半径可表示为
 | (7) |
像方光束束腰与透镜球面中心的距离可表示为
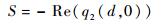 | (8) |
根据式(7)、式(8) 可以求出束腰和工作距离。
2 仿真分析 仿真所用的光子带隙光纤的为NKT公司产品HC-1550-02,光纤参数如表 1所示,表中:Λ为包层空气孔间距,D为纤芯直径,ω0为模场直径。
表 1 光子带隙光纤参数 Table 1 Parameters of photonic bandgap fiber
| 参数 | Λ/μm | D/μm | ω0/μm |
| 数值 | 3.8±0.1 | 10±1 | 9±1 |
表选项
C-lens入射光端面倾斜角θ=8°,透镜折射率n2=1.744,影响出射高斯光束在子午面和弧矢面的束腰半径WX、WY,工作距离 Sx、Sy的变量包括d、L、R,实际应考虑d、ω1、R、L、λ对工作距离及束腰半径的影响。
图 4为尾纤与C-lens透镜对工作距离和出射束腰半径的影响,透镜采用R1.9,可以看出,C-lens透镜倾斜角在子午面和弧矢面上对工作距离Sx、Sy和出射束腰半径WX、WY大小的影响几乎相同,子午面相对弧矢面略微向长距离d处偏移,这是因为:在子午面和弧矢面,尾纤与C-lens透镜前端面之间的传输矩阵相同,投射到C-lens透镜的光线不会随距离d的改变发生变化,因此α是定值,球面透镜对子午面和弧矢面的影响不随距离d影响,点精度也是定值。
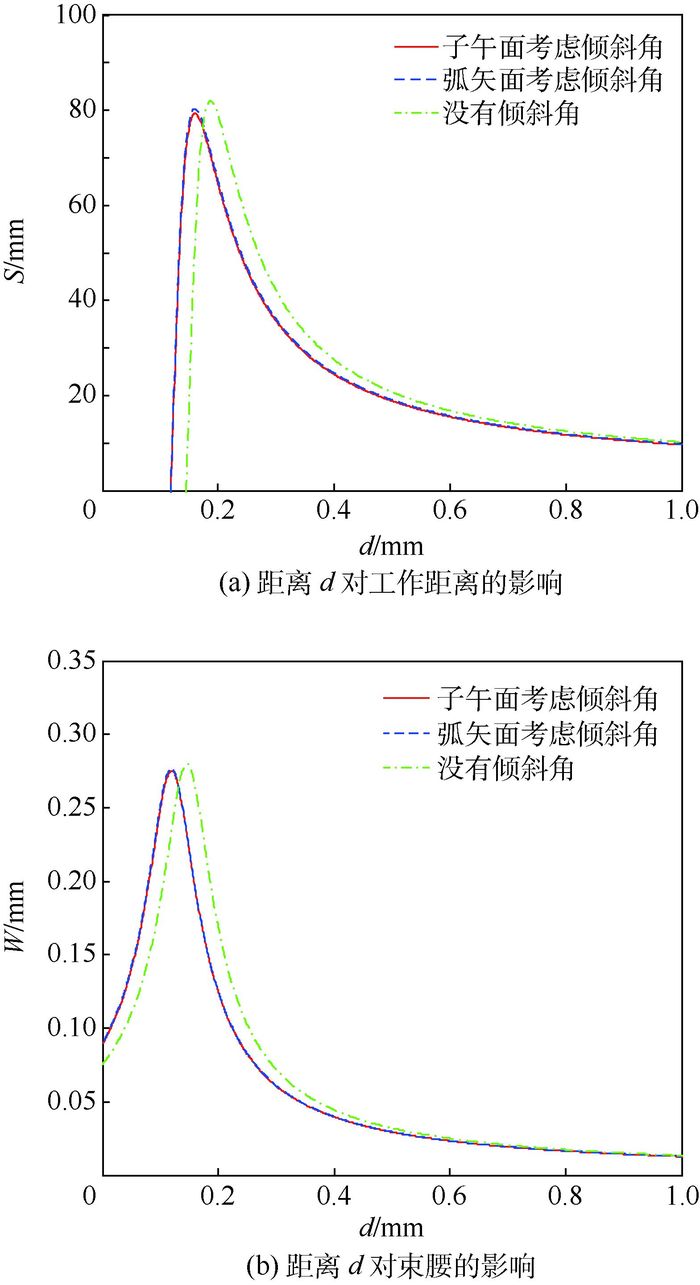 |
| 图 4 距离d对工作距离和束腰的影响(L=4.2 mm,R=1.9 mm,ω1=4.5 μm) Fig. 4 Influence of distance d on working distance and beam waist radius (L=4.2 mm, R=1.9 mm, ω1=4.5 μm) |
| 图选项 |
倾斜角的存在使得最大工作距离和最大出射束腰半径相对没倾斜角时向短距离d偏移。当间距d=0.13~0.278 mm时,工作距离S>40 mm,间距d=0.08~0.157 mm时,束腰半径W>0.2 mm,取d=0.13~0.157 mm时可同时保证在子午面和弧矢面工作距离大于40 mm、束腰半径大于0.2 mm。当d一定时,在子午面工作距离稍微小于弧矢面,保证子午面上的工作距离可以保弧矢面上的工作距离,且每个参数对子午面和弧矢面影响关系相似,因此以下以子午面对准直器的传输特性进行分析。
图 5为光纤模场对束腰和工作距离影响,可以发现光纤模场对透镜出射束腰和工作距离影响非常大,当ω1 < 5.2 μm时,可同时保证工作距离S>40 mm,束腰半径W>0.2 mm。由于光子带隙光纤模场设计灵活,通常可以满足这一要求。对于模场偏大的光子带隙光纤,其准直器的制作可以根据以下有关C-lens透镜球面透镜的曲率半径R和透镜长度L来选取和适合的C-lens透镜。
 |
| 图 5 模场对工作距离和束腰半径的影响(L=4.2 mm,R=1.9 mm,d=1.4 mm) Fig. 5 Influence of mode field on working distance and beam waist radius (L=4.2 mm, R=1.9 mm, d=1.4 mm) |
| 图选项 |
图 6为波长对束腰半径和工作距离影响,束腰半径和工作距离在短波长λ < 6 μm时随波长变化明显,λ>6 μm时变化趋于平缓,且随波长增加,工作距离和束腰半径均增加。波长λ>1 220 nm时,可同时满足工作距离S>40 mm、束腰半径W>0.2 mm的需求。如要需要满足更短波长的高斯光束准直,其分析与模场对工作距离和束腰影响相似,通过选取合适的C-lens透镜来满足应用需求。
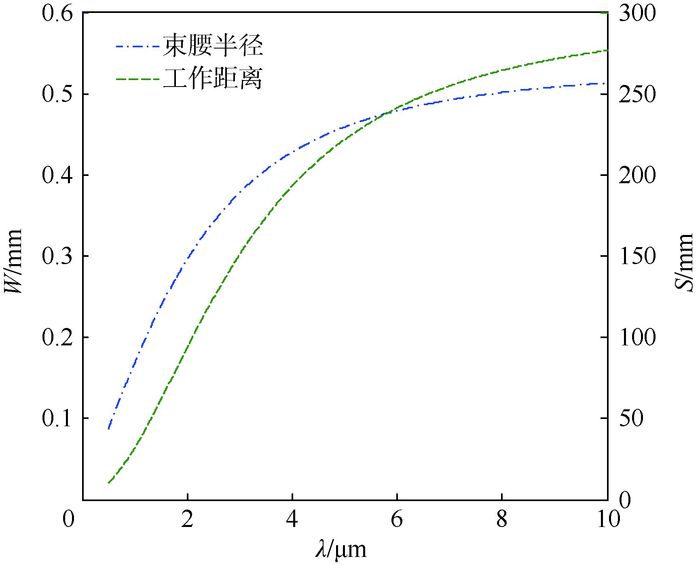 |
| 图 6 波长对束腰半径和工作距离影响(L=4.2 mm,R=1.9 mm,ω1=4.5 μm,d=1.4 mm) Fig. 6 Influence of wavelength on beam waist radius and working distance (L=4.2 mm, R=1.9 mm, ω1=4.5 μm, d=1.4 mm) |
| 图选项 |
通过以上有关模场和波长对工作距离和束腰分析可知,研究曲率半径R和透镜长度L同时对准直器工作距离和出射束腰影响是必要的,能够指导光子带隙光纤准直器C-lens透镜选取和制作。图 7和图 8为两者同时对工作距离和出射束腰的影响。从图 7和图 8可以发现成一系列锥状,并不是简单的单调关系,在固定的R(或L),满足要求的L(或R)在一个很小的范围内有明显的变化,有一个最佳值。
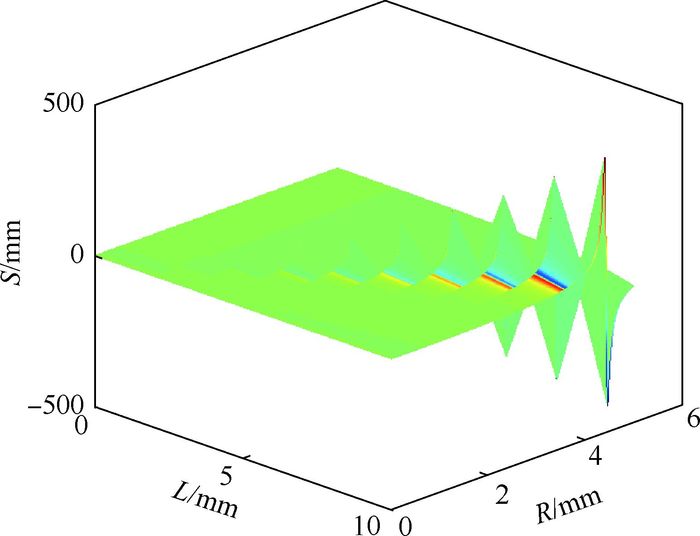 |
| 图 7 C-lens长度和曲率半径对工作距离的影响(d=1.4 mm) Fig. 7 Influence of C-lens length and radius of curvature on working distance (d=1.4 mm) |
| 图选项 |
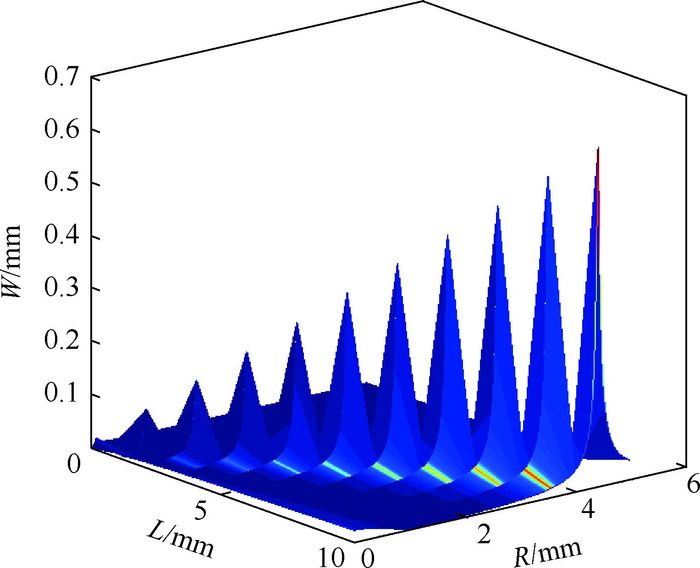 |
| 图 8 C-lens长度和曲率半径对束腰半径的影响(d=1.4 mm) Fig. 8 Influence of C-lens length and radius of curvature on beam waist radius (d=1.4 mm) |
| 图选项 |
随着R和L的不断增加,最大工作距离和束腰也在增加,当L>10 mm,R> 5 mm时,存在满足最大束腰半径W>0.6 mm,工作距离S>400 mm的点。
由于光子带隙光纤在包层直径为125 μm的成熟产品还没有,通过使用实芯的光子晶体光纤实验得到的耦合器附加损耗在2 dB左右,仍然很大,一部分原因是光纤本身损耗比较大,制作工艺不完善,另一部分原因在于相比光子带隙光纤,实芯光子晶体光纤需要研磨成斜8°,研磨会带来损耗,且由于实芯光子晶体光纤尾纤端面不能镀膜,存在反射损耗。
3 结论 本文根据所设计的光子带隙光纤准直器模型,利用矩阵光学原理,得到:
1) 光子带隙光纤准直器相比普通光纤准直器,由C-lens倾斜端面和球面引起的光斑椭圆化程度小,且由于光子带隙光纤端面没有反射,满足回波损耗的C-lens透镜前端面倾斜角可以进一步压缩,对出射高斯光束椭圆化影响进一步降低。
2) 光子带隙光纤模场对束腰和工作距离的影响非常明显,在光子带隙光纤的模场设计灵活的情况下,基于C-lens的光子晶体光纤准直器能够满足长工作距离、大出射束腰半径的要求。
光纤准直器的工作距离S=5 mm时,可满足微光学光器件对插入功能部件(晶体、光楔、滤波片等)的要求,由以上设计知,基于通信用R1.9的C-lens透镜和HC-1550-02光子带隙光纤的准直器在工作距离上大于40 mm,满足制作微光学光子带隙光纤耦合器、隔离器,可将耦合器和隔离器应用于全光子晶体光纤陀螺中。
参考文献
| [1] | 林学煌. 光无源器件[M].北京: 人民邮电出版社, 1998: 164-171. LIN X H. Optical passive devices[M].Beijing: Posts and Telecom Press, 1998: 164-171.(in Chinese) |
| [2] | 田燕宁, 方强, 王永昌. 双通道光环形器结构的设计及理论分析[J].中国激光, 2004, 31(11): 1398–1402. TIAN Y N, FANG Q, WANG Y C. Structure and characteristics of a double function optical circulator with double fiber tip and lens twice[J].Chinese Journal of Lasers, 2004, 31(11): 1398–1402.DOI:10.3321/j.issn:0258-7025.2004.11.025(in Chinese) |
| [3] | 禹培栋, 王国忠, 陈明华, 等. 光开关技术进展[J].半导体光电, 2001, 22(3): 149–154. YU P D, WANG G Z, CHEN M H, et al. Recent progress in optical switching[J].Semiconductor Optoelectronics, 2001, 22(3): 149–154.(in Chinese) |
| [4] | 廖延彪. 光纤光学[M].北京: 清华大学出版社, 2000: 54-90. LIAO Y B. Fiber optics[M].Beijing: Tsinghua University Press, 2000: 54-90.(in Chinese) |
| [5] | JOANNOPOULOS J D, JOHNSON S G, WINN J N, et al. Photonic crystals:Molding the flow of light[M].Princeton: Princeton University Press, 2011: 30-90. |
| [6] | 石飞飞. 光子晶体光纤设计与传感特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 5-9. SHI F F.Design and sensing characteristic on photonic crystal fibers[D].Harbin:Harbin Institute of Technology, 2013:5-9(in Chinese). |
| [7] | KIM H, KIM J, PAEK U C, et al. Tunable photonic crystal fiber coupler based on a side-polish technique[J].Optics Letters, 2004, 29(11): 1194–1196.DOI:10.1364/OL.29.001194 |
| [8] | JAROSZEWICZ L R, STASIEWICZ A K, MARC P, et al.Broadband photonic crystal fiber coupler with polarization selection of coupling ratio[C]//Proceedings of 4th European Workshop on Optical Fiber Sensors.Bellingham, WA:SPIE, 2010, 7653:76533W. |
| [9] | 代文, 杨远洪, 宋奎岩, 等. 基于渐变折射率透镜的低损耗1×N微结构光纤耦合方法[J].光学学报, 2014, 34(4): 77–82. DAI W, YANG Y H, SONG K Y, et al. Low-loss 1×N microstructrued fiber coupling method with a single gradient index lens[J].Acta Optica Sinica, 2014, 34(4): 77–82.(in Chinese) |
| [10] | 张璐. 光子晶体光纤的低损耗透镜耦合技术[J].光学学报, 2014, 34(1): 63–68. ZHANG L. Low-loss lens-coupling technique on photonic crystal fiber[J].Acta Optica Sinica, 2014, 34(1): 63–68.(in Chinese) |
| [11] | HIROOKA T, HORI Y, NAKAZAWA M. Gaussian and Sech approximations of mode field profiles in photonic crystal fibers[J].IEEE Photonics Technology Letters, 2004, 16(4): 1071–1073.DOI:10.1109/LPT.2004.824950 |
| [12] | 张虎. 空芯光子带隙光纤的结构设计和特性研究[D]. 北京: 北京邮电大学, 2009: 1-4. ZHANG H.Structure design and property research of hollow-core photonic bandgap fibers[D].Beijing:Beijing University of Posts and Telecommunications, 2009:1-4(in Chinese). |
| [13] | 龚文杰. C-Lens准直器特性的研究[D]. 哈尔滨: 哈尔滨工业大学, 2006: 2-16. GONG W J.Study of the C-lens collimator characteristics[D].Harbin:Harbin Industrial University, 2006:2-16(in Chinese). |
| [14] | 陆乔乔, 胡姝玲, 王鑫龙, 等. 大功率双包层光纤准直器的建模与仿真分析[J].红外与激光工程, 2014, 43(7): 2055–2060. LU Q Q, HU S L, WANG X L, et al. Modeling and stimulation of high-power double-clad fiber collimator[J].Infrared and Laser Engineering, 2014, 43(7): 2055–2060.(in Chinese) |
| [15] | 胡海蕾, 陈荣, 赖爱光, 等. C-lens准直特性分析[J].福建师范大学学报, 2005, 21(1): 36–40. HU H L, CHEN R, LAI A G, et al. Analysis of C-lens collimating propert[J].Journal of Fujian Normal University, 2005, 21(1): 36–40.(in Chinese) |
| [16] | 王素芹, 阮玉, 殷东亮, 等. C-lens准直器回波损耗的理论计算与分析[J].大气与环境光学学报, 2003, 16(1): 24–28. WANG S Q, RUAN Y, YIN D L, et al. The calculation and analyzing of the RL of C-lens collimator[J].Optoelectronic Technology & Information, 2003, 16(1): 24–28.(in Chinese) |
