湍流问题是当前航空航天设计过程中的关键问题之一。近几十年来，计算流体力学(Computational Fluid Dynamics, CFD)迅速发展，已成为研究湍流问题的重要手段^[1]。美国NASA在其《2030年CFD远景规划》报告中指出^[2]，CFD能够在有效降低设计过程中风险与费用的前提下，提供更加丰富的流动信息。同时，其认为湍流模型是影响CFD计算精度的最重要因素之一，必须对湍流模型开展持续深入的研究。
目前，常见的湍流模拟方法主要包括直接数值模拟(Direct Numerical Simulation, DNS)、大涡模拟(Large Eddy Simulation, LES)、雷诺平均Navier-Stokes(Reynolds Averaged Navier-Stokes, RANS)方法以及RANS/LES混合方法。DNS方法与LES方法计算精度高，但计算量很大，在当前计算条件下，两者离应用于工程实际流动还有较大差距。RANS方法计算量小，能够快速、经济地给出预测结果，但其普适性差，尤其对分离流动等非定常湍流问题难以给出令人满意的结果。RANS/LES混合方法结合RANS方法与LES方法各自的优点，能够在较小的计算量下(相较于LES方法)更为准确地模拟复杂流动问题(相较于RANS方法)。RANS/LES混合方法自提出以来受到了广泛关注，众多研究者发展了多种多样的混合方法^[3]。其中，应用最为广泛的是分离涡模拟(Detached Eddy Simulation, DES)类方法。Spalart等^[4]最早于1997年提出了SA-DES方法，其在近壁区回归为RANS模型，在远离壁面区域表现出LES求解的特性。随后，Strelets^[5]采用类似思想，基于Menter SST两方程模型发展了SST-DES方法。DES类方法在分离流动中表现出了较强的适用性，但同时其也存在一些缺陷^[6]，最为典型的问题之一是模化应力不足(Modelled Stress Depletion, MSD)问题。MSD问题主要是由边界层内网格不适当加密引起的。由于边界层内网格不适当加密(主要指流向和展向)，RANS/LES交界面向壁面移动，RANS模化区域减小，但此时的网格分辨率又无法支撑LES模式的准确求解，造成计算应力偏小，即出现MSD问题。MSD问题可能会导致计算所得壁面摩擦力降低，严重时会出现分离提前或非物理分离等现象。为解决该问题，Menter等^[7]率先提出边界层保护思想，采用SST模型中的F₁或F₂作为延迟函数，构造SST-DDES(Delayed DES)方法，保护边界层区域由RANS主导且不受网格加密影响。Spalart等^[8]受此启发，构造了更具一般性的延迟函数F_d，该延迟函数能应用于任意基于涡黏性模型的DES类方法中。虽然采用不同延迟函数的各DDES方法已得到了一定应用，但DDES方法还远未成熟，对不同延迟函数的作用机制与基本特性认识尚不够充分，尤其缺乏延迟函数在超声速分离流动中的相关研究。
为围绕延迟函数开展研究，本文选取超声速底部流动作为测试算例。超声速底部流动是广泛存在于导弹、火箭、再入飞船等航空航天飞行器绕流中的一类典型流动，其对飞行器气动特性尤其对超声速飞行器阻力有着重要影响。超声速底部流动虽几何外形简单，但包含自由剪切层、膨胀波、激波、分离、激波/漩涡干扰等复杂非定常流动现象。由于该流动的复杂性与重要意义，众多****对其开展了广泛的研究工作。美国伊利诺伊大学气体动力学实验室采用LDV(Laser Doppler Velocimeter)技术对超声速底部流动开展了深入的实验研究^[9-10]，给出了流场结构与详细的实验数据。部分研究者采用RANS模型对超声速底部流动进行了模拟^[11]，所得底部压力分布与实验存在较大差异。Fureby等^[12]采用LES方法对此流动开展研究，总体上得到了较为满意的结果，但预测所得边界层厚度及分离区大小均与实验有明显偏差。Peng^[13]采用RANS/LES混合方法，在底部压力的计算中表现出了较高精度，但所得分离区偏大。国内高瑞泽和阎超^[14]采用基于BL模型的混合方法、罗大海等^[15]采用PANS方法对超声速底部流动进行数值模拟，考察不同方法性能，取得了一些有意义的成果。
本文基于SST-DDES方法，对比F₁、F₂和F_d3种延迟函数，分析不同延迟函数的优缺点与适用性，对它们在超声速分离流动中的性能开展考察与评估。
1 计算方法 基于Menter SST两方程模型，可推导得出SST-DDES模型，具体模型方程为^[7]

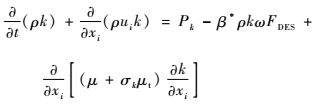(1)

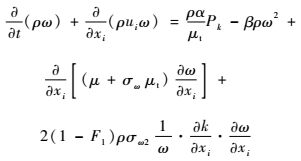(2)

式中：k为湍动能；ω为比耗散率；其他各项具体意义及模型常数详见文献[7]。
F_DES函数表达式为

(3)

式中：l_k-ω为湍流特征长度尺度；Δ为3个方向网格尺度Δx、Δy、Δz的最大值；C_DES为模型常数。在近壁区，F_DES取1，方法退化为原RANS模型方法；在分离区域，F_DES取大于1的值，方法表现出LES求解的特性。F_delay为SST-DDES方法中的延迟函数，其主要特性为在边界层内取1，保证近壁区的RANS模化；在远离壁面区域取0，SST-DDES方法回归到原SST-DES方法。本文中延迟函数F_delay采用3种不同形式F₁、F₂和F_d，下面对不同延迟函数进行简要介绍。
1) F₁函数
F₁函数表达式为

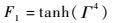(4)

式中：

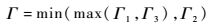(5)

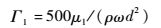(6)

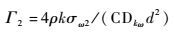(7)

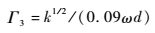(8)

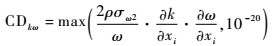(9)

其中：d为壁面距离；其余各项含义及常数与式(1) 和式(2) 中相同。
2) F₂函数
F₂函数表达式为

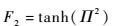(10)

式中：

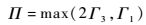(11)

其中：Γ₁和Γ₃如式(6) 和式(8) 所示。
3) F_d函数
F_d函数表达式为

(12)

式中：r_d为延迟因子，形式如下：

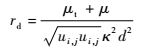(13)

其中：κ为卡门常数，取0.41；u_{i, j}为速度梯度；其余各项与前文一致。在近壁面对数率区，r_d=1；在远离壁面LES区域，r_d?1。
本文对以上3种不同延迟函数开展评价性研究，考察它们在超声速分离流动中的表现。
2 计算结果与分析 来流条件参照实验条件，来流马赫数Ma=2.46，来流静压P=31 415 Pa，来流静温T=145 K，底部圆柱面半径R=31.75 mm，对应的基于圆柱直径的雷诺数Re=2.858×10⁶。
计算模型和网格如图 1所示，网格生成参考文献[16]，在边界层、底部及尾迹区等流动关键部位进行网格加密，同时保证壁面第1层法向网格高度y^*＜1，总网格量约200万。计算方法参考课题组以往RANS/LES混合方法计算经验^{[14, 17]}，对流项采用5阶WENO的Roe格式离散，黏性项采用4阶中心差分格式离散。壁面条件采用无滑移绝热壁假设，物理时间推进步长Δt=5×10^-7 s。

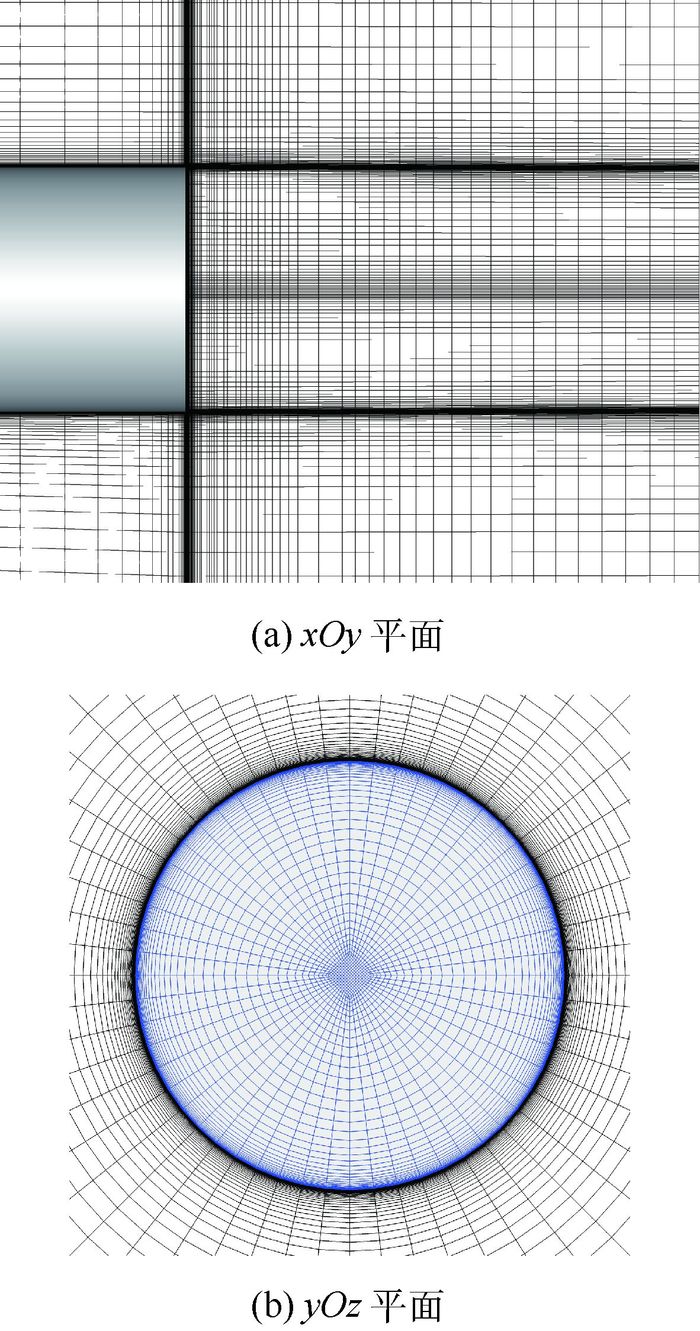图 1 底部流动外形和计算网格示意图 Fig. 1 Schematic diagram of configuration and computational grid for base flow

图选项

图 2为不同模型预测所得时均马赫数流场与实验结果的对比，各图中上半部分为实验结果，下半部分为计算结果。可以看出，三者相比，DDES-F_d在分离区内更大范围区域具有较大的回流速度，DDES-F₁与DDES-F₂所得回流速度分布较为相似，但分布形态上DDES-F₁与实验结果更为接近。同时，DDES-F₂与DDES-F_d预测的再附位置相较于实验有所延迟，所得分离区偏大，而DDES-F₁所得分离区大小与实验较为一致。

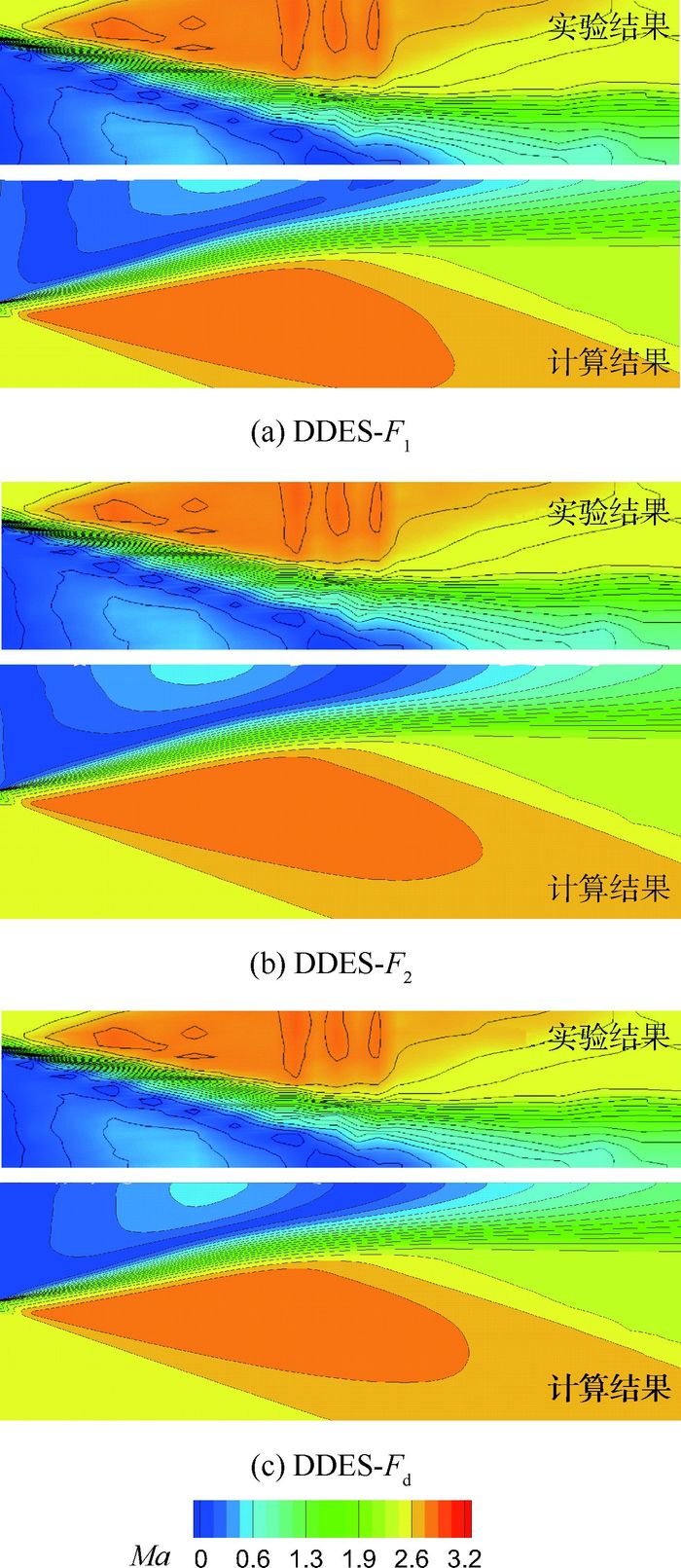图 2 对称面时均流场马赫数云图 Fig. 2 Mach number contours of time-averaged flow field in symmetry plane

图选项

图 3给出了各延迟函数分布与RANS、LES分区情况。总的来说，各延迟函数分布均在近壁区域取值为1，保证该区域内由RANS模型主导，符合其作用原理；区域划分方面，在近壁区和剪切层外的远场区域，模型趋于RANS模化，在分离区、剪切层以及尾迹区等复杂流动区域，模型趋于LES求解，以更为准确地刻画其中的非定常湍流脉动。同时对比可知，不同延迟函数的作用范围与分区情况存在差异：F₂保护范围最大，在近壁区较大范围内取值为1，并得到了最大的RANS区域；F_d保护范围最小，所得RANS模化区域也最小；F₁保护范围及分区情况介于两者之间，与F_d作用效果更为相似。此外，DDES-F₂所得RANS、LES过渡区域同样偏大，这与DDES方法中延迟函数能够实现快速切换的设计初衷相违背，可能对模型的求解能力产生影响。

图 3 不同延迟函数分布与RANS、LES区域划分云图 Fig. 3 Contours of distribution of different delayed functions and placement of RANS and LES regions

图选项

图 4为不同模型所得瞬时流场对比，以涡量云图形式给出，图中可以看到清晰的剪切层、边界层以及复杂的漩涡结构。在底部上游的附着流动区域，不同延迟函数所得边界层厚度无明显差异。在底部尾迹区内，DDES-F₁与DDES-F_d均捕捉到了丰富精细的分离流动结构，流动紊乱，包含较多的小尺度涡；相比较而言，DDES-F₂所得小尺度流动结构较少，湍流脉动稍弱，流场趋向于规则。分析认为这是由于F₂函数作用范围偏大，使得RANS模化区域偏大，损害了模型在尾迹区内对小尺度流动结构的求解能力。需要指出的是，瞬时流场的对比仅是定性分析，计算流场中更加丰富精细的流动结构并不一定意味着更加真实准确的结果。故下面将结合实验数据，开展详细系统的定量对比分析。

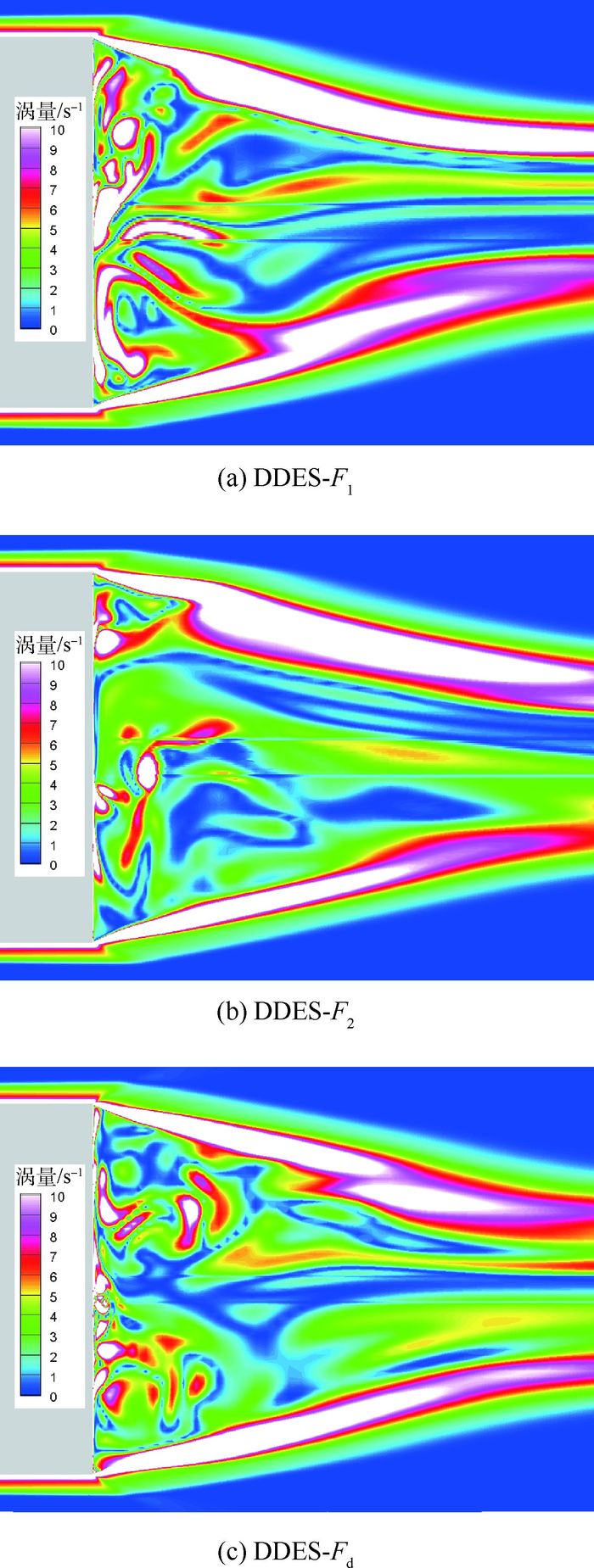图 4 对称面瞬时流场涡量云图 Fig. 4 Vorticity contours of instantaneous flow field in symmetry plane

图选项

图 5为不同延迟函数所得功率谱密度(PSD)对比。横轴代表频率f，低频对应大尺度结构，高频对应小尺度结构，纵轴为功率谱密度。由图 5可以看出，DDES-F₁与DDES-F_d所得结果较为相近，而DDES-F₂在高频区域结果偏低，说明其结果中小尺度湍流结构偏少，模型的求解能力受到影响。

图 5 功率谱密度分布 Fig. 5 Distribution of power spectral density

图选项

图 6为不同延迟函数所得时均底部压力系数C_p分布对比。图中：r为圆柱底部中心点到该处的径向距离。DDES-F₂所得压力系数分布沿径向存在一定变化，预测的底部中心处压力系数偏低，与实验存在差异。DDES-F₁与DDES-F_d所得压力系数分布相似，两者均预测到了较为平坦的压力分布曲线，分布规律与实验相一致，量值上略低于实验值，DDES-F₁与DDES-F_d预测结果优于DDES-F₂。

图 6 时均底部压力系数分布 Fig. 6 Distribution of time-averaged base pressure coefficient

图选项

图 7为尾迹中心线时均流向速度分布。在近尾迹区回流速度的预测上，DDES-F_d所得回流速度最大，DDES-F₂所得回流速度最小；在分离区大小的预测上，DDES-F₁所得分离区范围与实验最为接近，DDES-F₂与DDES-F_d所得再附位置推迟，预测的分离区范围偏大，与图 2中时均马赫数云图相一致。

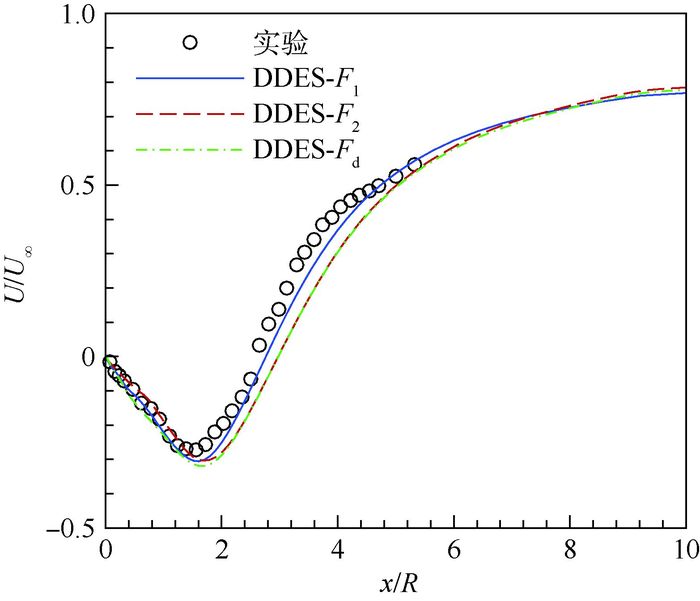图 7 尾迹中心线时均流向速度分布 Fig. 7 Distribution of time-averaged centerline streamwise velocity in wake

图选项

图 8给出了尾迹区不同站位处的时均流向速度分布。在x/R=0.157 5~1.259 8的近壁面分离区域，3种延迟函数在剪切层及其外部区域所得流向速度无明显差异，在剪切层内的回流区中(靠近中心线附近)，DDES-F₂所得回流速度偏小，与实验值存在一定差异，DDES-F₁与DDES-F_d的计算结果均与实验吻合较好，其中DDES-F_d预测精度略高于DDES-F₁。在x/R=1.889 8、2.519 7的流动再压缩和再附区域，DDES-F₂与DDES-F_d在中心线附近预测的回流速度偏大，表明计算得到的回流区较实验偏大，与图 2及图 7分析相一致，DDES-F₁预测的再附位置与实验十分接近，在该区域的表现优于其他模型。

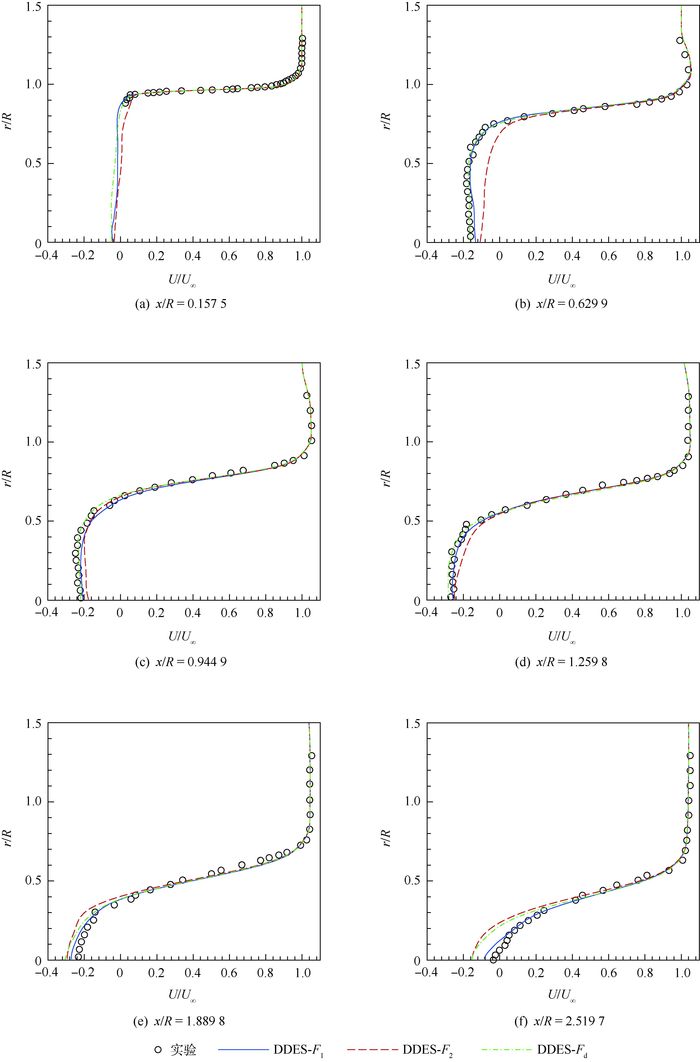图 8 不同站位的时均流向速度分布 Fig. 8 Distribution of time-averaged streamwise velocity at different locations

图选项

图 9为不同站位的雷诺剪切应力(U_∞²)分布对比，反映流场中速度脉动的模拟情况。DDES-F₂在各站位所得雷诺应力均低于其他两模型，其较大的RANS模化区域使得湍流脉动受到抑制，所得雷诺应力峰值明显低于实验值。DDES-F_d预测得到的速度脉动偏高，在图 9(b)站位中心线附近严重偏离实验值，在图 9(c)和图 9(d)站位所得雷诺应力峰值明显过冲。DDES-F₁计算结果与实验吻合程度较好，雷诺应力分布规律与实验十分接近，在图 9(a)~图 9(c)站位所得雷诺应力峰值略低于实验值。

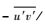
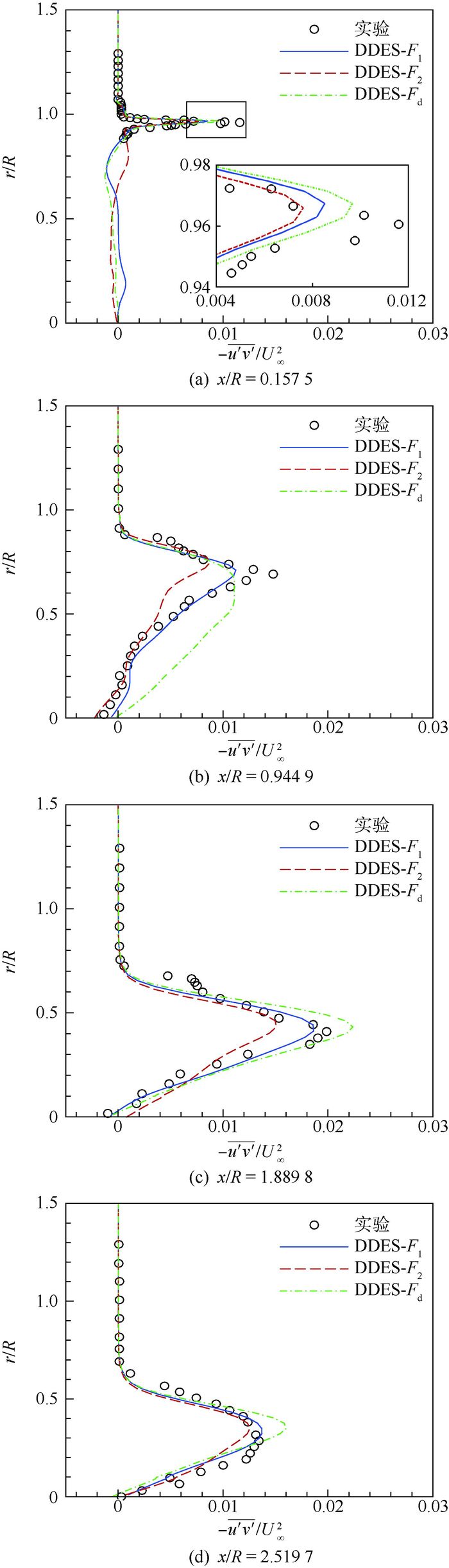图 9 不同站位的雷诺剪切应力分布 Fig. 9 Distribution of Reynolds shear stresses at different locations

图选项

3 结论 1) 在时均流场和时均量的对比中，在近尾迹区，DDES-F_d预测的回流速度最大，与实验值最为接近，DDES-F₁所得回流速度略低于实验值，而DDES-F₂计算结果明显偏低。在再附区附近，DDES-F₂与DDES-F_d高估了回流速度，预测的速度恢复偏慢，故再附位置延迟，得到了偏大的回流区，DDES-F₁在再附区的计算精度较高，与实验吻合较好。底部压力分布方面，DDES-F₂计算的压力分布沿径向呈现一定变化，与实验中平坦的压力分布存在差异，DDES-F₁与DDES-F_d预测的压力分布规律与实验一致，量值上略低于实验值。
2) 在瞬时流场和脉动量的对比中，DDES-F₂过多保护了边界层内RANS区域，模型表现出了较高的数值耗散，求解精度受到影响，所得小尺度涡结构偏少，湍流脉动受到抑制，预测的速度脉动低于实验值。DDES-F₁与DDES-F_d所得瞬时流场涡结构丰富，表现出了较强的对小尺度流动结构的捕捉能力，但DDES-F_d预测的速度脉动偏大，在部分站位偏离实验值，DDES-F₁则给出了令人满意的结果。
3) 延迟函数能够在近壁面起到相应的保护作用，但不同延迟函数的保护范围与分区特性存在明显差异。F₂函数在近壁面较大范围内取值为1，作用范围明显大于F₁与F_d，其对RANS区域的保护较为“保守”，所得RANS模化区域在3种模型中最大。F₁与F_d函数的作用效果较为相似，两者在底部附近所得RANS区域明显小于F₂计算结果。相比较而言，F_d函数保护范围最小。
4) 在延迟函数的选择上，本文认为F_d函数在实际应用中可能会更易出现保护效果不足问题；F₂函数则对模型的求解能力产生影响，对流动中的小尺度涡结构起到抑制作用，这对航空航天设计过程中气动力/热瞬态载荷和脉动的预测模拟不利；F₁函数兼顾保护作用与模型求解精度，本文推荐采用该延迟函数。
下一步工作中，将在更加复杂的工程实际湍流流动中，对不同延迟函数的性能、特点开展深入研究，以期为不同流动情况下延迟函数的选择给出指导与建议。同时在此基础上，寻求方法的发展改进，构造新型、高效的延迟函数与湍流模拟方法。

参考文献

[1]	阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J].力学进展, 2011, 41(5): 562–589. YAN C, YU J, XU J L, et al. On the achievements and prospects for the methods of computational fluid dynamics[J].Advances in Mechanics, 2011, 41(5): 562–589.DOI:10.6052/1000-0992-2011-5-lxjzJ2010-082(in Chinese)
[2]	SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study:A path to revolutionary computational aerosciences:NASA/CR-2014-218178[R].Hanover:NASA Center for Aerospace Information, 2014.
[3]	FR?HLICH J, VON TERZI D. Hybrid LES/RANS methods for the simulation of turbulent flows[J].Progress in Aerospace Sciences, 2008, 44(5): 349–377.DOI:10.1016/j.paerosci.2008.05.001
[4]	SPALART P R, JOU W H, STRELETS M, et al. Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach[C]//Proceedings of 1st AFOSR International Conference on DNS/LES, Advances in DNS/LES. Columbus:Greyden Press, 1997:137-147.
[5]	STRELETS M. Detached eddy simulation of massively separated flows:AIAA-2001-0879[R].Reston:AIAA, 2001.
[6]	SPALART P R. Detached-eddy simulation[J].Annual Review of Fluid Mechanics, 2009, 41: 181–202.DOI:10.1146/annurev.fluid.010908.165130
[7]	MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[C]//Turbulence, Heat and Mass Transfer 4. Redding:Begell House, Inc., 2003:625-632.
[8]	SPALART P R, DECK S, SHUR M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J].Theoretical and Computational Fluid Dynamics, 2006, 20: 181–195.DOI:10.1007/s00162-006-0015-0
[9]	HERRIN J L, DUTTON J C. Supersonic base flow experiments in the near wake of a cylindrical afterbody[J].AIAA Journal, 1994, 32(1): 77–83.DOI:10.2514/3.11953
[10]	BOURDON C J, DUTTON J C. Planar visualizations of large-scale turbulent structures in axisymmetric supersonic separated flows[J].Physics of Fluids, 1999, 11(1): 201–213.DOI:10.1063/1.869913
[11]	TUCKER P K, SHYY W. A numerical analysis of supersonic flow over an axisymmetric afterbody:AIAA-1993-2347[R]. Reston:AIAA, 1993.
[12]	FUREBY C, NILSSON Y, ANDERSSON K. Large eddy simulation of supersonic base flow:AIAA-1999-0426[R].Reston:AIAA, 1999.
[13]	PENG S H.Algebraic hybrid RANS/LES modelling applied to incompressible and compressible turbulent flows:AIAA-2006-3910[R].Reston:AIAA, 2006.
[14]	高瑞泽, 阎超. LES/RANS混合方法对超声速底部流动的应用[J].北京航空航天大学学报, 2011, 37(9): 1095–1099. GAO R Z, YAN C. LES/RANS hybrid method for supersonic axisymmetric base flow[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(9): 1095–1099.(in Chinese)
[15]	LUO D H, YAN C, WANG X Y. Computational study of supersonic turbulent-separated flows using partially averaged Navier-Stokes method[J].Acta Astronautica, 2015, 107: 234–246.DOI:10.1016/j.actaastro.2014.11.029
[16]	SIMON F, DECK S, GUILLEN P, et al. Reynolds-averaged Nacier-Stokes/large-eddy simulations of supersonic base flow[J].AIAA Journal, 2006, 44(11): 2578–2590.DOI:10.2514/1.21366
[17]	郑玮琳, 阎超. XY-SAS模型中不同网格尺度限制器的影响分析[J].北京航空航天大学学报, 2014, 40(12): 1725–1729. ZHENG W L, YAN C. Influence analysis on grid scale limiter of XY-SAS model[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(12): 1725–1729.(in Chinese)