直升机的使用环境往往十分恶劣，若热量在发动机表面积聚而不能散去，会导致动力舱温度异常升高而产生火灾。如果不能及时灭火，将会产生严重后果。随着直升机性能的提高，动力舱灭火系统保障直升机安全飞行的作用日益突出^[1]。美国“新一代灭火技术计划”^[2]曾优选七氟丙烷(HFC-227ea)作为哈龙1301(Halon1301)的替代灭火剂，然而与Halon1301相比，获得相同的灭火效果所需要替代灭火剂的质量与体积增加较多，因而还未见替代灭火剂用于军用飞机方面的公开报道。
目前我国军用直升机灭火系统中仍采用Halon1301作为灭火剂，因此，本文主要针对Halon1301和HFC-227ea进行分析。美军标MIL-E-22285(3)—1996^[3]规定从喷嘴开始释放灭火剂计时，释放规定质量的灭火剂所需时间不得高于1 s。由于室温下灭火剂的饱和蒸汽压较低，例如，25℃时Halon1301的饱和蒸汽压为1.61 MPa，HFC-227ea的饱和蒸汽压为0.47 MPa，不利于灭火时快速将灭火剂释放到防火区，因而工程上通常使用氮气作为增压介质充填到灭火瓶，提供释放灭火剂的驱动力。
美国NASA喷气动力实验室的Elliott等专门为Halon1301研制了HFLOW软件^[4]，美国国防部资助开发了基于Relap5的灭火系统仿真软件^[5]，美国国家标准及技术研究所(NIST)的Yang等为了计算氮气在灭火剂中的溶解度专门开发了PROFISSY软件^[6]，并开展了有关氮气和灭火剂的气液平衡试验^[7]。国内有关不同灭火剂所需氮气充填量的计算和试验还未见公开报道。已公开发表的文献多针对客机发动机舱灭火系统^[8]，主要采用GB 50163—1992^[9]和NFPA—2008^[10]提供的计算方法进行灭火剂用量的计算，并未涉及氮气充填量的计算。郑友兰等^{[1, 11]}通过对某型直升机灭火系统方案的确定以及系统关键参数匹配设计的探讨，分析了影响灭火系统管路设计的主要因素。但并未考虑瓶内氮气充填量对灭火剂释放过程的影响。灭火瓶内氮气充填量影响火灾时灭火剂的释放速率, 是设计机载灭火系统的重要参数之一。灭火瓶内存在二元高压混合物，包括氮气、灭火剂蒸汽和灭火剂液体。对其中氮气充填量、气相空间氮气和灭火剂蒸汽比例的准确计算，是计算灭火剂释放过程中氮气逸出压力和气体混合物的绝热指数的基础，从而为后续灭火剂释放过程的分析奠定了基础。由此可以看出，研究如何准确计算氮气的充填量及其在灭火瓶内的相态变化，对设计和分析机载灭火系统具有重要理论和工程应用价值。
Peng-Robinson(PR)状态方程的形式简单，通用性强，克服了Redlich-Kwong(RK)方程和Soave-Redlich-Kwong(SRK)方程计算液相密度精度较差的缺点，在临界点附近给出了较为接近实际的临界压缩因子(Z_c=0.307 4)。PR方程还可以比较准确地关联气液平衡试验数据，易于推广到混合体系^[12-14]。Wong-Sandler(WS)混合规则基于无限大压力下超额亥姆霍兹自由能A_∞^E ，并满足第二维里系数的边界条件，适用于极性流体及组分性质差异较大的混合体系^[15-16]。本文基于PR状态方程和WS混合规则，对不同充装工况下的氮气和灭火剂进行二元高压气液平衡计算，从而获得不同工况下的氮气充填量和瓶内气相空间氮气和灭火剂蒸汽的比例关系，并分析温度变化对压强和气相空间氮气摩尔分数的影响，为进一步分析氮气和灭火剂的混合物从灭火瓶的释放过程奠定了基础。
1 PR方程和WS混合规则 1.1 PR方程 Peng和Robinson^[17]提出的PR方程为

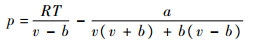(1)

式中：p为压力，Pa；R为通用气体常数，J/(mol·K)；T为热力学温度，K；v为摩尔体积，m³/mol；a和b为状态方程系数，a和b可由临界参数和偏心因子计算得到：

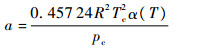(2)

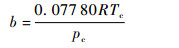(3)

式中:p_c和T_c分别为临界压力和临界温度；α(T)函数的定义为

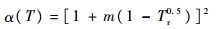(4)

式中：T_r=T/T_c为对比温度；m计算式为

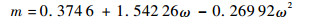(5)

式中：ω为偏心因子。
本文中氮气和灭火剂的临界参数及偏心因子如表 1所示^[18]。
表 1 氮气和灭火剂临界参数及偏心因子^[18] Table 1 Critical parameters and acentric factors of nitrogen and fire extinguishing agents^[18]

氮气和灭火剂	pc/MPa	Tc/K	ω
氮气	3.40	126.26	0.039
Halon1301	3.97	340.15	0.171
HFC-227ea	2.91	374.80	0.357

表选项






1.2 WS混合规则 PR方程用于氮气和灭火剂的高压气液平衡计算，需要结合相应的混合规则。本文采用1992年Wong和Sandler提出的WS混合规则^{[15-16, 19]}，该混合规则在大的温度、密度范围内，能够准确关联和预测复杂体系的物性和相平衡数据。WS混合规则的形式为

(6)

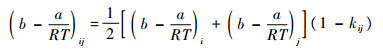(7)

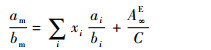(8)

式中：x_i和x_j为组分i与组分j在液相中的摩尔分数；a_m和b_m为混合物状态方程参数；a_i和b_i为纯物质状态方程参数；k_ij为二元交互作用参数；C为常数，对PR方程。本文采用Non-Random Two Liquid(NRTL)模型计算，其形式为

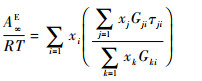(9)

式中：G_ji=exp(-α_jiτ_ji)为液相的相互作用能，α_ji为非随机参数，α_ji=0.30，τ_ji=(g_ji-g_ii)/(RT)，g_ji和g_ii分别为异类和同类分子间的相互作用能。
本文k_ij和(g_ji-g_ii)的取值来自文献[20]。
由PR方程和WS混合规则推导所得逸度系数计算式^[19]为

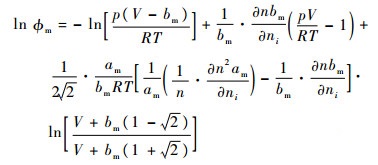(10)

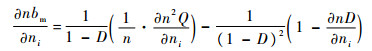(11)

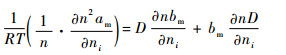(12)

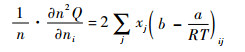(13)

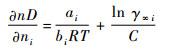(14)

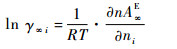(15)

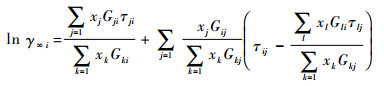(16)

式中：；Q=，a_ij和b_ij为PR方程参数；V为体积；n为摩尔数；n_i为组分i的摩尔数；γ_∞i为组分i的活度系数；τ_lj、τ_ji、τ_ij为NRTL模型参数。
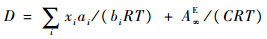
2 数值计算 确定灭火瓶内氮气充填量的已知条件是灭火瓶的有效容积V_bot、灭火剂充装量m_a、瓶内压力p和温度T。首先假定灭火瓶内气相和液相的氮气质量之和所占的摩尔分数Z_i=0.10，相平衡常数K_i(i=1，2)的初值选为理想状态下的计算值K_i⁰，然后在汽化分率e的迭代中视为常数。整个计算过程分为3层迭代：外层的z-循环，中间的K-循环，内层的e-循环，计算流程如图 1所示。

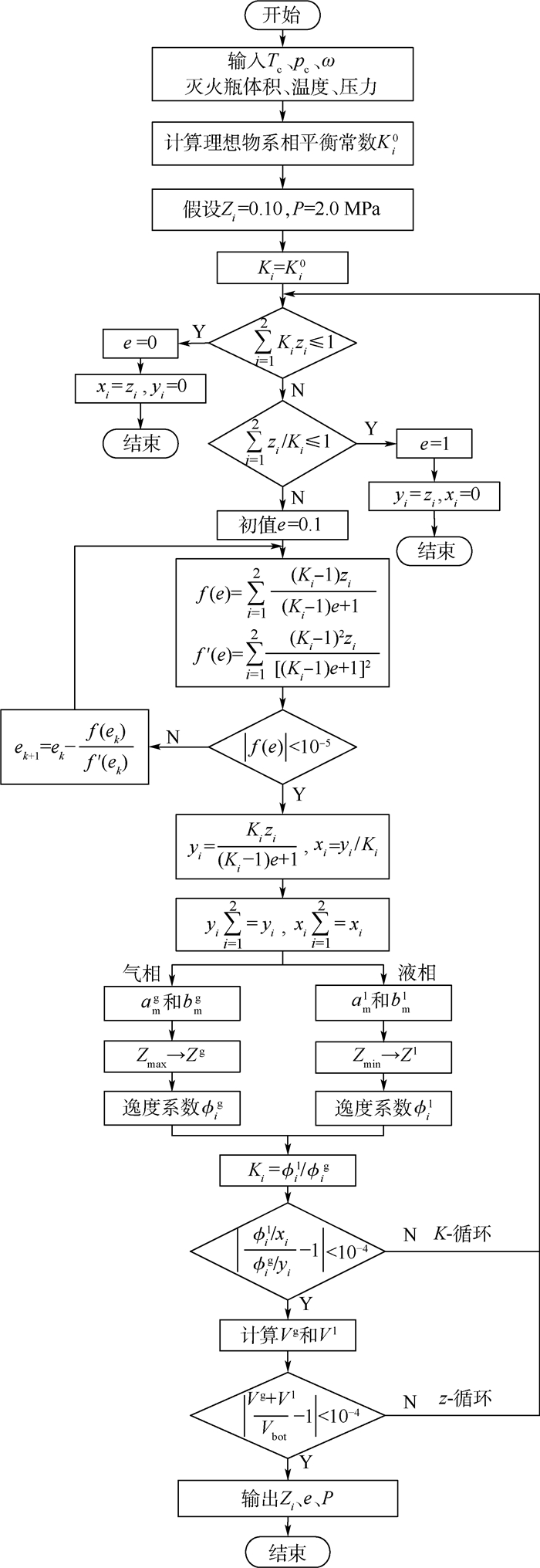yi—组分i气相摩尔分数；zi—组分i总摩尔分数；e—气化分率；ek—第k次计算的气化分率；f(e)—气化分率的迭代式；Zmax, Zmin—PR方程的最大压缩因子和最小压缩因子；Zl—液相压缩因子；Zg—气相压缩因子；Vg—气相体积；Vl—液相体积；K—相平衡常数；Φig—气相逸度系数；Φil—液相逸度系数。 图 1 氮气充填量计算流程图 Fig. 1 Calculation flowchart for filling mass of nitrogen

图选项

计算流程如下：
1)?假定Z_i初值为0.10，K_i的初值取理想物系相平衡常数，首先判断灭火瓶内氮气和灭火剂的组成是否处于两相区，然后进入最内层的e-循环。
2)?e-循环收敛后，计算氮气和灭火剂纯物质在PR方程中的系数a_i和b_i，结合WS混合规则计算混合物的a_m和b_m。
3)?分别计算气相和液相的压缩因子，然后得到气相和液相的逸度系数Φ_i^g、Φ_i^l和相平衡常数K_i，当残差|K_ix_i/y_i-1| < 1.0×10^-4时K-循环结束，转入z-循环。
4)?通过V^g=Z_maxRT/p和V^l=Z_minRT/p计算灭火瓶内气相体积和液相体积，当|(V^g+V^l)/V_bot-1.0| < 1.0×10^-4时z-循环收敛，输出计算结果。
3 计算结果与分析 3.1 氮气和Halon1301 文献[7]针对Halon1301进行了氮气充填试验，试验中灭火瓶的有效容积为(52.2±0.3)cm³，压力传感器的分辨率为6.9 kPa，K型热电偶的精度为±1℃，采用电子称测量整个试验装置充填氮气前后质量的变化，分辨率为0.1 g。采用本文提出的预测方法对灭火剂充装1/2灭火瓶和充装2/3灭火瓶工况下的氮气充填量进行了计算，并与文献[7]中的试验值、计算值进行了对比，如表 2和表 3所示。此外，表 2和表 3同时给出了基于文献[4]中HFLOW软件的设计方法所开发程序的计算结果。
表 2 Halon1301充填1/2灭火瓶试验工况 Table 2 Test conditions of Halon1301 filling one-half of fire agent bottle

灭火剂质量/g	压强/MPa	氮气充填量/g				误差/%
		试验值	文献[4]	文献[7]	本文计算值
40.9	2.89	0.7	0.748	0.75	0.719	2.71
40.9	4.29	1.4	1.511	1.53	1.479	5.64
40.7	4.29	1.4	1.512	1.53	1.480	5.71
注：误差=(本文计算值-试验值)/试验值×100%。

表选项






表 3 Halon1301充填2/3灭火瓶试验工况 Table 3 Test conditions of Halon1301 filling two-thirds of fire agent bottle

灭火剂质量/g	压强/MPa	氮气充填量/g				误差/%
		试验值	文献[4]	文献[7]	本文计算值
54.9	2.92	0.7	0.725	0.76	0.704	0.57
54.8	2.87	0.7	0.689	0.74	0.680	-2.86
54.9	4.25	1.4	1.413	1.48	1.393	-0.50
54.8	4.25	1.4	1.413	1.49	1.394	-0.43

表选项






由表 2和表 3可知，本文提出的基于PR方程和WS混合规则的预测方法，对Halon1301灭火剂计算得到的灭火瓶内氮气充填量，与试验测量值吻合较好。
对于Halon1301灭火剂充填1/2灭火瓶，本文计算的氮气充填量的平均误差约为4.7%，优于文献[7]中PROFISSY的平均误差8.7%、文献[4]中HFLOW的平均误差7.6%。对于Halon1301充填2/3灭火瓶，本文的平均误差约为1.1%，计算结果优于文献[7]中PROFISSY的平均误差6.6%，与文献[4]的计算结果相当。本文的计算方法误差较小，满足工程应用的精度，特别适合于灭火剂充填2/3灭火瓶的工况，确定灭火系统中瓶内的氮气充填量及氮气在气相和液相的比例关系。
3.2 氮气和HFC-227ea 对于HFC-227ea灭火剂，试验工况同3.1节的Halon1301灭火剂。对于HFC-227ea充填1/2灭火瓶和2/3灭火瓶工况下，氮气充填量的计算值与试验值的比较如表 4和表 5所示。
表 4 HFC-227ea充填1/2灭火瓶试验工况 Table 4 Test conditions of HFC-227ea filling one-half of fire agent bottle

灭火剂质量/g	压强/MPa	氮气充填量/g			误差/%
		试验值	文献[7]	本文计算值
36.5	2.90	1.2	1.24	1.251	4.25
36.6	2.93	1.2	1.26	1.272	6.00
36.5	4.29	1.9	1.95	1.965	3.42
36.6	4.28	1.9	1.94	1.966	3.47

表选项






表 5 HFC-227ea充填2/3灭火瓶试验工况 Table 5 Test conditions of HFC-227ea filling two-thirds of fire agent bottle

灭火剂质量/g	压强/MPa	氮气充填量/g			误差/%
		试验值	文献[7]	本文计算值
48.7	2.87	1.1	1.16	1.163	5.73
48.7	2.98	1.2	1.21	1.216	1.33
48.7	4.25	1.8	1.81	1.820	1.11
48.7	4.25	1.8	1.82	1.820	1.11

表选项






由表 4和表 5的结果对比可知，与Halon1301灭火剂相同，本文计算得到的灭火瓶内氮气充填量，与试验测量值吻合较好。
对于HFC-227ea灭火剂充填1/2灭火瓶和2/3灭火瓶的试验工况，平均误差分别为4.3%和2.3%，与文献[7]中PROFISSY的计算结果相近。
总的来说，本文提出的预测方法可以更准确地预测不同工况下，Halon1301灭火剂和HFC-227ea灭火剂在灭火瓶内所需的氮气充填量，为下一步计算瓶内氮气和灭火剂混合物的释放过程以及直升机动力舱灭火系统设计计算奠定了基础。
3.3 压强随温度的变化关系 由于直升机作战任务的需要，灭火瓶所处的环境温度可能发生较大变化。温度的变化会导致气相空间氮气和灭火剂蒸汽的增加或减少，使得灭火瓶内的压强随之发生变化。
图 2给出了灭火瓶内温度由-40℃增加至50℃时瓶内压强的变化曲线，计算工况与文献[16]的工况相同，详见表 6。

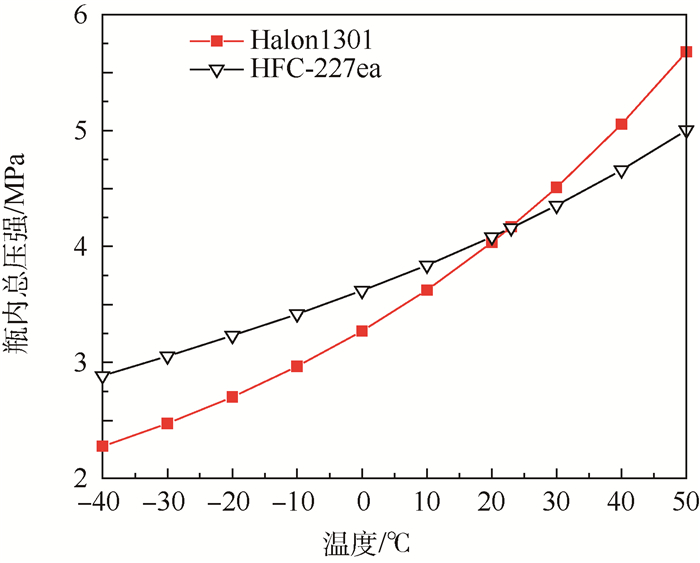图 2 总压强随温度的变化关系 Fig. 2 Variation of total pressure with temperature

图选项

表 6 灭火瓶内压强变化的计算工况 Table 6 Calculation cases for different pressure in fire agent bottle

灭火剂	压强/MPa	灭火瓶 体积/ cm3	灭火剂 质量/g	初始 温度/℃
Halon1301	4.17	53.2	32.0	23
HFC-227ea	4.16	53.2	26.3	23

表选项






由图 2可知，随着温度的逐渐增加，灭火瓶内的总压强显著的增加，特别是Halon1301灭火剂，随着温度的增加其压强增加的速率逐渐增大。当瓶内温度达到50℃时，充装Halon1301的瓶内压强高达近6.0 MPa。本文的预测方法，可以根据灭火系统设计使用的温度范围及初始的灭火瓶充装条件，计算得到灭火瓶内压强变化的范围，帮助灭火系统设计人员合理选择灭火瓶的材料，防止瓶内压强过高造成的危险。
3.4 氮气摩尔分数与温度的关系 图 3给出了灭火瓶内Halon1301灭火剂和HFC-227ea灭火剂气相空间氮气的摩尔分数的变化曲线，计算工况见表 6。
由图 3可知，随着温度的逐渐增加，无论是Halon1301灭火剂和HFC-227ea灭火剂，瓶内气相空间的氮气所占摩尔分数均逐渐降低，特别是Halon1301灭火剂，氮气的摩尔分数降低的速率逐渐加快，温度由-40℃增加到50℃时，氮气的摩尔分数由0.867降低到0.260。气相空间氮气和灭火剂蒸汽的比例变化，直接影响气体混合物的绝热指数^[15]，导致灭火剂释放速率的改变。

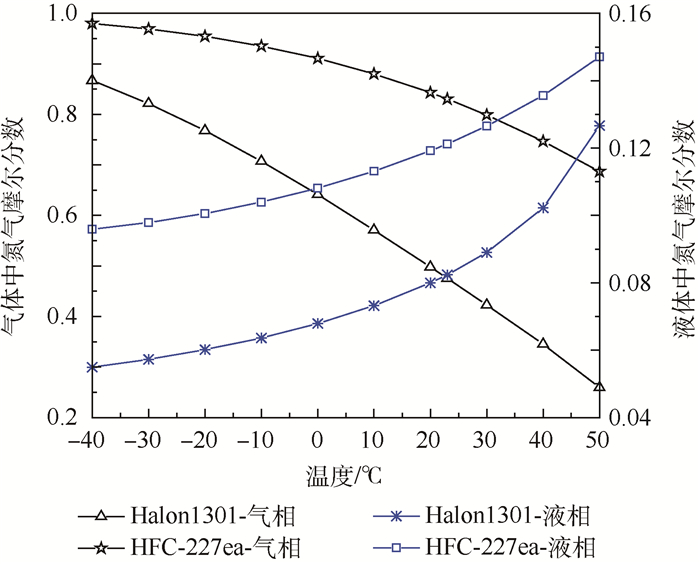图 3 氮气摩尔分数随温度的变化关系 Fig. 3 Variation of nitrogen mole fraction with temperature

图选项

4 结论 本文基于PR状态方程和WS混合规则预测了不同充装工况下灭火瓶内的氮气充填量。
1)?Halon1301充填1/2灭火瓶的试验工况，氮气充填量计算值与试验值平均误差约为4.7%；对充填2/3试验工况，平均误差约为1.1%，计算结果优于PROFISSY和HFLOW软件的计算结果。
2)?对于HFC-227ea灭火剂，本文结果与PROFISSY软件的计算精度相当。本文提出的预测方法，可获得较高的计算精度，可用于机载灭火系统的工程设计。
此外，本文还分析了瓶内总压强和气相空间氮气摩尔分数随温度的变化情况，为后续分析氮气和灭火剂的释放过程奠定了基础。

参考文献

[1]	郑友兰, 刘凯. 某直升机动力舱灭火系统的设计[J].直升机技术, 2004(3): 30–34.ZHENG Y L, LIU K. The design of helicopter powerplant fire extinguisher system[J].Helicopter Technique, 2004(3): 30–34.(in Chinese)
[2]	郑冬芳, 吴克安, 史婉君, 等. 美国哈龙替代灭火剂研究评估进展[J].有机氟工业, 2014, 4(4): 35–40.ZHENG D F, WU K A, SHI W J, et al. The development of U.S.next generation fire extinguishing agent assessments[J].Organo-Fluorine Industry, 2014, 4(4): 35–40.(in Chinese)
[3]	United States Navy.Extinguishing system, fire, aircraft, high-rate discharge type, installation and test of:NAVY MIL-E-22285(3)-1996[S].New York:US Military Specs, 1996:1-2.
[4]	ELLIOTT G, GARRISON P W, KLEIN G A, et al.Flow of nitrogen pressurized Halon 1301 in fire extinguishing systems:NASA-CR-174271[R].Washington, D.C.:NASA, 1984.
[5]	TUZLA K, PALMER T, CHEN J C, et al.Development of computer program for fire suppressant fluid flow[R].Bethlehem:Leihigh University, 1998:17-34.
[6]	YANG J C, CLEARY T G, VáZQUEZ I, et al. Optimization of system discharge[J].NIST Special Publication, 1995(890): 407–438.
[7]	YANG J C, CLEARY T G, VáZQUEZ I, et al. Measured and predicted thermodynamic properties of selected halon alternative/nitrogen mixtures[J].International Journal of Refrigeration, 1997, 20(2): 96–105.DOI:10.1016/S0140-7007(96)00070-9
[8]	李淑艳, 王新月, 卿雄杰, 等. 飞机/发动机灭火系统的设计与计算[J].西北工业大学学报, 2006, 24(1): 124–127.LI S Y, WANG X Y, QIN X J, et al. An engineering method for extinguishing incipient aircraft/engine fire[J].Journal of Northwestern Polytechnical Universtiy, 2006, 24(1): 124–127.(in Chinese)
[9]	中华人民共和国公安部.卤代烷1301灭火系统设计规范:GB 50163-1992[S].北京:中国标准出版社, 1992:8-10.Ministry of Public Security of the People's Republic of China.Code for design of Halon1301 fire extinguish system:GB-50163-1992[S].Beijing:Standards Press of China, 1992:8-10(in Chinese).
[10]	Technical Committee on Gaseous Fire Extinguishing Systems.Standard on clean agent fire extinguishing systems:NFPA-2008[S].Boston:Standards Council, 2007:28-36.
[11]	郑友兰, 金华, 付金云. 直升机灭火系统管路布局设计研究[J].直升机技术, 2009(2): 47–51.ZHENG Y L, JIN H, FU J Y. A study on tube distribution design for helicopter fire extinguishing system[J].Helicopter Technique, 2009(2): 47–51.(in Chinese)
[12]	胡芃, 陈龙祥, 陈则韶. HFC/HC三元混合工质气液相平衡推算[J].工程热物理学报, 2013, 34(4): 609–612.HU P, CHEN L X, CHEN Z S. Prediction of vapor-liquid equilibria for ternary HFC/FC mixtures[J].Journal of Engineering Thermophysics, 2013, 34(4): 609–612.DOI:10.1007/s10765-013-1439-6(in Chinese)
[13]	朱君悦, 段远源, 许心皓, 等. PR方程结合HV混合规则计算HFC/HFC和HFC/HC二元混合物气液相平衡[J].热科学与技术, 2012, 11(3): 241–245.ZHU J Y, DUAN Y Y, XU X H, et al. Calculation of vapor liquid equilibria of HFC/FC and HFC/FC binary mixtures using PR EOS with HV mixing rule[J].Journal of Thermal Science and Technology, 2012, 11(3): 241–245.(in Chinese)
[14]	LIN H, DUAN Y Y. Empirical correction to the Peng-Robinson equation of state for the saturated region[J].Fluid Phase Equilibria, 2005, 233(2): 194–203.DOI:10.1016/j.fluid.2005.05.008
[15]	SOLóRZANO-ZAVALA M, BARRAGáN-AROCHE F, BAZúA E R. Comparative study of mixing rules for cubic equations of state in the prediction of multicomponent vapor-liquid equilibria[J].Fluid Phase Equilibria, 1996, 122(1): 99–116.
[16]	FAU'NDEZ C A, VALDERRAMA J O. Modeling associating hydrocarbon+alcohol mixtures using the Peng-Robinson equation of state and the Wong-Sandler mixing rules[J].Comptes Rendus Chimie, 2013, 16(2): 135–143.DOI:10.1016/j.crci.2012.10.007
[17]	PENG D Y, ROBINSON D B. A new two-constant equation of state[J].Industrial & Engineering Chemistry Fundamentals, 1976, 15(1): 59–64.
[18]	YANG J C, BREUEL B D.Thermodynamic properties of alternative agents:NIST-SP-861[R].Boulder:Buiding and Fire Research Laboratory, 1994.
[19]	WONG D S H, SANDLER S I. A theoretically correct mixing rule for cubic equations of state[J].AIChE Journal, 1992, 38(5): 671–680.DOI:10.1002/(ISSN)1547-5905
[20]	LIM J S, KIM J. Vapor liquid equilibria of the binary systems nitrogen+bromotrifluoromethane, bromochlorodifluoromethane, 1, 1, 1, 2, 3, 3, 3-heptafluoropropane, and+trifluoroiodomethane from 293.2 to 313.2 K and 30 to 100 bar[J].Journal of Chemical and Engineering Data, 1997, 42(1): 112–115.DOI:10.1021/je960239o