随着导弹防御体系的发展，单枚导弹对目标进行打击突防难度越来越大，因此，为了增强突防能力，有必要研究多枚导弹协同制导方法^[1-3]。导弹之间通过信息共享实现配合、协作，共同完成打击任务，极大地增强了导弹的打击能力，增加了导弹的突防和摧毁目标的概率，还可以完成单枚导弹无法完成的任务。多枚导弹以一定的攻击角度同时对目标进行直接撞击，既可以增强弹头毁灭效果，还可以提高导弹的突防能力。因此，带有末端攻击角度约束^[4]的多导弹协同制导技术越来越引起各国****的关注。文献^[5]所研究的制导方法可以对导弹的飞行时间进行控制，即提出了一种飞行时间可控的制导律(Impact-Time-Control Guidance，ITCG)。文献^[6]在文献^[5]的基础上，研究了一种飞行时间和末端攻击角度同时可控的制导律(Impact-Time-Angle-Control Guidance，ITACG)。文献^[7]采用李雅普诺夫稳定性理论提出了一种三维平面内飞行时间和末端落角同时可控的制导律。近年来，印度****Padhi和Oza^[8-11]等提出了一种带有末端多约束的模型预测静态规划(MPSP)制导方法，该方法采用静态协态变量求解最优控制问题，可以节省制导方法运算时间，具有在线应用的潜力。受MPSP和模型预测控制(MPC)^[12-13]方法启发，文献^[14]对MPSP制导方法中的控制量进行一次形式参数化近似处理，给出了一种模型预测扩展控制(MPSC)制导方法。与MPSP制导方法相比，MPSC制导方法中的控制指令变化更加平缓，有利于控制量指令跟踪。
近几年国内外****对多导弹协同制导问题进行了大量研究。文献^[15]针对固定拓扑和切换拓扑两种情况，对多导弹协同拦截高超声速目标进行了研究，所给出的制导律具备较理想的作战效费比与弹道特性。文献^[16]所研究的制导律能够实 现时间和空间上的协同，即能够对导弹的攻击时间和攻击角度进行同时控制。文献^[17-18]所提出的制导方法也能够满足攻击时间和攻击角度约束，该方法是基于最优控制与滑模控制理论实现的。
本文提出运用MPSC制导方法进行多导弹协同制导律设计，不同于文献^[14]，MPSC制导原理推导时控制量参数化近似为二次形式。由于MPSC制导需要对初始控制量进行猜测并确定待飞时间，本文运用协同比例制导(CPN)^[19]方法对各枚导弹初始控制量进行猜测并对飞行时间进行约束控制，实现在MPSC制导体系下的带有末端攻击角度约束的多导弹协同(同时)攻击。
1 MPSC制导律设计 1.1 MPSC制导方法推导 对于一般形式的非线性系统，其状态方程和输出方程如下：

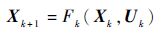(1)

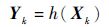(2)

式中： X ∈ R ⁿ为状态量； U ∈ R ^m为控制量； Y ∈ R ^p为输出量；k=1,2,…,N。
制导目标是找出合适的控制参数 U _k(k=1,2,…,N-1)，使得末端时刻的实际输出 Y _N与期望输出 Y _N^*满足： Y _N→ Y _N^*。运用线性化理论对式(1)和式(2)在各节点上进行离散化，得

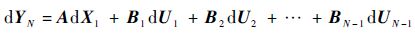(3)

式中：

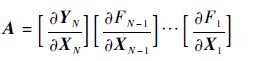(4)

B _k(k=1,2,…,N-1)为末端输出量与控制量 U _k之间的误差系数矩阵，表达式为

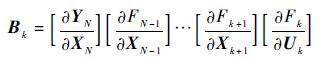(5)

由于初始状态 X ₁是确定的，因此，d X ₁=0，式(3)可简化为

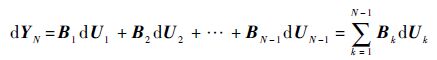(6)

通过迭代计算求解误差系数矩阵 B _k。首先，定义 B _N-1⁰如下：

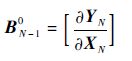(7)

然后，计算 B _k⁰(k=N-2,N-3,…,1)，如下：

(8)

最后，计算 B _k(k=N-1,N-2,…,1)，如下：

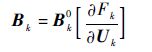(9)

式(6)~式(9)实现对误差系数矩阵 B _k的迭代计算，运算量大大减小。
控制量表达式采用二次形式，如下：

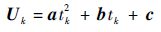(10)

式中： a 、 b 和 c 为当前控制量系数；t_k为时间节点。

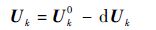(11)

结合式(10)、式(11)和式(6)，得

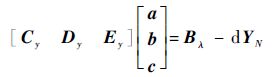(12)

式中：

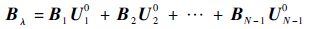(13)

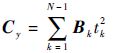(14)

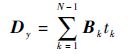(15)

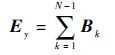(16)

当式(12)中方程个数小于等于系数 a 、 b 和 c 个数时，通过式(17)求解 a 、 b 和 c ：

(17)

如果式(12)中未知变量的个数大于方程数量，最优解可以通过极小化目标函数求解，选取性能指标函数为

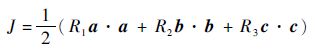(18)

式中：R₁,R₂,R₃>0。
考虑式(12)和式(18)，性能指标函数可以表示为

(19)

对式(19)进行变分运算，并结合式(14)、式(15)和式(16)，得

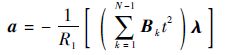(20)

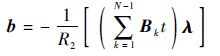(21)

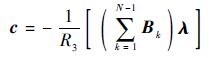(22)

将 a 、 b 和 c 分别代入式(12)，得

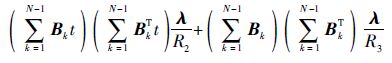(23)

即

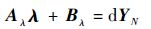(24)

式中：

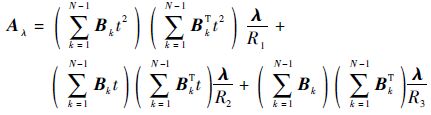(25)

由式(24)得

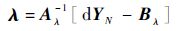(26)

因此，当前控制量为

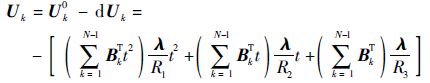(27)

1.2 制导问题描述 导弹运动方程如下：

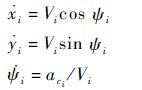(28)

式中：x_i、y_i和ψ_i为地面发射坐标系下导弹位移和速度矢量与基准线夹角；V_i为导弹的飞行速度；i为第i枚导弹；a_ci为法向加速度指令。
考虑到在攻击角度控制的导引律中，导弹速度变化的影响很小，为简化导引律设计过程，便于工程实现，假定导弹速度恒定。
导弹运动方程的离散形式如下：

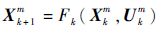(29)

式中：导弹i的状态量和控制量分别为

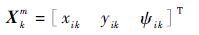(30)

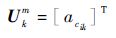(31)

其中：导弹i法向加速度指令a_cik近似为

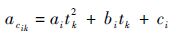(32)

基于MPSC制导方法的制导过程如下：
1) 通过第2节CPN制导律对初始控制量进行猜测，得到初始控制量a_cik，并确定飞行时间t_k。
2) 通过数值积分求解式(29)，得到导弹的末端状态 X _f=(x_if,y_if,ψ_if)，末端状态偏差d Y _N为

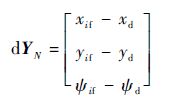(33)

式中：x_d、y_d和ψ_d为导弹期望末端状态。
3) 如果末端状态偏差d Y _N满足设计要求，程序结束；如果不满足要求，需要对法向加速度指令a_cik进行修正。计算 B _N-1⁰和 B _N-1如下：

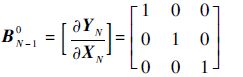(34)

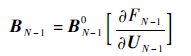(35)

4) 通过式(8)和式(9)计算 B _k和 B _k⁰(k=1,2，…,N-1)。
5) 求解出 B _k后，通过式(36)直接计算a_i、b_i和c_i：

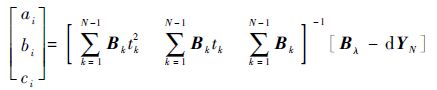(36)

6) 通过a_i、b_i和c_i计算导弹法向加速度指令a_cik。
2 基于CPN制导方法的初始控制量猜测 2.1 CPN制导原理 导弹M_i(i=1,2,…,m)相对地面静止目标T飞行示意图见图 1。图中：λ_i(i=1,2,…,m)为视线角；σ_i(i=1,2,…,m)为速度矢量与弹目视线夹角；r_i(i=1,2,…,m)为导弹与目标相对距离。假设各枚导弹的飞行速度V_i大小为常值。

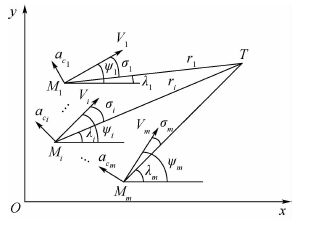图 1 导弹和目标相对运动示意图 Fig. 1 Engagement geometry of missile and target

图选项

CPN制导方法^[19]通过对式(37)中的比例导引系数 _i进行调节，使各枚导弹飞行时间趋于一致，实现协同攻击。

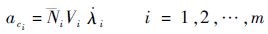(37)

式中：λ · _i为视线角速率。
假设比例导引系数N _i是时变的，形式如下：

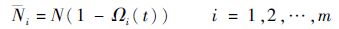(38)

式中：N为常值比例导引系数；Ω_i(t)为时变的增益系数。导弹飞行过程中通过对Ω_i(t)进行调节，即可完成对 _i的调节，从而实现法向加速度指令a_ci的控制。
定义导弹的待飞时间偏差为，即

(39)

式中：为预测的第i枚导弹的待飞时间，即

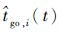
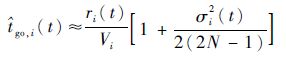(40)

式(39)可变换为

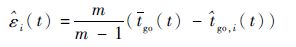(41)

式中：t _go(t)为所有导弹的平均待飞时间，即

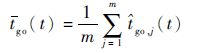(42)

定义导弹的待飞时间方差为Σ²(t)，如下：

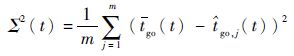(43)

通过对增益系数Ω_i(t)的调节，使得Σ²(t)=0，此时，各枚导弹即可以实现对目标的同时攻击。
把式(38)代入第i枚导弹与目标的相对运动方程，得

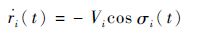(44)

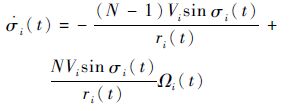(45)

现给出CPN制导律，如下：

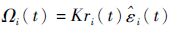(46)

式中：K为增益系数。r_i(t)→0， _i(t)→0时，Ω_i(t)→0，则式(38)中 _i(t)→N。
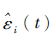
如果式(46)中增益系数K为正值，采用式(46)进行制导，由式(43)确定的导弹待飞时间方差为Σ²(t)在整个制导过程中不断减小。证明过程请参照文献^[19]。
2.2 初始控制量猜测仿真 两枚导弹对地面静止目标进行协同(同时)攻击，仿真参数见表 1。
表 1 初始控制量猜测仿真参数 Table 1 Simulation parameters for initial control guess

参数	导弹1(M1)	导弹 2(M2)
(xm,ym)/m	(1 180.0,2 080.0)	(0,0)
σ/(°)	-20	-5
V/(m·s-1)	290	300
(xT,yT)/m	(13 100.0,4 100.0)	(13 100.0,4 100.0)

表选项






仿真时，比例导引系数N=3时，导弹1和导弹2的飞行时间分别为45.8 s和42.2 s，两枚导弹的飞行时间偏差为3.6 s。运用CPN进行初始控制量猜测，并确定协同攻击时间。式(46)中K=40/(r ₀t _go,0)，r ₀和t _go,0分别为两枚导弹初始时刻的弹目平均距离和平均待飞时间。待飞时间变化曲线如图 2所示，待飞时间偏差变化曲线如图 3所示，CPN制导确定的两枚导弹飞行时间约为45.7 s，飞行时间偏差小于0.1 s。选择45.7 s作为MPSC制导两枚导弹的协同攻击时间。图 4为CPN制导过程中法向加速度指令，选择该指令作为MPSC制导的初始控制量。

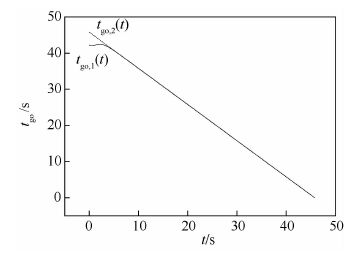图 2 待飞时间变化历程 Fig. 2 Time-to-go variation histories

图选项

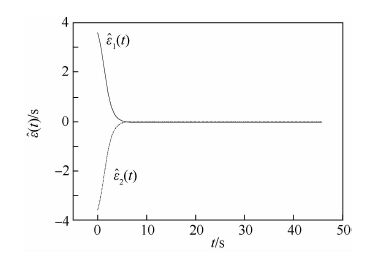图 3 待飞时间偏差变化历程 Fig. 3 Time-to-go error variation histories

图选项

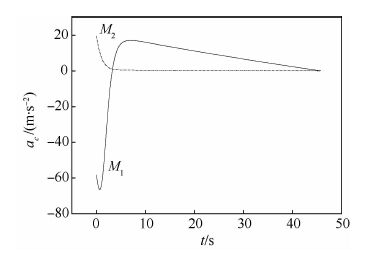图 4 法向加速度指令变化历程 Fig. 4 Normal acceleration command variation histories

图选项

3 数值仿真 仿真参数请参照表 1和表 2。第2.2节中CPN制导律给出的两枚导弹协同攻击时间为45.7 s。
表 2 末端时刻两枚导弹速度矢量与基准线期望夹角 Table 2 Final desired angle between velocity vector and reference line of two missiles

导弹	导弹1(M1)	导弹2(M2)
ψd /(°)	65.0	25.0

表选项






仿真迭代终止条件为：末端位移偏差小于1 m，末端速度矢量与基准线期望夹角偏差控制在±0.5°范围内。图 5为两枚导弹对目标同时攻击时的飞行轨迹变化曲线。图 6为速度矢量与基准线夹角的变化曲线。表 3给出了末端时刻两枚导弹的状态参数。由图 5、图 6和表 3可知，两枚导弹可以实现对目标协同攻击，末端时刻位移偏差小于0.5 m，角度偏差小于0.1°，即基于MPCP和CPN的制导方法在实现多导弹协同攻击的同时，还可以很好地满足末端攻击角度约束。图 7为两枚导弹初始控制量猜测法向加速度指令变化曲线。虽然命中目标时法向加速度指令不为零，但由于法向加速度指令采用二次形式近似，在整个制导过程中，法向加速度指令在有限范围内变化平缓，并没有出现突变。

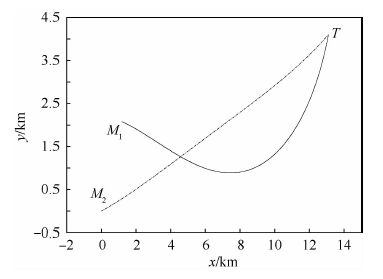图 5 两枚导弹飞行轨迹示意图 Fig. 5 Schematic diagram of flight trajectories of two missiles

图选项

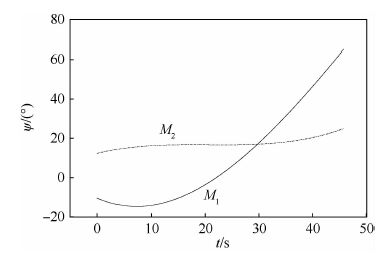图 6 速度矢量与基准线夹角的变化历程 Fig. 6 Variation histories of angle between velocityvector and reference line

图选项

表 3 末端时刻两枚导弹状态参数 Table 3 Final state parameters of two missiles

末端时刻状态参数	导弹1(M1)	导弹2(M2)
(xmf,ymf) /m	(13 099.2,4 099.5)	(13 100.3,4 100.8)
ψmf/(°)	64.9	25.0

表选项

图 7 初始控制量猜测法向加速度指令 Fig. 7 Normal acceleration command for initial control guess

图选项

CPN制导方法可以确定各枚导弹的攻击时间，攻击时间不用事先设定；MPSC制导方法可以对攻击角度进行控制。仿真表明，本文给出的MPSC制导体系的协同制导方法可以对攻击时间和攻击角度同时进行控制，实现多导弹协同攻击。与文献^[20]给出的带有攻击角度和时间约束的协同制导律相比，本文方法角度偏差可控制在0.1°范围内，协同攻击时末端角度控制精度更高。
4 结 论 针对多导弹协同制导问题，设计了一种二维平面内带有末端攻击角度约束的多导弹协同攻击制导律，得到以下结论：
1) 基于MPSC和CPN制导方法实现了满足末端攻击角度约束的多导弹协同攻击。
2) 通过CPN制导方法对初始控制量进行猜测并确定协同攻击时间，运用MPSC制导方法实现末端攻击角度约束。
3) 下一步将对三维空间多约束条件下的协同制导律作更深入的研究。

参考文献

[1]	?LEE J I,JEON I S,TAHK M J.Guidance law using augmented trajectory-reshaping command for salvo attack of multiple missiles[C]//UKACC International Control Conference 2006.Glasgow:UKACC,2006:766-771.
[2]	邹丽, 孔繁峨, 周锐, 等. 多导弹分布式自适应协同制导方法[J].北京航空航天大学学报, 2012, 38(1): 128–132.ZOU L, KONG F E, ZHOU R, et al. Distributed adaptive cooperative guidance for multi-missile salvo attack[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(1): 128–132.(in Chinese)
[3]	孙雪娇, 周锐, 吴江, 等. 多导弹分布式协同制导与控制方法[J].北京航空航天大学学报, 2014, 40(1): 120–124.SUN X J, ZHOU R, WU J, et al. Distributed cooperative guidance and control for multiple missiles[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(1): 120–124.(in Chinese)
[4]	范作娥, 于德海, 顾文锦. 带落角约束和目标机动补偿的三维制导律[J].系统工程与电子技术, 2011, 33(8): 1856–1859.FAN Z E, YU D H, GU W J. Three-dimensional guidance law with impact angle constraint and maneuvering target compensation[J].Systems Engineering and Electronics, 2011, 33(8): 1856–1859.(in Chinese)
[5]	JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J].IEEE Transactions on Control Systems Technology, 2006, 14(2): 260–266.DOI:10.1109/TCST.2005.863655
[6]	LEE J I, JEON I S, TAHK M J. Guidance law to control impact time and angle[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 301–310.DOI:10.1109/TAES.2007.357135
[7]	张友安, 马培蓓. 带有攻击角度和攻击时间控制的三维制导[J].航空学报, 2008, 29(4): 1021–1026.ZHANG Y A, MA P B. Three-dimensional guidance law with impact angle and impact time constraints[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 1021–1026.(in Chinese)
[8]	PADHI R, KOTHARI M. Model predictive static programming:A computationally efficient technique for suboptimal control design[J].International Journal of Innovative Computing,Information and Control, 2009, 5(2): 399–411.
[9]	DWIVEDI P N, BHATTACHARYA A, PADHI R. Suboptimal midcourse guidance of interceptors for high speed targets with alignment angle constraint[J].Journal of Guidance,Control,and Dynamics, 2011, 34(3): 860–877.DOI:10.2514/1.50821
[10]	OZA H B, PADHI R. Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles[J].Journal of Guidance,Control,and Dynamics, 2012, 35(1): 153–164.DOI:10.2514/1.53647
[11]	MAITY A,OZA H B,PADHI R.Generalized model predictive static programming and its application to 3D impact angle constrained guidance of air-to-surface missiles[C]//2013 American Control Conference(ACC).Piscataway,NJ:IEEE Press,2013:4999-5004.
[12]	CANNON M. Efficient nonlinear model predictive control algorithms[J].Annual Reviews in Control, 2004, 28(2): 229–237.DOI:10.1016/j.arcontrol.2004.05.001
[13]	SLEGERS N, COSTELLO M. Model predictive control of a parafoil and payload system[J].Journal of Guidance,Control,and Dynamics, 2005, 28(4): 816–821.DOI:10.2514/1.12251
[14]	PADHI R, CHAWLA C, DAS P G. Partial integrated guidance and control of interceptors for high-speed ballistic targets[J].Journal of Guidance,Control,and Dynamics, 2014, 37(1): 149–163.DOI:10.2514/1.61416
[15]	赵启伦, 陈建, 董希旺, 等. 拦截高超声速目标的异类导弹协同制导律[J].航空学报, 2016, 37(3): 936–948.ZHAO Q L, CHEN J, DONG X W, et al. Cooperative guidance law for heterogeneous missiles intercepting hypersonic weapon[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 936–948.(in Chinese)
[16]	张爱梅, 江加和. 基于相互通信的多导弹协同制导[J].应用科技, 2015, 42(2): 1–6.ZHANG A M, JIANG J H. Cooperative guidance for multi-missiles based on mutual communication[J].Applied Science and Technology, 2015, 42(2): 1–6.(in Chinese)
[17]	ZHAO S Y, ZHOU R, WEI C. Design and feasibility analysis of a closed-form guidance law with both impact angle and time constraints[J].Journal of Astronautics, 2009, 30(3): 1064–1085.
[18]	HARL N, BALAKRISHNAN S N. Impact time and angle guidance with sliding mode control[J].IEEE Transactions on Control Systems Technology, 2012, 20(6): 1436–1449.DOI:10.1109/TCST.2011.2169795
[19]	JEON I S, LEE J I, TAHK M J. Homing guidance law for cooperative attack of multiple missiles[J].Journal of Guidance,Control,and Dynamics, 2010, 33(1): 275–280.DOI:10.2514/1.40136
[20]	方研, 马克茂, 陈宇青. 带有攻击角度和时间约束的协同制导律设计[J].系统仿真学报, 2014, 26(10): 2434–2441.FANG Y, MA K M, CHEN Y Q. Cooerative guidance laws with constraints on impact time and terminal angle[J].Journal of System Simulation, 2014, 26(10): 2434–2441.(in Chinese)