随着城市规模急剧扩大，人员不断集中，形成了学校、医院、商业区等大型的人群密集区域。行人密集区域的设施设置不合理或者组织失策会产生拥挤的人群，一方面降低了人群流动的速度和效率，另一方面增加了安全隐患。小学放学过程就是典型的密集行人交通流运动过程。放学过程中，家长会聚集在校门附近。如果相应设施不合理或组织失策会造成大范围拥挤，延长放学过程学生疏散时间，同时也增加了安全隐患。
同其他交通方式相比，行人运动更随机、更复杂。行人交通流有以下特点：①行人转向和变速比机动车灵活，能随时根据周围环境选择合理甚至是任意的速度和路径；②步行受个人主观想法驱动，体型和肢体的灵活性使得行人几乎可以到达任何位置；③行人之间对避免碰撞要求不高，允许在拥挤状态下相互直接接触。基于以上特点，再加上人与人之间的相互作用，行人交通流现象非常复杂。
对行人流的研究已有60多年历史，主要行人流模型有元胞自动机模型、社会力模型和格子气模型等。Burstedde等^[1]利用“背景场”概念提出了二维行人流仿真模型，主要用于仿真有墙体的二维空间内行人流群体行为，发现了宏观的“成行”等现象。Helbing等^[2-4]在流体力学基础上提出了社会力模型，研究疏散状态下各异的疏散动作，发现了行人的自组织现象和在出口附近行人的“聚集”、“成拱”和“快即是慢”现象。Muramatsu等^[5]提出了格子气概念，用于模拟通道内的对向行人流，采用随机移动的气体分子模拟行人，行人依据相邻域的元胞占据情况，依照一定概率规则选择移动方向。杨立中等^[6-10]在模拟仿真中考虑了中国人的右行倾向。翁文国等^[11-12]在仿真中将行人基本运动分为平移、躲避和绕行。宋卫国等^[13]将社会力模型和格子气模型结合，在格子气模型中考虑力的影响，体现目标对行人的吸引及墙体、其余行人对当前行人的排斥。岳昊等^[14-16]研究了行人位置分布不均衡的多安全出口疏散过程，通过改进假想距离的计算方法和拥堵计算区域，实现疏散的动态平衡。任刚等^[17]通过行人行走倾向调查实验，建立考虑行走倾向的元胞自动机模型，构建行人复杂网络，通过仿真研究揭示双向行人流特点和自组织现象。周金旺等^[18-19]研究了成对行为对行人疏散的影响和不同成对模式对宏观疏散效果的影响，发现单人疏散总是比多人抱团疏散要快，行人大范围成对行为对疏散效率起消极作用，并排成对对疏散最不利。
目前对行人流的研究聚焦在疏散状态行人流，对特殊人群行人流(特别是小学生行人流)的研究相对较少。本文对小学放学过程的行人流(本文特指仅由家长和学生形成的这一类行人流)现象进行研究，利用元胞自动机模型，在静态场基础上提出了基于下一步距离收益的算法，利用北京航空航天大学附属小学(以下简称北航附小)放学时校门口的行人流进行仿真，探究影响小学生行人流疏散效率的因素，对提高小学生疏散效率、避免安全事故提供理论依据。
与普通行人流相比，放学过程中的行人流具有如下显著特点：
1) 接到孩子之前，家长和学生都单独移动；接到孩子后，家长与学生则成对运动。
2) 文献^[18]指出，“单个疏散比成对疏散快，成对行为对疏散产生阻碍作用”。行人流密度非常高，所以容易产生严重的拥堵现象。
3) 行人都会离开系统，所以行人移动具有明确的方向性。
1 模型 1.1 模型概述 放学过程中行人流比较密集，所以本文采用拥挤状态下的行人元胞尺寸，即0.4 m×0.4 m^[1]。元胞状态可以是空或被占据，也可以是墙体、进出口等。每个行人(学生、家长)只占用一个独立元胞；时间被离散成多个时间步；行人在每个时间步内可以移动到相邻元胞；行人最大步行速度为1 m/s^[18]；每个时间步至多移动一个元胞，单位时间步长为0.4 s；行人不可以穿越墙体。
行人在行走的过程中都带有目的性，会选择距离目的地近的路线以求尽可能快地到达目的地。现有行人流模型中，研究者为了反映固定目的地对行人的吸引，引入了“静态场”的概念^[1]。静态场在模拟行人向固定目的地移动方面已经广泛应用并取得很好的实用效果。为了表达目的地对行人的吸引，本文以中心元胞与目的地距离差为衡量参数。引入静态场是为了表明目的地对当前元胞的吸引程度，离出口越近则场强越大，行人总是趋向于移动到场强大的邻域元胞中。本文以行人考虑下一步移动所能达到的最大效益为原则，提出了以下Moore型邻域(见图 1)和算法：
1) 计算当前行人所在中心元胞与目标元胞的距离。
2) 计算8个邻域元胞与目标元胞的距离，(i=-1，0，1；j=-1，0，1) 。
3) R_{0, 0}-R_{i, j}为运动到第i行、第j列的邻域元胞的收益，R_{0, 0}-R_{i, j}为正，说明此次移动产生积极作用，R_{0, 0}-R_{i, j}为负，说明此次移动产生消极作用，其中:R_{0, 0}为第0行、第0列邻域元胞与目标元胞的距离；R_ij为第i行、第j列邻域元胞与目标元胞的距离。
4) P_{i, j}为移动到第i行、第j列的邻域元胞的概率。如果R_{0, 0}-R_{i, j}为最大，则P_{i, j}为1，否则为0。

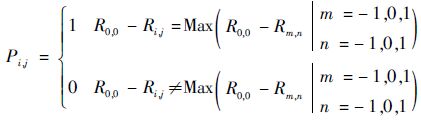图 1 基于静态场的Moore邻域 Fig. 1 Moore neighborhood based on static floor field

图选项

1.2 场景介绍 图 2(a)矩形区域为研究区域。通过对放学过程的观察，发现：

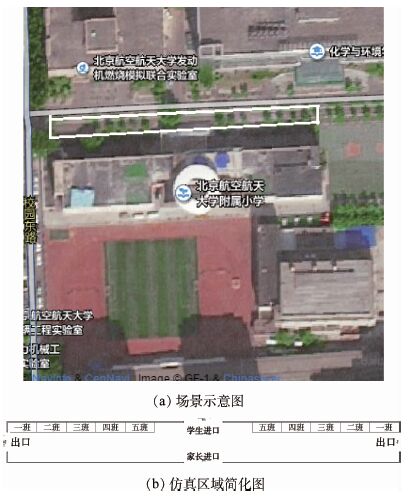图 2 北航附小门口示意图与仿真区域 Fig. 2 Schematic diagram of gate of Beihang University Affiliated Primary School and simulation area

图选项

1) 学生以班为单位有序排队从大门口移动到相应的等待区域，等待区域离校门越远的班级越早开始移动。学生严格按照排队顺序移动，不存在混乱和拥挤问题。由于学校规定家长需要在接送区域得到班主任确认后才能领走学生，所以不存在学生一出现在大门口就走向家长的情况。
2) 一部分家长提前进入系统，并随机分布在系统内；剩余家长在放学后陆续进入系统。
3) 学生队伍一旦出现在校门口，几乎所有家长都向接送区域移动。家长分散地进入接送区域寻找孩子，所以接送区域内的行人流相对有序，只有家长集中进入接送区域才会有明显的拥挤现象。
4) 家长接到小孩后就会离开接送区域，以出口为目标移动。出口处的行人比较分散，所以不会出现明显的拥挤现象。
根据上述现象对研究区域做如下简化：研究区域为80.8 m×8.8 m的矩形，除四周墙体的宽度，实际尺寸为80 m×8 m；出口宽度为4 m，学生进口宽度为8 m，家长进口宽度为8 m；每个班的接送区域为6 m×2 m的矩形区域，如图 2(b)所示。
1.3 更新规则 结合观察和研究可行性，本文给出如下基本假设：
1) 场景边界为墙体，行人从进口进入、出口离开(见图 2(b))。
2) 不考虑接送区域内家长和学生配对过程，将家长到达接送区域视为接到孩子。
3) 家长和学生都是完全理性的，而且在系统内运动时只考虑“静态场”。
根据元胞自动机模型更新规则、仿真场景和基本假设，提出如下规则：
1) 行人在每个时间步内至多移动一个元胞。
2) 仿真规模是由250名家长和250名学生构成的250对行人，其中每一对行人都有自己的编号。前100名家长提前分布在系统内，其中40%的家长集中分布在校门口附近，60%随机分布在其余位置。开始仿真时，剩余150名家长以1人/时间步的速率从入口进入系统。
3) 行人根据其编号划分为5类，分别对应5个不同的目的地。
4) 行人在判断下一步目标时，如果邻域是墙体或行人，该邻域元胞与出口的距离R_d设为无穷大(本文设为10 000个元胞长度)；如果邻域元胞为空元胞，计算其移动收益，行人在该时间步从当前元胞移动到移动收益最大的邻域元胞。
5) 行人一旦到达对应的接送区域，其上方元胞被对应学生占据，完成成对行为。此时，目的地变为出口，以出口作为目标移动。
6) 行人移动到出口，家长完成接送学生的行为，将从系统中移除。
7) 当多个行人竞争同一元胞，会产生移动冲突。文献^[2]比较了几种解决冲突的方法，并认为处理冲突的方式对仿真结果的影响非常小。所以，本文处理冲突时遵从编号小的行人移动到该目标元胞，其余竞争者移动到收益次大的邻域元胞。
8) 当第250名家长移动到出口，区域内没有任何行人，仿真结束。
2 仿真分析 实际上，同年级的250名学生同时放学，且一个年级放学时使用的区域是仿真区域的左侧或右侧，所以只需仿真左半侧区域。
图 3是不同时间步的行人位置情况。其中：图 3(a)是行人的初始分布；图 3(b)和图 3(c)表明行人进入系统以后，会在特定区域形成拥挤现象；图 3(d)表明拥挤情况随时间往班级接送区域移动，而且已经有部分家长与孩子完成了配对；图 3(e)~图 3(g)表明拥挤在消散，同时家长完成配对并往出口移动；图 3(h)和图 3(i)描述的是行人离开系统时的稀疏行人流状况。

图 3 行人疏散图 Fig. 3 Snapshot of pedestrian’s clearance

图选项

仿真结果表明，150个时间步以后，只有从家长入口进入的行人在系统中运动。由此可以预见如果行人进入系统的速率很小，系统的行人密度会降低，但行人进入系统的总时间会变长，疏散时间会增加。如果输入率很高，系统的行人密度会增加，出现拥挤现象，拥挤消散时间相应增加。但高输入率使得家长进入系统的时间较小，此时家长输入率对疏散时间的影响非常显著。
分别取家长输入率为5人/时间步、4人/时间步、3人/时间步、2人/时间步、1人/时间步、1人/2时间步、1人/3时间步、1人/4时间步，研究家长输入率对疏散时间的影响(见表 1和图 4)。
表 1 家长不同输入率下的平均疏散时间 Table 1 Average clearance time under different input rates of students’ parents

输入率/(人·时间步-1)	疏散时间/时间步					平均疏散时间/时间步
	仿真1	仿真2	仿真3	仿真4	仿真5
1/4	693	690	691	691	689	690.8
1/3	540	542	545	545	544	543.2
1/2	395	393	394	391	397	394.0
1	247	246	247	246	249	247.0
2	179	175	176	174	178	176.4
3	187	184	196	180	182	185.8
4	186	184	185	182	187	184.8
5	180	190	191	184	187	186.4

表选项

图 4 平均疏散时间与家长输入率之间的定量关系 Fig. 4 Quantitative relationships between average clearance time and input rate of students’ parents

图选项

其仿真结果表明：当输入率小于1人/时间步时，输入率与平均疏散时间负相关。当输入率大于1人/时间步时，不管输入率如何增大，平均疏散时间的变化都不显著。这说明只有在小输入率的情况下，家长输入率才对系统的疏散效率产生显著的影响。这是因为小输入率产生的是稀疏行人流。行人流的疏散时间基本上为常数，所以系统疏散时间基本上是由行人缓慢进入系统的总时间所决定的。而当输入率大于1人/时间步时，系统内逐渐产生了拥挤行人流，这使得行人间的排斥作用增强，行人之间对空间竞争的冲突使得整个行走过程的有效移动距离和有效移动时间步减少，导致系统疏散效率下降。在高输入率仿真中几乎都能看到行人围成一团的拥堵现象，且输入率越大，此现象越明显。拥堵的消散过程总是从外侧行人开始移动，由外到内慢慢消散。高输入率虽然减少了系统行人输入时间，但拥堵消散会浪费一定量时间，且两者之间的差异没有明确的定量关系，所以高输入率的变化与系统疏散平均时间的影响没有明显的定量关系。
初始分布人数对系统疏散时间的影响无法直观判断。通过改变模型的参数，进行多次仿真来探究初始分布行人数对疏散时间的影响，分别取初始分布人数为50、100、150、200进行仿真实验，其疏散时间如表 2和图 5所示。
表 2 不同初始分布人数的平均疏散时间 Table 2 Average clearance time under different number of pedestrian at initial stage

初始分布人数	疏散时间/时间步					平均疏散时间/时间步
	仿真1	仿真2	仿真3	仿真4	仿真5
50	297	298	296	298	296	297.0
100	247	246	247	246	249	247.0
150	197	198	204	197	197	198.6
200	182	185	180	182	186	183.0

表选项

图 5 平均疏散时间与初始分布人数之间的定量关系 Fig. 5 Quantitative relationships between average clearance time and number of pedestrian at initial stage

图选项

系统平均疏散时间与初始分布人数呈现负相关性。随着初始分布人数增加，家长入口输入的人数会减少，而输入率是定值，所以输入时间和系统疏散时间会减小。但并不是说初始分布人数越多，系统疏散效率越高，因为高密度的行人流使得系统因太拥堵而无法正常运行。
3 结论 根据小学生的行人流特征和运动规则，利用元胞自动机模型从微观角度分析了行人对距离收益的理性判断。对北航附小放学时行人疏散过程进行仿真，研究放学过程中家长接送孩子的行为，分析了系统行人输入率、初始分布人数对疏散效率的影响，其具体结果如下：
1) 行人输入率小于1人/时间步时，平均疏散时间随输入率减小而显著增大；行人输入率大于1人/时间步时，对平均疏散时间的影响没有明确的趋势。
2) 系统平均疏散时间与初始分布人数呈现负相关的关系。
以上研究结果发现，不考虑行人的差异性，可以得到一个最优的行人输入率和初始分布人数组合使得行人在最短的时间内全部离开系统。如果利用实测数据标定，可以得到一个符合实际情况的最优行人输入率和初始分布人数组合使得实际的行人运动达到效率最优。这两个参数在实际应用中可以通过管理控制实现。在放学区域的家长进口处控制进口宽度、设置相当数量的闸机或人工标志引导，以达到控制家长输入率的目的。控制系统内初始分布的人数，一方面要鼓励家长提早到接送区域等待学生的行为，以减少行人移动方向冲突产生的效率损失。另一方面也要防止初始分布人数过大产生严重拥堵。
然而，本文存在如下不足：缺乏实测数据支持、忽略行人的移动特性、缺少评价体系和反馈机制等。
但是，这些不足在现有研究中难以弥补，因此结合研究现状对未来研究做出如下展望：
1) 提高元胞模型精度。设置更小的元胞尺寸，每个行人占据多个元胞。理论上，元胞尺寸越小，刻画的微观行为越精确，仿真结果越真实。
2) 考虑行人相互作用和随机行为。本文仅把静态场对行人的作用作为行人移动的外在动力。而完整的行人系统应该考虑系统对行人的作用、行人对系统的作用、行人间的相互作用。而且，行人的行为并非完全理性，随机事件可以描述行人的非理性行为。
3) 引入实测数据。借助实测数据对行人流模型进行标定，对模型合理性做出评价，有利于用建模仿真手段解决实际问题。

参考文献

[1]	BURSTEDDE C, KLAUCK K, SCHADSCHNEIDER A, et al. Simulation of pedestrian dynamics using a two-dimensional cellular automaton[J].Physica A Statistical Mechanics & Its Applications, 2001, 295(3): 507–525.
[2]	HELBING D, MOLNáR P. Social force model for pedestrian dynamics[J].Physical Review E-Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1998, 51(5): 4282–4286.
[3]	HELBING D, JOHANSSON A. Pedestrian,crowd and evacuation dynamics[J].Encyclopedia of Complexity & Systems Science, 2009, 16: 697–716.
[4]	HELBING D, FARKAS I J, MOLNAR P, et al. Simulation of pedestrian crowds in normal and evacuation situations[J].Pedestrian & Evacuation Dynamics M Schreckenberg, 2002: 21–58.
[5]	MURAMATSU M, IRIE T, NAGATANI T. Jamming transition in pedestrian counter flow[J].Physica A Statistical Mechanics & Its Applications, 1999, 267(S3-4): 487–498.
[6]	YANG L Z, LI J, LIU S. Simulation of pedestrian counter-flow with right-moving preference[J].Physica A Statistical Mechanics & Its Applications, 2008, 387(13): 3281–3289.
[7]	YANG L Z, FANG W, FAN W. Modeling occupant evacuation using cellular automata-effect of human behavior and building characteristics on evacuation[J].Journal of Fire Sciences, 2003, 21(3): 227–240.DOI:10.1177/0734904103021003004
[8]	LIU S B, YANG L Z, FANG T Y, et al. Evacuation from a classroom considering the occupant density around exits[J].Physica A Statistical Mechanics & Its Applications, 2009, 388(9): 1921–1928.
[9]	朱孔金, 杨立中. 房间出口位置及内部布局对疏散效率的影响研究[J].物理学报, 2010, 59(11): 7701–7707.ZHU K J, YANG L Z. Research on the influence of the exit location and layout of the room on the evacuation efficiency[J].Acta Physics Sinica, 2010, 59(11): 7701–7707.(in Chinese)
[10]	杨立中, 李健, 赵道亮, 等. 基于个体行为的人员疏散微观离散模型[J].中国科学E辑:工程科学材料科学, 2004, 34(11): 1264–1270.YANG L Z, LI J, ZHAO D L, et al. The microscopic discrete evacuation model based on individual behavior[J].Science in China Ser E Engneering & Materials Science, 2004, 34(11): 1264–1270.(in Chinese)
[11]	WENG W G, SHEN S F, YUAN H Y, et al. A behavior-based model for pedestrian counter flow[J].Physica A Statistical Mechanics & Its Applications, 2007, 375(2): 668–678.
[12]	WENG W G, CHEN T, YUAN H Y, et al. Cellular automaton simulation of pedestrian counter flow with different walk velocities[J].Physical Review E-Statistical,Nonlinear,and Soft Matter Physics, 2006, 74(3): 92–100.
[13]	SONG W G, XU X, WANG B H, et al. Simulation of evacuation processes using a multi-grid model for pedestrian dynamics[J].Physica A Statistical Mechanics & Its Applications, 2006, 363(2): 492–500.
[14]	岳昊, 张旭, 陈刚, 等. 初始位置布局不平衡的疏散行人流仿真研究[J].物理学报, 2012, 61(13): 130509–1.YUE H, ZHANG X, CHEN G, et al. Simulation of pedestrian evacuation flow with unbalanced initial position layout[J].Acta Physics Sinica, 2012, 61(13): 130509–1.(in Chinese)
[15]	岳昊, 邵春福, 关宏志, 等. 基于元胞自动机的行人视线受影响的疏散流仿真研究[J].物理学报, 2010, 59(7): 4499–4507.YUE H, SHAO C F, GUAN H Z, et al. Simulation of pedestrian evacuation flow with affected visual field using cellular automata[J].Acta Physics Sinica, 2010, 59(7): 4499–4507.(in Chinese)
[16]	岳昊, 邵春福, 陈晓明, 等. 基于元胞自动机的对向行人交通流仿真研究[J].物理学报, 2008, 57(11): 6901–6908.YUE H, SHAO C F, CHEN X M, et al. Simulation of bi-directional pedestrian flow based on cellular automata model[J].Acta Physics Sinica, 2008, 57(11): 6901–6908.(in Chinese)
[17]	任刚, 陆丽丽, 王炜. 基于元胞自动机和复杂网络理论的双向行人流建模[J].物理学报, 2012, 61(14): 255–264.REN G, LU L L, WANG W. Modeling bi-directional pedestrian flow by cellular automata and complex network theories[J].Acta Physics Sinica, 2012, 61(14): 255–264.(in Chinese)
[18]	周金旺, 邝华, 刘幕仁, 等. 成对行为对行人疏散动力学的影响研究[J].物理学报, 2009, 58(5): 3001–3007.ZHOU J W, KUANG H, LIU M R, et al. Paired behavior effect on pedestrian evacuation dynamics[J].Acta Physics Sinica, 2009, 58(5): 3001–3007.(in Chinese)
[19]	薛鹏, 周金旺, 白克钊, 等. 多房间中人员在走廊疏散的元胞自动机模拟研究[J].广西师范大学学报:自然科学版, 2009, 27(3): 1–4.XUE P, ZHOU J W, BAI K Z, et al. Cellular automaton model of occupant evacuation from multi-room in corridor[J].Journal of Guangxi Normal University:Natural Science Edition, 2009, 27(3): 1–4.(in Chinese)