带攻击角度约束的导引律研究经过了40多年的发展,取得了一系列的研究成果。文献[2]提出了一种带攻击角度约束的最优导引律,采用强跟踪滤波器预测目标机动信息,但估计精度主要依赖于滤波器的性能;文献[3]提出了一种用于打击静止和慢速移动目标具有攻击角度约束的导引律,将通过比例导引律估计的攻击角度与期望攻击角度的误差反馈到制导指令中,修正角度误差最终得到期望攻击角度。
由于滑模变结构控制在滑动模态对参数摄动和外界干扰等具有不变性,因此广泛地应用于导引律的设计之中,通过在滑模面内引入攻击角度约束项,即可设计出带攻击角度约束的滑模导引律。文献[4-5]选取包含弹目视线角速率和期望视线角的线性滑模面,将目标运动视为有界干扰;文献[6]在文献[4]的线性滑模面的基础上,选取自适应指数趋近律来设计导引律,保证了到达条件及良好的动态特性。
传统滑模控制方法设计的线性滑模面,在系统状态到达滑模面后,只能渐进趋近于平衡点,不是有限时间收敛的;而终端滑模控制方法,能够实现系统状态的有限时间收敛,且比传统滑模控制具有更好的收敛性能[7]。文献[8-11]采用传统终端滑模面取代线性滑模面,设计了带攻击角度约束的导引律,满足有限时间收敛特性,但是由于控制指令中存在负指数项,会存在奇异问题。在文献[9]中,通过在负指数项引入一个变量β,当滑模面函数小于一定值时,设定β=0,以避免出现奇异问题,但降低了对期望视线角的跟踪精度,过程较为繁琐。文献[11]采用幂次趋近律,导致了系统状态离平衡点较远时,收敛速度较慢。
为了解决奇异问题,文献[12]提出了非奇异终端滑模控制方法,不仅解决了终端滑模控制的奇异性问题,还具有与终端滑模相似的特性,能够实现系统状态的有限时间收敛;文献[13-14]基于非奇异终端滑模控制方法,提出了带攻击角度约束的非奇异终端滑模导引律,获得了良好的制导性能,但采用等速趋近律,其收敛速度与开关项系数ε成正比关系,增加ε会增大抖振现象。针对此问题,文献[15]根据多模态滑模概念,设计分段切换函数,提出了一种快速终端滑模控制方法,实现系统状态全局快速收敛,但控制器形式较为繁琐。
为解决传统终端滑模导引律中存在的奇异问题和文献[11]中系统收敛速度较慢的问题,本文设计了一种快速收敛的非奇异终端滑模面,并对传统指数趋近律进行了改进,引入了状态变量的1阶范数,能够根据系统状态距离平衡点的远近自适应调整趋近速率,提高收敛速度;在此基础上,提出了一种自适应非奇异终端滑模控制方法,避免了非奇异问题,且提高了系统状态变量的全局快速收敛性。将所提方法用于导引律的设计中,进一步提出了一种带攻击角度约束的自适应非奇异终端滑模导引律(ANTSMG),实现了导弹对目标以期望攻击角度进行精确打击的作战要求。针对文献[13-14]中可能存在的抖振问题,采用高增益连续函数代替开关函数,大大削弱了抖振现象。本文所设计的导引律可以用于攻击固定、匀速运动和机动目标,适用范围广泛。从对比仿真实验结果可以看出,与传统滑模导引律和非奇异终端滑模导引律相比,本文所提导引律能够以更短的时间、更小的脱靶量和更高精度的期望攻击角度命中目标,验证了所提导引律的有效性和优越性。
1 弹目相对运动方程 为了方便对导引律进行研究,在惯性坐标系xOy中,建立导弹和目标在纵向平面内的相对运动关系,如图 1所示。图中:M和T分别表示导弹和目标;vm和vt分别为导弹和目标的速度;θm和θt分别为导弹的弹道倾角和目标的航迹倾角;am和at分别为导弹和目标的法向加速度;r为弹目之间相对距离;λ为弹目视线角;规定所有角度逆时针方向为正,反之为负。
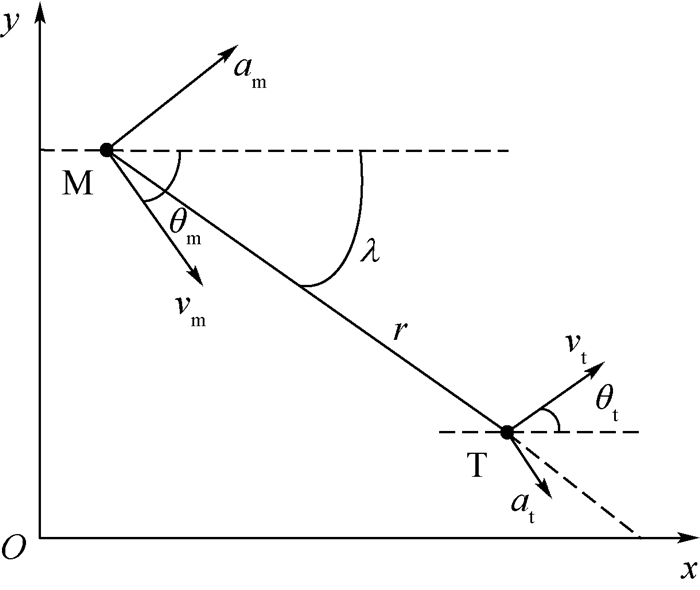 |
| 图 1 弹目相对运动关系 Fig. 1 Relationship of missile-to-target relative motion |
| 图选项 |
由图 1可得弹目相对运动方程为
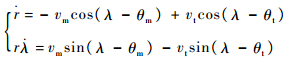 | (1) |
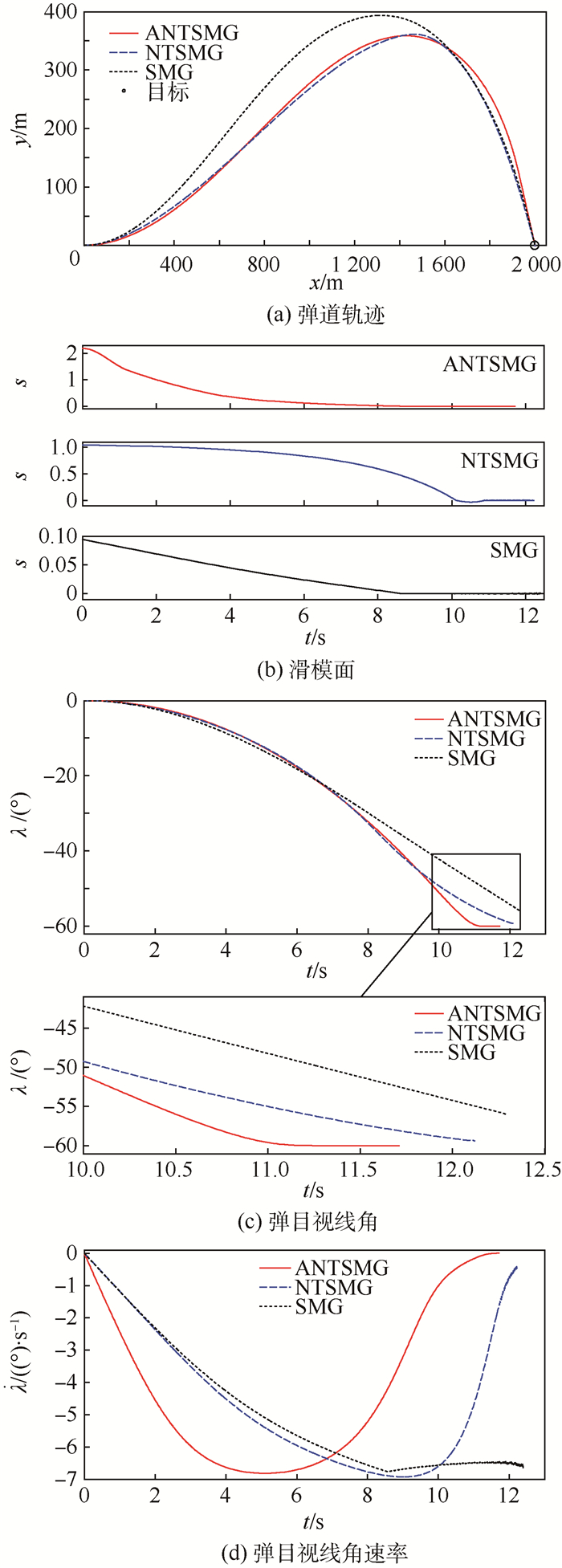 |
| 图 2 场景1的仿真实验结果 Fig. 2 Simulation experimental results of Situation 1 |
| 图选项 |
对式(1)两边求导,整理后可得
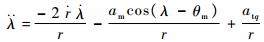 | (2) |
式中:atq=atcos(q-θt)为目标加速度在垂直于弹目视线方向上的分量。在实际场景中,目标的加速度信息很难获得,这里将atq视为有界干扰,可令|atq|≤|atmax|,|atmax|为目标最大加速度。
攻击角度表示弹目交战过程中导弹和目标的速度矢量之间的夹角,即θm-θt。攻击角度约束问题可以转化为视线角约束问题[16]。
2 自适应非奇异终端滑模控制 为证明和分析方便,首先对有限时间收敛的概念进行介绍。
针对如下非线性系统:
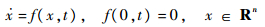 | (3) |
根据有限时间控制理论,有如下引理。
引理1[17]????假定存在一个定义在原点的邻域??U0?Rn上的光滑函数V(x),并且存在实数c > 0和0 < α < 1,使得V(x)在?上是正定的,且
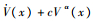
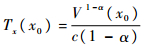 | (4) |
式中:x0为原点某一开邻域中的任何一点。如果?=Rn,并且V(x)是径向无界的,则系统的原点是全局有限时间稳定的。
引理2[18]????如果存在光滑、正定函数V(x),并且存在实数α, β>0,0 < γ < 1,满足如下不等式:
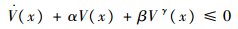 | (5) |
那么系统状态到达平衡点的时间为
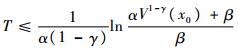 | (6) |
考虑如下非线性2阶系统:
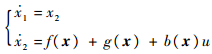 | (7) |
式中:x=[x1, x2]T;f(x)和b(x)为关于x的光滑非线性函数,且b(x) ≠ 0;u为控制输入;g(x)为有界干扰,且|g(x)|≤lg, lg为有界干扰的上界。
传统终端滑模控制在滑模面中引入非线性函数,以获得更好的收敛特性,其滑模面选取如下:
 | (8) |
式中:β > 0;p和q为正奇数,且q < p。
设计控制器为
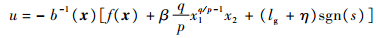 | (9) |
式中:η > 0。
从式(9)中可看出,由于存在x1q/p-1x2项,当x1 =0,x2 ≠ 0时,会出现奇异问题。当滑模面函数s=0时,x2=-βx1q/p,则x1q/p-1x2=-βx12q/p-1,若1 < p/q < 2,则可避免奇异问题。但是当s≠0时即到达滑模面之前,并不能保证不出现x1=0,x2 ≠ 0的情况,如果出现,就会发生奇异问题。文献[12]针对终端滑模控制的奇异问题,设计了一种非奇异终端滑模面,从而避免了奇异问题,滑模面切换的具体表达形式如下:
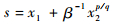 | (10) |
式中:β > 0;p 和q为正奇数,且q < p < 2p。
设计控制器为
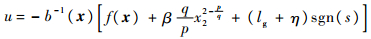 | (11) |
可以看出,采用式(10)的滑模面切换函数,所得控制量不存在负幂次方,避免了奇异问题。
由式(10)可知,当系统状态到达滑模面时,有
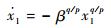 | (12) |
由式(12)可以看出,x1的指数项小于1,则系统状态在远离平衡点区域内,其收敛速度相比线性滑模面较为缓慢。为进一步提高系统趋近于平衡点的收敛速度,本文设计了一种快速收敛的终端滑模面切换函数:
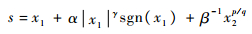 | (13) |
式中:α>0;γ >1,且γ>p/q。
为抑制抖振,减小系统状态到达滑模面的时间,改善系统性能,选取一种自适应指数趋近律:
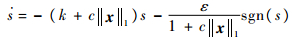 | (14) |
式中:
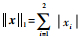
传统的指数趋近律?=-ks-εsgn(s),其系数k和ε是固定的,不能够随着系统状态的变化而自适应地调整。本文所选趋近律式(14)引入了系统状态变量的1阶范数,使得随着系统状态距离平衡点的远近进行自适应地调整趋近速率。式(14)中的第1项为指数趋近项,当‖x‖1很大时,其趋近速率要大于传统的指数趋近律,从而能够缩短到达滑模面的时间,并且第2项的等速趋近项的系数远小于传统趋近律;当‖x‖1较小时,通过增大系数c缩短滑模到达时间,并且能够减小变结构项系数,大大削弱系统抖振;当‖x‖1趋近于零时,所提自适应指数趋近律就变为了传统的指数趋近律。
对于本文所设计滑模面式(13)和趋近律式(14),有如下定理。
定理1????对于非线性系统式(7),选取式(13)所示的滑模面,系统到达滑模面后,系统状态能够在有限时间收敛到平衡点,且收敛时间要小于传统非奇异终端滑模控制。
证明????当系统状态到达滑模面时,即s=0,则由式(7)可得
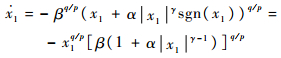 | (15) |
证毕
为了方便证明,对终端滑模控制中相关时间量进行定义。
定义1????系统状态从初始位置(x1(0), x2(0))到达滑模面的时间为tr,到达点坐标为(x1(tr), x2(tr))。
定义2????系统从到达点(x1(tr), x2(tr))沿滑模面运动到平衡点(0, 0)的时间为tc。
由定义2可知,x1 (tc)=0,对式(15)两边求积分得
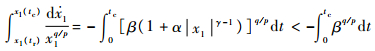 | (16) |
则
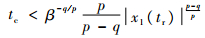 | (17) |
文献[7]给出了传统非奇异终端滑模控制tc的表达式:
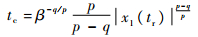 | (18) |
可以看出,系统状态能够在有限时间收敛到平衡点,且本文设计的滑模面切换函数相比较传统非奇异终端滑模面,其收敛时间更短。 证毕
定理2????对于非线性系统式(7),选取式(13)和式(14)所示的滑模面和趋近律,设计如下控制器:
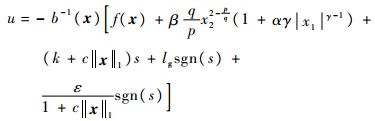 | (19) |
则系统式(7)是有限时间收敛的。
证明
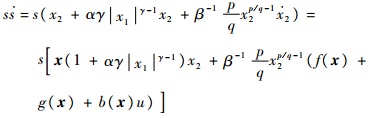 | (20) |
令
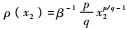
 | (21) |
当x2 ≠ 0时,ρ(x)>0,则
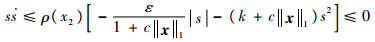 | (22) |
满足滑模可达条件。
当x2=0时,将式(19)代入式(7)得
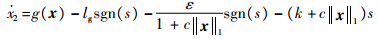 | (23) |
则有
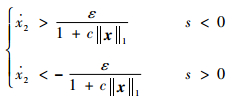 | (24) |
由式(20)可以看出,s ≠ 0,x2=0时,x2不是稳态,且在有限时间内x2将变为非零的状态,又由式(22)可知,系统状态在有限时间内能够到达滑模面,系统(7)是有限时间收敛的。 证毕
综上所述,本文所提自适应非奇异终端滑模控制方法能够使系统状态在有限时间内收敛到滑模面,并且到达滑模后,相比传统非奇异终端滑模控制方法,能够以更短的时间收敛至平衡点。
3 带攻击角度约束的导引律设计 基于本文提出的自适应非奇异终端滑模控制方法,设计滑模面为
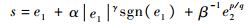 | (25) |
式中:e1=λ-λd;e2=?1;λd为期望的攻击角,假定为常数,则
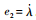
选取如式(14)所示的自适应指数趋近律:
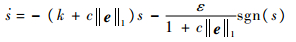 | (26) |
式中:
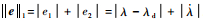
根据所设计滑模面和趋近律,可设计如下所示的带攻击角度约束的导引律:
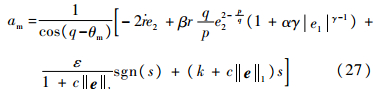 | (27) |
定理3????对于式(1)和式(2)所描述的弹目相对运动非线性方程,设计如式(27)所示的导引律,系统状态能够有限时间收敛到滑模面,弹目视线角跟踪误差e1和视线角速率e2能够在有限时间内收敛到零,且不会出现奇异问题。
证明????根据系统状态运动的2个阶段进行分析。
1)?滑模到达阶段。系统状态在趋近律作用下,趋近于滑模面的过程。
选取如下Lyapunov函数:
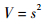 | (28) |
对式(28)两边求导,并将式(25)代入得
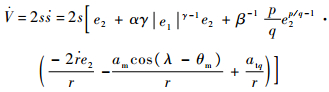 | (29) |
将式(27)代入式(29)中得
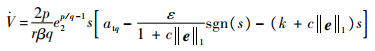 | (30) |
对于固定或者匀速运动的目标,此时at=atq=0,则式(30)可变换为如下形式:
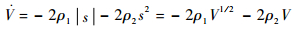 | (31) |
式中:
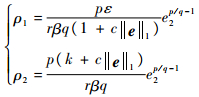 | (32) |
显然,ρ1, ρ2≥0,由引理1可知,系统状态是有限时间收敛的,由引理2可知, 系统状态收敛到滑模面s=0的时间为
 | (33) |
式中:e2 ≠ 0;s(0)为s的初值。
下面对e2=0的情况进行讨论,将式(27)代入式(2)得
 | (34) |
从式(34)可以看出,e2=0不是一个稳定状态,因此,系统状态能够在有限时间收敛到滑模面。
对于机动目标,即at ≠ 0,式(30)可表述为如下形式:
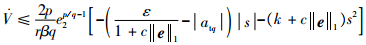 | (35) |
如果
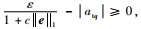
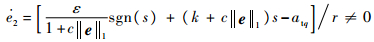 | (36) |
同理,e2=0不是一个稳定状态,系统状态能够在有限时间收敛到滑模面。
2)?沿滑模面运动阶段。系统状态到达滑模面后,沿滑模面趋近于平衡点的过程。
下面对系统状态到达滑模面后的运动状态进行讨论,此时s=0,代入式(25)得
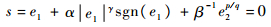 | (37) |
由定理1可知,系统状态能够在有限时间收敛到平衡点,且收敛时间满足tc < βq/p·
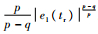
综上,本文所设计导引律能够使系统状态在有限时间收敛到滑模面,弹目视线角跟踪误差e1和视线角速率e2能够在有限时间内收敛到零,且不会出现奇异问题。????证毕
本文所设计导引律满足系统状态的有限时间快速收敛特性,但导引律式(27)中存在变结构项,会出现抖振现象。针对抖振问题,可以采用高增益连续函数s/(s+δ)代替符号函数sgn(s),则导引律的形式可以改进为
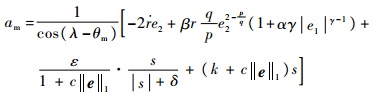 | (38) |
式中:δ>0,为一较小数,一般称为边界厚度,也称为消颤因子。
由式(38)可以看出,δ与制导控制指令的大小成反比关系,较小的δ能够增强控制效果,但是取值过小会增大抖振。因此,需要根据实际情况选取适当的δ值,达到消弱抖振的同时不影响控制效果。
4 仿真分析 本节基于弹道仿真,对本文所提带攻击角度约束的导引律的制导性能进行仿真验证与分析。在惯性坐标系下,设定导弹的初始位置为坐标原点,即(0, 0) m,导弹的速度vm=180 m/s,目标的初始位置为(2 000, 0) m,运动中目标的速度vt=20 m/s,设导弹的初始弹道倾角为θm0,目标运动时的初始航迹倾角为θt0。ANTSMG的相关制导参数设置如下:α=1, β=0.5, γ=3, p=5, q=3, ε=k=100, c=5, δ=0.001。
为了对比分析所提导引律的制导效果,更全面地考察导引律的制导性能,在仿真实例中引入文献[13]所提的带攻击角度约束的非奇异终端滑模导引律(NTSMG),其具体表达形式如下:
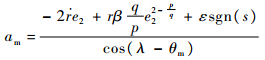 | (39) |
式中:滑模面切换函数s=e1+β-1e2p/q。相关参数设置为:β=0.2, p=5, q=3, ε=100。
为了验证所提导引律的收敛特性和抑制扰动方面的性能,文献[6]所提带攻击角度约束的传统滑模导引律(SMG),其表达形式如下:
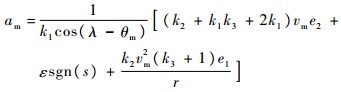 | (40) |
式中:滑模面切换函数s=k1e2+k2vme1/r。且采用指数趋近律,相关参数设置为k1=k2=k3=1, ε=20。
根据所打击目标不同的运动状态,设计3个仿真场景进行仿真实验分析。
1)?场景1。打击固定目标,θm0=0°,λd=90°,vt=0 m/s,at=0 m/s2,仿真实验结果如图 2所示。
从图 2(a)可以看出,3种导引律都是通过提升弹道的方式对目标进行打击,以获得期望的攻击角度;导弹在ANTSMG的作用下,弹道高度最低、路径较短,能够有效减少攻击时间,并且在制导末端ANTSMG的弹道曲率较大,导弹将以较大的攻击角度命中目标。由图 2(b)可以看出,在3种导引律的作用下,滑模面s均能在有限时间内收敛到零,且在ANTSMG和SMG作用下,相比NTSMG系统状态能够较早地到达滑模面,这主要由于前两者采用了指数趋近律,加快了到达滑模面的速度。从图 2(c)和图 2(d)中可以看出,在ANTSMG的作用下,在最后1 s左右弹目视线角λ和弹目视线角速率
导弹在ANTSMG、NTSMG和SMG 3种导引律作用下,其攻击时间和脱靶量分别为:11.72 s,0.08 m;12.23 s,0.22 m;12.41 s,0.41 m。相比后两者,ANTSMG在攻击时间上分别减少了0.51 s和0.69 s,在脱靶量方面降低了0.14 m和0.33 m。
对于固定目标,根据导弹初始弹道倾角和攻击角度约束的不同,还进行了5种情形的仿真:θm0分别取30°和60°,λd=-60°;θm0分别取0°、 30°和60°,λd=-75°。由于篇幅有限,这里只给出ANTSMG、NTSMG和SMG在这5种情形下的攻击时间、脱靶量和攻击角度偏差的结果,如表 1所示。可以看出,ANTSMG在攻击时间、脱靶量和攻击角度偏差方面要优于另外2种导引律。
表 1 打击固定目标仿真实验结果 Table 1 Simulation experimental results of attacking fixed target
| 导引律 | 攻击时间/s | 脱靶量/m | 攻击角度偏差/(°) |
| ANTSMG | 12.01 | 0.51 | 0.01 |
| 12.17 | 0.25 | 0.01 | |
| 12.29 | 0.43 | 0.01 | |
| 12.30 | 0.37 | 0.04 | |
| 12.45 | 0.50 | 0.10 | |
| NTSMG | 12.31 | 0.58 | 0.20 |
| 12.50 | 0.29 | 0.10 | |
| 12.44 | 0.57 | 1.50 | |
| 12.51 | 0.89 | 0.30 | |
| 12.71 | 0.87 | 0.50 | |
| SMG | 12.85 | 0.34 | 3.40 |
| 13.59 | 0.61 | 1.60 | |
| 13.05 | 0.58 | 2.80 | |
| 13.71 | 0.84 | 0.80 | |
| 14.69 | 0.51 | 2.30 |
表选项
2)?场景2。打击匀速运动目标,θm0=0°,λd=-60°,vt=15 m/s2,at=0 m/s,θt0=120°,仿真实验结果如图 3所示。在ANTSMG的作用下, s和λ均能严格收敛到0和-60°;在NTSMG作用下,s和λ只能分别收敛到|s| < 0.05,-59.3° < λ < -59.0°;在SMG的作用下,s和λ只能分别收敛到|s| < 0.01,-56.7° < λ < -56.0°,且前者较后两者收敛速度更快,时间更短。
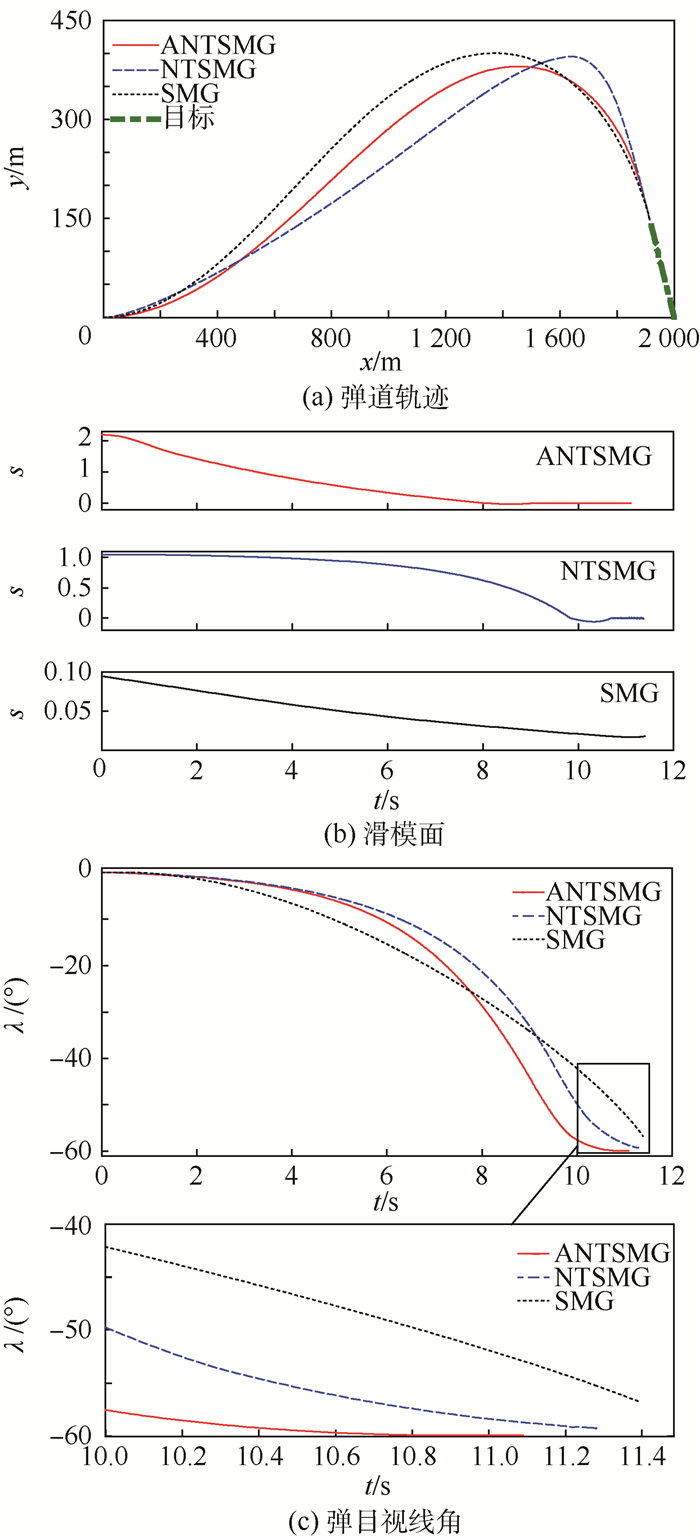 |
| 图 3 场景2的仿真实验结果 Fig. 3 Simulation experimental results of situation 2 |
| 图选项 |
在ANTSMG、NTSMG和SMG 3种导引律作用下,攻击时间和脱靶量分别为:11.11 s,0.25 m;11.38 s,0.83 m;11.42 s,1.24 m。因此,相比NTSMG和SMG,ANTSMG方法在攻击时间上分别减少了0.27 s和0.31 s,在脱靶量方面分别降低了0.58 m和0.99 m。
针对匀速运动目标,还进行了以下2种情形的仿真:λd=-60°,θm0分别取30°和60°。这里只给出3种导引律作用下的攻击时间、脱靶量和攻击角度偏差的实验结果,如表 2所示。可以看出,对于目标运动带来的扰动,ANTSMG和NTSMG的制导性能变化不大,体现了良好的抗扰动能力。
表 2 打击匀速运动目标仿真实验结果 Table 2 Simulation experimental results of attacking constant speed target
| 导引律 | 攻击时间/s | 脱靶量/m | 攻击角度偏差/(°) |
| ANTSMG | 11.26 | 0.12 | 0.08 |
| 11.40 | 0.31 | 0.01 | |
| NTSMG | 11.60 | 0.34 | 0.30 |
| 11.76 | 0.28 | 0.20 | |
| SMG | 12.07 | 0.97 | 3.90 |
| 12.77 | 0.62 | 2.50 |
表选项
3)?场景3。打击机动目标,θm0=0°,λd=-60°,vt=-15 m/s,at=10cos t m/s2,θt0=120°。仿真实验结果如图 4所示,为节省篇幅,滑模面曲线未给出。可以看出,在ANTSMG的作用下,s和λ均能严格收敛到|s| < 0.01和-60°;在NTSMG和SMG的作用下,s和λ分别收敛到|s| < 0.1、-58.1° < λ < -57.4°和|s| < 0.03、-54.3° < λ < -53.0°。说明相比非有限时间收敛的SMG,具有有限时间收敛特性的ANTSMG和NTSMG对未知的目标机动这一干扰有着很好的抑制作用。
 |
| 图 4 场景3的仿真实验结果 Fig. 4 Simulation experimental results of situation 3 |
| 图选项 |
在ANTSMG、NTSMG和SMG 3种导引律作用下,攻击时间和脱靶量分别为:11.24 s,0.32 m;11.55 s,0.94 m;11.63 s,1.36 m。相比NTSMG和SMG,ANTSMG方法在攻击时间上分别减少了0.31 s和0.39 s,在脱靶量方面分别降低了0.62 m和1.04 m。
针对机动目标,还对at=5 m/s2其他条件不变的情形进行了仿真,ANTSMG、NTSMG和SMG 3种导引律的攻击时间、脱靶量和攻击角度偏差分别为:11.84 s,0.12 m,0.01°;12.14 s,0.39 m,1.10°;12.20 s,0.67 m,4.60°。
由以上3种场景的仿真结果可以看出,相比NTSMG和SMG,本文所设计的导引律在攻击时间、脱靶量和攻击角度偏差是减小的,在攻击时间方面分别降低了0.21~0.36 s和0.31~2.24 s;在脱靶量方面分别减小了-0.03~0.52 m和-0.17~0.99 m;攻击角度偏差下降了0.1°~1.5°和0.5°~4.6°。这在实际作战中是很有意义的,更短的攻击时间和更小的脱靶量能够满足快速精确命中目标的要求,更大的攻击角度能够有效提高战斗部的毁伤效能。从仿真结果还可以看出, ANTSMG全局收敛时间要明显快于NTSMG和SMG,验证了所选取的非奇异终端滑模面和指数趋近律能够有效提高系统状态的全局快速收敛性。通过上述仿真实验,验证了所设计导引律的有效性。
5 结论 本文基于终端滑模控制和有限时间控制理论,设计了带攻击角度约束的自适应非奇异终端滑模导引律,通过理论分析和大量仿真实验验证,可以得出以下结论:
1)?采用快速收敛的非奇异终端滑模面,在不存在奇异问题的情况下,能够实现制导系统状态在有限时间内严格收敛的平衡点,且比传统非奇异终端滑模控制的收敛速度更快,选取自适应指数趋近律,能够根据系统状态距平衡点的远近自适应增大趋近速率,同时减小变结构项系数,实现系统状态全局有限时间快速收敛的同时有效削弱了抖振。
2)?所设计导引律相比非奇异终端滑模导引律和线性滑模导引律,具有更高的命中精度和更小的攻击角度跟踪误差,以及更短的攻击时间。
3)?本文所设计导引律不需要任何近似处理,形式较为简单,易于工程实现。
由于制导参数的选择对导引律的性能影响很大,后续的研究可以考虑如何对制导参数进行优化并考虑自动驾驶仪的动态特性。
参考文献
| [1] | 蔡洪, 胡正东, 曹渊. 具有终端角度约束的导引律综述[J].宇航学报, 2010, 31(2): 315–323.CAI H, HU Z D, CAO Y. A survey of guidance law with terminal impact angle constraints[J].Journal of Astronautics, 2010, 31(2): 315–323.(in Chinese) |
| [2] | SONG T, SHIN S, CHO H. Impact angle control for planar engagements[J].IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1439–1444.DOI:10.1109/7.805460 |
| [3] | LEE C H, KIM T H, TAHK M J. Interception angle control guidance using proportional navigation with error feedback[J].Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1556–1561.DOI:10.2514/1.58454 |
| [4] | SONG J M, ZHANG T Q. Passive homing missile's variable structure proportional navigation with terminal angular constraint[J].Chinese Journal of Aeronautics, 2001, 14(2): 83–87. |
| [5] | ZHOU D, QU P P, SUN S. A guidance law with terminal impact angle constraint accounting for missile autopilot[J].Journal of Dynamic Systems, Measurement, and Control, 2013, 135(5): 051009.DOI:10.1115/1.4024202 |
| [6] | 吴鹏, 杨明. 带终端攻击角度约束的变结构制导律[J].固体火箭技术, 2008, 31(2): 116–120.WU P, YANG M. Variable structure guidance law with terminal attack angle constraint[J].Journal of Solid Rocket Technology, 2008, 31(2): 116–120.(in Chinese) |
| [7] | 穆朝絮, 余星火, 孙长银. 非奇异终端滑模控制系统相轨迹和暂态分析[J].自动化学报, 2013, 39(6): 902–908.MU C X, YU X H, SUN C Y. Phase trajectory and transient analysis for nonsingular terminal sliding mode control systems[J].Acta Automatica Sinica, 2013, 39(6): 902–908.(in Chinese) |
| [8] | ZHOU D, SUN S, TEO K L. Guidance law with finite time convergence[J].Journal of Guidance, Control, and Dynamics, 2009, 32(6): 1838–1846.DOI:10.2514/1.42976 |
| [9] | KUMAR S R, RAO S, GHOSE D. Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints[J].Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1230–1246.DOI:10.2514/1.55242 |
| [10] | ZHANG Y X, SUN M W, CHEN Z Q. Finite-time convergent guidance law with impact angle constraint based on sliding-mode control[J].Nonlinear Dynamics, 2012, 7(3): 619–625. |
| [11] | 张运喜, 孙明玮, 陈增强. 滑模变结构有限时间收敛制导律[J].控制理论与应用, 2012, 29(11): 1413–1418.ZHANG Y X, SUN M W, CHEN Z Q. Sliding mode variable structure finite-time convergence guidance law[J].Control Theory & Applications, 2012, 29(11): 1413–1418.(in Chinese) |
| [12] | FENG Y, YU X H, MAN Z H. Non-singular terminal sliding mode control of rigid manipulators[J].Automatica, 2002, 38(12): 2159–2167.DOI:10.1016/S0005-1098(02)00147-4 |
| [13] | ZHOU H B, SONG S M, XU M Y, et al.Design of terminal sliding-mode guidance law with attack angle constraint[C]//25th Chinese Control and Decision Conference.Piscataway, NJ:IEEE Press, 2013:556-560. |
| [14] | KUMAR S R, RAO S, GHOSE D. Nonsingular terminal sliding mode guidance with impact angle constraints[J].Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1114–1130.DOI:10.2514/1.62737 |
| [15] | 赵霞, 姜玉宪, 吴云洁, 等. 基于多模态滑模的快速非奇异终端滑模控制[J].北京航空航天大学学报, 2011, 37(1): 110–113.ZHAO X, JIANG Y X, WU Y J, et al. Fast nonsingular terminal sliding mode control based on multi-sliding-mode[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(1): 110–113.(in Chinese) |
| [16] | 刁兆师, 单家元. 带末端攻击角约束连续有限时间稳定制导律[J].宇航学报, 2014, 35(10): 1141–1149.DIAO Z S, SHAN J Y. Continuous finite-time stabilization guidance law for terminal impact angle constrainted flight trajectory[J].Journal of Astronautics, 2014, 35(10): 1141–1149.(in Chinese) |
| [17] | HONG Y G. Finite-time stabilization and stabilizability of a class of controllable systems[J].Systems & Control Letters, 2002, 46(4): 231–236. |
| [18] | YU S H, YU X H, SHIRINZADEH B Y, et al. Continuous finite-time control for robotics manipulators with terminal sliding mode[J].Automatica, 2005, 41(11): 1957–1964.DOI:10.1016/j.automatica.2005.07.001 |
