全文HTML
--> --> -->2004年以来, 复杂网络理论在复杂性系统的研究中得到了广泛的应用[9-12]. 气候系统作为非线性复杂巨系统之一[13-15], 其内部存在典型的非线性相互作用[16]. Tsonis和Roebber[17]率先提出了气候系统复杂网络的概念, 旨在利用复杂网络这一工具从整体论的角度开展气候异常问题研究. 500 hPa高度场的关联网络中, 网络的超级节点可以让气候系统更具有稳定性, 物质和能量的传输也更为高效[18]. 龚志强等[19-21]研究了全球表面气温场网络的动力学统计性质和北半球环流系统的结构特征, 实现了复杂网络理论在气候诊断分析中的应用.
气候系统复杂网络已有一部分研究聚焦于ENSO现象, Proc. Natl. Acad. Sci.连续刊登文章介绍基于复杂网络理论的ENSO事件识别和预测研究[22,23]. ENSO复杂网络的研究成果主要包括: 1)定量刻画了与ENSO相联系的全球遥相关特征. Tsonis和Swanson[18]采用月尺度资料揭示了El Ni?o网络的连通度较La Ni?a网络显著降低, 指出前者网络的稳定性相对较低, 造成El Ni?o年全球温度的可预测性较La Ni?a年偏低. Yamasaki等[24]采用逐日资料也揭示了全球不同区域的温度网络结构特征在El Ni?o年份对应网络中连边数较La Ni?a的情况显著减少. 2)不同类型ENSO事件的客观识别. Radebach等[25]系统分析了全球气候网络空间结构的时间演化特征, 初步建立了这种演化与两类ENSO事件的联系. Wiedermann等[26]基于动态的全球温度网络定量描述了不同类型ENSO事件的网络局地性和发散性结构特征, 结合网络传递性变量定义了一种能够有效区别中部型和东部型ENSO事件的新指数. Lu等[27]也利用气温网络参数—总节点度指标成功区分出EP型和CP型ENSO事件. 3)利用气温网络相变刻画海温状态的转变. Lu等[28]将海温强异常事件等效视为海温强迫对气温网络的攻击, 利用气温网络中的相变指标指示热带太平洋地区海温状态的转变, 并作为评判气候系统是否变化的依据. 可以看出, 与ENSO相关的复杂网络研究中, 目前多为构建全球地表温度网络, 通过分析El Ni?o/La Ni?a年的网络特征量的变化来实现监测、诊断和预测研究. 值得注意的是, 相关成果大多未涉及一个共性问题: ENSO事件中赤道中东太平洋的海温异常, 在不同关键海区的网络结构特征和气候要素会有怎样的差异, 以及海温升高究竟如何引起全球温度网络结构特征的变化.
本文首先分别构建了El Ni?o和La Ni?a事件对应的全球气温关联网络, 分析La Ni?a事件网络(以下简称La Ni?a网络)和El Ni?o事件网络(以下简称El Ni?o网络)的结构特征量的差异性, 然后区分不同关键海区对网络特征差异的影响, 最后联系海气相互作用探究ENSO关键区域海温升高与全球气温关联网络结构特征变化之间的可能联系, 浅析ENSO事件网络结构特征发生改变的原因.
2.1.资 料
本研究选取的气象要素资料均来自为避免极地格点距离较近引起的高度相关性, 本文选取70°N—70°S以内的格点构建网络. 沿纬向29个格点, 沿经向72个格点, 总共2088个格点作为网络的节点. 为消除季节变化趋势, 对格点的温度序列作距平值处理(原始值减去每个月的气候平均值). 为研究冷暖ENSO事件的网络结构特征的差异性, 对于Ni?o3.4指数距平的3个月滑动平均值, 将连续5个月
2
2.2.全球ENSO气温关联网络的构建
图1给出了El Ni?o事件和La Ni?a事件中全球所有格点间气温序列的皮尔逊相关系数概率分布图. 可以看出, El Ni?o事件对应的节点间的相关系数在0值附近的峰值要高于La Ni?a的情况. 此外, 对格点的气温序列作随机化处理[20], 即将每一对节点中1个节点的时间序列的顺序打乱重排后, 计算两个节点的时间序列相关联的相关系数, 随机化处理可以破环原来时间序列的周期性和趋势特征等, 同时显著减弱两个序列之间的相关性. 结果发现, 经随机化处理的El Ni?o和La Ni?a序列的相关系数具有明显的正态分布特征, 其概率分布在0值附近的峰值明显增大, 且El Ni?o和La Ni?a两种情况的相关系数概率分布曲线近乎重合. 由此说明, 全球气温节点间存在具有物理意义的相关性特征, 且这种相关强度在La Ni?a年份要强于El Ni?o年份, 而气温序列的随机化处理则会严重破坏此类特征.
图 1 不同ENSO相位下格点气温序列相关系数概率分布, 其中shuffled表示对格点气温序列作了随机化处理Figure1. Probability distribution of correlation coefficient of grid temperature series under different ENSO phases, where shuffle represents randomization of grid temperature.
为了较好地定义网络中节点对之间的连边, 计算了所有可能节点对的时间序列之间的皮尔逊相关系数. 这里设定一个阈值Q, 只有当节点间的相关系数绝对值|
对于复杂网络而言, 通常是借助网络结构特征量进行分析研究. 本文从系统内部关联作用的强弱、不同尺度下连边数目的多少、格点要素变化的区域同步性特征和信息的传递效率4个方面定义结构特征量, 定量描述系统的关联结构复杂性.
1)连通度, 又称区域权重连通度. 本文将节点间的连接强度按照节点密度的大小乘以一定的系数, 消除了纬度差异带来的节点分布不均匀的问题. 如果节点i与位于
2)连通距离, 又称链路距离. 若两个格点之间有连边, 则它们间的地表实际距离即为连通距离, 公式如下[32]:
式中la代表纬度, lo代表经度, R是地球半径为6371 km. 连通距离用来统计网络连边距离数量分布的变化, 连通距离值大, 代表节点间存在越远距离的遥相关作用.
3)集聚系数. 在节点i相连的
4)特征路径长度. 在关联网络中, 节点i与相互连接的节点j所要经过的最少连边数为最短路径长度
3.1.全球网络特征
图2给出了ENSO气温网络结构特征量的空间分布图. 如图2(a)中连通度的空间分布所示, El Ni?o和La Ni?a气温关联网络都是具有超级节点的网络, 但El Ni?o网络连通度的值是明显小于La Ni?a的. 全球连通度高的区域主要集中在热带的赤道大西洋、赤道印度洋、西太平洋和中东太平洋4个部分, 在温带地区也存在少量超级节点, 而且连通度在南北半球并不是对称分布. 图2(b)和图2(c)给出了集聚系数和最短路径长度的空间分布, 可以看出它们与连通度的分布也有一定的对应关系, 这表明三者在反映网络的体系结构时具有很好的一致性, 而且在热带地区气温链接保存得更加完好.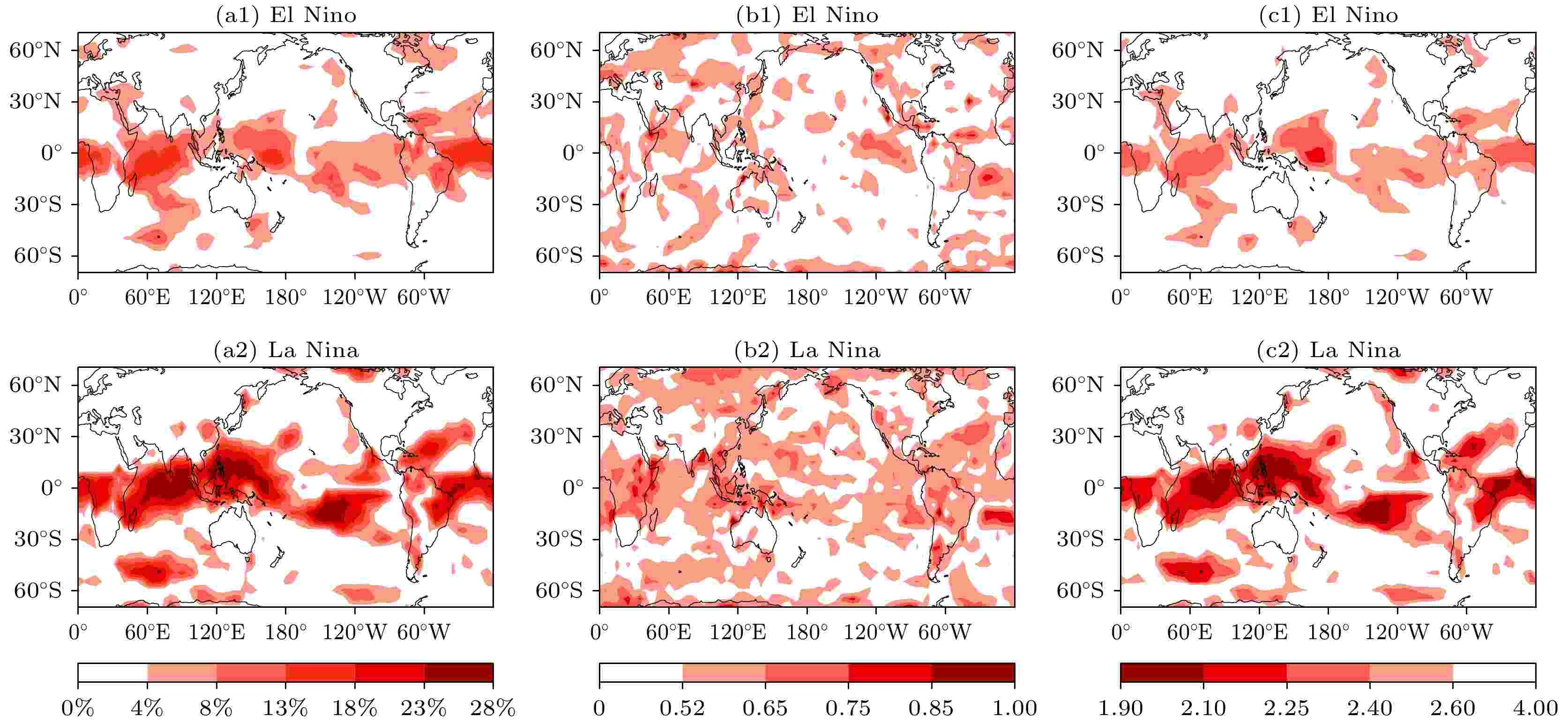
图 2 网络特征量空间分布 (a1), (a2)连通度; (b1), (b2)集聚系数; (c1), (c2)特征路径长度Figure2. Spatial distribution of network characteristic quantity: (a1), (a2) Connectivity degree; (b1), (b2) agglomeration coefficient; (c1), (c2) characteristic path length.
为了区分温带与热带的网络结构特征差异性, 以南北纬30°为界, 划分为北温带、热带和南温带3个区域分别计算网络结构特征, 并给出概率分布, 此处差异率定义为
| ${ \widetilde {C}_{\mathrm{E}\mathrm{l}\;\mathrm{N}\mathrm{i}{\tilde {\rm{n} } }\mathrm{o} } }$ | ${\widetilde {C}_{\mathrm{L}\mathrm{a}\;\mathrm{N}\mathrm{i}{\tilde {\rm{n} } }\mathrm{a} } }$ | 差异率D | |
| 全球 | 0.035 | 0.055 | 55% |
| 北温带 | 0.024 | 0.025 | 2% |
| 热带 | 0.057 | 0.097 | 72% |
| 南温带 | 0.020 | 0.033 | 63% |
表1连通度平均值与差异率
Table1.Average connectivity and difference rate.
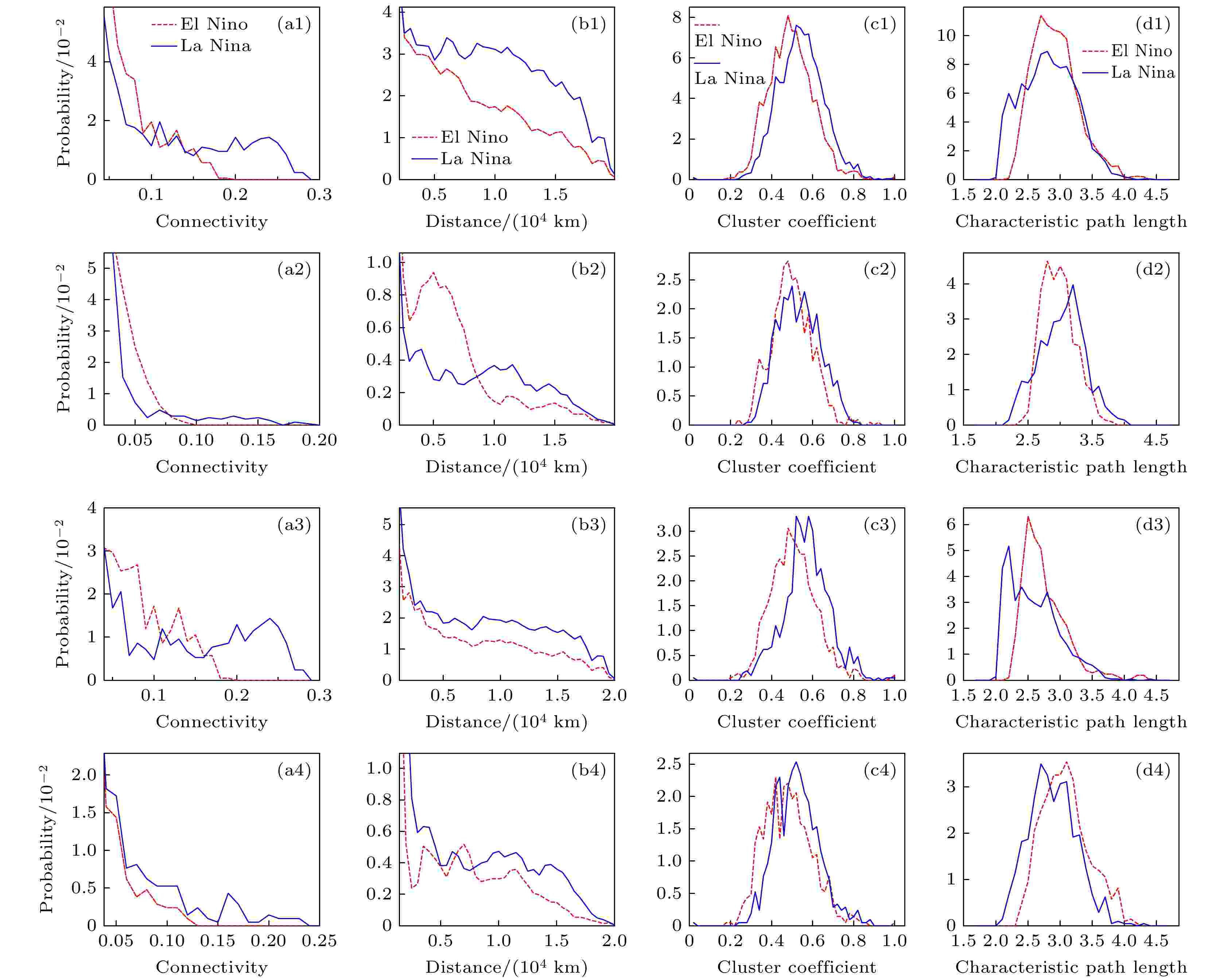图 3 不同区域网路特征量的概率分布 (a1)?(a4)连通度; (b1)?(b4)连通距离; (c1)?(c4)集聚系数; (d1)?(d4)最短路径长度. 由上到下4行依次对应全球网络、北温带网络、热带网络和南温带网络Figure3. Probability distribution of (a1)?(a4) connectivity degree, (b1)?(b4) connectivity distance, (c1)?(c4) agglomeration coefficient, and (d1)?(d4) shortest path length of different regional network characteristic quantities. From top to bottom, four rows correspond to the global network, the northern temperate network, the tropical network, and the southern temperate network.
2
3.2.关键区影响性分析
从图2可以看出, 气温网络中热带海洋区域对连通性具有重要的影响, 因此, 考虑了各大洋关键区对全球气温网络的影响. 为了避免区域范围不同可能导致的不平衡性, 尽量保持各个关键区面积相等(表2). 确定区域后, 分别计算了区域内节点与全球其他区域节点气温序列的相关, 以此来分析不同关键区域对全球气温关联网络(大洋关键区-全球气温关联网络)的作用.| 纬度 | 经度 | |
| 赤道大西洋 | 5°N—10°S | 40°W—10°E |
| 赤道印度洋 | 10°N—5°S | 60°E—100°E |
| 赤道西太平洋 | 20°N—5°N | 110°E—150°E |
| 赤道东太平洋 | 5°N—5°S | 170°W—120°W |
表2各大洋关键区的划分范围
Table2.Range of key regions in the oceans.
大洋关键区-全球气温关联网络的连通度空间分布如图4所示. 可以看出, 大洋关键区-全球气温关联网络中连通度表现出与全球网络类似的特征. 除了大西洋关键区中两者网络差别较小外, 赤道印度洋、赤道西太平洋和赤道东太平洋关键区与全球气温网络的连通度都表现出El Ni?o事件远低于La Ni?a事件的特征. 通过对连通度和连通距离概率分布(图5)的分析可以看到, La Ni?a网络比El Ni?o网络拥有更高的连通度分布和更多数量的链接, 这使得前者具有更高的信息传递能力, 且稳定性更高. 此外, 由图4可以看出, 在不同相位的ENSO事件中, 赤道印度洋、赤道大西洋以及赤道东太平洋关键区之间的连通度分布始终存在, 表明这几块区域间气温的关联性较强, 这可能与热带地区存在的Hadley等纬向环流有关, 即赤道区域的海温变化可以加强或者减弱纬向环流, 并通过它影响到大气内部作用, 传递给其他遥相关区域.
图 4 大洋关键区-全球气温关联网络连通度的空间分布图 (a1), (a2)大西洋关键区与全球相关; (b1), (b2)印度洋关键区与全球相关; (c1), (c2)赤道西太平洋关键区与全球相关; (d1), (d2)赤道东太平洋关键区与全球相关Figure4. Spatial distribution of the connectivity between key regions of the ocean and global temperature network: (a1), (a2) Atlantic Ocean key region relevant to global; (b1), (b2) Indian Ocean key region relevant to global; (c1), (c2) equatorial western Pacific key region relevant to global; (d1), (d2) equatorial eastern Pacific key region relevant to global.
图 5 大洋关键区-全球气温关联网络连通性的概率分布图 (a1)?(a4)连通度; (b1)?(b4)链路距离. 其中(a1), (a2)为大西洋关键区与全球相关, (b1), (b2)为印度洋关键区与全球相关, (c1), (c2)为赤道西太平洋关键区与全球相关, (d1), (d2)为赤道东太平洋关键区与全球相关Figure5. Probability distribution of the connectivity between key regions of ocean and global temperature correlation network: (a1)?(a4) Connectivity degree; (b1)?(b4) link distance. Panels (a1), (a2) correspond to the key region of the Atlantic Ocean relevant to global, panels (b1), (b2) correspond to the key region of the Indian Ocean relevant to global, panels (c1), (c2) correspond to the key region of the equatorial western Pacific relevant to global, panels (d1), (d2) correspond to the key region of the equatorial eastern Pacific relevant to global.
4.1.El Ni?o和La Ni?a年大洋关键区海气要素异常特征
为了进一步分析ENSO不同相位时全球气温关联网络结构特征差异的成因, 本节分别给出了El Ni?o和La Ni?a年份对应的全球海温距平和长波辐射的合成图(图6). 可以看出, 海温和净长波辐射空间分布的特征是一致的, El Ni?o事件对应赤道东太平洋、赤道印度洋和赤道大西洋的海温异常偏高, 这些区域的海洋向大气释放热量, 长波辐射转为负值, 海气热交换较强, 并通过Walker环流和Hadley环流等影响全球其他区域的气温. 赤道西太平洋由于受赤道Walker环流的影响, El Ni?o事件主要呈现海温偏低, 对外长波辐射偏弱, 海气作用较弱的特征. La Ni?a年则表现出与El Ni?o年基本相反的特征. 图7给出了4个大洋关键区域的海温距平和长波辐射距平、垂直速度距平的概率分布图. 可以看出, 海温距平中赤道东太平洋、赤道印度洋和赤道大西洋3个关键海区海温距平的概率分布曲线在La Ni?a年较El Ni?o年的情况均明显向左偏移, 而赤道西太平洋则向右偏移, 这与图6中海温距平分布基本一致. 在长波辐射和垂直速度距平的概率分布中赤道东太平洋和赤道印度洋在La Ni?a年向右偏移的特征较为明显, 而赤道大西洋虽然海温偏低, 但长波辐射向右偏移不明显, 垂直速度场出现了向左偏移的特征. 此外, 赤道西太平洋则表现出与赤道中东太平洋相反的特征. 所以我们推测, 正是由于ENSO现象中某些区域海温的变化使得全球气温出现波动, 导致气温网络连通性发生改变.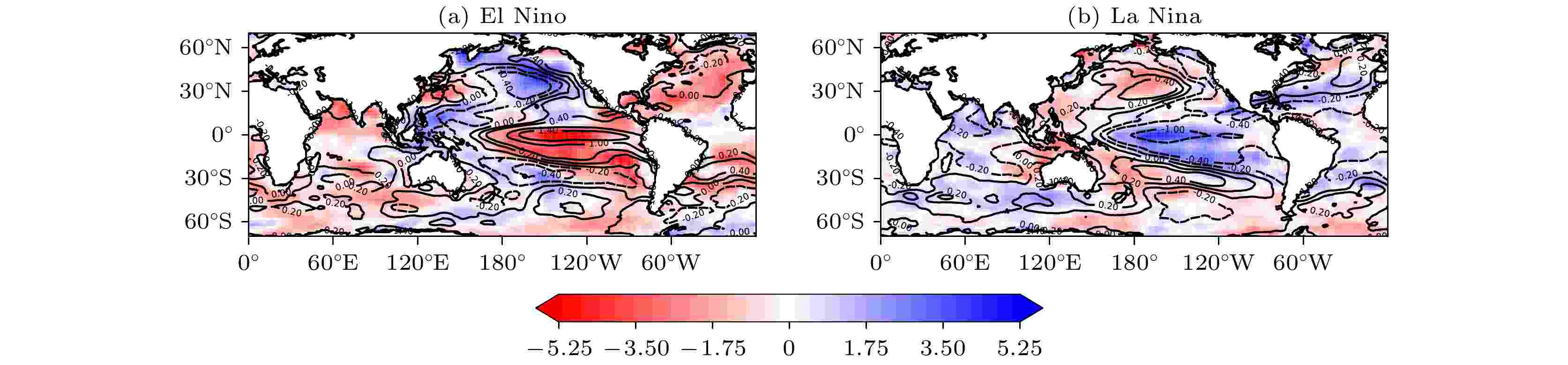
图 6 El Ni?o和La Ni?a事件对应的海温距平(等值线, 单位: ℃)和净长波辐射距平(填色部分, 单位: 
Figure6. Spatial distribution diagram of SST anomaly (isolines, unit: ℃) and net long-wave radiation anomaly (color filling, unit:
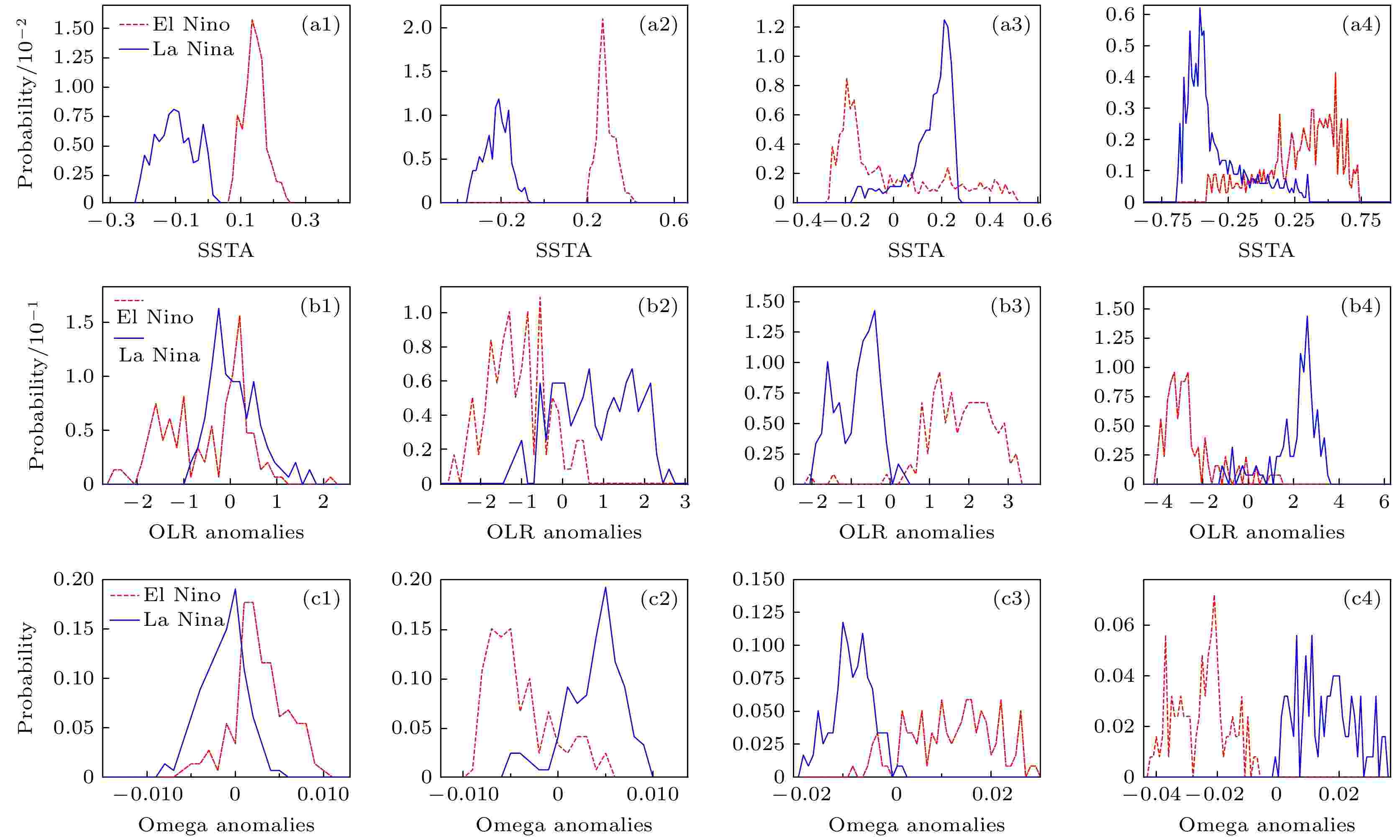图 7 各关键区海温距平((a1)?(a4))、长波辐射距平((b1)?(b4))和垂直速度距平((c1)?(c4))的概率分布? (a1)?(c1)赤道大西洋; (a2)?(c2)赤道印度洋; (a3)?(c3)赤道西太平洋; (a4)?(c4)赤道东太平洋Figure7. Probability distribution of SST anomaly ((a1)?(a4)), long-wave radiation anomaly ((b1)?(b4)) and vertical velocity anomaly ((c1)?(c4)) in each key area: (a1)?(c1) Equatorial Atlantic Ocean; (a2)?(c2) equatorial Indian Ocean; (a3)?(c3) equatorial western Pacific; (a4)?(c4) equatorial eastern Pacific.
2
4.2.海温对全球气温网络结构的影响
Ni?o3.4指数是判别ENSO事件的常用指标, 故本节探究Ni?o3.4指数区域海温变化对全球气温网络结构的影响. 分析区域海温升高对气温网络结构特征量、净长波辐射和垂直速度场的改变, 具体做法如下: 1)选取Ni?o 3.4指数, 计算1950—2020年的每年11月到次年3月的平均海温并排序, 得到海温升序序列; 2)取窗口宽度为30 a, 滑动步长为1 a, 计算每一个窗口的平均海温(图8); 3) 构建各窗口所对应的30 a气温关联网络, 计算网络结构特征量.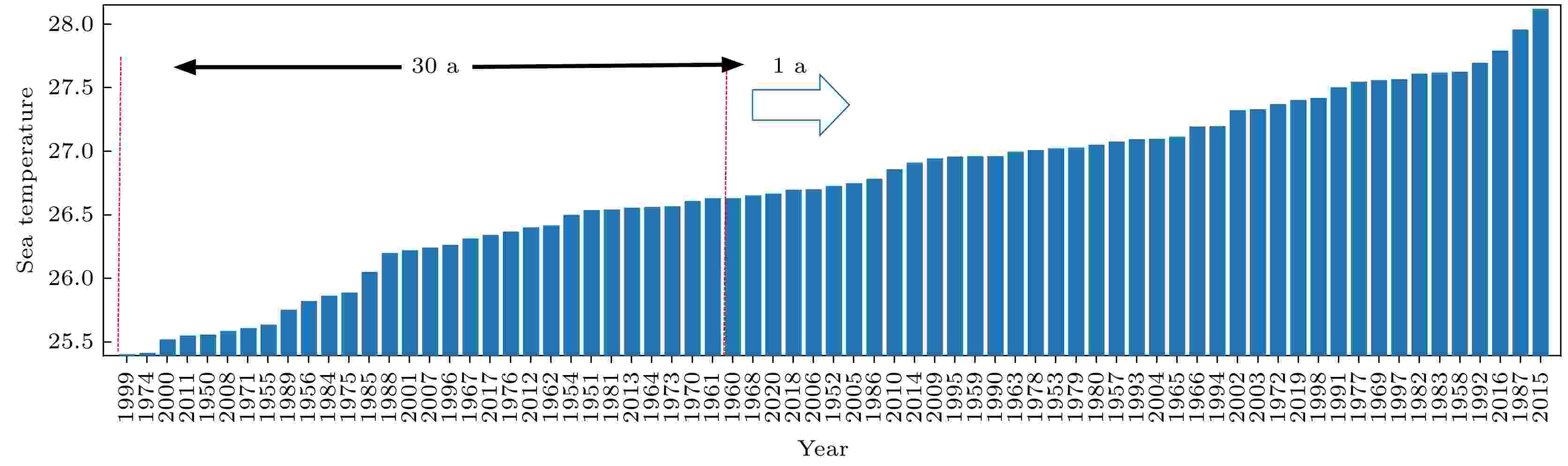
图 8 排序后Ni?o 3.4区域冬半年的海温均值序列, 虚线内窗口宽度30 a, 滑动步长为1 aFigure8. Sequence of mean SST of winter half year in Ni?o 3.4 region after sorting. The window width in the dashed line is 30 a, and the sliding step length is 1 a.
图9给出了全球气温网络结构特征量与Ni?o 3.4区域海温之间的对应关系. 可以看出, 随着Ni?o 3.4区域海温的升高, 全球气温网络连通性呈现波动下降的趋势, 连通距离也具有类似的特征, 而特征路径长度则表现出相反的变化特征, 即全球温度网络的连通性与Ni?o 3.4区域的海温之间存在反向变化的关系.
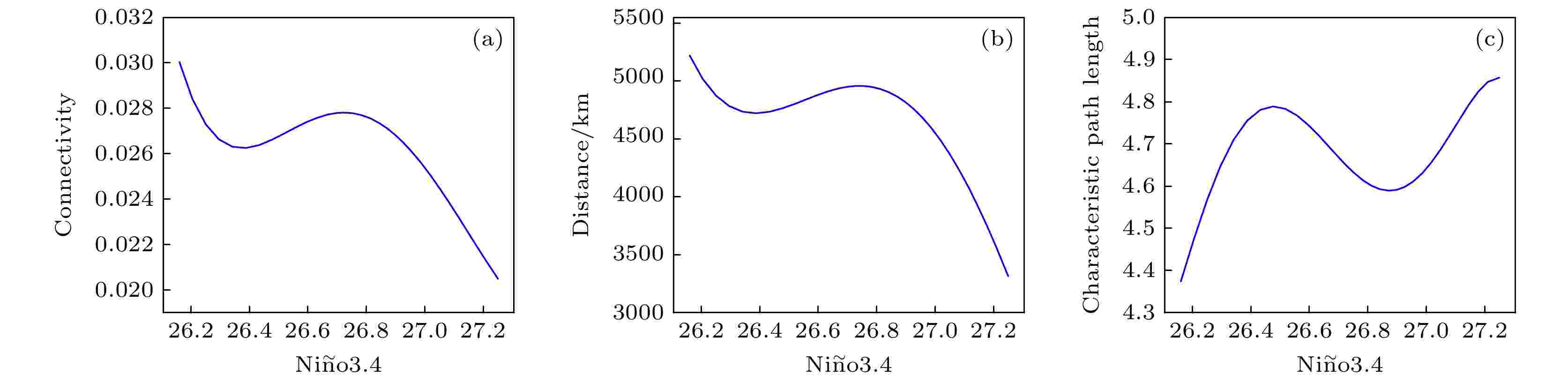图 9 全球气温关联网络结构特征量平均值随Ni?o3.4区域海温升高变化特征 (a) 连通度; (b) 连通距离; (c)特征路径长度Figure9. Variation characteristics of the mean value of structural characteristics of global temperature correlation network with the rise of SST in Ni?o3.4 region: (a) Connectivity degree; (b) connectivity distance; (c) characteristic path length.
此外, 从图10可以看出, 随着Ni?o 3.4区域海温的升高, 赤道东太平洋区域的长波辐射、垂直速度均呈现线性减少的趋势, 由正距平转为负距平, 表明海洋与大气之间的热力交换和动力作用由正作用转为负作用; 赤道西太平洋区域则与之相反, 由负距平转为正距平, 即海洋与大气之间的热力交换和动力作用由负作用转为正作用. 与赤道东、西太平洋这两个区域不同的是, 赤道印度洋和大西洋区域的变化幅度较小. 因此可以说, 相较于印度洋和大西洋, 赤道东、西太平洋区域的海气热对流作用十分强烈, 这在一定程度上会加剧网络的不稳定性, 进而造成网络连通性的降低.
图 10 大洋关键区域长波辐射、垂直速度场随Ni?o3.4指数升高的变化特征Figure10. Variation characteristics of long wave radiation and vertical velocity fields in key regions of the ocean with Ni?o3.4 index increasing.
为了进一步分析海温变化影响气温网络连通性的变化机理, 计算了不同纬度区域平均的格点气温方差变化, 结果如图11所示. 可以看出, 北温带区域气温变化的方差随着Ni?o 3.4区域海温的升高呈上升的趋势, 南温带区域也有类似的特征. 因此, Ni?o 3.4区域海温的升高会加剧东西太平洋海温梯度的明显变化, 加强东西太平洋关键区的海气相互作用, 造成低纬度与中高纬度之间气温变化的一致性减弱, 相互作用增强, 南北温带区域气温波动加大, 导致气温网络大量链路的断裂, 网络连通性明显下降, 故而造成El Ni?o全球气温关联网络的连通性明显低于La Ni?a的情况. Tsonis和Swanson[18]的研究也表示, 正是因为El Ni?o年中月平均气温变化的方差要比La Ni?a年大出20%, 快速而剧烈的气温涨落破坏了网络中格点之间稳定的链接, 才会导致前者网络的可预测性下降.
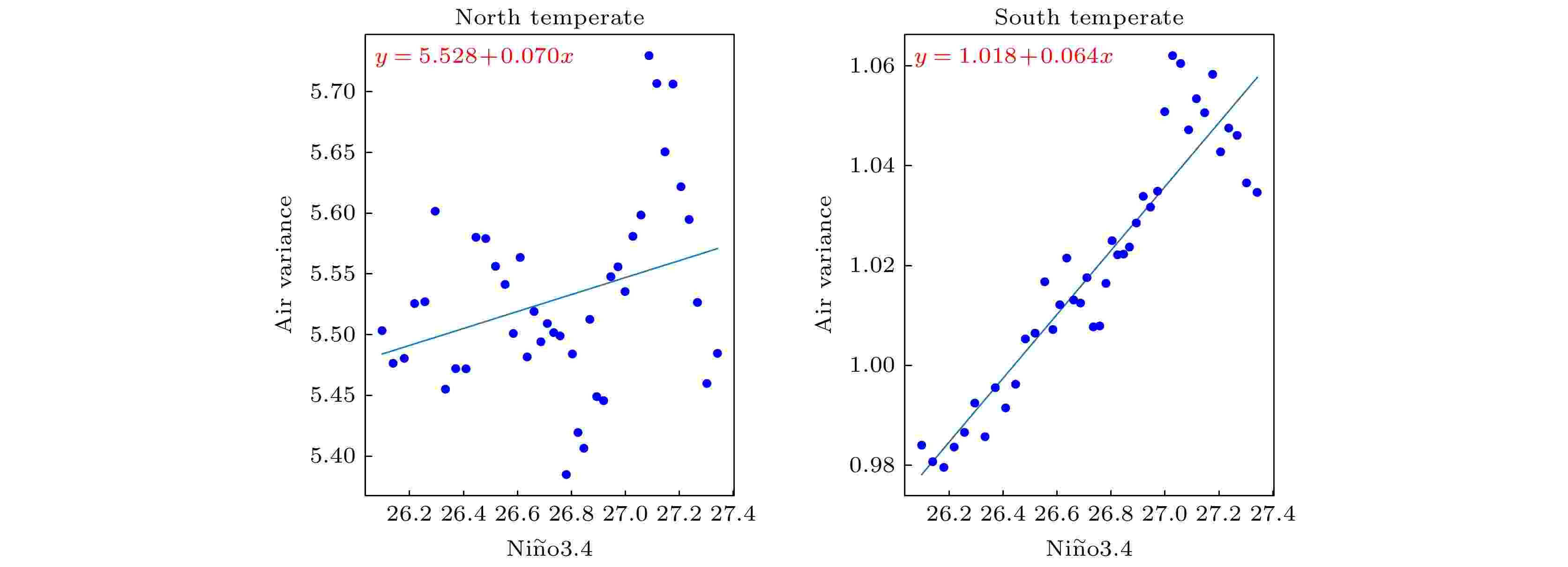图 11 南温带(30°S?65°S)和北温带(30°N?65°N)平均气温方差随Ni?o3.4区域海温升高的变化图Figure11. Variance of mean temperature in the south and north temperate regions (30°S?65°S, 30°N?65°N) with the increase of SST in Ni?o3.4.
1)与La Ni?a网络相比, El Ni?o网络中格点温度序列间的相关性减弱, 气温网络的连通度显著偏低, 连通性下降, 网络信息传递效率减弱, 这种特征在热带和南温带区域尤为显著.
2)大洋关键区-全球气温关联网络的特征量差异表明, 赤道东太平洋、赤道西太平洋、赤道印度洋和赤道大西洋区域对全球ENSO气温关联网络连通度影响相对较大, 在El Ni?o网络中的减少异常明显, 是导致两类网络结构特征差异性的4块关键区域. 其中差异性最为显著的是赤道东太平洋区域, 正好对应于ENSO现象发生的区域.
3)对Ni?o 3.4区域的海温采用窗口为30 a, 步长为1 a的滑动平均值升序处理, 构建对应的30 a气温关联网络并计算结构特征量, 发现随着Ni?o3.4区域的海温升高, 赤道东、西太平洋关键区域的海洋-大气热力和动力作用明显增强, 对外长波辐射加强, 对流活动增加, 低纬度与中纬度区域的相互作用增强, 导致南北温带气温变化的方差加大, 造成4大关键区格点气温序列与全球其他地区的相关性减弱, 全球温度关联网络连通性下降.
温度关联网络不仅可以帮助我们理解不同区域之间内在的联系, 也可以作为评估ENSO影响性的指标. 本研究表明, 一些除了气温之外的动力学因素也是导致ENSO不同相位下网络结构特征差异的可能原因, 为此有必要在未来进一步考虑不同气象要素构建的气候网络, 分析其中的结构特征将进一步明确ENSO影响性的物理机理.
