删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Nb<sup>5+</sup>掺杂钛酸锶结构与性能的第一性原理研究

本站小编 Free考研考试/2021-12-29
摘要:本文选取SrTiO3材料进行B位Nb5+离子掺杂改性, 采用第一性原理计算了不同含量(0%, 12.5%和25%)Nb5+掺杂SrTiO3的电子结构、光学、力学和热学性质. 结果表明, 当Nb5+掺杂浓度上升, 材料晶胞参数增大; Nb5+掺杂后SrTiO3由间接带隙化合物转变为直接带隙化合物, Nb5+掺杂使材料反射系数、吸收系数、能量损耗下降、脆性降低, 当Nb5+掺杂浓度上升, 材料体弹性模量不变, 剪切模量与杨氏模量减小, 泊松比增大, 德拜温度降低, 晶格热导率与理论最低晶格热导率减小.
关键词: Nb5+掺杂SrTiO3/
第一性原理/
光学性能/
热学性能

English Abstract


全文HTML

--> --> -->
1.引　言
钛酸锶(SrTiO3)是一种宽禁带氧化物(3.2 eV)[1], 其在室温下属于顺电体, 居里温度Tc = 106 K, 当温度低于居里温度时, SrTiO3由立方相转为四方相[2]. SrTiO3具有高介电常数、低介电损耗和卓越的热稳定性, 使其在光催化[3]、可逆电阻开关[4]、高温固体氧化物燃料电池材料[5]、氧化物电子器件、传感器[6]、电容器[7]、压敏电阻[8]和氢燃料制备[9]等方面具有广泛的应用. 例如SrTiO3单晶介电性能优异, 室温下介电常数约为300, 在射频应用中前景较好. SrTiO3单晶由于具有与超导材料相近的点阵常数, 可用于超导薄膜的基底, 其折射率较高(2.4), 可广泛用于如镜头等光学器件[10]. 外延SrTiO3薄膜介电常数高、介电常数可调性较好, 可应用于制造微波可调器件[11].
本征SrTiO3属于绝缘体, 在经过掺杂改性后SrTiO3可转变为半导体, 成为性能优异的电子功能陶瓷材料. 因此, 研究者尝试给SrTiO3材料进行掺杂改性, 最常见的方法是A位或B位的阳离子替代[12], 如使用La3+、Nb5+对SrTiO3进行掺杂. 当Sr2+或Ti4+离子部分被La3+或Nb5+离子取代时, 可提高电导率. 其中, 由于Nb5+与Ti4+半径相近, 因此可进行掺杂, 而不影响立方晶系钙钛矿结构稳定性. 由于Nb5+化合价高于Ti4+, 在掺杂时将向体系中引入电子, 因此 SrTiO3经Nb5+施主掺杂后可由绝缘体转变为n型半导体. Nb5+掺杂SrTiO3不仅可作为电子器件的电极, 而且可用于生产新型半导体器件如高温超导薄膜的基片材料和p-n结等器件[13]. Tomio等[14]利用脉冲激光沉积技术制备出Nb5+掺杂的SrTiO3薄膜, 通过改变Nb5+掺杂含量来调控材料的电导率. Bakhshi[15]使用溶胶凝胶法结合放电等离子体烧结制备出Nb5+掺杂SrTiO3/TiO2纳米复合材料, 降低了热导率.
除了实验研究工作外, 众多****也对SrTiO3材料进行了理论计算研究, 特别是使用第一性原理计算了本征及掺杂SrTiO3材料的电子结构和物理性质[16-22]. 例如Benrekia等[16]计算了本征SrTiO3的电子结构, 结果表明带隙为1.76 eV, 本征SrTiO3为间接带隙化合物. Ghebouli等[17]计算了钙钛矿SrTiO3的电子结构、弹性性质和光学性质, 结果表明SrTiO3的杨氏模量E为271.8 GPa、泊松比为0.236, 同时发现随着压力的增大, SrTiO3的介电常数实、虚部和折射率将减小. Yun[18]构建了2 × 2 × 2的SrTiO3超晶胞, 掺杂12.5%的La3+, Sb5+, Nb5+取代Sr2+和Ti4+, 结果表明Nb5+, La3+, Sb5+掺杂SrTiO3材料体系的可见光透过率均高于未掺杂SrTiO3. Guo等[19]利用第一性原理研究SrTi1–xNbxO3(x = 0.125, 0.25, 0.5)的电子结构, 分别建立了SrTi0.875Nb0.125O3(2 × 2 × 2超晶胞), SrTi0.75Nb0.25O3(1 × 2 × 2超晶胞)和SrTi0.5Nb0.5O3(1 × 2 × 2超晶胞), 结果表明随着Nb5+掺杂浓度上升, 晶格常数增大. Eglitis等[20]以及Nishiyama等[21]建立了包含40个原子的2 × 2 × 2的SrTi1–xNbxO3超晶胞, 计算了Nb5+掺杂SrTiO3的电荷密度图(001)平面, 以及Nb5+掺杂的SrTiO3的电子态和成键态, 结果表明Nb5+的4d轨道会削弱Ti4+离子和O2–离子之间的共价性, 掺入电子使远距离库仑力减小, 近距离弹性力增大, 从而使离子极化率降低.
从目前的文献报道来看, 研究人员大多构建包含40个原子的2 × 2 × 2的SrTiO3超晶胞, 令Nb5+离子取代每8个Ti4+离子中一个, 重点研究了掺杂对SrTiO3材料电子结构的影响, 而关于Nb5+掺杂对SrTiO3材料光学和热学性质的影响报道较少, 特别是Nb5+离子掺杂浓度为25%的SrTiO3材料结构与性能的第一性原理计算研究鲜有报道. 因此, 本文采用基于密度泛函理论的第一性原理平面波赝势方法研究了不同浓度Nb5+掺杂对SrTiO3的电子结构、光学、力学、热学性质的影响规律, 为获得具有良好性能的SrTiO3材料提供理论基础.
2.计算方法与模型
2
2.1.计算方法
-->

2.1.计算方法

本文的计算工作是采用Materials Studio 8.0 软件包中的CASTEP 模块完成的[23]. 计算基于密度泛函理论(DFT)的平面波超软赝势法, 采用广义梯度近似(GGA)下的PBE (Perdew-Burke-Ernzerhof)泛函来展开交换关联能[24]. 对于布里渊区k点的积分运算, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3三种超晶胞均取k值为5 × 5 × 5. 计算时Sr, Ti, O, Nb四种原子价电子构型分别取4s24p65s2, 3s23p63d24s2, 2s22p4和4s24p64d45s1. 计算过程中能量收敛精度为1.0 × 10–5 eV/atom, 原子的最大位移为0.0001 nm, 截断能取380 eV, 晶体内应力收敛标准为0.05 GPa, 原子间的相互作用力收敛标准为0.3 eV/nm. 首先构建2 × 2 × 2的三种超晶胞, 其次对所构建的晶胞进行几何优化, 最后在几何优化后的晶胞基础上进行物理性质的计算.
2
2.2.结构模型
-->

2.2.结构模型

SrTiO3晶胞属于立方晶系, 晶体结构属于空间群Pm3m (O${}^1_{\rm{h}} $), 晶胞参数a = b = c = 0.3905 nm[14], Sr2+占据晶胞8个顶角A位的位置, Ti4+位于晶胞的体心B位的位置, 阴离子O2–位于面心, 配位数分别为12, 6, 6. CASTEP 模块一般用于计算周期性结构体系材料, 计算时, 软件将体系的周期性晶格简化为最小对称单元; 对于非周期性结构体系材料, 程序包会对其进行周期性化处理, 即使用超晶胞. SrTiO3属于立方晶系钙钛矿结构, 其晶胞结构具有周期性. 其最小对称单元为包含15个原子的 1 × 1 × 1模型. 但由于 1 × 1 × 1晶胞模型只含有一个Ti4+, 不适用于进行Nb5+掺杂研究. 若构建包含135个原子的3 × 3 × 3的SrTiO3超晶胞, 则计算量过大, 同时Nb5+掺杂的可能位置组合过多, 不同位置Nb5+取代对晶胞性能影响不同. 因此本文选取了包含40个原子的2 × 2 × 2超晶胞作为SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的计算模型: 其中SrTi0.875Nb0.125O3为一个Nb5+离子替换一个Ti4+离子; SrTi0.75Nb0.25O3为两个Nb5+离子按最邻近位置分别替换两个Ti4+离子. 三种超晶胞构型分别如图1(a)—1(c)所示.
图 1 晶胞结构　(a) SrTiO3; (b) SrTi0.875Nb0.125O3; (c) SrTi0.75Nb0.25O3
Figure1. Cell structure: (a) SrTiO3; (b) SrTi0.875Nb0.125O3; (c) SrTi0.75Nb0.25O3.

3.结果与讨论
2
3.1.电子结构
-->

3.1.电子结构

表1列出了弛豫后SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3三种超晶胞的晶胞参数, 并与实验数据[14]进行了对比. 可以看到所计算的SrTiO3晶胞参数为0.3939 nm, 比实验数据大0.87%(小于1%), 同时所计算的SrTi0.875Nb0.125O3和SrTi0.75Nb0.25O3晶胞参数与实验值[14]相符, 这表明所建立的晶体结构模型是合理的.
GGA(380 V)Experimental resultsError
(380 eV)/%
SrTiO30.39390.3905 (PDF 84-0444)0.87
SrTi0.875Nb0.125O30.39570.3950[14]0.18
SrTi0.75Nb0.25O30.39720.3980[14]–0.20


表1SrTi1–xNbxO3晶胞参数(a = b = c, 单位: nm)
Table1.Cell parameters of SrTi1–xNbxO3 (a = b = c, unit: nm).

由表1可以看到掺杂Nb5+后, SrTiO3的晶体结构并未发生明显变化, 仍然保持立方晶系. 随着Nb5+离子的掺入, 晶胞参数均有着不同程度的增大, 且随着掺入Nb5+离子浓度的增大, 晶胞参数进一步增大, 原因是Nb5+离子的半径(0.064 nm)大于原Ti4+离子(0.061 nm), 从而引起晶胞畸变而产生轻微的扩张. 当Nb5+离子掺入浓度增大时, 更多的Nb5+离子取代Ti4+离子, 从而导致晶胞参数进一步增大.
在几何优化后, 进行了能带结构的计算, 得到了本征SrTiO3能带结构如图2(a)所示. 由图可知SrTiO3的本征费米能级位于价带顶, 其能带价带顶在R点, 导带底在Γ点, 故可分析出钛酸锶是间接带隙化合物, 这与Benrekia等[16]所分析的一致. 计算得到的带隙是1.837 eV, 与文献[16, 22]报道的带隙一致. 然而SrTiO3带隙实验值为3.2 eV[25], 这是由于PBE泛函会显著低估带隙[16]. 尽管计算值与实验值有一定差距, 由于计算所选参数一致, 所得到的能带结构变化规律是可信的, 不会影响Nb5+掺杂SrTiO3电子结构的理论分析.
图 2 能带结构图　(a) SrTiO3; (b) SrTi0.875Nb0.125O3; (c) SrTi0.75Nb0.25O3
Figure2. Band structure: (a) SrTiO3; (b) SrTi0.875Nb0.125O3; (c) SrTi0.75Nb0.25O3.

采用第一性原理计算的SrTi0.875Nb0.125O3与SrTi0.75Nb0.25O3的能带结构图如图2(b)和2(c)所示. 本征SrTiO3的费米能级位于价带顶, 而随着Nb5+离子的掺入, 费米能级进入导带, 这主要是由于掺杂向体系中引入多余的电子填满价带, 电子转移进入导带. 随着Nb5+离子掺杂浓度的增大, 费米能级进一步深入导带, 表明Nb5+离子比Ti4+离子放出了更多的电子, 使体系载流子浓度升高, 且体系简并化. Nb5+掺杂改变了钛酸锶的导电性, 使材料从绝缘性向金属性转变, 显示出金属行为[18]. Nb5+掺杂令体系的价带顶位置改变, 由R点改为Γ点, 但导带底位置未发生变化, 始终都在Γ点. 因此, Nb5+掺杂使SrTiO3由间接带隙化合物转为直接带隙化合物, 且随着Nb5+离子掺杂浓度的增大, 带隙由1.924 eV增大为1.939 eV.
图3为SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的态密度(PDOS)图. 由图3(a)可见, 未掺杂钛酸锶主要由O 2p轨道构成价带顶, Ti 3d轨道构成导带底, 这说明共顶点连接的钛氧八面体决定了钛酸锶的电子结构. 由图3(b)、(c)可见, 掺杂钛酸锶主要由O2p轨道构成价带顶, Ti3d和Nb4d轨道构成导带底, Nb5+离子对导带的构成起到了很大的贡献, 引起材料能带结构的改变, 而Sr轨道能级对于价带顶、导带底贡献较少. 未掺杂钛酸锶的费米能级位于价带顶, 随着Nb5+离子的掺入, 态密度向能量较低方向移动, 费米能级的位置发生变动, 其进入导带, 且随着Nb5+离子掺入浓度的增大, 费米能级进入导带的位置越深, 费米能级处电子态密度值越大, 这与之前能带结构的分析一致.
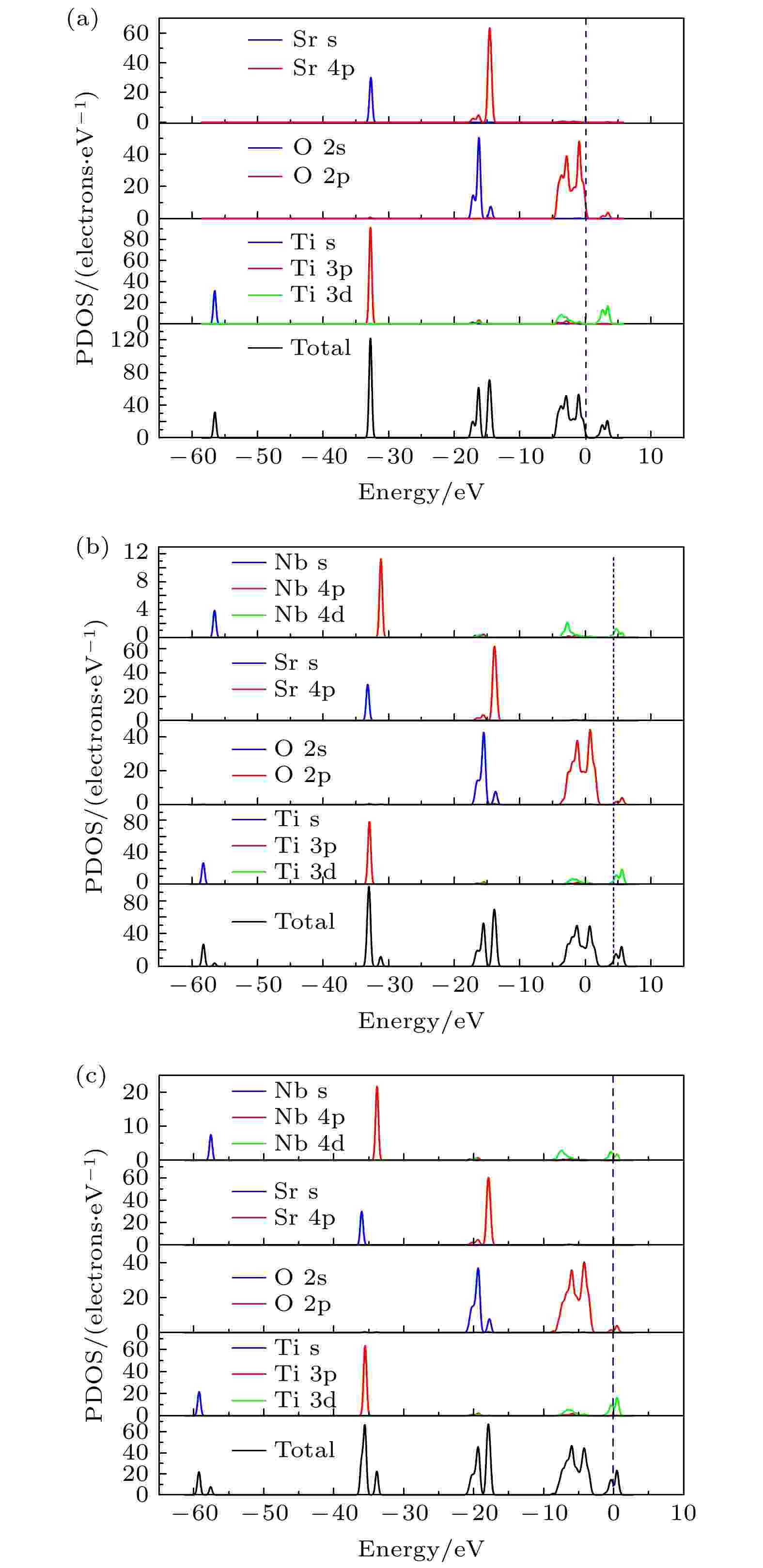图 3 态密度图　(a) SrTiO3; (b) SrTi0.875Nb0.125O3; (c) SrTi0.75Nb0.25O3
Figure3. Density of states: (a) SrTiO3; (b) SrTi0.875Nb0.125O3; (c) SrTi0.75Nb0.25O3.

导带底和价带顶的结构与晶体结构的对称性和价键特性密切相关, 结合能带结构图2及态密度图3可知, 当Nb5+掺杂后, 晶胞参数发生变化, 晶体结构的对称性受到影响. 当Nb5+离子替换Ti4+离子进入SrTiO3晶格后, 与周围邻近的O2–离子杂化成键, 发生的相互作用限制了部分s轨道的电子. Nb5+离子的电子占据d轨道, 引起了电子波函数交叠, 从而影响了费米能级附近的电子能带结构, 导致了价带顶部位较大程度的变化[26]. 由态密度图3(b)和3(c)可见, Nb-4d轨道占据态密度的价带顶及导带底, Nb-4d轨道态密度最高峰位于价带顶, 故Nb5+对价带顶电子结构影响较大, 而对导带底的电子结构影响较小. 因此, 由于杂质能级Nb-4d的出现, 价带顶的电子结构发生改变, 而导带底的位置变化不大, 电子跃迁由间接带隙变为直接带隙.
2
3.2.光学性质
-->

3.2.光学性质

当光在介质中传播时, 光子电场的扰动导致电子发生从被占态到未占态的光学跃迁. 在线性光学响应范围内, 物质的光学特性可以通过复介电常数ε(ω)来描述, 该函数表示系统对具有小波矢的外部电磁场的线性响应:
$ \varepsilon \left( \omega \right) = \varepsilon_1\left( \omega \right) + {\rm{i}}\varepsilon_2\left( \omega \right). $
介电常数在宏观上揭示了与固体光学性质有关的常数, 介电常数虚部ε2(ω)是由布里渊区从被占态到未占态的所有可能的直接跃迁之和计算得到[27]:

$ \varepsilon_{\rm{2}}\left( \omega \right) = \frac{{\rm{π}}}{{\varepsilon 0}}\left( {\frac{{\rm{e}}}{{m\omega }}} \right)\sum\limits_{{\rm{V,C}}}^{} {\left\{ {\int\nolimits_{{\rm{BZ}}}^{} {\frac{{2{\rm{d}}K}}{{{{\left( {2{\rm{π}}} \right)}^2}}}{{\left| {\alpha M_{\rm{V,C}}} \right|}^2}\delta \left[ {E_{\rm{C}}\left( K \right)} \right] - \left[ {E_{\rm{V}}\left( K \right) - h\omega } \right]} } \right\}} . $
介电常数实部ε1(ω)则可以利用Kramers-Kronig色散关系通过ε2(ω)求出:
$ \varepsilon_1\left( \omega \right) = 1 + \frac{{2{\rm{e}}}}{{\varepsilon_0{m^2}}}\sum\limits_{{\rm{V,C}}}^{} {\int\nolimits_{BZ}^{} {\frac{{2{\rm{d}}K}}{{{{\left( {2{\rm{π}}} \right)}^2}}}\frac{{{{\left| {\alpha M_{\rm{V,C}}\left( K \right)} \right|}^2}}}{{\left[ {E_{\rm{C}}\left( K \right) - E_{\rm{V}}\left( K \right)} \right]/h}}\frac{1}{{[{{E_{\rm{C}}\left( K \right) - E_{\rm{V}}\left( K \right)}}]/{{{h^2}}} - {\omega ^2}}}} } . $

其中C和V分别表示价带和导带, BZ是第一布里渊区, K为电子波矢量, α是矢量势A的单位方向矢量, EC(K)和EV(K)分别是导带和价带的本征能级, ω表示入射光的频率. 当光发射向一种材料时, 光子能量会以以下方式慢慢消失: 一部分会被物质吸收, 第二部分将反射回空间, 第三部分将被折射, 最后一部分是物质内的缓慢能量损失. 因此, 本文由介电常数实部ε1(ω)与虚部ε2(ω)参数推导计算了SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的折射系数n(ω)、消光系数k(ω)、吸收系数I(ω)、反射系数R(ω)和能量损失谱L(ω)[27]. 由于计算的带隙值低于实验值, 为了使光学性质计算符合实验值, 添加了剪刀算符(1.36 eV)以修正光学性质的计算结果.
SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的介电常数实部与虚部曲线如图4(a)所示, 其介电常数实部、虚部在0—8 eV范围内有明显的差异, 在高于8 eV范围内则较为相似. SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的介电常数实部分别在5.35 eV, 5.70 eV和5.85 eV取得负值, 其静态介电常数分别为2.53, 2.15和2.12, 介电常数虚部分别在5.07 eV, 5.29 eV和5.42 eV取得最大值, 其值分别为5.45, 4.85和4.69. 介电常数虚部与光的吸收有关, 其在5—6 eV的峰高而尖锐, 这主要是由O2p轨道与Ti3d轨道电子跃迁引起的.
图 4 SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的光学性质　(a) 介电常数实部与虚部; (b)折射系数与消光系数
Figure4. Optical properties of SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3: (a) Real and imaginary part of the dielectric function; (b) refraction coefficient and extinction coefficient.

SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的折射系数n(ω)与消光系数k(ω)如图4(b)所示. 由于折射系数和消光系数可近似于介电常数实部和虚部的平方根[27], 可以看到其变化趋势基本一致. 在4—5 eV范围内, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3均具有较高折射系数. 当光子能量为0 eV时, 其静态折射率分别等于1.58, 1.47, 1.46. 在5—6 eV范围内, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3均具有较高消光系数, 并分别在5.51 eV, 5.76 eV和5.92 eV取得最大值, 其值分别为1.60, 1.45和1.42. 研究表明, Nb5+掺杂使材料消光系数降低, 并使其整体向高能区移动.
SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的吸收系数如图5(a)所示. 在4—9 eV范围内, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3均具有较高吸收系数, 其吸收系数分别在5.76 eV, 5.97 eV, 6.26 eV取得最大值, 其值分别为145393.4 cm–1, 137189.7 cm–1, 139038.5 cm–1. 掺杂使材料吸收系数下降, 但当掺杂浓度上升时, 吸收系数反而增大. 吸收主要集中在低能区, 在高能区(> 10 eV)范围吸收较少.
图 5 SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的吸收系数与 (a)能量和 (b)波长的关系图
Figure5. Relationship between absorption coefficients of SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3 and (a) energy; (b) wavelength.

为了更清楚地讨论吸收系数与波长的关系, 绘制了吸收系数随波长的变化曲线如图5(b)所示. 波长为390—760 nm时对应可见光, 其能量范围是1.64—3.19 eV. 可以看到, 未掺杂SrTiO3与掺杂SrTiO3均在可见光范围内有着较低吸收, 而在紫外光区有着较高吸收, 吸收系数数量级达105 cm–1. 材料的吸收边与带隙相关, 实验测得钛酸锶吸收边为380 nm[28], 与本文计算结果一致, 其所关联带隙为3.2 eV. 由于掺杂使材料带隙增大, 故导致材料吸收边向高能区移动, 随着掺杂浓度增大, 吸收边深入高能区, 吸收边蓝移, 主要是由于Nb5+掺杂向体系引入了更多的电子(载流子), 使费米能级进入导带, 费米能级下的价带全部被电子占据, 电子需要更高的能量进行跃迁. 而掺杂后体系吸收系数减小, 主要是由于杂质离子在导带底占据较小的态密度值, 从而导致电子跃迁到导带的概率降低[18].
当介电常数实部ε1(ω) < 0时, 光不能透过固体传播, 与此同时n(ω) < k(ω), 表明此时材料体系具有较高的反射系数[27]. SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的反射系数如图6(a)所示. 在5—9 eV范围内, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3均具有较高反射系数, 其反射系数分别在8.198 eV, 8.069 eV, 8.197 eV取得最大值, 其值分别为0.69, 0.56, 0.56. 掺杂使材料反射系数下降, 当掺杂浓度上升, 反射系数峰向高能区移动. 未掺杂钛酸锶反射跨度明显大于掺杂钛酸锶的反射跨度.
图 6 SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的光学性质　(a)反射系数; (b)能量损失谱
Figure6. Optical properties of SrTiO3, SrTi0.875Nb0.125O3 and SrTi0.75Nb0.25O3 (a) Reflection coefficient; (b) energy loss spectrum.

能量损失函数表示光子通过均匀介质时光子能量的损失, 其特征峰与等离子体震荡有关[29]. SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的能量损失谱如图6(b)所示. 在8—9 eV范围内, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3具有较高能量损失, 其能量损耗分别在8.45 eV, 8.41 eV, 8.54 eV取得最大值, 其值分别为23.86, 12.96, 12.82, 此时介电常数实部ε1(ω) = 0, 吸收系数与反射系数急剧下降. 当光子能量大于10 eV时, 未掺杂SrTiO3与掺杂SrTiO3能量损失基本为0, 这与消光系数k(ω)为0相对应. 掺杂使材料能量损耗降低, 当掺杂浓度上升, 能量损耗峰向高能区移动.
随着Nb5+掺杂浓度提高, 材料体系吸收边蓝移, 在可见光区1.64—3.19 eV材料体系具有较低的吸收系数、反射系数、能量损耗, 这表明Nb5+掺杂钛酸锶材料体系是潜在的可见光区透明材料. Yun[18]计算发现, Nb, La, Sb掺杂SrTiO3材料体系可见光透过率均高于未掺杂SrTiO3; Kumar[30]使用脉冲激光沉积技术在SrTiO3(100)衬底上制备了透过率高达91%的Nb5+掺杂的SrTiO3薄膜. 本文计算结果与上述文献报道结果一致, 表明Nb5+掺杂有利于提高SrTiO3材料透过率. 同时由于Nb5+掺杂为n型掺杂, 掺杂使体系电子浓度增加, 使电导率提高[14], 故Nb5+掺杂钛酸锶材料在可见光范围内透明导电, 有望用于制备透明导电氧化物薄膜.
2
3.3.力学性质
-->

3.3.力学性质

研究材料的力学性质, 如弹性常数、杨氏模量、泊松比和压缩性等, 对材料的工业应用具有重要意义. 弹性性质与晶体的许多固态性质有关, 如熔点、比热容和德拜温度等, 可以提供有关晶体各向异性和晶体结构稳定性的重要信息[31]. 弹性常数的数目与结构的对称性有关, SrTiO3晶胞属于立方晶系, 因此有3个独立的弹性刚度张量(Cij), 分别为C11, C12, C44. 立方晶系的晶体稳定标准为
$ \left\{ \begin{aligned}&C_{11} + 2C_{12} > 0, ~~ C_{11} - C_{12} > 0 \\&C_{11} > 0, ~~ C_{44} > 0 \end{aligned} \right\} . $
所计算的SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的弹性刚度张量(Cij)如表2所示, 并与文献[16, 32]报道的数据进行了对比, 可以看到计算的SrTiO3弹性刚度张量值C11, C22与实验值接近, C44比实验值小. 这可能是由于计算采用理想模型, 而实验时样品会产生电离杂质、空位等晶格缺陷所致, 但计算所选参数一致, 所得到的弹性刚度张量变化规律是可信的. 由表中数据分析可知, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3均符合此力学判据.
SrTiO3 (Caculation)[16]SrTiO3 (Experiment)[32]SrTiO3SrTi0.875Nb0.125O3SrTi0.75Nb0.25O3
C11318.6317.0311.1299.1306.3
C1299.3102.597.2105.9122.9
C44109.8123.5109.499.479.3


表2SrTi1–xNbxO3弹性刚度张量 (单位: GPa)
Table2.Elastic constants (Unit: GPa) of SrTi1–xNbxO3.

采用弹性刚度张量C11, C12, C44可计算出材料的体弹性模量B、剪切模量G、杨氏模量E与泊松比σ[33], 如表3所示. 晶体具有多种组成方式, 其性质也各不相同, 晶体的组成的改变会对材料的性质产生影响. 当Nb5+引入材料体系中, Ti4+被替换, 使Ti-O八面体产生畸变, 且掺杂离子对近邻几何结构产生了影响, 从而改变材料力学性能. 由表3数据可以看出, SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的体弹性模量B几乎相同, 掺杂未使材料的体弹性模量发生改变. 而随着Nb5+掺杂浓度增大, SrTiO3材料体系的剪切模量G与杨氏模量E降低, 泊松比σ降低.
ParametersSymbelSrTiO3SrTi0.875Nb0.125O3SrTi0.75Nb0.25O3
Bulk elastic modulus/GPaB168.8169.7166.0
Shear modulus/GPaG108.3100.878.3
G/B/0.640.590.47
Young's modulus/GPaE267.7252.4202.9
Poisson's ratio/(m·s–1)σ0.2360.2520.296


表3SrTi1–xNbxO3力学性能参数
Table3.Mechanical property parameters of SrTi1–xNbxO3.

由剪切模量和体积模量的比值(G/B)能够表征材料韧脆性能[34]. 当G/B > 0.5时, 表示材料是脆性材料; 当G/B < 0.5时, 表示材料是韧性材料. G/B的值越大, 则表示材料脆性越大, 更容易脆性断裂. 计算SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的 G/B值如表3所示, 可以看到, 掺杂浓度较低时, G/B值均大于0.5, 属于脆性材料, 且随着Nb掺入浓度的增大, 其G/B值降低, 表明掺入Nb5+使SrTiO3材料的脆性降低, 能够改善SrTiO3材料的力学性能.
剪切模量G与材料的硬度有关, 材料的剪切模量G越低, 则材料的硬度越低[35]. 剪切模量G与杨氏模量E可反应晶胞中原子作用力的大小, 晶胞中原子作用力越小, 则材料弹性模量越小. 从表3可见, Nb5+掺杂使材料的剪切模量G减少, 表明材料晶胞中原子作用力减弱, 导致抗剪切应变的能力减弱, 更容易发生剪切变形. Nishiyama等[21]计算发现Nb5+的掺入会削弱Ti—O键, 引起晶格畸变, 从而导致晶胞对称性降低. SrTi0.75Nb0.25O3的晶胞对称性最低, 而未掺杂SrTiO3晶胞对称性较好. 不同Nb5+掺杂浓度使材料的剪切模量G与杨氏模量E改变, 原因在于Nb5+掺杂使晶胞的对称性降低, 取代原子引起的尺寸和耦合力失调使晶格畸变, 应变场波动导致晶格弛豫, 从而使晶胞更容易变形[36], 使杨氏模量与剪切模量降低, 从而降低体系硬度. 而未掺杂SrTiO3晶胞对称性较高, 从不同方向施压晶胞变形较难, 故其剪切模量G与杨氏模量E较高.
2
3.4.热学性质
-->

3.4.热学性质

德拜温度是反映原子之间结合力的重要物理量, 对应于晶格振动的最高频率, 是描述材料晶格振动与比热、熔点的物理量. 当德拜温度越高, 表明原子之间作用力越强, 熔点越高. 由杨氏模量E、体弹性模量B和剪切模量G可以计算出SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的压缩波速、剪切波速、德拜温度等参数[33]如表4所示, 从表4可见, 随着Nb5+掺杂浓度增大, 材料的压缩波速、剪切波速、德拜温度下降, 表明Nb5+掺杂使材料的原子作用力减弱, 熔点降低, 这与之前关于剪切模量与杨氏模量的分析一致.
ParametersSymbelSrTiO3SrTi0.875Nb0.125O3SrTi0.75Nb0.25O3
Compression wave velocity/(m·s–1)vp7916.57745.67241.4
Shear wave velocity/(m·s–1)vs4655.34460.23897.8
Average wave velocity/(m·s–1)vm4876.24694.34351.6
Debye temperature/KΘD630.7603.9557.7


表4SrTi1–xNbxO3的声速和德拜温度
Table4.Calculated sound velocity and Debye temperature of SrTi1–xNbxO3.

对于大多数完美的电绝缘材料来说, 热传输主要是声子-声子散射. 结合声速和弹性特性, 可计算材料的晶格热导率. Slack导出了本征晶格热导率的定量表达式[37]. 图7(a)显示了采用Slack模型计算的κSlack随温度变化的关系, 可以看到, 根据Slack模型所计算的未掺杂SrTiO3与掺杂SrTiO3的晶格热导率随温度升高而降低, 在室温下热导率为5.7—8.2 W/(m·K), 在1000 K高温下热导率为1.3—2.4 W/(m·K). 当温度很高接近熔点时, 材料热导率不受温度影响, 可根据Clark模型计算理论最低晶格热导率kmin[38], 采用Clark模型计算出的SrTiO3、SrTi0.875Nb0.125O3、SrTi0.75Nb0.25O3理论最低晶格热导率κmin如图7(b)所示, 随着Nb5+掺杂浓度的升高, 理论最低晶格热导率κmin降低, 当Nb5+掺杂浓度为25%时, 理论最低晶格热导率κmin为1.396 W/(m·K).
图 7 SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3的热导率　(a) κslack; (b) κmin
Figure7. Thermal conductivity of SrTiO3, SrTi0.875Nb0.125O3, SrTi0.75Nb0.25O3: (a) κslack; (b) κmin.

Zhang等[39]采用水热法制备了Nb5+掺杂钛酸锶样品, 在1000 K时, 其热导率为3.2 W/(m·K), 此时晶格热导率为2.5 W/(m·K). Okhay等[40]制备的Nb5+掺杂钛酸锶材料, 在1160 K时热导率为2.9 W/(m·K), 此时晶格热导率为2.3 W/(m·K). 本文采用第一性原理计算出的κslack、理论最低晶格热导率κmin与实验结果[39-41]接近. 且κslack和κmin均随着Nb5+掺杂浓度的增大而降低, 表明Nb5+掺杂能有效降低材料晶格热导率, 从而降低材料的总热导率, 这是由于随着Nb5+掺杂浓度增大, 晶胞对称性降低, 取代原子引起的尺寸和耦合力失调使晶格畸变, 应变场波动导致晶格弛豫, 弛豫减慢了声子的传播速度, 抑制了材料的热传导作用[36]. 同时在高温时, 由于掺杂离子Nb5+与Ti4+的质量差异, 掺杂离子有效散射了短波长声子, 这对降低晶格热导率做出了贡献[42].
4.结　论
1)对SrTiO3晶体结构的几何优化与电子结构计算表明, Nb5+离子掺杂使材料晶胞参数增大, 且随着掺入Nb5+离子浓度的增大, 晶胞参数进一步增大. 未掺杂SrTiO3主要由O2p轨道构成价带顶, 由Ti3d轨道构成导带底; Nb5+掺杂SrTiO3由O2p轨道构成价带顶, 由Ti3d和Nb4d轨道构成导带底. SrTiO3是间接带隙化合物, 掺杂Nb5+后转变为直接带隙化合物.
2) Nb5+掺杂钛酸锶光学性质的计算表明, 当Nb5+掺杂浓度增大, 介电常数实部峰值增大, 介电常数虚部峰值减小, 实部和虚部介电峰位置均向高能区移动; 在4—5 eV范围内, 掺杂SrTiO3材料体系均具有较高折射系数; 在5—6 eV范围内, 掺杂SrTiO3材料体系均具有较高消光系数; Nb5+掺杂使材料反射系数、吸收系数、能量损耗下降, 可见光范围内光学透过率上升.
3) Nb5+掺杂钛酸锶力学性质的计算表明, 当Nb5+掺杂浓度增大, 材料体弹性模量几乎不改变, 而剪切模量与杨氏模量减小, 泊松比增大, Nb5+掺杂使SrTiO3材料的抗剪切变形能力、硬度和脆性降低, 韧性增大.
4) Nb5+掺杂钛酸锶热学性质的计算表明, 未掺杂SrTiO3与掺杂SrTiO3的晶格热导率随温度升高而降低, 在室温下热导率为5.7—8.2 W/(m·K), 在1000 K高温下热导率为1.3—2.4 W/(m·K). 当Nb5+掺杂浓度增加, SrTiO3材料的德拜温度减小, 晶格热导率与理论最低晶格热导率均减小.
相关话题/材料 计算 结构 电子 光学
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • Ti, V, Co, Ni掺杂二维CrSi<sub>2</sub>材料的电学、磁学及光学性质的第一性原理研究
    摘要:二维磁性材料的研究是一大热点,其中单层CrSi2表现出优良的磁性,有望应用于自旋电子学等领域,但金属性限制了其部分层面的应用与发展.采用基于密度泛函理论的第一性原理赝势平面波方法研究了不同元素(Ti,V,Co,Ni)、不同掺杂浓度(原子百分比为3.70%,7.41%,11.1%)对二维CrSi ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 掺杂维度和浓度调控的δ掺杂的La:SrTiO<sub>3</sub>超晶格结构金属-绝缘体转变
    摘要:利用密度泛函理论计算,本文系统研究了δ掺杂的La:SrTiO3超晶格结构的电子性质随掺杂维度和掺杂浓度改变而变化的规律性.该结构通过在SrTiO3等间距的单元层中掺入一定浓度的La来实现.在25%La掺杂浓度下,随着相邻掺杂层间距从1个单层增加到5个单层,掺杂维度从三维过渡到二维,超晶格从金属 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于电荷和热输运的石墨烯热电子器件性能优化
    摘要:科研人员近年来提出了石墨烯热电子能量转换器件(graphenethermionicenergyconverter,GTEC)的模型,对其物理机理与参数优化展开了研究,为高品位热能开发提供了新途径.然而,空间电荷积累和近场热辐射效应对GTEC能量转换性能的影响却鲜有报道.本文结合热电子发射、朗缪 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于测量的量子计算研究进展
    摘要:相比于量子门电路模型,基于测量的量子计算模型为实现普适量子计算提供了另一途径,且经过近二十年的发展其内涵已得到了极大丰富.本文对基于测量的量子计算模型的研究历史和现状进行综述.首先简要介绍该模型的基本理论,包括量子图态等资源态的概念和工作原理、模型的计算普适性和经典模拟方法、在相关量子信息处理 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 硅和锗量子计算材料研究进展
    摘要:半导体量子点量子计算是实现固态量子计算的重要途径之一,高质量量子计算材料制备是其中的关键.硅和锗材料能够实现无核自旋的同位素纯化,满足量子比特对长退相干时间的要求,同时与当前的硅工艺兼容,是实现半导体量子计算的重要材料平台.本文首先概述了近年来半导体量子点量子计算领域取得的重要进展,然后详细介 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 三元Hf-C-N体系的空位有序结构及其力学性质和电子性质的第一性原理研究
    摘要:采用第一性原理方法,研究了三元Hf-C-N体系的空位有序结构及其力学性质和电子性质.首先采用第一性原理和进化算法,预测得到8种可能存在的热力学稳定的Hf-C-N空位有序结构;这些结构都具有岩盐结构,与实验发现的无序固溶体的结构类型一致.本文的预测结果证明了Hf-C-N空位化合物能够以有序结构形 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • AlGaN/GaN高电子迁移率晶体管的栅极电容模型
    摘要:AlGaN/GaN高电子迁移率晶体管的栅极电容由本征电容和边缘电容组成.边缘电容分为外部边缘电容和内部边缘电容,内部边缘电容相比外部边缘电容对器件的开关转换特性更为敏感.本文基于内部边缘电容的形成机理,推导了内部边缘电容Cifs/d模型,进一步的分析表明,其与器件的栅极偏置强相关;基于Ward ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 聚甲基丙烯酸甲酯与碳纳米管纳米复合材料玻璃化转变及其非线性力学行为的分子动力学模拟
    摘要:短纤维结构对聚合物材料玻璃化转变温度及非线性力学具有非常重要的影响.本文利用粗粒化分子动力学方法研究了碳纳米管(CNTs)含量对聚甲基丙烯酸甲酯(PMMA)玻璃化转变、扩散系数及非线性力学特性的影响.分子动力学模拟结果显示:短CNTs纤维的加入的确会改变PMMA体系的玻璃化转变温度,模拟结果与 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于MXene涂层保护Cs<sub>3</sub>Sb异质结光阴极材料的计算筛选
    摘要:以锑化铯(Cs3Sb)为代表的碱金属型半导体光阴极具有高量子效率、低电子发射度、光谱响应快等特点,可作为理想的新型电子发射源.然而Cs3Sb中碱金属敏感于含氧气体,从而导致其结构不稳定,工作寿命低,影响电子发射效率.利用超薄层状的二维材料进行涂层保护Cs3Sb基底,有望构建新型高性能光阴极材料 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 渔网超结构的等离激元模式及其对薄膜电池的陷光调控
    摘要:渔网超结构具有平面、近光学无损、特定光场中可以激发表面等离激元等特点,在增强光子器件的响应效率方面极具潜力.本文基于时域有限差分方法和严格耦合波分析,系统研究了渔网超结构的等离共振模式及其对晶硅薄膜电池的光波调控性能.研究结果表明,渔网结构对光波的吸收、散射和消光特性强烈依赖金属层的厚度、线宽 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.