摘要: 科研人员近年来提出了石墨烯热电子能量转换器件(graphene thermionic energy converter, GTEC)的模型, 对其物理机理与参数优化展开了研究, 为高品位热能开发提供了新途径. 然而, 空间电荷积累和近场热辐射效应对GTEC能量转换性能的影响却鲜有报道. 本文结合热电子发射、朗缪尔空间电荷、非平衡态热力学和涨落电动力学等理论, 考虑热电子输运、近场热辐射输运、牛顿换热的相互作用对GETC的影响, 进而构建完善的物理模型. 首先, 分析极板温度恒定时的电流密度、阴极板附加势垒、功率密度、转换效率、热流对电压和真空间隙的依赖特性, 结果表明真空间隙对功率密度的影响显著, 而对效率的影响较小, 可在不同的电压处获得最高功率密度和效率. 其次, 分析了极板温度受能量平衡约束条件下, 功率密度与效率随电压的变化情况, 研究发现: 相比于恒温模型, 牛顿换热对功率密度的影响显著, 而对效率的影响较小; 在最优功率密度时的阳极板温度高于环境温度, 而最优效率时的阳极板温度趋于环境温度; 折衷考虑功率密度和效率, 确定了电压、真空间隙和阳极板温度的优化区间. 本文所获结果可为实际器件的研制提供理论支撑.
关键词: 石墨烯 /
热电子输运 /
近场热输运 /
功函数 /
朗缪尔空间电荷理论 English Abstract Performance optimization of graphene thermionicdevices based on charge and heat transport Liao Tian-Jun 1 ,Yang Zhi-Min 2 ,Lin Bi-Hong 3 1.Department of Physics and Energy, Chongqing University of Technology, Chongqing 400054, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 12004327), the Chongqing Research Program of Basic Research and Frontier Technology, China (Grant No. cstc2020jcyj-msxmX0001), the Science and Technology Research Program of Chongqing Municipal Education Commission, China (Grant No. KJQN201901144), and the Scientific Research Foundation of Chongqing University of Technology, China (Grant No. 2019ZD22).Received Date: 10 June 2021Accepted Date: 22 July 2021Available Online: 15 August 2021Published Online: 20 November 2021Abstract: In recent years, researchers have proposed a model of graphene thermionic energy converter (GTEC) for the utilization of high-grade thermal energy, which is used to extensively study the physical mechanism and parametric optimization. However, the influences of space charge accumulation and near-field radiative effects on the GTEC’s energy conversion performance are rarely reported. In the present work, the theories of thermionic emission, Langmuir space charge, non-equilibrium thermodynamics, and fluctuating electrodynamics are used to construct an improved model, in which the coupling effects of thermionic transport, near-field radiative heat transfer, and Newton heat transfer are considered. Firstly, the dependence of additional potential barrier, current density, power density, efficiency, and heat flows on the voltage and the vacuum gap are analyzed by neglecting the Newton heat transfer. The results show that the vacuum gap has a significant influence on the power density, while it has a negligible effect on the efficiency, the optimal power density and efficiency can be obtained at two different voltages. Secondly, the variations of power density and efficiency with voltage are analyzed on condition that the electrodes’ temperatures are restricted by the energy balance equation. It is found that Newton heat transfer has a significant influence on the power density, while it has a negligible effect on the conversion efficiency; the anode’s temperature at the optimal power density is higher than the ambient temperature, and the temperature at the optimal efficiency is close to the ambient temperature; the optimal regions of voltage, vacuum gap, and anode’s temperature are determined by considering the trade-off between power density and efficiency. The results obtained in this work can provide a theoretical basis for the development of practical devices.Keywords: graphene /thermionic transport /near-field heat transport /work function /Langmuir space charge theory 全文HTML --> --> --> 1.引 言 热光伏器件[1 -3 ] 和热电子器件[4 -7 ] 是全固态能量装置, 可以被核能[8 ,9 ] 、燃料电池[10 ,11 ] 、聚焦太阳能[12 ,13 ] 等高品位热源驱动而产生电能, 具有较高的能量转换效率, 在新能源开发领域具有广阔应用前景. 为了提供新型高效热电子能量转换方案, Liang 和Ang[14 ] 、Mishra等[15 ] 借助石墨烯高熔点和奇特二维狄拉克锥结构特性, 提出了单层石墨烯热电子转换器件(graphene thermionic energy converter, GTEC)的模型, 应用统计物理和热电子发射理论, 导出了不同于传统Richardson-Dushman方程的阴极板电流密度解析式, 揭示了阴极板功函数和温度对电流密度、功率密度和效率的影响, 产生了一些新机理. Mishra等[16 ] 和Yang等[17 ] 分别研究了多层石墨烯TEC的物理机理和太阳能驱动多层石墨烯TEC的参数优化设计问题, 拓展了石墨烯在TEC中的应用. 廖天军等[18 ] 研究了GTEC内远场辐射以及高低温端的牛顿换热对伏安特性和能量转换性能的影响, 通过两极板功函数的优化, 获得了最高功率密度和效率, 提供了参数优化区间, 揭示了热源温度和石墨烯费米能级对优化性能的影响, 相比于文献[14 ]的研究, 能量转换性能有一定提升. Hu等[19 ] 利用石墨烯作为阳极板材料, 使其在低温条件下具有较低的逆向电流密度, 提高GTEC的净电流密度, 同时在阳极板表面放置光学反射器, 使其抑制阳极板对远场红外辐射光子的吸收, 降低阳极板温度, 从而提高能量转换性能. 通过数值模拟, 获得了GTEC在 1940 K 时的最大效率76.6%和功率密度95.1 W·cm–2 , 提供了不同热源温度下的参数优化判据. 值得注意的是, 廖天军等[18 ] 、Hu等[19 ] 研究中GTEC忽略了空间电荷积累效应对热电子的传输性能的显著影响, 从而获得了极高的理论性能极限. 理论上, 设计亚微米尺度的真空间距, 可降低空间电荷积累效应对GTEC的影响, 但也将带来极板间近场热辐射损耗和阳极板温度升高, 进而影响能量转换性能[14 ] . 因此, 有必要全面考虑热电子输运和近场热辐射输运耦合作用对GTEC的影响, 将真空间隙设计在实验可行区域, 为器件的研制提供理论支撑.2.基于电-热输运特性的功率密度和转换效率 由于传统热电子转换器件(thermionic energy converter, TEC)电极材料中的电子能量-动量函数关系为抛物线型, 而石墨烯无质量狄拉克费米子具有线性能带结构, 其电子能量-动量遵循相对论色散关系, 导致石墨烯在高温和低温热源激发下具有较高和较低的电流密度[14 ] , 因此, 本文采用石墨烯作为TEC的阴极和阳极材料, 可提高净电流密度. 另外, 石墨烯具有较低的红外热发射率, 其作为TEC电极材料可以减少器件内部的不可逆辐射热损失, 从而提高能量转换效率[20 ] . 图1(a) 为GTEC结构示意图, 其中石墨烯覆盖金属钨表面而构成阴、阳极极板, 高温阴极板具有较高的热电子正向电流密度$ {J_{\text{1}}} $ , 低温阳极板具有较低的逆向电流密度$ {J_{\text{2}}} $ . 当GTEC与高温热源接触时, 温度为$ {T_{\text{1}}} $ 的阴极板单位时间吸收热量$ {q_{\text{H}}} $ 和温度为${T_{\text{2}}}$ 的阳极板单位时间释放热量$ {q_{\text{L}}} $ , 同时热电子克服阴极板功函数的束缚而逸出表面, 通过宽度为$ d $ 的真空被阳极板吸收, 然后流经外部负载回到阴极, 构成回路, 从而实现热能到电能的转换. 在能量转换过程, 因热电子传输, 导致单位时间离开阴极板的热量和进入阳极板的热量分别为$ {q_{\text{1}}} $ 和$ {q_{\text{2}}} $ . 当$ d $ 远小于热辐射特征波长$ {\lambda _{{\text{th}}}} = {{c\hbar } \mathord{\left/ {\vphantom {{c\hbar } {\left( {{K_{\text{B}}}{T_1}} \right)}}} \right. } {\left( {{K_{\text{B}}}{T_1}} \right)}} $ 或与其相当时[5 ] , 两极板近场辐射交换热流为$ {q_{{\text{NF}}}} $ , 其中$ \hbar = {h \mathord{\left/ {\vphantom {h {2{\text{π }}}}} \right. } {2{\text{π }}}} $ 为约化普朗克常数, $ c $ 为真空光速, $ {K_{\text{B}}} $ 为玻尔兹曼常数.图 1 GTEC的结构和能带示意图 (a)结构; (b)能带Figure1. The structure and band diagrams of the GTEC: (a) Structure; (b) band图1(b) 为GTEC能带示意图, $ {E_{{\text{F, 1}}}} $ 和$ {E_{{\text{F, 2}}}} $ 分别为阴极板和阳极板石墨烯的费米能级, ${V_{{\text{fb}}}} = $ $ {{\left( {{E_{{\text{F, 2}}}} - {E_{{\text{F, 1}}}}} \right)} / e}$ 为平带电压, $ e $ 为基元电荷, 功函数$ {\phi _{\text{1}}} $ 和$ {\phi _{\text{2}}} $ 决定于两极板表面真空能级与相应费米能级的差值, 空间电荷积累效应在两极板间产生的静电势与基元电荷的负值$ - e $ 相乘为势函数$ \phi \left( x \right) $ [21 ,22 ] , 它是位置$ x $ 的函数, $ \phi \left( x \right) $ 负梯度为电子在传输过程中受到的电场力, 势函数在$ {x_{\text{M}}} $ 的最高值$ {\phi _{\text{M}}} $ 与两极板表面真空能级的差值为附加势垒$ {\phi _{{\text{M1}}}} $ 和$ {\phi _{{\text{M2}}}} $ [21 ,22 ] .$ {\phi _{\text{M}}} $ 恰好在阴极板表面时, 则所有热发射电子处于正向加速电场, 均能通过真空间隙到达阳极, 从而产生阴极板饱和电流密度$ {J_{{\text{1 S}}}} $ . 当$ {\phi _{\text{M}}} $ 恰好在阳极板表面, 则所有热发射电子需要克服反向电场力而减速到达阳极. 当$ {\phi _{\text{M}}} $ 位于两极板之间时, 在$ {x_{\text{M}}} \leqslant x \lt d $ 区域, 电子处于加速电场, 速度区间为$ {v_{\text{0}}} \leqslant {v_x} \leqslant \infty $ , 其中$ {v_{\text{0}}} = \sqrt {{{2\left[ {{\phi _{\text{M}}} - \phi \left( x \right)} \right]} \mathord{\left/ {\vphantom {{2\left[ {{\phi _{\text{M}}} - \phi \left( x \right)} \right]} m}} \right. } m}} $ , $ m $ 为电子质量; 在$ 0 \lt x \leqslant {x_{\text{M}}} $ 区域, 一部分电子以动能由0到$ {\phi _{\text{M}}} - \phi \left( x \right) $ 返回阴极, 一部分电子向阳极板运动, 动能范围为0到$ \infty $ , 则速度区间为 $- {v_{\text{0}}} \leqslant $ $ {v_x} \leqslant \infty$ .$ \phi \left( x \right) $ 决定于泊松方程[21 ,22 ] :$ {\varepsilon _{\text{v}}} = {\text{8}}{\text{.85}} \times 1{{\text{0}}^{ - 14}}{\text{ F}} \cdot {\text{c}}{{\text{m}}^{ - 1}} $ 为真空介电常数, 电子密度函数$N(x)$ 为[21 ,22 ] :$ {\psi _{\text{M}}} $ 在$ 0 \lt x \lt d $ 区域, 速度分布函数$ f\left( {x, v} \right) $ 为[21 ,22 ] :$ g\left( u \right) $ 为单位阶跃函数, $\gamma =\dfrac {\left[ {{\phi _{\text{M}}} - \phi \left( x \right)} \right]} {\left( {{K_{\text{B}}}{T_{\text{1}}}} \right)}$ 为无量纲参数, $ N\left( {{x_{\text{M}}}} \right) $ 是在$ {x_{\text{M}}} $ 处的电子数密度.2 )式和(3 )式, $ N\left( x \right) $ 可进一步表示为[21 ,22 ] :4 )式, 泊松方程可改写为:$\xi = {\left( {x - {x_{\text{m}}}} \right)}/ {{x_{\text{0}}}}$ , ${x_0} = \sqrt {{\varepsilon _{\text{v}}}{{{K_{\text{B}}}{T_{\text{1}}}} /{\left[ {2{e^2}N\left( {{x_{\text{M}}}} \right)} \right]}}} $ $ = {\left( {\dfrac{{\varepsilon _{\text{v}}^2 K_{\text{B}}^3}}{{2{\text{π }}m{e^2}}}} \right)^{0.25}}\dfrac{{T_1^{0.75}}}{{J_1^{0.5}}}$ , $ {J_{\text{1}}} $ 为阴极板工作电流密度. 结合边界条件 $ \gamma \left( {\xi = 0} \right) = 0 $ 和$\gamma ( \xi = 0 ) = 0$ 和$\gamma '( \xi = $ $ 0) = 0$ , 数值求解(5 )式, 可获得函数$ \gamma \left( \xi \right) $ .$ {\phi _{\text{M}}} $ 处于$ 0 \lt x \lt d $ 区域, 阴极板工作电流密度$ {J_{\text{1}}} $ 为:$ {\phi _{\text{M}}} $ 处于$ x = 0 $ , 阴极板饱和电流密度$ {J_{{\text{1 S}}}} $ 满足:3 )式, (6 )式和(7 )式, 可导出阴极板饱和电流密度${J_{{\text{1S}}}}$ 与工作电流密度$ {J_1} $ 的关系式:$ {J_{{\text{1 S}}}} $ 为[14 ] $A = {{eK_{\text{B}}^{\text{3}}} /{\left( {{\text{π }}{\hbar ^3}v_{\text{f}}^2} \right)}} = 0.01158\, {\text{A}} \cdot {\text{c}}{{\text{m}}^{ - {\text{2}}}} \cdot {{\text{K}}^{ - {\text{3}}}}$ 是石墨烯的热电子发射常数, $ {v_{\text{f}}} \approx {10^8}{\text{ cm}} \cdot {{\text{s}}^{ - 1}} $ 为费米速率.$ {\phi _{\text{M}}} $ 位于$ x = 0 $ , 阳极板表面到势垒最高处的距离$ d $ 经无量纲化后为${\xi _{{\text{2 S}}}} = {\left( {\dfrac{{2{\text{π }}m{e^2}}}{{\varepsilon _{\text{v}}^2 K_{\text{B}}^3}}} \right)^{0.25}}\dfrac{{J_{1{\text{S}}}^{0.5}d}}{{T_1^{0.75}}}$ , 可得$ {\phi _{{\text{M2}}}} = \gamma \left( {{\xi _{{\text{2 S}}}}} \right){K_{\text{B}}}{T_{\text{1}}} $ , 则阳极板逆向电流密度$ {J_{\text{2}}} $ 为:$ {\phi _{\text{M}}} $ 位于$ x = 0 $ , GTEC的功率密度$ P $ 为:$V = {{\left( {{\phi _{\text{1}}} - {\phi _{\text{2}}} - {\phi _{{\text{M2}}}}} \right)} /e}$ 为输出电压, $J = {J_{{\text{1S}}}} - $ $ {J_2}$ 为净电流密度.$ {q_{\text{1}}} $ 和$ {q_{\text{2}}} $ 可分别表示为:$ {\phi _{\text{M}}} $ 位于$ x = d $ , GTEC的功率密度$ P $ 为:$ {J_{2{\text{S}}}} $ 为:$ {q_{\text{1}}} $ 和$ {q_{\text{2}}} $ 可表示为:$ {\phi _{\text{M}}} $ 位于$ 0 \lt x \lt d $ , GTEC的功率密度$ P $ 为:$ {J_{\text{1}}} $ 和$ {J_2} $ 可分别表示为[13 ] :$ {q_{\text{1}}} $ 和$ {q_{\text{2}}} $ 可表示为[23 ] :$ \left( {{\phi _{\text{1}}} + {\phi _{{\text{M1}}}} + 3{K_{\text{B}}}{T_{\text{1}}}} \right) $ 和$ \left( {{\phi _{\text{2}}} + {\phi _{{\text{M2}}}} + 3{K_{\text{B}}}{T_{\text{2}}}} \right) $ 分别为每个电子从阴极板和阳极板表面逸出所携带的热流, $ \left( {{\phi _{\text{1}}} + {\phi _{{\text{M1}}}} + 3{K_{\text{B}}}{T_{\text{2}}}} \right) $ 是电子从阳极板表面逸出到达阴极板所携带的热流率, $( {\phi _{\text{2}}} + {\phi _{{\text{M2}}}} + $ $ 3{K_{\text{B}}}{T_{\text{1}}} )$ 是电子离开阴极板到达阳极所携带的热流率, $ 3{K_{\text{B}}}{T_{\text{1}}} $ 和$ 3{K_{\text{B}}}{T_{\text{2}}} $ 分别是阴、阳极板电子越过势垒后的平均热动能.$ {q_{\text{H}}} $ 和流入阳极板的热量$ {q_{\text{L}}} $ 可表示为[5 ] :$ {q_{\text{H}}} $ 和$ {q_{\text{L}}} $ 可表示为[18 ] :$ {U_{\text{H}}} = {U_{\text{L}}} = 0.10\, {\text{W}} \cdot {\text{c}}{{\text{m}}^{ - 2}} \cdot {{\text{K}}^{ - 1}} $ 为换热系数, $ {T_{\text{H}}} = 1500\, {\text{K}} $ 为热源温度, ${T_{\text{L}}} = 300\, {\text{K}}$ 为环境温度.$ {q_{{\text{NF}}}} $ 由传播波和倏逝波引起的热流$ {q_{{\text{Evan}}}} $ 和$ {q_{{\text{Prop}}}} $ 两部分组成, 基于涨落电动力学理论, $ {q_{{\text{Evan}}}} $ 和$ {q_{{\text{Prop}}}} $ 可分别表示为[24 ,25 ] $ \Theta \left( {\omega , T} \right) = {\left\{ {\exp \left[ {{{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {\left( {{K_{\text{B}}}T} \right)}}} \right. } {\left( {{K_{\text{B}}}T} \right)}}} \right] - 1} \right\}^{ - 1}} $ 为玻色-爱因斯坦分布函数, 上标$ j = {\text{s}}, {\text{p}} $ 代表电场矢量垂直和平行于辐射面的$ {\text{s}} $ 和$ {\text{p}} $ 两个偏振方向, $ \beta $ 为平行于极板表面的波矢分量, ${k_{{z\text{v}}}} = {[{({\omega /c})^2} - {\beta ^2}]^{0.5}}$ 为波矢垂直于真空中能量传递方向的分量, $ R_{\text{i}}^{\text{s}} $ 和$ R_{\text{i}}^{\text{p}} $ 为两极板表面的菲涅尔反射系数[25 ] :$ i = 1, 2 $ 代表阴极和阳极, ${k_{{ {z}}i}} = [{\varepsilon _{{\text{W, }}i}}{({\omega / c})^2} - $ $ {\beta ^2}]^{0.5}$ 介质内波矢在$ z $ 方向的分量, $ \chi $ 为真空磁导率, $ {\sigma _{\text{G}}} $ 为石墨烯电导率.$ {\varepsilon _{{\text{W, }}i}} $ 与电导率$ {\sigma _{{\text{W, }}i}} $ 、电子弛豫时间$ {\tau _{{\text{W, }}i}} $ 和光子角频率$ \omega $ 之间的函数关系为[5 ] $ {\tau _{{\text{W, }}i}} = {\left( {{{10}^7}T_i^{\text{2}} + 2 \times {{10}^6}T_i^3} \right)^{ - 1}} $ , 电导率$ {\sigma _{{\text{W, }}i}} $ 决定于极板工作温度$ {T_i} $ .$ {\sigma _{{\text{G, }}i}} $ 可由G. W. Hanson的近似公式给出[26 ] $ {\mu _{{\text{G, }}i}} $ 和$ {\tau _{{\text{G, }}i}} $ 分别为石墨烯的化学势和电-声弛豫时间.3.性能优化 为了揭示空间电荷积累效应对GTEC能量转换性能的影响, 将极板温度恒定为${T_1} = 1500\; {\text{K}}$ 和${T_2} = $ $ 300\; {\text{K}}$ . 选取参数${\mu _{{\text{G, }}i}} = 0.{\text{1}}0\;{\text{ eV}}$ , ${\tau _{{\text{G, }}i}} = {10^{ - 13}}\;{\text{ s}}$ , ${E_{{\text{F, 1}}}} = 0.{\text{4}}0\;{\text{ eV}}$ , ${E_{{\text{F, 2}}}} = 0.{\text{8}}0\;{\text{ eV}}$ , ${\phi _{\text{1}}} = 1.70\;{\text{ eV}}$ 和${\phi _2} = 1.50\;{\text{ eV}}$ , 通过数值模拟, 可绘制三个不同真空间隙$ d $ 条件下, GTEC的净电流密度$ J $ 与阴极板势垒高度$ {\phi _{{\text{M1}}}} $ 、功率密度$ P $ 与转换效率$ \eta $ 、热流$ {q_1} $ 和$ {q_2} $ 随电压$ V $ 的变化关系曲线, 如图2 所示. 从图2(a) 可看出电压$ V $ 从$ 0\, {\text{V}} $ 增加至开路电压$ {V_{{\text{OC}}}} = 2.05\, {\text{V}} $ , 则净电流密度$ J $ 从短路电流密度${J_{{\text{SC}}}} = 303.50 \; {\text{A}}/{\text{c}} {{\text{m}}^{ 2}}$ 递减至 $0\; {\text{A}} \cdot {\text{c}}{{\text{m}}^{ - 2}}$ , 这是由于阳极板在${T_{\text{2}}} = 300\; {\text{K}}$ 低温条件下产生的逆向电流密度${J_{\text{2}}}$ 较小, 其对净电流密度$ J $ 的影响较小, 则$ J $ 主要决定于阴极板的电流密度$ {J_1} $ , 而(2 )式决定了电流密度$ {J_1} $ 随阴极板附加势垒$ {\phi _{{\text{M1}}}} $ 的增加而递减, 又因为空间电荷积累效应引起的阴极板附加势垒$ {\phi _{{\text{M1}}}} $ 随电压$ V $ 的升高而递增, 当$ V = {V_{{\text{OC}}}} $ 时, $ {\phi _{{\text{M1}}}} $ 达到最高值, 因此, 净电流密度$ J $ 是电压$ V $ 的单调递减函数.图 2 三个不同真空间隙条件下, GTEC的净电流密度$ J $ 与阴极板势垒高度$ {\phi _{{\text{M1}}}} $ 、功率密度$ P $ 与转换效率$ \eta $ 、热流$ {q_1} $ 和$ {q_2} $ , 以及近场辐射热流与阴极板热流的比值$ {{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}} $ 随电压$ V $ 的变化关系曲线 (a)$ J $ 与$ {\phi _{{\text{M1}}}} $ ; (b)$ P $ 与$ \eta $ ; (c)$ {q_1} $ 和$ {q_2} $ ; (d)$ {{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}} $ Figure2. The curves net electrical current density $ J $ and cathode’s additional barrier $ {\phi _{{\text{M1}}}} $ , power density $ P $ and efficiency $ \eta $ , heat flow rates $ {q_1} $ and $ {q_2} $ , and the ratio of $ {q_{{\text{NF}}}} $ to $ {q_{\text{H}}} $ varying with the voltage $ V $ for given three values of $ d $ : (a)$ J $ and$ {\phi _{{\text{M1}}}} $ ; (b)$ P $ and$ \eta $ ; (c)$ {q_1} $ and$ {q_2} $ ; (d)$ {{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}} $ .$ {V_{{\text{fb}}}} $ 处可获得最高功率密度[27 ] , 而图2(b) 显示GTEC在$ {V_P} = $ $ 0.377{\text{ V}} $ 处可获得最高功率密度${P_{\max }} = 54.7\, {\text{W}}/{\text{c}}{{\text{m}}^{2}}$ , 电压优化值$ {V_P} $ 小于平带电压${V_{{\text{fb}}}} = ( {E_{{\text{F, 2}}}} - {E_{{\text{F, 1}}}} ) / e = $ $ 0.40{\text{ eV}}$ , 这是由于热电子的输运特性导致GTEC在平带电压$ {V_{{\text{fb}}}} $ 处的功率密度不是最优; 另一方面, GTEC在${V_\eta } = 1.09{\text{ V}}$ 处可获得最高效率$ {\eta _{\max }} = 0.338 $ , 而$ {V_\eta } $ 高于$ {V_P} $ . 由于在两极板温差$ \left( {\Delta T = {T_1} - {T_2}} \right) $ 恒定的条件下, 热流$ {q_{\text{1}}} $ 包含的$ \left( {{q_{{\text{Evan}}}} + {q_{{\text{Prop}}}}} \right) $ 不受电压$ V $ 的影响, 而热电子对热流$ {q_{\text{1}}} $ 的贡献依赖于电压$ V $ , 如图2(c) 所示, 从而导致方程${{{\text{d}}\left( {{P/ {{q_{\text{1}}}}}} \right)} / {{\text{d}}V}} = 0$ 的数值解$ V = {V_\eta } $ 高于$ {V_P} $ . 利用$ {V_P} = 0.377{\text{ V}} $ , 可确定电流密度的优化值${J_P} = 145.10\, {\text{A}}/ {\text{c}}{{\text{m}}^{2}}$ , 从$ {V_P} $ 和$ {J_P} $ 的值可看出GTEC是电压值较小而电流密度较大的能源装置, 实际应用中需要将多个小尺寸GTEC串联在一起, 以提高装置的负载驱动能力. 根据$ {V_{{\text{OC}}}} $ , $ {J_{{\text{SC}}}} $ , $ {V_P} $ 和$ {J_P} $ , 可引入一个伏安特性因子$f = {{{V_P}{J_P}} / {\left( {{V_{{\text{OC}}}}{J_{{\text{SC}}}}} \right)}}$ 来评估GETC的电学性能, $ f $ 值越接近于1, 电学性能就越高. 从图2(b) 可看出结构参数$ d $ 对功率密度$ P $ 的影响显著, 优化电压$ {V_P} $ 随$ d $ 的增加而右移, 效率$ \eta $ 和电压优化值$ {V_\eta } $ 随结构参数$ d $ 的增加基本保持不变, 其物理机理是: 附加势垒高度$ {\phi _{{\text{M1}}}} $ 随$ d $ 的增加而升高, 如图2(a) 所示, 则空间电荷积累效应对阴极板热激发电子传输的阻碍作用就越强, 阴极板的电流密度$ {J_1} $ 就越小, 需要提高输出电压才能获取最高功率密度$ {P_{\max }} $ ; 从图2(b) 和图2(c) 可看出功率密度$ P $ 和阴极板热流$ {q_{\text{1}}} $ 随$ d $ 的增加均呈下降趋势, 其导致结构参数$ d $ 的变化对$ \eta $ 和$ {V_\eta } $ 的影响较小.图2(c) 可看出两个热流$ {q_{\text{1}}} $ 和$ {q_2} $ 随$ V $ 的增加而单调下降, 这是由于阴极板附加势垒高度$ {\phi _{{\text{M1}}}} $ 随$ V $ 的增加而升高, 最高势垒$ {\phi _{\text{M}}} $ 也相应增加, 导致两极板的热电子可越过$ {\phi _{\text{M}}} $ 的数目减少, 因此, 热流$ {q_{\text{1}}} $ 和$ {q_2} $ 均减少. 在$ {V_P} \leqslant V \leqslant {V_\eta } $ 区域, 热流$ {q_{\text{1}}} $ 的下降幅度高于功率密度$ P $ , 因此效率$ \eta $ 随电压$ V $ 的升高而增加; 在$ {V_\eta } \leqslant V \leqslant {V_{{\text{OC}}}} $ 区域, 热流$ {q_{\text{1}}} $ 的下降幅度低于功率密度$ P $ , 因此效率$ \eta $ 随电压$ V $ 的增加而下降. 图2(c) 显示随$ d $ 的增加, 热流$ {q_{\text{1}}} $ 和$ {q_2} $ 均减少, 这是由热电子输运和热输运共同所致. 由于在短路和开路状态下GTEC不产生电功率, 则$P = {q_{\text{1}}} - $ $ {q_2} = 0$ , 因此, 两个热流$ {q_{\text{1}}} $ 和$ {q_2} $ 在短路和开路状态下相等$ \left( {{q_{\text{1}}} = {q_2}} \right) $ , 这与图2(c) 中的结果相吻合.$ P $ 与效率$ \eta $ 的乘积在${V_P} \leqslant V \leqslant $ $ {V_\eta }$ 范围内可达最大值, 因此$ {V_P} \leqslant V \leqslant {V_\eta } $ 是GTEC的优化区间. 从图2(d) 看出真空间隙$ d $ 对近场辐射热流与阴极板热流比值${{{q_{{\text{NF}}}}}/{{q_{\text{H}}}}}$ 的影响较小, 而${{{q_{{\text{NF}}}}}/{{q_{\text{H}}}}}$ 是电压$ V $ 的单调递增函数, 当$ V = {V_\eta } $ , ${{{q_{{\text{NF}}}}}/{{q_{\text{H}}}}}$ 达上界${\left( {{{{q_{{\text{NF}}}}} /{{q_{\text{H}}}}}} \right)_{{\text{ub}}}} = 0.0831$ , 则热电子输运能量损失占总热流$ {q_{\text{H}}} $ 的比例约为60%, 由此说明空间电荷积聚效应对GTEC转换效率的影响占主导.图2 看出在开路电压$ {V_{{\text{OC}}}} $ 左侧的一部分区域, 真空间隙$ d $ 对GTEC能量转换性能的影响较小, 这是由于该区域的附加势垒$ {\phi _{{\text{M1}}}} $ 随真空间隙$ d $ 的增加而不发生变化. 图2 还表明在恒定温差$ \left( {\Delta T = {T_1} - {T_2}} \right) $ 条件下, 减小真空间隙$ d $ 可提高GETC的净电流密度$ J $ 和功率密度$ P $ , 但实际应用中需合理设计$ d $ , 一方面, $ d $ 越小, 对真空技术工艺的要求就越高, 同时两极板之间微纳尺度近场热辐射输运产生的能量损失越高, 这将使阳极板的温度$ {T_2} $ 升高, 从而导致恒定温差物理模型失效; 另一方面, 真空间隙$ d $ 越大, 热电子输运产生的能量损失就越大, 这也将导致两个极板的温差减小, 从而影响器件的电学特性和转换效率. 因此, 考虑器件高低温端的牛顿换热, 建立非恒温器件模型, 并结合当前真空技术, 将$ d $ 设计在合理区域, 这对于GTEC理论设计和实际应用是有益的, 下部分将讨论这一关键问题.$ d = 1.5\, {\text{μm}} $ , 当(25 )式和(26 )式的高温端和低温端的牛顿传热被考虑时, 阴极板温度$ {T_1} $ 和阳极板温度$ {T_{\text{2}}} $ 可通过数值求解能量平衡方程获得. $ {T_1} $ 和$ {T_{\text{2}}} $ 以及功率密度$ P $ 与效率随电压$ V $ 的变化关系曲线, 如图3 所示, 其中$ {V_P} $ 和$ {V_\eta } $ 分别是在最大功率密度和最大效率时的优化电压, $ {T_{1 P}} $ 和$ {T_{1\eta }} $ 是阴极板优化温度, $ {T_{2 P}} $ 和$ {T_{2\eta }} $ 是阳极板优化温度. 图3(a) 显示考虑牛顿传热后, $ {V_P} $ 高于平带电压$ {V_{{\text{fb}}}} $ , $ {T_1} $ 随电压$ V $ 的增加而升高, $ {T_{\text{2}}} $ 随电压$ V $ 的增加而下降. 对比图2(b) 和图3(b) , 可得出$ {P_{\max }} $ 下降幅度较大, 而效率下降幅度较小, 这是由${T_{1 P}} \ll $ $ {T_{\text{H}}}$ 、${T_{2 P}} \gg {T_{\text{L}}}$ 、$ {T_{1\eta }} \to {T_{\text{H}}} $ 和$ {T_{2\eta }} \to {T_{\text{L}}} $ 所致. 由于功率密度与效率的乘积$ P \times \eta $ 在图 3 极板温度$ {T_1} $ 与$ {T_{\text{2}}} $ 和功率密度$ P $ 与效率$ \eta $ 随电压$ V $ 的变化曲线, 其中$d = 1.5\, {\text{μm}}$ (a)$ {T_1} $ 与$ {T_{\text{2}}} $ ; (b)$ P $ 与$ \eta $ Figure3. The curves cathode’s operating temperature $ {T_1} $ and anode’s operating temperature $ {T_{\text{2}}} $ and power density $ P $ and efficiency $ \eta $ varying with the voltage $ V $ , where $d = 1.5\, {\text{μm}}$ : (a)$ {T_1} $ and $ {T_{\text{2}}} $ ; (b)$ P $ and $ \eta $ .33 )式为$ V $ 的优化区间, 调节负载, 可使$ V $ 处于该优化区域. 根据(33 )式, 可确定阴极板温度和阳极板温度的优化区间:35 )式的温度区间内, 阳极板温度高于环境温度, 通过能源梯级利用系统的构建, 可减少阳极板余热排放, 提高转换效率[28 -30 ] . 根据$ {V_P} $ 、$ {V_\eta } $ 、$ {T_{1 P}} $ 、$ {T_{1\eta }} $ 、$ {T_{2 P}} $ 和$ {T_{2\eta }} $ , 可确定电流密度$ J $ 在在最大功率密度和最大效率时的的优化值$ {J_P} $ 和$ {J_\eta } $ , 则电流密度$ J $ 的优化区间为:$ d $ 的减小分别被削弱和增强, 因此, 通过$ d $ 的优化设计可改善GTEC的性能. 图4(a) 显示存在优化间距$ d = {d_P} $ 和$ d = {d_\eta } $ 使GTEC分别获得最高功率密度$ {P_{\text{M}}} = 10.62\, {\text{W}} \cdot {\text{c}}{{\text{m}}^{ - 2}} $ 和效率$ {\eta _{\text{M}}} = 33.2{{\text{%}}} $ . 折衷考虑功率密度和转换效率, 则$ d $ 应位于以下区间:图 4 (a)最高功率密度$ {P_{\max }} $ 与效率$ {\eta _{\max }} $ 和(b)优化电压$ {V_P} $ 和$ {V_\eta } $ 以及优化比值$ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_P} $ 和$ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_\eta } $ 随真空间隙$ d $ 的变化曲线Figure4. The curves (a) the maximum power density $ {P_{\max }} $ and efficiency $ {\eta _{\max }} $ and (b) the optimum operating voltages $ {V_P} $ and $ {V_\eta } $ , and the optimum ratios $ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_P} $ and $ {\left( {{{{q_{{\text{NF}}}}} \mathord{\left/ {\vphantom {{{q_{{\text{NF}}}}} {{q_{\text{H}}}}}} \right. } {{q_{\text{H}}}}}} \right)_\eta } $ varying with the vacuum gap $ d $ .图4(b) 显示在$ {d_P} \leqslant d \leqslant {d_\eta } $ 区间内, $ {V_P} $ 和$ {V_\eta } $ 分别维持在0.551 V和1.03 V. 图4(b) 还显示${\left( {{{{q_{{\text{NF}}}}} / {{q_{\text{H}}}}}} \right)_\eta }$ 高于${\left( {{{{q_{{\text{NF}}}}} /{{q_{\text{H}}}}}} \right)_P}$ , 这是由于(34 )式和(35 )式决定了最大效率$ {\eta _{\max }} $ 时的温差$( {{T_{1, \eta }} - {T_{2, \eta }}})$ 高于最大功率密度$ {P_{\max }} $ 时的温差$( {{T_{1, P}} - {T_{2, P}}} )$ , 从而导致${\left( {{{{q_{{\text{NF}}}}} / {{q_{\text{H}}}}}} \right)_\eta } \gt $ $ {\left( {{{{q_{{\text{NF}}}}} / {{q_{\text{H}}}}}} \right)_P}$ . 由于在$ {d_P} \leqslant d \leqslant {d_\eta } $ 区间内的比值${{{q_{{\text{NF}}}}}/ {{q_{\text{H}}}}}$ 较小, 这说明空间电荷效应对GTEC性能的影响占主导.$ d \gt {\lambda _{{\text{th}}}} $ 条件下的远场辐射热流$ {q_{{\text{FF}}}} $ :$F = 0.13 \times {\text{1}}{0^{ - 12}}\, {\text{W}} \cdot {\text{c}}{{\text{m}}^{ - 2}} \cdot {{\text{K}}^{ - 4}}$ 为石墨烯表面热发射率0.023[20 ] 与斯特藩-玻尔兹曼常数的乘积. 给定$d = 4\; {\text{μm}} \gt {\lambda _{{\text{th}}}}$ , 在同时考虑远场热辐射效应和空间电荷效应条件下可获得$ {P_{\text{M}}} = 9.81\, {\text{W}} \cdot {\text{c}}{{\text{m}}^{ - 2}} $ 和${\eta _{\text{M}}} = 31.2{{\text{%}} }$ , 它们低于图4(a) 的$ {P_{\text{M}}} $ 和$ {\eta _{\text{M}}} $ . 进一步分析可知功率密度与效率随着$ d $ 的增大而减小. 这表明本文基于空间电荷效应和近场热辐射效应研究 GTEC的性能, 获得的优化结果是很有意义的, 根据(33 )式—(37 )式选择参数, 可确保GTEC操作在最优区域.4.结论与展望 24.1.结 论 4.1.结 论 本文协同考虑热电子输运和近场热辐射输运的耦合作用对GETC能量转换性能的影响, 开展了理论分析与参数优化研究, 所获得的主要结论如下:$ \left( {{T_1} - {T_2}} \right) $ 小于$ \left( {{T_{\text{H}}} - {T_{\text{L}}}} \right) $ , 而最优转换效率时的极板温差$ \left( {{T_1} - {T_2}} \right) $ 趋于$ \left( {{T_{\text{H}}} - {T_{\text{L}}}} \right) $ , 从而导致低温端牛顿换热对GETC的功率密度的影响显著, 而对效率的影响较小. 折中考虑功率密度和效率, 确定了电压、真空间隙和极板温度的优化判据. 另外, 研究发现近场热辐射条件下所获得的最优性能优于远场热辐射条件下所获得的最优性能, 这说明基于空间电荷效应和近场热辐射效应的器件性能优化研究是意义的.4.2.展 望 -->4.2.展 望 1) 本文未考虑石墨烯掺杂[31 ] 、本征缺陷(点缺陷, 单空穴缺陷, 多重空穴缺陷, 线缺陷和面外碳原子引入缺陷)与外引入缺陷[32 ,33 ] 和工作温度[34 ] 对费米能级、费米速率、化学势、导电率、电子弛豫时间等参数的影响, 有必要深入揭示这些因素对GTEC热-光-电特性和能量转换性能的影响, 使GETC的模型更加完善, 建立既便于理论分析又便于实验研制的参数优化设计准则.$ m_{\text{e}}^* $ 、材料功函数$ \phi $ 等物理特性, 另外材料的光学特性也是重点考察因素, 因为它影响TEC内部的辐射换热性能. 随着新型材料的不断涌现, TEC的物理模型也将更加丰富. 
















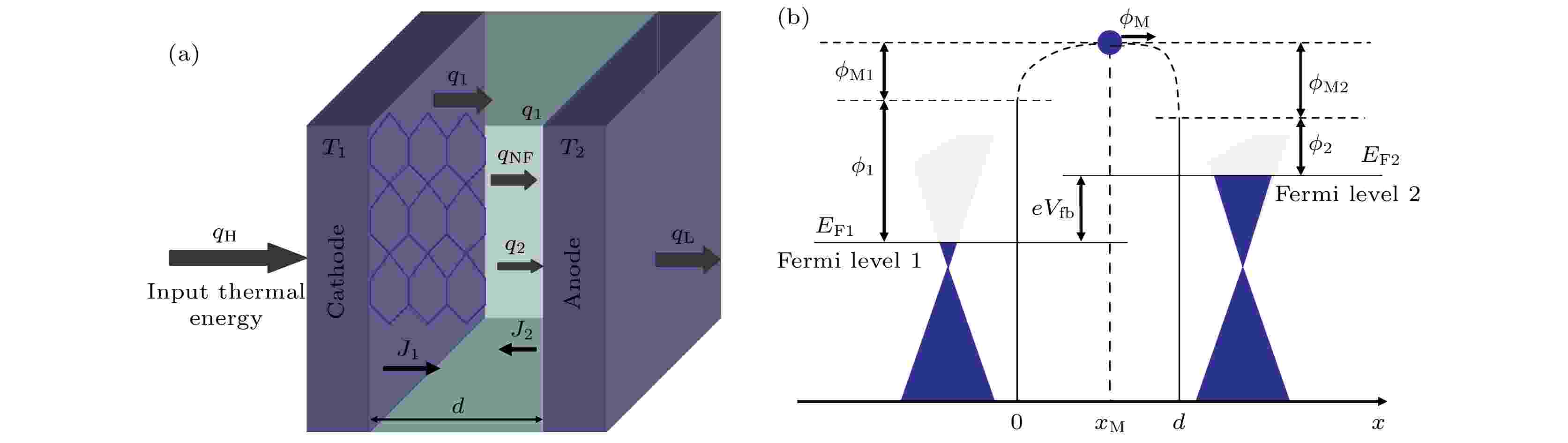 图 1 GTEC的结构和能带示意图 (a)结构; (b)能带
图 1 GTEC的结构和能带示意图 (a)结构; (b)能带






























































































































































































































 图 2 三个不同真空间隙条件下, GTEC的净电流密度
图 2 三个不同真空间隙条件下, GTEC的净电流密度










































































































































































































































































































































































































 图 3 极板温度
图 3 极板温度
































































 图 4 (a)最高功率密度
图 4 (a)最高功率密度















































