摘要:二维磁性半导体由于兼具磁性、半导体性和特殊的二维结构而受到人们的广泛关注, 为纳米级自旋电子和光电子器件的研发应用和相关的基础理论研究提供了新的思路和平台. 基于第一性原理计算, 在对一系列二维双金属碘化物CrTMI₆的交换能进行初步筛选的基础上, 选出了具有铁磁性的CrMoI₆单层结构. 进一步计算表明, CrMoI₆单层的电子能带结构展示出理想的半导体特性, 计算得到的带隙约为1.7 eV, 而且还具有很大的磁各向异性能(741.3 μeV/TM). 通过基于海森伯模型的蒙特卡罗模拟预测这一材料的居里温度达到92 K, 约为CrI₃单层的2倍. 此外, 分子动力学和声子谱的计算还证明了其良好的热稳定性和动力学稳定性. 这类可以通过合金化方法合成的磁性过渡金属卤化物将进一步拓展二维磁性材料家族及其在自旋电子学器件领域的应用.
关键词: 二维材料/
磁性半导体/
居里温度/
磁各向异性

English Abstract

全文HTML

--> --> -->

二维材料在电子、光电子、催化、电池、生物医学、传感器、磁性等领域展现出了越来越广泛的应用潜力^[1-6]. 2017年, 具有本征铁磁性的二维CrI₃和Cr₂Ge₂Te₆在实验上被成功剥离^[7,8], 这是人们首次通过实验确认的具有长程铁磁序的二维半导体材料. 这一突破不仅为探索二维磁体的各种物理机制提供了平台, 也预示着二维材料将进一步拓展到数据存储、磁电传感器、逻辑器件等基于磁性材料的器件领域^[9-11]. 但是, 二维磁性半导体材料除了面临产量化制备和环境稳定性等二维材料的共同难题以外, 还存在着特有的居里温度普遍较低的困难. 这导致二维铁磁耦合很难在较高温度下得以维持. 例如, 已有的CrI₃单层的居里温度低于45 K, Cr₂Ge₂Te₆双层的居里温度仅为20 K, 均远远低于室温甚至是液氮温度, 这极大地限制了它们的实际应用. 因此, 如何通过各种途径来提高二维磁性半导体材料的居里温度是当前该研究领域需要解决的重要问题之一.
通过对已有的铁磁材料进行合金化掺杂是提高材料居里温度的一个有效方法. Xue等^[12]在单层CrCl₃中利用同价W原子取代50%的Cr原子, 发现单层CrWCl₆具有很强的面外磁各向异性以及强的自旋轨道耦合, 居里温度达到了76 K; Guan等^[13]通过在二维MnS₂铁磁半导体中引入Re原子, 构建等价合金化合物Mn_xRe_1–xS₂, 将居里温度提高到室温以上. 引入Mn-Re相互作用后, 也看到了自旋耦合的显著增强. 因此, 基于现有磁性二维半导体材料构建合金化合物很有可能实现提高居里温度的目的. 本文基于实验报道的单层CrI₃构建了合金化合物CrTMI₆, 其中的过渡金属TM遍历了元素周期表中第四、第五周期的过渡金属元素. 通过基于第一性原理的高通量计算, 选定了一个具有较大铁磁交换能的二维本征铁磁半导体CrMoI₆作为进一步研究的对象. 通过声子谱计算和从头算分子动力学(AIMD)模拟证实了其动力学和热力学稳定性. 考虑了自旋轨道耦合后的理论计算表明, CrMoI₆单层具有相当大的磁各向异性能, 易磁轴垂直于材料所在的二维平面. 蒙特卡罗模拟预测得到单层CrMoI₆的居里温度约为92 K, 达到CrI₃单层的2倍以上.

本文主要采用基于密度泛函理论的第一性原理计算方法, 通过应用软件VASP(Vienna ab-initio simulation package)^[14]来研究材料的电子结构和磁性质. 计算过程中广义梯度近似(GGA)下PBE(Perdew-Burke-Ernzerhof)泛函用于优化结构^[15], 同时考虑了体系中的自旋极化作用. 投影缀加平面波(projected augmented wave, PAW)方法用于描述离子实和价电子间的相互作用^[16]. 平面波截断能设置为500 eV, 并采用Γ中心的Monkhorst-Pack方法^[17]进行第一布里渊区采样. 对于2×2超胞结构的优化, k点网格的选取为3×3×1, 能量收敛精度为10^–6 eV, 力收敛精度为0.01 eV; 在对能带等电子结构计算时则采用了25×25×1的网格来获得更高的精度. 离子弛豫总能量收敛的标准是10^–6 eV, 原子之间相互作用力的收敛标准为0.01 eV/?. 为了防止周期性边界条件可能带来的平面重叠干扰, 在垂直于平面方向设置了18 ?的真空层. 本文采用基于海森伯模型的蒙特卡罗模拟方法预估了材料的居里温度^[18]. 在稳定性计算中, 采用了密度泛函微扰理论计算声子谱来判断材料的动力学稳定性^[19], 并在正则系统中使用AIMD方法测试了材料的热稳定性.

2

-->

3.1.高通量筛选二维合金化合物CrTMI₆

基于单层CrI₃的晶体结构搭建二维合金化合物CrTMI₆, 其中TM代表的是元素周期表中第四、第五周期的过渡金属元素, 如图1(a)所示. 具体来说, 从单层CrI₃的2$ \times $2超胞结构入手, 使过渡金属元素替换超胞中50%的Cr原子, 形成CrTMI₆双金属碘化物. 针对这些结构, 计算了每一种材料的铁磁和反铁磁结构的能量. 筛选准则为总交换能E_ex的正负号和大小, 这里交换能为反铁磁耦合的超胞能量减去铁磁耦合的能量, 即$ {E_{{\text{ex}}}} = {E_{{\text{AFM}}}} - $$ {E_{{\text{FM}}}} $. 若结果为正值, 表示铁磁耦合更稳定; 若为负值则表示反铁磁耦合更稳定. E_ex绝对值越大一般情况下说明耦合就越强. 考虑到计算量的问题, 这里只计算了如图1(b)所示的合金原子分布结构和基于该结构的两种反铁磁态和铁磁态的能量对比作为粗筛的依据.
图 1 (a)二维等价合金化合物CrTMI₆中TM元素的选取示意图; (b)高通量计算中考虑的单层CrTMI₆的铁磁构型和两种反铁磁构型; (c)使用GGA+U方法前后单层CrTMI₆材料的交换能. 其中E_ex1 = E_AFM1 – E_FM, E_ex2 = E_AFM2 – E_FM; E(U)_ex1和E(U)_ex2为使用GGA+U后的相应值
Figure1. (a) Schematic diagram of the selection of TM element in the two-dimensional equivalent alloy compound CrTMI₆; (b) ferromagnetic configuration and two antiferromagnetic configurations of monolayer CrTMI₆ considered in high-throughput calculations; (c) exchange energy of CrTMI₆ monolayer before and after GGA+U method applied, where E_ex1 = E_AFM1 – E_FM, E_ex2 = E_AFM2 – E_FM; E(U)_ex1 and E(U)_ex2 are the corresponding values using GGA+U.

基于GGA+PBE计算结果, 得到了9种铁磁材料(E_ex1和E_ex2均为正)和10种反铁磁材料(E_ex1和E_ex2均为负或任一为负), 如图1(c)和表1所示. 为了考虑d电子之间较强的库仑相互作用, 使用GGA + U^[20,21]方法再次计算交换能. 在不同的过渡金属元素U值的选取上, 使用文献提供的每种过渡金属元素相应价态的参数来描述它们的d轨道电子, 具体数值见表2. 计算后发现部分材料的磁性耦合基态发生了变化: 有4种材料由铁磁性转变为反铁磁性, 分别为CrTiI₆, CrCoI₆, CrNbI₆, CrVI₆; 有两种材料由反铁磁性转变为铁磁性, 分别为CrRuI₆, CrMnI₆. 因此, 若按照GGA + U的结果来看, 得到了6种铁磁材料和13种反铁磁材料(图1(c)及表1). 值得注意的是, 在整个过程中, CrMoI₆单层的磁性耦合情况没有发生变化. 而且, 在铁磁材料中, CrMoI₆的总交换能最大, 即铁磁耦合最强. 因此, 在后面的内容中, 将围绕CrMoI₆单层材料进行更为深入的研究. 为了结果的准确性, 上述所有不同结构加U后的能量都在对应磁性耦合状态下重新进行结构优化后得到.

材料	交换能/eV
	Eex1	Eex2	E(U)ex1	E(U)ex2
CrMoI6	219.40	315.84	108.58	196.34
CrZnI6	62.14	62.06	33.52	34.48
CrScI6	19.53	19.49	23.13	23.00
CrRhI6	17.97	17.94	25.99	25.91
CrYI6	10.65	10.66	13.90	13.88
CrTiI6	72.12	146.71	150.49	–82.80
CrRuI6	–101.15	66.06	14.58	–8.83
CrCoI6	25.84	25.88	80.72	–235.76
CrMnI6	–150.41	–150.73	150.10	157.28
CrAgI6	–29.97	4.74	21.69	–32.62
CrCdI6	–20.45	–52.78	–39.27	9.51
CrCuI6	–52.43	–132.37	–7.68	–65.38
CrNiI6	–194.93	–231.25	–51.18	–45.46
CrPdI6	–313.25	–359.92	–24.18	–67.84
CrZrI6	–290.64	–385.45	2.73	–77.70
CrFeI6	–292.42	–399.20	–62.40	–121.16
CrTcI6	–98.88	–146.83	–301.14	–1104.20
CrNbI6	65.53	337.29	–698.92	–681.61
CrVI6	219.46	211.92	–776.31	–718.52

表1单层CrTMI₆的2×2超胞的交换能
Table1.Exchange energy of 2×2 supercells of CrTMI₆ monolayer.

材料	U/eV
V	3.1[22]
Cr	3.5[22]
Mn	3.9[22]
Fe	4.0[22]
Co	3.4[22]
Ni	6.0[22]
Cu	4.0[22]
Zn	5.0[23]
Nb	2.0[24]
Mo	3.5[22]
Tc	2.3[24]
Ru	2.4[24]
Rh	2.8[24]
Pd	3.3[24]
Ag	5.1[25]
Cd	6.0[25]

表2过渡金属元素TM所使用的U值
Table2.Value of U used for the transition metal element TM.

2 -->

3.2.单层CrMoI₆的结构特性及稳定性

针对单层CrMoI₆, 在上述的基本构型之外, 进一步设计了6种可能的合金原子排列结构(图2(a)). 对于Cr原子和Mo原子, 使用表2中所列的对应值来适当地考虑强关联电子. 计算结果表明, C2构型的能量最低, 这一结构中存在Mo(Cr)原子的二聚体, 这可能是使该结构相对稳定的原因. 如图2(b)所示, C2构型中的Mo原子间的平均距离约为6.5 ?, Mo和Cr原子相互间隔或过于聚集都会造成能量的略微上升.
图 2 (a)单层CrMoI₆可能存在的6种不同构型; (b) C1—C6各构型相对C2构型平均到每个化学式的能量差和Mo-Mo间的平均距离; (c)单层CrMoI₆的声子谱; (d)时长10 ps, 温度300 K的分子动力学模拟下, 系统温度和总能量的变化以及模拟结束时的结构
Figure2. (a) Six possible configurations of CrMoI₆ monolayer that may exist; (b) energy difference of C1?C6 configuration relative to C per chemical formula and the average bond distance between Mo-Mo; (c) phonon spectrum of CrMoI₆ monolayer; (d) molecular dynamics simulation with duration of 10 ps, 300 K and the variation curves of system temperature and total energy, as well as the structure at the end of simulation.

结构稳定性是二维材料在实验制备和应用中的首要条件. 因此, 对单层CrMoI₆的动力学稳定性和热稳定性进行了计算评估. 首先, 计算了单层CrMoI₆的声子谱结构, 如图2(c)所示, 在整个布里渊区内, 声子谱没有虚频, 说明它具有良好的动力学稳定性. 图2(d)给出了300 K温度下单层CrMoI₆在AIMD模拟过程中总能量的波动以及模拟10 ps后的晶体结构. 计算中使用了Nosé-Hoover方法^[26]进行控温, 在正则系统中每个温度的步长为1 fs. 从图2(d)可以看出, 整个模拟过程中, 能量和系统温度波动都较小, 且所有原子都在平衡位置附近振动, 二维周期性结构始终能够得以保持. 以上计算结果表明, 单层CrMoI₆具有良好的热稳定性, 预测可以在室温范围内稳定存在.
2 -->

3.3.单层CrMoI₆的磁性耦合与能带

为了进一步验证单层CrMoI₆更倾向于铁磁耦合, 考虑图3(a)所示的6种可能的反铁磁耦合结构. 计算结果表明, 铁磁态的能量最低, 相比反铁磁构型中能量最低的AFM1, 铁磁态平均到每个化学式的能量低约25 meV, 如图3(b)所示. 基于优化后的结构可以发现, Cr-I-Mo, Cr-I-Cr和Mo-I-Mo的键角均位于94°—95°区间内, 根据Goodenough-Kanamori-Anderson (GKA)规则^[27-29], 这类键角在90°左右的磁性离子间的超相互作用(super-exchange interaction)一般会带来材料的铁磁序, 这可以解释上述计算得到的铁磁耦合下单层CrMoI₆能量最低的结果.
图 3 (a)单层CrMoI₆的6种反铁磁构型示意图; (b)不同反铁磁构型相对于铁磁构型平均到每个化学式的能量差; (c)单层CrMoI₆的能带结构示意图, 红色实线表示自旋向上通道, 蓝色实线表示自旋向下通道; (d) Cr, Mo合金体系的轨道演化及能级差示意图; (e)单层CrMoI₆的自旋向上状态的分轨道能带结构, Cr的$ {\text{e}}_{\text{g}} $和${\text{t}}_{\text{2g}}$轨道分别用浅蓝色和深蓝色表示, Mo的$ {\text{e}}_{\text{g}} $和${\text{t}}_{\text{2g}}$轨道分别用浅红色和深红色表示, 灰色表示Cr, Mo和I原子的s轨道以及p轨道; (f)使用HSE06杂化泛函计算得到的单层CrMoI₆的能带结构图
Figure3. (a) Schematic diagram of six antiferromagnetic configurations of CrMoI₆ monolayerand (b) energy difference per formula of different antiferromagnetic configurations. (c) Band structure of CrMoI₆ monolayer. The solid red and blue lines represent the spin-up and spin-down channels, respectively. (d) schematic diagram of orbital evolution and energy level difference of Cr and Mo alloy systems. (e) Band structure of CrMoI₆ monolayer in the spin-up state. The $ {\text{e}}_{\text{g}} $ and ${\text{t}}_{\text{2g}}$ orbitals of Cr and Mo atoms are shown in light blue, dark blue, light red and dark red, respectively. The s and p orbitals of Cr, Mo, and I atoms are shown in gray. (f) Band structure of CrMoI₆ monolayer calculated with HSE06 functional.

针对单层CrMoI₆的铁磁耦合结构, 首先使用DFT+U的方法计算其电子能带结构, 如图3(c)所示. 单层CrMoI₆的能带结构在自旋向上和自旋向下通道都表现出了半导体特性, 自旋向上通道的带隙为0.97 eV, 自旋向下通道的带隙为2.9 eV. 从整体来看, 价带顶和导带底均由自旋向上的电子提供, 和单层CrI₃的能带结构类似^[30]. 进一步分析发现, CrMoI₆的结构可划分为多个CrI₆和MoI₆八面体, 八面体晶体场会使d轨道能级分裂为能量较低的$ {\text{t}}_{{2 {\rm{g}}}} $态(包含$ {\text{d}}_{{xy}}\text{, }\text{}{\text{d}}_{{yz}}\text{和}{\text{d}}_{{xz}} $轨道)和能量较高的$ {\text{e}}_{\text{g}} $态(包含$ {\text{d}}_{{{z}}^{\text{2}}} $和${\text{d}}_{{{x}}^{{2}}{-}{{y}}^{{2}}}$轨道). 理想状态下, 体系中Cr³⁺和Mo³⁺都具有3个d轨道电子, 按照洪特规则, 它们应该在各自$ {\text{t}}_{\text{2g}} $态的三个轨道上填充3个相同自旋的电子, 而能量较高的$ {\text{e}}_{\text{g}} $态则无电子占据, 如图3(d)所示. 计算得到的Cr和Mo离子的局域磁矩为2.95μ_B, 符合上述预测. 图3(e)是计算得到的多数占据自旋通道(即自旋向上通道)的各轨道投影能带图, 其中Cr原子的$ {\text{e}}_{\text{g}} $和$ {\text{t}}_{2{\rm{g}}} $轨道分别用浅蓝色和深蓝色实心圆表示, Mo原子$ {\text{e}}_{\text{g}} $和$ {\text{t}}_{2{\rm{g}}} $轨道分别用浅红色和深红色实心圆表示, 灰色实线表示Cr, Mo和I原子的s轨道以及p轨道. 可以看到, Mo原子的$ {\text{e}}_{\text{g}} $态轨道能量最高, 其次是Cr原子的$ {\text{e}}_{\text{g}} $态轨道, 这两组轨道主要分布在费米面以上, 没有电子占据. 而在费米面以下, Mo原子的$ {\text{t}}_{2{\rm{g}}} $态轨道也在Cr原子的$ {\text{t}}_{2{\rm{g}}} $态之上, 证实了图3(d)中的分析结果. 为了更准确地描述单层CrMoI₆的电子能带结构, 使用HSE06泛函计算了它的能带(图3(f)). 计算结果表明, 在HSE06泛函下单层CrMoI₆自旋向上和自旋向下的带隙分别提高到1.7和4.2 eV, 但能带的基本结构和带边位置都没有变化, 因此对上述的结论没有影响.
2 -->

3.4.磁各向异性与居里温度

磁各向异性是二维长程磁有序存在的必要条件, 通过加入自旋轨道耦合修正计算了单层CrMoI₆自旋取向沿不同方向的磁各向异性能(MAE). MAE沿x(100), y(010)和z(001)方向的角度依赖的计算公式如下:

$ MAE\left( {\theta ,\varphi } \right) = E\left( {\theta ,\varphi } \right) - E\left( {\theta = 0,\varphi = 0} \right) \text{, } $

其中θ和φ对应的方向角如图4(a)所示. 从计算结果可以看出, 单层CrMoI₆的易磁轴(MAE能量为0的方向)垂直于xy平面, 即易磁轴的方向始终都指向二维材料平面外. 计算得到每个磁性原子沿z方向的能量比x方向和y方向分别低997.4和741.3 μeV(见图4(b)和图4(c)). 这样大的磁各向异性能在二维磁性材料中并不多见, 预测对材料抵抗热扰动来稳定长程磁性耦合有重要作用.
图 4 (a) θ和φ的示意角度及xy轴在结构平面上的方向; (b)全空间内的磁各向异性能分布; (c)垂直于y轴方向的xz平面内的磁各向异性能分布极坐标图; (d)交换相互作用J₁—J₆的示意图; (e)单层CrMoI₆的磁矩及磁化率随温度的变化曲线; (f)单层CrI₃的磁矩及磁化率随温度的变化曲线
Figure4. (a) Schematic angles of θ and φ and the direction of the xy axis on the structure plane; (b) distribution of magnetic anisotropy energy in the whole space; (c) polar coordinate diagram of magnetic anisotropic energy distribution in the xz plane perpendicular to the y axis; (d) schematic diagram of exchange interaction J₁–J₆; The magnetic moment and susceptibility of (e) CrMoI₆ monolayer and (f) CrI₃ monolayer as a function of temperature.

居里温度是铁磁材料实际应用的一个关键参数, 使用基于海森伯模型的蒙特卡罗方法计算单层CrMoI₆的居里温度. 考虑到Cr原子和Mo原子的磁矩及交换相互作用的不同, 将二者区分开来考虑, 取最近邻Cr$ - $Cr(J₁), Cr$ - $Mo(J₂), Mo$ - $Mo(J₃), 次近邻Cr$ - $Cr(J₄), Cr$ - $Mo(J₅), Mo$ - $Mo(J₆)6种交换相互作用(见图4(d)), 则系统的自旋哈密顿量可写为

$ H = - \sum\limits_m {\sum\limits_{ij} {{J_m}{\boldsymbol{S}_i} \cdot {\boldsymbol{S}_j}} } - {\sum\limits_i {A\left( {S_i^Z} \right)} ^2} \text{, } $

其中, S_i和S_j为每个局域磁矩的自旋向量, J_m(m = 1, 2, ···, 6)代表上述6种交换相互作用参数, A是各项异性能参数, 表示为

$ A = {{MAE}}/{{{{\left| S \right|}^2}}} . $

结合之前获得的铁磁和反铁磁耦合状态的能量差, 可以得到各交换作用参数为: J₁ = 5.00×10^–3, J₂ = 4.16×10^–3, J₃ = 2.47×10^–3, J₄ = 0.616×10^–3, J₅ = 0.375×10^–3, J₆ = 0.538×10^–3. 在蒙特卡罗模拟中, 使用100×100的超胞, 在每个温度下模拟10^–7步, 同时所有磁位的自旋都是随机翻转的. 从图4(e)可以看出, CrMoI₆的磁化率在92 K时达到峰值, 同时磁矩的变化率也达到最大值, 说明此温度即为单层CrMoI₆的居里温度. 同时也计算了单层CrI₃的居里温度, 结果为43 K (图4(f)), 与实验值45 K符合较好, 说明了本文计算方法的可靠性.
2 -->

3.5.应力对磁性耦合的影响

在实验和应用过程中, 二维材料容易因衬底等外部因素的影响而受到应力作用, 并导致应变的产生, 这种应变往往会影响二维材料的物理性能. 因此, 本文进一步研究了应变对单层CrMoI₆的磁性影响. 首先施加等比例的双轴应变, 体系总能量和交换能E_ex的变化如图5(a)所示. 拉伸时反铁磁和铁磁的交换能会进一步增加, 而压缩时则会降低. 我们认为这是磁性离子间的直接相互作用和超相互作用竞争的结果. 磁性离子间的直接相互作用倾向于反铁磁耦合, 而前面提到的键角接近90°的超相互作用则带来铁磁耦合. 当拉伸时, 如图5(b)和图5(c)所示, 磁性离子间距增加, 直接相互作用减弱, 所以铁磁耦合增强. 而压缩时, 磁性离子间距减小, 直接相互作用增强, 所以铁磁耦合强度减弱. 另外, 我们发现键角偏离平衡位置也会减弱超相互作用带来铁磁耦合效果, 从图5(b)和图5(c)可以看到, 无论拉伸还是压缩, TM—I—TM的键角都会偏离原来的值, 造成图5(a)中铁磁耦合的减弱, 只是这种影响弱于离子间距改变对直接相互作用造成的影响. 图5(d)为在x, y单一方向施加应变的结果, 交换能的变化趋势和双轴应变的情况类似, 但变化幅度不同. 能量沿x方向变化较为平缓, 而y方向变化较为陡峭, 很显然这是由沿y方向的应变对磁性离子的间距影响更大造成的.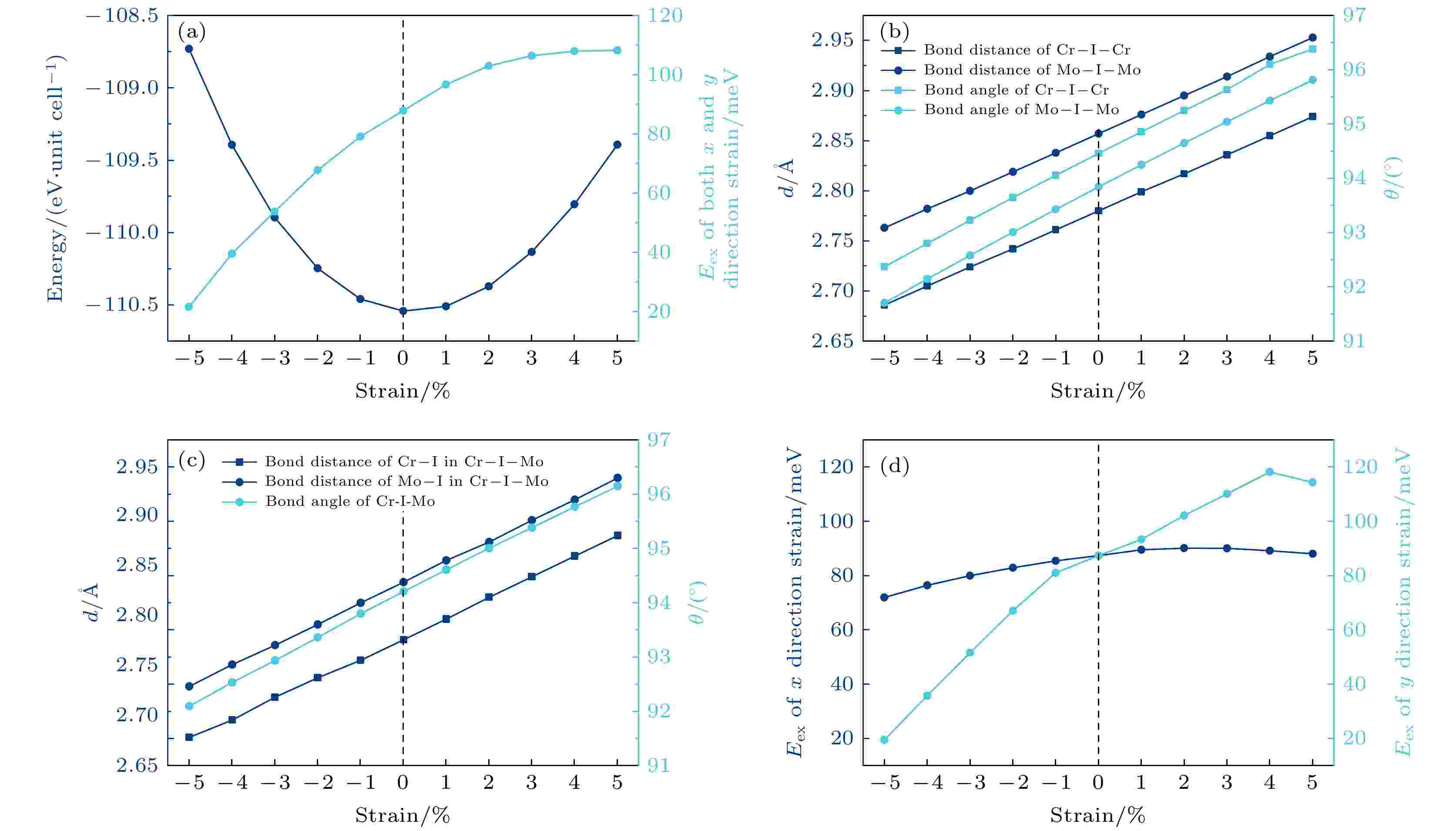
图 5 (a)双轴应变下CrMoI₆单层的交换能以及总能量的变化; (b)施加拉伸及压缩应变时Cr—I—Cr和Mo—I—Mo的键长与键角随应变大小的变化; (c)施加拉伸及压缩应变时Cr—I—Mo的键角以及其中Cr—I和Mo—I的键长随应变大小的变化; (d)单轴应变下的交换能随应变大小的变化
Figure5. (a) Variation of exchange energy and total energy of CrMoI₆ monolayer under biaxial strain; (b) variation of bond lengths and bond angles of Cr—I—Cr and Mo—I—Mo with strain under tensile and compressive strain; (c) variation of the bond angles of Cr—I—Mo and the bond lengths of Cr—I and Mo—I as a function of strain under tensile and compressive strain; (d) variation of exchange energy with strain under uniaxial strain.

通过第一性原理计算预测了一种稳定的CrMoI₆二维本征铁磁性材料. CrMoI₆单层是一种半导体材料, 其自旋向上和自旋向下通道的带隙分别为1.7和4.2 eV. 同时, 它具有面外易磁轴和相当大的磁各向异性能, 有作为高密度磁存储器件的优良性能. 海森伯模型下的蒙特卡罗模拟预测单层CrMoI₆的转变温度为92 K, 是单层CrI₃的两倍以上. 另外, 在施加压缩和拉伸应变的情况下, 其铁磁耦合表现出了较强的稳定性. 分子动力学模拟及声子谱计算也进一步表明这一材料有着良好的热力学稳定性和动力学稳定性.