摘要: X射线荧光CT(X-ray fluorescence computed tomography, XFCT)是一种使用X射线荧光(X-ray fluorescence, XRF)实现功能性成像的新技术, 在生物医学成像中表现出较大潜力. 但是, X射线穿过生物体的同时还会产生大量康普顿散射光子, 对XRF信号的采集形成很强的背景噪声; 因此, 如何有效消除康普顿散射噪声对于提高XFCT成像质量至关重要. 本文研究总结了XFCT成像过程中涉及的物理过程, 包括: 荧光的产额、退激发时间、荧光发射角分布、荧光偏振态、康普顿散射角分布与散射光偏振态, 并通过研究荧光与散射光物理性质的差异寻找去除康普顿散射噪声的方法. 经过物理过程推导和分析计算, 发现: 1) 高原子序数元素的K层荧光退激发时间极短, 在现有探测器的时间分辨率条件下, 无法分辨散射光与荧光; 2) K层发射荧光的角分布各向同性, 康普顿散射角分布在与入射光偏振方向附近取得最小值, 而且入射光线偏振度越高, 散射光的微分截面越小, 偏振光源将有利于减少康普顿散射噪声; 3) K层荧光线偏振度为零, 而康普顿散射光子在一些散射方向上具有一定线偏振度, 因此偏振态的差异可能用于降低康普顿散射噪声.
关键词: X射线荧光 /
计算机断层成像 /
偏振X光 /
康普顿散射 /
功能成像 English Abstract Calculation and analysis of key physical problems: Fluorescence yield, deexcitation time, scattering and polarization in X-ray fluorescence CT imaging Zhang Zhi-Zhen 1,2 ,Li Liang 1,2 1.Department of Engineering Physics, Tsinghua University, Beijing 100084, China Fund Project: Project supported by the Grant from National Key R and D Program of China (Grant No. 2018YFC0115502)Received Date: 21 April 2021Accepted Date: 21 May 2021Available Online: 07 June 2021Published Online: 05 October 2021Abstract: X-ray fluorescence computed tomography (XFCT) is a molecular imaging technique with great potential applications in biomedical imaging, in which used is the primary X-ray to excite element probes with high atomic number inside samples or tissues for functional imaging. However, owing to the limitation of molecular sensitivity and spatial resolution, the XFCT has not been widely used in the molecular imaging. A large number of Compton scattering photons are produced as the broadband primary X-ray passes through the samples or tissues, forming a strong noise background in the collected XRF signal, which is a major cause of limited molecular sensitivity. Therefore, eliminating the Compton scattering noise is very important for improving molecular sensitivity. In this paper, we summarize the main physical processes involved in the imaging process of XFCT, including the angle distribution and polarization state of the fluorescence and Compton scattering photons, fluorescence yield and deexcitation time of K-shell vacancy. The above physical processes are the main limitations of the imaging quality of XFCT. Through the derivation and analysis of physical processes, we explore the possibility of using these physical effects to reduce the Compton scattering noise and draw some conclusions below. 1) The deexcitation time of K-shell vacancy of the element with high atomic number is very short, consequently the scattered light and fluorescence cannot be distinguished between each other under the time resolution condition of the existing detector. 2) The angular distribution of the K-shell fluorescence emission is isotropic, and the differential cross section of Compton scattering reaches a minimum value near the polarization direction of the incident light of which the minimum decreases as the linear polarization degree of the incident light increases. Therefore, the polarized light source is beneficial to reducing the Compton scattering noise. 3) The linear degree of polarization of K-shell fluorescence is zero, while the Compton scattering photons possess a certain linear degree of polarization in some scattering directions, so the difference between polarization states may be helpful in reducing the Compton scattering noise.Keywords: X-ray fluorescence /computed tomography /polarized X-rays /Compton scattering /functional imaging 全文HTML --> --> --> 1.引 言 X射线荧光CT(X-ray fluorescence computed tomography, XFCT)是一种针对高原子序数元素的功能成像技术. XFCT通过探测X射线与物体内高原子序数元素发生光电效应后产生的XRF得到物质内该元素的浓度分布图像, 所以兼具透射型CT结构成像和发射型CT功能成像的优点. Boisseau和Grodzins[1 ] 利用美国国家同步辐射光源首次实现XFCT实验. 同步辐射光源具有准单能和高线偏振度的特性, 是XFCT成像的理想光源, 但是因为同步辐射占用场地和成本高昂的问题, 所以基于同步辐射的XFCT系统很难应用于实际医学应用中. X光机相比于同步辐射具有巨大的灵活性和经济性优势, 近年来有很多基于X光机的XFCT系统设计的研究[2 -9 ] . 因为X光机光源采用电子轫致辐射的方式产生X射线, 所以其能谱是分布范围较大的连续谱并且不具备线偏振特性. 相比于同步辐射光源, X光机光源会产生更大的散射背景, 严重影响了XFCT的成像质量.[10 ] . 第一种方法对光源单能性要求很高, 一般采用同步辐射源. 第二种方法利用散射光子能量连续分布的特点, 通过三次多项式拟合的方式估计散射, 进而在数据中减去散射的贡献[2 ] , 该方法对探测器的能量分辨率要求高, 一般使用单像素X射线谱仪采集荧光信号, 导致扫描时间很长.[11 ] 蒙卡模拟研究了逆康普顿光源线偏振特性对XFCT成像质量的影响, 发现逆康普顿光源能抑制XFCT成像的康普顿散射背景约1.6倍.2.XFCT成像方法和物理原理 在XFCT所涉及的能量范围内, X射线与物质相互作用方式有光电效应、相干散射和康普顿散射. 在X射线能量为几十keV时, 相干散射截面与康普顿散射截面相当, 所以在处理XFCT散射问题时相干散射和康普顿散射一般都要考虑, 其中相干散射主要沿着小角方向散射, 对光子的传播会有影响, 但通过后面的讨论可以看出, 在大角度方向康普顿散射是主要的.[2 -12 ] , 其中基于小孔成像、扇束X射线源和XRF探测器阵列的成像系统设计能大幅提高扫描速度[5 ] , 其XFCT实验布置示意图如图1 所示. 小孔准直器作用是使XRF探测器具有空间分辨能力. 示意图中被扫描物体是一个包含四个小圆柱的大圆柱模型, 四个小圆柱里含有不同浓度的某种高原子序数元素的溶液. 图1 中描绘了某一条光路以及该路径上可能产生的XRF光子和散射光子, 入射光与溶液中的重金属元素原子发生光电效应, 重金属原子发射荧光(特征X射线), 荧光经过小孔后, 被XRF探测器阵列探测, 同时散射光子也会进入XRF探测器, 形成散射背景. XRF探测器可通过设置能窗阈值得到入射到每个探测器单元的相应能窗的光子计数. X射线探测器阵列用于传统的透射型CT成像, 其得到的衰减系数分布图可用于XFCT成像的衰减校正.图 1 基于小孔成像方式的XFCT实验设置Figure1. Experimental setup based on pinhole imaging.[13 ] :I 表示光强度; ${P_1}$ 和${P_2}$ 表示在与传播方向垂直的平面内成$45^\circ $ 夹角的两对正交方向下分别测量得到的平面偏振度; ${P_3}$ 表示圆偏振度. 光束的线偏振度和圆偏振度定义分别为[14 ] ${P_{\rm{L}}}$ 表示线偏振度; ${P_{\rm{C}}}$ 表示圆偏振度; ${I_{{\rm{max}}}}$ 和${I_{{\rm{min}}}}$ 分别表示经过理想线偏振片后光强的最大与最小值; ${I_{\rm{R}}}$ 和${I_{\rm{L}}}$ 分别表示光束中右旋光和左旋光的强度. 定义归一化Stokes矢量为$ {\xi _1} = - 1 $ 对应的线偏振方向为x 轴, 则$ {\xi _1} = + 1 $ 对应的线偏振方向为y 轴, 传播方向为z 轴正向, 并规定: 迎着光子传播方向(z 轴正向)看时, 绕z 轴顺时针旋转角度为正, 绕z 轴逆时针旋转角度为负, 则在旋转$\psi $ 角度后的新正交方向下的Stokes矢量$ {\left[ {1, \zeta } \right]^{\rm{T}}} $ 与原正交方向下的Stokes矢量$ {\left[ {1, {\boldsymbol{\xi }}} \right]^{\rm{T}}} $ 由变换矩阵${\boldsymbol{M}}$ 联系, 即$ {\left[ {1, \zeta } \right]^{\rm{T}}} = {\boldsymbol{M}}{\left[ {1, {\boldsymbol{\xi }}} \right]^{\rm{T}}} $ . ${\boldsymbol{M}}$ 的非零元为$4 \times 4$ 变换矩阵T 联系相互作用前后的Stokes矢量:$ {\left[ {\begin{array}{*{20}{c}}{{I_0}}&{{{\boldsymbol{P}}_0}} \end{array}} \right]^{\rm{T}}} $ 表示入射光Stokes矢量; $ {\left[ {\begin{array}{*{20}{c}}I&{\boldsymbol{P}} \end{array}} \right]^{\rm{T}}} $ 表示散射光Stokes矢量.3.K层荧光物理性质 23.1.荧光产额 3.1.荧光产额 某个壳层或子壳层的荧光产额定义为该壳层产生一个空穴后, 通过发射荧光退激发的概率. K壳层产生空穴后, 不同跃迁方式产生的荧光的能量和强度不同. 一般地, 壳层越高的电子通过退激发填充K层空穴, 产生的荧光的能量越高, 某种荧光的强度正比于该荧光对应跃迁的分支比. 荧光产额的半经验公式[15 ] :${\omega _{\rm{K}}}$ 表示K层荧光产额; Z 表示原子序数; ${C_i}$ 表示拟合参数. (6 )式中参数${C_i}$ 可以由实验得到的不同元素荧光产额数据拟合得到. Bambynek等[15 ] 和Hubbell等[16 ] 结合理论计算与实验给出拟合参数和元素荧光产额数据表.${\omega _{\rm{K}}}$ 是原子序数Z 的增函数, 对$Z > 60$ 的元素, ${\omega _{\rm{K}}} > 90\%$ , 所以高原子序数原子的K层空穴态通过发射荧光退激的概率最大. 因此XFCT应该选择高原子序数元素作为荧光元素, 在高Z 元素范围内荧光产额基本饱和, 提高Z 对增加荧光产额的收益很低, 但提高Z 可增大荧光能量, 能量高的光子更容易穿透物体被探测器采集到, 从而降低统计噪声.α 代表来自L层电子的跃迁产生的荧光, Kβ 表示来自M层及更高层电子跃迁产生的荧光, 同一组内的荧光能量相近. Ertu?ral等[17 ] 给出了原子序数16≤Z ≤92 范围内59种元素的Kβ /Kα 荧光强度比测量值, Scofield[18 ] 给出了10≤Z ≤98原子序数范围内Kβ /Kα 荧光强度比理论计算值, 从实验和理论计算结果可以看出, 荧光强度比Kβ /Kα 随原子序数增大而增大, 对于$Z > 60$ 的元素, Kβ /Kα 荧光强度比在0.3左右. 通过荧光强度比和K层荧光产额${\omega _{\rm{K}}}$ 可以得到K层不同能量荧光的产额.3.2.荧光退激发时间 -->3.2.荧光退激发时间 如果荧光退激发半衰期很长, 且长于探测器的时间分辨率, 那么可以采用极短时间的X光脉冲作为光源, 在散射光子到达探测器后, 延迟一段时间采集荧光光子, 这样就可以在时间上分开散射和荧光从而去除康普顿散射背景; 如果探测器的时间分辨率大于荧光退激发半衰期, 那么荧光和散射光子到达探测器的平均时间差小于探测器时间分辨率, 从而无法分辨荧光和散射光子. 为了证明这种方法是否可行, 需要计算荧光退激发时间. 原子发生光电效应后处于激发态, 激发态是不稳定的, 假设t =0时刻原子处于激发态, 则在以后的t 时刻体系仍然停留在这个态的概率是$\tau $ 是激发态平均存在时间, 亦称激发态寿命, 其与激发态能级宽度$ \varGamma $ 关系为K 层荧光分宽度$ {\varGamma _{\rm{R}}} $ 与K 层荧光产额的关系是[15 ] $Z > 40$ 的元素, K 层空穴态能级宽度半经验公式为[15 ] 8 )式和(9 )式得到K 层荧光寿命${\tau _{\rm{K}}}$ 为$Z{\rm{ = 64}}$ ), K层荧光寿命为0.03 ps. 当前对伽马光子探测器时间分辨率要求最高的PET设备的符合时间分辨率在百皮秒量级[19 ] , 远大于中高原子序数元素的K层荧光退激发时间, 因此, 无法通过时间差别来分辨荧光与散射光子进而减少散射背景.3.3.荧光发射角分布与线偏振度 -->3.3.荧光发射角分布与线偏振度 原子内壳层荧光发射角分布和偏振态在理论和实验上已经有很多研究[20 -26 ] : 若空穴态的总角动量量子数$J = 1/2$ , 则荧光发射角分布各向同性且线偏振度为零[20 ] ; 若$J > 1/2$ , 则荧光发射一般各向异性并且部分偏振[22 ] . 因为K层空穴态$J = 1/2$ [22 ] , 所以K层空穴态发射荧光的角分布各向同性且线偏振度为零. L, M等不同子层具有不尽相同的总角动量量子数, 而且某些子层的空穴态会通过Coster-Kronig跃迁将空穴转移到其他子层, 因此L, M等壳层的空穴态发射荧光更加复杂多样, 剔除Coster-Kronig效应的影响后, 不同子层空穴态发射荧光角分布与线偏振度也满足上述角动量规则[24 ] .4.XFCT中的散射 24.1.散射光角分布 4.1.散射光角分布 实验室参考系下单个自由电子与线偏振光的康普顿散射截面Klein-Nishina公式为[25 ] ${r_0}$ 是经典电子半径; k 和${k_0}$ 分别是出射和入射光子能量, 以电子静质量能为单位; e ' e ${\rm{d}}\varOmega $ 是立体角元. 假设在出射方向n e' e n n ${\rm{d}}{\sigma _{{\rm{KN}}}}{\rm{/d}}\varOmega$ [27 ] . 散射方向和偏振方向如图2 所示, 入射光沿Z 轴正向入射, 用矢量${{\boldsymbol{k}}_0}$ ($\left| {{{\boldsymbol{k}}_0}} \right| = {k_0}$ )表示; 散射光沿$\overrightarrow {OS} $ 方向出射, 用矢量${\boldsymbol{k}}$ ($\left| {\boldsymbol{k}} \right| = k$ )表示. ${\boldsymbol{e}}$ 是描述入射光偏振方向的单位矢量, $ \theta = \angle SOZ $ 是散射角, $\varphi = \angle AOX$ 是散射的方位角. y 和y' 表示垂直于散射平面$SOX$ 的线偏振方向, x 和x' 表示平行于平面$SOX$ 的线偏振方向, 位于平面$x'Sy'$ 内的e ' 表示散射光的偏振方向, e ' 与y' 夹角为$\beta $ , 显然, x' , y' 和e ' 垂直${{\boldsymbol{k}}_{\rm{f}}}$ . 从图2 描述的几何关系得到 ${( {{\boldsymbol{e}} \cdot {\boldsymbol{e}'}} )^2} = {\cos ^2}\beta ( 1 - {{\sin }^2}\theta {{\cos }^2}\varphi )$ .图 2 偏振康普顿散射示意图Figure2. Schematic diagram of polarized Compton scattering.x' 和y' 的分截面求和得到入射光为线偏振光且不测量散射光偏振的实验中的截面[25 ] 为${P_{\rm{L}}}$ ($0 < {P_{\rm{L}}} < 1$ )的部分偏振光, 不测量散射光偏振的实验中的康普顿散射截面为[28 ] 图2 中X 轴方向取为入射光透过理想偏振片后的透射强度最大方向. 注意到公式中$k/{k_0} = $ $ 1/[ 1 + k_0 (1 - \cos \theta) ]$ 与方位角$\varphi $ 无关, 所以公式对$\varphi $ 积分后得到截面沿散射角$\theta $ 的分布与线偏振度${P_{\rm{L}}}$ 无关, 进而总截面与${P_{\rm{L}}}$ 无关.14 )式的最小值, 做变换$x = k/{k_0}$ , 则$x \in [1/\left( {1 + 2{k_0}} \right), 1]$ . 记(15 )式右边方括号内的项为函数$g(x, \varphi )$ , 则$\partial g/\partial x$ 在$x = 1/\left( {1 + 2{k_0}} \right)$ 处的值为$ f({k_0}, a) $ 和$h(x, a)$ 为$ f({k_0}, a){\rm{ = 0}} $ , 得到${k_0}$ 关于a 的唯一解, 记为${k_0} = K(a)$ . 易知, 当$ f({k_0}, a) \leqslant 0 $ 时, 方程$ h(x, a) = $ $ 0 $ 在定义域内存在唯一解, 记为$x = X(a)$ . 讨论函数(15)的最小值得到如下结论: 若${k_0} < K(1 + {P_{\rm{L}}})$ , 则函数(15)的最小值在$x = X(1 + {P_{\rm{L}}}), ~\varphi = 0, ~\pi$ 处取得; 若${k_0} \geqslant K(1 + {P_{\rm{L}}})$ , 则函数(15)的最小值在$x = 1/(1 + 2{k_0})$ 处取得.$K(1 + {P_{\rm{L}}}) \geqslant K(1) \approx 1.74$ , 荧光CT所用X射线能量一般小于0.2个电子静能(100 keV), 远小于$K(1)$ , 所以最终得到截面最小值点对应的$ {\theta _{{\rm{min}}}} $ :${\theta _{{\rm{min}}}}$ 随偏振度P 的变化如图3 所示, 可见荧光CT所用的X光能量范围内, 微分截面最小值对应散射角在90°附近. 偏振度越高且入射能量越低, 则${\theta _{{\rm{min}}}}$ 越接近90°. 由于部分偏振光可以统计描述为完全偏振光(${P_{\rm{L}}} = 1$ )和一个完全非偏振光(${P_{\rm{L}}} = 0$ )的叠加, 所以最小微分截面方向接近入射光完全偏振成分的电矢量方向.图 3 不同入射能量时, ${\theta _{{\rm{min}}}}$ 随线偏振度变化Figure3. ${\theta _{{\rm{min}}}}$ varying with polarization for different incident energy.图4 描述了不同入射能量下, 微分截面最小值随偏振度的变化. 可见在荧光CT成像的能量范围内, 随入射光偏振度的增大, 最小微分截面值减小. 这为荧光CT去散射提供了思路, 即入射光偏振度越高, 在$\theta = {\theta _{{\rm{min}}}}, \varphi = 0\;{\rm{ or }}\;\pi $ 处的康普顿散射本底越低.图 4 不同入射能量时最小微分截面随偏振度的变化Figure4. Minimum differential cross section varying with polarization for different incident energy.$S(q, Z)$ , 则一个原子的非相干散射微分截面为[29 ] Z 是原子序数; $x = \sin (\theta /2)/{\lambda _0}$ ,${\lambda _0}$ 是入射光子波长(单位为?).非相干散射函数的理论计算方法和数值表可在相关文献中查寻[30 -33 ] . 非相干散射函数满足$0 \leqslant S(x, Z)/Z \leqslant 1$ , 对于低Z 原子的散射, 只有在x 较小(软X射线或小角度散射, $x < 1$ )时, $S(x, Z)/Z$ 才显著小于1. 例如100 keV入射光子, 波长约为0.124 ?, 入射到氧原子($Z{\rm{ = 8}}$ ), 散射角满足$\theta < 4^\circ $ 才使$S(x, Z)/Z < $ $ 0.5$ , 实际实验中, 入射光束总有发散角和宽度, 在小散射角处测量荧光信号存在很强的入射光背景, 所以实验设置应该在较大角度处测量荧光信号, 因此在这个测量角度范围内单个自由电子微分截面最小值的分析依然是有效的, 即考虑非相干散射函数后, 入射光线偏振优势方向是依然是近似的散射强度最小点.$k = {k_0} \to 0$ 时得到单个自由电子的Thomson散射截面公式:${P_{\rm{L}}}$ , 则相应的散射截面公式为22 )式易知, 最小微分截面方向为$\theta = {\pi }/2$ 且$\varphi = 0,~\;{\pi }$ , 所以最小微分截面方向为入射光完全偏振成分的电矢量方向. 从经典电动力学角度出发也可以得到相同的散射截面公式, 即电子在入射光电场驱动下振动辐射电磁波.[25 ] $ F(x, Z) $ 是原子形状因子, 可通过文献[30 -32 ]查询原子形状因子和理论计算方法. 原子形状因子随x 的变化趋势与非相干散射函数相反, x 越大$ F(x, Z) $ 越接近零, 相反地, x 趋于零时$ F(x, Z) $ 趋于Z .20 )式和(23 )式, 一个原子的康普顿散射与相干散射微分截面的总和为20 )式、(23 )式和(24 )式忽略光的偏振对原子形状因子和散射因子的影响[26 ] , 所以根据(14 )式和(22 )式的最小值的讨论, 一个原子的总微分截面的最小值点一定满足$\varphi = 0,~\pi $ .[34 ] $m(x)$ 表示分子干涉函数; $ s(x) $ 和$ f(x) $ 表示采用独立原子模型(independent atomic modelling, IAM)计算得到的非相干散射函数和分子形状因子[33 ] , 即${F_i}(x, {Z_i})$ 表示分子中第i 种元素原子的形状因子; $ {S_i}(x, {Z_i}) $ 表示第i 种元素的非相干散射函数; ${n_i}$ 表示分子中第i 种元素的原子个数; $m(x)$ 表示分子干涉函数[34 ] .$\varphi = 0, {\text{π}}$ 处的微分散射截面随散射角$\theta $ 的分布如图5 所示. 从图5(a) 可以看出, 相干散射微分截面随散射角增大快速减小, 在大角度处, 微分散射截面由主要由非相干散射贡献. 由图5(b) 中总微分截面角分布随线偏振度的变化可知, 线偏振度越高, 垂直方向散射的微分截面越小. ${P_{\rm{L}}} = {\rm{0}}{\rm{.5}}$ 时不同入射光能量下的总微分截面如图5(c) 所示, 可见在XFCT的光源能量范围内, 不同能量光子的水分子散射截面最小值均在入射光线偏振优势方向附近, 且该方向上微分截面相近.图 5 $\varphi = 0{\rm{ , \pi }}$ 处微分截面随散射角变化 (a) ${P_{\rm{L}}} = 1$ 时相干、非相干和总微分截面; (b) 不同线偏振度时的总微分截面; (c) ${P_{\rm{L}}} = $ $ {\rm{0}}{\rm{.5}}$ 时不同入射能量下的总微分截面Figure5. Differential cross section varying with $\theta $ at $\varphi = 0{\rm{ , \pi }}$ : (a) Incoherent, coherent and total differential cross section at ${P_{\rm{L}}} = 1$ ; (b) total differential cross section varying with $\theta $ for different ${P_{\rm{L}}}$ ; (c) total differential cross section varying with $\theta $ for different incident energy at ${P_{\rm{L}}} = {\rm{0}}{\rm{.5 }}$ 4.2.散射光的偏振 -->4.2.散射光的偏振 联系康普顿散射前后光束Stokes矢量的变换矩阵T [25 ] ${{\boldsymbol{k}}_{\boldsymbol{0}}} = {k_0}{{\boldsymbol{n}}_{\boldsymbol{0}}}$ , ${\boldsymbol{k}} = k{\boldsymbol{n}}$ , ${\boldsymbol{S}}$ 是电子初始自旋方向, ${{\boldsymbol{n}}_{\rm{0}}}$ 是入射光动量方向, ${\boldsymbol{n}}$ 是散射光动量方向. 在各向同性材料中, 电子初始自旋方向的平均值为$\overline {\boldsymbol{S}} = $ $ 0$ , 所以矩阵T ${\boldsymbol{S}}$ 的矩阵元为零. 在变换矩阵T 成立的坐标系中要求垂直散射平面方向完全线偏振光的归一化Stokes矢量为$ {\left[ {\begin{array}{*{20}{c}}{\rm{1}}&1&0&0 \end{array}} \right]^{\rm{T}}} $ , 即y 和y' 轴垂直于散射平面, 由图2 易知, 坐标系$xOy$ 可由$XOY$ 绕$OZ$ 轴旋转$\psi = - \varphi $ 得到, 则由(4a )式、(4b )式和(4c )式可知, 在$XOY$ 坐标系内Stokes矢量为$ {\left[ {\begin{array}{*{20}{c}}{\rm{1}}&{ - P_{\rm{L}}^{({\rm{i}})}}&0&{P_{\rm{C}}^{({\rm{i}})}} \end{array}} \right]^{\rm{T}}} $ 的入射光转换到坐标系$xOy$ 后归一化Stokes矢量变为$ {\left[ {{I_{\rm{f}}}, {\boldsymbol{\zeta '}}} \right]^{\rm{T}}} $ , 即:29 )式可得散射光的线偏振度$ P_{\rm{L}}^{({\rm{f}})} $ 为29 )式亦可得到散射光偏振的主方向与散射平面法向夹角β , 符号规定为: 迎着光子动量方向, 在表示散射光偏振的局部坐标系$x'Sy'$ 内, y' 轴以最小角度旋转到e ' , 若其旋转方向为顺时针, 则β 为正, 否则为负. 规定β 的符号后, 在局部坐标$x'Sy'$ 旋转β 角得到的新坐标系中, 散射光Stokes矢量的第二个分量应达到正的最大值, 据此条件可求得${\rm{atan}} 2\left( {y, x} \right)$ 为双参数反正切函数.$ \varphi = 0 \; {\rm{ or \; \pi }} $ 散射平面上散射光的归一化Stokes矢量、线偏振度和偏振主方向角为β 分别为$\theta = {\rm{π}}/2 \; {\rm{ , }} \; \varphi = 0 {\rm{,\; \pi }}$ 散射方向上散射光的归一化Stokes矢量和线偏振度为图6 展示了在不同入射光能量下$\varphi = 0,{\rm{~ \pi }}$ 散射平面内$ \xi _2^{({\rm{f}})} $ 随散射角$\theta $ 的变化. 图7 展示了不同能量下$\theta = {\rm{π}}/2 \; {\rm{ , }} \; \varphi = 0, \;{\rm{\pi }}$ 散射方向上散射光线偏振度随入射光线偏振度的变化. 若入射光为完全线偏振光($ P_{\rm{L}}^{({\rm{i}})} = 1 $ ), 则$\theta = {\rm{π}}/2 \; {\rm{ , }} \; \varphi = 0,\;{\rm{\pi }}$ 散射方向上散射光的线偏振度$ P_{\rm{L}}^{({\rm{f}})} $ 为零, 这与(12 )式是相符的. 从图6 可以看出, 在XFCT所涉及的能量范围内, 相同散射角处不同能量下散射光线偏振度差距较小, 而在$\theta = {\rm{π}}/2$ 附近, 部分偏振的入射光, 其散射光也具有较高偏振度. 从图7 可知, 只有当入射光线偏振度接近完全线偏振时, $\theta = {\rm{π}}/2$ 的散射光的偏振度才显著降低.图 6 $\varphi = 0\;{\rm{ or\; \pi }}$ 处$ \xi _2^{({\rm{f}})} $ 随散射角变化Figure6. $ \xi _2^{({\rm{f}})} $ varying with $ \theta $ at $\varphi = 0,\;{\rm{\pi }}$ .图 7 不同能量下$\theta = {\rm{π}}/2{\rm{ , }}\varphi = 0,\;{\rm{\;\pi }}$ 处散射光线偏振度随入射光线偏振度变化Figure7. The linear polarization of scattering photons $ P_{\rm{L}}^{({\rm{f}})} $ varying with $ P_{\rm{L}}^{({\rm{i}})} $ at $\theta = {\rm{π}}/2{\rm{ , }}~\varphi = 0,\;{\rm{ \pi }}$ for different incident energy.30 )式、(31 )式和(32a )式可知: 完全非偏振入射光的散射光的偏振主方向始终垂直于散射平面, 部分偏振入射光的散射光偏振; 部分偏振入射光在$\varphi = 0,\;{\rm{\pi }}$ 平面内的散射光偏振度是散射角的函数, 且存在两个零点, 左零点左侧和右零点的右侧偏振优势方向平行于散射平面, 在两个零点之间, 偏振优势方向垂直于散射平面, 在两个零点处散射光完全非偏振; 在$\varphi = 0,\; {\rm{ \pi }}$ 散射平面内, 完全线偏振入射光的散射光在$\theta \ne {\rm{π}}/2$ 时的偏振优势方向均平行于散射平面, 在$\theta = {\rm{π}}/2$ 时散射光完全非偏振.5.结 论 本文分析了XFCT的物理过程及其性质. 计算荧光退激发时间和荧光产额发现, 中高Z 元素荧光产额基本饱和, 而荧光退激发时间远远小于现有探测器时间分辨率, 因此, 荧光退激发时间无法用于分辨散射光与荧光, 提高原子序数可以增加荧光的能量, 荧光能量越高, 其穿透性越强, 有助于提高探测到的荧光光子数, 减小统计噪声, 提高信噪比. 偏振光源有助于减少康普顿散射背景, 入射光偏振度不影响康普顿散射总截面, 但对截面的角分布有影响, 部分偏振入射光在偏振方向附近具有最小的散射截面, 在此方向上探测荧光光子有助于降低康普顿散射背景, 并且对于完全非偏振或部分偏振的入射光, 在大部分方向上的散射光仍然具有一定的线偏振度, 而K层荧光线偏振度为零, 因此荧光和散射光线偏振度差异可以用于进一步降低荧光探测中的康普顿散射背景, 由于实际成像过程的复杂性, 通过偏振性质来减少散射背景需要进一步模拟和实验验证.  图 1 基于小孔成像方式的XFCT实验设置
图 1 基于小孔成像方式的XFCT实验设置































































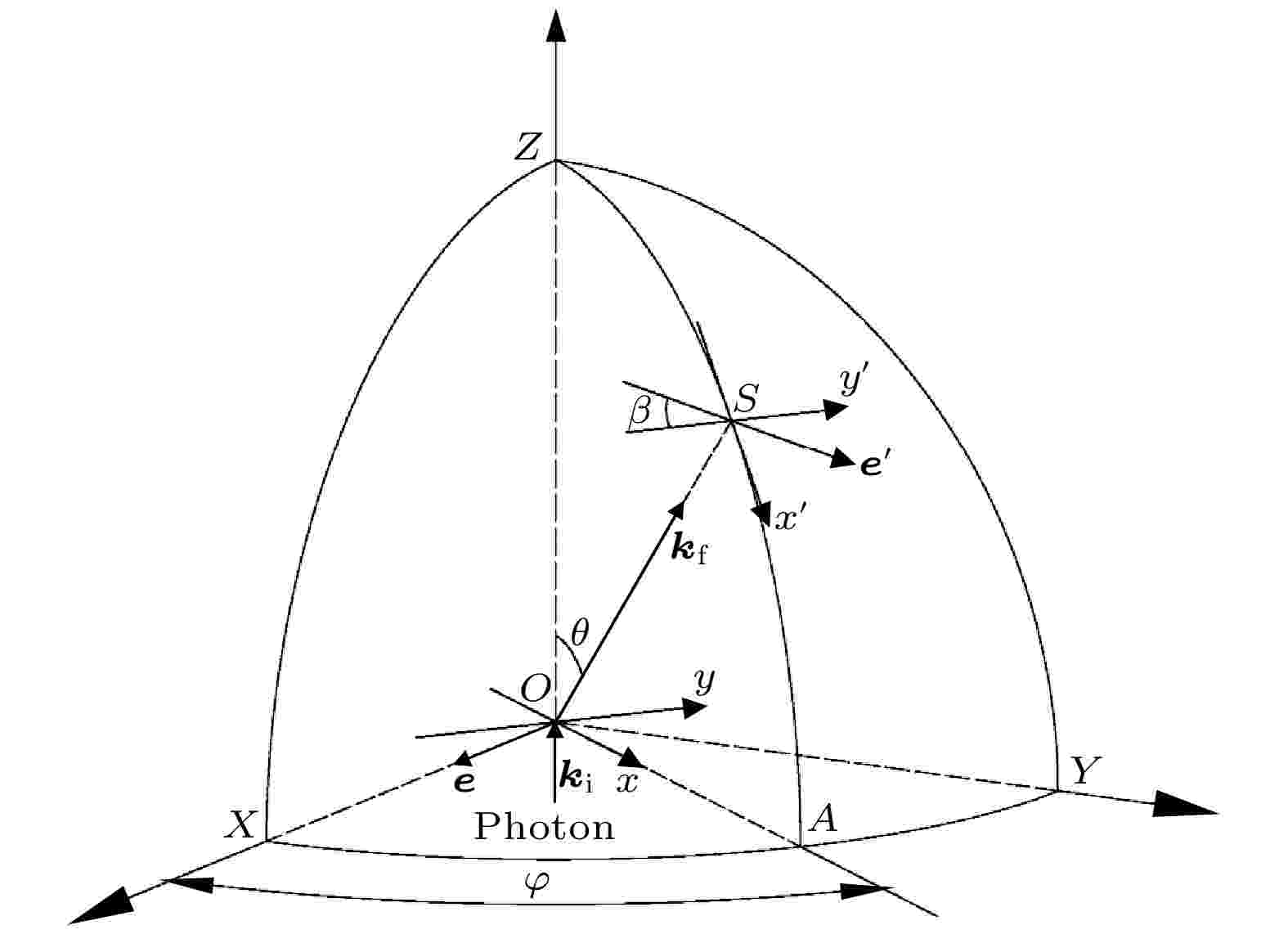 图 2 偏振康普顿散射示意图
图 2 偏振康普顿散射示意图







































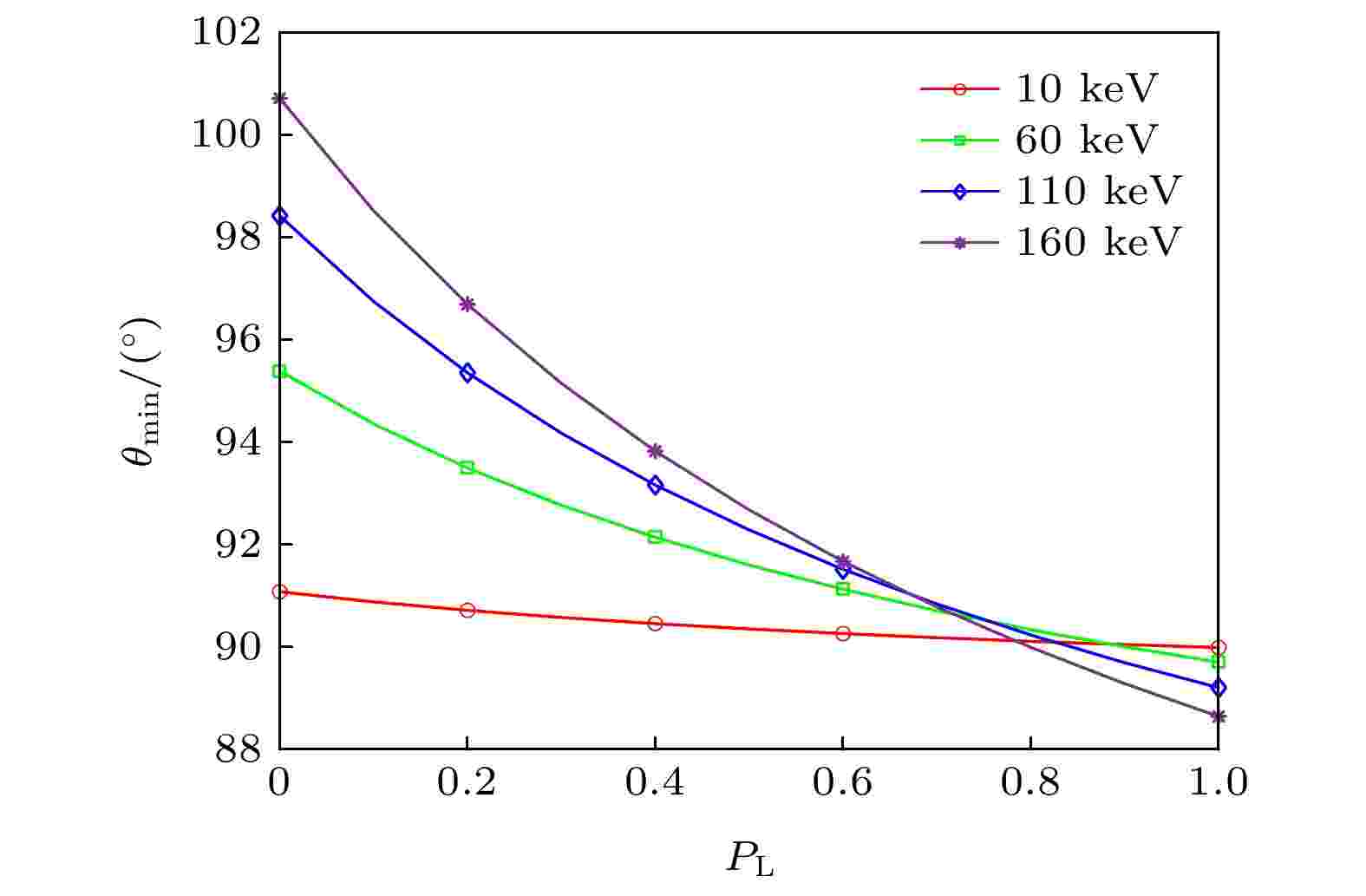 图 3 不同入射能量时,
图 3 不同入射能量时, 


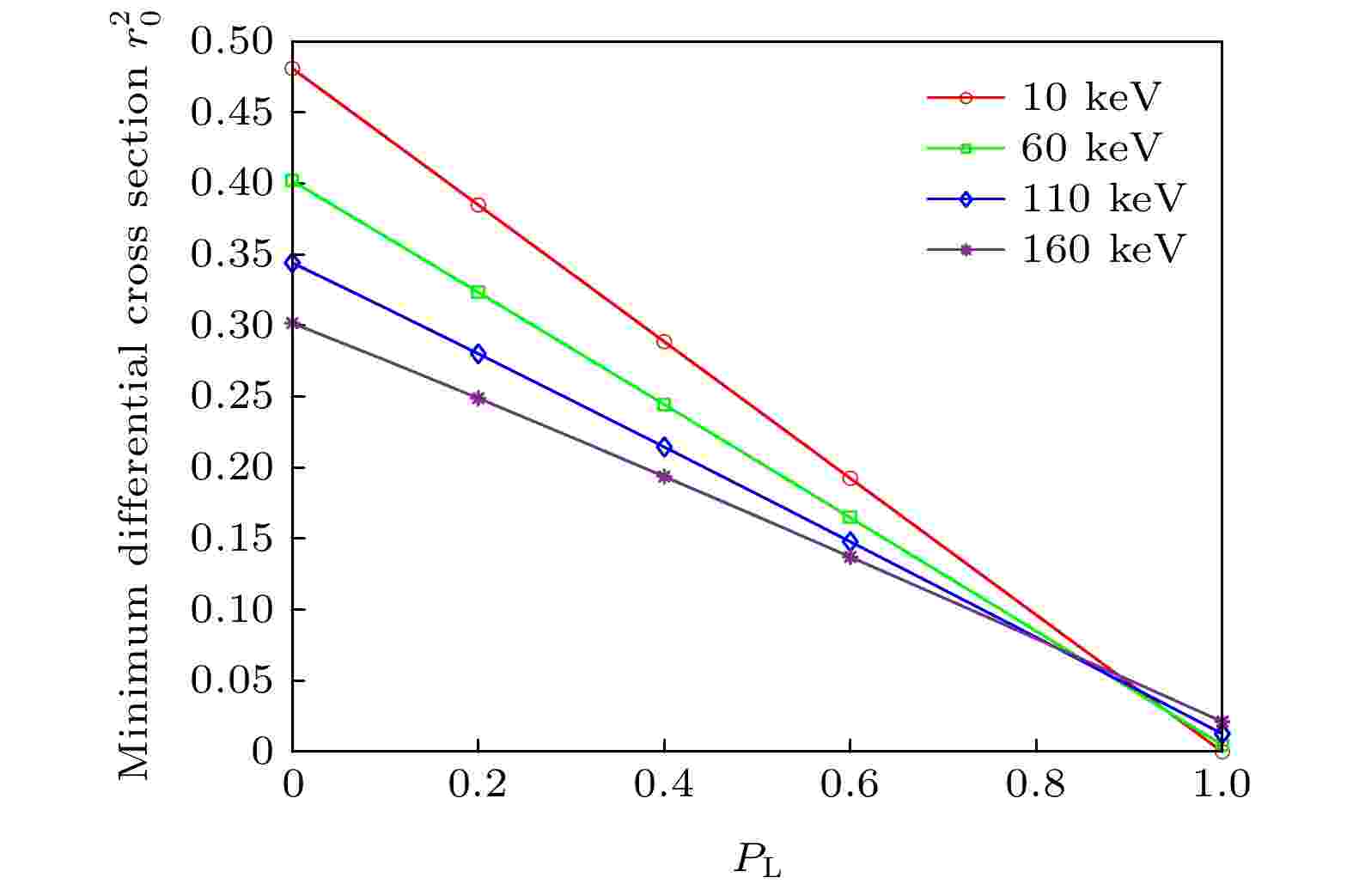 图 4 不同入射能量时最小微分截面随偏振度的变化
图 4 不同入射能量时最小微分截面随偏振度的变化

































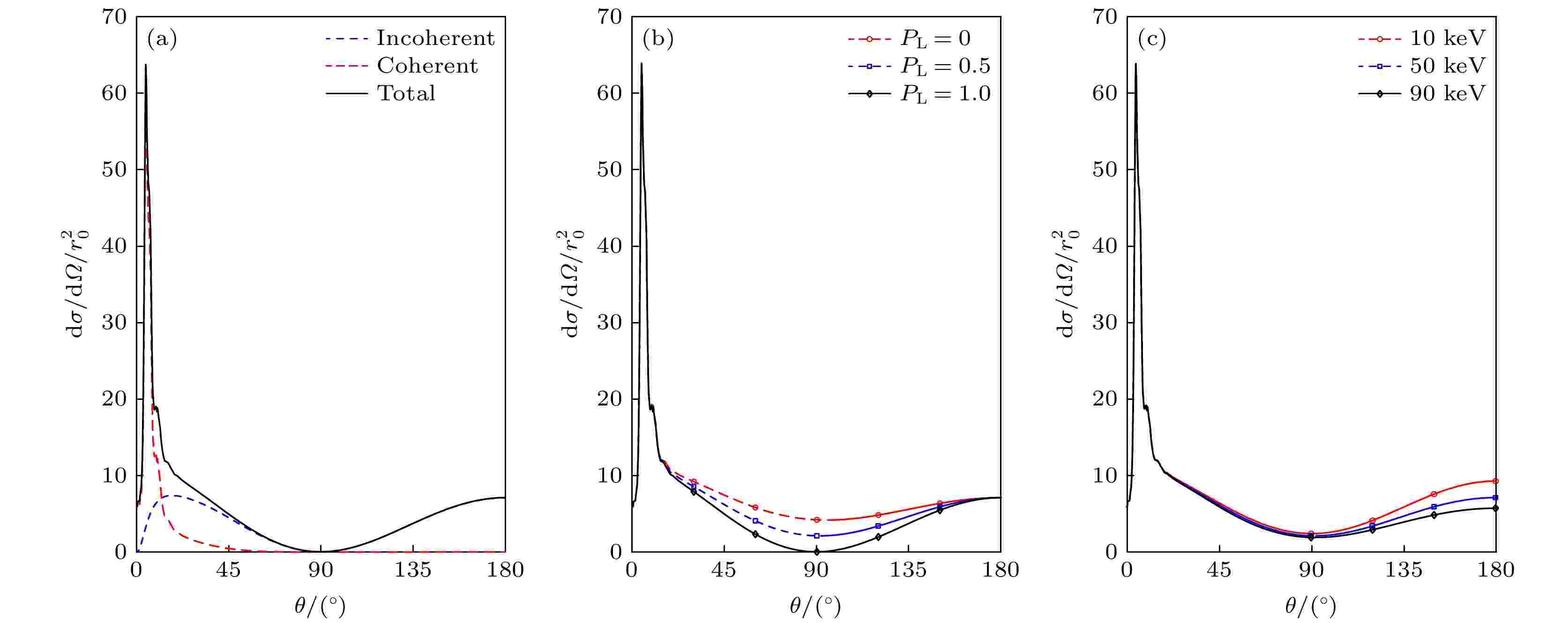 图 5
图 5 


























































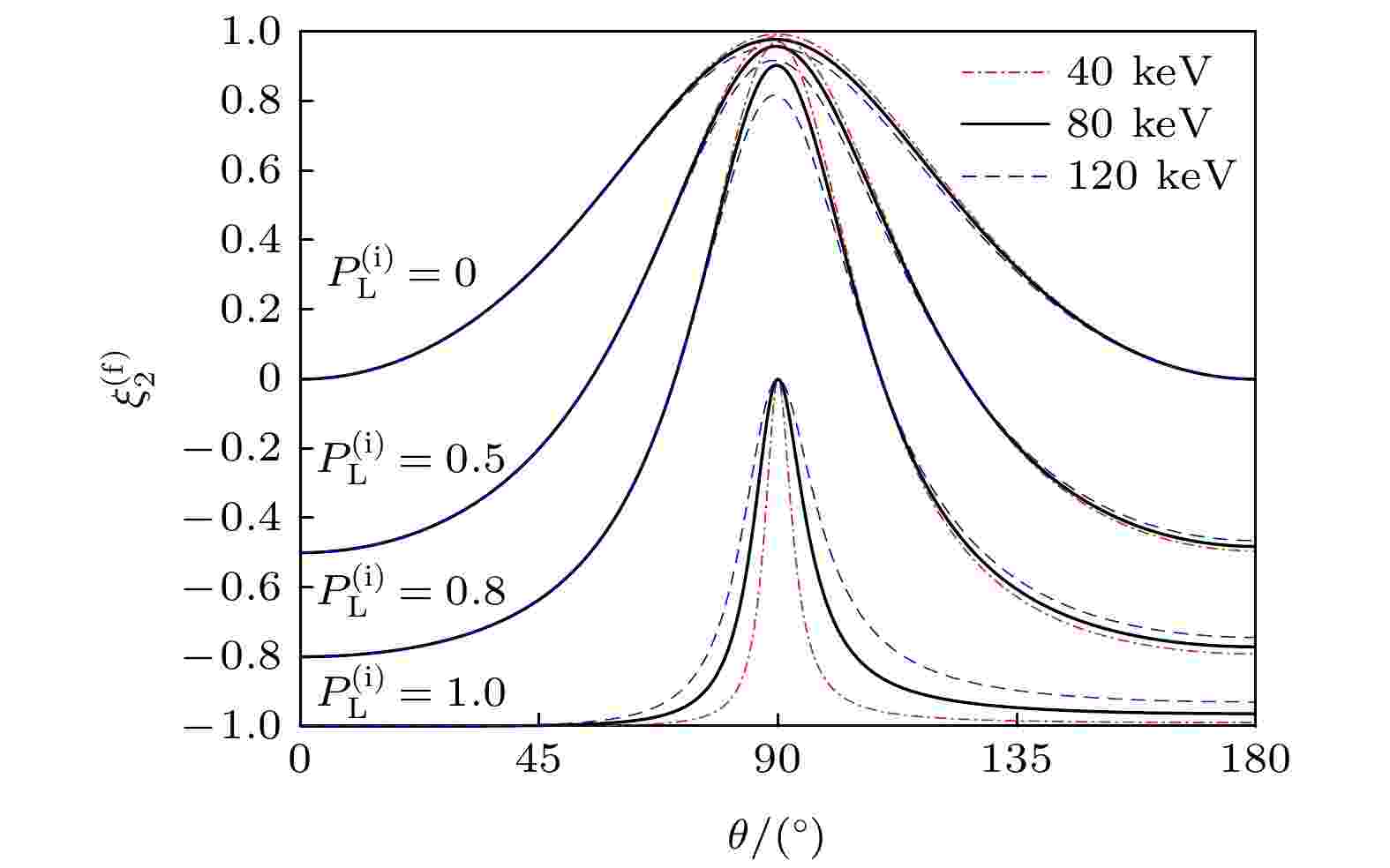 图 6
图 6 




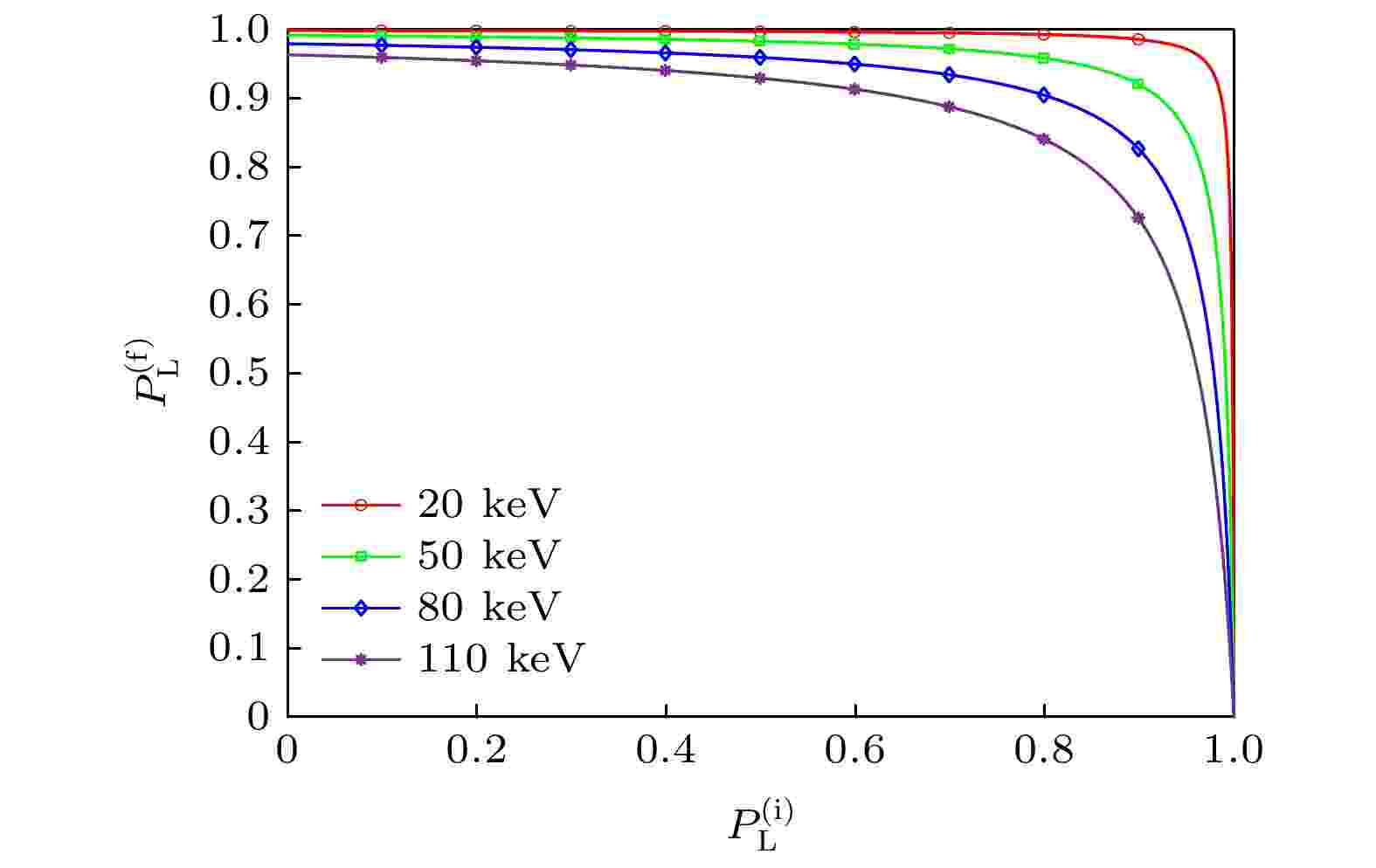 图 7 不同能量下
图 7 不同能量下







