CuBiI三元化合物晶体结构预测及光电性能第一性原理研究

全文HTML

--> --> -->

1.引　言

作为新兴的三元金属卤化物光电材料, 甲基铵碘化铅(MAPbI₃)引起了人们的广泛关注. 在过去十年中, 其功率转换效率迅速提高, 目前已超过25.7%^[1-3]. 然而, MAPbI₃的空气不稳定性及铅的高毒性阻碍了其商业化应用^[4,5]. 人们尝试用其他金属, 如Sn, Ge, Sb和Bi来取代三元金属卤化物中的铅 ^[6-9]. Sn²⁺, Ge²⁺离子在潮湿环境下容易发生氧化, 致使Sn基和Ge基卤化物太阳能电池的功率转化效率降低^[10,11]. Bi基金属卤化物因其优良的空气稳定性得到了广泛的研究^[12-19], 值得注意的是, 三元金属卤化物AgBiI具有多种组分比结构(AgBiI₄, AgBi₂I₇, Ag₂BiI₅, Ag₃BiI₆, AgBi₃I₁₀)、合适的光学带隙(1.71—1.83 eV)、宽的光吸收谱^[15-19].
Lu等^[15]用溶液法合成了一种环境友好、性能稳定的全无机卤化铋银AgBiI₄太阳能吸收层材料, 表现出优异的空气稳定性. Kulkarni等^[16]采用溶剂工程技术在较低温度下获得均匀无针孔的AgBi₂I₇薄膜, 组装成的太阳能电池具有光、热和湿度的长期稳定性. Ramachandrana等^[17]通过溶解碘化银和碘化铋后真空退火制备碘化银铋薄膜, X射线衍射分析表明薄膜结构为Ag₂BiI₅, 具有1.71 eV的带隙, 使用其组装成的可见光探测器表现出良好的响应性、灵敏度和入射光强度依赖性. Yi等^[19]报道了一种用于太阳能电池的新型Bi基类钙钛矿材料AgBi₃I₁₀, 其晶体结构由AgI₆和BiI₆八面体构成, 研究表明其光学带隙为1.80 eV, 同时具有良好的空气稳定性.
综合考虑丰度和成本因素, CuBiI三元化合物更具有研究价值. 目前仅报道过Cu₂BiI₅和CuBiI₄两种组分的结构, 光伏领域的研究仅局限于CuBiI₄化合物^[20-23]. Hu等^[21]利用低温溶液法合成了均匀致密的CuBiI₄薄膜, 带隙为2.67 eV, 利用其组装成的太阳能电池在光照条件下保持良好的稳定性. Zhang等^[22]在室温下采用直接金属表面元素反应的方法合成了均匀致密的CuBiI₄薄膜, 禁带宽度为1.81 eV. CuBiI三元化合物是否还存在着其他稳定组分结构, 其电学和光学性质, 以及光伏性能等均值得进一步研究.
本文采用基于遗传算法的晶体结构预测软件USPEX (universal structure predictor: evolutionary xtallography)对CuBiI三元化合物(CuBi₂I₇, Cu₂BiI₅, Cu₂BiI₇, Cu₃BiI₆, Cu₃Bi₂I₉, CuBi₃I₁₀, Cu₄BiI₇)的晶体结构进行了系统的研究. 共预测了12种热力学、晶格动力学和弹性力学稳定的CuBiI三元化合物晶体结构. 同时计算了它们的能带结构, 发现不同晶体结构的带隙值存在明显差异(1.13—3.09 eV). 在可见光区域中, Cu₂BiI₅, Cu₂BiI₇, CuBi₂I₇和Cu₄BiI₇表现出极强的光吸收能力, 光吸收系数均接近4 × 10⁵ cm^–1, 超过了CH₃NH₃PbI₃. 此外, CuBiI三元化合物晶体结构(Cu₂BiI₇-P1)的SLME值高达31.63%, 表明了其具有光电吸收材料的潜质.

2.计算方法

本文使用基于遗传算法的晶体结构预测软件USPEX, 对CuBiI三元化合物进行晶体结构预测. 在晶体结构搜索的过程中, 第一代100个结构通过随机算法产生. 接下来每一代的结构将分别通过遗传操作(50%), 软模变异操作(20%), 置换操作(10%)和随机的方式(20%)产生. 上一代群体中能量最低的60%个体用于下一代结构的产生. 通常, 全局优化需要大约20代或更多^[24,25].
所有的计算均采用基于密度泛函理论(density functional theory, DFT)的第一性原理从头算程序包(vienna ab-initio simulation package, VASP)来完成^[26]. 电子交换相关能和离子势分别采用 Perdew-Burke-Ernzerhof (PBE)参数化的广义梯度近似(generalized gradient approximation, GGA)^[27]和投影缀加波(projected augmented wave, PAW)方法^[28]来描述. 平面波截断能量设为600 eV. K点网格使用以G点为中心的Monkhorst-Pack网格方法^[29], 网格间距为2π × 0.03 ?^–1. 收敛标准设为总能量小于1 × 10^–8 eV, 每个原子受力小于0.001 eV/?.
利用基于密度泛函微扰理论(density functional perturbation theory, DFPT)的PHONOPY程序计算CuBiI三元化合物的声子谱, 分析其动力学稳定性^[30]. 根据应力-应变的方法计算弹性常数矩阵, 验证CuBiI三元化合物的力学稳定性^[31,32]. 同时采用更加精确的杂化泛函(heyd-scuseria-ernzerhof, HSE)方法^[33,34]计算电子结构、光吸收谱、光转换效率.

3.结果与讨论

3.1.结构预测

-->

3.1.结构预测

采用机器学习方法, 以形成焓为标准, 基于稳定存在的BiI₃, CuI, CuI₂以及AgBiI三元化合物的组分比设计了7种CuBiI三元化合物, 分别为CuBi₂I₇, Cu₂BiI₅, Cu₃BiI₆, Cu₄BiI₇, Cu₃Bi₂I₉, CuBi₃I₁₀, Cu₂BiI₇. 其中, Cu₂BiI₇的Cu离子为+2价, 其他CuBiI化合物的Cu离子为+1价. 然后以焓值为适应度函数, 基于“能量越低, 结构越稳定”的原则, 对这7种CuBiI三元化合物进行定成分晶体结构预测, 从预测结构中选择稳定和亚稳结构(亚稳结构与稳定结构之间焓值差在100 meV/atom以内).
进一步计算了CuBi₂I₇, Cu₂BiI₅, Cu₃BiI₆, Cu₄BiI₇, Cu₃Bi₂I₉, CuBi₃I₁₀, Cu₂BiI₇的稳定以及亚稳结构的声子色散谱, 确定了12个动力学稳定的晶体结构. 结合成分比以及对称性对12个动力学稳定结构进行命名, 分别为CuBi₂I₇-P1, CuBi₂I₇-P1-II, Cu₂BiI₅-P1, Cu₂BiI₅-Cm, Cu₃BiI₆-P3, Cu₃BiI₆-R3, Cu₄BiI₇-P3, Cu₄BiI₇-P1, Cu₃Bi₂I₉-P1, CuBi₃I₁₀-P1, Cu₂BiI₇-P1, Cu₂BiI₇-P1-II. 图1给出了12个动力学稳定结构的声子谱, 在整个布里渊区范围内, 12个结构的声子谱均没有出现虚频, 声学和光学分支之间没有明显的间隙, 存在重叠部分, 可以有效增强声学支光学支的散射.

图 1 12个CuBiI三元化合物结构的声子色散谱图　(a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II
Figure1. Phonon dispersion spectra for the 12 structures of CuBiI ternary compound: (a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II.

表1给出了12个稳定结构的空间群、晶胞内原子数、体积以及形成能. 12种结构分别属于三斜晶系(CuBi₂I₇-P1, CuBi₂I₇-P1-II, Cu₂BiI₅-P1, Cu₄BiI₇-P1, Cu₃Bi₂I₉-P1, CuBi₃I₁₀-P1, Cu₂BiI₇-P1, Cu₂BiI₇-P1-II)、单斜晶系(Cu₂BiI₅-Cm)和三方晶系(Cu₃BiI₆-P3, Cu₃BiI₆-R3, Cu₄BiI₇-P3). 为了判定这些结构的热力学稳定性, 按照以下公式计算了其形成能:

Structure name	Space group	Number of/ (atoms·unit cell^–1)	Volume/ (?³·unit cell^–1)	${{E} }_{\rm{form} }$/ (eV·atoms^–1)	Structure name	Space group	Number of/ (atoms·unit cell^–1)	Volume/ (?³·unit cell^–1)	${{E} }_{\rm{form} }$/ (eV·atoms^–1)
CuBi₂I₇-P1	P1	10	474.24	–0.362	CuBi₂I₇-P1-II	P1	10	465.35	–0.385
Cu₂BiI₅-P1	P1	8	295.03	–0.287	Cu₂BiI₅-Cm	Cm	16	742.54	–0.290
Cu₃BiI₆-P3	P3	10	404.63	–0.265	Cu₃BiI₆-R3	R3	30	1318.62	–0.244
Cu₄BiI₇-P1	P1	12	428.29	–0.237	Cu₄BiI₇-P3	P3	12	451.33	–0.231
Cu₃Bi₂I₉-P1	P1	14	645.41	–0.294	CuBi₃I₁₀-P1	P1	14	691.08	–0.402
Cu₂BiI₇-P1	P1	10	420.79	–0.225	Cu₂BiI₇-P1-II	P1	10	420.68	–0.226

表112个CuBiI三元化合物结构的结构名称、空间群、晶胞内原子数、体积及形成能
Table1.Structure name, space group, number of atoms per unit cell, volume of the unit cell and formation energy for the 12 structures of CuBiI ternary compound.

$\begin{split}&{E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}= \\\;&\frac{\left[E\left({{{\rm{Cu}}}_{x}{{\rm{Bi}}}_{y}{\rm{I}}}_{z}\right)-xE({\rm{Cu}})-yE({\rm{Bi}})-{z}E({\rm{I}})\right]}{x+y+z},\end{split}$

式中, $E\left({{{\rm{Cu}}}_{x}{{\rm{Bi}}}_{y}{\rm{I}}}_{z}\right)$

是${{\rm Cu}_{x}{\rm Bi}_{y}{\rm{I}}}_{z}$

晶胞的能量; $ {E}_{\mathrm{C}\mathrm{u}} $

, $ {E}_{\mathrm{B}\mathrm{i}} $

, $ {E}_{\mathrm{I}} $

是单个Cu, Bi, I原子的能量; x, y, z分别为晶胞内Cu, Bi, I原子个数.
为了进一步判定12个CuBiI三元化合物结构的力学稳定性, 计算了这些结构的弹性常数. 对于不同的晶系, 力学稳定性判断条件不同. 单斜结构包含13个独立的弹性常数, 三方结构存在8个独立的弹性常数, 可通过Born-Huang稳定性公式^[31]来判定力学稳定性. 三斜结构具有21个独立的弹性常数, 由Born-Huang稳定性准则可知, 需要弹性矩阵的正定型来保证力学稳定性^[32]. 12个结构的弹性系数C_ij列于表2, 均满足于Born-Huang稳定性准则, 表明了12个结构的力学稳定性.

C_ij/GPa	CuBi₂I₇-P1	CuBi₂I₇-P1-II	Cu₂BiI₅-P1	Cu₂BiI₅-Cm	Cu₃BiI₆-P3	Cu₃BiI₆-R3	Cu₄BiI₇-P1	Cu₄BiI₇-P3	Cu₃Bi₂I₉-P1	CuBi₃I₁₀-P1	Cu₂BiI₇-P1	Cu₂BiI₇-P1-II
C₁₁	8.34	9.03	39.90	4.76	11.99	17.59	23.63	32.25	17.16	2.82	9.71	3.12
C₂₂	12.61	14.16	29.93	35.09	—	—	18.34	—	20.42	9.34	14.12	10.34
C₃₃	8.35	9.00	35.71	5.64	5.92	5.05	23.61	8.90	11.86	8.62	14.43	26.51
C₄₄	3.52	3.62	10.18	1.73	1.01	3.53	6.87	1.41	3.91	3.27	6.46	7.16
C₅₅	3.74	2.99	9.96	—	—	—	7.83	—	3.56	1.91	3.73	4.52
C₆₆	2.41	4.43	6.77	1.24	4.42	6.13	8.72	11.26	6.01	1.93	3.13	3.18
C₁₂	4.73	4.45	9.13	1.63	3.01	5.22	4.56	9.71	6.13	1.96	4.71	3.19
C₁₃	2.61	2.57	14.13	2.77	1.33	2.99	7.76	3.30	3.14	2.11	5.61	6.45
C₁₄	–2.07	–0.04	4.02	—	0.04	1.7	–1.84	0.28	0.51	–0.63	–0.17	–0.32
C₁₅	0.18	0.21	0.18	–0.67	–0.15	–0.38	2.85	0.06	–0.79	–0.21	–2.11	0.54
C₁₆	0.79	2.27	0.12	—	—	—	–0.27	—	–0.51	0.86	–1.73	–0.32
C₂₃	2.69	2.76	14.94	2.42	—	—	5.49	—	6.79	2.98	7.51	7.18
C₂₄	–2.53	0.12	5.64	—	—	—	–0.99	—	2.280	–0.05	–2.43	2.11
C₂₅	0.28	0.16	0.17	–0.12	—	—	2.68	—	0.49	–0.09	–3.12	1.54
C₂₆	0.49	1.72	–0.02	—	—	—	0.04	—	0.41	1.47	1.35	1.01
C₃₄	–1.69	–0.27	5.74	—	—	—	–0.56	—	2.53	–0.89	–1.51	0.36
C₃₅	–1.76	0.39	0.12	–0.90	—	—	3.43	—	–0.21	–2.38	–3.43	1.76
C₃₆	1.47	1.17	–0.04	—	—	—	1.72	—	0.80	0.81	0.13	–0.48
C₄₅	–0.41	0.83	0.13	—	—	—	–0.47	—	0.21	0.85	1.26	0.19
C₄₆	–0.10	0.42	0.01	0.12	—	—	1.75	—	0.34	–0.62	–2.13	–0.69
C₅₆	–0.58	–0.29	1.485	—	—	—	–1.07	—	0.94	–0.53	0.82	0.72

表212个CuBiI三元化合物结构的弹性系数(C_ij)
Table2.Calculated elastic constants for the 12 structures of CuBiI ternary compound.

2

3.2.晶体结构

-->

3.2.晶体结构

12个CuBiI三元化合物结构的主要特征在于, 存在Cu—I和Bi—I键以及I原子的配位多面体. 表3总结了12个结构的晶格常数以及Cu/Bi—I键长. 下面对12个晶体结构进行详细的描述.

Structure name	a/?	b/?	c/?	α/(°)	β/(°)	γ/(°)	Cu—I/?	Bi—I/?
CuBi₂I₇-P1	7.93	7.94	7.92	97.67	82.58	76.98	2.53—2.55	3.02—3.32
CuBi₂I₇-P1-II	8.05	7.85	7.75	97.64	100.86	100.78	2.54—2.55	3.03—3.22
Cu₂BiI₅-P1	4.42	7.62	9.57	95.94	103.35	106.82	2.59—2.67	3.09—3.18
Cu₂BiI₅-Cm	16.64	4.33	12.22	90.00	122.51	90.00	2.57—2.72	2.84—3.50
Cu₃BiI₆-P3	7.89	7.89	7.54	90.00	90.00	120.00	2.54—2.61	3.02—3.29
Cu₃BiI₆-R3	11.40	11.40	11.72	90.00	90.00	120.00	2.52—2.56	3.05—3.35
Cu₄BiI₇-P1	7.61	7.79	7.64	101.68	100.50	98.22	2.56—2.74	3.06—3.22
Cu₄BiI₇-P3	8.32	8.32	7.52	90.00	90.00	120.00	2.64—2.68	3.09—3.22
Cu₃Bi₂I₉-P1	7.67	8.59	9.85	84.58	88.98	86.74	2.55—2.70	2.99—3.28
CuBi₃I₁₀-P1	9.46	10.12	7.85	103.09	106.70	77.25	2.53—2.54	2.99—3.32
Cu₂BiI₇-P1	7.33	7.90	7.92	104.09	108.49	81.74	2.59—2.64	3.05—3.34
Cu₂BiI₇-P1-II	9.00	7.78	7.20	109.91	89.24	64.61	2.58—2.70	2.98—3.34

表312个CuBiI三元化合物结构的晶格常数以及Cu/Bi—I键长
Table3.Lattice constants and Cu/Bi—I bond length for the 12 structures of CuBiI ternary compound.

图2给出了CuBi₂I₇ (CuBi₂I₇-P1, CuBi₂I₇-P1-II)晶体结构的主视图和俯视图, 两个结构均属于三斜晶系. CuBi₂I₇-P1结构沿着[010]方向, 配位八面体BiI₆通过共享边的形式形成了八面体BiI₆链; 在[100]方向, BiI₆链彼此之间通过共享点连接成重复单元; 在[001]方向, 重复单元通过片状CuI₃共享边或者共享点构成三维空间结构. CuBi₂I₇-P1-II结构在[010]方向与CuBi₂I₇-P1相似, 配位八面体BiI₆通过共享边形成BiI₆链; 在[100]方向, BiI₆链之间通过共享点的方式连接成空间结构, 并且片状结构CuI₃通过共享边和共享点的方式依附在BiI₆链上.

图 2 CuBi₂I₇-P1的晶体结构　(a) 主视图; (b) 俯视图. CuBi₂I₇-P1-II的晶体结构 (c) 主视图; (d) 俯视图
Figure2. Crystal structure of CuBi₂I₇-P1: (a) Front view; (b) top view. Crystal structure of CuBi₂I₇-P1-II: (c) Front view; (d) top view

图3给出了Cu₂BiI₅ (Cu₂BiI₅-P1, Cu₂BiI₅-Cm)晶体结构的主视图和俯视图. Cu₂BiI₅-P1结构属于三斜晶系, 在[010]方向, 配位四面体CuI₄通过共享点的方式形成CuI₄链; 在[001]方向, 八面体BiI₆以共享点的方式连接在CuI₄链上; 在[100]方向, 配位四面体CuI₄彼此之间通过共享点连接, 同样八面体BiI₆以共享边的方式连接. Cu₂BiI₅-Cm结构属于单斜晶系, 该结构中Cu原子存在两种配位环境: 四面体CuI₄与片状结构CuI₃. 在[010]方向, 配位八面体BiI₆以共享边的方式连接, 四面体CuI₄和片状结构CuI₃依次通过共享边的方式交替连接, [001]方向, 四面体CuI₄与八面体BiI₆以共享边的方式连接成重复单元.

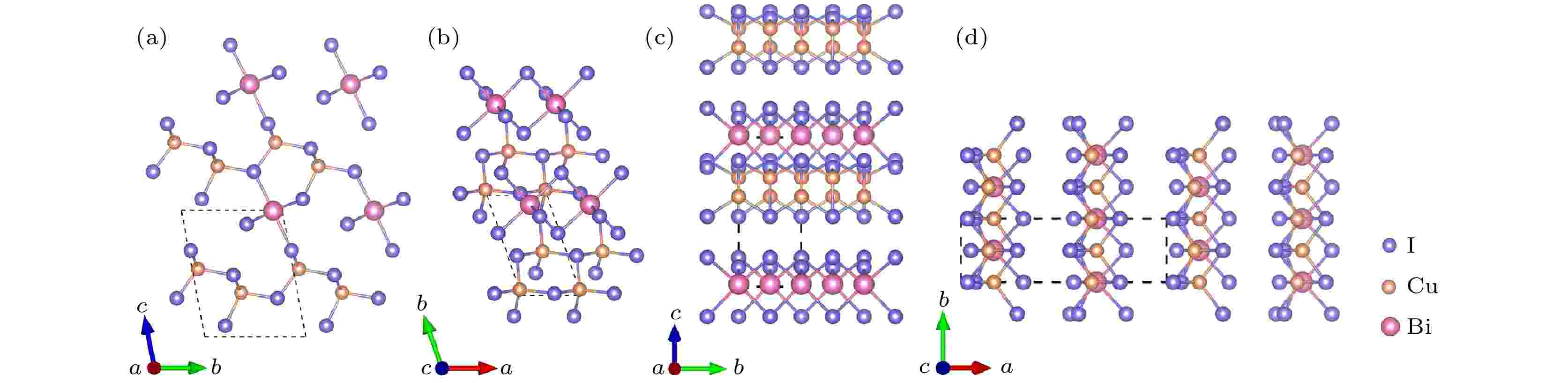图 3 Cu₂BiI₅-P1的晶体结构　(a) 主视图; (b) 俯视图. Cu₂BiI₅-Cm的晶体结构 (c) 主视图; (d) 俯视图
Figure3. Crystal structure of Cu₂BiI₅-P1: (a) Front view; (b) top view. Crystal structure of Cu₂BiI₅-Cm: (c) Front view; (d) top view.

图4给出了Cu₃BiI₆ (Cu₃BiI₆-P3, Cu₃BiI₆-R3)晶体结构的主视图和俯视图, 两个结构均属于三方晶系. Cu₃BiI₆-P3为[001]方向的层状结构, 每层由配位八面体BiI₆与片状结构CuI₃构成: Bi原子位于顶点位置, 与周围的六个I原子形成配位八面体BiI₆, Cu原子与周围三个I原子形成片状结构CuI₃, 每个八面体BiI₆与周围三个片状结构通过共享边构成重复单元, 并依次通过共享点的形式连接成层状结构. Cu₃BiI₆-R3结构是由八面体BiI₆与片状结构CuI₃构成的三维结构: 八面体BiI₆与片状结构CuI₃通过共享边连接成重复单元, 该重复单元在[010]或者[001]方向, 均通过八面体BiI₆与三个片状结构CuI₃的共享点构成三维空间结构.

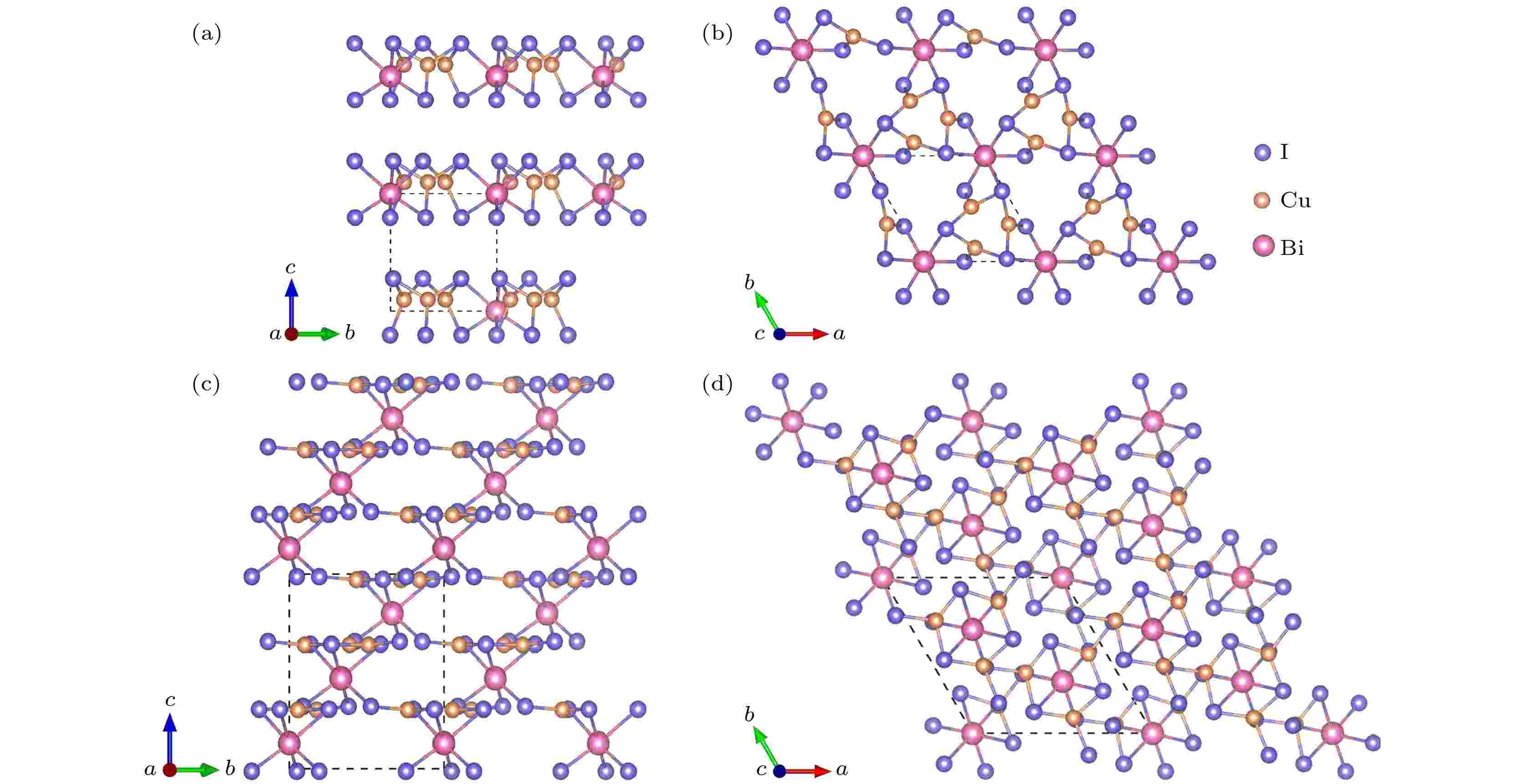图 4 Cu₃BiI₆-P3的晶体结构　(a) 主视图; (b) 俯视图. Cu₃BiI₆-R3的晶体结构 (c) 主视图; (d) 俯视图
Figure4. Crystal structure of Cu₃BiI₆-P3: (a) Front view; (b) top view. Crystal structure of Cu₃BiI₆-R3: (c) Front view; (d) top view.

图5给出了Cu₄BiI₇ (Cu₄BiI₇-P1, Cu₄BiI₇-P3)晶体结构的主视图和俯视图. Cu₄BiI₇-P1结构属于三斜晶系, 该结构中的Cu原子存在两种配位环境: 四面体CuI₄与片状结构CuI₃. 两个八面体BiI₆之间通过两组共享边的片状结构CuI₃与四面体CuI₄相连成空间结构. Cu₄BiI₇-P3结构属于三方晶系, 该结构为[001]方向的层状结构, 每层由配位八面体BiI₆与配位四面体CuI₄构成: [100]方向或者[010]方向, 原子排列方式相同: 两个八面体BiI₆之间均由两个共享边的四面体CuI₄通过共享点或者共享边相连成层状材料.

图 5 Cu₄BiI₇-P1的晶体结构　(a) 主视图; (b) 俯视图. Cu₄BiI₇-P3的晶体结构 (c) 主视图; (d) 俯视图
Figure5. Crystal structure of Cu₄BiI₇-P1: (a) Front view; (b) top view. Crystal structure of Cu₄BiI₇-P3: (c) Front view; (d) top view.

图6给出了Cu₃Bi₂I₉-P1和 CuBi₃I₁₀-P1晶体结构的主视图和俯视图. Cu₃Bi₂I₉-P1与CuBi₃I₁₀-P1结构均属于三斜晶系. 对于Cu₃Bi₂I₉-P1结构, 在[100]方向, 八面体BiI₆彼此通过共享边形成BiI₆链, 四面体CuI₄通过共享点或边的方式连接在BiI₆链上, 形成重复的单元; 在[001]方向, 该重复单元通过四面体CuI₄之间的点共享构成的三维空间结构. CuBi₃I₁₀-P1结构为[100]方向的层状结构, 每层由配位八面体BiI₆与片状CuI₃结构构成: 在[010]或[001]方向, 八面体BiI₆均通过共享边的方式连接, 而片状CuI₃结构以共享边或共享点的方式嵌入八面体BiI₆堆垛的间隙中, 以此构成了层状结构.

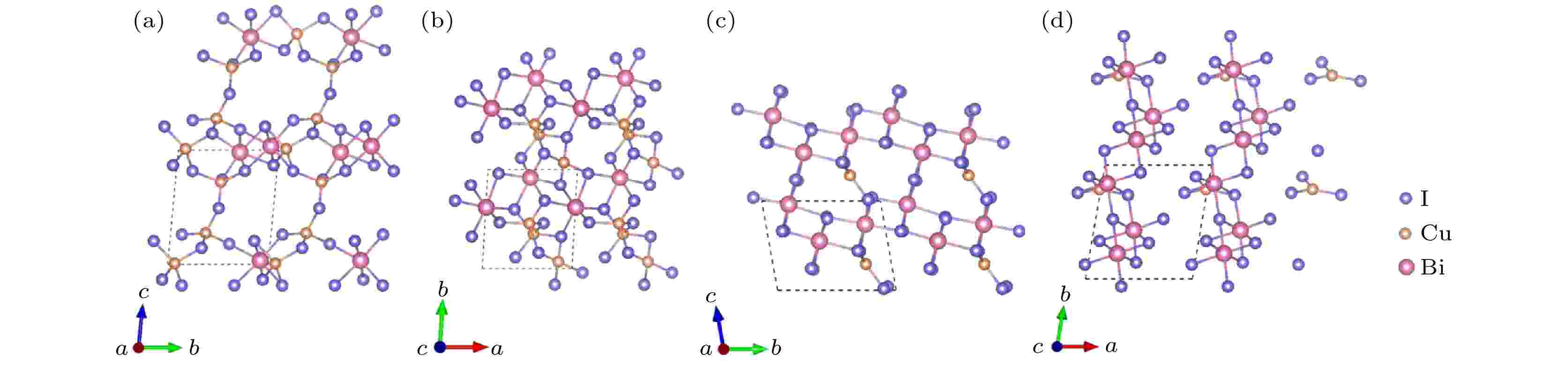图 6 Cu₃Bi₂I₉-P1的晶体结构　(a) 主视图; (b) 俯视图. CuBi₃I₁₀-P1的晶体结构 (c) 主视图; (d) 俯视图
Figure6. Crystal structure of Cu₃Bi₂I₉-P1: (a) Front view; (b) top view. Crystal structure of CuBi₃I₁₀-P1: (c) Front view; (d) top view

图7给出Cu₂BiI₇ (Cu₂BiI₇-P1, Cu₂BiI₇-P1-II)晶体结构主视图和俯视图. Cu₂BiI₇-P1与Cu₂BiI₇-P1-II结构均属于三斜晶系, Cu₂BiI₇-P1结构为[100]方向的层状结构, 每层由配位八面体BiI₆与配位四面体CuI₄构成: 在[001]方向或[010]方向, 八面体BiI₆与四面体CuI₄通过共享边或共享点的方式交替相连成层状结构, 且四面体CuI₄之间相互共享边. Cu₂BiI₇-P1-II与Cu₂BiI₇-P1相似, 也为[100]方向的层状结构, 不同之处在于[010]方向, 八面体BiI₆与四面体CuI₄之间仅通过共享边的方式连接, 且四面体CuI₄之间不存在边共享.

图 7 Cu₂BiI₇-P1的晶体结构　(a) 主视图; (b) 俯视图. Cu₂BiI₇-P1-II的晶体结构 (c) 主视图; (d) 俯视图
Figure7. Crystal structure of Cu₂BiI₇-P1: (a) Front view; (b) top view. Crystal structure of Cu₂BiI₇-P1-II: (c) Front view; (d) top view

2

3.3.电子结构

-->

3.3.电子结构

分别采用PBE和HSE06计算了12个CuBiI三元化合物结构的能带结构, 如图8所示. 带隙值以及导带底和价带顶位置如表4所列. 与PBE计算值相比, HSE06计算值更大. CuBi₂I₇-P1, Cu₂BiI₅-Cm, Cu₃Bi₂I₉-P1和CuBi₃I₁₀-P1结构为直接带隙半导体, 有利于光子的垂直跃迁. CuBi₂I₇-P1与Cu₂BiI₅-Cm价带顶(valence band maximum, VBM)和导带底(conduction band minimum, CBM)均在G (0 0 0)点, Cu₃Bi₂I₉-P1的VBM和CBM在F (0 0.5 0)点, CuBi₃I₁₀-P1的VBM和CBM在Z (0 0 0.5)点. CuBiI三元化合物其他结构均为间接带隙半导体. 12个结构带隙值为1.13—3.09 eV. 其中, Cu₂BiI₅-P1 (1.56 eV), Cu₂BiI₇-P1 (1.13 eV)及Cu₂BiI₇-P1-II (1.40 eV)的带隙值相对较小, 接近于光吸收的最佳带隙值(1.40 eV), 适合作为太阳能电池中的光吸收材料. Cu₃BiI₆-R3 (2.81 eV)与Cu₃BiI₆-P3 (3.09 eV)的带隙值偏大, 接近于紫外光能量, 不利于可见光吸收. 其他结构的带隙均在可见光能量范围(1.64—3.19 eV)内, 且具有较宽的可见光吸收谱, 具备优良太阳能吸收材料潜质.

图 8 12个CuBiI三元化合物结构的能带结构图 (红色, HSE06方法计算结果; 蓝色, PBE方法计算结果)　(a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II
Figure8. Band structure for the 12 structures of CuBiI ternary compound calculated by the PBE (blue lines) and HSE06 (red lines) methods: (a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II.

Structure name	E_g/eV		VBM	CBM	Bader charge			SLME/%
Structure name	HSE06	PBE	VBM	CBM	Cu/(e·atom^–1)	Bi/(e·atom^–1)	I/(e·atom^–1)	SLME/%
CuBi₂I₇-P1	2.39	1.48	0 0 0	0 0 0	0.33	1.08	–0.36	10.75
CuBi₂I₇-P1-II	2.13	1.21	0 0 0	0 0.5 0	0.33	1.09	–0.36	9.50
Cu₂BiI₅-P1	1.56	0.84	0 0 0.5	0 0.5 0	0.34	1.04	–0.34	22.20
Cu₂BiI₅-Cm	1.87	0.89	0 0 0	0 0 0	0.29	1.07	–0.33	7.50
Cu₃BiI₆-P3	3.09	1.97	0.05 0 0	0 0 0.5	0.29	1.08	–0.33	2.86
Cu₃BiI₆-R3	2.81	1.85	0 0 0	0.5 0 0.5	0.31	1.01	–0.32	5.49
Cu₄BiI₇-P1	2.19	1.22	0 0 0	0 0.5 0	0.30	1.03	–0.32	15.77
Cu₄BiI₇-P3	2.21	1.21	0 0 0.06	0 0 0.5	0.32	1.06	–0.33	13.61
Cu₃Bi₂I₉-P1	2.03	1.17	0 0 0.5	0 0 0.5	0.34	1.02	–0.34	19.02
CuBi₃I₁₀-P1	2.36	1.41	0 0.5 0	0 0.5 0	0.33	1.09	–0.36	4.17
Cu₂BiI₇-P1	1.13	0.50	0 0 0	0 0.5 0	0.37	1.09	–0.26	31.63
Cu₂BiI₇-P1-II	1.40	0.60	0 0 0	0 0.5 0.5	0.35	1.06	–0.25	28.30

表412个CuBiI三元化合物结构的带隙值(HSE06和PBE方法计算结果), 价带顶与导带底位置, Bader电荷转移以及SLME (spectroscopic limited maximum efficiency)值
Table4.Band gaps (E_g) calculated by the HSE06 and PBE method, positions of VBM and CBM, Bader charge and the spectroscopic limited maximum efficiency (SLME) values for the 12 structures of CuBiI ternary compound.

图9给出了CuBiI三元化合物12个结构的总态密度(total density of states, TDOS), 投影态密度(projected density of states, PDOS)和价带顶、导带底的电荷密度分布图. 12个结构的价带顶均由Cu-3d和I-5p轨道杂化而成. Cu₃BiI₆-R3的导带底主要由Bi-6p和I-5p轨道组成, Cu-3d有少许贡献; Cu₂BiI₇的两个结构(Cu₂BiI₇-P1, Cu₂BiI₇-P1-II)的导带底主要来自I-5p轨道, Cu-3d有少许贡献. 对于Cu₂BiI₇-P1结构, 在2.7—4.0 eV范围内Bi-6p和I-5轨道杂化. Cu₂BiI₇-P1-II结构在2.5—3.2 eV范围内, 也存在Bi-6p和I-5p轨道杂化; 其他结构的导带底均由Bi-6p和I-5p轨道杂化而成.

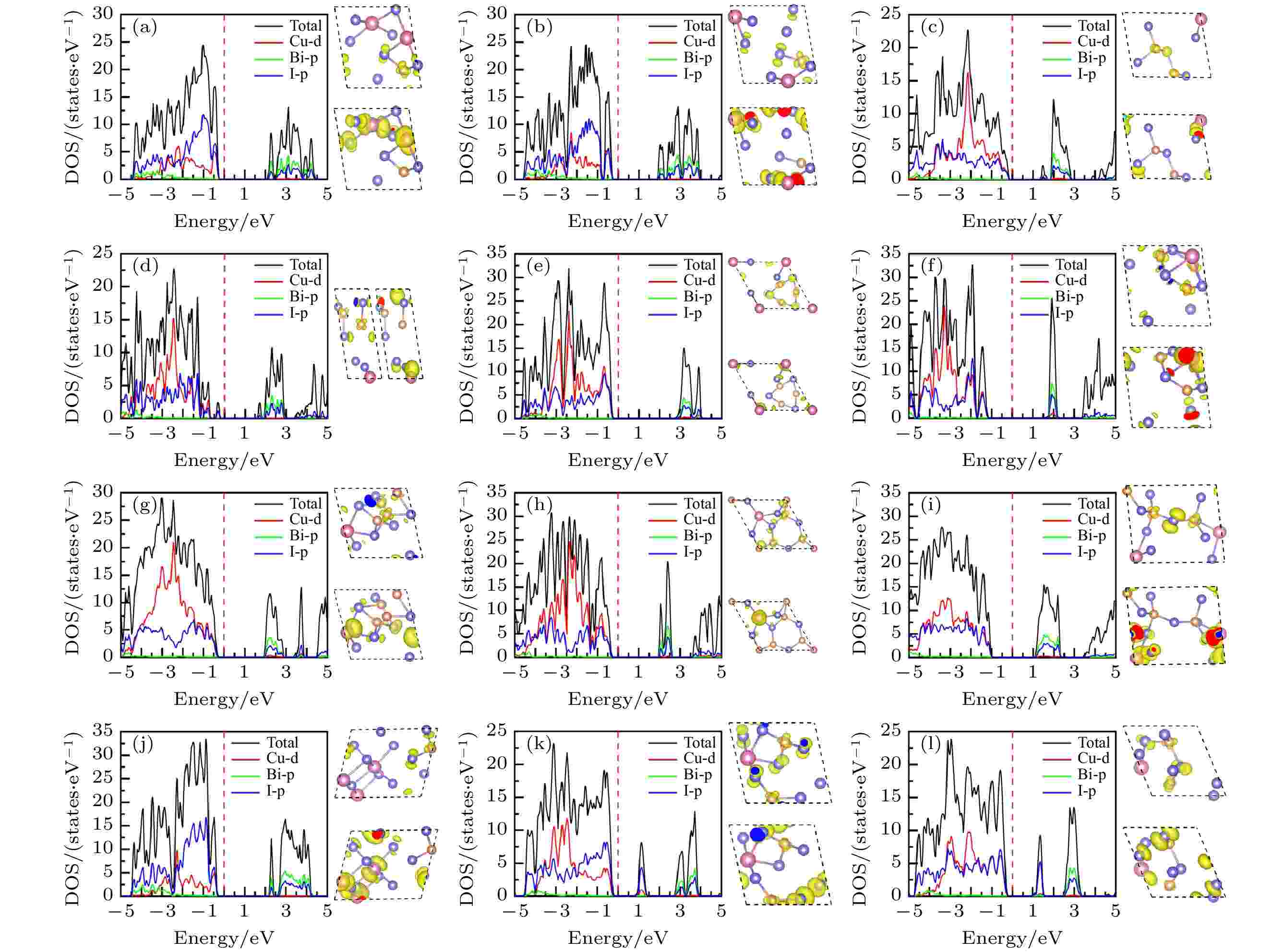图 9 12个CuBiI三元化合物结构的总态密度、投影态密度图以及价带顶、导带底(从左到右或从上到下)的电荷密度分布图　(a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II
Figure9. Total density of state (TDOS), projection density of state (PDOS) and charge density distribution (Left to right or top to bottom) at CBM and VBM for the 12 structures of CuBiI ternary compound: (a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II.

为了进一步分析化学键, 计算了CuBiI三元化合物12个结构的电子局域函数(electron localization function, ELF). 图10给出了CuBiI三元化合物12种结构的电子局域函数分布图. I原子核的ELF值接近于1, 电子在此处高度局域; Bi原子附近的ELF值约为0.50, 电子均匀分布; Cu原子核附近的ELF值约为0.25, 电子离域分布. 值得注意的是, Bi原子和I原子之间的ELF数值约为0.28, 而Cu原子和I原子之间的ELF约为0.22, 共价属性相对较低.

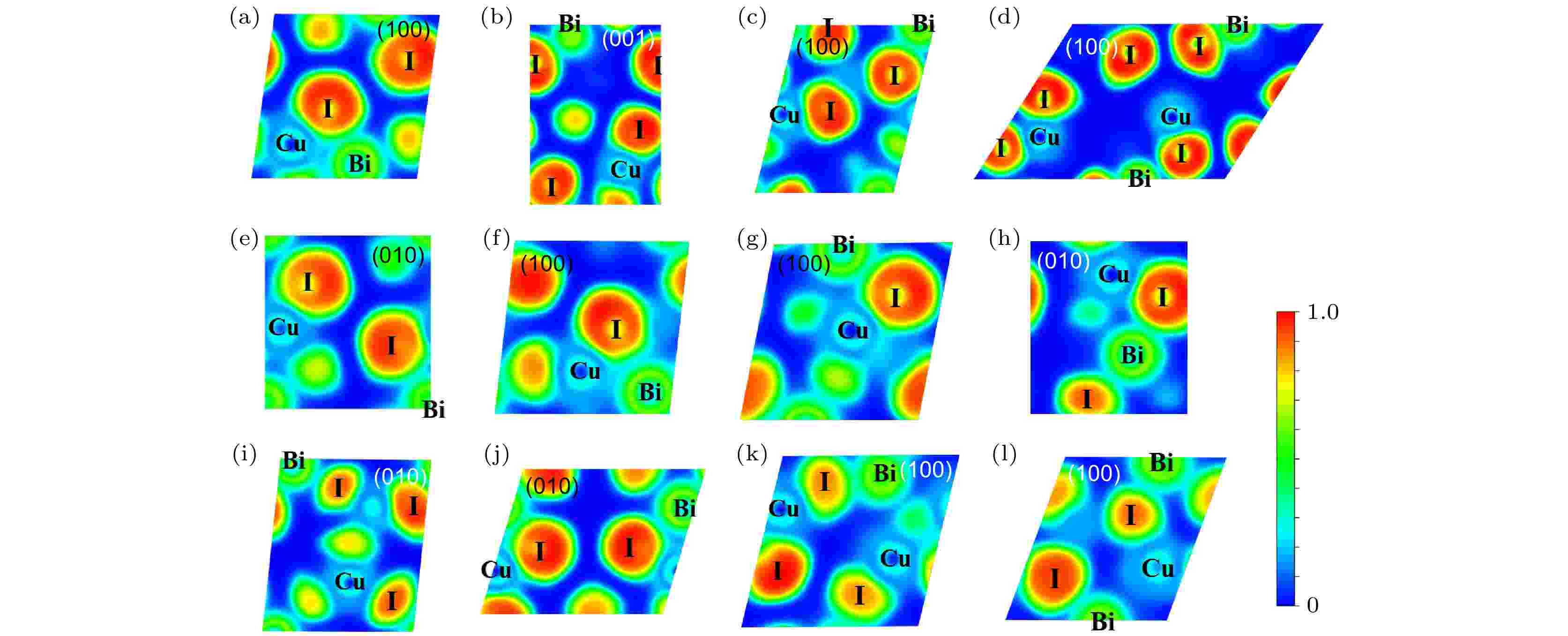图 10 12个CuBiI三元化合物结构的电子局域函数分布图　(a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II
Figure10. Electron localization function (ELF) for the 12 structures of CuBiI ternary compound: (a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P3; (h) Cu₄BiI₇-P1; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II.

进一步计算了 Bader 电荷以分析Cu, Bi原子与I原子之间的电子转移情况, 计算结果见表4. Cu原子和Bi原子分别失去0.29e—0.37e和1.03e—1.09e电子, I原子获得0.25e—0.36e电子. Cu, Bi和I的Bader电荷与通常的纯离子键相互作用(例如Cu⁺/Cu²⁺, Bi³⁺, I^–)偏离, 表明了Cu, Bi原子与I原子之间离子键和共价键相互作用共存. PDOS也证实了Cu/Bi—I的共价相互作用, Cu-3d/Bi-6p 轨道和 I-5p轨道存在着明显的耦合作用. 因此, CuBiI三元化合物12个结构中Cu—I, Bi—I键具有强的离子性, 弱的共价性.
2

3.4.光吸收性质

-->

3.4.光吸收性质

吸收系数α是反映光吸收强度的重要参数^[35,36], 可通过以下公式得到:

$\alpha \left(\omega \right)=\sqrt{2}\omega {\left[\sqrt{{{\varepsilon }_{1}\left(\omega \right)}^{2}+{{\varepsilon }_{2}\left(\omega \right)}^{2}}-{\varepsilon }_{1}\left(\omega \right)\right]}^{\tfrac{1}{2}},$

其中, $ {\varepsilon }_{1}\left(\omega \right) $

和$ {\varepsilon }_{2}\left(\omega \right) $

分别代表介电函数的实部和虚部. 虚部$ {\varepsilon }_{2}\left(\omega \right) $

根据电子跃迁选择定则, 由占据态的电子波函数之间的矩阵元得到:

${\varepsilon _2}(\omega) = \frac{{2{e^2}{\rm{\pi }}}}{{\varOmega {\varepsilon _0}}}\mathop \sum \limits_{k,{\rm{v}},{\rm{c}}} {| {\langle {\psi _k^{\rm{c}}{\rm{|}}\hat ur{\rm{|}}\psi _k^{\rm{v}}} \rangle } |^2}\delta ({E_k^{\rm{c}} - E_k^{\rm{v}} - E}),$

其中, e为电子电荷, $ \varOmega $

为原胞体积, $ {\varepsilon }_{0} $

为真空介电常数, k为波矢, 上标c和v表示导带和价带, $ {\psi }_{k}^{\mathrm{c}} $

和$ {\psi }_{k}^{\mathrm{v}} $

分别是k点处的导带和价带的波函数, $\hat{u}r$

为动量跃迁矩阵, $ {E}_{k}^{\mathrm{c}} $

和$ {E}_{k}^{\mathrm{v}} $

分别表示导带和价带的本征能级, E是光子能量, δ是克罗内克函数, $ \omega $

为入射光子频率. 实部$ {\varepsilon }_{1}\left(\omega \right) $

可以通过Kramers-Kronig关系由$ {\varepsilon }_{2}\left(\omega \right) $

得出^[37]:

${\varepsilon }_{1}\left(\omega \right)=1+\frac{2}{\mathrm{\pi }}P{ {\int _0^\infty}}\frac{{\omega '}{\varepsilon }_{i}\left({\omega '}\right)}{{\omega }^{'2}-{\omega }^{2}}\mathrm{d}{\omega '}, $

其中P代表主值积分.
为了更准确地描述CuBiI三元化合物12个结构的光学性质, 采用HSE06方法计算光吸收系数. 图11为CuBiI三元化合物中12个结构的光吸收谱. Cu₂BiI₇两个结构(Cu₂BiI₇-P1与Cu₂BiI₇-P1-II)的吸收起点位于红外光区, 吸收覆盖了整个可见光区. 相比之下, 其他结构的吸收光谱有显著的紫移, 吸收谱起点由其带隙值决定. 从吸收起点开始, CuBiI三元化合物中12个结构的光吸收强度均随着能量增加呈现上升的趋势. 在可见光能量范围内, 12种结构的吸收强度有着明显的差异. CuBi₂I₇-P1, Cu₂BiI₅-P1, Cu₄BiI₇-P1, Cu₂BiI₇-P1-II和Cu₃Bi₂I₉-P1在可见光高能量区域的吸收系数接近于4 × 10⁵ cm^–1, 超过了CH₃NH₃PbI₃^[38]. 宽可见光范围内高吸收系数表明有能力捕获更多的光子, 产生电子和空穴对. 另外, Cu₃BiI₆-R3和Cu₃BiI₆-P3具有较宽的带隙值(2.81 eV和3.09 eV), 仅在可见光高能量处具有较高的吸光强度.

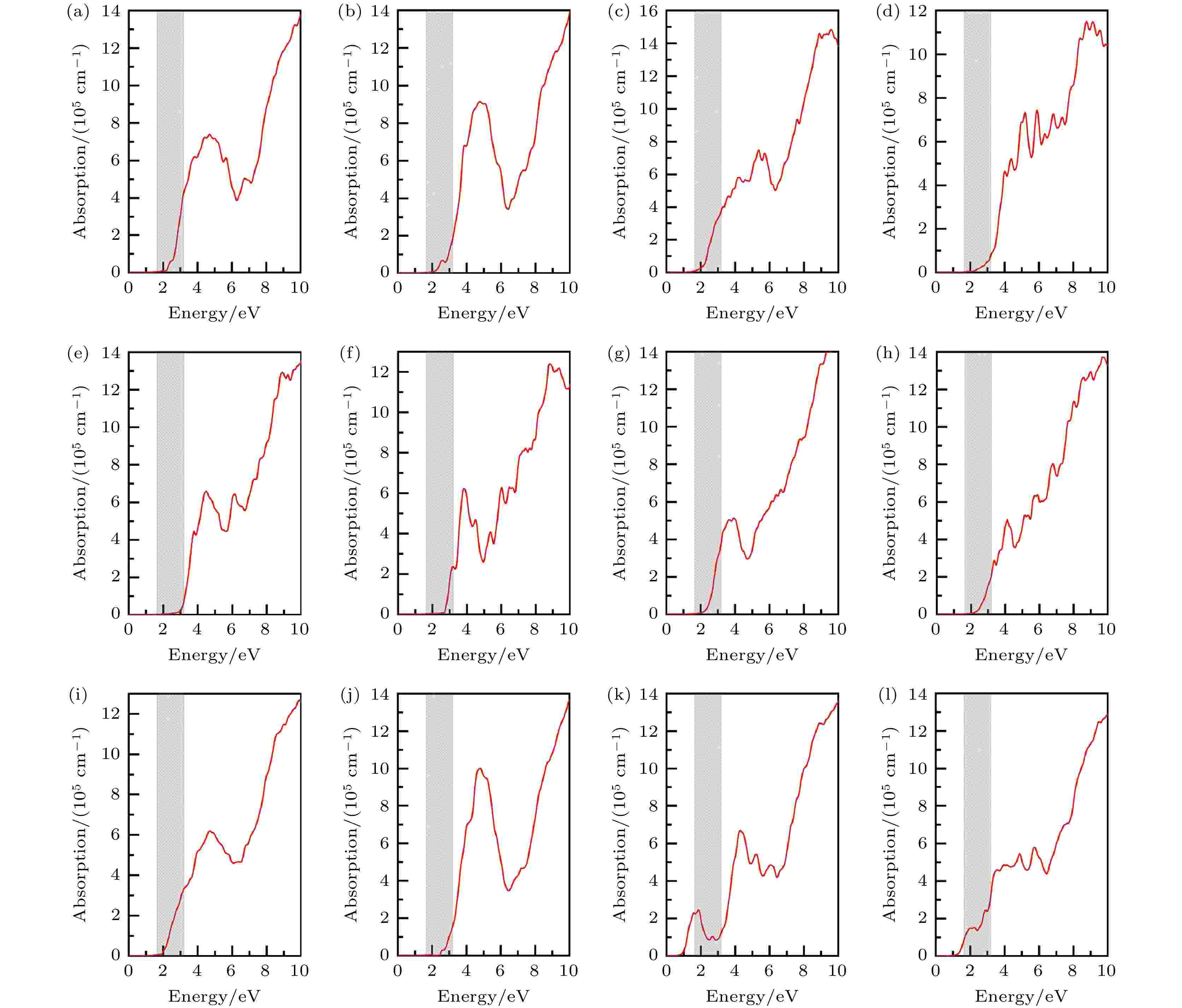图 11 12个CuBiI三元化合物结构的光吸收谱, 灰色区域代表可见光能量范围(1.64—3.19 eV)　(a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II; (c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II
Figure11. Optical absorption spectrum for the 12 structures of CuBiI ternary compound. The gray area represents the Visible energy range (1.64–3.19 eV): (a) CuBi₂I₇-P1; (b) CuBi₂I₇-P1-II;(c) Cu₂BiI₅-P1; (d) Cu₂BiI₅-Cm; (e) Cu₃BiI₆-P3; (f) Cu₃BiI₆-R3; (g) Cu₄BiI₇-P1; (h) Cu₄BiI₇-P3; (i) Cu₃Bi₂I₉-P1; (j) CuBi₃I₁₀-P1; (k) Cu₂BiI₇-P1; (l) Cu₂BiI₇-P1-II.

2

3.5.功率转换效率

-->

3.5.功率转换效率

传统的肖克利-奎塞尔(Shockley-Queisser, SQ)法预测光电转换效率依赖于材料的带隙, 并未考虑光吸收谱, 因此SQ方法预测的光电转换效率在很多情况下并不准确的. 相对于SQ方法, 光谱有限最大效率(spectroscopic limited maximum efficiency, SLME)法运用了热动力学方法, 考虑了特定的吸收光谱以及电子空穴复合过程对光电转换效率的影响, 得到的光电转换效率会更加符合实际情况^[39,40]. 本文采用了SLME方法计算太阳能电池的最大理论功率转换效率:

$\eta =\frac{{P}_{\mathrm{m}}}{{P}_{\mathrm{i}\mathrm{n}}},$

其中P_m和P_in为太阳光谱的最大功率密度和入射功率密度, 如下所示:

${P}_{\mathrm{m}}=JV=\left[{J}_{\mathrm{s}\mathrm{c}}-{J}_{0}\left({\mathrm{e}}^{\tfrac{q}{kT}}-1\right)\right]V,$

${P}_{\mathrm{i}\mathrm{n}}=\int _{0}^{\infty }E{I}_{\mathrm{s}\mathrm{u}\mathrm{n}}\left(E\right)\mathrm{d}E,$

式中, J是总电流密度, V是穿过吸收层的电压电势, k是玻尔兹曼常数, T为温度. 根据以下关系式, 短路电流密度J_sc和反向饱和电流密度J₀为:

${J}_{\mathrm{s}\mathrm{c}}=q\int _{0}^{\infty }\left(1-{\mathrm{e}}^{-2\alpha \left(E\right)L}{I}_{\mathrm{s}\mathrm{u}\mathrm{n}}\left(E\right)\right)\mathrm{d}E,$

${J}_{0}=\frac{q}{{f}_{\mathrm{r}}}\int _{0}^{\infty }\left(1-{\mathrm{e}}^{-2\alpha \left(E\right)L}{I}_{\mathrm{b}\mathrm{b}}\left(E,T\right)\right)\mathrm{d}E,$

其中L, I_sun, I_bb分别为薄膜材料的厚度, 1.5 G太阳光谱和黑体光谱的光子通量. α是通过第一性原理计算得出的吸收系数. 辐射复合分数($ {f}_{\mathrm{r}} $

)按以下关系式估算:

${f}_{\mathrm{r}}={\mathrm{e}}^{\left(\tfrac{{E}_{\mathrm{g}}^{\mathrm{d}\mathrm{a}}-{E}_{\mathrm{g}}}{kT}\right)},$

式中, $ {E}_{\mathrm{g}}^{\mathrm{d}\mathrm{a}} $

和$ {E}_{\mathrm{g}} $

分别为光学带隙和基本带隙. 可以看出, SLME不仅依赖于光子吸收率($ \alpha \left(E\right) $

), 还依赖于辐射电子-空穴复合分数($ {f}_{\mathrm{r}}) $

. 另外, 因为SLME的数值与材料的带隙紧密相关, 所以采用HSE方法计算所得的带隙来计算SLME.
图12为SLME方法预测的CuBiI三元化合物12个结构的光电转换效率. 当吸收层的厚度很小(t < 0.10 μm)时, 由于吸收层对光的吸收很弱, 导致光电转换效率也较低; 当吸收层厚度较大(t > 1 μm)时, 光电转换效率与吸收层厚度不再具有依赖关系, 基本保持最大光电转换效率. 在实验中, 太阳能电池一般会做成薄膜结构, 厚度大概在0.50 μm左右. 表4给出了t = 0.50 μm时CuBiI三元化合物12个结构的光电转换效率. 光电转换效率与能带值以及可见光区域光吸收强度有着密切的联系. Cu₂BiI₇-P1与Cu₂BiI₇-P1-II的带隙值小, 位于红外光能量范围内, 在整个可见光吸收范围内(1.64—3.14 eV)均有较强的吸收强度, 且Cu₂BiI₇-P1为直接带隙, 在受到光电子激发时, 价带顶的电子直接跃迁到导带, 因此Cu₂BiI₇-P1与Cu₂BiI₇-P1-II的光电转换效率最大, 分别为31.63%和28.30%. 相反, Cu₃BiI₆-P3, Cu₃BiI₆-R3和CuBi₃I₁₀-P1结构的带隙值大很多, 与理想的太阳能电池吸收材料的带隙(1.40 eV)相差很大, 且在可见光范围内的光吸收系数小, 即对太阳光的利用率很低, 导致其光电转换效率极小(2.86%, 5.49%和4.17%). 此外, Cu₂BiI₅-P1, Cu₄BiI₇-P1, Cu₃Bi₂I₉-P1结构在可见光范围内高的光吸收系数(4 × 10⁵ cm^–1)使得其具有较大的光电转换效率.

图 12 SLME方法预测的12个CuBiI三元化合物结构的光电转换效率与吸收层厚度的关系
Figure12. Photoelectric conversion efficiency of 12 structures of CuBiI ternary compound with respect to the absorption layer thickness predicted by SLME method.

4.结　论

采用晶体结构预测软件USPEX对CuBiI三元化合物(CuBi₂I₇, Cu₂BiI₅, Cu₂BiI₇, Cu₃BiI₆, Cu₃Bi₂I₉, CuBi₃I₁₀, Cu₄BiI₇)进行了全局结构搜索. 通过综合分析热力学、动力学以及机械稳定性, 确定了12种稳定结构: CuBi₂I₇-P1, CuBi₂I₇-P1-II, Cu₂BiI₅-P1, Cu₂BiI₅-Cm, Cu₂BiI₇-P1, Cu₂BiI₇-P1-II, Cu₃BiI₆-P3, Cu₃BiI₆-R3, Cu₄BiI₇-P1, Cu₄BiI₇-P3, Cu₃Bi₂I₉-P1, CuBi₃I₁₀-P1. HSE方法计算12个结构的带隙为1.13—3.09 eV, 表明成分比对带隙调控有着重要影响. 电子局域函数与Bader电荷分析表明Cu—I, Bi—I键具有强的离子性, 弱的共价性. 重要的是, 高的光吸收系数(4 × 10⁵ cm^–1)和高功率转换效率(31.63%)表明CuBiI三元化合物具有作为优良光电吸收材料的潜质. 本文的研究为CuBiI三元化合物在太阳能电池吸收材料的研究和应用提供了设计思路和理论支持.

本站小编 Free考研考试/2021-12-29

English Abstract

Structure prediction of CuBiI ternary compound and first-principles study of photoelectric properties

Corresponding author:Fan Xiao-Li, xlfan@nwpu.edu.cn

全文HTML

3.1.结构预测

3.2.晶体结构

3.3.电子结构

3.4.光吸收性质

3.5.功率转换效率

相关话题/结构 计算 光电 电子 材料

领限时大额优惠券,享本站正版考研考试资料!

混合时钟驱动的自旋神经元器件激活特性和计算性能

磁制冷材料LaFe<sub>11.5</sub>Si<sub>1.5</sub>基合金成分与磁相变温度关系的高通量计算

Be, Si掺杂调控GaAs纳米线结构相变及光学特性

适用400 Gbit/s接收系统的铟磷基低暗电流高带宽倏逝波耦合光电探测器阵列

富锂锰基三元材料Li<sub>1.208</sub>Ni<sub>0.333</sub>Co<sub>0.042</sub>Mn

中子辐照对掺镱光纤材料光学特性的影响

低温下InAs纳米结构在GaAs(001)表面形成机制的研究

电磁超构表面与天线结构一体化的低RCS阵列

基于非对称结构全介质超材料的类电磁诱导透明效应研究

X射线荧光CT成像中荧光产额、退激时间、散射、偏振等关键物理问题计算与分析