删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

磁制冷材料LaFe<sub>11.5</sub>Si<sub>1.5</sub>基合金成分与磁相变温度关系的高通量计算

本站小编 Free考研考试/2021-12-29
摘要:获得具有不同磁相变温度的La(Fe, Si)13基合金对拓宽磁制冷工作温区具有重要意义. 借助第一性原理模拟软件AMS-BAND模块并结合平均场理论对LaFe11.5Si1.5基磁制冷合金的磁相变温度进行了高通量计算. 研究了Mn, Co, Ni, Al和Fe缺位掺杂对LaFe11.5Si1.5基合金体系相变温度的影响, 得到了成分与磁相变温度的关系图. 利用高通量第一性原理计算可以有效地降低研究成本, 提高科研效率, 并能够对后续实验选取具有合适磁相变温度的磁制冷材料提供技术支持.
关键词: 高通量计算/
磁制冷/
磁相变温度/
第一性原理

English Abstract


全文HTML

--> --> -->
1.引　言
制冷技术在日常生活、 工业生产、 农牧医疗和国防军事等领域都发挥着举足轻重的作用. 气体压缩式制冷是目前最常采用的制冷技术, 但存在着制冷工质不够环保和制冷效率较低等问题. 基于材料磁熵变的磁制冷技术采用固体磁性材料作为制冷工质, 水等流体作为换热介质, 具有零GWP (global warming potential), 零ODP (ozone depletion potential), 低噪音以及便于小型化等特点, 是一种绿色环保的新型制冷技术. 磁制冷效率可达卡诺循环的 30%—60%, 而气体压缩制冷的效率一般仅为 5%—10%. 环境友好和高效节能的磁制冷技术日益受到国际社会的高度重视.
通常用磁热效应来衡量材料的磁制冷性能. 磁热效应是指外磁场变化引起磁性材料内部磁熵改变并伴随着吸热和放热的一种物理现象, 是磁性材料的固有特性, 通常用绝热温变和等温磁熵变表征[1]. 高性能磁制冷材料的探索最初是从金属Gd开始的, 其居里温度为294 K, 是一类二级磁相变材料. 1976年, 美国国家航空航天局的 Brown[2]首次采用金属 Gd 作为磁制冷工质, 在7 T的超导磁场和无热负荷的条件下获得了47 K的温度差. 为了拓宽其制冷温区, 多个课题组在Gd基合金中开展了磁制冷的研究工作[3-5]. 1997年, Gschneidner和Pecharsky[6,7]在Gd的三元合金Gd-Si-Ge中获得了巨大的室温磁热效应, 其中Gd5Si2Ge2的最大磁热效应可达Gd最大值的两倍, 是一种具有巨磁热效应的一级磁相变材料. 由于一级磁相变材料明显具有较大的磁制冷效应, 随后越来越多的研究工作都聚焦在探索具有大磁热效应的一级磁相变合金材料中, 并陆续发现了La(Fe, Si)13合金[8,9], Mn-Fe-P-As[10], Ni-Mn基铁磁形状记忆合金[11,12]以及${\rm{Mn}} M' X$ (M为过渡金属)X(X为Si或Ge)合金[13]等. 其中, La(Fe, Si)13基合金因磁熵变大, 相变温度易调, 滞后小, 原料丰富以及价格低廉等原因已经成为国际上公认的最具应用潜力的室温磁制冷材料之一.
作为一种典型的一级磁相变材料, La(Fe, Si)13基合金只在相变温度处表现出大的磁熵变, 所以工作区间仅集中在相变点附近较窄的温区, 给实际应用带来了困难. 通过提高外加磁场强度的方法可以起到拓宽磁制冷温区的效果, 但目前磁制冷机普遍采用永磁体, 其提供的磁场强度有限. 为了能在更宽的温度范围内获得大的磁热效应, 目前的磁制冷机大都采用在磁回热器热交换流体流动的方向填充多组具有不同相变温度的磁制冷工质, 希望通过多层工质叠加形成的复叠结构来拓宽制冷温区[14]. 美国宇航公司搭建的原型磁制冷机中使用了6 层La-Fe-Si-H 作为复叠制冷工质, 其磁相变温度较均匀地分布在30.5—40.3 K之间[15], 零负载时系统最大温跨达到了18 K. 根据文献报道, 利用多层磁工质复叠来进行磁制冷是目前最大制冷量原型机[15]和最高效率原型机[16]的常见技术方案.
基于上述分析, 在具有巨磁熵变的一级磁相变材料中, 调节其磁相变温度以获得不同温区下的大磁熵变是磁制冷的一个重要研究方向. La(Fe,Si)13基稀土磁制冷材料中, Mn的掺入可以提高合金的稳定性, 并且La(Fe, Mn, Si)13H合金的磁相变温度可以达到室温[17]. 掺Co和Ni同样也可以提高磁相变温度. 2002年, 胡凤霞等[18]利用Co替代Fe所获得的LaFe11.2Co0.7Si1.1合金的磁相变温度可以提高到274 K, 最大磁熵可达20.3 J/(kg·K). Moreno等[19]发现, 在LaFe11.6Si1.4合金中掺入不同浓度的Ni可以提高磁相变温度, 但是随着Ni浓度的升高, LaFe11.6–xNixSi1.4由一级相变变为二级相变. 2008年, 沈俊[20]研究了La1–xRxFe11.5Si1.5 (R = Ce, Pr, Nd)化合物的磁相变和磁热效应, 发现稀土R替代La会引起晶格收缩, 使Fe-Fe原子间的交换作用减弱, 但导致R-Fe交换作用增强, 从而提高了磁相变温度.
为了获得不同相变温度的磁制冷材料, 目前所采用的研究模式主要是传统炒菜方式, 即利用不同元素替代的方式去逐一合成这些材料再测量它们的磁相变温度. 这将导致研究成本过高, 效率过低, 不利于高性能磁制冷材料的高效研发. 材料基因技术是近年来兴起的材料研发的新模式, 它借鉴人类基因组计划的理念, 通过高通量的计算、 制备和表征等手段来研究材料的组成和结构等与材料性能间的关系. 这种全新的研究理念能缩短材料研发周期、 降低材料研发成本, 在材料研究领域日益受到高度重视.
本文从材料基因技术出发, 以具有巨磁热效应的La(Fe, Si)13基稀土合金为研究对象, 基于高通量的第一性原理计算, 研究了Co, Mn, Ni和Al等多种元素掺杂对体系磁相变温度的影响并构筑了磁相变温度相图, 预测符合实际应用的合金成分, 为获得具有不同磁相变温度的La(Fe, Si)13基稀土磁制冷材料提供了研究基础.
2.理论与实验方法
2
2.1.计算模型
-->

2.1.计算模型

本文以LaFe11.5Si1.5为例来估算不同元素掺杂对其磁相变温度的影响. 根据文献报道, La(Fe, Si)13基材料是具有立方NaZn13型结构的化合物, 空间群为Fm–3c(Oh6). 为了获得Si的占位信息, 首先分析未掺杂Si时LaFe13体系中每种原子的占位情况: LaFe13体系的每个晶胞中有8个La原子和104个Fe原子, Fe原子分别占据FeI(8b位)和FeII(96i位)两个不同的晶位. 其中, 8个La原子和8个FeI原子形成CsCl结构, 每个La原子被24个FeII原子包围. FeI原子被由12个FeII原子所组成的二十面体包围, 具有面心立方的局域环境. FeII原子被9个最近邻的FeII原子和1个FeI原子所包围. 当掺入Si后, LaFe11.5Si1.5体系中的12个Si原子随机占据FeII原子的位置[21], 晶体结构如图1所示.
图 1 LaFe11.5Si1.5基合金晶体结构示意图
Figure1. Schematic image of the crystal structure of LaFe11.5Si1.5-based alloy.

为解释稀土-过渡族化合物的磁性, Beth[22-27]提出了一种模型: 在Fe, Co和Ni中, 仅有5%甚至更少的3d电子被看作是真正的巡游电子, 其余3d电子仍具有局域性, 在库仑作用下, 以被极化的巡游3d电子为媒介, 局域的3d电子之间产生Ruderman-Kittel-Kasuya-Yosida (RKKY)长程相互作用. La(Fe, Si)13基稀土磁制冷材料的交换作用可以用RKKY机制来描述. 进一步地, 根据海森伯模型[28]和平均场理论, 可以通过公式$ {T}_{\mathrm{C}}= $$ {\Delta E}/({3 N{k}_{\mathrm{B}}}) $估算该体系的磁相变温度[29], 其中$ {k}_{\mathrm{B}} $为玻尔兹曼常数, N为磁性原子数, ?E为体系铁磁和反铁磁态下的能量差(EAFM–EFM). 本文用第一性原理模拟软件AMS-BAND (BAND2017.114)[30,31]模块进行相关计算, 此模块已引入相对论效应, 所用基组为全电子高精度基组, 并具有并行效率高的优势, 可用于计算具有较多核外电子的稀土合金体系. 对体系进行几何优化和单点能计算时, 参数设置为: 基组选用TZP, 泛函取广义梯度近似(GGA-PBE)[32], 布里渊区K点取5×5×5, 能量收敛标准为10–6 Hartree, 力收敛标准为10–4 Hartree/?.
2
2.2.实验方法
-->

2.2.实验方法

为了验证磁相变温度的估算结果, 除了与部分文献报道结果相对比外, 还制备了三种合金成分进行了实验研究. 在实验中所用的原材料La, Co, Mn, Fe和Si的纯度均为99.9％, 按LaFe11.5Si1.5, LaFe11.25Mn0.125Co0.125Si1.5和LaFe11Mn0.375Co0.125Si1.5化学配比配料后, 将原材料放入充有高纯氩气的电弧炉中, 反复熔炼以保证合金均匀. 经熔炼所得的铸锭样品封在高真空的石英管中, 在1373 K温度下退火7 d后将样品快速淬入冰水混合物中. 利用美国Quantum Design公司的VersaLab测试了所得样品的热磁曲线. 测量时, 测试模式选择“扫场模式”, 变温速率为1.5 K/min, 所加外场为500 Oe. 样品的热磁曲线如图2所示, 所对应的磁相变温度定义为dM/dT的极值.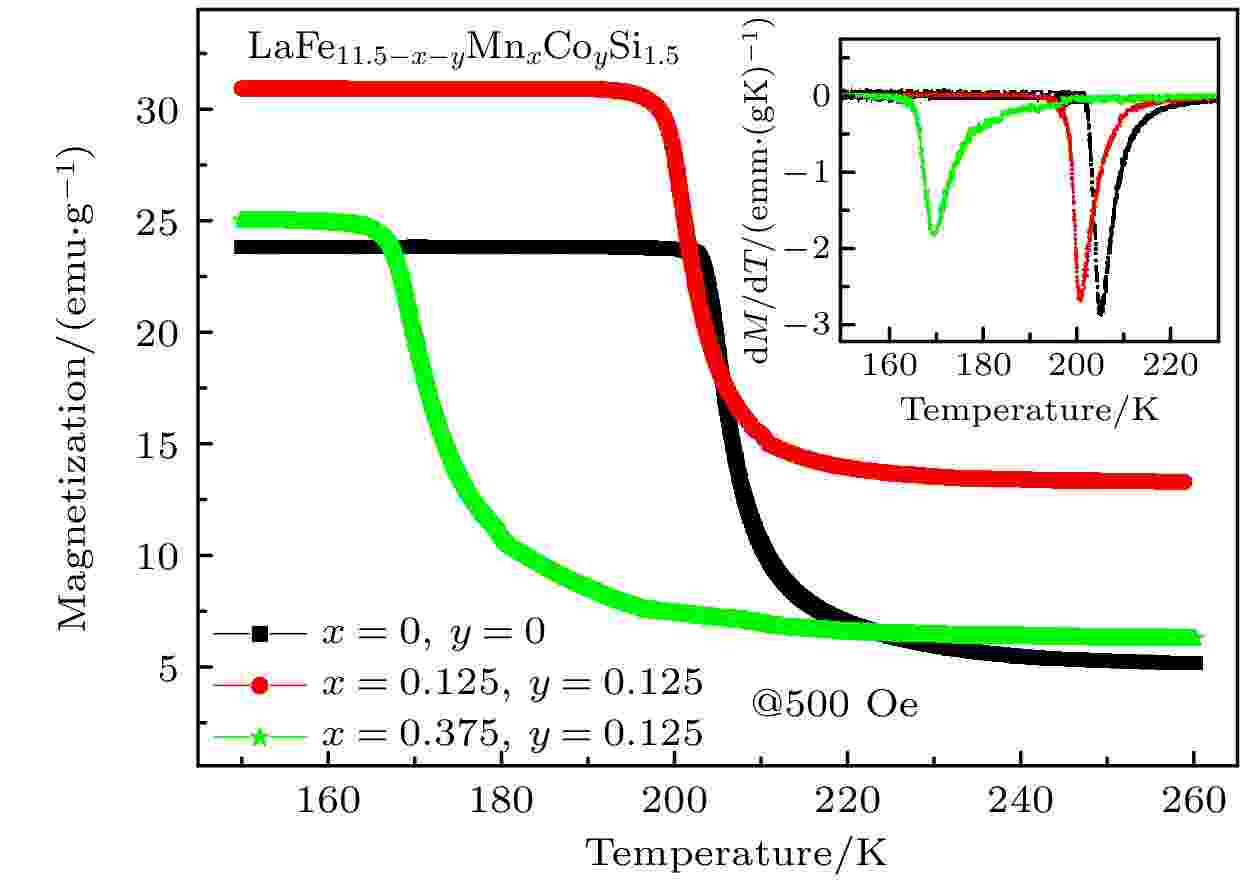
图 2 LaFe11.5–x–yMnxCoySi1.5合金热磁曲线; 插图是dM/dT曲线
Figure2. Thermomagnetic curves of LaFe11.5–x–yMnxCoySi1.5 alloys, inset is the dM/dT.

3.结果与讨论
2
3.1.LaFe11.5Si1.5合金磁相变温度的估算
-->

3.1.LaFe11.5Si1.5合金磁相变温度的估算

首先对具有不同晶格常数的LaFe11.5Si1.5合金体系进行几何优化. 通过拟合E-a曲线可以确定体系能量最低时的晶格常数a0 = 11.453 ?, 这与相应的实验值11.464或11.475 ?[33,34]之间的误差不超过0.2%; 然后对该晶格常数下的体系进行加U几何优化得到最终LaFe11.5Si1.5结构; 最后结合平均场理论估算磁相变温度, 计算体系铁磁态和反铁磁态的单点能. 由于LaFe11.5Si1.5基合金为强关联体系, 因此需要对La-d轨道进行加U处理[35]. 通过对多个U值的测试, 发现当U = 0.39 eV时估算得到的LaFe11.5Si1.5磁相变温度为191.4 K, 与实验报道的183.0—198.0 K[33,34,36]非常接近, 与实验值204.0 K (图2)也仅有6%的误差.
2
3.2.Co, Mn, Ni, Al掺杂对LaFe11.5Si1.5基合金体系磁相变温度的影响
-->

3.2.Co, Mn, Ni, Al掺杂对LaFe11.5Si1.5基合金体系磁相变温度的影响

基于上述计算参数, 利用高通量第一性原理计算研究了Co, Mn, Ni和Al等元素掺杂以及Fe缺位对LaFe11.5Si1.5合金体系磁相变温度的影响. 首先研究了LaFe11.5–xTx Si1.5 (T = Co, Mn, Ni, Al)等单掺合金体系的磁相变温度. 通过比较掺杂原子分别占据FeI或FeII位时体系的单点能, 发现所有的掺杂元素倾向于占据FeII位. 当用Mn元素替代Fe时, 随着Mn含量的升高, 估算出的磁相变温度随之降低, 与实验趋势相符[37]. 当x为0.125时, 估算得LaFe11.375Mn0.125Si1.5的磁相变温度为179.1 K, 与之前实验报道的具有相似成分的LaFe11.4Mn0.1Si1.5材料的磁相变温度181.0 K接近[37]. 随着Mn含量增加到x = 0.25, 估算LaFe11.25Mn0.25Si1.5的磁相变温度为167.8 K, 非常接近文献报道的实验值168 K[37]. 当单掺杂Co和Ni元素时, 体系的磁相变温度随着掺杂量的增加而升高, 与实验报道的趋势一致[38]. 在利用Ni进行掺杂, 当y取0.125时, 估算得到的LaFe11.375Ni0.125Si1.5的磁相变温度为192.3 K, 接近文献报道的具有相近成分LaFe11.385Ni0.115Si1.5的实验值195.0 K[38].
在上述工作的基础上, 研究了多元合金LaFe${}_{11.5-x-y} $MnxCoySi1.5, LaFe${}_{11.5-x-y} $MnxAlySi1.5, LaFe${}_{11.5-x-y} $MnxNiySi1.5和LaFe$ {}_{11.5-x-y} $MnxNiyCo0.125Si1.5体系 (x = 0, 0.125, 0.25, 0.375; y = 0, 0.125)的磁相变温度并构筑了成分与磁相变温度相图. 对于Mn, Co共掺杂的LaFe$ {}_{11.5-x-y} $MnxCoySi1.5体系, 构筑的成分-磁相变温度相图如图3(a)所示. 当x = 0, y = 0.125时, 体系磁相变温度从LaFe11.5Si1.5的191.4 K提高到192.6 K. 保持Co含量y = 0或0.125不变, 此时体系的磁相变温度随Mn含量的增加而逐渐降低. 为了验证Mn, Co共掺杂体系中估算磁相变温度的准确性, 对x取0.125和0.375时所对应成分LaFe11.375–xMnxCo0.125Si1.5的磁相变温度进行了实验验证. 如图2所示, 当x = 0.125或0.375时, 实验测量所得到的磁相变温度分别为200.0或170.0 K, 与理论估算的179.6 (x = 0.125)或157.7 K (x = 0.375)的误差分别为10.2%和7.2%.
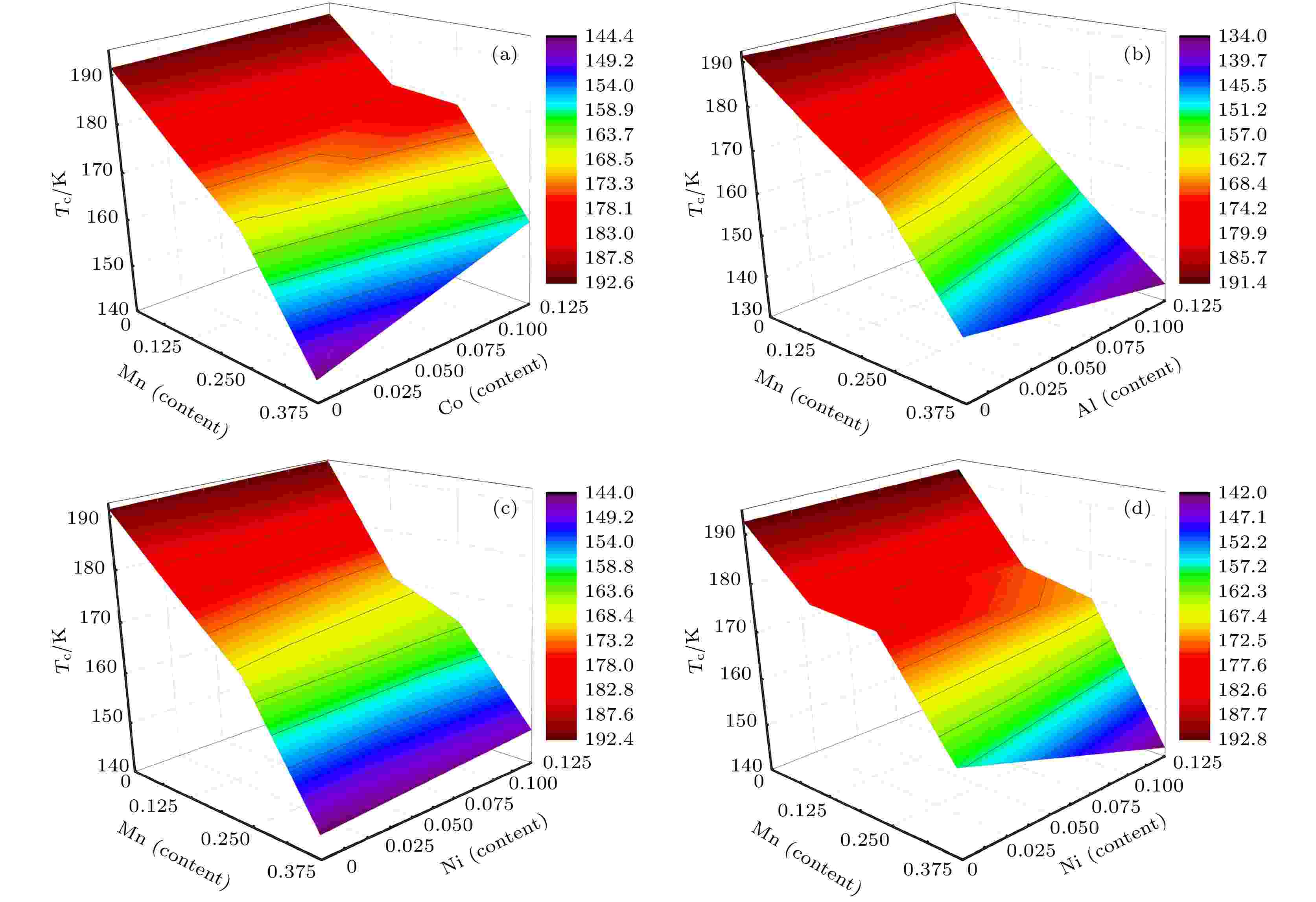图 3 合金体系相变温度相图　(a) LaFe11.5–x–yMnxCoySi1.5; (b) LaFe11.5–x–yMnxAlySi1.5; (c) LaFe11.5–x–yMnxNiySi1.5; (d) LaFe11.375–x–yMnxNiyCo0.125Si1.5
Figure3. The phase diagrams of phase transition temperature: (a) LaFe11.5–x-yMnxCoySi1.5; (b) LaFe11.5–x–yMnxAlySi1.5; (c) LaFe11.5–x–yMnxNiySi1.5; (d) LaFe11.375–x–yMnxNiyCo0.125Si1.5 alloys.

在LaFe11.5Si1.5合金中同时掺杂Mn和Al原子, 估算LaFe11.5–x–yMnxAlySi1.5体系的磁相变温度并给出了磁相变温度随成分变化的相图. 如图3(b)所示, 随着Al和Mn的掺入, 体系的磁相变温度逐渐降低, 在LaFe11Mn0.375Al0.125Si1.5体系中出现了磁相变温度最低值134.2 K. 紧接着, 研究了LaFe11.5–x–yMnxNiySi1.5合金体系的磁相变温度. 根据如图3(c)所示的成分-磁相变温度相图可以看出, 当Mn含量一定时, Ni的掺入提高了体系的磁相变温度. 而当Ni含量一定时, 体系的磁相变温度则随Mn含量的增加逐渐降低. LaFe11.5–x–yMnxNiySi1.5体系的磁相变温度最高和最低值分别为192.3和144.4 K. 进一步地, 本研究小组研究了Mn, Ni和Co三元共掺体系LaFe11.375–x–yMnxNiyCo0.125Si1.5, 其成分-磁相变温度相图如图3(d)所示. 随着Mn含量的增加, 磁相变温度呈下降趋势; 而随着掺杂Ni含量增加, 体系磁相变温度逐渐升高, 在LaFe11.25Ni0.125Co0.125Si1.5中磁相变温度达到最高值192.8 K.
2
3.3.Fe缺位对LaFe11.5Si1.5基合金体系磁相变温度的影响
-->

3.3.Fe缺位对LaFe11.5Si1.5基合金体系磁相变温度的影响

元素缺位也是一种有效调控磁相变温度的手段[39,40]. 本研究组研究了Fe缺位对LaFe11.5Si1.5基合金体系磁相变温度的影响. 如前所述, 在LaFe11.5Si1.5中, 每个晶胞中有92个Fe原子, Fe可以占据FeI或FeII位. 当缺失1个Fe原子, 分别对FeI或FeII缺位时体系的能量进行对比, 发现相同缺失浓度下, FeI缺失时体系的能量较低. 所以在下面的计算中, 将FeI位设为Fe的缺失位点. 当不掺杂任何元素, FeI位缺失一个Fe原子时, LaFe11.375Si1.5的磁相变温度为160.0 K, 与LaFe11.5Si1.5的191.4 K相比有所下降. 进一步地, 对FeI位缺失一个Fe原子时多元掺杂合金体系LaFe$ _{11.375-x-y} $MnxNiySi1.5, LaFe$ _{11.375-x-y} $MnxCoySi1.5, LaFe$ _{11.25-x-y} $MnxNiyCo0.125Si1.5及LaFe$ _{11.25-x-y} $MnxCoyNi0.125Si1.5的磁相变温度进行了估算. 如图4所示, 在FeI位缺失一个Fe原子时, 掺杂Mn, Co和Ni时体系的磁相变温度变化的总体趋势与不缺位时类似.
图 4 合金体系相变温度相图　(a) LaFe11.375–x–yMnxNi ySi1.5; (b) LaFe11.375–x–yMnxCoySi1.5; (c) LaFe11.25–x–yMnxNiyCo0.125Si1.5; (d) LaFe11.25–x–yMnxCoyNi0.125Si1.5
Figure4. The phase diagrams of phase transition temperature: (a) LaFe11.375–x–yMnxNi ySi1.5; (b) LaFe11.375–x–yMnxCoySi1.5; (c) LaFe11.25–x–yMnxNiyCo0.125Si1.5; (d) LaFe11.25–x–yMnxCoyNi0.125Si1.5 alloys.

这样, 通过高通量第一性原理计算的方法估算了Co, Mn, Ni和Al等元素掺杂以及Fe缺位时LaFe11.5Si1.5基合金体系的磁相变温度, 为实验上筛选具有合适磁相变温度的La(Fe, Si)13基磁制冷材料提供了技术支持.
2
3.4.PDOS分析及Fe磁矩变化
-->

3.4.PDOS分析及Fe磁矩变化

磁制冷材料磁矩的大小是影响其磁熵变值的一个重要因素. 为了研究Al, Co, Mn, Ni等元素掺杂对LaFe11.5Si1.5合金体系磁矩的影响, 分别计算了LaFe11.375T0.125Si1.5体系投影态密度(PDOS)和元素掺杂后Fe的磁矩.
图5为LaFe11.375T0.125Si1.5体系的PDOS分布. 从图5(a)中可以看出, 当掺入原子Al时, Al自旋向上(正)和自旋向下(负)的PDOS值几乎是对称的, 因此Al没有磁性. Al-p主要在–10—–5 eV, 对PDOS有贡献. 虽然Al-p对体系PDOS的贡献很小, 但是Al-p与Fe-d的PDOS峰一一对应, 表明Al-p与Fe-d有一定的杂化. 在费米能级附近, Fe-d自旋向上电子主要占据价带, Fe-d自旋向下电子几乎均匀分布于价带和导带. Fe-d自旋向上和向下电子PDOS的不对称分布使得FeI和FeII的平均磁矩分别为1.716μB/FeI和2.150μB/FeII, 与计算得出的LaFe11.5Si1.5体系中FeI和FeII的平均磁矩1.758μB/FeI和2.179μB/FeII相比有所减小.
图 5 LaFe11.5–xTxSi1.5 (T = Al, Co, Mn, Ni)合金体系的PDOS图
Figure5. The PDOS of LaFe11.5–xTxSi1.5 (T = Co, Mn, Ni, Al) alloys.

当掺杂Co原子时, 发现费米能级附近电子自旋向上电子态密度主要分布在价带, 并且PDOS主要由Co-d与Fe-d共同贡献且二者PDOS峰耦合很好; Fe自旋向下电子态密度几乎均匀分布在费米能级两侧的价带和导带, 而Co-d轨道自旋向下PDOS值相对Fe-d向价带方向有明显的移动, 导致Co-d与Fe-d的PDOS耦合较差(图5(b)). Fe-d自旋向上和向下的PDOS值分布明显不对称, 计算得出FeI和FeII的平均磁矩分别为1.758μB/FeI和2.174μB/FeII, 相比于掺Al体系, Co掺杂体系中FeI和FeII的平均磁矩都有所增大, 与LaFe11.5Si1.5体系中FeI和FeII的磁矩几乎一致.
Mn原子掺杂相比于Co和Al的掺杂, 情况有所不同. 如图5(c)所示, Mn-d的PDOS峰相对于Fe-d向右偏移, 并且自旋向上电子态密度最高峰出现在费米能级处, Mn-d与Fe-d耦合较强, 峰值一一对应; 而在能量为–5.00—0.25 eV, Mn-d与Fe-d自旋向下的PDOS杂化增强; 能量高于0.25 eV时, PDOS主要由Mn-d贡献, 且与Fe-d耦合变差. Fe-d自旋向上和向下的PDOS值分布更加不对称, 导致FeI和FeII的平均磁矩分别为1.773μB/FeI和2.188μB/FeII, 与LaFe11.375Co0.125Si1.5相比, 磁矩进一步增加, 相比于LaFe11.5Si1.5体系中FeI和FeII的磁矩1.758μB/FeI和2.179μB/FeII也有所增加. 掺杂Ni时, LaFe11.375Ni0.125Si1.5合金的PDOS分布与掺Co时相似(图5(d)). 相比于Co-d的PDOS分布, 自旋向下Ni-d的PDOS峰明显向左偏移, 导致自旋向上与向下PDOS分布比较对称. Fe-d的PDOS存在明显的不对称分布, 估算LaFe11.375Ni0.125Si1.5合金中Fe的磁矩分别为1.743μB/FeI和2.175μB/FeII, 相比于LaFe11.5Si1.5体系中FeI和FeII的磁矩有所减小.
从上述结果可以得出, 相比于LaFe11.5Si1.5体系, 掺杂Ni和Al时FeI和FeII磁矩稍微减小; 掺杂Co时FeI和FeII磁矩几乎不变, 只有掺入Mn时磁矩才有所增加. 进一步地, 对多元掺杂LaFe11.375–xMnxCo0.125Si1.5合金体系的磁矩进行了计算, 研究了该体系中Fe磁矩随Mn含量增加的变化趋势. 如图6所示, 随着Mn含量增加, 每个FeI和FeII原子的磁矩都受到不同程度的影响, 平均磁矩都有所增加, 由1.758μB/FeI和2.179μB/FeII (x = 0) 分别增加到1.802μB/FeI和2.213μB/FeII (x = 0.375).
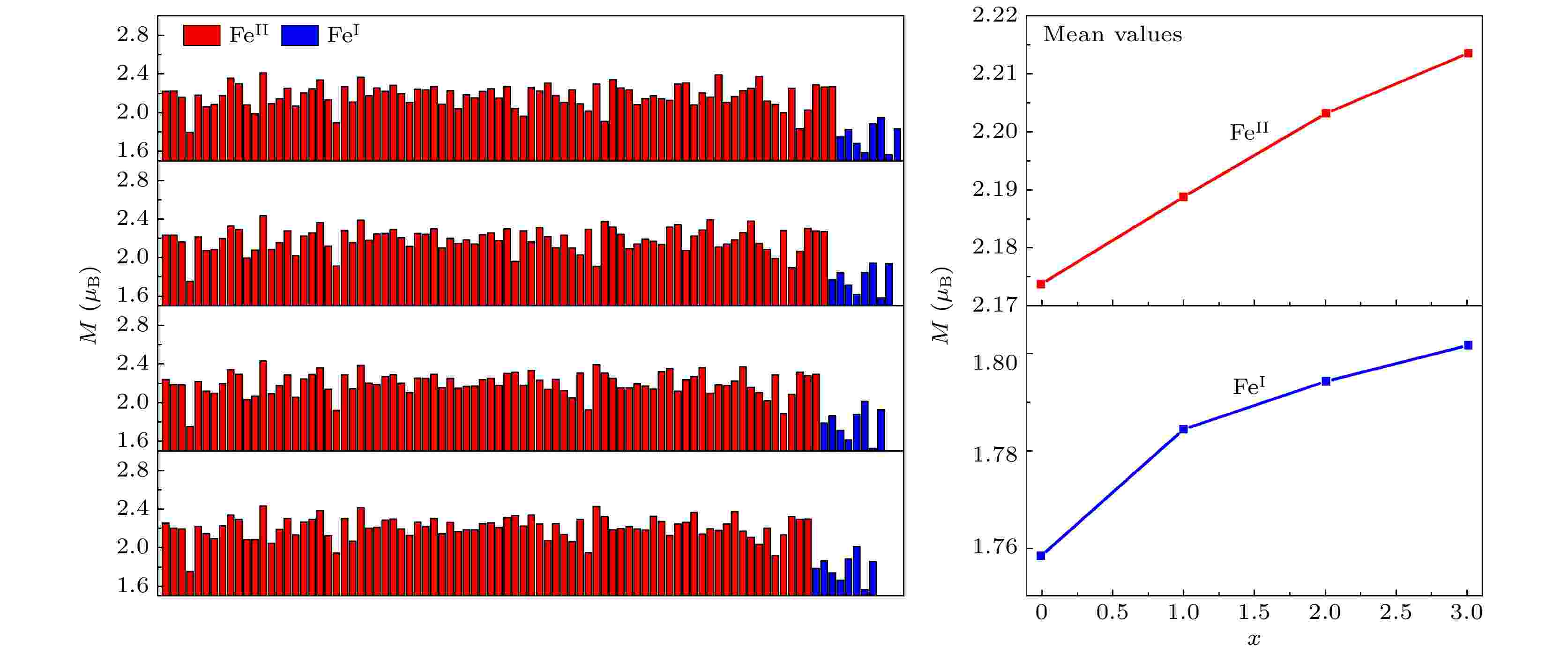图 6 LaFe11.375–xMnxCo0.125Si1.5合金体系中Fe的磁矩
Figure6. The magnetic moment of Fe atom in LaFe11.375–xMnxCo0.125Si1.5 alloys.

4.结　论
利用高通量第一性原理计算研究了Co, Mn, Ni, Al及Fe缺位掺杂对LaFe11.5Si1.5基合金体系磁相变温度的影响. 首先估算单掺体系的磁相变温度并与文献报道的实验结果进行对照, 发现计算方法有较高的准确性; 然后对多元掺杂的LaFe11.5Si1.5基合金体系进行了高通量第一性原理计算, 结果表明, Mn和Fe缺位的掺入使得体系磁相变温度降低, 而掺杂Co和Ni可以提高体系的磁相变温度; 掺杂Mn时可以提高Fe的磁矩. 根据计算给出的LaFe11.5Si1.5基合金体系中的成分-磁相变温度相图, 可以在109.4—192.8 K宽的温度范围内选择合适的合金成分. 高通量第一性原理计算可以降低研究成本, 提高科研效率, 为后续实验选取合适的磁制冷材料提供研究基础和技术支持.
本文的数值计算是在南京大学高性能计算中心的计算机集群上完成的, 感谢南京大学高性能计算中心提供计算平台.
相关话题/材料 计算 实验 电子 技术
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 混合时钟驱动的自旋神经元器件激活特性和计算性能
    摘要:自旋神经元是一种新兴的人工神经形态器件,其具有超低功耗、强非线性、高集成度和存算一体等优点,是构建新一代神经网络的强有力候选者.本文提出了一种磁场辅助磁弹应变驱动的混合时钟自旋神经元,利用OOMMF微磁学仿真软件建立了该神经元器件的微磁学模型,基于LLG方程建立了其数值仿真模型,利用所设计的自 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 富锂锰基三元材料Li<sub>1.208</sub>Ni<sub>0.333</sub>Co<sub>0.042</sub>Mn
    摘要:采用基于密度泛函理论的第一性原理方法,计算了$R\bar{3}m$相的富锂锰基三元正极材料Li1.208Ni0.333Co0.042Mn0.417O2的晶体结构、电子结构以及缺陷性质.结果表明,Li1.208Ni0.333Co0.042Mn0.417O2是一种具有直接带隙的磁性半导体材料,其价 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 原位表征技术在全固态锂电池中的应用
    摘要:近年来,可移动消费电子与电动汽车等产业发展迅速,迫切需要发展高能量密度与高安全稳定性的锂电池,以提高这些设备的长续航与长期稳定运行的能力.这使得全固态锂电池极具潜力,并获得迅速发展.然而,高性能全固态锂电池的发展需要对其充放电机制与性能衰减机理等有深入的认识,对电池内部及界面的微观结构、物相组 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 中子辐照对掺镱光纤材料光学特性的影响
    摘要:采用改进型化学气相沉积法结合稀土螯合物掺杂制备了系列掺镱光纤预制棒及光纤,并测试了光纤(预制棒)辐照、退火前后的光学性能.结果表明:中子辐照后掺镱光纤材料中与Al相关的缺陷浓度增多,导致光纤材料在可见光区域吸收损耗增加.Ce离子的掺杂可缓减铝氧空位中心(Al-OHC)等色心缺陷的增加,从而有效 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于非对称结构全介质超材料的类电磁诱导透明效应研究
    摘要:本文设计了一种非对称结构的类电磁诱导透明超材料结构,利用时域有限差分方法对其光学特性和类EIT效应进行了仿真分析,建立了其耦合洛伦兹模型,并对所设计超材料结构的类EIT效应进行了模拟分析.结果表明:利用两个长短不同的硅块明模和明模之间的耦合,在1555nm附近实现了类电磁诱导透明效应;通过对该 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • X射线荧光CT成像中荧光产额、退激时间、散射、偏振等关键物理问题计算与分析
    摘要:X射线荧光CT(X-rayfluorescencecomputedtomography,XFCT)是一种使用X射线荧光(X-rayfluorescence,XRF)实现功能性成像的新技术,在生物医学成像中表现出较大潜力.但是,X射线穿过生物体的同时还会产生大量康普顿散射光子,对XRF信号的采集 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Si<sub><i>n</i></sub>团簇/石墨烯(<i>n</i> ≤ 6)结构稳定性和储锂性能的第一性原理计算
    摘要:目前,硅/碳复合材料是锂离子电池最有潜在应用前景的高容量负极材料之一,硅与碳材料的界面状态是影响其电化学性能的重要因素.本文在作为碳材料结构单元的石墨烯表面构建了Sin(n≤6)团簇,采用基于密度泛函理论(DFT)的第一性原理方法研究了Sin团簇/石墨烯(Sin/Gr)的几何构型、结构稳定性和 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 背电极材料、结构以及厚度等影响钙钛矿太阳能电池性能的研究
    摘要:背电极是影响钙钛矿太阳电池性能的一个重要因素.本文采用COMSOL软件仿真研究了背电极材料、结构、厚度对电池性能的影响规律.发现相对于背电极金属的功函数,其阻值对电池性能影响小.背电极结构除了阻值会影响电池性能,还存在影响电池性能的其他因素.蜂窝结构背电极中,考虑制作难易程度的情况下,圆形半径 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高海拔宇宙线观测实验中scaler模式的模拟研究
    摘要:位于四川省稻城县海子山的高海拔宇宙线观测站(LHAASO)包含3个子阵列,即地面粒子探测器阵列(KM2A)、水切伦科夫探测器阵列(WCDA)和广角大气切伦科夫望远镜阵列(WFCTA).作为LHAASO实验的主阵列,KM2A由5195个地面电磁粒子探测器(ED)和1188个地下缪子探测器(MD) ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 水团簇掺杂实验方法研究进展
    摘要:水是空间中最常见的分子之一,也是地球上生物赖以生存的最有价值的物质资源.水团簇的研究对于水资源的实际利用具有重要作用,同时水团簇还可作为理想的水微观模型,可拓展物理化学基础科学的发展,并为溶剂和溶质之间尺寸依赖的解离性质及相互作用等研究提供借鉴.另外一方面,气相酸性混合水团簇近年来引起了学界高 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.