摘要:铝合金中Fe元素的含量直接影响合金的塑性、耐热性、强度及抗应力腐蚀性能, 其成分的定量分析是合金成分在线检测的重要环节. 为了提高铝合金中Fe元素定量分析精度, 把空间约束纳秒激光诱导击穿光谱技术与梯度下降法相结合. 通过采集激光诱导铝合金等离子体发射光谱, 发现在平板空间约束下的等离子体辐射强度有明显增强, 在间距为10 mm时的等离子体发射光谱增强约2.3倍. 分别利用内标法和梯度下降法建立定标模型, 对比两种模型的拟合系数、均方根误差和平均相对误差. 在平板约束条件下, 相比于内标法, 梯度下降法得到的Fe元素定量分析参数R²从95.22%提升到了99.22%, 训练集均方根误差从质量分数0.1409%下降到了0.0731%, 测试集均方根误差从质量分数0.1401%下降到了0.0756%, 平均相对误差从6.8893%下降到3.5521%. 与内标定标模型相比, 梯度下降定标模型的精确度和稳定性都有所提高, 空间约束LIBS结合梯度下降法可以有效地降低合金基体效应和自吸收效应对定量分析的影响.
关键词: 激光诱导击穿光谱/
梯度下降/
空间约束/
铝合金

English Abstract

全文HTML

--> --> -->

铝合金是世界上使用量第二大的金属材料, 仅次于钢. 由于其强度高、密度低、塑性好, 广泛应用于建筑、航空、交通、电子等诸多领域^[1]. 铝合金中元素的含量将直接影响铝合金的组织和性能, 其中Fe元素含量对铝合金的强度、塑性和应力腐蚀性有重要影响^[2]. 在铝合金铸造过程中, Fe元素质量分数小于0.6%时, 会造成不易成型而脱模现象, 当Fe元素质量分数大于1.2%时, 会降低铸件品质并缩短铝合金的使用寿命, 因此对铝合金中Fe元素的定量分析是铝合金铸造过程中的重要环节之一.
传统的铝合金成分检测技术主要有电感耦合等离子体原子发射光谱法、火花源原子发射光谱法和X射线荧光法^[3-5], 这些方法都需要对样品进行预处理, 无法进行铝合金原位快速检测. 激光诱导击穿光谱技术(laser induced breakdown spectroscopy, LIBS)是一种多元素同时分析的化学计量方法, 由于具有无需样品制备、原位和在线分析能力, 目前LIBS已广泛适用于土壤重金属污染检测^[6]、大气污染成分检测^[7]、爆炸物成分检测^[8]、生物癌症诊断^[9]、金属冶炼过程检测等领域^[10], 已成为化学计量分析领域的“Super Star”.
LIBS用于金属成分检测过程中, 涉及包括高功率激光与物质相互作用、激光等离子体膨胀、等离子体与环境空气作用等复杂的物理过程, 使得空气环境下相邻激光脉冲诱导靶材产生的等离子体的空间形态有一定的差异性^[11], 从而在固定探测立体角内的等离子体发射光谱强度随激光脉冲个数有一定的起伏, 影响了LIBS技术的探测精确度, 因此LIBS技术存在一定的实验重复性差和探测精度低等技术缺陷^[12], 限制了LIBS技术的发展和应用. 针对LIBS技术实验重复性差和探测精度低等技术问题, 目前相关研究人员主要在LIBS实验方案设计和LIBS光谱数据处理两方面开展工作. 在LIBS实验方案设计方面, 主要开展了双脉冲激发、磁场约束、空间约束等方法提高等离子体的时空稳定性, 从而提高LIBS技术的探测精度. Guo等^[13]利用半球腔空间约束LIBS对钢样品进行定量分析, 无腔体和有腔体下Mn I 476.64/Fe I 492.05 nm的相关系数R²分别为0.945 和0.989, 通过空间约束提高了钢样品中微量元素(V, Cr和Mn)的检测精度; Li等^[14]提出了圆柱腔空间约束LIBS技术来提高煤中碳含量的测量精度, 具有圆柱腔约束组合模型的R²达到0.99; Ren等^[15]提出了一种将空间约束激光诱导击穿光谱技术与纳米颗粒相结合的方法提高微量元素检测精度. 在LIBS光谱数据处理方面, 主要利用LIBS结合机器学习算法提高LIBS定量分析精度. Tian等^[16]采用LIBS技术分别结合内标法、偏最小二乘(PLS)和支持向量机(SVM)三种回归模型对三种海鲜中的磷酸盐进行定量分析, 其中SVM模型的R²最高为0.9904; Hao等^[17]利用LIBS与PLS回归模型结合提高铁矿石酸度的测量精度, 测试样品酸度的平均相对误差(average relative error, ARE)达到3.65%; Rao等^[18]将回归集成模型与LIBS结合对硅元素含量进行预测, 并将其预测准确性与传统主成分回归(PCR)、PLS和人工神经网络(ANN)回归模型进行对比. LIBS 技术现阶段在光谱数据处理领域存在的主要问题是重复性差和分析精度低, 解决方法主要有单变量光谱归一化^[16]、等离子体图像^[19]、机器学习多变量回归^[20]、黑体辐射定标^[21]等, 其中单变量分析(内标法等)的光谱数据处理通常会导致较差的分析性能, 基于化学计量学或机器学习方法的多元分析已被证明能够提供可靠的校准模型, 从而提高LIBS测量的分析精度.
梯度下降法是在20世纪80年代由Hinton^[22]提出的, 梯度下降法在特征变量较大时也可以运行良好, 通过代价函数迭代的方法可以更直观地进行极小值寻优, 在非矩阵层面对光谱数据进行运算, 简化了计算流程, 提高了运算效率. 因此本文提出基于平板空间约束LIBS技术结合梯度下降法对铝合金样品中的Fe元素进行定量分析, 对结合空间约束和梯度下降法的定标模型进行评估, 在此基础上, 开展LIBS技术结合梯度下降方法提高铝合金中Fe元素的探测精度.

空间约束ns-LIBS实验装置如图1所示. 实验采用波长1064 nm、脉冲宽度10 ns、重复频率10 Hz的Nd:YAG激光器, 激光光束通过由半波片和格兰棱镜组成的能量衰减系统调节激光脉冲能量, 通过焦距为120 mm的平凸石英透镜(L1)聚焦到铝合金样品表面产生等离子体. 等离子体辐射光谱由焦距为75 mm的收集透镜L2聚焦到配有ICCD (1024 × 1024 pixel, DH334)的中阶梯光栅光谱仪(Mechelle 5000, Andor)的光纤探头内. 为避免对铝合金样品表面同一位置的过度烧蚀, 样品在三维电动平移台上以0.5 mm/s的速度做“弓”字形运动. 实验过程中, 激光能量为80 mJ, ICCD的门宽为1 μs, 光谱探测延时为1 μs. 为了减小激光能量波动对LIBS光谱强度的影响, 每组光谱数据采集50发脉冲做平均, 并且相同实验条件下重复5次. 实验采用6种铝合金标准样品(LD7.8), 该样品由西南铝业集团有限责任公司研制, 铝合金标准样品的Fe元素含量如表1所列. 实验均在标准大气压、室内温度为22 °C、空气相对湿度为25%条件下开展.
图 1 空间约束ns-LIBS实验装置图
Figure1. Experimental setup diagram of spatial confinement nanosecond laser-induced breakdown plasma.

样品	E311	E312a	E313	E314	E315	E316
Cu	4.51	2.45	1.52	3.33	0.927	5.55
Mg	0.428	1.370	0.897	1.800	2.260	0.074
Fe	0.454	1.230	0.908	1.610	1.870	0.115
Ni	1.550	1.090	2.020	0.624	0.153	2.250
Mn	0.095	0.119	0.239	0.184	0.287	0.054
Si	0.094	0.724	1.220	0.371	1.530	0.090
Zn	0.140	0.220	0.334	0.166	0.367	0.084
Ti	0.02100	0.07800	0.12000	0.05500	0.16100	0.00095

表1铝合金标样元素成分表(质量分数百分比)
Table1.Element composition of standard aluminum alloy sample (weight percent)

梯度下降法又称最速下降法, 是一种用于求解函数极小值的算法, 常被用来求解无约束最优化问题, 其每一步主要对目标函数的梯度向量进行求解, 搜索方向为当前位置的负梯度方向^[23,24], 参数集的函数表征为

$ h({\boldsymbol{x}};{\boldsymbol{\theta}} ) = {\theta _0}{\text{ + }}{\theta _1}{x_1} + \cdots + {\theta _n}{x_n} = {{\boldsymbol{\theta}} ^{\text{T}}}{\boldsymbol{x}}, $

其中${\theta _{\text{i}}}~(i = 0, 1, 2, \cdots, n)$为模型参数, ${x_i}~(i = 0, 1, $$ 2, \cdots, n)$为每个样本的n个特征值.
代价函数为

$\begin{split}&J\text{(}{\theta }_{0},{\theta }_{1}\text{, }\cdots,{\theta }_{n})\\=\;&\frac{1}{2m}{\sum\limits_{j=1}^{m}\left[{h}_{\theta }({x}_{0}^{(j)},{x}_{1}^{(j)},\cdots \text{, }{x}_{n}^{(j)})-{y}_{j}\right]} ^{2},\end{split}$

其中, m为样本个数. 梯度下降法的核心思想是对${\theta _0}, {\theta _1}, \cdots, {\theta _n}$, 学习率$\alpha $和迭代次数等参数进行初始化. 具体过程如下:
1)对代价函数求导得到下降梯度, 表达式为

$ \frac{\partial }{{\partial {\theta _{\text{i}}}}}J({\theta _{\text{0}}},{\theta _{\text{1}}}, \cdots,{\theta _n}); $

2)利用学习率与梯度的乘积表征该位置的下降距离, 即$\alpha \dfrac{\partial }{{\partial {\theta _i}}}J({\theta _{\text{0}}}, {\theta _{\text{1}}}, \cdots, {\theta _n})$;
3)重置初始参数$\theta $, 更新${\theta _i}$表达式,

$ {\theta _i} = {\theta _i} - \alpha \frac{\partial }{{\partial {\theta _i}}}J({\theta _{\text{0}}},{\theta _{\text{1}}}, \cdots,{\theta _n}). $

通过对学习率和参数初始值的优化, 使代价函数的值达到最小, 导出参数从而实现对新数据的预测. 先将实验获取的铝合金LIBS光谱数据进行均值归一化处理, 然后利用梯度下降算法对铝合金LIBS光谱数据进行处理, 从而对铝合金中的Fe元素进行定量分析计算, 计算流程如图2所示.
图 2 梯度下降算法流程图
Figure2. Flowchart of gradient descent algorithm.

2

-->

4.1.LIBS光谱增强

优化平板空间约束光谱增强效果最好实验条件(激光能量80 mJ、板间距10 mm、光谱探测延时7 μs)下的铝合金LIBS光谱如图3所示, 选取247—277 nm范围内Fe谱线较丰富的LIBS光谱波段作为铝合金中的Fe成分分析对象. 在平板空间约束条件下, 纳秒激光烧蚀诱导铝合金产生的等离子体发射光谱强度存在明显增强, 且谱线Fe I 274.9 nm增强了2.3倍. 这是由于纳秒激光烧蚀铝合金诱导产生的等离子体快速向外膨胀, 同时伴随产生冲击波向外快速膨胀. 当向外膨胀的冲击波遇到平板空间约束障碍物时, 反弹膨胀传输的冲击波压缩等离子体羽, 使等离子体羽体积变小, 增加等离子羽体内的粒子间碰撞几率, 使低激发态原子经碰撞激发跃迁至高激发态的原子数增加, 从而实现了等离子体发射光谱的增强^[25-27]. 等离子体光谱稳定性是评价LIBS实验重复性的重要参数, 在优化的平板空间约束实验条件下, LIBS谱线中Fe元素 Fe I 274.9 nm特征光谱及270 nm处的背景光谱的相对标准偏差(relative standard deviation, RSD)值分别为3.48%和2.56%, 而无空间约束下对应的光谱RSD值分别为10.13%和7.32%. 结果表明, 空间约束不仅能够增强LIBS光谱强度, 同时还能降低LIBS光谱的RSD, 提高LIBS光谱稳定性, 从而提高了LIBS实验重复性.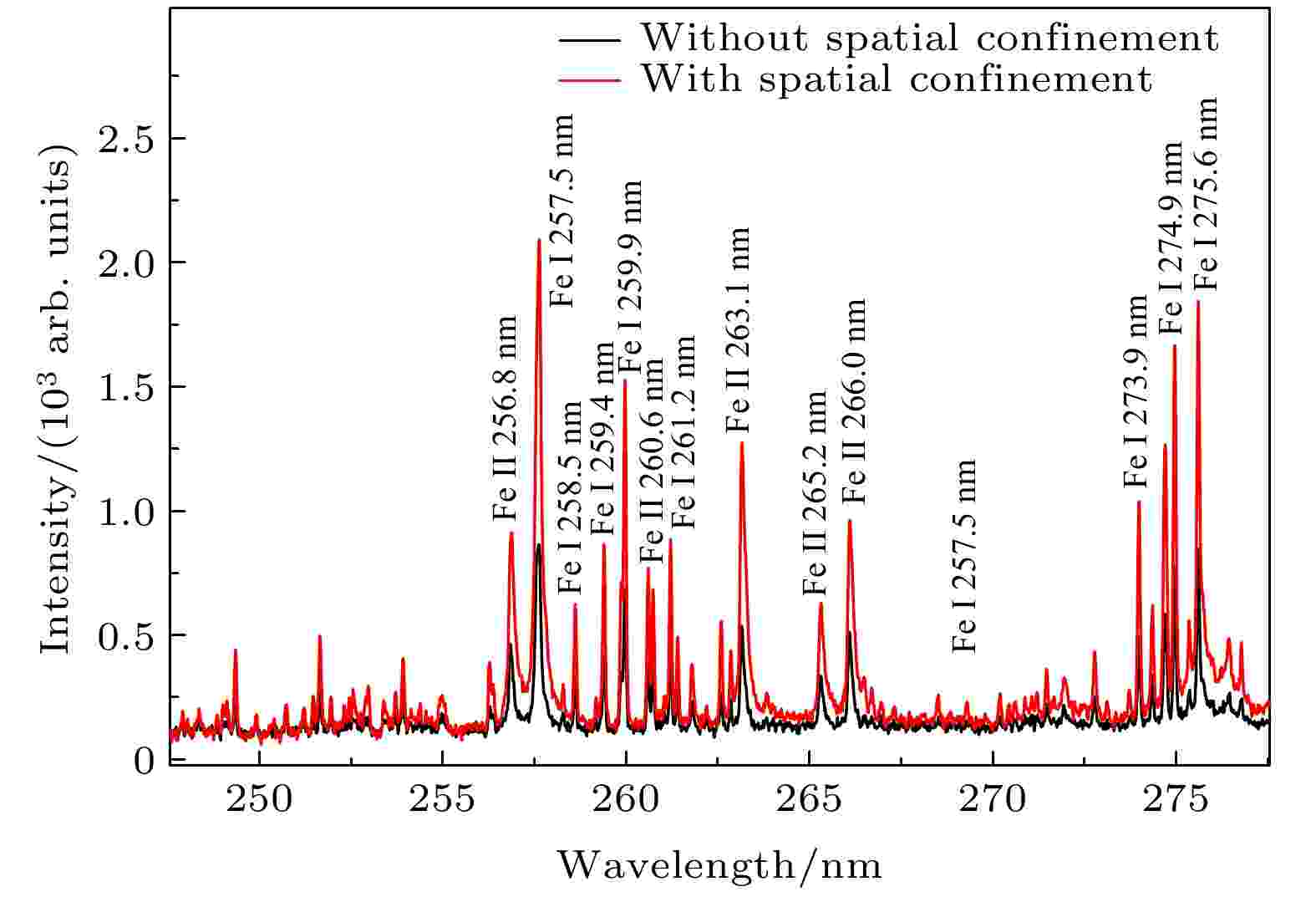
图 3 空间约束纳秒激光诱导击穿光谱
Figure3. Nanosecond laser-induced breakdown spectroscopy with and without parallel plates confinement.

2 -->

4.2.定量分析

内标法是LIBS分析中应用较广泛的定量分析方法, 通过内标元素的元素峰高或归一化光谱强度来补偿LIBS检测中的基体效应^[28]. 选择Al II 288.2 nm作为内标参考线, 以Fe元素的Fe I 274.9 nm谱线作为定量分析谱线. 在相同的实验条件下, 将每个浓度的铝合金样品采集5组LIBS光谱数据, 其中3组数据作为训练集, 2组作为预测集, 得到有/无空间约束条件下铝合金中Fe元素的LIBS定量分析结果如图4所示. 可以看到, 无空间约束条件下铝合金中Fe元素LIBS定量分析参数R², 训练集均方根误差(root mean square error calibration, RMSEC), 测试集均方根误差 (root mean square error prediction, RMSEP)和ARE值分别为90.66%, 0.1903% (质量分数), 0.1910% (质量分数)和9.2220%, 板间距为10 mm的平板空间约束条件下的铝合金中Fe元素LIBS定量分析参数R², RMSEC, RMSEP和ARE值分别为95.22%, 0.1409% (质量分数), 0.1401% (质量分数)和6.8893%. 结果表明, 空间约束提高了铝合金中Fe元素LIBS定量分析精度和准确度. 但是, LIBS内标法获得的Fe元素的标准浓度与预测浓度的共线性不高, 定标曲线的R²值有待提高.
图 4 Fe元素的LIBS内标法定标曲线, 图中的含量均为质量分数
Figure4. Calibration curve of internal standard method, concentrations in the figure are all the weight concentration.

选取分析谱线Fe I 274.9 nm, Fe I 275.6 nm, Fe I 273.9 nm和Fe I 259.9 nm作为输入变量建立Fe的梯度下降定标模型. 设定初始参数θ₀—θ₄为0, 设定学习率取值范围为0—10 (学习率的常用变化范围不超过10), 最大迭代次数10000次. 无空间约束时, 通过运算得到在学习率α = 0.1时, Fe的定标模型代价函数局部最优, 此时迭代次数为2000次. 当α > 0.1时, 代价函数呈发散状, 无法进行收敛. 有空间约束时, 通过运算得到在学习率α = 0.3时, Fe的定标模型代价函数局部最优, 此时迭代次数为1000次. 当α > 0.3时, 代价函数呈发散状, 无法进行收敛. 收敛曲线如图5所示.
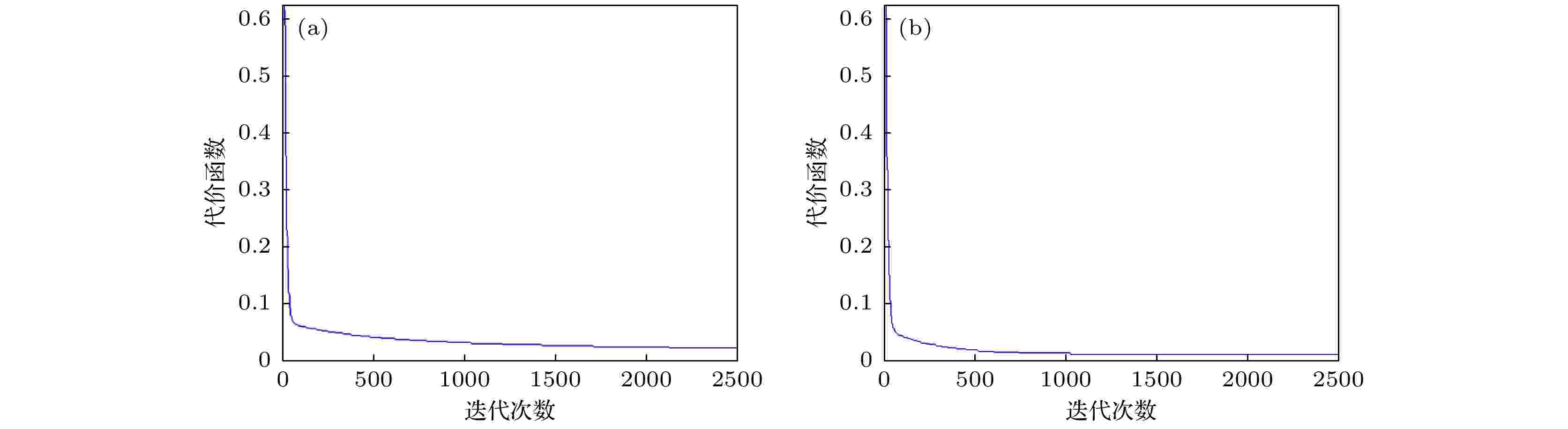图 5 代价函数随迭代次数的变化图　(a) 无约束; (b) 约束
Figure5. Graph of the change of the cost function with the number of iterations: (a) Without spatial confinement; (b) with spatial confinement.

对应的有/无平板空间约束条件下结合梯度下降法的铝合金中Fe元素的LIBS定标曲线如图6所示. 可以看出, 无空间约束条件下, 采用梯度下降法获得的Fe元素的定量分析参数R², RMSEC, RMSEP和ARE分别为97.12%, 0.1467% (质量分数), 0.1124% (质量分数)和7.1373%, 而在板间距为10 mm的平板空间约束条件下, 采用梯度下降法获得的Fe元素的定量分析参数R², RMSEC, RMSEP和ARE分别为99.22%, 0.0731% (质量分数), 0.0756% (质量分数)和3.5521%.
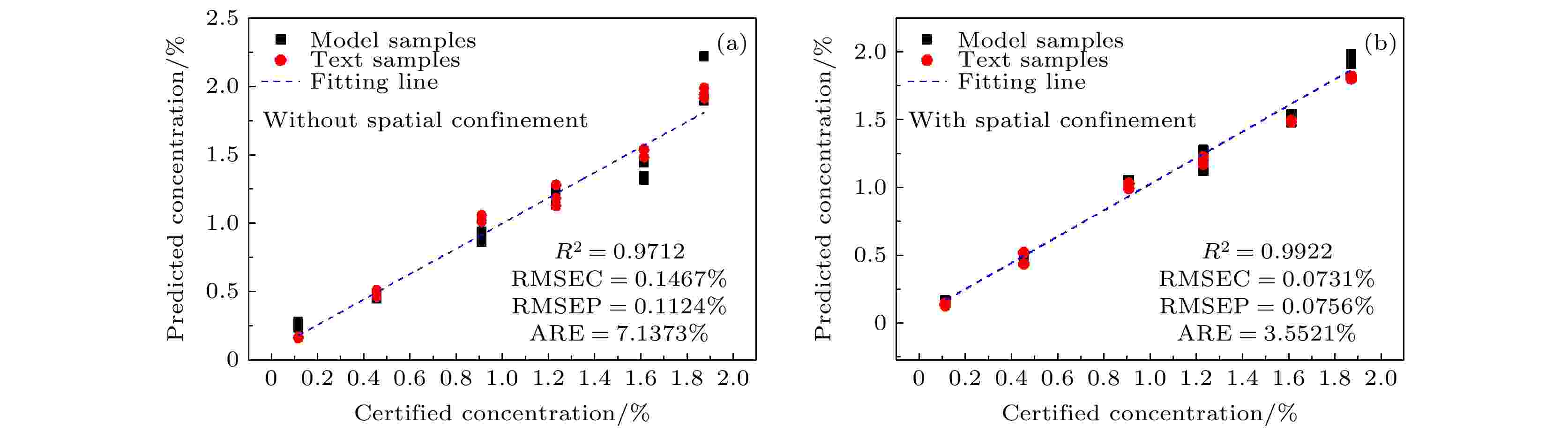图 6 Fe元素梯度下降法LIBS定标曲线, 图中的含量为质量分数
Figure6. Calibration curve of gradient descent, concentrations in the figure are all the weight concentration.

有/无平板空间约束条件下内标法和梯度下降法的铝合金中Fe元素的定量分析参数R², RMSEC, RMSEP和ARE的对比如表2所列. 相比于内标法, 结合梯度下降法的铝合金中Fe元素LIBS定标曲线的R²有了很大的提高, 而RMSEC, RMSEP和ARE参数均有所降低. 结果表明, 在平板空间约束条件下结合梯度下降法的LIBS技术对铝合金中Fe元素的定量模型精度、准确度和稳定性都有大幅度的提高. 这是由于空间约束可以增强特征谱线的强度, 进一步提高信噪比, 同时增强等离子体的稳定性, 实现元素定量分析精度的提高; 而梯度下降作为机器学习算法之一, 其模型稳定性高, 适合较大的LIBS光谱数据量, 通过代价函数迭代的方法可以更直观地进行极小值寻优, 在非矩阵层面对数据进行运算, 效率较高. 因此, 将LIBS与梯度下降法相结合是一种检测合金中痕量元素含量的可行方法.

	内标法			梯度下降
	无约束	约束		无约束	约束
R2	0.9066	0.9522		0.9712	0.9922
RMSEC/%	0.1903	0.1409		0.1467	0.0731
RMSEP/%	0.1910	0.1401		0.1124	0.0756
ARE/%	9.2220	6.8893		7.1373	3.5521

表2定量分析参数对比, 含量为质量分数
Table2.Comparison of the quantitive analysis parameters, the concentrations are the weight concentration.

本文开展了平板空间约束结合梯度下降算法提高铝合金中Fe元素的LIBS检测精度研究. 对比无空间约束条件下, Fe元素分析谱线Fe I 274.9 nm光谱增强因子为2.3, 而RSD值从10.13%降低到3.48%, 表明空间约束能够增强LIBS光谱, 同时提高了光谱稳定性. 分别利用内标法和梯度下降对铝合金标样中的Fe元素建立LIBS定标模型, 平板空间约束条件下, 内标法获得的铝合金中Fe元素的LIBS定量分析参数R², RMSEC, RMSEP和ARE分别为95.22%, 0.1409% (质量分数), 0.1401% (质量分数)和6.8893%, 而采用梯度下降法得到的铝合金中Fe元素的LIBS定量分析参数R², RMSEC, RMSEP和ARE分别为99.22%, 0.0731%(质量分数), 0.0756% (质量分数)和3.5521%. 结果表明, 平板空间约束结合梯度下降法的LIBS技术对铝合金中Fe元素的定量模型精度、准确度和稳定性都有大幅度的提高, 能够提高LIBS实验的重复性和定量分析精度, 为合金中痕量元素的检测提供可行的方法.