全文HTML
--> --> -->当前, 对空间太阳电池阵各层胶接结构应力应变问题的研究不断深入[15-21]. Wang等[15]利用解析法研究了材料热膨胀系数对温度场中太阳电池板最大应力的影响, 指出聚酰亚胺薄膜及与其相部的硅橡胶中存在最大应力, 选用较低热膨胀系数的聚酰亚胺薄膜可显著降低空间太阳电池阵最大应力值. Liu等[16]以太阳翼在轨运行期间热变形和热应力变化规律为研究对象, 利用有限元建立电池翼热变形模型, 研究变工况太阳电池翼在轨热应力和热变形规律, 研究发现, 空间太阳电池翼基板制作时选用高导热系数材料可有效减小热变形量. Wang等[17]利用MSC-Marc软件研究了热循环条件下太阳电池板单元结构热应力分布及演变规律, 结果表明该结构在低温保温阶段的最大正应力及最大剪切应力远大于高温保温阶段的最大应力, 且太阳电池板最大应力值随热循环的增大而增大.
目前, 对于空间太阳电池阵应力应变的研究主要集中在理论及建模计算等方面[22-23], 而对于空间太阳电池阵在模拟空间热循环温度场作用下的实时应变研究却鲜有报道, 这对科研人员在地面研究空间太阳电池阵减应力问题时缺少直接对比数据. 因此, 本文通过构建空间太阳电池阵应变传感器测试方法, 实现了对空间太阳电池阵在模拟真空热循环温度场作用下的应变实时监测, 同时获得了空间太阳电池阵的应变规律以及空间太阳电池片的断裂应变值. 本研究对提升空间太阳电池阵的抗形变能力提供了重要参考依据.
2.1.实验材料
实验样品为上海空间电源研究所研制的光电转化效率为30%空间用砷化镓太阳电池. 选用电池尺寸为40.3 mm × 60 mm × 0.27 mm.选用电池的表面使用硅橡胶粘贴抗辐照玻璃盖片. 空间太阳电池通过硅橡胶粘贴在碳纤维铝蜂窝基板上.
2
2.2.热真空循环实验
热真空循环实验使用上海空间电源研究所KM1热真空试验系统. 真空度设置为 < 1.0 × 10–3 Pa, 热真空循环温度范围148—408 K, 循环周期1.5周, 高温和低温段各保温120 min.2
2.3.应变测试
应变测试使用江苏东华测试公司DH3820高速静态应变数据采集仪.选用的应变传感器为中航电测BAB250系列高温应变片. 选用的胶黏剂为B-711中航电测常温固化耐高温贴片胶.
2
2.4.应变传感器原理
应变数据采集是基于测量物体受力变形产生应变, 利用应变传感器将形变信号转换为电阻变化. 通常是将应变传感器粘合在基体上, 当基体受力发生应力变化时, 应变传感器也一起产生形变, 使应变片的阻值发生改变, 之后将信号传输给处理电路显示. 基体发生膨胀时, 粘贴在其表面的应变传感器随之发生拉伸形变, 可采集到正向应变数据; 基体发生收缩时, 应变传感器发生压缩形变, 可采集到负向应变数据.应变传感器的主体部分由基体材料、金属应变丝或应变箔、绝缘保护片和引出线等组成, 如图1(a)所示. 自主研制的空间太阳电池阵应变测试系统由热真空试验系统、太阳模拟灯阵、罐内外数据传输系统、应变传感器、空间太阳电池阵、数据转换系统组成, 如图1(b)所示.
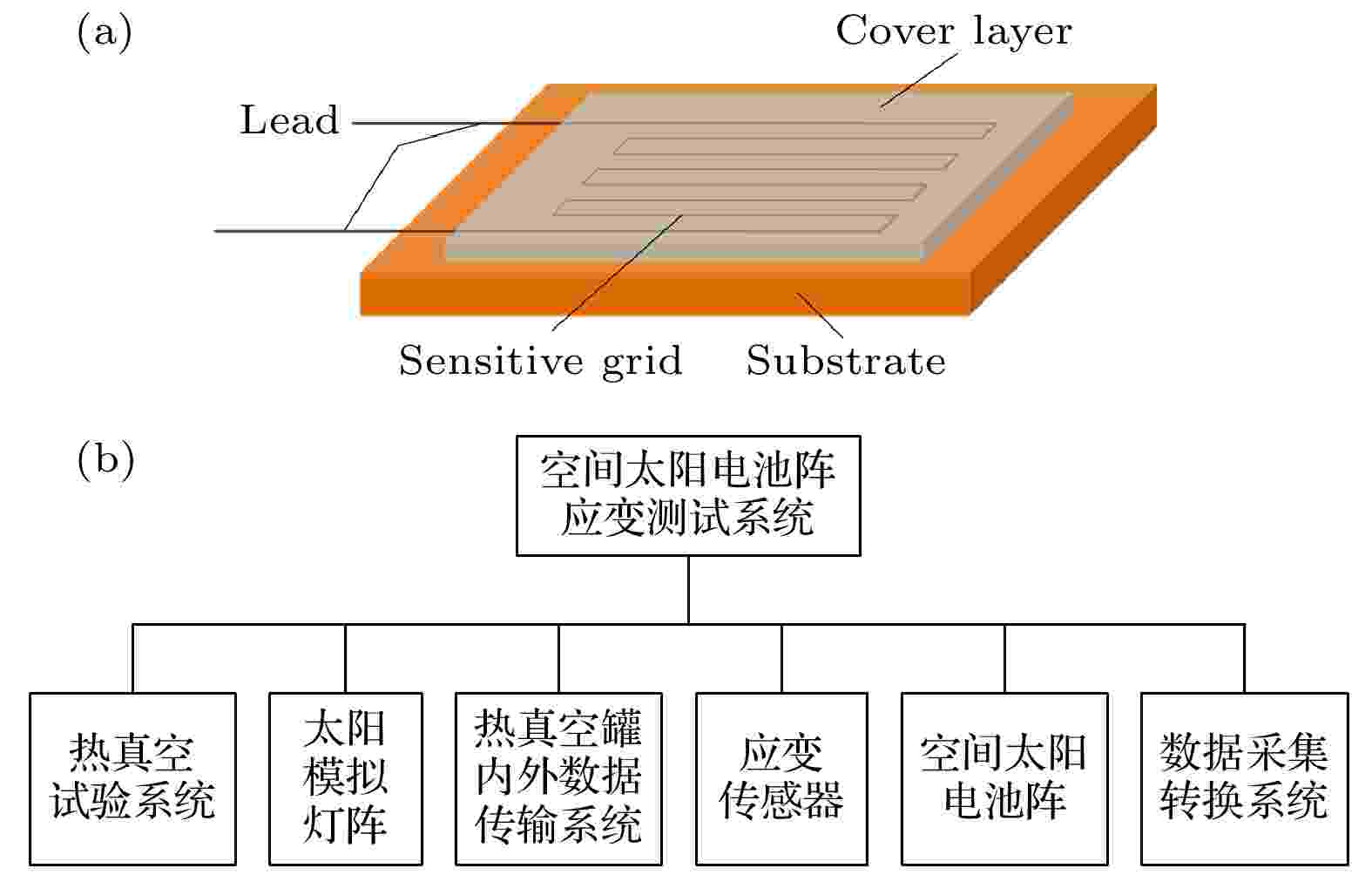图 1 (a) 应变传感器的基本构造; (b)空间太阳电池阵应变测试系统组成Figure1. (a) Basic structure of a strain sensor; (b) composition of space solar array strain test system.
3.1.不同粘接状态太阳电池应变分析
应变传感器粘贴示意如图2(a)所示. 热真空循环实验全程应变测试系统信号采集电路连接方式如图2(b)所示, 粘贴在太阳电池片上的应变传感器引出线与空间级导线焊接; 焊接完成后所有应变传感器信号汇总到热真空罐内电连接器, 该电连接器经罐壁上的转接电缆与罐外电缆连接, 罐外电缆与应变采集器相连, 采集器对信号进行处理, 通过计算机上安装的软件输出应变曲线.
图 2 (a)电池粘贴应变传感器示意图; (b)应变信号采集线路连接示意图; (c)热真空实验温度曲线; (d)空间太阳电池热真空实验应变数据, 黑色为粘接在太阳翼基板上电池应变数据, 红色为未粘接自由状态电池应变数据Figure2. (a) Schematic diagram of strain sensor pasted on a space solar cell; (b) schematic diagram for strain signal collection circuit; (c) temperature curve of thermal vacuum test; (d) strain curves of space solar cell during thermal vacuum test. The black line is strain data for solar cells bonded on the substrate, and the red one for free solar cells not bonded on substrate.
对两类粘接状态的空间太阳电池进行了应变采集. 两类电池分别为粘接在太阳翼基板上的太阳电池(简称为粘接电池)以及未粘接固定的自由状态太阳电池(简称为自由电池). 在模拟空间热真空环境下, 将两类粘接状态的空间太阳电池随环境热应力场发生的应变情况进行了全程监测和对比.
结合图2(c)热真空实验温度曲线和图2(d)空间太阳电池热真空实验应变数据, 将本次热真空实验简化分为5个阶段, 分别为抽真空段(I)、升温段(II)、降温段(III)、升温段(IV)和随炉冷却段(V). 抽真空段(I), 两类粘接状态电池迅速由0降至–200 με后稳定在–35 με. 这是由于罐内气压的迅速变化, 太阳电池阵中胶粘剂内的残留气体被抽走, 应变传感器采集到了变化明显的压缩形变; 当真空罐内气压逐渐减小至10–2—10–3 Pa时, 气压变化缓慢, 应变数据较为平稳. 升温段(II), 当罐内温度由298 K开始升高时, 应变值随温度升高发生负向增大, 到达高温408 K时, 两类粘接状态电池发生了450 με压缩形变. 这是由电池各层热膨胀系数差异所致, 顶层抗辐照玻璃盖片的热膨胀系数(5.5 × 10–7 K–1)远远小于底部的盖片胶(2.0 × 10–4 K–1)、锗衬底(6.0 × 10–6 K–1)、以及金属电极层(1.8 × 10–5 K–1)的热膨胀系数, 因此升温段能监测到明显的压缩形变. 当温度由408 K降低时, 两类电池发生拉伸形变, 见降温段(III). 在408—330 K段平均温度变化速率为2.2 K/min, 电池形变速率大于6.5 με/min. 从243—148 K, 电池形变速率随温度缓慢降低. 至148 K时, 拉伸形变达到最大值, 粘接电池应变量为870 με, 自由电池应变量为820 με. 根据Ⅲ段应变值变化趋势, 粘接电池的应变量比自由电池高90—120 με, 这极有可能跟粘接电池与铝蜂窝基板的底片胶在低温下变脆变硬有关.
在升温段(IV), 温度由148 K快速升至408 K, 平均温度变化速率2.6 K/min, 两类电池均发生870—920 με的收缩应变, 该变化原因同升温段(II). 将低温段与高温段最大应变绝对值相加, 得到实验全周期两类电池发生的最大应变总量, 自由电池为1270 με, 粘接电池为1320 με. 第3010 min, 热真空罐停止加热, 进入随炉冷却段(V), 两类电池随温度降低发生缓慢拉伸形变. 由曲线可知, 至出罐时自由电池和粘接电池分别发生了194 με和322 με的拉伸净应变.
对热真空循环实验前后太阳电池的光电性能进行了测试, 如图3(a)所示. 热真空循环实验后太阳电池的IV曲线与实验前基本重合, 空间太阳电池阵未发生力学破坏时, 电池的电性能不发生改变. 通过热真空循环实验, 得到两类空间太阳电池片在真空温度场下的应变规律, 如图3(b)所示. 空间太阳电池在高温发生压缩形变, 低温发生拉伸形变, 形变速率与温变速率成正比. 从进罐至出罐, 自由电池和粘接电池分别发生194 με和322 με的拉伸净应变. 将低温段与高温段最大应变绝对值相加, 得到实验全周期两类电池最大形变总量, 自由电池和粘接电池分别为1270 με和1320 με.
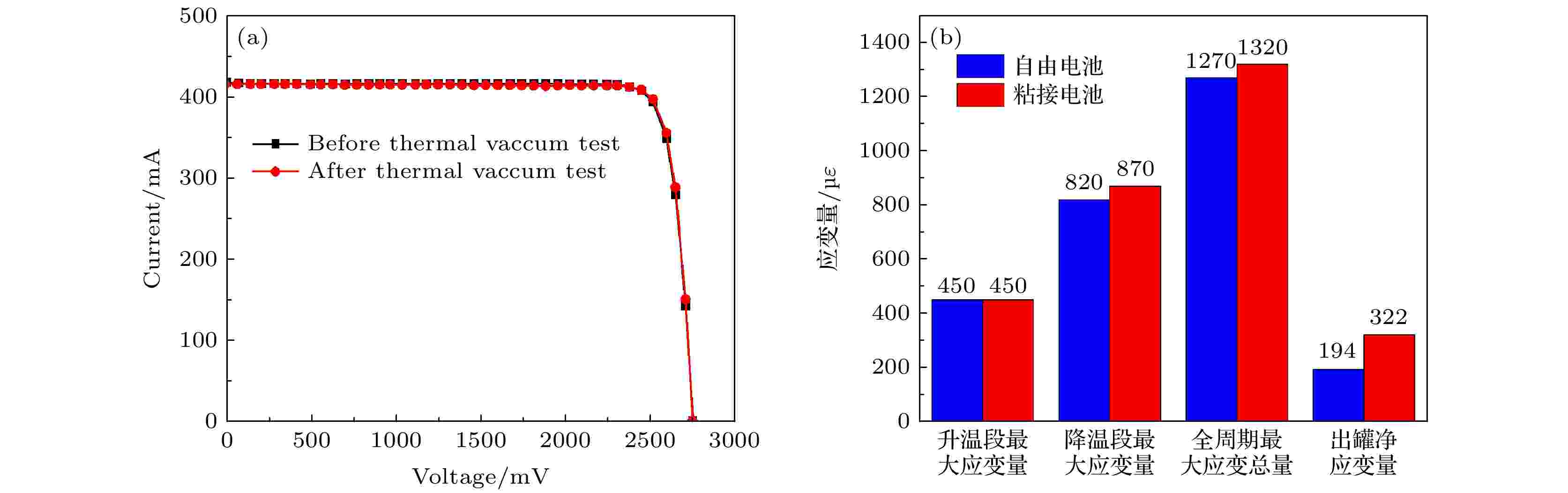图 3 (a) 热真空循环实验前后空间太阳电池的IV曲线; (b) 两类空间太阳电池阵应变规律总结Figure3. (a) IV curves of space solar cell before and after thermal vacuum test; (b) strain summary of free and pasted space solar cells.
2
3.2.不同太阳电池区域应变分析
本小节研究同片电池不同区域在真空热循环温度场下应变规律. 将一片太阳电池分为电池中心区域和围绕电池中心的边缘区域. 在这两个区域各粘贴一片应变传感器采集数据, 如图4(a)所示. 将电池置于热真空环境中开展1.5循环实验(图4(b)), 应变测试系统采集数据如图4(c)所示.
图 4 (a) 同片电池粘贴应变传感器的示意图; (b) 热真空实验温度曲线; (c) 同片空间太阳电池不同位置热真空实验应变数据, 红色为太阳电池中心区域应变数据, 黑色为太阳电池边缘区域应变数据; (d) 同片空间太阳电池片应变规律总结Figure4. (a) Schematic diagram of strain sensors pasted on one space solar cell; (b) temperature curve of thermal vacuum test; (c) strain curves test from different area in one space solar cell during thermal vacuum test, where the red line is strain data from the middle area of the solar cell, and the black one from the edge area of the solar cell; (d) strain summary of one space solar cell.
电池中心区域应变值如图4(c)中红色曲线所示, 其变化规律与图2(d)中电池形变规律基本一致, 即高温发生压缩应变, 低温发生拉伸应变. 在高温408 K最大应变值为–345 με, 在低温148 K最大应变值为910 με, 实验全程最大应变总量为1255 με. 全周期至出罐发生245 με拉伸应变.
同片电池的边缘区域形变如图4(c)中黑色曲线所示. 在升温段(Ⅱ), 边缘区域发生先拉伸后压缩的形变, 这可能与多层结构形变的综合作用有关. 在降温段(Ⅲ), 最大应变量为400 με, 为中心区域形变值的一半. 在随炉冷却(V)过程, 2210 min之前边缘区域发生较快压缩形变, 2210 min之后应变变化缓慢, 至出罐时应变量为–115 με, 其原因可能是太阳电池阵多种材料热膨胀系数差异以及起主导作用的因素不同所致. 尽管目前尚无法精确测出每层材料在真空温度场下的应变变化值, 但通过地面实测以及理论推导分析, 可有效地得出空间太阳电池阵应变规律并针对性采取减应力措施.
空间太阳电池片中心及边缘区域在真空温度场下的应变规律总结如图4(d)所示, 同片电池中心区域发生了245 με的拉伸净应变, 边缘区域发生了–115 με的压缩净应变. 将低温段与高温段的最大应变值相加, 得到同片电池中心区域与边缘区域的最大应变总量分别为1255 με和590 με. 中心区域的应变量比边缘区高113%.
2
3.3.空间太阳电池断裂应变分析
3.1和3.2节对电池在真空温度场下的应变值进行了全程监测, 测得高低温条件下的应变总量. 本小节对空间太阳电池的断裂应变值定量测试. 使用空间太阳电池弯曲工装进行实验, 如图5(a)和图5(b)所示, 将两块弯曲半径相同的凹凸组合模块可构成一组弯曲半径. 在空间太阳电池表面粘贴应变传感器, 将电池依次放入弯曲半径由大到小的工装中进行弯曲实验, 直到电池发生断裂为止. 使用应变传感器采集全过程的应变值, 得到电池在每个弯曲半径下的应变值. 获得最小弯曲半径的同时, 得到太阳电池在最小弯曲半径下断裂应变值.
图 5 (a) 弯曲实验工装凸槽; (b)弯曲实验工装凹槽; (c)太阳电池断裂应变数据曲线; (d)空间太阳电池断裂实物图Figure5. (a) Convex equipment for bending test; (b) concave equipment for bending test; (c) rupturing strain curve of space solar cell; (d) picture of a ruptured space solar cell.
使用应变传感器连续记录了5组弯曲半径(依次为15 cm, 12.5 cm, 10 cm, 7.5 cm, 5 cm)下电池的应变值(图5(c)). 测试过程只有在放入凹凸组合模块时电池会发生明显的应变变化, 在移动及转移组合块的过程均不会使电池发生明显的形变, 即每次进行弯曲测试之前电池的初始应变值均可以认为是0 με, 这就避免了引入其他应变的可能. 由图5(c)可知电池的弯曲半径由15 cm逐渐减小至7.5 cm时, 应变值由810 με增大至1550 με. 电池在弯曲半径为5 cm时发生了断裂, 测试该条件下的应变值2080 με, 即为电池弯曲碎裂的应变值, 如图5(d)所示.
表1统计了不同弯曲半径条件下电池应变值. 将断裂前应变值对弯曲半径作图, 得到弯曲半径-应变散点图(见图6). 将数据线性拟合得到斜率为–88.9的拟合直线. 由拟合数据可得电池未发生断裂时, 电池的弯曲半径与应变值呈线性变化趋势, 这符合弹性变形阶断应力应变呈线性变化的规律. 弯曲半径5 cm时断裂应变值2080 με远大于线性外推得出的应变值. 实验得出空间太阳电池在受到外力时, 发生弯曲断裂的应变值为2080 με.
| 弯曲半径/cm | 20 | 17.5 | 15 | 12.5 | 10 | 7.5 | 5 |
| 电池应变值/με | 401 | 577 | 810 | 945 | 1210 | 1550 | 2080 |
表1不同弯曲半径条件下电池应变值
Table1.Strain data of space solar cell under different bending radius conditions.
图 6 不同弯曲半径下电池应变值拟合曲线Figure6. Strain data fitting curve of space solar cell under different bending radius.
