摘要:磷化铟(InP)具备电子迁移率高、禁带宽度大、耐高温、耐辐射等特性, 是制备空间辐射环境下电子器件的重要材料. 随着电子器件小型化, 单个重离子在器件灵敏体积内产生的位移损伤效应可能会导致其永久失效. 因此, 本文使用蒙特卡罗软件Geant4模拟空间重离子(碳、氮、氧、铁)在InP材料中的输运过程, 计算重离子的非电离能量损失(non-ionizing energy loss, NIEL), 得到重离子入射InP材料的位移损伤规律, 主要结论有: 1) NIEL值与原子序数的平方成正比, 重离子原子序数越大, 在InP材料中产生位移损伤的能力越强; 2)重离子NIEL比次级粒子NIEL大3—4个量级, 而NIEL与核弹性碰撞产生的反冲原子的非电离损伤能成正比, 说明重离子在材料中撞出的初级反冲原子是导致InP材料中产生位移损伤的主要原因; 3)空间辐射环境中重离子数目占比少, 一年中重离子在0.0125 mm³ InP中产生的总非电离损伤能占比为2.52%, 但重离子NIEL值是质子和α粒子的2—30倍, 仍需考虑单个空间重离子入射InP电子器件产生的位移损伤效应. 4)低能重离子在较厚材料中完全沉积导致平均非电离损伤能分布不均匀(前高后低), 使NIEL值随材料厚度的增大而略微减小, 重离子位移损伤严重区域分布在材料前端. 研究结果为InP材料在空间辐射环境中的应用打下基础.
关键词: 磷化铟/
位移损伤/
Geant4/
非电离损伤能

English Abstract

全文HTML

--> --> -->

InP作为重要的第二代半导体材料, 禁带宽度大、电子迁移率高、耐高温、抗辐照性能优于硅和砷化镓, 是航天器电子器件的首选材料之一^[1]. 航天器远地飞行状态下, 主要受到来自银河宇宙射线的背景辐射(85%为质子, 15%为α粒子, 1%为重离子)以及太阳耀斑爆发产生的大量重离子、α粒子、高能质子和电子辐射, 统称为宇宙射线(cosmic ray, CR)^[2]. 研究表明, 空间辐射环境中电子器件的位移损伤效应是导致其电学性能永久失效的主要因素之一^[3], 且InP材料多被用于光电器件, 光电器件对于位移损伤效应的敏感性强于其他器件. 空间重离子占比小但能量大, 可以穿过外层材料进入航天器内部, 且随着电子器件小型化, 单个高能重离子在电子器件灵敏体积处产生的位移损伤, 即可造成电子器件灵敏体积处的永久损伤^[4]. 因此, 研究空间重离子入射InP材料产生的位移损伤规律, 可以为InP材料在航天器中的应用打下基础.
目前, 国内外关于空间重离子入射InP材料产生的位移损伤规律未见文献报道, 研究主要集中于低能质子、电子^[5-12]、离子注入^[13-16]在InP材料或电子器件中产生的辐照效应. 实验方面, Yamaguchi等^[5]采用地面实验装置探究InP单晶材料和太阳能电池经低能质子(1—10 MeV)和电子(1 MeV)辐照后的电学性能变化. Kamarou等^[15]使用快重离子氙(375 MeV)、金(593 MeV)注入InP单晶材料, 得到离子注入后的缺陷退火机制. 模拟方面, Summers等^[17]使用SRIM软件得到不同能量的质子和电子入射Si, InP, GaAs产生的NIEL值, 发现实验得到的电学损伤因子与NIEL相关, 可以衡量电子器件经辐照后的电学性能退化程度, 将不同种类和能量的粒子对电子器件的电学性能影响转化为NIEL进行比较是一种可靠的处理手段.
本文使用Geant4软件^[18]模拟空间重离子在InP材料中的输运过程, 比较重离子及其次级粒子在InP材料中的NIEL值, 得到重离子在InP材料中产生的平均非电离损伤能随深度分布规律, 同时将空间主要辐射粒子(氢、氦、碳、氮、氧、铁)分别以实际年注入量的入射数目入射InP材料, 计算空间主要辐射粒子的总非电离能量沉积, 得到重离子在空间主要辐射粒子中的总非电离能量沉积占比. 该工作对InP基电子器件在航天领域的应用有重要意义.

2

-->

2.1.几何结构

根据文献[5]得到InP材料作为基底厚度是500 μm, 同时为了探究厚度对重离子在InP中产生的NIEL值的影响, 将InP材料厚度分别设置为500 μm, 1000 μm, 5000 μm, 横截面为500 μm × 500 μm.
2 -->

2.2.物理过程

Geant4软件在核技术领域应用较广^[19-22], 可以模拟多种能量、多种粒子在具有复杂几何结构、材料构成的器件中的输运过程. 本文利用Geant4软件和程序库, 使用QGSP_BIC物理模型模拟空间重离子在InP中的输运过程. QGSP_BIC物理模型包含了电磁相互作用(多次散射、电离、光电效应、韧致辐射)和强子相互作用(弹性散射、非弹性散射和原子核嬗变), 使用的数据库文件是基于Livermore实验室的ENSDF, EEDL, EPDL97, EADL库, 最高可模拟10 TeV的入射粒子在材料中的输运过程. 同时在电磁相互作用中增加了G4ScreenedNuclearRecoil类, 模拟反冲原子的核阻止本领, 该类由Weller等^[23]开发, 用于计算库仑散射对NIEL的贡献, Weller等^[24]也验证了该类在计算质子入射GaAs, Si等材料的NIEL值时的准确性和可靠性. Raine等^[4]也使用G4ScreenedNuclearRecoil类计算质子和中子入射Si产生的NIEL. 说明G4ScreenedNuclearRecoil类适用于计算带电粒子在材料中产生的NIEL.
重离子与物质相互作用过程主要有核弹性碰撞和核外电子非弹性碰撞. 核弹性碰撞为带电粒子与靶原子核的库仑场作用发生弹性散射, 使原子核反冲带走带电粒子的一部分能量, 将这种能量损失称为非电离能量损失. 核外电子非弹性碰撞为带电粒子与靶原子核外电子发生库仑作用, 使电子获得能量被击出, 靶原子失去电子变为离子, 同时带电粒子的能量减小, 运动速度降低, 将这种能量损失称为电离能量损失.
位移损伤是指核弹性碰撞产生的初级反冲原子(primary knock-on atom, PKA)离开晶格位置, 继续发生弹性碰撞过程, 产生次级反冲原子(secondary knock-on atom, SKA), 若次级反冲原子获得的能量足够大, 也会继续发生弹性碰撞, 进而形成级联碰撞, 产生点缺陷、团簇、位错环等晶格缺陷. 而这些缺陷多处于电子器件的深能级处, 可以俘获少数载流子, 影响少数载流子数目和寿命, 进而使得电学器件开路电压、短路电流、最大电功率、暗电流等电学特性发生变化, 改变器件的电学性能.
由于重离子与核外电子发生非弹性碰撞的产物在材料中形成位移损伤的方式与PKA相同, 因此将非弹性碰撞产物与初级反冲原子统称为PKA, 用于探究重离子及其PKA在InP材料中产生的位移损伤大小.
2 -->

2.3.粒子源设置

宇宙射线主要由质子(H)、α粒子(He)、空间重离子组成, 其中空间重离子主要种类有碳(C)、氮(N)、氧(O)、铁(Fe), 因此选取这4种粒子作为入射粒子. 粒子源以面源入射, 大小与材料横截面(500 μm × 500 μm)相同. 粒子源能量选取考虑到航天器外层镀有薄铝合金, 航天器内部电子系统的辐射环境应为经过铝层屏蔽后的宇宙射线, 因此选取经过100 mil (2.54 mm, 国际默认值)厚的铝层屏蔽后的宇宙射线能谱图作为此次模拟能谱. 如图1(a)所示, 是CREME96^[25]数据库中得到的宇宙射线能谱图, 图1(b)为经过100 mil厚的铝层屏蔽后的宇宙射线能谱图. 可以观察到, 经过铝层屏蔽后的宇宙射线能谱在低能部分占比增多, 且能量从1 MeV/nuc降至0.1 MeV/nuc(其中nuc表示核子数, 而质量数越大的粒子核子数越多, 如C的核子数为12, 所以1 MeV/nuc对于C而言, 实际动能有12 MeV.), 高能部分占比减少, 能谱峰值向左移动. 说明经过外层镀铝合金屏蔽后的宇宙射线能谱存在更多的低能重离子, 对于航天器内部电子器件造成位移损伤的概率更大. 从图1能谱可知, 质量数越大的粒子能谱范围越广.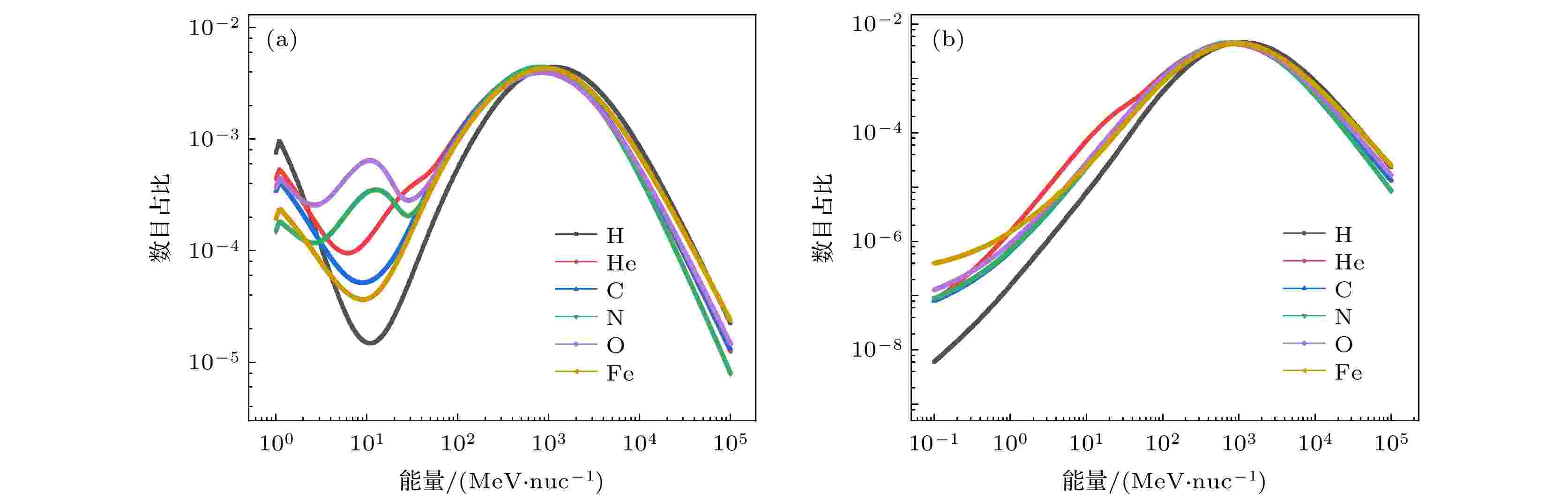
图 1 能谱图　(a)宇宙射线能谱图; (b) 100 mil Al屏蔽后的宇宙射线能谱图
Figure1. Energy spectrum: (a) Cosmic ray energy spectrum; (b) 100 mil Al shielded cosmic ray energy spectrum.

2 -->

2.4.位移损伤计算

NIEL是指单个粒子在单位质量厚度上非电离能量损失^[26], 单位为MeV·cm²/g. NIEL值越大, 表明粒子在材料中的非电离能量沉积越多, 产生位移损伤的能力越强. NIEL计算方式如下:

${\rm{NIEL}} = \frac{{{N_{\rm{A}}}}}{A}{\sum\nolimits_i \sigma _i}(E){E_{{\rm{dam}}}}(E),$

式中, $ {N}_{\mathrm{A}} $为阿伏伽德罗常数, A为靶原子质量数, E为反冲原子动能, $ {\sigma }_{i}\left(E\right) $为第i个反冲原子的离位反应截面. ${E_{{\rm{dam}}}}(E) $为能量为E的反冲原子在材料中的非电离损伤能.
Jun等^[27]在计算NIEL时, 将反应截面与非电离损伤能的乘积求和简化为

${\sum\nolimits_i \sigma _i}(E){E_{{\rm{dam}}}}(E) = \frac{{{T_{{\rm{dam}}}}}}{{{N_{\rm{v}}}h}},$

式中, $ {T}_{\text{dam}} $是平均非电离损伤(位移损失)能, 将反冲原子$ {E_{{\rm{dam}}}}(E) $加和除以入射粒子数即可得到, $ {N}_{\mathrm{v}} $是原子密度, h为靶材料厚度.
进一步推导得:

${\rm{NIEL}} = {{{T_{{\rm{dam}}}}}}/({{\rho h}}),$

式中, ρ为靶材料密度, InP材料密度取4.56 g/cm³.
$ {E_{{\rm{dam}}}}(E) $用Robinson等^[28]和Akkerman等^[29,30]修正的Lindhard分离函数得到:

${E_{{\rm{dam}}}}(E) = \frac{E}{{1 + {k_{\rm{d}}}g({\varepsilon _{\rm{d}}})}},$

${k_{\rm{d}}} = \frac{{0.0793Z_1^{2/3}Z_2^{1/2}{{({A_1} + {A_2})}^{3/2}}}}{{{{(Z_1^{2/3} + Z_2^{2/3})}^{3/4}}A_1^{3/2}A_2^{1/2}}},$

${\varepsilon _{\rm{d}}} = \frac{E}{{30.724{Z_1}{Z_2}\sqrt {Z_1^{2/3} + Z_2^{2/3}} (1 + {A_1}/{A_2})}},$

$g\left( {\varepsilon_{\rm{d}}}\right) = \left\{\begin{aligned}&{\varepsilon_{\rm{d}}} + 0.40244\varepsilon_{\rm{d}}^{3/4} + 3.4008\varepsilon_{\rm{d}}^{1/6}, \\&\quad\quad\quad\quad\quad\quad\quad {(E > 200\;{\rm{keV}}),}\\& 0.742{\varepsilon_{\rm{d}}} + 1.6812\varepsilon_{\rm{d}}^{3/4} + 0.90565\varepsilon_{\rm{d}}^{1/6},\\&\quad\quad \quad\quad\quad\quad\quad {(E < 200\;{\rm{keV}}),}\end{aligned} \right.$

式中, Z₁, Z₂是晶格原子和反冲原子的原子序数, A₁, A₂是晶格原子和反冲原子的质量数. 对于化合物而言, 原子序数和质量数取化合物组成元素的加权平均数, 即:

$Z_{2,{\rm{average}}} =\frac{{\displaystyle\sum\nolimits_i {{n_i}{Z_i}} }}{{\displaystyle\sum\nolimits_i {{n_i}} }},$

$A_{2,{\rm{average}}} =\frac{{\sum\nolimits_i {{n_i}{A_i}} }}{{\sum\nolimits_i {{n_i}} }},$

式中, $ {n}_{i} $为元素i在化合物中的原子密度. 对于InP材料, 取$ Z_{2, {\rm{average}}} = 32$, $ A_{2, {\rm{average}}} = 72.3$.
Akkerman-Robinson-Lindhard修正函数被广泛应用于NIEL值的计算^[31,32], 由于Geant4程序中自带的G4LindhardPartition函数并没有包含Akkerman等^[29,30]的修正部分, 重新编译G4LindhardPartition函数, 使其包含Akkerman等^[29,30]的修正计算. 之后利用自行编译的G4Lind- hardPartition函数得到InP材料中入射粒子及PKA的非电离损伤能E_dam(E), 代入(2)式即算出NIEL值.
2 -->

2.5.物理过程可靠性验证

国内外对带电粒子入射硅(Si)的非电离能量损失规律及NIEL值计算资料丰富^{[4,17,19,27,33]}, 因此为验证程序可靠性, 使用薄靶近似法^[19]计算1—300 MeV单能质子入射Si和InP产生的NIEL值, 即取材料厚度为入射粒子在材料中射程的1/10, 材料长宽为厚度的10倍. 该方法的优点在于减少入射粒子在材料中慢化导致的NIEL值误差, 同时保证材料中产生足够多的PKA数目, 避免统计性误差. Geant4模拟参数设置及计算结果如表1所示, Si和InP射程由SRIM^[34]软件计算得到.

质子能量/MeV	Si射程/mm	Si厚度/mm	NIEL/(MeV·cm2·g–1)	InP射程/mm	InP厚度/mm	NIEL/(MeV·cm2·g–1)
1	0.016	0.0018	0.07004	0.013	0.0015	0.0558
2	0.048	0.0050	0.03763	0.038	0.0040	0.0302
5	0.216	0.0220	0.01519	0.164	0.0180	0.0135
10	0.709	0.0750	0.00968	0.518	0.0550	0.0079
20	2.390	0.2400	0.00759	1.680	0.2000	0.0051
50	12.180	1.2200	0.00483	8.320	1.0000	0.0037
100	41.620	4.1800	0.00265	27.530	3.0000	0.0034
200	138.630	14.0000	0.00148	90.270	9.5000	0.0032
300	273.570	28.0000	0.00138	176.860	18.0000	0.0033

表1Geant4模拟相关参数和NIEL计算值
Table1.Geant4 Simulated parameters and NIEL.

如图2所示, 将本文Si和InP的NIEL计算值与Jun等^[27]和Dale等^[33]计算结果做对比, 发现NIEL值变化趋势相同, 即NIEL值随质子能量的增大而减小, 说明低能质子在材料中产生的位移损伤大于高能质子. 原因在于高能质子与原子核发生弹性碰撞的反应截面小, 因此产生的NIEL值小. 数值方面, 本文计算值与文献值相近, 数据符合一致性较好, 说明本文程序适用于计算带电粒子在InP中产生的NIEL.
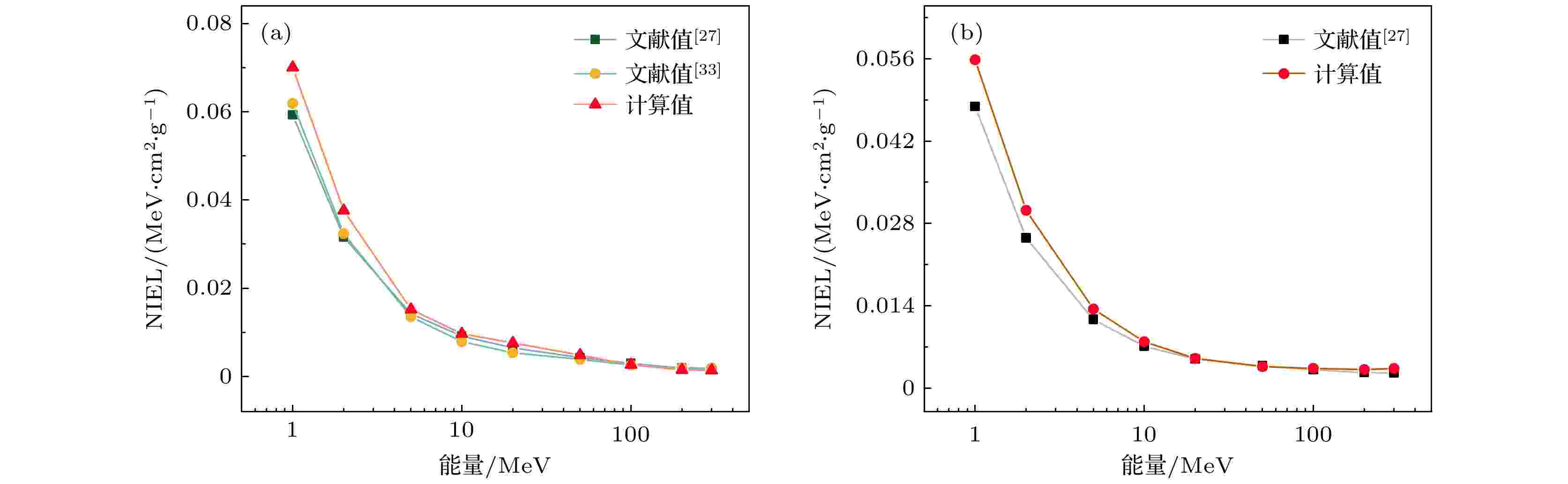图 2 1?300 MeV质子入射(a) Si 和(b) InP的NIEL计算值
Figure2. 1?300 MeV proton NIEL for (a) Si and (b) InP.

2 -->

2.6.设计方案

关于InP辐照效应的研究多为H, He, 因此本文在部分模拟中加入了H, He粒子的计算, 将 C, N, O, Fe的计算结果与H, He做对比, 研究H, He, 空间重离子位移损伤机制的异同. 采用三种方法探究重离子入射InP材料产生的位移损伤: 1)将H, He, C, N, O, Fe 分别以10⁶个粒子数目打入InP材料, 取InP材料厚度为500 μm, 比较质子、α粒子和重离子入射同一厚度的InP材料产生的NIEL; 2)从CREME96^[25]数据库中得到H, He, C, N, O, Fe的年注入量, 以空间环境中粒子年注量的数目打入InP材料, 取InP材料厚度为500 μm, 统计一年中不同粒子在InP材料中的非电离能量沉积; 3)将C, N, O, Fe 分别以10⁶个粒子数目打入InP材料, 取InP材料厚度为500, 1000, 5000 μm, 比较相同粒子数下不同重离子入射不同厚度的InP材料产生的NIEL, 具体设计方案如表2.

	粒子种类	粒子数目	InP材料厚度/μm
方法一	H	106	500
	He	106	500
	C	106	500
	N	106	500
	O	106	500
	Fe	106	500
方法二	H	12728631	500
	He	1187039	500
	C	30945	500
	N	8389	500
	O	29305	500
	Fe	3200	500
方法三	C	106	500, 1000, 5000
	N	106	500, 1000, 5000
	O	106	500, 1000, 5000
	Fe	106	500, 1000, 5000

表2重离子入射InP材料的设计方案
Table2.Design scheme of heavy ion incident on InP.

2

-->

3.1.相同粒子数下不同宇宙粒子入射InP产生的NIEL

由于在Geant4程序中对于粒子能量的设置是采用能谱概率取值的方法, 为了保证能谱取值的遍历性和数据的可靠性, 数据都是经过10次计算后取平均值得到.
由(1)式可知, NIEL值与粒子在材料中撞出的反冲原子的非电离损伤能$ {E_{{\rm{dam}}}}(E) $有关, 因此入射粒子的NIEL值通过计算其产生的PKA非电离损伤能得到, 而PKA的NIEL值通过计算PKA撞出的SKA的非电离损伤能得到. 如表3所示, 列出H, He, C, N, O, Fe入射500 μm厚的InP材料的相关信息: 入射粒子及其PKA的NIEL值、NIEL占比及变异系数. 其中, NIEL占比等于各自NIEL值除以入射粒子及PKA 的NIEL之和, 变异系数等于标准差除以平均值. 变异系数约在10^–2量级, 说明10次计算数据离散程度较小, 平均值具有代表性.

粒子 种类	统计 种类	NIEL/ (MeV·cm2·g–1)	NIEL 占比/%	变异 系数
H	H	0.004316	98.365	0.03953
	PKA	7.1739×10–5	1.635	0.08716
He	He	0.00861	96.443	0.02208
	PKA	3.17556×10–4	3.557	0.04532
C	C	0.0165	99.906	0.01073
	PKA	1.54785×10–5	0.094	0.20895
N	N	0.01798	99.928	0.01309
	PKA	1.2888×10–5	0.072	0.30657
O	O	0.02132	99.936	0.01548
	PKA	1.3566×10–5	0.064	0.20082
Fe	Fe	0.11922	99.976	0.00507
	PKA	2.9332×10–5	0.024	0.15543

表3宇宙射线粒子及其PKA在500 μm 厚的InP中产生的NIEL统计表
Table3.NIEL of cosmic ray particles and their PKA produced in 500 μm InP.

分析表3数据可知, 相较于H, He, 重离子的NIEL值占比更大, 达99%以上, 而重离子PKA产生的NIEL值占比仅为0.024%—0.094%. 原因在于重离子PKA在材料中产生的SKA数目少且其非电离沉积能量小, 可以忽略重离子的SKA在材料中产生的位移损伤, 研究重离子的PKA在InP材料中产生的位移损伤.
比较6种入射粒子的NIEL值, 发现NIEL值与原子序数的平方成正比, 这一趋势与文献[35]结论相符. 原因在于弹性散射截面与入射粒子原子序数的平方成正比. 入射粒子原子序数越大, 弹性散射截面越大, 在InP材料中产生位移损伤的能力越强, 即NIEL值越大. 对于同一厚度的InP材料, C, N, O, Fe的NIEL值比H, He高1—2个量级, 说明空间重离子在InP 材料中产生非电离能量沉积并造成位移损伤的概率远大于H, He, 需要关注空间辐射环境下单个重离子入射InP电子器件导致的位移损伤效应.
2 -->

3.2.年注量入射数目下的不同宇宙粒子入射InP产生的非电离能量沉积

根据CREME96数据库提供的能谱数据可知, H, He, C, N, O, Fe粒子数目在宇宙射线中的占比为99.7%, 可以认为宇宙射线在电子器件中非电离能量沉积近似等于这6种粒子非电离能量沉积之和. 本节内容选取H, He, C, N, O, Fe作为代表粒子探究一年中宇宙射线在InP材料中产生的总非电离能量沉积. 6种粒子在500 μm × 500 μm平面上一年内注入的总数目为13987508个, 在表4中列出了各粒子的入射数目、非电离损伤能、非电离损伤能占比(各粒子非电离损伤能与6种粒子非电离损伤能之和的比值)以及变异系数. 变异系数在10^–2量级, 说明10次计算的非电离损伤能平均值具有代表性.

粒子 种类	入射 数目	非电离 损伤能/MeV	非电离损 伤能占比/%	变异 系数
H	12728631	12380.55	82.14	0.01366
He	1187039	2312.76	15.34	0.02426
C	30945	116.995	0.78	0.07564
N	8389	33.99	0.23	0.01548
O	29304	142.74	0.95	0.05274
Fe	3200	86.27	0.56	0.01301

表4不同粒子在0.125 mm³ InP产生的非电离损伤能统计表
Table4.Total non-ionization damage energy produced by cosmic particles in 0.125 mm³ InP.

由表4可知, 在0.125 mm³ InP材料中沉积的非电离损伤能最多的是H, 占比为82.14%, 与大多数理论和实验结果相符, He的非电离损伤能占比达到了15.34%, C, N, O, Fe重离子的非电离损伤能总占比为2.56%. 即使重离子的NIEL值高于H, He, 但是重离子在空间辐射环境中的数目少, 因此在InP中产生的总非电离损伤能占比较低.
C和O的数目以及NIEL值接近, 因此非电离损伤能占比接近, 分别为0.78%和0.95%, 而N的NIEL值居中且数目较少, 其非电离损伤能占比最低为0.23%. Fe的数目最少但NIEL值比C, N, O大1个量级, 因此3200个Fe离子入射0.125 mm³ InP产生的非电离损伤能在空间重离子中不可忽视, 占比达到0.56%. 以上统计有效对比了空间辐射环境中不同粒子产生的非电离损伤能, 为InP材料在空间中的应用提供参考数据.
2 -->

3.3.不同重离子入射不同厚度的InP材料产生的NIEL及其深度分布

如表5所示, 统计了C, N, O, Fe在不同厚度(500, 1000, 5000 μm)的InP材料中产生的NIEL平均值及变异系数, 变异系数在10^–2量级, 说明数据离散程度较小, NIEL平均值具有代表性.

重离子种类	材料厚度/μm	NIEL均值	变异系数
C	500	0.0165	0.01073
	1000	0.01639	0.00631
	5000	0.01539	0.00664
N	500	0.01798	0.01309
	1000	0.01755	0.01031
	5000	0.01628	0.00723
O	500	0.02132	0.01548
	1000	0.02087	0.00724
	5000	0.01878	0.00349
Fe	500	0.11922	0.00507
	1000	0.11591	0.00382
	5000	0.09486	0.00303

表5重离子在500, 1000, 5000 μm InP产生的NIEL统计表
Table5.NIEL of heavy ion produced in 500, 1000, 5000 μm InP.

由表5可知, 随着材料厚度的增加, NIEL值出现变小的趋势, 但是数值变化不大. 重离子在500 μm和1000 μm的InP中的NIEL值相差不大, 下降比例从500 μm到1000 μm约为0.6%—2.7%; 重离子在1000 μm 和5000 μm InP中的NIEL值相差略多, NIEL值从1000 μm到5000 μm下降比例约为6%—18%. 猜测原因在于当材料厚度增加后, 能谱中的中高能粒子的射程远大于5000 μm, 在InP 材料中产生均匀损伤, 而低能粒子会在材料前端发生完全沉积, 导致材料后端非电离损伤能相对降低, 使得NIEL值减小. 但是空间能谱中低能粒子数目占比小, 所以随着材料厚度的增大, 低能粒子在材料中的非均匀位移损伤对NIEL值的影响不显著, 即NIEL值减小幅度低.
由(3)式可知, 在材料种类确定的情况下, NIEL的计算与平均非电离损伤能T_dam和材料厚度有关, 为了验证上述猜想, 需进一步研究空间重离子在InP材料中产生的T_dam随深度分布情况. 由于重离子在500 μm和1000 μm InP中的T_dam随深度分布与5000 μm InP前端分布相同, 因此只给出重离子在5000 μm InP材料中T_dam随深度的分布.
如图3所示, 实心球为10次计算得到的T_dam平均值, 阴影部分为10次计算结果的标准差. 由于粒子与物质相互作用发生概率为泊松分布, 同一能量粒子两次打入材料, 发生非电离反应的位置可能不同, 且本文使用从能谱中按概率取值的方式设置入射粒子动能, 增加了数据选取的随机性, 导致T_dam随深度的分布会出现数据涨落, 波动较大, 但依然可以得到重离子入射InP产生的T_dam随深度的分布趋势, 即T_dam随入射深度的增大而减小, 详细分析见下文. 图中标准差量级均为10^–2, 但是由于Fe的T_dam波动较大, 在2.5 keV范围内波动, 而其他离子T_dam仅在0.2 keV范围内波动, 因此Fe的阴影区域相较于其他离子的阴影区域要小, 但从计算精度而言, C, N, O, Fe的标准差均在同一量级. 同时, 因为Fe的质量数为56, 将图1(b)横坐标乘以56, 得到其能量范围为5.6—5600000 MeV, 相较于C, N, O的能量范围, Fe的能量取值范围更广, 所以Fe的T_dam波动更大.
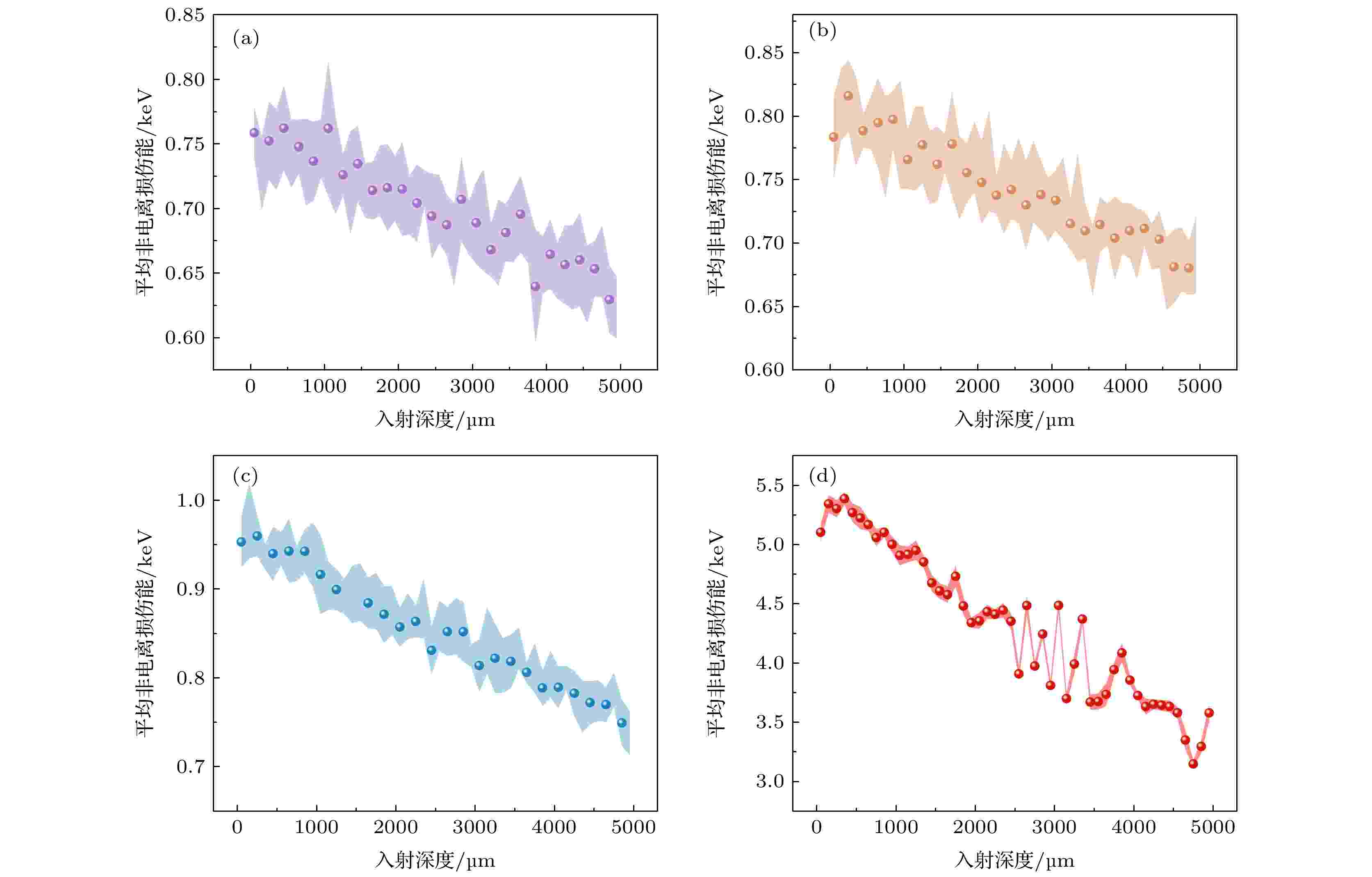图 3 不同种类重离子(a) C, (b) N, (c) O, (d) Fe入射5000 μm InP产生的平均非电离损伤能随深度分布图
Figure3. Distribution average non-ionization damage energy of different heavy ions (a) C, (b) N, (c) O, (d) Fe with depth in 5000 μm InP

由图3可知, C, N, O, Fe入射InP材料产生的T_dam随深度增加而减少, 入射深度小于1000 μm时, T_dam的下降趋势尚不明显, 则表5中NIEL值下降比例小. 当入射深度大于1000 μm后, T_dam近似成线性下降, 材料后端的非电离能量沉积相较于前端减少很多, 则表5中NIEL值下降比例增大. 综上可知, 随着材料厚度的增大, 低能重离子在较厚材料前端发生完全沉积, 导致材料整体的位移损伤分布不均匀, 即T_dam在材料中出现下降情况, 进而使NIEL值减小.
分析图3纵坐标可知, 随着原子序数的增大, C, N, O, Fe入射InP材料产生的T_dam的分布区间从0.63—0.77 keV逐渐上升为3.5—5 keV, 说明随着原子序数的增大, T_dam也逐渐增大, 则总非电离损伤能增大. 与表3中NIEL值随原子序数的增大而增大的趋势相同. 说明质量数大的重离子在InP材料中非电离能量沉积多, 产生位移损伤的能力强. 因此, 空间辐射环境中需要关注低能重离子入射InP电子器件产生的位移损伤.

本文使用Geant4模拟空间重离子(C, N, O, Fe)入射InP产生的位移损伤, 主要结论有: 1)在500 μm InP中, 比较H, He, C, N, O, Fe的NIEL值, 发现NIEL值与原子序数的平方成正比, Fe NIEL值最大. 同时比较了6种粒子及其PKA的NIEL值, H, He NIEL值比PKA的大1—2个量级, 而重离子NIEL值比PKA大3—4个量级, 说明空间重离子在InP材料中产生的位移损伤主要与重离子产生的PKA有关, 重离子产生的SKA在InP材料中的位移损伤可忽略; 2)在实际应用中, 由于空间重离子数目占比小, 一年中H, He在0.125 mm³ InP中产生的非电离损伤能在空间辐射环境中占比达97.44%, 重离子占比仅为2.56%, 但重离子NIEL值约是H, He的2—30倍, 单个空间重离子在InP电子器件中的位移损伤效应不可忽略; 3)统计了C, N, O, Fe在500, 1000, 5000 μm InP中的NIEL值及T_dam随深度分布, 发现NIEL值随厚度增大而减小, 但减小幅度不大, 原因在于当低能离子射程小于InP材料厚度时, 在材料前端发生完全沉积, 导致后端非电离能量沉积相对变小, 进而使NIEL值随深度增大而减小. 进一步分析T_dam随深度分布可知, T_dam随粒子入射深度的增加而减小, 验证了上述说法的正确性, 同时说明空间重离子在InP材料中产生的位移损伤严重区域主要分布在材料前端.
综上可知, 空间辐射环境中需要考虑低能高原子序数离子在InP电子器件中产生的位移损伤效应. 本文的工作对于InP电子器件在空间环境中的应用有重要意义, 为InP电子器件在轨性能预测和屏蔽防护设计提供参考数据.