全文HTML
--> --> -->柔性无机电子技术将传统无机半导体材料与柔性衬底集成, 并基于力学结构设计, 减小了器件变形过程中应变对无机功能单元的影响[5]. 该技术涉及物理、电子、材料、微纳加工、大规模制造和系统集成等多门学科, 需要综合考虑电场、力场、热场等多场耦合效应来发展柔性器件、电路、系统的设计理论和实现方法, 因此将为上述学科带来理论和实践上的新突破.
在物理层面上, 柔性无机电子技术的发展将拓宽传统半导体物理在应力条件下对能带和载流子输运机制的理解, 揭示受力形变条件下化学键、分子链及晶格结构的形变对其物理性质的影响规律. 同时, 可发现柔性电子材料和器件在受结构和外力影响的情况下新颖的微观和宏观物理效应, 发展出新的机理和应用.
在器件与系统层面上, 柔性无机电子技术的发展有利于揭示器件中关键材料的形变与器件物性的变化规律, 发展可延展柔性器件在大变形工作环境下的性能评价和失效分析标准; 发展基于柔性无机电子技术的集成方法学和系统设计理论有助于突破感知、计算、通信、能量和执行等覆盖信息技术全功能链的关键技术, 将在信号、激励、执行等层面实现信息与现有生物系统的无缝集成, 实现人-机-物的高度共融.
基于此, 本文将围绕柔性无机电子技术及半导体材料性能调控进行重点阐述, 详细介绍柔性无机电子技术中的两大关键技术:减薄技术及转印技术, 并探究两大关键技术对半导体电子器件性能的影响; 随后就应变-能带结构耦合关系在低维半导体材料及间接带隙半导体材料中的应用进行概述, 针对目前外界手段所引入多为拉应力且应变多为固定值的局限性, 以屈曲模型的研究为例, 阐明柔性电子技术应用于半导体材料性能调控的独特优势, 为设计优化半导体器件提供新的思路(图1)[6-10].
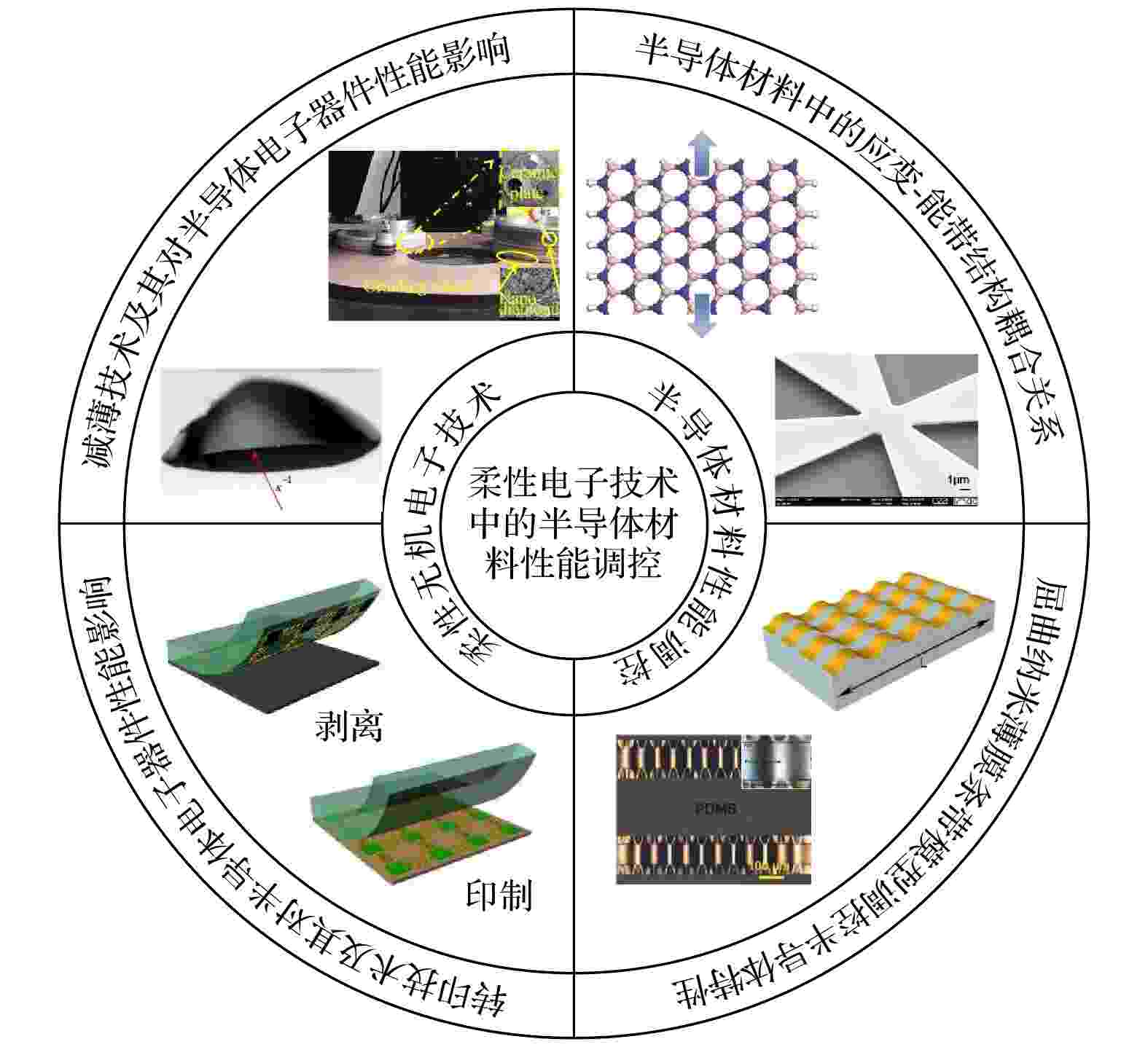图 1 柔性无机电子技术与半导体材料性能调控相结合, 设计优化半导体器件[6-10]Figure1. Combine flexible inorganic electronics with the property regulation of semiconducting materials to design and optimize semiconductor devices[6-10].
2.1.概 述
柔性无机电子技术依托高性能的无机半导体材料, 可与传统的互补金属氧化物半导体(complementary metal-oxide-semiconductor, CMOS)电路相兼容, 通过结构优化, 使器件、电路与系统从形态上体现出可弯曲/可折叠/可延展等特性, 使得柔性电子系统具有空间结构的高度适应性. 实现系统的柔性化可分为以下三种情况: 一是无机半导体器件或芯片等功能单元的柔性化; 二是对互连线进行结构设计实现柔性化; 三是通过异质集成将上述功能单元与互连线封装于柔性材料中.接下来就以上三种情况所涉及的方法与技术进行相应介绍, 重点阐述基于纳米金刚石颗粒的减薄技术及转印技术, 并探究其对半导体电子器件性能的影响.2
2.2.减薄技术及其对半导体电子器件性能的影响
半个多世纪以来, 集成电路一直遵循摩尔定律快速发展. 而随着晶体管尺寸的不断减小与集成度的不断提升, 制备超薄半导体器件以及有效解决散热问题是亟待解决的关键. 减薄技术无疑是解决该问题的有效途径之一: 一般来说, 本征衬底材料对于芯片不但没有功能用途, 甚至还会影响到散热和传输速度等性能参数. 对晶圆/芯片进行减薄, 去除基底材料, 可以有效减小芯片的封装体积、提高芯片散热效率, 进而提升系统的集成度.半导体材料减薄后的曲率和减薄后材料的厚度以及减薄过程中产生的失配应变有关, 厚度越薄、失配应变越大, 曲率越大, 减薄后的半导体材料越容易碎裂, 从而更难获得超薄半导体材料. 材料的抗弯刚度同厚度成三次方关系, 制备柔性半导体材料的一大重要方向即是降低材料的厚度, 故厚度薄、曲率小的半导体材料是制备柔性半导体材料的理想状态, 根据变形模式与厚度、失配应变之间的关系可知, 减小失配应变才可以获得超薄、小变形的半导体材料[9].
目前的减薄技术主要包括湿法腐蚀[11]化学机械抛光[12]、等离子腐蚀[13]、研磨以及磨削[14]等. 其中最常用的减薄技术为研磨、磨削以及湿法腐蚀等. 研磨及磨削技术避免了湿法腐蚀所引入的化学溶液腐蚀与损伤等, 且具备较高的加工效率、较低的成本与较高的成品率, 被广泛应用于半导体行业中. 然而, 一方面, 目前的研磨及磨削技术大多针对晶圆级进行减薄处理, 并没有办法减薄小尺寸的半导体芯片; 另一方面, 普通的化学抛光垫或砂纸颗粒太大, 无法实现高集成度、功能复杂芯片的精细研磨. 因此, 目前传统意义上的减薄工艺不适用于超薄半导体器件的发展, 更为重要的是定量研究在减薄过程中所引入的应变对器件性能影响有着十分重要的意义.
金刚石是碳的一种结晶态, 是一种原子晶体, 由于碳原子体积小, 原子间的共价键短、结合力强等, 因而具有极高的硬度、耐腐蚀性和耐磨性. 采用负氧平衡爆轰合成法可以得到粒度小、外貌为球形或类球形的纳米金刚石, 这类金刚石多用于制作抛光剂, 可以对半导体材料、光学材料、生物陶瓷等材料进行精密抛光. 纳米金刚石高硬度和高模量的特性使其可以磨削半导体材料的表面, 进而去除半导体器件的原始衬底. 在减薄的过程中, 纳米金刚石颗粒在均布压力的作用下会嵌入到芯片背面内部, 同时附着有纳米金刚石颗粒的减薄盘的旋转方向同芯片的旋转方向相反, 故而在旋转力的作用下, 金刚石颗粒不停地磨削芯片背面, 进而不断地减薄芯片. 纳米金刚石颗粒的类球形形貌, 可以有效减小纳米金刚石颗粒在磨削过程中对半导体芯片的损伤; 减薄盘和芯片相反的旋转方向控制, 保证了接触面积及研磨力的恒定, 从而确保加工状态的稳定, 有效避免了减薄过程中常见的中凸及边塌现象. 同时, 通过控制金刚石颗粒粒径大小、金刚石颗粒浓度、均布压力以及减薄盘的转速, 可以控制减薄速度并优化减薄质量, 从而获得性能良好的超薄芯片. 基于此技术, 清华大学冯雪研究小组发展了一套无化学损伤、自动可控的柔性半导体器件制备流程, 并据此制备了柔性可延展光电子器件及系统(图2(a)), 实现了血氧及血压的无创、长时间动态监测[15,16].
图 2 芯片减薄表征及性能测试 (a) 发光二极管(红光, 砷化镓)及光电探测器(硅)减薄后厚度方向和功能层表面SEM图片; 超薄半导体光电器件性能测试: 发光器件(红外光及红光LED)的电致发光(electro luminescence, EL)光谱, 以及光电探测器的绝对光谱响应(absolute specular reflectance, ASR)[15,16]. (b) MOS管减薄后光镜图; 减薄前后转移特性曲线及输出特性曲线对比Figure2. Characterization and properties of the thin-film semiconductors fabricated by thinning process: (a) SEM images show the thickness of the ultrathin red light LED and photodetector. Insets is the microstructure of the chips after thinning via the nano-diamond thinning process. Electroluminescence (electro luminescence, EL) spectra of light-emitting elements (infrared light and red light) and the absolute spectral responsibility (absolute specular reflectance, ASR) of photodetector used in the skin-like device[15,16]; (b) optical image of the MOSFET after thinning process. The comparison of transfer characteristics at Vd = 3 V and output characteristics at Vg = 3 V of MOSFET between thin-film and original semiconductors.
金属-氧化物半导体场效应晶体管(metal-oxide-semiconductor field-effect transistor, MOSFET, MOS管)作为最基础的半导体器件在微电子领域发挥着极其重要的作用, 利用纳米金刚石颗粒减薄技术可将其减薄至10 μm左右, 通过光学显微镜观察MOS管的功能表面未发现明显的划痕或损伤, 通过测试对比其减薄前后转移特性曲线以及输出特性曲线定量研究了减薄所引入的应变对MOS管的电学特性的影响 (图2(b)). 转移特性曲线描述当漏极-源极电压为常量时, 漏极电流Id与栅极-源极电压Vg之间的函数关系; 输出特性曲线描述当栅极-源极电压为常量时, 漏极电流Id与漏极-源极电压Vd之间的关系. 观察可见, 减薄前后的MOS管特性曲线基本重合, 其开启电压、可变电阻区及恒流区等并没有发生明显变化, 这充分说明纳米金刚石减薄技术将MOS管减薄至10 μm左右对其电学性能基本不会造成影响.
总之, 基于纳米金刚石颗粒的减薄技术是一种高效的超薄半导体制备工艺. 这种技术不仅可以针对半导体芯片进行减薄, 同样可以应用于半导体晶圆的减薄, 且基本不会影响到半导体器件性能, 为发展超薄半导体器件提供了一条行之有效的途径.
2
2.3.可延展柔性结构设计
在实现了无机半导体器件或芯片等功能单元的减薄处理后, 需要进一步针对互连线进行结构设计, 从而确保集成电路在极大的拉伸应变下仍不出现裂纹并正常工作, 于是, 研究者们相继发展了基于屈曲模型的波浪结构法和岛桥结构法等.在力学领域, 对于柔性结构早有诸多理论研究. 在这些理论之中, 屈曲模型被认为是实现柔性、可延展结构的一种有效的途径. 2006年, 美国西北大学Rogers 研究小组[5]通过预应变控制方法在聚二甲基硅氧烷(polydimethylsiloxane, PDMS)基底上制备了波纹状单晶硅条(图3(a)), 成功地通过屈曲结构实现了无机半导体材料柔性化. 测试结果显示器件在承受较大变形的情况下电学性能无明显下降. 波浪结构凭借易于制备、较大延展性等优点, 被广泛应用于可延展电子器件制备中[17-19]. 该工作为无机半导体器件可延展柔化奠定了基础.
图 3 可延展柔性结构设计 (a) 单晶硅条带在PDMS基体上形成波浪结构的扫描电子显微镜照片[5]; (b) 砷化镓纳米条带在PDMS基体部分粘合形成波浪结构的扫描电子显微镜照片[20]; (c) 硅纳米薄膜在PDMS基体上的岛桥结构扫描电子显微镜照片[22,23]; (d) 蛇形导线岛桥结构互连的可拉伸CMOS反相器阵列的扫描电子显微镜照片[22,23]Figure3. Designs of the flexible and stretchable structure: (a) SEM images of wavy, single-crystal Si ribbons[5]; (b) SEM images of an array of gallium arsenide nanoribbons in buckled shapes where bonding to the PDMS substrate occurs only at the positions of the troughs, as illustrated in the top inset[20]; (c) SEM image of a silicon nanomembrane in a buckled, mesh layout on PDMS[22,23]; (d) SEM images of an array of stretchable CMOS inverters with noncoplanar bridges that have serpentine layouts[22,23].
由于在波浪结构中, 薄膜和基体在变形中是完全粘合的, 故其弯曲或拉伸性能受材料属性的影响较大. Sun等[20]对波浪结构进行了改进, 仅让一部分薄膜与基体粘合, 释放预应变后只有未粘合的薄膜发生屈曲, 形成可控屈曲的波浪结构(图3(b)). 美国西北大学黄永刚研究小组[21]对这种结构进行分析, 进一步证明了该屈曲结构的波长和幅值与材料属性无关, 拓宽了波浪结构在可延展柔性电子器件制备中的应用范围.
受可控屈曲的波浪结构的启发, Kim 等[22,23]提出了岛桥结构法, 进一步提高了半导体器件的柔性和延展性, 并减小了拉伸过程中功能薄膜所承受的应变. 在这种方法中, 功能组件(岛)通过化学方法粘合在经过预拉伸的基体上, 组件之间通过导线(桥)进行互连, 导线与基体之间不发生粘合. 释放预应变后, 导线发生面外屈曲而拱起(图3(c)), 从而提高了柔性电子器件的延展性. 但是由于直导线的尺寸受到了岛与岛之间间距的影响, 因此结构的可延展性有限. 为继续提升延展率, Kim 等将互连部分设计为蛇形结构, 相比于直导线, 蛇形结构在相同的岛间距内长度更大(图3(d)). 故而当对器件进行拉伸时, 蛇形导线会发生更大的面外弯曲和扭转(即面外屈曲), 从而承担了电子器件几乎全部的应变, 而其中的半导体功能组件几乎不承受应变, 最终器件的可延展性能可达到100%. 研究者们基于岛桥结构发展了具有更小失真和更广视角的仿生电子眼相机[24]、柔性LED显示器[25]等器件. 为了进一步提高柔性无机电子的柔性和延展性, 研究者们在岛桥结构的基础上, 对蛇形线的几何构型进行拓展, 得到了多级分形互连导线结构等[26], 并应用于锂电池的结构设计中, 实现了延展率为300%的可无线充电的锂电池[27].
利用以上设计可以有效地提高器件整体柔性与可延展性, 将功能单元中的应变控制在材料失效极限以下, 从而降低了应变所引起的半导体性能改变, 使得电子器件可以承受拉伸、扭转、弯曲等复杂变形, 极大拓宽了柔性无机电子的应用范围, 现已成为微电子与集成电路革新性发展的方向之一.
2
2.4.转印技术及其对半导体电子器件性能的影响
在实现了器件的减薄处理及可延展柔性结构设计后, 需要将超薄半导体器件同可延展柔性互连线集成并封装于系统中. 在柔性无机电子技术中, 转印是实现异质集成必不可少的关键工艺. 转印技术是将不同功能、不同材料、不同尺寸的无机功能单元从源基底组装到柔性目标基底上最终形成柔性集成器件的过程, 该技术的核心是能够高效并行地将功能单元从源基底完整剥离, 并精确地按器件的结构有序地释放并搭接为具有特定功能的复杂系统[28,29]. 目前应用最为广泛的即是基于印章的转印技术, 一般包括剥离与印制两个步骤: 剥离过程指的是用柔性印章将源基底上刻蚀完的薄膜器件(空间有序的功能单元)撕起; 印制过程指的是在经过对准后, 将之前柔性印章上所粘附的器件(空间有序的功能单元)印制在新的目标基底上. 整个过程如图4(a)所示.
图 4 转印技术 (a) 基于率相关印章的转印技术[32]; (b) 基于磁控的转印技术[38]; (c) 基于液滴的转印技术[39]Figure4. Transfer printing techniques: (a) Kinetically controlled transfer printing[32]; (b) magnetically actuated transfer printing[38]; (c) transfer printing using droplet stamps[39].
转印过程涉及界面粘附调控和断裂的力学控制过程, 其力学机理为软印章、硬薄膜和基底三者间形成的两个界面的竞争断裂, 即两个或多个界面同时受到外力作用产生破坏倾向时, 界面强度的高低将决定哪个是首先破坏的界面, 因此如何调控界面的强度是转印技术进一步发展和完善的关键[30,31].
通常用界面的临界能量释放率Gcrit (即单位面积界面破坏所需要的最小能量)作为界面强度的衡量, 在剥离与印制过程中都是界面中强度较小者(也即是临界能量释放率较小者)首先发生破坏, 故
剥离过程:
印制过程:
由于硬薄膜和基底均处于弹性变形状态, 所以二者间的界面称为弹性界面, 此界面的临界能量释放率
除以上介绍的率相关印章转印技术外, 近年来, 研究者们还发展了基于微结构的转印技术[34]、基于形状记忆聚合物的转印技术[35,36]、基于胶带的转印技术[37]、基于磁控的转印技术(图4(b))[38]以及基于液滴的转印技术(图4(c))[39]等. 转印技术扩大了电子器件的应用范围, 利用其制备的电子器件表现出的优良性能, 在显示、能源、医疗健康及人机交互中等领域具有广泛的应用前景[40-45].
但是目前在纳米器件的转印, 三维复杂曲面的转印和大规模、高效、精准转印方面仍存在巨大的挑战, 相信随着科技的发展, 研究者们将在不久的将来攻克掉这些难题.
2
2.5.柔性无机电子技术在健康医疗中的应用
基于上述设计方法与关键技术, 柔性无机电子器件近些年来已取得长足的进步[46-48], 尤其在柔性传感领域, 凭借柔性和可延展性, 其可与皮肤、心脏、神经等共形贴合, 被广泛用于检测生物体生理参数, 如: 柔性无创血糖传感器[49]、软硬材料上制备的温度传感器[50]、类皮肤压力传感器[51]、超柔变形传感器[52]、利用攀爬现象制备的可用于神经电刺激及电信号采集的螺旋电极(图5(a))[53]、与软体手集成的高性能柔性触觉传感器(图5(b))[54]、可延展柔性血氧及血压传感器(图5(c))[16]及高密度超薄超柔脑电极[55]等, 实现了血糖、温度、心率、血氧、血压及生物电信号等多种生理信息的精准监测.
图 5 可延展柔性传感器在健康医疗中的应用 (a) 用于神经电刺激与电信号采集的螺旋电极[53]; (b) 与假手集成的柔性触觉传感器[54]; (c) 可延展柔性血氧及血压监测系统[16]Figure5. Applications of stretchable and flexible electronics: (a) Climbing-inspired twining electrodes using shape memory for peripheral nerve stimulation and recording[53]; (b) flexible tactile sensor integrated with a soft prosthetic hand[54]; (c) wearable skin-like optoelectronic systems for cuff-less continuous blood pressure monitor[16].
2
2.6.小 结
综上所述, 一方面, 研究柔性无机电子技术中的减薄、转印关键技术及对半导体电子器件性能的影响对于评估分析可延展柔性器件在大变形工作环境下的性能变化具有十分重要的意义, 结合可延展柔性结构设计将有望推动基于力学优化的半导体器件的结构设计, 从而有效规避变形等引起的器件性能改变; 另一方面, 通过合理设计结构引入单轴或双轴应变来调控半导体材料的物理性质, 进而设计优化半导体器件近些年受到诸多关注.3.1.概 述
随着集成电路的高速发展, 硅基CMOS器件特征尺寸不断缩小且集成度与复杂度急剧增强, 单个晶体管的尺寸越来越接近物理和技术的双重极限, 摩尔定律陷入瓶颈. 为延续摩尔定律, 应变硅凭借其载流子迁移率高、能带结构可调, 并与硅的微电子技术相兼容等优异特性得到广泛关注与应用, 已成为高速高性能半导体器件与集成电路的研究发展重点[56-59], 目前可以通过衬底引入双轴应变或半导体工艺引入单轴应变来增强载流子迁移率. 以上利用应变来调控材料(三维的块材、二维的薄膜或者一维的量子点等多尺度多形态材料)宏观物理性质的过程称为“应变工程”. 目前, 应变工程已广泛应用于调控半导体能带、铁电及介电材料性能、多铁性薄膜电磁性能等领域[60-64].半导体材料的光电性质本质上取决于其能带结构, 主要包括能隙、态密度等, 因此正确理解半导体能带结构对于研究其光电特性尤为重要. 鉴于此, 江崎和朱兆祥等提出“能带工程”的概念, 即创造人工改性半导体材料能带的工程: 能隙作为半导体材料的本征特性之一, 源自于材料内稳定的周期性晶体势场. 故当晶体的晶格受到应变而发生畸变时, 原本稳定的周期性晶体场便发生改变, 材料的本征能隙也会相应地发生变化. 对材料的物理参数和几何参数进行设计和生长(如调节材料原子组分和各层材料的掺杂浓度、引入应变、生长异质结构等), 以改变其能带结构并调控材料能隙大小, 可以优化其电、光学性质, 从而获得性能更加优越的新器件材料[65-69].
2
3.2.半导体材料中的应变-能带结构耦合关系
在能带工程中, 研究应变-能带结构间的耦合关系是重中之重. 将应变与材料能带结构相结合, 不仅会更深入理解材料特性并探索到新的物理现象, 而且对于人工设计半导体器件并调控其性能具有重要指导作用. 同时, 将原位应变调控技术和能带工程以及设计新型半导体功能结构相结合, 进一步实现材料光电性能的多参量调控, 也是未来研究的重点方向之一. 一直以来, 对半导体材料施加应力主要通过外延来实现, 即利用生长材料与基底的晶格不匹配所导致的位错获得本征内应力[70,71], 这种方法简单且易于实现, 但所得到的应力是单一的双轴面内应力, 不存在梯度分布, 且一旦材料与基底体系确定后, 应力水平便固定不变.随着微纳技术的发展, 部分半导体材料可以通过新型生长技术制备成纳米线、纳米管等低维材料, 并结合微观应力加载平台, 搭配精细化的实验测量仪器, 这给应变调控半导体特性带来了契机. 低维材料因某一维度的尺寸在分子乃至原子的尺度范围, 从而使得应变的引入强烈扰动材料的能带结构, 一定程度上对应变调控效应有放大的作用; 且低维材料如纳米线等屈服强度较块体材料或传统电子材料大大增强, 从而可以更有效地通过引入应变调控其电学及光学性能[72-76]. Wei 等[77]针对不同尺寸(直径)的氧化锌纳米线进行单轴拉伸研究其能隙的改变, 对直径100 nm的纳米线施加7.8%的拉应变, 其能隙改变量可达110 meV(图6(a)). Signorello 等[78]对GaAs/Al0.3Ga0.7As/GaAs的核壳结构纳米线施加3.5%的拉应变时, 其带隙可以降低296 meV, 为基于半导体纳米线的光电器件利用应变效应实现宽波段范围内的光学特性调控提供了非常好的借鉴思路, 其核壳结构的加载方式与能隙变化图如图6(b)所示. 除了研究应变对纳米线的调控, 诸多对于较为新颖的单原子层材料的应变调控同样受到关注. Qi 等[6]研究了不同宽度的六方氮化硼纳米条带在施加不同的单轴拉伸下能隙的变化, 其中对宽为6 nm的条带施加10%的拉伸应变实现了其能隙从3.5 eV降低到1.0 eV, 意味着六方氮化硼的能隙可以在弹性应变范围内降低至单晶硅的能隙水平, 为利用弹性应变工程调控二维纳米条带的光学及电学特性提供了新的思路. Conley 等[79]对单层以及双层二硫化钼施加单轴拉应变均观测到了能隙改变量与应变之间的近似线性关系: 单层约45 meV/%, 双层约120 meV/%. Lloyd 等[80]通过气压诱导双轴应变实现了单层二硫化钼薄膜能隙的连续可逆调控, 其中在微米大小的区域内可引入5.6%的双轴应变且能隙改变量达500 meV(图6(c)), 为研究双轴应变对其他二维半导体材料性能的影响提供了借鉴意义.
图 6 低维材料中的应变-能带结构耦合关系 (a) 单轴拉伸调控氧化锌纳米线[77]; (b) 单轴拉压调控GaAs/Al0.3Ga0.7As/GaAs核壳结构纳米线[78]; (c) 双轴应变调控单层二硫化钼薄膜[80]Figure6. Applications of strain effects on band structures to low-dimensional materials: (a) The shifts of the near-band-edge (NBE) peak for the 100 nm nano-wire (NW) by tension and the photon energy versus strain curves for ZnO NWs with different diameters[77]; (b) schematic of a GaAs-Al0.3Ga0.7As-GaAs core-shell nanowire and photoluminescence (PL) spectra measured for different values of applied uniaxial stress[78]; (c) the monolayer MoS2 bulged up or down depending on whether Δp is positive or negative and in situ measurements of PL spectra for a monolayer device[80].
另一方面, 研究应变-能带结构间的耦合关系将有望突破间接带隙半导体材料在光发射领域的受限. 通过对间接带隙半导体材料如锗, 施加相应的应变, 增加其光激发效率, 可以拓展其在光电发射器件领域应用的潜能[81-85]. Sánchez-Péreza 等[86]将不同厚度的锗纳米薄膜转印至柔性聚酰亚胺薄膜(polyimide, PI)上, 并通过加压的方式引入双轴应变, 最大应变在2%左右. 研究发现, 随着施加的拉应变的增加, 厚度为40 nm的锗薄膜的光致发光强度明显增强, 其引入应变示意图及随应变变化的光致发光光谱图如图7(a)所示; Süess 等[87]通过结构设计锗微桥应变结构, 将应变集中于窄桥区域, 从而成功地在悬浮的锗微桥中引入了高达3.1%的单轴拉应变, 实验测到其光致发光强度为体材料的25倍. 该方法同CMOS工艺相兼容, 且得到的应变值较大, 因而受到了广泛的关注, 锗微桥及光致发光光谱如图7(b)所示; Bao 等[88]在微桥结构中的平板区域通过刻蚀弧形分布式布拉格反射器光栅来引入光反馈(图7(c)), 结合1.6%的单轴拉应变锗以及Q值大于1100的光学谐振腔, 观察到了低温(80 K)的光抽运激射, 且阈值功率仅为3 kW/cm2, 从而论证了拉应变的锗材料作为低阈值硅基激光器的可行性.
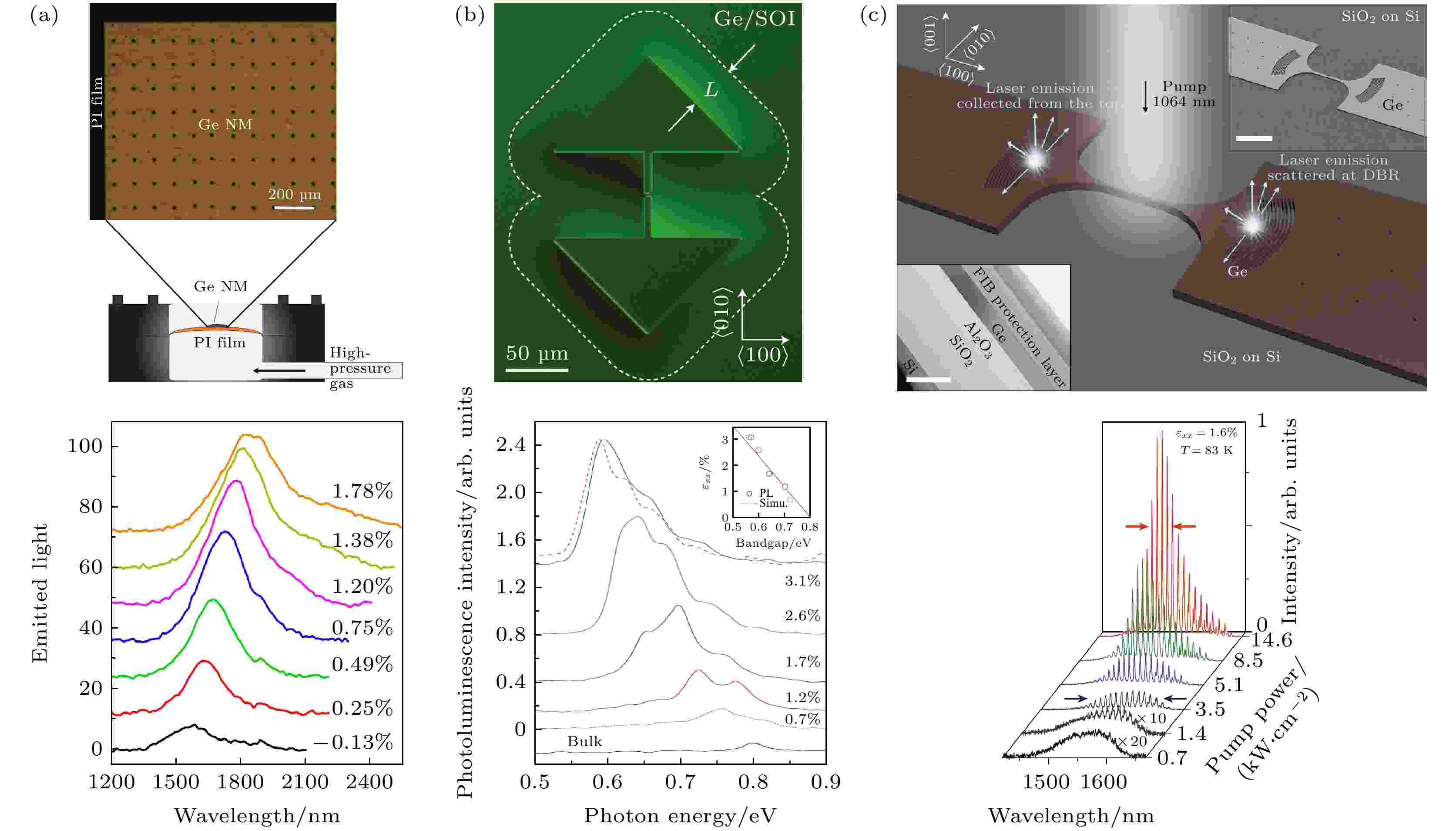图 7 锗材料中的应变-能带结构耦合关系 (a) 双轴应变调控锗纳米薄膜[86]; (b) 锗微桥应变结构及光致发光谱(室温)[87]; (c) 单轴拉应变锗DBR激光器及不同泵浦光功率下的光致发光谱(80 K)[88]Figure7. Applications of strain effects on band structures to Ge material: (a) Ge nanomembranes(NMs) and schematic sample mount and PL spectra of a 40 nm thick Ge NM at different levels of biaxial tensile strain[86]; (b) differential interference contrast light-microscopy image of a Ge/SOI structure and μPL spectra taken from structures with increasing longitudinal strain up to 3.1% and excitation in the center of the constriction[87]; (c) Schematic illustration of a typical Ge nanowire laser consisting of a strained nanowire surrounded by a pair of distributed Bragg reflectors (DBRs) on the stressing pads and power-dependent photoluminescence spectra of a 1.6% strained Ge nanowire with DBRs showing a gradual transition from broad spontaneous emission to multimode lasing oscillation (threshold, 3.0 kW/cm2)[88].
然而, 以上所阐述的通过外界手段所引入的设计大多局限于拉应力且应变多为固定值, 到目前为止, 定量地引入压应力仍然是一大难题, 而柔性电子技术的发展为此提供了契机.
2
3.3.屈曲纳米薄膜条带模型调控半导体特性
将屈曲模型同半导体材料性能调控相结合, Wang 等[89]提出一种转印方法, 将脆性的无法直接拉伸或压缩的纳米级AlxGa1–xAs条带集成至预拉伸的软基底上, 释放预应变后利用结构屈曲得到了稳定的余弦形的波浪状周期结构, 借助微区拉曼谱(μ-Raman)和微区光致发光谱(μ-PL)的表征手段, 分析了一维屈曲模型下的AlxGa1–xAs薄膜表面部分所受应变以及能隙随具体位置的分布规律. 结果表明GaAs的能隙可以在结构上形成周期性的调控. 该方法为连续应变调控脆性的半导体材料提供了技术和理论支撑, 未来可以继续拓展应用在一些需要材料性能周期性变化的新兴领域之中.研究所涉及的功能纳米条带AlxGa1–xAs多层材料通过金属有机化合物化学气相淀积(metal-organic chemical vapor deposition, MOCVD)生长在
图 8 功能纳米条带屈曲图及能隙与形貌叠加图[89] (a) GaAs纳米条带屈曲制备流程示意图; (b) 屈曲条带光镜图及3D形貌图; (c) 单个周期内GaAs的能隙变化与形貌变化叠加图Figure8. Buckling-based method for measuring the strain-photonic coupling effect of GaAs nanoribbons[89]: (a) Schematic procedures of fabricating the AlxGa1–xAs wavy geometry on PDMS; (b) optical microscope image, 3D microstructure, and profile details of a single ribbon for three samples; (c) band gap mapping by PL scanning within one period in the wavy ribbon.
为了直观地观察到屈曲结构所导致的GaAs能隙的改变, 研究中采用PL光谱观察到GaAs条带在一个周期内能隙的连续周期性变化(图8(c)). 图8(c)中反映一个周期的“谷”处呈现能隙的最大值, 而“峰”处为能隙的最小值, 从“谷”到“峰”, 能隙逐渐连续的变窄, 且呈现伴随屈曲结构一致的周期性改变.
研究发现由应变导致的GaAs的特性发生的周期性改变同屈曲形貌的周期性变化类似, 进一步说明了研究所提出的这种一维屈曲形貌周期性改变材料禁带宽度的方法在未来有可能应用在某些要求同一材料必须具备周期性变化性能的领域之中.
屈曲结构在连续调控半导体量子阱结构中同样取得了较好的研究结果. Zhang 等[92]进一步研究了Al0.3Ga0.7As/GaAs/Al0.3Ga0.7As量子阱结构在一维屈曲下的连续周期性能带分布, 研究所涉及的量子阱结构通过分子束外延生长在
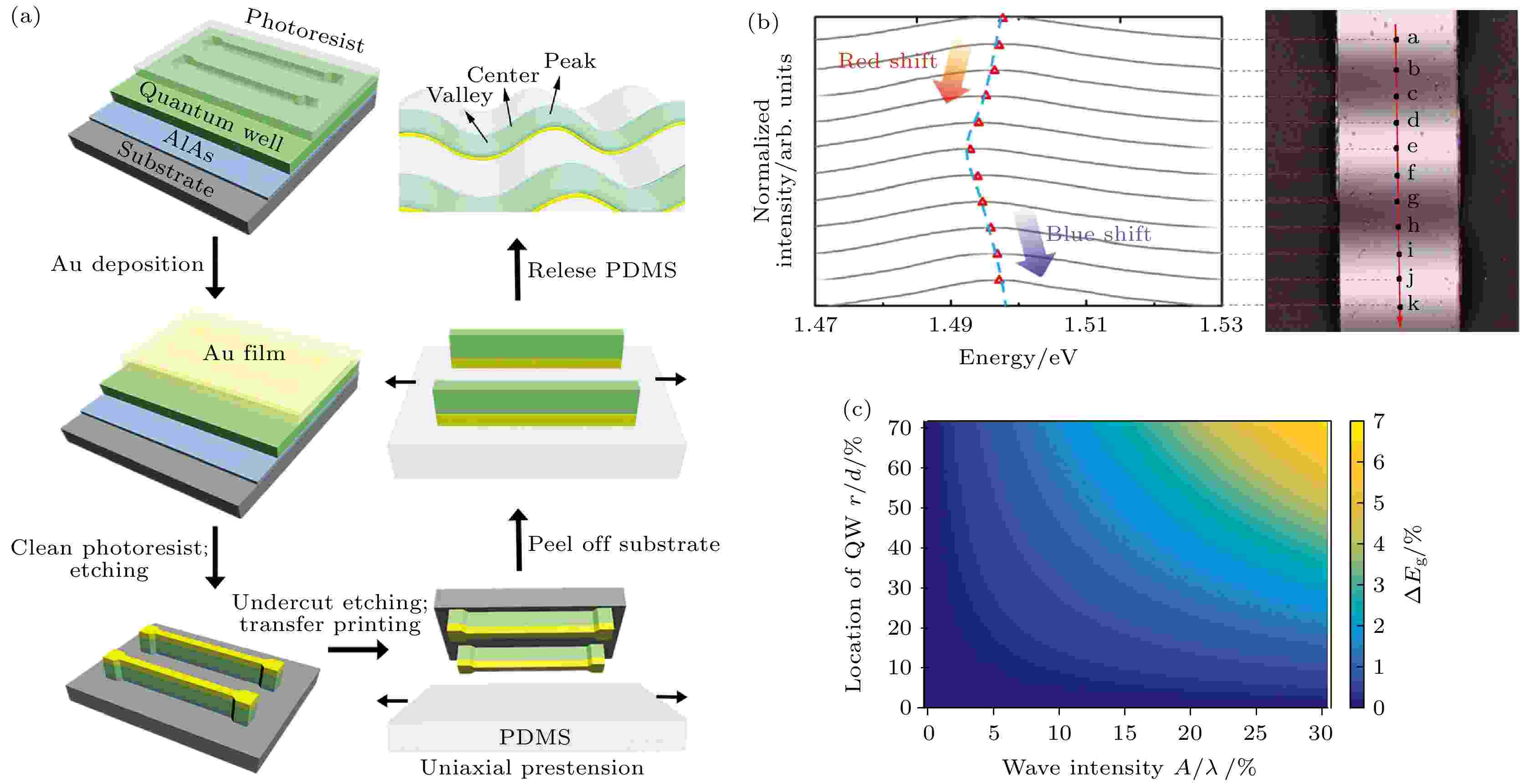图 9 半导体量子阱结构的应变调控[92] (a) Al0.3Ga0.7As/GaAs/Al0.3Ga0.7As量子阱结构屈曲制备流程示意图; (b) 量子阱结构屈曲条带的能隙分布; (c) 量子阱结构实现能隙调控优化示意图Figure9. Strain engineering in quantum well embedded in wavy nanoribbons[92]: (a) Schematic procedures of fabricating the wavy quantum well nanoribbons (QWNRs) on PDMS; (b) strain effect on the photonic property of the wavy QWNR; (c) band gap variation of a single QWNR as a function of wave intensity A/λ and the location of QW r/d within the fracture limit of the nanoribbon.
实验最后进一步研究了在满足结构未断裂的基础上, 通过调节量子阱结构的相对位置(r/d)以及屈曲结构的波形(A/L)实现能隙调控的最大化. 将能隙的改变率同两个外界可控的无量纲量绘制于图9(c)中, 可发现在r/d = 73.3%且A/L = 30.7%时能隙改变率可达到6.7%.
该实验通过简单而切实可行的屈曲结构实现了量子阱结构能隙的连续周期性调控, 测得一周期内能隙改变量可达3.6 meV, 这为设计带隙可调的量子阱发射器提供了借鉴思路.
2
