摘要:基于电磁加载装置CQ-4, 建立了一种同步开展透明材料折射率和高压声速测量的实验方法. 完成了聚甲基丙烯酸甲酯(PMMA)窗口材料14 GPa斜波压缩实验, 利用多点双光源外差位移干涉测速仪(dual laser heterodyne velocimetry, DLHV), 获得了PMMA样品后表面的速度历史曲线. 速度曲线表现出明显的双波结构, 表明PMMA样品出现了弹塑性转变. 通过实验数据处理, 一发实验同步获取了PMMA的折射率-粒子速度光学特性和拉氏声速-粒子速度动力学特性.
关键词: 聚甲基丙烯酸甲酯/
折射率/
拉氏声速/
斜波加载

English Abstract

全文HTML

--> --> -->

近些年发展的磁驱动斜波加载技术^[1], 对应热力学路径中的等熵线, 等熵线介于等温线和冲击绝热线之间, 因此该实验技术被誉为联系准静态和冲击加载技术的桥梁. 斜波压缩过程加载压力平滑上升、材料中不形成冲击波强间断, 样品经历连续的热力学过程, 实验记录材料物理量从初始状态到终态连续变化过程, 在热力学平面上对应一条等熵线. 利用斜波加载实验技术, 国内外已广泛开展了各种材料状态方程等物性研究和透明材料折射率研究^[2-7], Hayes等^[3]开展了蓝宝石窗口的折射率和等熵线研究, 数据处理中的原位粒子速度是借助反积分方法计算得到的, 这一步数据处理需要电极板和透明材料的状态方程及其动力学参数. 利用相似的方法, Fratanduono等^[4,5]、Nazarov等^[6]和张旭平等^[7]陆续开展了LiF, MgO, LiF和石英窗口的折射率研究. 本研究对之前的实验方法进行优化, 建立了一种同步开展透明材料光学和动力学特性研究的新实验方法, 单发实验可同时获得其折射率-粒子速度和高压声速-粒子速度等关系. 而且新的实验方法, 不需要预先知道透明材料的动力学物性参数, 即可直接开展新研制未知透明材料的物性研究.
聚甲基丙烯酸甲酯(polymethyl methacrylate, PMMA) 是一种典型的无色透明聚合物, 俗称有机玻璃, 具有良好的光学、力学和化学性能且价格低廉, 已被广泛应用于航空航天、船舶、建筑和医疗械等各行各业, 人们也对其屈服、黏性、软化和损伤等机械特性开展了广泛的研究^[5,8-13]. 另外, 在材料高压物性研究中, 由于PMMA在较宽的压力范围内具有良好的透光性且物性简单, 常被作为低阻抗光学窗口^[14,15]. Chhabildas和Asay^[16]基于阻抗梯度飞片斜波加载技术开展了LiF和PMMA两种透明窗口的折射率研究, 只给出了折射率随压力变化的规律. 国内郝龙等^[17]利用多发冲击实验, 获得了PMMA材料在冲击压力6—50 GPa区间内的冲击波速-粒子速度数据, 同时获得了冲击压缩条件下PMMA样品材料的高压折射率与密度的变化关系以及界面粒子速度修正系数. 现阶段PMMA材料的物性研究工作主要依托静高压和冲击加载实验技术开展.
本研究利用新的实验方法, 开展了斜波加载下有机玻璃窗口材料14 GPa压力内的光学和动力学响应研究, 通过1550 nm波长激光干涉测速技术测量PMMA的后表面速度曲线, 获得PMMA窗口材料在0—14 GPa范围的折射率-粒子速度和高压声速-粒子速度关系.

2

-->

2.1.磁驱动斜波压缩实验

斜波压缩实验在中国工程物理研究院流体物理研究所的磁驱动加载装置CQ-4^[18]上开展. CQ-4装置由储能、开关和传输三部分组成, 加载电流上升沿约600 ns, 电流峰值可达4 MA. 磁驱动加载实验加载原理见图1所示, 具体见文献[1], 种涛等^[19]指出斜波压缩实验的加载均匀性优于1%, 罗斌强等^[20]分析了磁驱动斜波加载实验的不确定度, 结合理论分析和实验证明了磁驱动斜波加载是一种可靠的精密物理实验技术. 实验采用激光波长1550 nm的DLHV^[21]开展速度测试, DLHV利用上、下变频两种工作模式对速度信号频率进行变换, 使得其在100 m/s以内低速段和10 km/s以上的高速段测量同时具有高的时间分辨率和测量精度.
图 1 磁驱动加载原理及样品布局
Figure1. Schematic diagram of magnetically driven ramp wave loading and layout of the samples.

为了在一发实验中同时获取PMMA材料的折射率和动力学参数, 实验负载区布局见图1所示. 实验有4个测试点(图中红点位置): PMMA样品(图中蓝色)后表面3个测试位置(ch1—ch3), 铝极板后表面1个测试位置(ch4). 其中ch1和ch2位置处样品厚度相同, ch1处PMMA样品后表面粘PMMA窗口, PMMA窗口下表面镀约0.3 μm厚镀铝反射膜、上表面镀1550 nm增透膜, 测试界面速度; ch2处样品后表面镀约0.3 μm厚铝反射膜, 测试样品后表面自由面速度. ch3处布局与ch1处相同, 窗口尺寸相同, 样品直径相同、厚度相差约0.2 mm. ch4处铝极板后粘LiF窗口, LiF窗口上表面镀约0.3 μm厚镀铝反射膜、下表面镀1550 nm增透膜, 测量铝极板/LiF窗口界面速度.
磁驱动加载实验负载区的加载电极选择电导率高、物性单一的材料, 常用材料为无氧铜、硬铝和纯铝, 本实验选择声阻抗较低的纯铝为加载电极材料. 根据以上实验设计思路, 参考纯铝电极^[22]、PMMA^[23]样品和LiF^[24]窗口材料的初始物性参数以及斜波加载实验具体实验方法^[25], 具体实验条件见表1.

实验编号	位置	材料	尺寸/(mm × mm)
shot163	ch1	纯铝	1.006 × 10.0 (厚 × 宽)
		PMMA	Ф10.0 × 1.485
		PMMA	Ф10.0 × 4.000
	ch2	纯铝	1.002 × 10.0 (厚 × 宽)
		PMMA	Ф10.0 × 1.483
	ch3	纯铝	1.007 × 10.0 (厚 × 宽)
		PMMA	Ф10.0 × 1.263
		PMMA	Ф10.0 × 3.987
	ch4	纯铝	1.008 × 10.0 (厚 × 宽)
		LiF	Ф10.0 × 3.601

表1实验条件
Table1.Experimental condition.

2 -->

2.2.数据处理方法

结合ch1和ch2处两条实测粒子速度(也叫表观粒子速度^[2,3,5], u_a)曲线, 可获取PMMA材料折射率随粒子速度(或密度)变化规律. 由于实验加载均匀性良好, 可认为4个位置加载历史一致, ch1和ch2处极板厚度和样品厚度相等, 两个样品后界面原位粒子速度(u_p)相等. 在加载压力不高、样品温升较小的条件下, ch2处记录的自由面速度可乘以0.5直接转换为原位粒子速度; ch1处样品和窗口为同种材料, 记录的表观粒子速度只需通过折射率修正即可转换为原位粒子速度.
获取PMMA材料折射率参数后, 对ch1和ch3处记录的两条表观粒子速度进行折射率修正, 即可转换为两条原位粒子速度曲线, 再利用斜波压缩实验台阶样品Lagrange数据处理方法^[26], 可获得PMMA材料高压声速-粒子速度关系、压力-比容关系等动力学特性.

2

-->

3.1.实验结果

实验测试速度曲线见图2所示, 由Al/LiF界面速度可得实验加载压力峰值约14 GPa. 由图可得, ch1和ch2位置样品厚度相同, 波形相似, 速度起跳时刻、弹塑性转变和卸载时序完全一致, 由于PMMA样品后表面阻抗匹配不同波形幅值存在差异; ch1和ch3位置样品厚度不同、后表面窗口相同, 速度波形完全相同, 似乎进行了整体平移.
图 2 实验速度曲线
Figure2. Experimental velocity curve.

2 -->

3.2.折射率修正计算

在带窗口测量界面速度历史的高压物理实验中, 假设忽略激光在窗口中穿过期间窗口材料的密度变化, 激光在窗口中的光学厚度可以表示为

$ Z\text{(}t)={\int_{{\text{窗口厚度}}}n(x,t){\rm{d}}x} , $

其中Z为光学厚度; n为窗口材料的折射率; x为空间位置; t为时间. DLHV记录的速度是表观粒子速度u_a, 有

${u_{\rm{a}}} = \frac{{{\rm{d}}Z}}{{{\rm{d}}t}}.$

结合以上假设和(1)式及(2)式, Hayes^[2]给出任意加载条件写激光干涉测速时窗口的折射率修正关系为

$\frac{{{\rm{d}}{u_{\rm{a}}}}}{{{\rm{d}}{u_{\rm{p}}}}} = n - \rho \frac{{{\rm{d}}n}}{{{\rm{d}}\rho }} = f(\rho ), $

其中ρ为窗口材料的密度. 假设密度和折射率是原位粒子速度的函数, 积分可得折射率为

$n(\rho ) = \rho \left[ {\frac{{{n_0}}}{{{\rho _0}}} - \int_{{\rho _0}}^\rho {\frac{{f\left( {{\rho ^\prime }} \right)}}{{{\rho ^{\prime 2}}}}} {\rm{d}}{\rho ^\prime }} \right].$

当f(ρ) = C为常数时, (4)式转化为与冲击加载时形式相同的折射率修正关系式:

$ n{\text{(}}\rho ) = C{\text{ + (}}{n_0} - C)\frac{\rho }{{{\rho _0}}} . $

对ch2位置表观粒子速度进行两倍粒子速度近似, 获取原位粒子速度u_p, ch1位置记录的是表观粒子速度, 对u_a-u_p曲线的进行拟合, 见图3所示, 有u_a = –0.00657(± 0.0012)+1.06(± 0.0014)u_p, 取初始折射率n₀ = 1.485^[27], 由(5)式可得折射率与密度的关系为

$ n(\rho ) = 1.06( \pm 0.0014) + 0.425\frac{\rho }{{{\rho _0}}} . $

图 3 表观速度-原位粒子速度关系
Figure3. u_a-u_p relationship of PMMA.

2 -->

3.3.动力学响应

得到PMMA材料折射率参数后, 对ch1和ch3位置表观速度进行折射率修正, 可计算得两个位置的原位粒子速度, 见图4所示. 需指出, 由于样品和窗口为同种材料, 阻抗完全一致, 数据处理时省去了阻抗匹配计算原位粒子速度这一过程, 也减少了阻抗匹配带来的误差. 由图4可得, 相同厚度PMMA样品原位粒子速度波形在加载段完全重合, 在约2.3 μs开始分离, 这是由于卸载波到达ch2位置PMMA样品后表面中心位置, 破坏了它的一维应变压缩状态.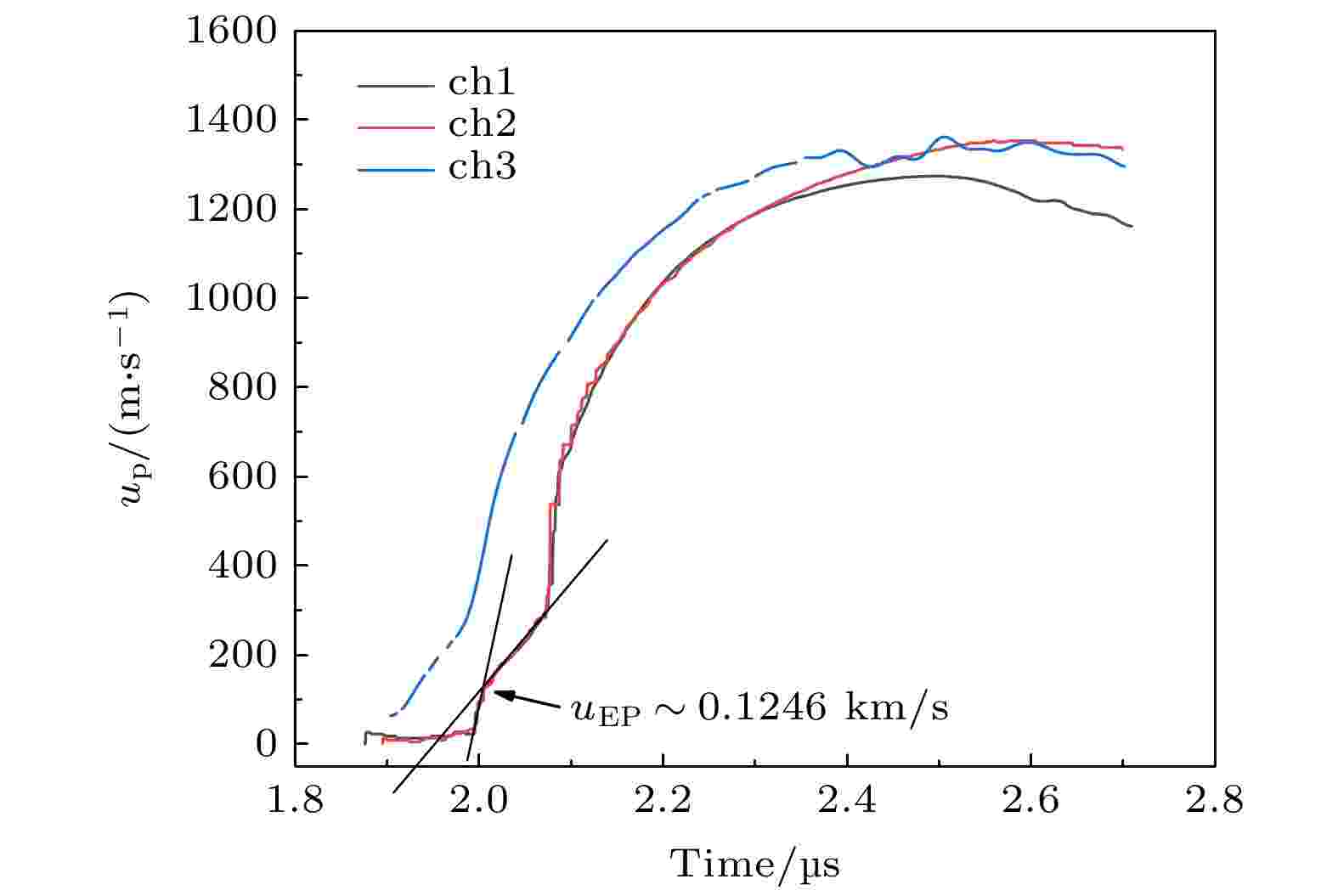
图 4 原位粒子速度波形
Figure4. true particle velocity waveforms.

利用斜波加载实验台阶样品Lagrange数据处理方法^[25], 计算得PMMA材料拉氏声速(c_L)-原位粒子速度(u_p)关系, 见图5所示. 由图得, c_L-u_p关系可分为两部分, 拉氏声速起始段的下降, 对应弹塑性转变过程, 之后全部为塑性段, 对应体波声速. 对塑性段声速数据进行线性拟合, 得c_L = c₀+2λu_p = 2.268+2 × 1.05u_p. PMMA初始密度ρ₀ = 1.181 g/cm³, 初始声速c₀ = 2.268 km/s, 计算得到PMMA的弹性极限σ_IEL = ρ₀c_Lu_EP = 0.37 GPa. 采用线弹塑性模型假设, 弹性极限${\sigma _{{\text{IEL}}}} = Y{{(1 - }}v)/(1 - 2 v)$, 其中Y为屈服强度, ν为泊松比. PMMA泊松比取值0.399^[2], 可得其屈服强度Y = 0.127 GPa.
图 5 拉氏声速-原位粒子速度关系
Figure5. Lagrange sound speed- true particle velocity relationship.

结合磁驱动加载装置CQ-4和激光干涉测速技术, 建立了一种同时测量透明材料折射率和高压声速的实验方法. 完成了14 GPa压力内PMMA材料的斜波压缩实验. 首先, 结合相同厚度样品后界面速度和自由面速度计算了PMMA折射率随密度变化关系, $ n(\rho ) = 1.06( \pm 0.0014) + 0.425\rho /{\rho _0} $; 然后, 利用折射率系数对正对不同厚度样品界面速度进行修正, 得到台阶样品的原位粒子速度, 由于样品和窗口为同一种材料, 这一步不需要进行阻抗匹配修正; 最后, 采用斜波加载实验台阶样品Lagrange数据处理方法, 计算得到了PMMA材料拉氏声速-原位粒子速度关系c_L = c₀+2λu_p = 2.268+2 × 1.05u_p.
感谢吴刚、胥超、税荣杰对 CQ4 实验装置的运行和邓顺益在实验数据测试中的帮助!