摘要: 旋涡对声波的散射问题是声波在复杂流场中传播的基本问题, 在声源定位、声目标识别及探测、远场噪声预测等方面具有重要的学术研究价值和工程应用价值, 如飞行器的尾涡识别、探测及测距, 湍流剪切流中声目标预测, 声学风洞试验中声学测量和声源定位等. 声波穿过旋涡时会产生非线性散射现象, 其物理机理主要与声波波长和旋涡半径的长度尺度比相关. 本文采用高阶精度高分辨率线性紧致格式, 通过求解二维非定常Euler方程, 数值模拟了平面声波穿过静止等熵涡的物理问题. 通过引入声散射截面法, 分析了不同声波波长与旋涡半径的长度尺度比对声波脉动压强、声散射有效声压以及声散射能量的影响规律. 研究表明: 随着声波波长与旋涡半径的长度尺度比逐渐增加, 旋涡流场对声场的影响逐渐减弱, 声散射有效声压影响区域先逐渐增大随后逐渐减小, 声散射能量最大值呈现4种不同的变化阶段.
关键词: 声散射 /
静止等熵涡 /
声散射截面 /
长度尺度比 English Abstract Numerical study on spatial scale characteristics of sound scattering by a static isentropic vortex Wang Yi-Min 1,2 ,Ma Rui-Xuan 1,3 ,Wu Cong-Hai 1,2 ,Luo Yong 1,2 ,Zhang Shu-Hai 1,2 1.State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China Fund Project: Project supported by the Key Program of the National Natural Science Foundation of China (Grant No. 11732016), the Science and Technology Program of Sichuan Province, China (Grant No. 2018JZ0076), and the National Numerical Windtunnel projectReceived Date: 30 December 2020Accepted Date: 06 May 2021Available Online: 07 June 2021Published Online: 05 October 2021Abstract: The scattering of acoustic waves by a vortex is a fundamental problem of the acoustic waves propagation in complex flow field, which plays an important role in academic research and engineering application for sound source localization, acoustic target recognition and detection, the far field noise prediction, such as aircraft wake vortex identification, detection and ranging, acoustic target forecasting in turbulent shear flow, acoustic measurement and sound source localization in wind tunnel test, etc. The nonlinear scattering phenomenon occurs when acoustic wave passes through the vortex, which is mainly related to the length-scale ratio between the wavelength of acoustic wave and the core radius of the vortex. In this paper, a plane acoustic wave passing through a stationary isentropic vortex is numerically simulated by solving a two-dimensional compressible, unsteady Euler equation. A sixth-order linear compact finite difference scheme is employed for spatial discretization. Time integration is performed by a four-stage fourth-order Runge-Kutta method. The eighth-order spatial compact filter scheme is adopted to suppress high frequency errors. At the far field boundaries, buffer layer is applied to handle the outgoing acoustic wave. Under the matching condition, the accuracy of the numerical results is verified by comparing with the previous direct numerical simulation results. The acoustic scattering cross-section method is introduced to analyze the effects of different length-scale ratio on the acoustic pulsation pressure, acoustic scattering effective sound pressure and acoustic scattering energy. Scattering occurs when sound waves pass through the vortex, the acoustic field in front of the vortex is basically unaffected, and the acoustic wave front remains intact. A “vacuum” region is formed slightly below the acoustic field directly behind the vortex, and two primary interference bands and several secondary interference bands are formed on the upper and lower sides of the vortex. As the length-scale ratio increases, the sound scattering decreases and the influence of the vortex flow field on the acoustic field gradually weakens. The influence region of effective sound pressure of acoustic scattering is mainly concentrated behind the vortex. With the increase of the length scale ratio, the influence gradually increases and extends to the upstream, and then the influence region gradually decreases to the vicinity of the vortex. When the length scale ratio is greater than or equal to 6, the location of the maximum effective sound pressure of sound scattering jumps from the upper right to the lower right of the vortex. The influence of acoustic wave wavelength change on the acoustic scattering energy can be divided into three parts. With the increase of the length scale ratio, the maximum sound scattering energy presents four different stages.Keywords: acoustic scattering /static isentropic vortex /acoustical scattering cross-section /length-scale ratio 全文HTML --> --> --> 1.引 言 旋涡对声波的散射问题是声波在复杂流场中传播的基本问题, 在声源定位、声目标识别及探测、远场噪声预测等方面具有重要的学术价值和工程应用价值, 在大气声学、水声学、气动声学中都有广泛应用, 如飞行器的尾涡识别、探测及测距, 湍流剪切流中声目标预测, 声学风洞试验中声学测量和声源定位等. 近场声源向远场辐射的声波须穿越以旋涡为主导的非均匀流场, 声波会发生折射、散射等现象, 统称为广义散射[1 ] .[2 ] 和Miles[3 ] 分别采用几何声学方法对声波穿过两种不同流速流体形成的交界面时发生反射、全反射、折射等现象进行了分析, 发现声波入射角、反射角以及折射角都与流体马赫数相关. 后来, Amiet[4 ,5 ] 和Schlinker[6 ] 发现平行剪切流动的厚度对声波穿过平行剪切流动的折射效应影响较小, 可以忽略, 并采用理论分析方法研究了声波穿过剪切层的折射特性, 给出了声波校正公式, 该公式已经成为现在风洞试验中普遍采用的噪声校正方法. 但Amiet等采用的是理想的平行剪切层, 与实际情况有着明显的偏差. 实际剪切层是一个随时空演化的涡层, 其强度、结构和厚度随时间和空间而变化. 随后很多****[7 -24 ] 尝试对其进行改进, 改进方式主要分为两种思路; 一是从传统声学方法和剪切层形成的多种因素(风速、扩张角、厚度、强度)入手来完善Amiet理论, 二是以Candel, Colonius为代表的****[15 , 16 ] 希望从旋涡声散射机理研究中找到剪切层修正的理论依据.[7 ] 采用线化欧拉方程(linearlised Euler equations[8 ] , LEE)计算了二维高斯脉冲声波穿过无厚度剪切层的声场, 并对Amiet理论进行了验证. 张军等[9 ] 通过声学风洞试验对比分析了4种不同剪切层修正方法, 发现当气流马赫数$ Ma\leqslant 0.3 $ , 测量角$ 40{°} \leqslant \varTheta_{n}\leqslant $ $ 140{°} $ 的条件下, 各种方法和Amiet[4 ,5 ] 方法对声波相位修正的精度误差小于1%. 张军等[10 ] 提出了一种适用于空间弯曲剪切层的三维剪切层相位修正方法, 扩展了剪切层相位修正的应用范围, 但是这类基于几何声学的修正方法只适用于高频声波. 倪章松等[11 ] 对开口风洞剪切层的参数影响和流场特性进行了深入研究, 发现开口风洞剪切层的轴向速度剖面强自相似. 王李璨等[12 -14 ] 采用LEE数值模拟了声波穿过自相似风洞剪切层的声场, 并对剪切层的厚度、扩张角和强度对声传播和声源定位进行了系统研究, 随后发展了一套三维剪切层修正方法, 并运用到了三维热射流剪切层中声波传播、声源定位与修正问题的研究中[14 ] . 但LEE方法有其自身的局限性, LEE忽略了背景流场与声波的非线性作用, 特别是在温度较高的热射流中可能会影响最终结果的精度.[15 ] 首次采用数值计算的手段研究了旋涡声散射问题, 数值求解了近似抛物方程, 并且提出对于声波穿过剪切层的研究应该以声波与单个旋涡相互作用的机制为基础. 1980年, Schlinker和Amiet[6 ] 对声波穿过剪切流动的散射效应进行了实验研究, 发现声波垂直于开口射流中心轴线时, 散射影响最小. 1994年, Colonius等[16 ] 采用数值模拟和声比拟理论, 系统研究了声波穿过旋涡的散射特征, 比较了观测位置和旋涡强度对声散射的影响, 指出了传统声比拟理论的局限性, 发现对于紧致涡, 声比拟理论是有效的, 而对于非紧致涡, 声比拟理论结果与DNS结果存在很大差异. 2004年, Symons等[17 ] 采用LEE模拟了低频声波在大气湍流中传播发生散射的现象, 但是缺乏对高频声波的声散射特性方面的研究. 文献[18 -21 ]采用点声源替代了经典的平面声波模型, 研究了Rankine涡对长波声散射的影响, 得到了与前人一致的结果. 2012年, Cheinet等[22 ] 采用二阶中心差分格式, 通过求解LEE数值模拟了声波穿过马赫数$ Ma \leqslant $ $ 0.125 $ 的涡流场. 但是为了获得高分辨率的散射声场, 二阶格式所需网格规模比高阶格式大很多. Ke等[23 ] 采用高阶WENO(weighted essentially non-oscillatory)格式数值模拟了声波穿过单个静止旋涡、静止旋涡对和运动旋涡对的情况, 发现当低频声波穿过低马赫数的涡流场时, 散射声场才满足随距离呈“$ 1/r $ ”衰减的规律. 最近, Clair和Gabard[24 ] 采用LEE研究了运动旋涡声散射的频谱展宽特性以及与波长的关系, 并采用Helmholtz数对声波与旋涡的尺度进行了分类, 但是关于声波波长与旋涡声散射的影响机制仍停留在定性关系.2.理论方法 22.1.控制方程 2.1.控制方程 大多数文献采用LEE求解旋涡声散射问题, 然而当声波波长远小于旋涡半径时, 声波与旋涡相互作用会产生非线性耦合效应, 此时LEE会失效. 本文采用二维Euler方程进行旋涡声散射计算, 其守恒形式为$ {\boldsymbol{U}} $ 为守恒变量, 具体形式为$ \rho $ 是流体介质密度, $ u $ 和$ v $ 分别是$ x $ 和$ y $ 方向上的速度分量, $ E $ 是单位体积的总能量, 定义为$ p $ 是流体介质的压强; $ \gamma $ 是比热比, 对于空气$ \gamma $ 的值可取为1.40; F G $ x $ 和$ y $ 方向的无黏流通矢量, 表达式为2.2.数值方法 -->2.2.数值方法 声学脉动量和流体动力学量之间数量级的差异很大, 一般在4个数量级以上[1 ] , 所以计算气动声学问题需要数值格式具有高精度、高分辨率、低色散和低耗散等特性. 本文采用六阶线性中心紧致格式[25 -27 ] , 具体形式为[25 ] , 具体形式为$ N = 4 $ , 详细参数可以参考文献[27 ].[28 ] , 具体形式为2.3.物理模型 -->2.3.物理模型 物理模型如图1 所示, 一个波长为$ \lambda $ 的平面声波从左往右穿越一个涡核半径为$ R_{\rm c} $ 的等熵涡, 在$ R_{\rm c} $ 处速度达到最大, 为$ U_0^* $ , 此时环量为$ \varGamma _0^{*} $ . 计算域包括物理域和缓冲层[29 ] . 其中, 物理域是边长为$ \max \left\{ {\left[ - 10 R_{\rm c} ,\; 10 R_{\rm c} \right], \;\left[ { - 5\lambda,\; 5\lambda } \right]} \right\} $ 的正方形区域. 缓冲层为图1 中灰色区域, $ x $ 方向宽度为$\max \big\{ 2.5\lambda, $ $ \; 99\Delta x \big\}$ . 另外半径为$ r $ 的虚线环线表示观测声散射环线.图 1 平面声波穿过旋涡的示意图Figure1. Schematic diagram of acoustic wave propagating through a vortex2.3.1.声波初始条件 -->2.3.1.声波初始条件 平面声波采用单频正弦形式, 无量纲形式为$ \rho _{\rm a} $ , $ u_{\rm a} $ , $ v_{\rm a} $ , $ p_{\rm a} $ 分别表示平面声波的密度脉动、$ x $ 方向速度分量、$ y $ 方向速度分量、脉动压强; $ \varepsilon $ 是声波幅值; $ \bar{\omega} $ 是角频率, 其定义为$ c_\infty $ 是声速, $ f $ 是声波频率, 定义为2.3.2.旋涡初始条件 -->2.3.2.旋涡初始条件 静止等熵涡[30 ,31 ] 的初始条件:$ \rho_\infty $ 、声速$ c_\infty $ 、压强$ p_\infty $ , 且满足$ {\rho_\infty} {c_\infty^{2}} = \gamma p_\infty $ , $ \gamma $ = 1.4. 旋涡强度为 $M_{\rm v} = U_0^{*} / c_\infty$ , $ r $ 是旋涡半径, 其定义为$\left( x_{\rm v}, y_{\rm v} \right)$ 是旋涡的中心.2.3.3.缓冲层 -->2.3.3.缓冲层 添加缓冲层是为了抑制边界处的声波反射和避免从边界外引入伪波, 保证物理域计算结果是纯净无污染的. 本问题中, 声波反射主要发生在出口边界处, 而入口边界和上、下边界处基本无反射, 故在出口边界处添加缓冲层, 其具体形式为$ x\left( i \right) $ 是$ x $ 方向网格节点$ i $ 上的坐标值, $ {x_{\rm out}} $ 是缓冲层开始处的坐标值, $ {L_x} $ 是$ x $ 方向边界处的坐标值. ${U_{\rm v}}$ 是旋涡流场的初始值, 是一个定常的空间分布量. 另外系数$ \sigma $ 的大小根据需要来选取, 一般取0.1.2.3.4.声散射计算方法 -->2.3.4.声散射计算方法 声波穿过旋涡发生散射, 散射的压强分量定义[23 ] 为$ p\left( {x, y, t} \right) $ 是声波与旋涡相互作用的瞬时流场压强. $ {p^{\rm a}}\left( {x, y, t} \right) $ 是对应声波在没有旋涡的自由空间中传播的瞬时脉动压强, 是一个随时间变化的非定常量. $ {p^{\rm v}}\left( {x, y, t} \right) $ 是对应旋涡(本文为静止等熵涡)的压强, 是一个确定的压强分布. $ {\bar p_{\rm sc}}\left( {x, y, t} \right) $ 是声波与旋涡相互作用发生散射的瞬时脉动压强. $ \varepsilon $ 是入射声波的幅值, ${p_{\rm sc}}\left( {x, y, t} \right)$ 是声波与旋涡相互作用发生散射的脉动压强$ {\bar p_{\rm sc}}\left( {x, y, t} \right) $ 与入射声波幅值$ \varepsilon $ 的比值, 即采用入射声波幅值$ \varepsilon $ 进行无量纲化.${p_{\rm rms}}$ 代表旋涡对声波散射的强弱, 定义[23 ] 为$ {\rm d}t $ 是计算时间步长, $ T $ 是统计总时间. 即, 在一个给定的时间$ T $ 内, 对散射瞬时压强 $ {p_{\rm sc}\left( {x, y, t} \right)} $ 的平方取时间平均的均方根值, 称之为散射有效声压$ {p_ {\rm rms}\left( {x, y} \right)} $ . 平面声波穿过旋涡发生散射达到周期性后开始进行数据统计, 为了减小随机性误差, 本文在流场达到周期性稳定后再记录20个周期来计算散射有效声压${p_ {\rm rms}}(x, y)$ .[16 ] 、Clair和Gabard[24 ] 的研究中, 仅采用某个固定半径处圆周上的散射有效声压$ {p_{\rm rms}\left( {x, y} \right)} $ 来表示散射的强弱以及空间分布情况, 难以直观地比较不同情况下的散射强度. 为了进一步比较分析不同声波波长对旋涡声散射的影响机制, 本文引入声散射截面(acoustical scattering cross-section, ASCS)方法[32 -34 ] . 声散射截面是一种分析声散射能谱的方法, 一般应用在三维流场结构或物体对声波的散射现象分析中, 例如声呐、水下遥测、海洋声学、声空化和医疗及工业超声波等. 为了分析二维旋涡声散射能谱, 其定义为$ r $ 的圆周上, 对散射有效声压${p_{\rm rms}}\left( {x, y} \right)$ 的平方进行积分, 得到该半径 $ r $ 圆周上的声散射能量.2.4.数值验证 -->2.4.数值验证 为了验证计算结果的可靠性, 本文采用Colonius等[16 ] 和Clair[24 ] 的算例进行数值计算, 并与文献数据进行对比验证.${c_\infty } = 1, \;{\rho _\infty } = 1, \;{{ {R}}_{\rm c}} = 1$ , 旋涡强度为$ {M_{\rm v}} = 0.125 $ , 平面声波波长$ \lambda = 4{R_{\rm c}} $ . 声学脉动量和流体力学量一般相差4—5个量级, 为了使平面声波处于线性扰动区, 声波压强幅值大小为$ \varepsilon = {10^{ - 5}}{p_\infty } $ . 为了保证旋涡计算的精细程度, 一般在一个旋涡核半径$ R_{\rm c} $ 之内有8—10个点; 为了保证平面声波的分辨率, 一个波长$ \lambda $ 之内有20个点, 故$ \Delta x = \Delta y = \min \left\{ {{{{R_{\rm c}}} / {10}},\; {\lambda / {20}}} \right\} $ . 当声散射稳定后, 开始统计声波脉动, 并持续20个周期, 时间步长满足$ c_\infty \Delta t / \Delta x = 0.1 $ .$ {M_{\rm v}} = 0.125 $ , 核半径$ {R_{\rm c}} = 1 $ 的静止等熵涡的初始分布情况如图2 所示.图 2 静止等熵涡初始分布 (a) 密度; (b) 速度; (c) 压强; (d) 涡量Figure2. Initial distribution of stationary isentropic vortices: (a) density; (b) velocity; (c)pressure; (d) vorticity.[16 ] 和Clair[24 ] 的结果对比如图3 所示. 数值计算结果与Clair[24 ] 和Colonius[16 ] 中结果符合很好. 这证明了本文数值计算结果的可靠性.图 3 散射有效声压在半径为$r = 8{R_{\rm c}}$ 圆周上的分布及其与文献[16 , 24 ]的对比Figure3. The distribution of root-mean-square pressure of scattered wave on a circle with radius $8 R_{\rm c}$ (comparison between numerical results and that of reference[16 , 24 ])3.数值结果与分析 为了更好地说明旋涡声散射与声波波长与旋涡半径的长度尺度比的关系, 定义声波波长与旋涡半径的长度尺度比为$r_{\rm L}$ ,$r_{\rm L}$ 的大小来研究声波波长对旋涡声散射的影响情况.3.1.脉动压强与声波波长的关系 3.1.脉动压强与声波波长的关系 研究声波脉动压强与长度尺度比$ r_{\rm L} $ 的变化情况, 可以更深入了解长度尺度比$ r_{\rm L} $ 对声场的影响情况. 声波脉动压强定义为$ \bar p'\left( {x, y, t} \right) $ 是声波与旋涡相互作用后, 减去旋涡背景流场后的声波脉动量, $ p'\left( {x, y, t} \right) $ 是将声波脉动量$ \bar p'\left( {x, y, t} \right) $ 与入射声波幅值$ \varepsilon $ 的比值.图4 给出了声波脉动压强云图随着长度尺度比$r_{\rm L}$ 大小的变化情况, 图中黑色圆表示旋涡的涡核位置情况, 声波脉动压强取值范围为$ \left[ -1.0, 1.0\right] $ . 从图4 可以看出, 当 $ r_{\rm{L}} = 0.1 $ 时, 旋涡左侧的声波脉动压强几乎没改变, 在旋涡右后方出现了大片“空白”的低脉动区域, 近似于没有声波的“真空地带”, 而声波被挤压到了“真空地带”的上下两侧, 在上方形成了一个三角区, 内部具有一定结构; 在下方形成了一条类似于压缩波的粗线. 当$ r_{\rm L} = 0.5 $ 和$ r_{\rm L} = 1.0 $ 时, 真空地带在逐渐减小, 上下两侧向内展开. 特别是当$ r_{\rm L} > 5.0 $ 时, 声波脉动压强几乎不发生改变, 波阵面呈初始的垂直于$ x $ 轴的直线. 因此, 随着长度尺度比$ r_{\rm L} $ 的增大, 旋涡流场对声场的影响逐渐减小.图 4 声波脉动压强随长度尺度比$r_{\rm L}$ 的变化云图 (a) $ r_{\rm L} = 0.1 $ ; (b) $ r_{\rm L} = 0.5 $ ; (c) $ r_{\rm L} = 1.0 $ ; (d) $ r_{\rm L} = 5.0 $ ; (e) $ r_{\rm L} = 10.0 $ ; (f) $ r_{\rm L} = 20.0 $ Figure4. The contour of the change of acoustic wave pressure with the length-scale ratio $ r_{\rm L} $ : (a) $ r_{\rm L} = 0.1 $ ; (b) $ r_{\rm L} = 0.5 $ ; (c)$ r_{\rm L} = 1.0 $ ; (d) $ r_{\rm L} = 5.0 $ ; (e) $ r_{\rm L} = 10.0 $ ; (f) $ r_{\rm L} = 20.0 $ .[35 ] . 平面声波波阵面穿过旋涡后, 由于旋涡的非均匀分布会在旋涡后方上下两侧形成两个主干涉条带和多个次级干涉条带, 且干涉条带整体形状呈半弧形, 这说明越靠近旋涡涡核, 散射越强. 本文中的旋涡均为逆时针旋转, 且当$ r_{\rm L} = 0.5 $ 和$ r_{\rm L} = 1.0 $ 时涡核内部的声波波阵面由竖直变为逆时针旋转了一个角度, 且从左向右, 角度逐步增大, 这也说明旋涡内的速度对声波波阵面产生了一定的偏折.3.2.散射有效声压与声波波长的关系 -->3.2.散射有效声压与声波波长的关系 图5 给出了散射有效声压$ p_{\rm rms} $ 随着长度尺度比$ r_{\rm L} $ 的变化情况, 图中黑色圆表示旋涡的涡核位置, 散射有效声压$ p_{\rm rms} $ 的取值范围为$ \left[ 0,\; 3.0 \right] $ . 从图5 可以看出, 声散射基本发生在旋涡右后方. 当$ r_{\rm L} = 0.1 $ 时, 在旋涡位置处有清晰的回纹结构, 并在右上方一定倾角处呈三角形排列着多个红色的“尖峰”. 当$ r_{\rm L} = 0.5 $ 和$ r_{\rm L} = 1.0 $ 时, 相比于$ r_{\rm L} = 0.1 $ , 旋涡附近结构消失了, 右上角只剩下一个减弱的红色“尖峰”, 位置更接近于旋涡边缘. 当$ r_{\rm L }= 5.0 $ 时, 红色“尖峰”包裹着旋涡正上方, 且在右下方也产生了另一个近似对称的红色“尖峰”, 后方的影响区域分开, 并向两侧扩展. 当$ r_{\rm L} = 10.0 $ 时, 红色“尖峰”进入到旋涡内侧且处于右下角, 并且影响区域呈蝴蝶状. 当$ r_{\rm L} = 20.0 $ 时, 影响区域再次大幅减小, 只在旋涡涡核位置还有微弱影响. 此外, 随着长度尺度比$ r_{\rm L} $ 的增大, 红色“尖峰”的值从2.5左右降到了0.1左右.图 5 散射有效声压$ p_{\rm rms} $ 随长度尺度比$ r_{\rm L} $ 的变化云图 (a) $ r_{\rm L} = 0.1 $ ; (b) $ r_{\rm L} = 0.5 $ ; (c) $ r_{\rm L} = 1.0 $ ; (d) $ r_{\rm L} = 5.0 $ ; (e) $r_{\rm L} = $ $ 10.0$ ; (f) $ r_{\rm L} = 20.0 $ Figure5. The contour of the change of the root-mean-square of scattering pressure with the length-scale ratio $ r_{\rm L} $ : (a) $ r_{\rm L} = 0.1 $ ; (b) $ r_{\rm L} = 0.5 $ ; (c) $ r_{\rm L} = 1.0 $ ; (d) $ r_{\rm L} = 5.0 $ ; (e) $ r_{\rm L} = 10.0 $ ; (f) $ r_{\rm L} = 20.0 $ .$ r_{\rm L} $ 的变化情况, 选取观测半径为$ r = 8 R_{\rm c} $ 圆周上的散射有效声压分布进行分析比较, 如图6 所示. 可以看出, 当$ r_{\rm L} = 0.1 $ 时存在多个波峰波谷, 随着长度尺度比$ r_{\rm L} $ 的增大, 波峰数量减少; 当$ r_{\rm L} = 4.0 $ 和$ r_{\rm L} = 5.0 $ 时, 角度在$ \left[ -90^ \circ, \;90^ \circ \right] $ 范围有两个高波峰, 角度在$ \left[ -180^ \circ, \;-90^ \circ \right] $ 和$ \left[ 90^ \circ,\; 180^ \circ \right] $ 范围内有两个即将突起的小波峰; 当$ r_{\rm L} = 10.0 $ 和$ r_{\rm L} = $ $ 20.0 $ 时, 直接出现4个不同高度的波峰, 并且随着长度尺度比$ r_{\rm L} $ 增大, $ \left[ -90^ \circ,\; 90^ \circ \right] $ 角度范围内的波峰高度逐渐减小, 而$ \left[ -180^ \circ,\; -90^ \circ \right] $ 和$ \left[ 90^ \circ,\; 180^ \circ \right] $ 范围内波峰高度逐渐增大. 另外, 峰值最高的两个波峰都在$ 0^ \circ $ 附近, 并且当$ r_{\rm L} = 0.1 $ 和$ r_{\rm L} = 0.5 $ 时最高波峰在$ 0^ \circ $ 右侧, 而$ r_{\rm L} > 1.0 $ 时最高波峰在$ 0^ \circ $ 左侧. 因此, 随着长度尺度比$ r_{\rm L} $ 增大, 最高波峰从$ 0^ \circ $ 右侧转变到左侧, 即最高波峰从旋涡右上方转变到了右下方(如图5 所示).图 6 散射有效声压在半径为$ r = 8 R_{\rm c} $ 圆周上的分布 (a) 全局图; (b) 局部放大图1; (c) 局部放大图2Figure6. The distribution of root-mean-square pressure of scattered wave on a circle with radius $ 8 R_{\rm c} $ : (a) Global; (b) zoomed 1; (c) zoomed 2.$ r_{\rm L} $ 的变化, 本文统计了散射有效声压最大值及其位置半径和角度随长度尺度比$ r_{\rm L} $ 的变化情况, 如图7 所示. 可以看出, 当$ {r_{\rm L}} \leqslant 1.0 $ 时, 散射有效声压最大值的大小及位置变化剧烈. 当$ {r_{\rm L}} > 1.0 $ 时, 散射有效声压最大值$p_{{\rm rms}\; {\rm max }}$ 逐渐减小, 如图7(a) 所示. 对于散射有效声压取最大值时的观测半径$ R $ , 当$ {r_{\rm L}} \in \left[ {1.0,\; 6.7} \right] $ 时, $ R\left( {p_{{\rm rms}{\rm max}}} \right) $ 在2.0左右; 当$ {r_{\rm L}} \geqslant 6.8 $ 时, $ R\left( {p_{{\rm rms}\;{\rm max}}} \right) $ 在0.5左右. 对于散射有效声压取最大值时位置点的角度$ \theta $ , 当$ {r_{\rm L}} \leqslant 5.9 $ 时, $ \theta \left( {p_{{\rm rms}\;{\rm max}}} \right) \in \left[ {{{20}^ \circ },\; {{60}^ \circ }} \right] $ ; 当${r_{\rm L}} \geqslant 6.0$ 时, $\theta \left( {p_{{\rm rms}\;{\rm max}}} \right) \in $ $ \left[ { - {{80}^ \circ },\; - {{40}^ \circ }} \right]$ , 并且当${r_{\rm L}} \geqslant 7.5$ 时, $\theta \left( {p_{{\rm rms}\;{\rm max}}} \right) = $ $ - {63.6^ \circ }$ 保持不变(如图5 中$r_{\rm L} = 10.0$ 和$ r_{\rm L} = 20.0 $ ).图 7 散射有效声压最大值随长度尺度比的变化曲线 (a) 散射有效声压最大值; (b) 散射有效声压最大值点的半径; (c) 散射有效声压最大值点的角度Figure7. The curve of the root-mean-square pressure of scattered wave with $r_{\rm L}$ value: (a) $ {p_{{\rm rms}\;{\rm max}}} $ ; (b) $ R\left({p_{{\rm rms}\;{\rm max}}} \right) $ ; (c) $ \theta \left( {p_{{\rm rms}\;{\rm max}}} \right) $ .3.3.声散射能量与声波波长的关系 -->3.3.声散射能量与声波波长的关系 本节采用声散射截面法计算了声散射能量随观测半径$ R $ 的变化情况, 结果如图8 所示. 可以看出, 当$ {r_{\rm L}} \in \left[ {0.1, \;5} \right] $ 时, 声散射截面$ \varSigma $ 的值随观测半径$ R $ 先增大, 后减小, 随后趋近于某个值保持不变. 特别是当$ {r_{\rm L}} = 0.1 $ 时, 声散射截面$\varSigma$ 在随观测半径$ R $ 增大过程中出现了两次小的波动(如图8(a) 所示), 第一次是近似正弦波动变化, 在$ R = 0.3 $ 处到达波峰, 随后在$ R = 0.4 $ 处到达波谷. 第二次是以$ R = 0.78 $ 为中心的近似立方抛物线增长的变化. 当$ {r_{\rm L}} = 0.2 $ 时, 总散射截面$\varSigma$ 在随观测半径$ R $ 增大过程中出现近似正弦波动变化(类似$ {r_{\rm L}} = 0.1 $ 的第一次波动), 在$ R = 0.66 $ 处到达波峰, 随后在$ R = 0.8 $ 处到达波谷. 当$ {r_{\rm L}} \in \left[ {6,\; 30} \right] $ 时, 总散射截面值$\varSigma \left( {R = 0.5} \right)$ 随着尺度比$ r_{\rm L} $ 的增大而增大, 原来$\varSigma \left( {R = 2.0} \right)$ 左右处的峰值随着尺度比$ r_{\rm L} $ 的增大而减小(如图8(c) 所示), 并且在 $ r_{\rm L} = 10.0 $ , $ r_{\rm L} = 20.0 $ 和$ r_{\rm L} = 30.0 $ 时, 总散射截面峰值$\varSigma \left( {R = 0.5} \right)$ 呈平方倍数增长.图 8 声散射能量$ \varSigma $ 随观测半径$ R $ 的变化曲线 (a) $r_{\rm L} \in $ $ \left ( 0.1, \, 1.0 \right)$ ; (b) $ r_{\rm L} \in \left ( 2.0, \, 5.0 \right) $ ; (c) $ r_{\rm L} \in \left ( 6.0, \, 30.0 \right) $ Figure8. The curve of acoustical scattering cross-section with observed radius: (a) $ r_{\rm L} \in \left ( 0.1, \, 1.0 \right) $ ; (b) $ r_{\rm L} \in \left ( 2.0, \, 5.0 \right) $ ; (c) $ r_{\rm L} \in \left ( 6.0, \, 30.0 \right) $ .图8 中每条曲线的峰值$\varSigma_ {\max}$ 及所在的观测半径$ R $ 与长度尺度比$ r_{\rm L} $ 的变化关系, 如图9 所示. 在文献[15 -23 ]中, 声波散射随着波长的增大而减小, 但我们的计算中高频声波与旋涡的相互作用具有较强非线性. 随着长度尺度比$ r_{\rm L} $ 的增大, 散射截面最大值$\varSigma_{\max}$ 的变化情况呈现了4个阶段的变化(如图9(a) 中的I, II, III, IV4个阶段), 采用分段有理函数拟合, 得到:图 9 声散射能量随尺度比的变化曲线 (a) $\varSigma_{\max }$ ; (b) $R\left(\varSigma_{\max }\right )$ Figure9. The curve of acoustical scattering cross-section with $ r_{\rm L} $ value: (a) $\varSigma_{\max }$ ; (b) $R\left( \varSigma_{\max }\right )$ .$ y_i (i = 1, 2, 3, 4) $ 表示声散射截面最大值$\varSigma_{\rm max}$ , $ x $ 表示长度尺度比$ r_{\rm L} $ . 图9(a) 中黑色圆点表示数值计算结果, 红色曲线是上述4条分段拟合曲线. 从图9(a) 可以看出, 拟合曲线与数值计算结果完全符合.23 )式可以看出, 在第I阶段, 散射截面最大值$\varSigma_{\max}$ 与长度尺度比$ r_{\rm L} $ 立方的倒数成正比; 在第II, III, IV阶段, 散射截面最大值$\varSigma_{\max}$ 与长度尺度比$ r_{\rm L} $ 平方的倒数成正比, 如下式:图9(b) 给出了散射能量在不同长度尺度比$ {r_{\rm L}} $ 中取最大值时的观测半径$ R $ , 其随着长度尺度比$ {r_{\rm L}} $ 的变化情况. 当${r_{\rm L}} \leqslant 1.25$ 时, 观测半径$ R $ 出现了图9(a) 中类似的波动, 但并不是直接相关; 当$ {r_{\rm L}} \in \left[ {1.25, \;9.6} \right] $ 时, 观测半径$ R $ 基本在2.2附近; 当${r_{\rm L}} \geqslant 9.7$ 时, 观测半径$ R $ 直接跳到了0.5处. 这是由于总散射截面值$\varSigma \left( {R = 0.5} \right)$ 处在逐渐增大, 恰好在观测半径$R = $ $ 9.7$ 处超过总散射截面值$\varSigma \left( {R = 2.3} \right)$ , 与图8(c) 的结果一致.3.4.物理机理的初步讨论 -->3.4.物理机理的初步讨论 根据吴介之[35 ,36 ] 关于波涡相互作用的研究结果, “波与涡之所以能相互作用, 是因为涡中本来就有波, 或者有形成波的条件. 换言之, 波涡相互作用的核心是涡流中不稳定波的受迫激发和入射波与不稳定波之间的耦合”. 声波是一种纵波, 对外的表现为膨胀过程, 对流场而言, 则是一种微弱的强迫扰动. 因此平面声波从开始接触到穿越旋涡的整个过程, 入射声波刺激旋涡向外辐射不稳定波. 不稳定波与入射声波会发生线性叠加和非线性耦合两种作用, 最终表现为散射波形态, 如图4 中的干涉条带.图4 所示. 特别是声波波长越小, 在旋涡涡核内声波波数越多, 如图4(a) —(c) 中有多个声波, 而图4(d) —(f) 中一个整周期声波都没有. 另外声波以声速传播, 相同时间传播的距离是一个常值, 波长越小, 单位时间通过旋涡的整周期声波越多, 如图10 所示.图 10 声波幅值随时间的变化曲线Figure10. The variation of acoustic wave amplitude with time$ \lambda = 1, 2, 4 $ )穿过涡核半径为1的旋涡, 得到散射压强分布, 如图11 所示. 长度为4时, 具有4个$ \lambda = 1 $ 的完整波形, 2个$ \lambda = 2 $ 的完整波形, 1个$ \lambda = 4 $ 的完整波形. 从图11 可以看出, 当$ \lambda = 1 $ 时, 声散射压强最强; 即相同时间情况下, 波长越小, 声波穿过旋涡后的散射压强越大.图 11 声散射压强云图 (a) $ \lambda = 1 $ ; (b) $ \lambda = 2 $ ; (c) $ \lambda = 4 $ Figure11. The contour of sound scattering pressure: (a) $ \lambda = 1 $ ; (b) $ \lambda = 2 $ ; (c) $ \lambda = 4 $ .$ \bar{\omega} = 2\pi c_\infty /\lambda $ 越大, 声波幅值变化越快, 即作用在旋涡的强迫扰动变化越快, 受激辐射的不稳定波也越强. 然而, 波长越小, 单个波长的声波波阵面越容易被破坏, 如图4(a) 中涡核内部的波阵面直接断裂向后偏移, 而图4(b) 和图4(c) 涡核内部声波波阵面仅仅是偏折一定角度. 此时强不稳定波与结构遭到破坏的波阵面在向后传播的过程中, 发生了强非线性作用, 使得后方的干涉条带向两侧偏折角度大, 直接导致旋涡正后方的空白区域, 且产生很多细小的结构, 如图4(a) 中旋涡后方的散射图像. 总的来说, 声波波长越小, 旋涡受激产生的不稳定波越强, 声波波阵面越容易被旋涡破坏, 随后二者的强非线性作用导致旋涡后方的散射图像越复杂. 如图4 所示, 当声波波长逐渐增大, 涡核内部声波波阵面从断裂到偏折角度, 直至未发生改变, 对应着旋涡后方干涉条带从两侧逐渐向内靠拢, 直到后面未发生改变.图5(a) —(d) ), 波动持续最强的空间点处于旋涡涡核后方, 且波长越大, 越靠近涡核边界. 当声波波长较大时(如图5(e) 和图5(f) ), 波动持续最强的空间点处于涡核内部右下方. 详细分布可以参考图7(b) , 当$r_{\rm L} \geqslant 6.8 \approx 2.2 \pi$ 时, 声波与旋涡相互作用最强是在旋涡$ 0.5 R_{\rm c} $ 处; 当$r_{\rm L} \geqslant 1.0$ 时, 声波与旋涡相互作用最强是在旋涡$ 2 R_{\rm c} $ 处;当$ r_{\rm L} < 1.0 $ 时, 声波波阵面的破坏程度不一, 形成细小结构与强不稳定的非线性作用, 无法形成一个近似稳定的最强相互作用区间, 所以最强相互作用点在来回振荡.图9 所示), 但当$r_{\rm L} < 1.0$ 时内部反复振荡, 同散射有效声压的变化类似, 当然具体的物理机理还需要进一步的研究阐释.4.结 论 本文对正弦声波与静止等熵涡相互作用进行了数值模拟. 通过改变旋涡左侧入射声波的波长, 研究了不同波长的声波对旋涡声散射的影响规律, 得到了以下结论.${r_{\rm L}} \geqslant 6$ 时, 声散射有效声压最大处位置从旋涡右上方跳转到右下方.$ {r_{\rm L}} \in \left[ {0.3, 6} \right] $ 时, 声散射能量随观测半径的增大, 先增大, 再减小, 最后基本保持不变; 当长度尺度比$ {r_{\rm L}} < 0.3 $ 时, 在声散射能量增大的过程中还有一定的波动; 当长度尺度比 $ {r_{\rm L}} > 6 $ 时, 在观测半径$ R = 0.5 $ 处声散射能量与长度尺度比呈平方增长, 而观测半径$ R = 2 $ 左右处声散射能量逐渐下降. 声散射能量最大值随长度尺度比的增大, 呈现出4个不同阶段. 
































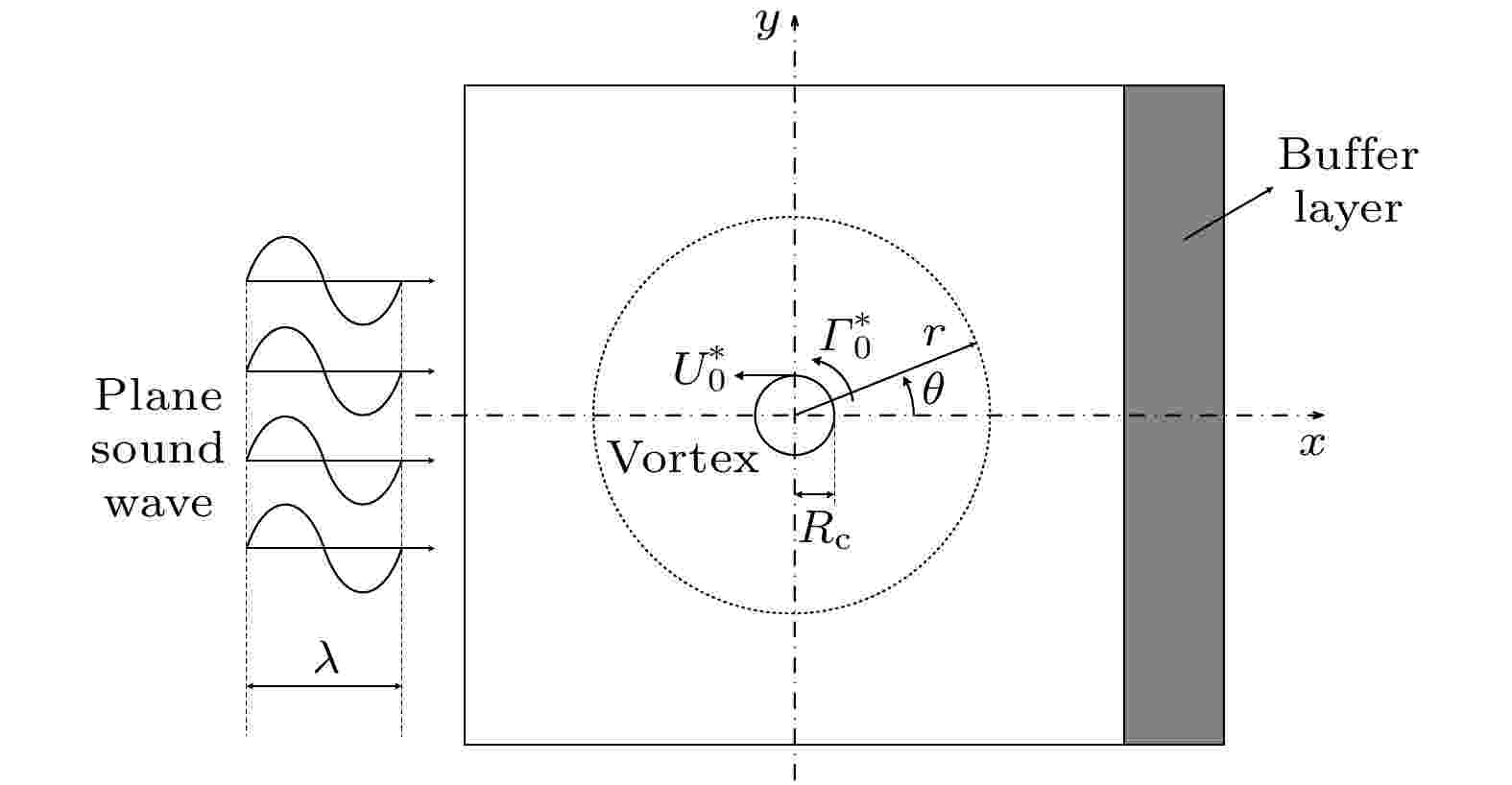 图 1 平面声波穿过旋涡的示意图
图 1 平面声波穿过旋涡的示意图





































































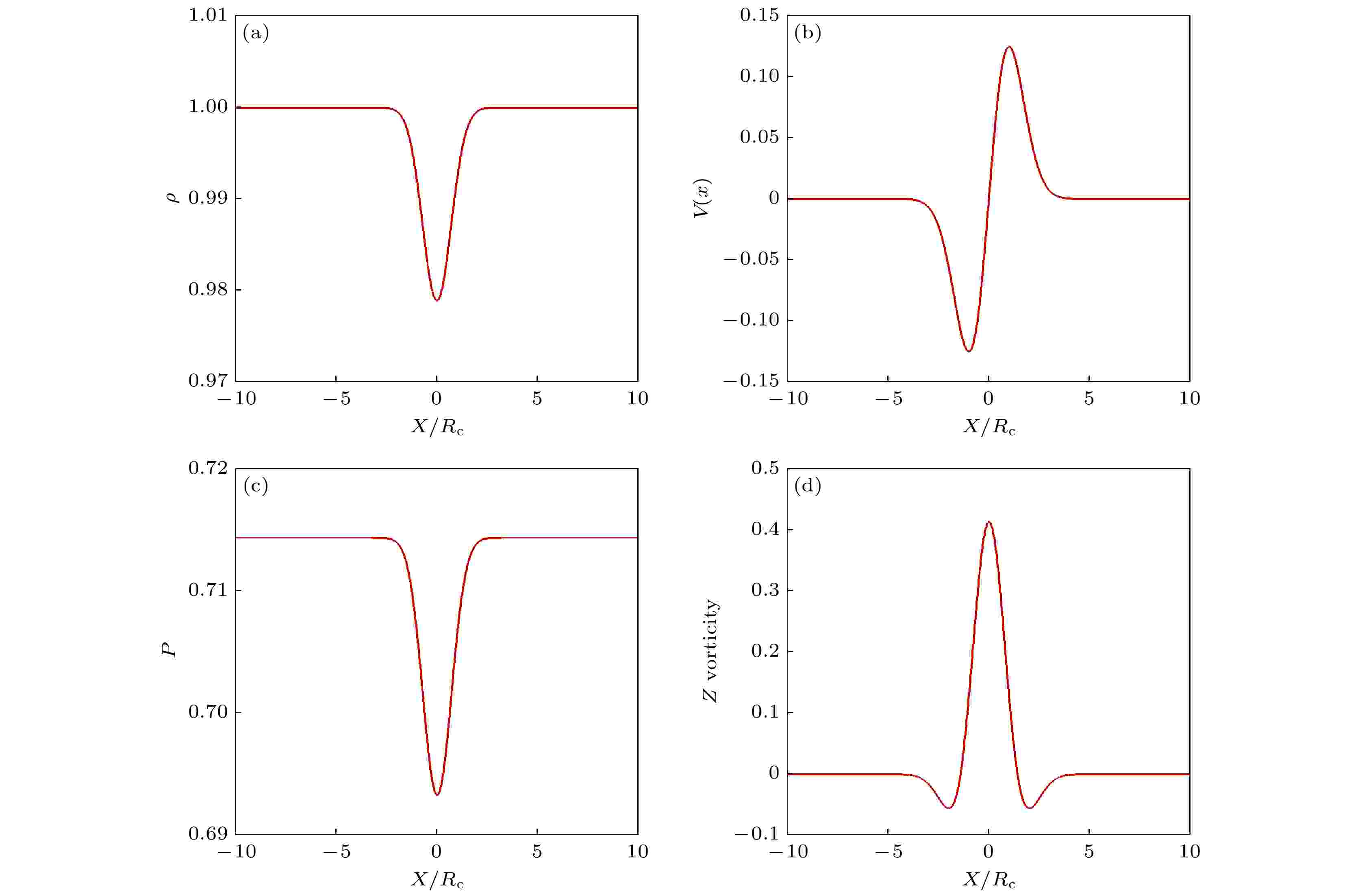 图 2 静止等熵涡初始分布 (a) 密度; (b) 速度; (c) 压强; (d) 涡量
图 2 静止等熵涡初始分布 (a) 密度; (b) 速度; (c) 压强; (d) 涡量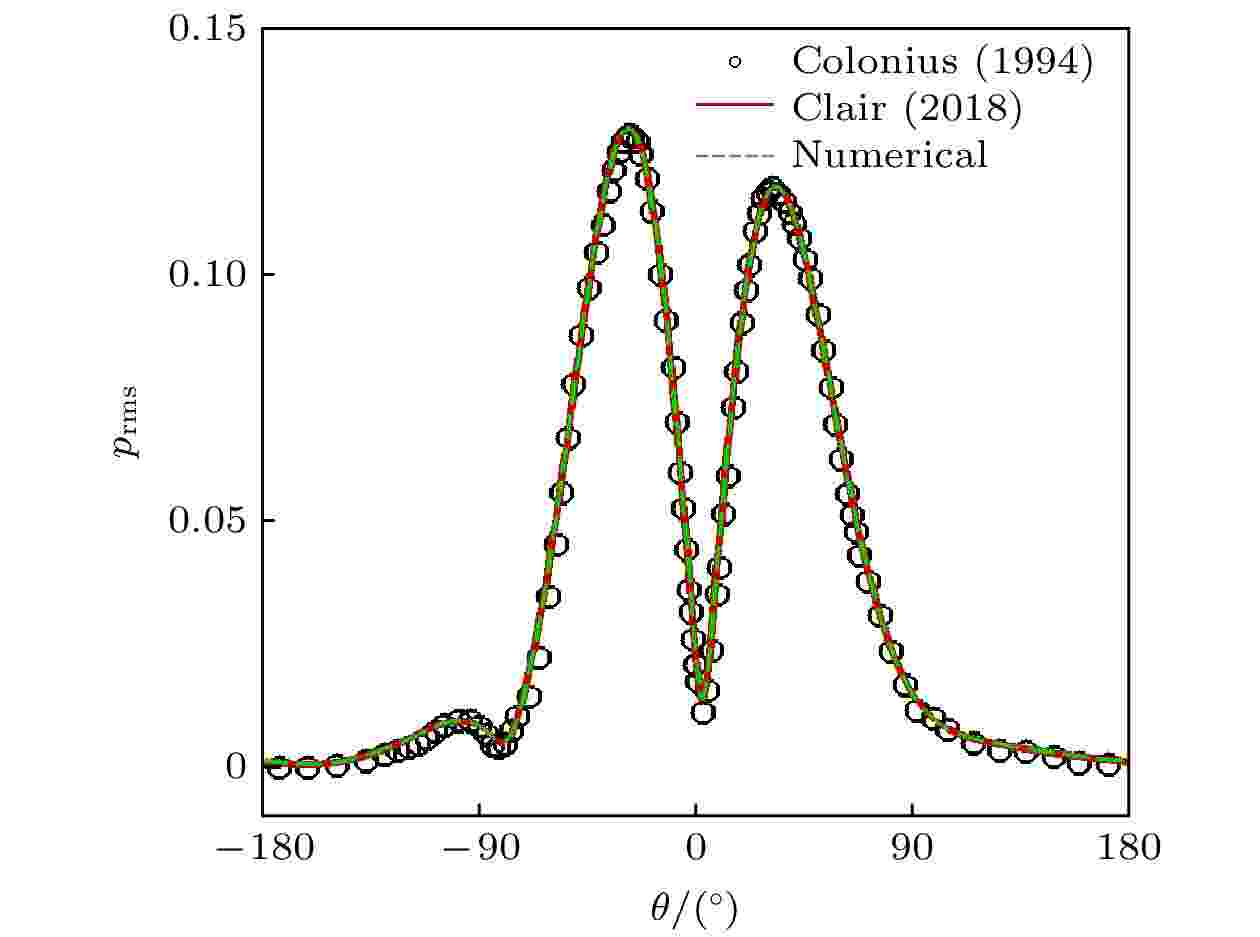 图 3 散射有效声压在半径为
图 3 散射有效声压在半径为





















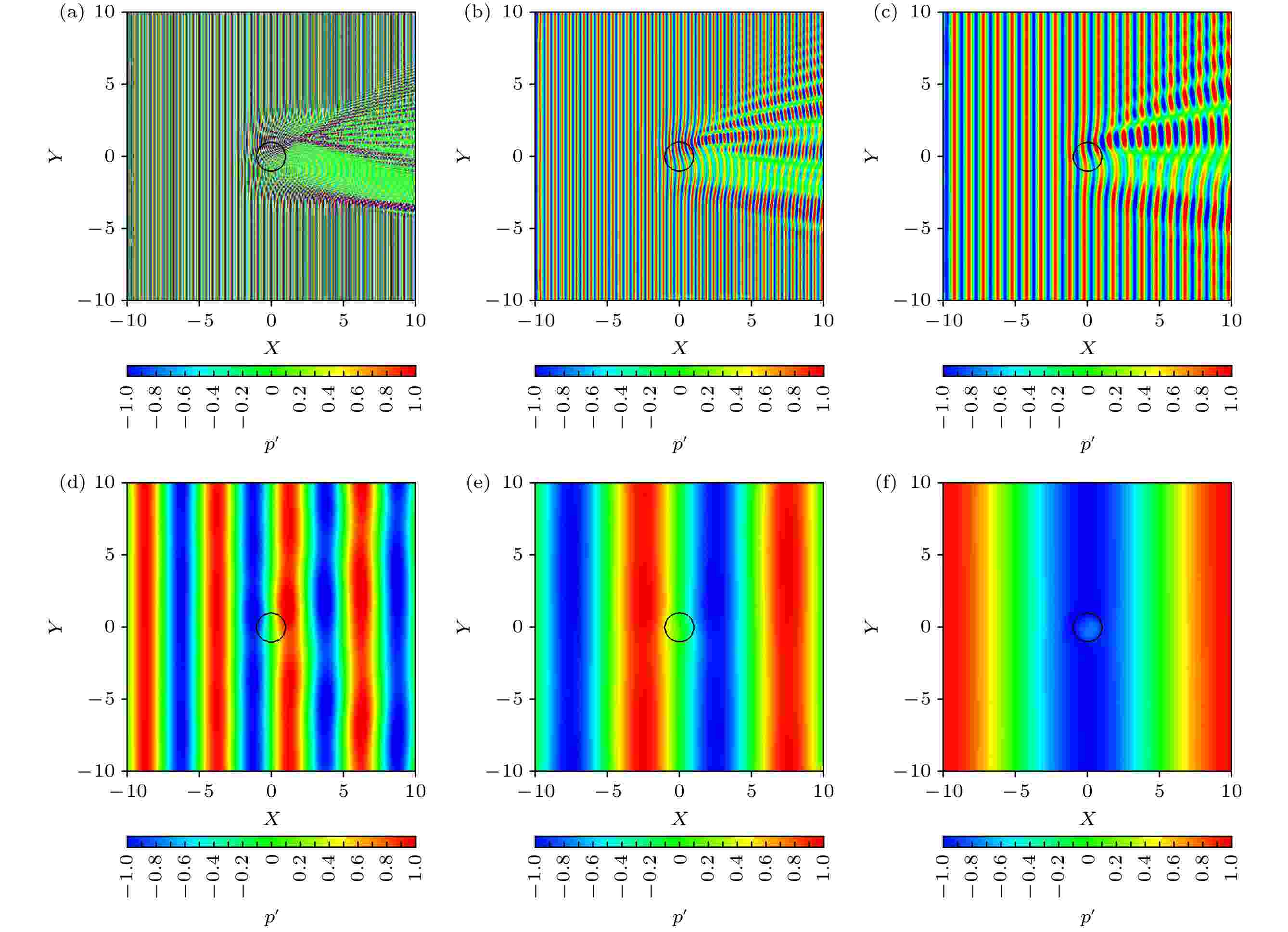 图 4 声波脉动压强随长度尺度比
图 4 声波脉动压强随长度尺度比

































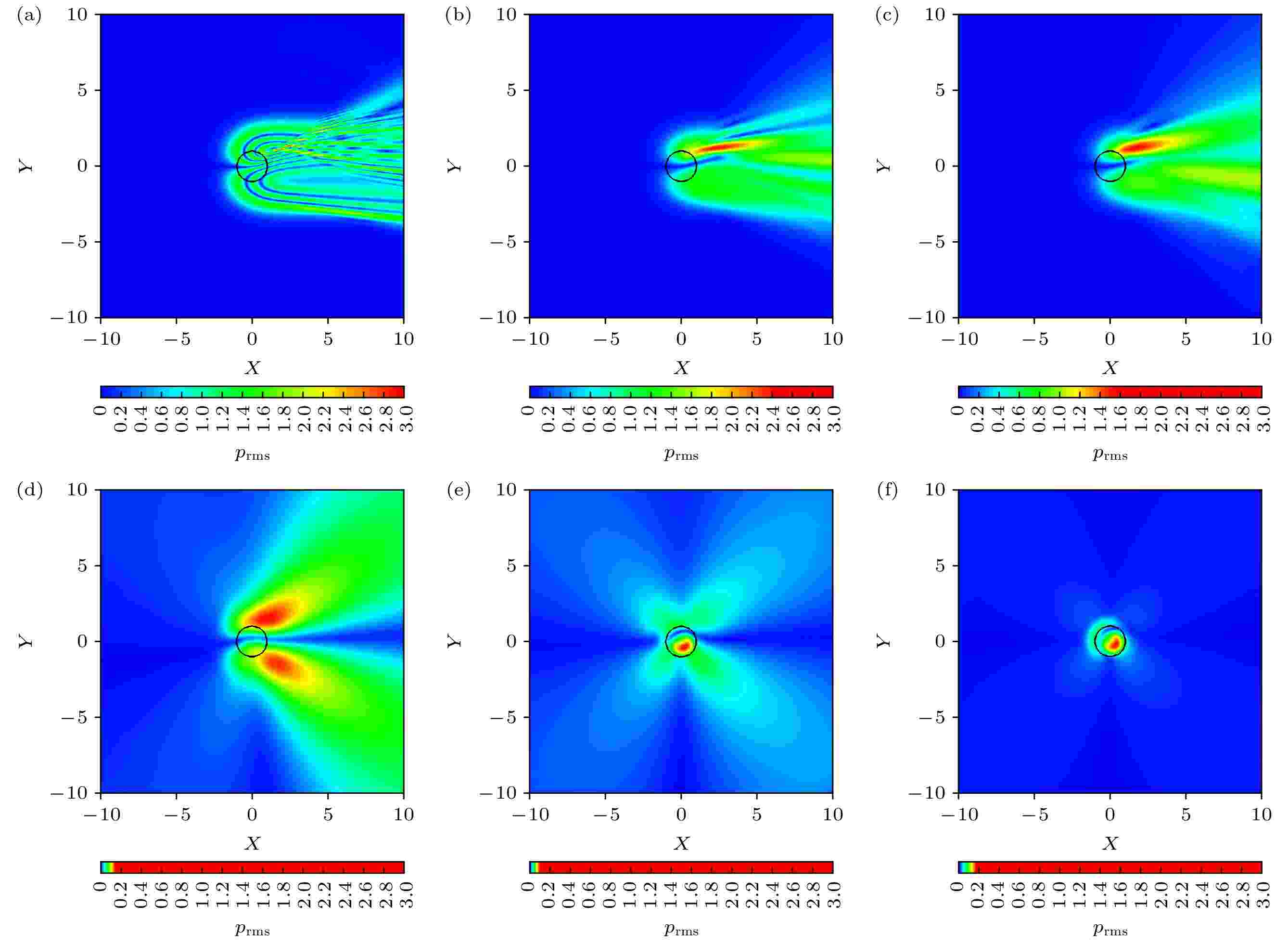 图 5 散射有效声压
图 5 散射有效声压



































































 图 6 散射有效声压在半径为
图 6 散射有效声压在半径为
























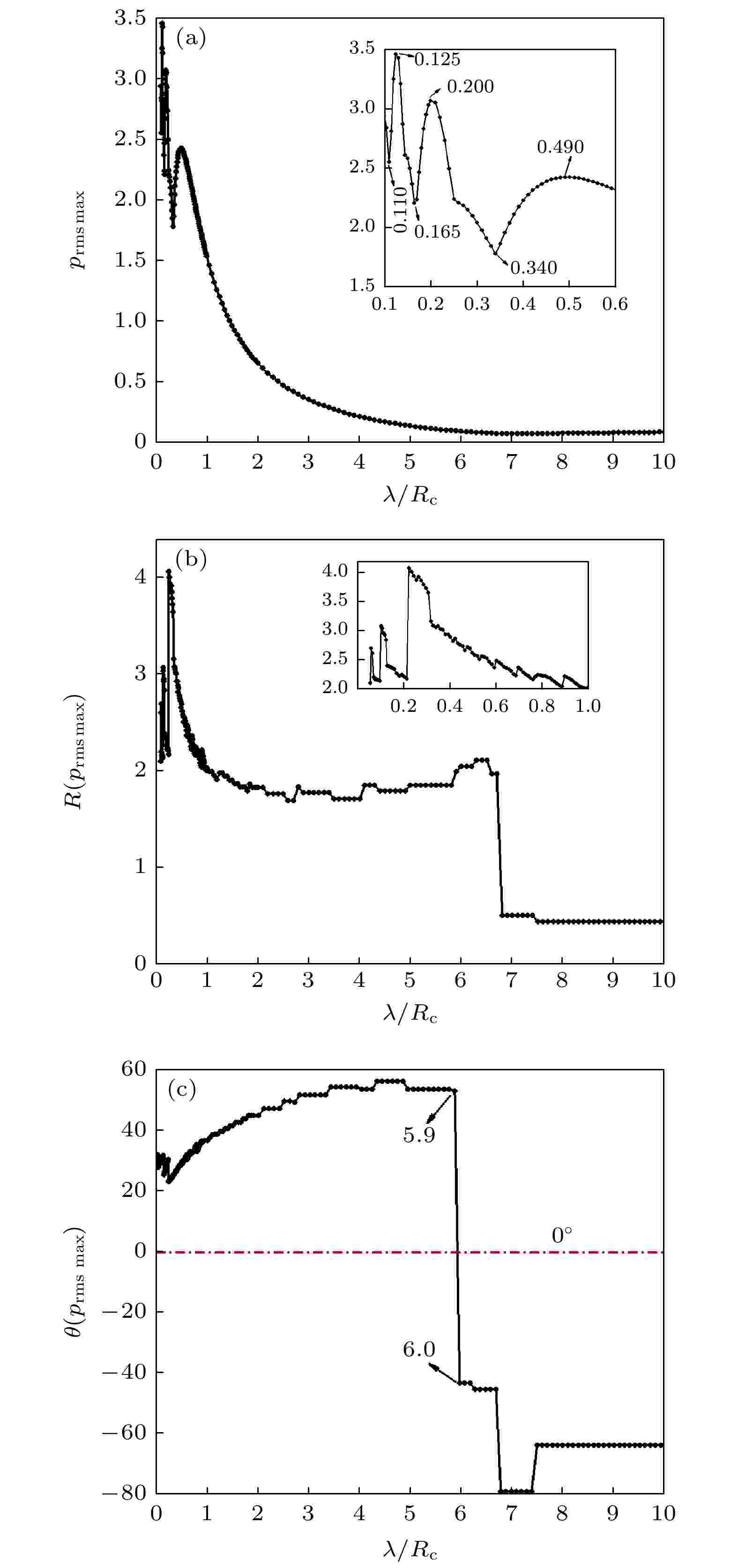 图 7 散射有效声压最大值随长度尺度比的变化曲线 (a) 散射有效声压最大值; (b) 散射有效声压最大值点的半径; (c) 散射有效声压最大值点的角度
图 7 散射有效声压最大值随长度尺度比的变化曲线 (a) 散射有效声压最大值; (b) 散射有效声压最大值点的半径; (c) 散射有效声压最大值点的角度
















































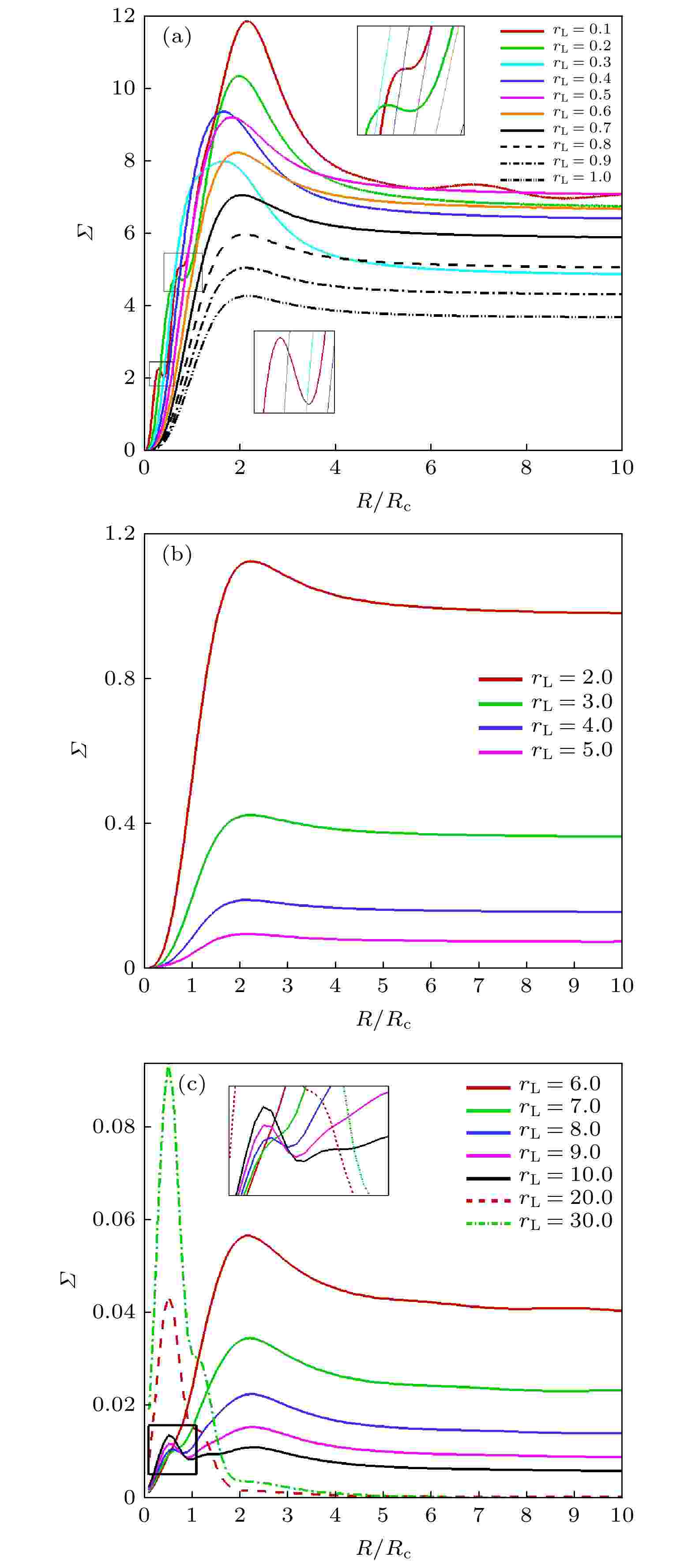 图 8 声散射能量
图 8 声散射能量















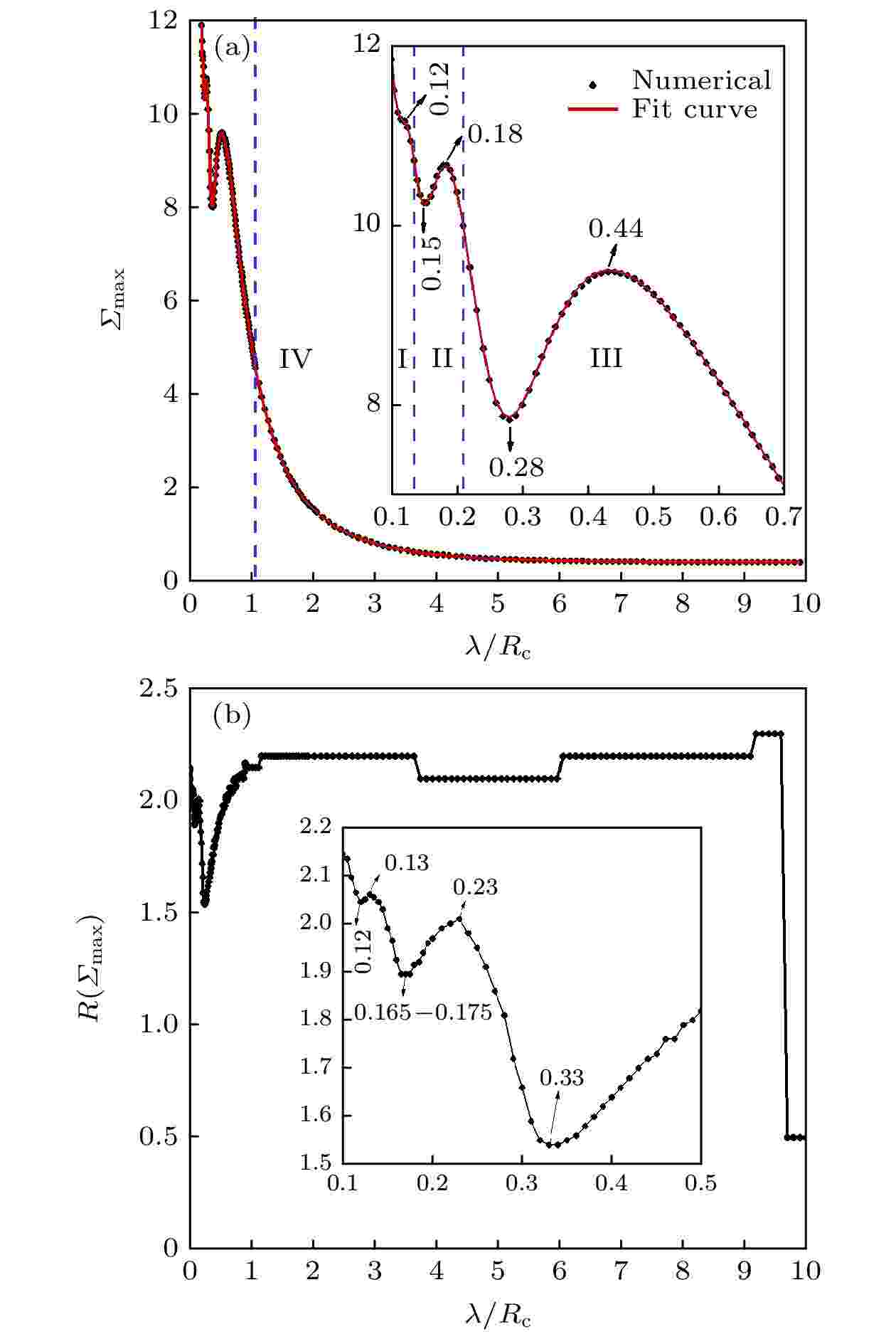 图 9 声散射能量随尺度比的变化曲线 (a)
图 9 声散射能量随尺度比的变化曲线 (a) 











































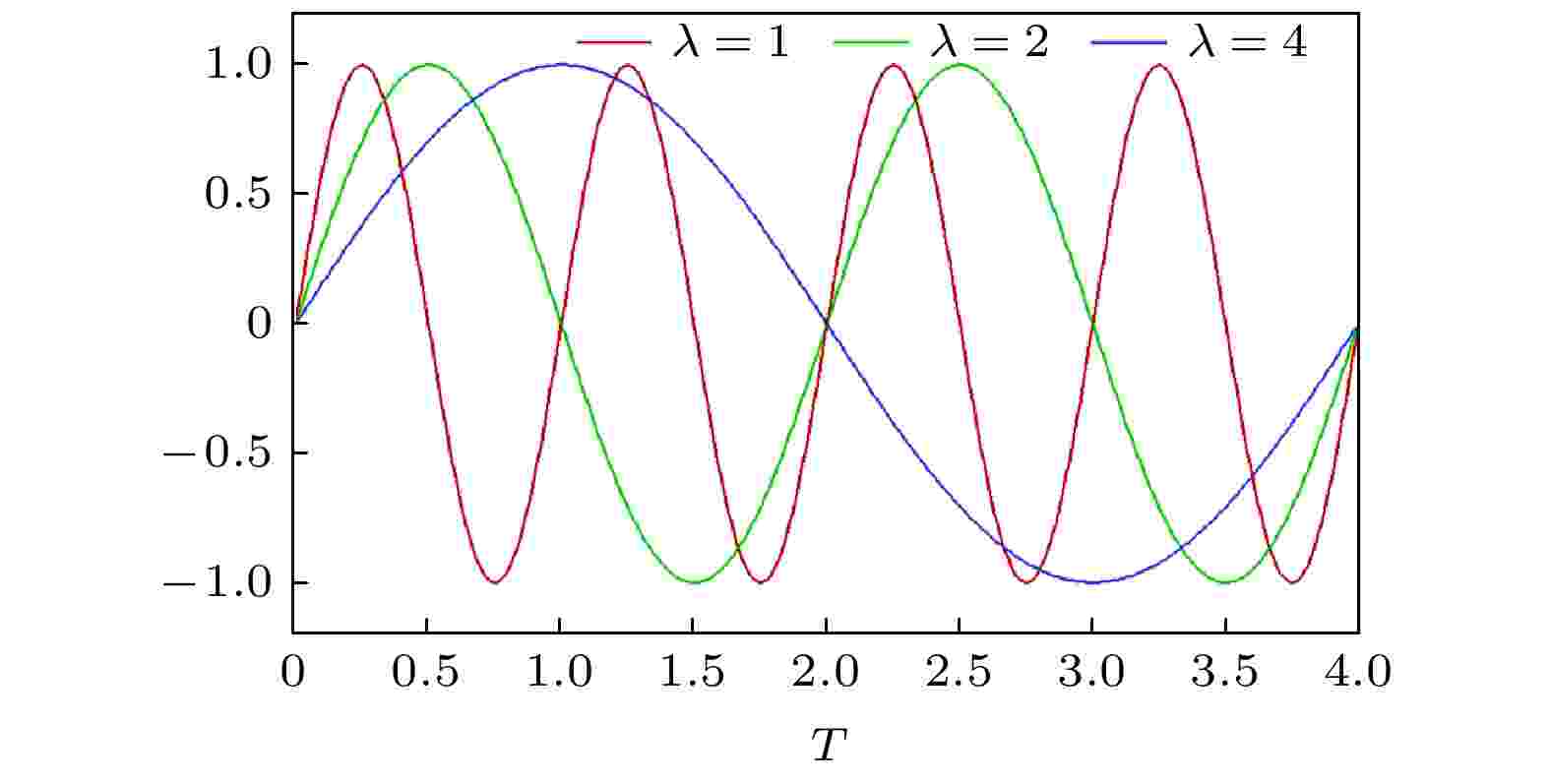 图 10 声波幅值随时间的变化曲线
图 10 声波幅值随时间的变化曲线






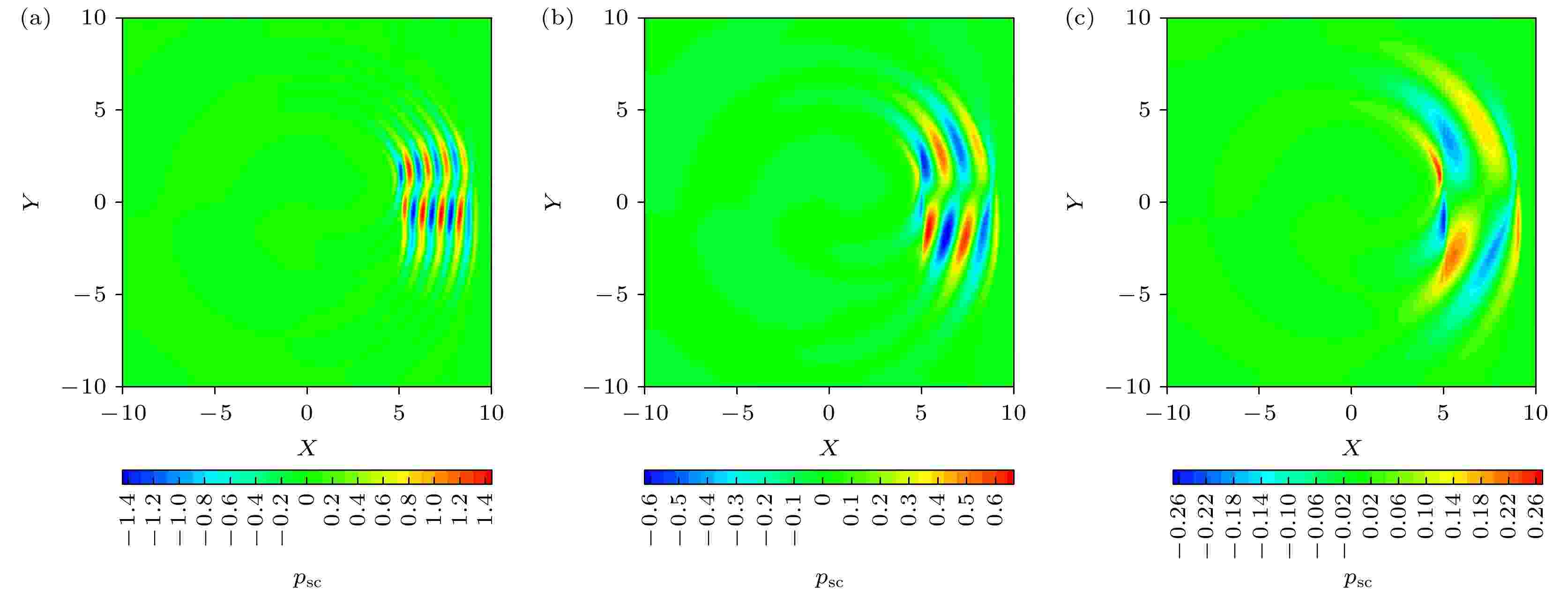 图 11 声散射压强云图 (a)
图 11 声散射压强云图 (a) 


















