摘要:辐射冲击波波后物质具有辐射属性, 它通过扰动界面引起的Richtmyer-Meshkov(RM)不稳定性的增长有别于通常的冲击波. 在高功率激光装置上开展冲击波波后辐射效应对界面不稳定性增长影响的实验研究, 认识波后辐射对界面增长的影响过程及规律, 有助于提高高能量密度条件下RM不稳定性演化规律的认识水平及预测能力. 基于神光III原型高功率激光装置, 设计并开展了两种激光驱动条件下的界面流体力学不稳定性实验, 研究波后辐射效应对界面RM不稳定性增长的影响. 实验中在较高功率密度驱动条件下CHBr扰动样品未见明显的扰动增长, 结合模拟分析发现较高功率密度条件下辐射前驱波波阵面和冲击波波阵面明显分离, 辐射前驱波在冲击波到达扰动界面前烧蚀扰动界面, 改变了界面的初始状态, 界面不稳定性增长过程中密度梯度的增大和界面Atwood数的减小抑制了界面RM不稳定性的增长.
关键词: 辐射冲击波/
Richtmyer-Meshkov不稳定性/
密度梯度尺度/
烧蚀速度/
Atwood数

English Abstract

全文HTML

--> --> -->

辐射冲击波条件下的界面流体力学不稳定性现象普遍存在于天体物理中, 例如超新星爆发、超新星遗迹、原恒星的吸积与生长等^[1-3]. 在超新星爆发过程中产生的向外运动的高速冲击波具有辐射属性, 会改变冲击波的结构, 进而影响冲击波过界面时引发的界面Richtmyer-Meshkov(RM)不稳定性的发展^[4,5]. 在惯性约束聚变中, 同样存在辐射冲击波条件下的界面RM不稳定性增长现象^[6,7], 例如冲击波在通过双壳层点火靶的泡沫层时具有辐射属性, 它会影响界面处的RM不稳定性增长. 因此, 在高功率激光装置上开展冲击波波后辐射属性对RM不稳定性增长影响的实验研究, 认识波后辐射对界面增长的影响过程及规律, 有助于提高极端条件下流体演化规律的认识水平及预测能力.
基于高功率激光装置, 国际上开展了少量的辐射冲击波物理研究工作, 辐射冲击波的产生会加速能量的损失, 从而改变冲击波的速度和强度, 目前主要工作集中于辐射冲击波的产生和结构测量方面, 例如测量辐射冲击波的温度、速度及辐射前驱波的电子密度和速度等. 由于驱动能量的限制, 现阶段实验研究材料以气体材料为主, 例如Xe气^[8-15], 而在固体材料研究方面的工作则相对开展较少^[16]. 随着美国国家点火装置(NIF)的投入使用, 激光输出能量提升至1.8 MJ, 在NIF装置上开展的球几何内爆实验中, CH材料中冲击波速度可达约300 km/s, 因此可研究辐射冲击波对CH材料状态方程和密度分布的影响^[7,17]. 在辐射冲击波对界面不稳定性增长影响研究方面, 相关工作正处于起步阶段, 2018年Huntington等^[18]和Kuranz等^[19]在NIF装置上开展了间接驱动条件下爆炸波(blast wave)引起的界面不稳定性增长研究, 实验中爆炸波进入低密度泡沫材料后产生的辐射效应抑制了减速阶段的界面Rayleigh-Taylor (RT)不稳定性增长. NIF装置上实验采用间接驱动的方式, 具有驱动源均匀、驱动尺度大的优点, 但在输出能量相对较小的激光装置上, 则很难采用间接驱动的方式在固体材料中产生辐射冲击波.
前述NIF装置上的界面不稳定性实验中, 冲击波从高密度材料进入低密度泡沫材料, 因此实验研究的是波后辐射效应对正在发生的减速阶段界面RT不稳定性增长的影响. 在天体物理现象或者惯性约束聚变研究中, 辐射冲击波形成后, 波后辐射向各方向传播, 不仅作用于已经发生流体力学不稳定性增长的扰动界面, 还会辐射烧蚀冲击波未传播到的扰动界面, 影响后续冲击波通过界面后的RM不稳定性增长, 目前这部分相关工作尚未见公开报道. 本工作基于神光Ⅲ原型装置的驱动能力, 把扰动样品置于低密度泡沫之后, 研究波后辐射效应造成的界面初始状态的改变对随后界面发生的RM不稳定性增长的影响.

RM不稳定性是冲击波加速两种不同密度流体导致的界面失稳现象. 不管是冲击波从低密度流体到高密度流体, 还是冲击波从高密度流体到低密度流体, 都会产生RM不稳定性. RM不稳定性的增长的来源是冲击波通过扰动界面时的涡量沉积. 在流体运动过程中, 涡量场的变化为涡量动力学方程所制约, 斜压粘性流体的涡动力学方程可表示为^[20,21]

$ \frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = (\omega \cdot \nabla )v - \omega (\nabla \cdot v) + \frac{1}{{{\rho ^2}}}\nabla \rho \times \nabla p + \upsilon {\nabla ^2}\omega, $

其中υ是黏性; ω表示涡量, (1)式称作弗里德曼-赫姆霍兹方程. 式中右边第三项表示斜压流体产生的涡量, 这个涡量的存在引起了界面的RM不稳定性增长. Richtmyer将冲击波加速界面近似看作瞬时加速过程, 并认为波后流体不可压, 根据RT不稳定性的线性不可压理论, 得到了RM不稳定性线性增长公式:^[22]

$ \frac{{{\rm{d}}\eta }}{{{\rm{d}}t}} = {A^*}Uk\eta _0^*,~~ A > 0, $

其中U表示界面的运动速度; k表示扰动波数; A^*和$ \eta _0^* $表和示冲击波通过扰动界面后的界面扰动幅值和Atwood数, Atwood数A = (ρ₂–ρ₁)/(ρ₂ + ρ₁), ρ₁, ρ₂分别表示扰动界面两侧的密度. 根据(2)式可知RM不稳定性的增长与Atwood数、初始扰动幅值和界面运动速度密切相关. Atwood数由界面两侧的密度决定, 因此界面两侧的密度变化会影响RM不稳定性的增长.

为了研究冲击波后辐射效应对界面RM不稳定性增长的影响, 首先要在材料中产生具有辐射属性的冲击波. 当冲击波强度和波后物质温度足够高, 波后物质产生的辐射能流与进入波后物质的能流接近时, 冲击波将转变为辐射冲击波. 冲击波波后物质产生的辐射能流与进入波后物质的能流比值可表示为^[3]

$ R = \frac{{U_{\rm{s}}^5}}{\rho }\sigma {\left( {\frac{1}{{{k_{\rm{B}}}}}\frac{{A{m_{\rm{p}}}}}{{1 + z}}\frac{{2\left( {\gamma - 1} \right)}}{{{{\left( {\gamma + 1} \right)}^2}}}} \right)^4}, $

其中U_s是冲击波速度; A是平均原子质量; k_B是Boltzmann常数; m_p是质子质量; γ为冲击波波后材料的多方系数. 随着R值的增大, 波后辐射效应逐渐增强.
由(3)式可知高原子序数、低密度材料较易产生具有辐射属性的冲击波. Reighard等^[8]和Chantal等^[9]分别在Omega和PALS激光装置上进行了Xe气辐射冲击特性实验研究, 确认了当冲击波速度达到几十km/s时, 即可产生辐射冲击波. Xe气虽然对激光驱动能力要求较低, 但对高功率激光实验所需的微靶制备能力要求较高, Xe气需密封在激波管内, 存在密封保气问题. 2018年NIF装置上开展的辐射冲击波条件下的界面不稳定性实验采用SiO₂泡沫作为产生辐射冲击波的材料, 它的优点为SiO₂泡沫是固体材料, 便于加工, 不存在漏气的问题, 不利之处是与Xe气相比, 原子序数相对较低, 密度较高, 冲击波速度需要在150 km/s以上才能产生明显的辐射效应^[4,18]. 对于CH泡沫材料, 由于其原子序数更低, 需要冲击波速度达到200 km/s以上才能产生辐射效应. 结合目前具备的制靶能力, 现阶段采用固体材料作为辐射冲击波的产生材料.
本文采用一维辐射流体力学程序Multi-1D模拟泡沫材料中的冲击波速度, 评估神光Ⅲ原型装置是否能产生辐射冲击波. 神光Ⅲ原型装置具有八束驱动激光束, 上、下各四束激光以45o倾角的方式注入靶室, 单束激光在1 ns方波驱动条件下, 输出能量的技术指标为200—800 J. 实验中激光束需从一端烧蚀平面样品, 因此最多只能采用四束激光作为驱动束. 为提高泡沫材料中的冲击波速度, 实验采用上端四束激光作为驱动束, 每束激光驱动能量为800 J, 驱动波形为1 ns方波.
本文研究的是波后辐射效应造成界面初始状态的改变对随后界面发生的RM不稳定性增长的影响, 因此在靶设计中冲击波应首先进入泡沫样品, 然后通过泡沫样品与CHBr(掺Br原子比3%)样品的扰动界面, 具体结构如图1所示. 为提高泡沫材料中的冲击波速度, 激光驱动端第一层材料为CH烧蚀增压层^[23], 厚度为15 μm, 需保证烧蚀阶段CH层不被烧穿; 第二层材料为Al, 为预热屏蔽层, 厚度为10 μm; 第三层材料为泡沫材料, 密度为20 mg/cm³, 厚度根据泡沫中冲击波速度进行优化; 第四层材料为CHBr, 厚度为25 μm. 神光Ⅲ原型装置在采用Φ500 μm的连续相位板(CPP)进行束匀滑的条件下, 单端驱动最高激光功率密度可达1.6 × 10¹⁵ W/cm², 在此驱动条件下模拟两种泡沫材料中的冲击波运动轨迹, 结果如图2所示. 在相同激光功率条件下, CH泡沫中冲击波速度可达180 km/s, 但无法达到产生辐射冲击波的条件; SiO₂泡沫中冲击波速度约为170 km/s, 虽然与CH泡沫相比略小, 但满足产生辐射冲击波条件. 综合考虑材料密度、原子序数、靶制备难度、激光驱动能力等因素, 选择SiO₂泡沫作为产生辐射冲击波的材料.
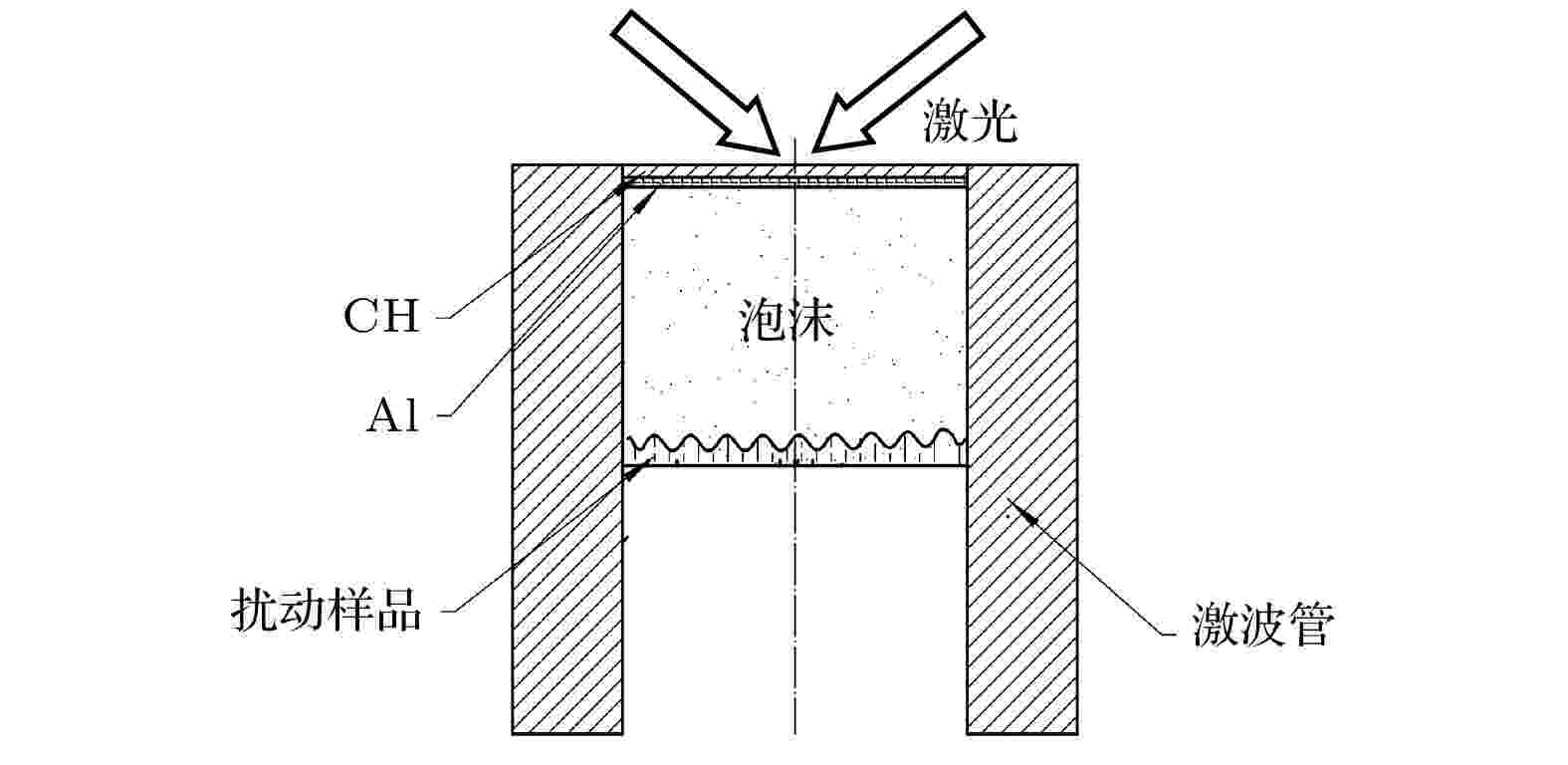图 1 激光驱动界面不稳定性研究主靶结构示意图
Figure1. Schematic view of the hydrodynamic instability target driven by laser.

图 2 两种泡沫材料中冲击波的运动轨迹
Figure2. Shock trajectory in two foam materials.

根据上述分析, 实验选择SiO₂泡沫作为产生辐射冲击波的材料, 在神光Ⅲ原型高功率激光装置上研究了冲击波波后辐射效应对RM不稳定性增长的影响. 靶结构如图1所示, 为便于观测, 激波管制作为矩形激波管, 管壁厚度为200 μm, 激波管内部开孔尺寸200 μm × 500 μm; 第一层和第二层材料分别为CH和Al; 第三层材料为SiO₂泡沫, 密度为20 mg/cm³, 厚度为380 μm; 第四层扰动样品为CHBr, 其与SiO₂泡沫接触面为正弦单模扰动界面, 波长为50 μm, 初始扰动幅度为5 μm, 平均厚度为25 μm. 实验前采用X射线检测装置对静态靶进行CT照相, 测量结果如图3所示, 图中Al样品呈现规则的单模周期结构, 样品尺寸满足设计需求.
图 3 界面不稳定性研究主靶CT图像
Figure3. Photo of the hydrodynamic instability target taken by CT.

通过调节入射激光的功率密度, 可改变泡沫材料中的冲击波速度, 在SiO₂泡沫中产生有、无辐射效应的冲击波, 进而研究冲击波的辐射效应对RM不稳定性增长的影响. 实验采用两种驱动设置, 一种驱动条件为4×800 J, 4表示驱动激光束的数目, 800 J表示每束激光的输出能量, 激光驱动波形为1 ns方波, 采用焦斑500 μm的CPP, 激光功率密度为1.6×10¹⁵ W/cm²; 另一种驱动条件为4 × 500 J, 激光驱动波形为1ns方波, 采用焦斑500 μm的CPP, 激光功率密度1×10¹⁵ W/cm².
实验在神光Ⅲ原型激光装置上开展, 实验排布如图4所示, 原型装置上四路激光直接辐照主靶上端面, 产生向下传播的冲击波, 冲击波通过扰动界面会使界面产生RM不稳定性增长. 图中背光靶与主靶通过靶架连接, 原型装置专用的背光驱动束激光辐照钒样品, 产生约5.2 keV的X光作为X光阴影照相的背光源. 实验采用球面弯晶成像系统测量不同时刻的界面不稳定性增长数据, 与传统的X光针孔成像相比, 球面弯晶成像系统具有空间分辨高(约5 μm)、单色性(谱分辨 > 1000)好的优点. 球面弯晶成像系统目前不具备时间分辨能力, 因此实验采用多发次、短脉冲背光打靶的方式获得不同时刻的界面扰动增长阴影图像, 实验中背光设计脉宽为0.5 ns, 实际打靶激光脉宽的涨落小于10%, 图像的时间分辨约为0.5 ns.
图 4 激光驱动界面不稳定性实验示意图
Figure4. Schematic of the laser driven hydrodynamic instability experiment.

实验中激光烧蚀CH样品产生向下传播的冲击波, 冲击波穿过CH层、Al层进入低密度泡沫区后速度迅速提升, 由于CH层和Al厚度较薄, 冲击波在进入SiO₂泡沫层的同时会产生向上运动的稀疏波, 当稀疏波达到CH层上端面时, 驱动激光束仍未结束, 因此会再次产生一个向下运动的冲击波, 第二个冲击波在SiO₂泡沫层中追上第一个冲击波, 会进一步提高泡沫中的冲击波速度. 当冲击波通过CHBr样品的扰动面后, 涡量的沉积引起界面发生RM不稳定性增长, 由于驱动源持续时间较短, CHBr层加速阶段持续时间约为0.5 ns, 界面经历短暂加速后以接近匀速的方式运动, 因此本实验条件下界面扰动增长以RM不稳定性增长为主.
由于SiO₂泡沫不透明度较低, 冲击波波后产生的辐射能量在泡沫中沉积较少, 会在冲击波前产生辐射前驱波, 因此冲击波后辐射效应会在冲击波到达扰动样品之前烧蚀CHBr扰动界面, 改变扰动界面处的密度分布, 界面初始状态的改变会影响涡量的沉积, 进而改变界面的RM不稳定性增长.
实验设计开展了两种激光功率密度(1 × 10¹⁵和1.6 × 10¹⁵ W/cm²)条件下的界面不稳定性实验, 不同时刻的界面不稳定性增长图像分别如图5和图6所示. 图5和图6中不同时刻的数据来自不同的实验发次, 实验通过控制制靶精度和激光驱动能量来实现实验数据的可重复性. 在靶制备过程中, 要求正弦初始扰动幅值的制靶精度控制在5 μm ± 0.5 μm范围内. 在激光能量输出方面, 要求实际的输出能量与设计输出能量的偏差控制在15%以内, 实际的激光输出能量如表1和表2所列, 可见实际输出能量与设计输出能量的偏差控制优于设计需求. 图5显示激光功率密度为1 × 10¹⁵ W/cm²时, 扰动前期增长不明显, 后期出现了尖钉结构, 扰动增长因子GF≈10, 扰动增长因子的定义为界面经不稳定性增长后的扰动幅值与初始界面扰动幅值的比值^[24]. 图6显示当功率密度为1.6 × 10¹⁵ W/cm²的实验时, 两个测量时刻都未观察到明显的界面扰动增长.
图 5 激光功率密度1 × 10¹⁵ W/cm²条件下CHBr样品的RM不稳定性增长图像
Figure5. RM growth image at a laser intensity of 1 × 10¹⁵ W/cm².

图 6 激光功率密度1.6 × 10¹⁵ W/cm²条件下CHBr样品的界面不稳定性增长图像
Figure6. RM growth image at a laser intensity of 1.6 × 10¹⁵ W/cm².

发次号	记录图像 时刻/ns	设计能 量/J	实际输出 能量/J	实际输出能量与 设计能量偏差/%
057	5	2000	1931	–3.45
056	6	2000	1983	–0.85
054	8	2000	1988	–0.60

表1激光功率密度1 × 10¹⁵ W/cm²条件下激光参数统计
Table1.Laser parameters at a laser intensity of 1 × 10¹⁵ W/cm².

发次号	记录图像 时刻/ns	设计能 量/J	实际输出 能量/J	实际输出能量与 设计能量偏差/%
061	5	3200	3080	–3.75
055	8	3200	2812	–12.1

表2激光功率密度1.6 × 10¹⁵ W/cm²条件下激光参数统计
Table2.Laser parameters at a laser intensity of 1.6 × 10¹⁵ W/cm².

根据单模样品界面RM扰动增长规律, 随着时间的增长, 波谷处的物质会向波峰处运动, 导致波峰区域物质越来越多, 波谷区域的物质越来越少, 对获取的扰动样品的阴影图像区域(如图5中5 ns图像黄框部分)进行Y轴方向的积分平均, X光强度的周期扰动结构会逐渐明显. 对图5和图6扰动样品处进行Y轴方向积分平均计算, 获得不同激光功率密度条件下不同时刻扰动样品X光阴影图像沿X轴方向的光强分布分别如图7和图8所示, 图中纵轴尺度一致. 从X光光强分布可以看出, 在较低功率密度条件下CHBr样品存在明显的单模周期结构, 并且随着时间的增大, 周期结构的对比度增强, 说明尖钉气泡结构在不断增长, 而在较高功率密度条件下则未见明显的周期结构. 结合扰动样品侧向背光照相阴影图像的直接观测结果, 可知在激光功率密度1.6 × 10¹⁵ W/cm²条件下扰动界面未发生明显的RM不稳定性增长.
图 7 激光功率密度1 × 10¹⁵ W/cm²条件下CHBr样品阴影区X轴方向光强分布
Figure7. Horizontal lineouts of perturbation sample images at a laser intensity of 1.6 × 10¹⁵ W/cm².

图 8 激光功率密度1.6 × 10¹⁵ W/cm²条件下CHBr样品阴影区X轴方向光强分布
Figure8. Horizontal lineouts of perturbation sample images at a laser intensity of 1 × 10¹⁵ W/cm².

2

-->

5.1.辐射前驱波的形成

冲击波通过扰动界面会引起界面产生RM不稳定性增长, 实验中冲击波从轻介质进入重介质, 界面扰动增长如(2)式所示. 从RM不稳定性增长公式可知, 扰动增长速率正比于界面运动速度. 在相同的靶结构条件下, 界面运动速度与驱动源强度正相关, 理论上激光功率密度1.6 × 10¹⁵ W/cm²条件下的界面扰动增长速率应高于激光功率密度1 × 10¹⁵ W/cm²条件下的界面扰动增长速率, 但在实验中却观察到较高激光功率密度条件下未发生明显的RM不稳定性增长, 这与扰动界面初始状态的改变有关.
实验通过控制入射激光能量产生有、无辐射效应的冲击波. 随着入射激光能量的提升, 冲击波后辐射效应逐渐增强, 辐射效应会加热波前物质, 提高冲击波波前物质的温度, 表现为在冲击波波前产生一个辐射前驱波阵面^[16,25,26], 并且辐射前驱波阵面与冲击波阵面的间距随着冲击波速度的提升而增大, 辐射前驱波会在冲击波到达扰动界面前改变界面初始状态.
辐射前驱波的形成与冲击波速度密切相关, 采用Multi-1D模拟不同激光功率密度条件下的各层物质的运动速度、密度、压力及电子温度, 可以给出不同驱动条件下冲击波速度和辐射前驱波速度. 激光功率密度1.6 × 10¹⁵ W/cm²条件下Multi-1D模拟得到的各层物质的运动如图9所示, 图中绿色表示CH样品, 黑色表示Al样品, 青色表示SiO₂泡沫, 枚红色表示CHBr样品, 根据泡沫材料中的密度变化给出冲击波的运动轨迹, 如图中红线所示, 可知冲击波在SiO₂泡沫中存在两种速度, 1.1 ns前SiO₂泡沫中冲击波速度约为100 km/s, 1.1 ns后SiO₂泡沫中冲击波速度约为170 km/s. 不同的冲击波速度会造成不同的波后温升, 而波后辐射效应与波后电子温度正相关^[3], 波后温升引起的辐射流F∝T_e⁴, T_e表示波后物质的电子温度.
图 9 模拟激光功率密度1.6 × 10¹⁵ W/cm²条件下各层物质运动及冲击波、辐射前驱波阵面
Figure9. Simulated shock trajectory, radiative precursor trajectory and the movement of materials at a laser intensity of 1.6 × 10¹⁵ W/cm².

辐射前驱波的形成表现为冲击波波前物质电子温度的升高. 模拟获得的SiO₂泡沫中和CHBr样品中的电子温度分布如图10所示, 1.1 ns前冲击波速度较低时, SiO₂泡沫中冲击波波后电子温度较低(约40 eV), 1.1 ns冲击波提速后电子温度迅速升至约80 eV. 定义冲击波波前物质温度升高到30 eV的位置处为辐射前驱波阵面, 在图9中做出SiO₂泡沫中的辐射前驱波阵面, 可知1.1 ns前冲击波速度较低时, 辐射前驱波阵面与冲击波阵面未分离, 说明冲击波后辐射效应不明显; 1.1 ns后电子温度的升高使波后辐射流提高约16倍, 使辐射前驱波运动速度提升至约270 km/s, 辐射前驱波阵面与冲击波阵面明显分离. 模拟显示辐射前驱波提前冲击波约0.7 ns到达CHBr扰动界面, 波后辐射效应烧蚀界面, 在冲击波到达界面前改变了界面的初始状态.
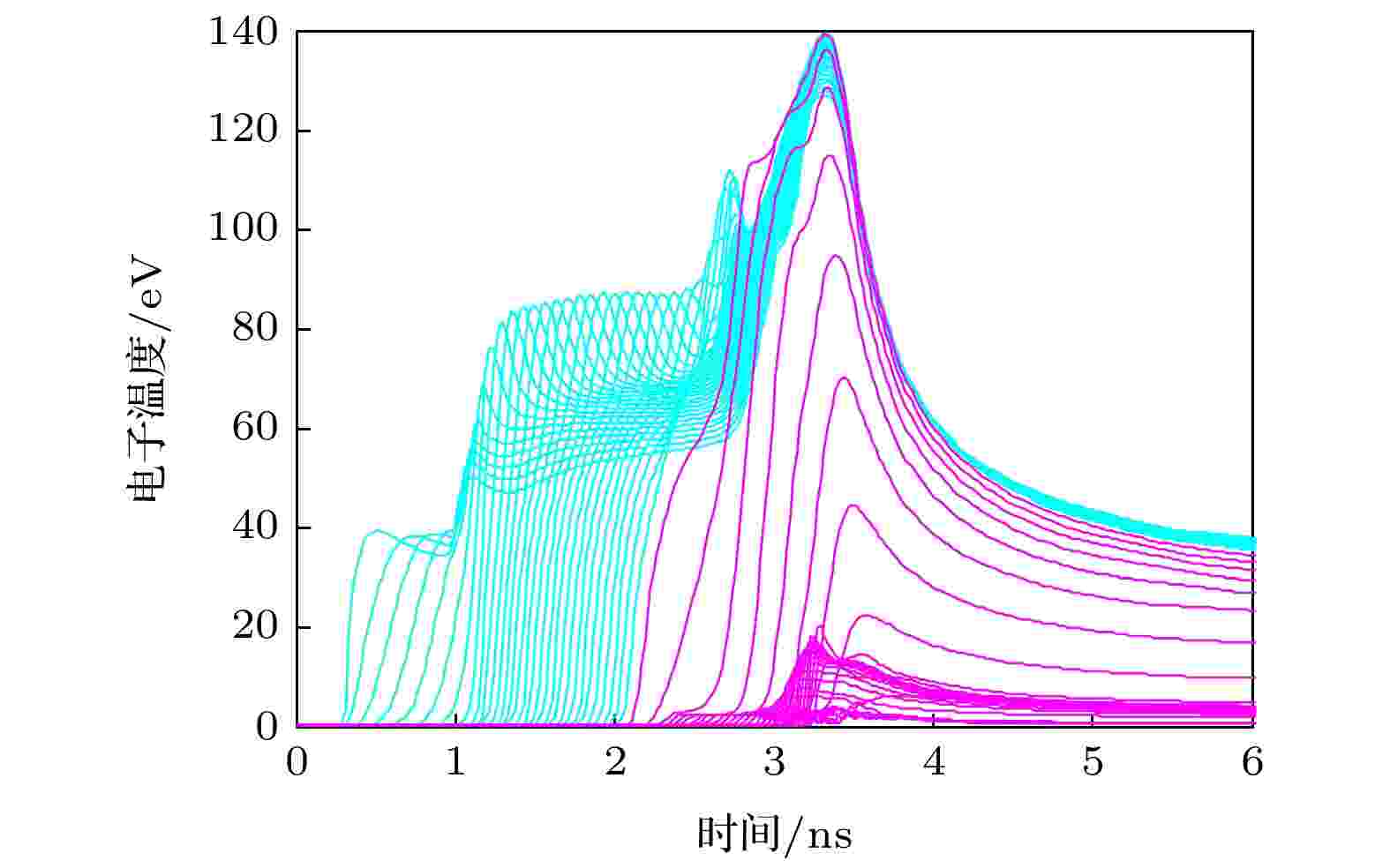图 10 模拟SiO₂泡沫和CHBr层电子温度变化
Figure10. One-dimensional profiles of electron temperature of SiO₂ foam and CHBr.

波前电子密度N_e的提升同样可反映辐射前驱波的形成. 模拟两个典型时刻(泡沫材料中冲击波加速前后)SiO₂泡沫中的电子温度和电子密度分布如图11所示, 当冲击波速度较低时, 波前电子密度不发生改变, 如图11(a)所示, 当冲击波速度提升至约170 km/s时, 波前电子密度提升接近2个量级, 如图11(b)所示, 说明冲击波提速后辐射前驱波形成. 结合电子密度和电子温度的变化, 证实较高功率密度条件下冲击波提速后产生了辐射前驱波.
图 11 模拟不同时刻SiO₂泡沫中电子密度和电子温度的变化　(a) 0.9 ns; (b) 2.0 ns
Figure11. Simulated one-dimensional profiles of electron temperature and electron density at different time: (a) 0.9 ns; (b) 2.0 ns.

为了研究波后辐射效应对界面不稳定性增长规律的影响, 实验通过降低激光功率密度, 获得辐射效应不占优条件下的界面不稳定性增长数据, 用于与具有波后辐射效应影响的界面RM不稳定性增长数据进行比对研究. 采用Multi-1D模拟激光功率密度1 × 10¹⁵ W/cm²条件下各层物质运动、冲击波轨迹和辐射前驱波轨迹如图12所示, 1.2 ns前SiO₂泡沫中的冲击速度约为70 km/s, 1.2 ns后冲击波速度提升至约130 km/s, SiO₂泡沫中冲击波后电子温度从约30 eV升至约60 eV, 模拟显示, 冲击波加速后虽有辐射前驱波存在, 但两者分离并不明显, 辐射前驱波仅提前冲击波约0.2 ns到达扰动样品. 模拟两个典型时刻(泡沫材料中冲击波加速前后)SiO₂泡沫中的电子温度和电子密度分布如图13所示, 当冲击波速度较低时, 波前电子密度不发生改变, 当冲击波速度提升至约130 km/s时, 波前电子密度虽然提升, 但波前电子密度升高区域宽度较窄约20 μm (较高功率密度条件下电子密度升高区域约90 μm, 如图11所示), 说明辐射前驱波虽有形成, 但它与冲击波阵面距离较近, 在冲击波到达扰动样品前对界面状态的改变能力较弱.
图 12 模拟激光功率密度1 × 10¹⁵ W/cm²条件下各层物质运动及冲击波、辐射前驱波阵面
Figure12. Simulated shock trajectory, radiative precursor trajectory and the movement of materials at a laser intensity of 1 × 10¹⁵ W/cm².

图 13 模拟不同时刻SiO₂泡沫中电子密度和电子温度的变化　(a) 1.2 ns; (b) 2.5 ns
Figure13. Simulated electron density and electron temperature in SiO₂ foam for different time: (a) 1.2 ns; (b) 2.5 ns.

2 -->

5.2.较高激光功率密度条件下界面扰动增长致稳机制分析

实验显示较高激光功率密度条件下扰动界面未发生明显的RM不稳定性增长, 说明存在着界面致稳效应. 根据(3)式可知辐射能流与进入波后物质的能流的比值R与冲击波速度的五次方成正比, 根据模拟给出的SiO₂泡沫中的冲击波速度, 计算得出两种激光功率密度条件下比值R相差4倍, 说明教高功率密度条件下泡沫材料中波后辐射能流明显提升. 在较高功率密度条件下, 辐射前驱波在约2.2 ns到达CHBr样品, 提前冲击波0.7 ns, 在冲击波到达扰动样品前波后辐射效应烧蚀CHBr样品, 使CHBr样品温度升高到约60 eV. 通过模拟计算得到的冲击波到达样品前的CHBr样品的烧蚀速度如图14(a)所示, 烧蚀速度随着扰动界面处温度的升高而提升. 烧蚀效应的存在使扰动界面处的密度分布发生改变, 通过模拟可知烧蚀面处密度的变化使扰动界面处的密度梯度标长在冲击波到达前升至μm量级, 如图14(b)所示. 波后辐射效应对扰动界面的烧蚀改变了界面的初始状态, 进而影响冲击波过界面后引起的界面RM不稳定性增长.
图 14 模拟激光功率密度1.6 × 10¹⁵ W/cm²条件下 (a) CHBr样品烧蚀速度, (b)界面处密度梯度标长
Figure14. Simulated (a) ablation velocity and (b) density-gradient scale length on the surface at a laser intensity of 1.6 × 10¹⁵ W/cm².

在界面不稳定性发展过程中, 密度梯度效应会抑制不稳定性的增长. 较高激光功率驱动条件下波后辐射效应改变了界面初始状态, 使界面的密度梯度分布变缓, 这会增大冲击波通过扰动界面后CHBr样品的密度梯度尺度. 模拟两种驱动条件下冲击波通过界面后的密度梯度尺度变化如图15所示, 图中定义冲击波通过扰动界面的时刻为0时刻, 模拟显示较高激光功率驱动条件下密度梯度尺度明显高于较低激光驱动条件下的密度梯度尺度. 因此波后辐射效应造成的界面初始状态变化提高了界面处的密度梯度尺度, 抑制了界面的不稳定性增长. 在较低激光功率密度实验条件下, 辐射前驱波与冲击波分离不明显, 冲击波到达扰动界面前界面状态未发生明显改变, 界面扰动增长为经典的双介质界面RM不稳定性增长, 因此实验测量到较低功率密度条件下界面扰动发展至尖钉气泡结构.
图 15 模拟两种激光功率密度条件下界面处密度梯度标长变化
Figure15. Simulated density-gradient scale length on the surface at the different laser intensity.

根据RM不稳定性的增长规律, 界面扰动增长还与界面的Atwood数密切相关, 由于波后辐射效应改变了扰动界面处的初始状态, 因此界面处的Atwood数也随之发生改变. 模拟两种激光功率密度条件下的Atwood数变化如图16所示, 在较高功率密度条件下, 波后辐射效应烧蚀扰动界面, 在冲击波达到界面前已使Atwood数降低, 当冲击波到达扰动界面后压缩CHBr样品, 使界面Atwood数出现短暂的上升, 但在冲击波通过扰动界面后Atwood数迅速下降至0.1; 而在较低功率密度条件下界面Atwood数缓慢下降, 最终的Atwood数约是较高功率密度条件下的4倍. 因此冲击波波后辐射烧蚀效应引起的Atwood数的快速下降也是较高功率密度条件下未观测到界面扰动增长的一个原因.
图 16 模拟两种激光功率密度条件下扰动界面处的Atwood数变化
Figure16. Simulated Atwood number on the surface at the different laser intensity.

基于神光Ⅲ原型激光装置研究了冲击波波后辐射效应对界面RM不稳定性增长的影响, 在较高激光功率密度条件下初始单模CHBr样品界面未观测到明显的扰动增长, 而在低功率密度条件下观测到了尖钉结构的形成. 原因在于较高功率密度条件下辐射效应在冲击波到达扰动样品前烧蚀扰动样品, 改变了CHBr样品的初始状态, 增大了冲击波通过扰动界面后界面的密度梯度标长，减小了界面处的Atwood数, 从而抑制了RM不稳定性的增长.