摘要:二维磁性材料的研究是一大热点, 其中单层CrSi₂表现出优良的磁性, 有望应用于自旋电子学等领域, 但金属性限制了其部分层面的应用与发展. 采用基于密度泛函理论的第一性原理赝势平面波方法研究了不同元素(Ti, V, Co, Ni)、不同掺杂浓度(原子百分比为3.70%, 7.41%, 11.1%)对二维CrSi₂电子结构、磁学及光学性质的影响, 期望改善二维CrSi₂材料的相关性质, 也为开发基于二维CrSi₂的电子器件提供有效的理论基础. 研究表明: 二维CrSi₂在远红外以及紫外范围内的吸收系数与反射系数都很强, 表现出优异的光学性质. 在原子百分比为3.70%的浓度下掺杂Ti, V, Ni后, 成功打开了二维CrSi₂的带隙, 导致其分别向间接半导体、稀磁半导体和半金属铁磁体转变, 同时, 掺杂能对单分子层CrSi₂的磁性进行有效的调控. 掺杂后的二维CrSi₂拥有良好的光学性质, 多数掺杂体系的光学性质峰值增大并发生蓝移, 但在原子百分比为11.1%的掺杂浓度下, 吸收峰红移. 二维CrSi₂有望成为高稳定性的新型自旋电子器件的制备材料.
关键词: 二维CrSi₂材料/
电子结构/
磁学性质/
光学性质

English Abstract

全文HTML

--> --> -->

石墨烯^[1]的问世开启了材料科学领域新的篇章, 其单分子层结构具有优异的性能, 包括量子霍尔效应、优秀的透光率、低电阻率和高载流子迁移率等^[2-5], 在超级电容储能、半导体和光电器件及航空航天多方面展现出了无穷的潜力. 2018年, “魔角”石墨烯^[6]的提出, 进一步推动了二维材料超导及转角电子学^[7]等领域的突破式发展, 开拓了二维材料研究和应用的新维度, 二维材料举世瞩目, 吸引了众多****对这种原子层量级的超薄材料进行探索与研究^[8-14], 随着研究的深入, 二维材料家族被不断丰富与拓宽, 如过渡金属碳化物^[15,16]、黑磷^[17,18]、硼纳米片^[19-21]、六方氮化硼^[22]、半导体材料过渡金属硫化合物^[23-29]和类水滑石材料^[30]等.
与此同时, 具有磁性的二维材料成为了新的研究热点, 2010年, Dzade等^[31]从一个平面蜂窝晶格出发, 在过渡金属元素吸附到与石墨烯有着相似结构硅稀^[32,33]的单层结构中时, 发现二维过渡金属硅化物CrSi₂表现为金属和铁磁性. 过渡金属硅化物是由非金属硅原子进入过渡金属的晶格形成的金属间化合物, 具有高度的稳定性^[34], 由于具有特殊的物理和化学特性, 如良好的传热性和优异的耐高温、耐腐蚀等性质, 被广泛用于电加热组件电路、磁性材料及高温抗氧化涂料^[35,36]等领域. CrSi₂同多数过渡金属硅化物一样有着良好的热电与光学性质, 在微电子及光电子领域有着广阔的应用前景, 但遗憾的是, 本征三维CrSi₂及在掺杂铁磁性Co元素后也并未表现出理想的磁性^[37-39], 这限制了其在自旋电子学等领域的应用与发展. 目前****对CrSi₂材料的研究, 主要分为实验和理论两方面. 在实验方面, Dasgupta等^[40]通过制备单晶CrSi₂材料, 得出三维CrSi₂属于一种间接带隙半导体, 禁带宽度为0.35 eV, 室温块体态的塞贝克系数大约为96 μV/K、电导率约为10³/(Ω·cm)、热导率约为10 W/m·K. Nagai H等^[41]用Cu替代三维CrSi₂中的Si原子, 提高了ZT值, 也降低了CrSi₂材料的热导率. Naval等^[42]采用放电等离子烧结方法研究了CrSi₂/7.5%SiGe (7.5%为质量分数)纳米复合材料中CrSi₂材料的热电性质. 在理论方面, 掺杂引起三维CrSi₂材料电学与光学性质的变化己被广泛研究^[43,44].
与三维材料相比, 具有特殊物理性能的二维材料在自旋电子学^[45,46]、磁存储^[47,48]、分子尺度电子器件^[49,50]等领域具有重要的应用, 潜力也因其量子尺寸效应呈现出广泛的新特性^[51]. 二维金属硅化物因为在硅基器件技术中的重要应用而备受关注^[52,53]. 2013年, Viet等^[54]分别研究了在弯曲和平面硅烯表面附着Cr元素的二维材料, 发现CrSi₂(B)表现半金属性, 带隙为0.28 eV, 磁性为铁磁性, CrSi₂(PL)为金属, 表现出反铁磁性. 近年来, Chen和Yan^[55]通过切割三维CrSi₂材料来计算其表面特征, 得出与Dzade等^[31]一致研究的结论: 二维CrSi₂材料具有金属和铁磁FM特性, 同时Chen和Yan^[55]还研究了一个Ti, Fe和Mn元素、近邻V元素掺杂对二维CrSi₂的电学和磁学性质的影响, 结果表明: Mn掺杂的二维CrSi₂在远红外和真空紫外的光学性质优异, 但是未涉及不同浓度下掺杂Ti, V二维CrSi₂光学特征及能带结构的研究, 主要关注掺杂体系的磁性^[56-58].
电子工业需要高质量的、柔性的并且薄的半导体材料, 以便补充常规材料由于几何形状或尺寸而无法应用的工况, 随着自旋电子材料的飞速发展, 人们对二维材料的需求越来越大, 如果能在材料中同时应用电荷和电子的自旋属性, 出现所谓的稀磁半导体, 则有望在自旋电子器件中发挥巨大作用. 常规的二维材料不具备磁性, 主流的以获得磁性材料为目的的方法是对二维材料进行空穴或者原子的吸附, 而对于磁性材料磁矩的调控又是一个极为重要的课题, 单分子层的CrSi₂表现出优良的性质, 有望成为新型二维磁性材料, 其性质与Cr元素核外3d态自旋电子数相关, 如果通过掺杂拥有相同3d态过渡金属族元素, 来增强或者削弱Cr元素核外自旋电子数, 那么就能实现CrSi₂材料性质的有效调控. 采用基于密度泛函理论的第一性原理赝势平面波方法研究了切割三维CrSi₂(001)面得到的单分子层结构, 并分析掺杂对二维CrSi₂材料的电学、磁学及光学等性质的影响, 旨在通过理论分析为材料的制备和应用提供指导.

2

-->

2.1.三维与二维CrSi₂的结构模型

三维CrSi₂材料是一种新型的环境友好半导体材料, 具有优异的高温稳定性、抗氧化性、高效的热功率和高电导率, 晶胞为C40的六方晶体, 空间点群为P6₂22, 晶格常数为a = b = 0.4379 nm, c = 0.6324 nm, 晶面角为α = β = 90°, γ = 120°^[59]. 图1为CrSi₂的晶体结构模型, 其原胞中含有6个Si原子和3个Cr原子, 原子摩尔比为2∶1. CrSi₂与硅衬底之间具有较小的晶格错配率, 有利于薄膜在硅基上外延生长^[60], 三维CrSi₂的基本性质如表1所列.
图 1 三维CrSi₂晶体模型
Figure1. Three-dimensional CrSi₂ crystal model.

	CrSi2	Si	Cr
带隙类型[44,55-58]	间接带隙	间接带隙	无带隙
带隙/eV[44,55-58]	0.38	0.853	0.00
磁矩/μB[55-58]	0.00	0.00	0.00
基态能/eV[55-58]	–32199.36	0.00	0.00
热导率/(W·MK–1)[40]	10	150	91.3
电导率/(Ω·cm)[40]	103	—	—

表1三维CrSi₂的基本性质
Table1.Basic properties of three-dimensional CrSi₂

石墨烯以C元素为主体, 以sp²轨道杂化的方式键连构成蜂窝状结构, 二维CrSi₂具有类似石墨烯的蜂窝状结构, 由于层与层之间的范德瓦耳斯力较弱, 理论上可以通过微机械劈裂技术形成单层的CrSi₂^[61,62].
对应于图1中的CrSi₂晶体结构模型, 结合图2可以观察其层间距离与层内成键的基本情况, 可以发现, 晶体层内键长最大值为2.566 ?, 对应中间层的Si—Cr成键; 键长最小值为2.532 ?, 来自最下层的相邻Si—Cr键, 同时可以看到, 晶体层间有成键, 成键最大值为3.061 ?, 最小值为2.459 ?, 基于上述对三维CrSi₂晶格结构的分析, 在原胞的基础上构建了2 × 2 × 1的CrSi₂三维超胞结构, 对有关性质计算后用来同二维CrSi₂作对比研究. 单分子层的CrSi₂通过切割几何优化后的三维CrSi₂(001面)并建立3 × 3 × 1的扩胞模型而来, 如图3所示.
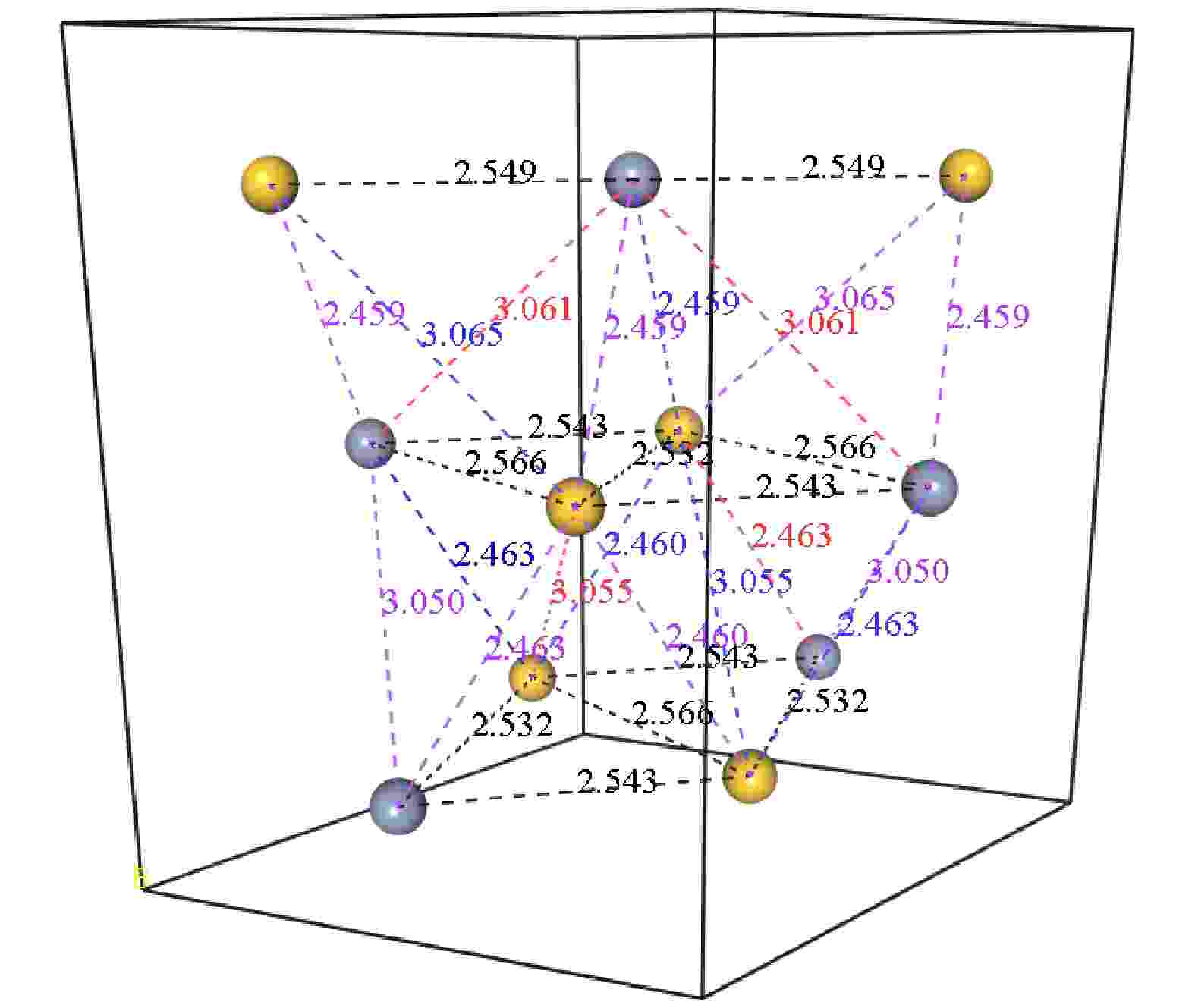图 2 三维CrSi₂晶体的成键模型
Figure2. Bonding models of three dimensional CrSi₂ crystals.

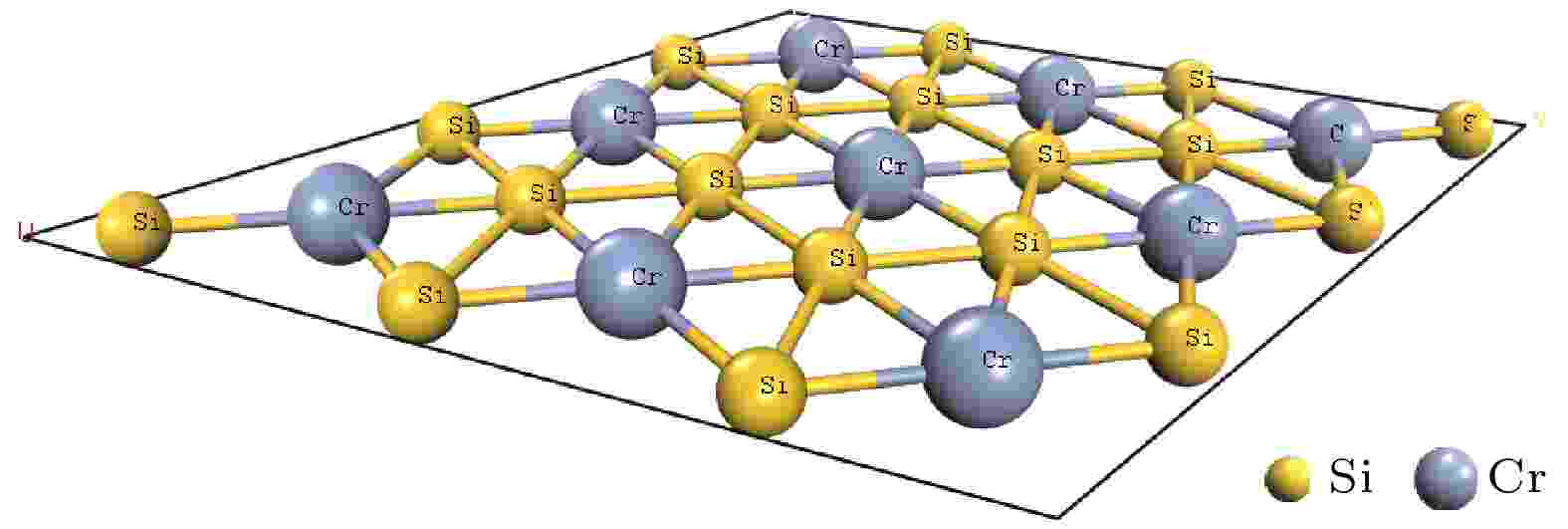图 3 二维CrSi₂结构模型
Figure3. Two-dimensional structure model of CrSi_2.

三维及二维CrSi₂经过几何优化后的结果如表2所列, 其中三维CrSi₂的晶格常数为a = b = 0.438 nm, c = 0.632 nm, 晶面角为α = β = 90°, γ = 120°. 几何优化后单层CrSi₂的晶格常数为a = b = 0.441 nm, c = 1.5 nm.

Model	a/nm	b/nm	c/nm	Vo/nm3
3D-CrSi2	0.438	0.438	0.632	0.107
2D-CrSi2	0.441	0.441	1.5	2.274

表2三维及二维CrSi₂的结构优化结果
Table2.Structural optimization results of three-dimensional and two-dimensional CrSi₂.

在进行相关性质的模拟计算前, 首先需要考察模型的稳定性. CrSi₂几何优化结果显示其晶体模型整体上无不规则变化, 但这些结构的相对稳定性仍不确定, 2018年Chen等^[62]对二维CrSi₂材料进行第一性原理计算发现, 三维CrSi₂及切割其(001)面而得到的单分子层结构中, 声子谱的计算结果显示二者均未在虚频出现震动, 模型是相对稳定的, 基于此, 我们继续开展下一步研究.
2 -->

2.2.二维CrSi₂掺杂模型

过渡金属元素 3d 壳层的电子结构如表3所示, Ti和V元素的电子轨道结构分别为3d²4s²和3d³4s², 表现为顺磁性, 顺磁离子在结合成固体时, 由于有不满的内壳层因而可以保持固有磁矩, 表现出较强的磁性, 成为磁性深入研究的主要对象. Co和Ni元素的电子轨道结构分别为3d⁷4s²和3d⁸4s², 它们的3d轨道是根据Hundt准则和Pauli不相容性原理排列的, 有不成对的电子会产生磁矩, 表现为铁磁性.

原子序数	21	22	23	24	25	26	27	28	29	30
元素名	Sc	Ti	V	Cr	Mn	Fe	Co	Ni	Cu	Zn
磁性	顺磁性	顺磁性	顺磁性	反铁磁性	反铁磁性	铁磁性	铁磁性	铁磁性	无磁性	无磁性
轨道结构	3d14s2	3d24s2	3d34s2	3d54s1	3d54s2	3d64s2	3d74s2	3d84s2	3d104s1	3d104s2
3d电子数及其自旋排布	↑	↑ ↑	↑ ↑ ↑	↑ ↑ ↑ ↑ ↑	↑ ↑ ↑ ↑ ↑	↑↓ ↑ ↑ ↑ ↑	↑↓ ↑↓ ↑ ↑ ↑	↑↓ ↑↓ ↑↓ ↑ ↑	↑↓ ↑↓ ↑↓ ↑↓ ↑↓	↑↓ ↑↓ ↑↓ ↑↓ ↑↓
4s轨道电子数	2	2	2	1	2	2	2	2	1	2

表3过渡金属元素3d壳层的电子结构
Table3.Electronic structure of 3d shell of transition metal elements.

选取顺磁Ti, V元素和铁磁Co, Ni元素对二维CrSi₂在原子百分比为3.70% (一个掺杂元素)、7.41% (两个掺杂元素)与11.1% (三个掺杂元素)浓度(如无特殊说明, 后文的浓度数据均为原子百分比)下的掺杂体系进行研究, 图4为Ti在不同浓度下替换Cr原子, 即掺杂二维CrSi₂的模型, 其余V, Co及Ni元素的掺杂对应位置及浓度均同Ti掺杂的模型相同, 仅以Ti在不同掺杂浓度下的模型表示.
图 4 不同浓度下Ti掺杂二维CrSi₂的模型　(a)原子百分比为3.70%; (b) 原子百分比为7.41 %; (c) 原子百分比为11.1%
Figure4. Model of Ti doped two-dimensional CrSi₂ at different concentrations: (a) Atomic percentage is 3.70%; (b) atomic percentage is 7.41%; (c) atomic percentage is 11.1%.

2 -->

2.3.计算细节

计算中采用Materials Studio软件包中的Visualizer模块建立CrSi₂的结构模型, 然后通过VASP软件包对模型进行几何结构优化. 对于三维CrSi₂, 采用广义梯度近似(GGA)方法中的PBE泛函来描述交换关联效应, 截断能设置为400 eV, 收敛精度为10^–6 eV/atom, 倒空间由K点网格均匀间距的Gamma方案均匀采样, K点网格为3 × 3 × 4, 晶格常数和原子位置完全松弛, 直到每个原子上的力小于0.03 eV/?.
对二维CrSi₂体系进行收敛性测试, K点设置为2 × 2 × 1, 截断能取为140—340 eV的范围, 每隔20 eV进行一次测试, 结果如图5所示. 可以看出, 当ECUT < 200 eV时, 体系的总能出现不规则震荡, 当200 eV < ECUT < 260 eV, 体系的能量随着截断能的增大缓慢上升, 在ECUT>300 eV以后, 体系的总能不再随着ECUT的改变而改变(< 0.002 eV), 根据能量的收敛性, 选择截断能为300 eV, 收敛精度为10^–6 eV/?, 在计算能带时, 二维材料的布里渊区种类比较少, 这里选择的高对称点为G-X-H₁-C-H-Y-G. 通过在掺杂体系的c方向上添15 ?的真空层, 来防止层与层之间的相互作用, 其次对模型进行优化与计算, 对计算后的有关性质进行对比分析, 以此来探究单层CrSi₂的性质变化规律.
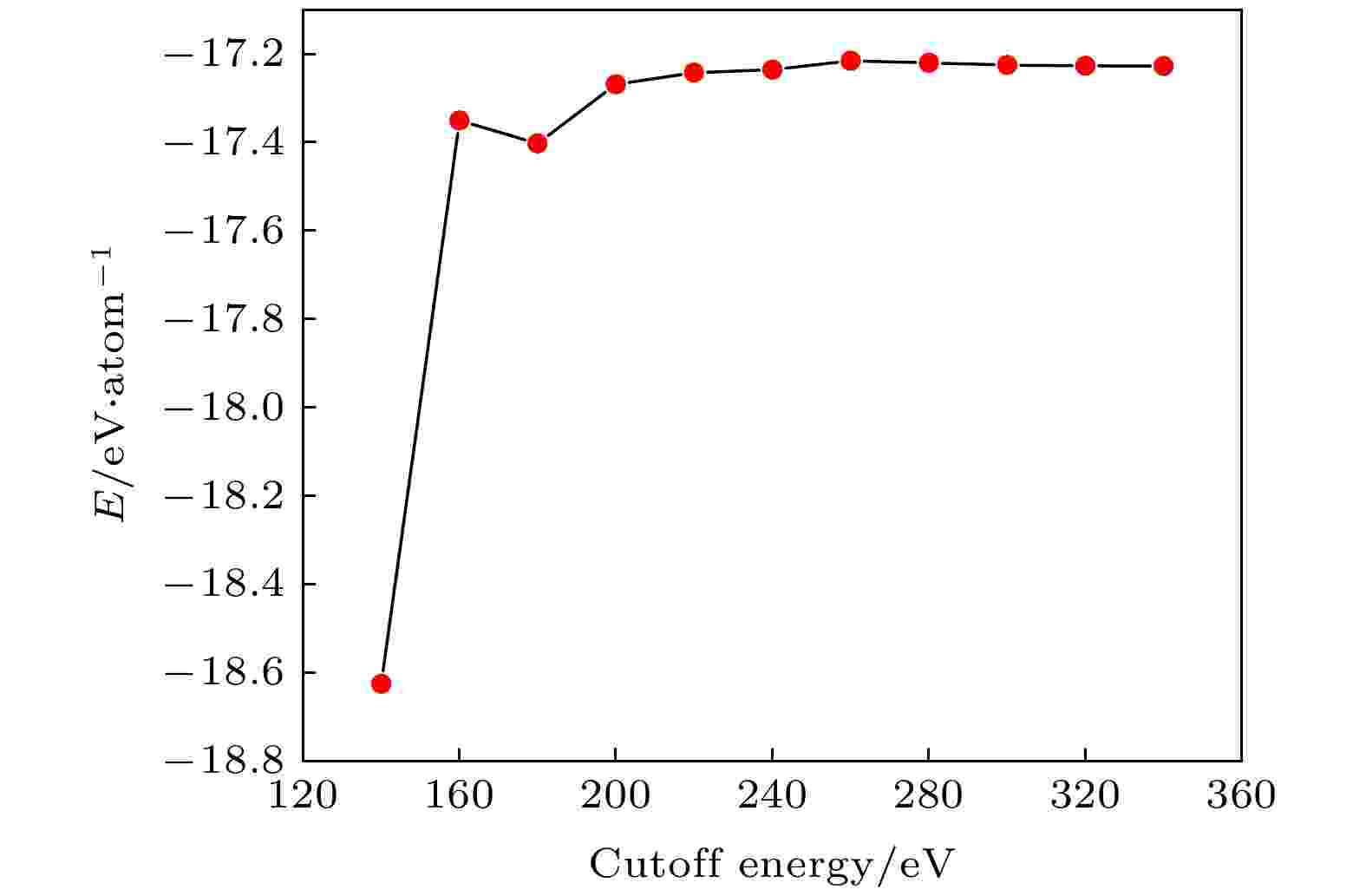图 5 截断能与总能量的关系
Figure5. Relationship between truncation energy and total energy.

2

-->

3.1.电子结构

3 -->

3.1.1.能带结构

图6(a)为三维CrSi₂费米面附近的能带结构图, 计算显示其导带在高对称点G点到达最低, 为0.182 eV, 价带在高对称点Z点到达最高, 为–0.184 eV, 因此, 本征三维CrSi₂的带隙为0.366 eV, 结果与闫万珺等^[43,44]以及Chen和Yan^[55]的理论计算值相近. 图6(b)和图6(c)显示, 二维CrSi₂上、下旋能带结构的带隙均为零且互相具有不对称性, 表明其呈现出金属性和磁性, 这与以往的研究结论一致^[33,55].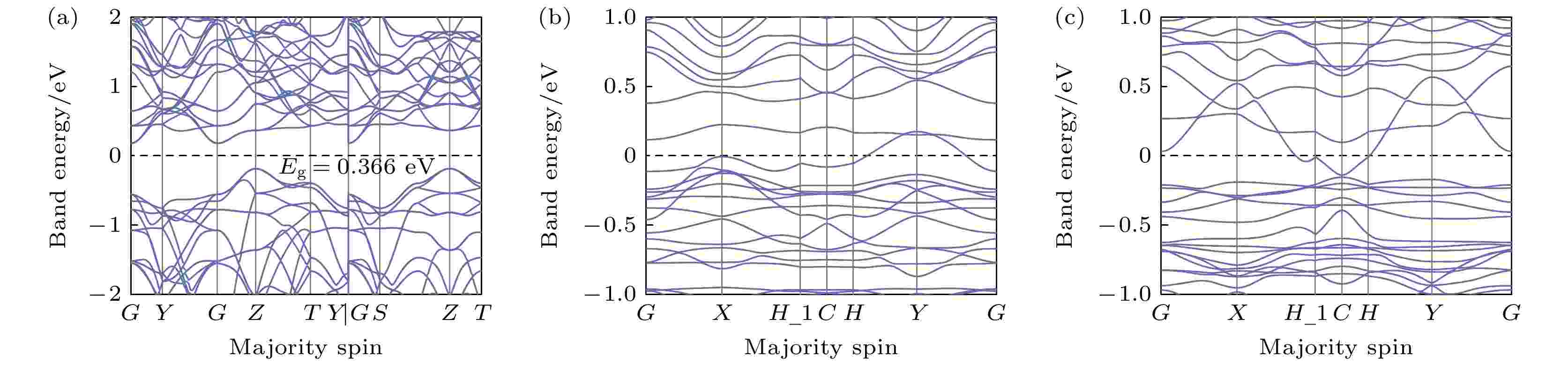
图 6 能带结构图　(a)三维CrSi₂的能带结构图; (b)二维CrSi₂的上旋电子能带结构; (c)二维CrSi₂的下旋电子能带结构
Figure6. Energy band structure diagram: (a)Energy band structure diagram of three-dimensional CrSi₂; (b) spin up electron band structure of two-dimensional CrSi₂; (c) spin down electron band structure of two-dimensional CrSi₂.

图7为在3.70%, 7.41 %及11.1%浓度下Ti, V, Co, Ni掺杂二维CrSi₂的上旋及下旋电子能带结构. 掺杂浓度为3.70%时, Ti, V, Ni掺杂的二维CrSi₂分别表现为间接半导体、稀磁半导体和半金属铁磁体, 在3.70%的浓度下掺杂Co及7.41%和11.1%浓度下掺杂的二维CrSi₂能带图中, 导带或价带均有超过费米能级, 体系表现为金属性, 同时, 除在浓度为3.70%掺杂Ti的二维CrSi₂不具有磁性外, 其余掺杂体系的上、下旋能带结构均不对称, 表现为磁性.
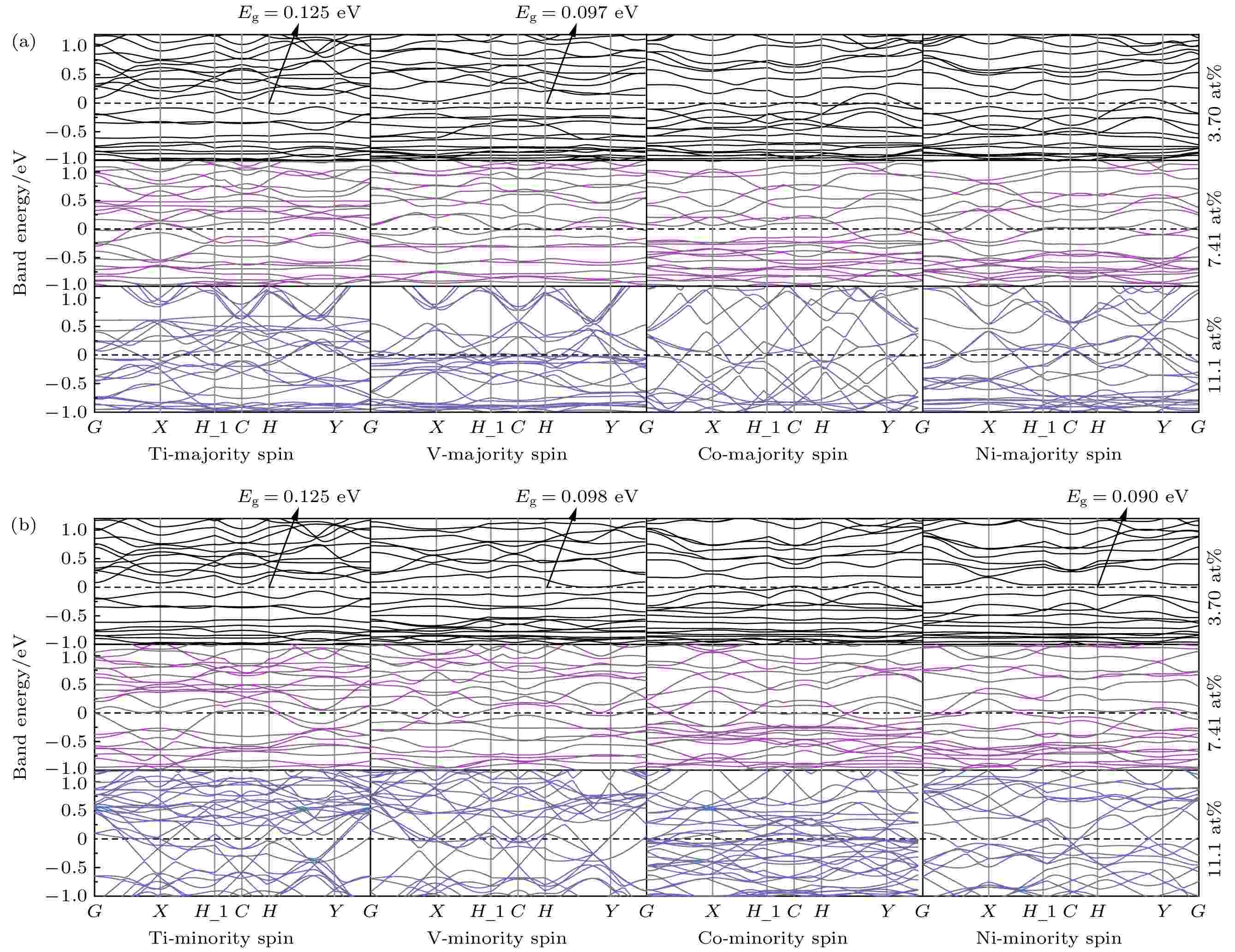图 7 Ti, V, Co和Ni在3.70%, 7.41%, 11.1%浓度掺杂下二维CrSi₂的能带结构　(a)上旋电子能带结构; (b)下旋电子能带结构
Figure7. Band structure of Ti, V, Co and Ni in two-dimensional CrSi₂ doped with the concentration of 3.70%, 7.41% and 11.1%: (a) Spin up electron band structure; (b) spin down electron band structure.

对3.70%浓度下掺杂Ti, V, Ni后二维CrSi₂的能带结构进一步分析可知: Ti掺杂的CrSi₂磁矩变为0 μB, 且表现为间接带隙半导体的性质, 其导带最低点和价带最高点分别在点C和点Y处, 值分别为0.058和–0.067 eV, 因此禁带宽度为0.125 eV. V掺杂的二维CrSi₂体系具有磁性, 自旋向上的能带中导带在X点到达最小值0.027 eV, 价带在C点到达最大值–0.07 eV, 出现0.097 eV的带隙, 自旋向下的能带图中, 分别在Y和G点到达导带底与价带顶, 同样出现0.098 eV的带隙. 分析可知, 掺杂V后的二维CrSi₂, 兼具半导体和磁性材料的性质, 符合稀磁半导体的描述. 稀磁性半导体具有磁性和半导体双重特性, 如掺杂后的GaAs和TiO₂等^[63,64], 为了能同时实现自旋与电荷两个自由度的调控与应用, 研究人员需要准备磁性半导体, 这种材料为开拓半导体技术新领域提供了有利条件, 对于自旋电子学器件的研发与应用极具意义, 具有十分广阔的前景. 2005年, 《Science》杂志报道了这种材料, 并发出能否创造具有室温工作磁性半导体的疑问^[65,66], 引发了广泛关注^[67-72].
在3.70%浓度下掺杂Ni后二维CrSi₂自旋向下的能带结构中, 导带在G点到达最小值0.042 eV, 价带在C点到达最大值–0.048 eV, 出现0.09 eV的带隙; 自旋向上的能带中, 价带穿过费米能级并在Y点到达价带顶, 对应能量为0.074 eV, 在C点到达导带底, 能量为0.053 eV. 由此可知, 在该浓度下掺杂Ni后的二维CrSi₂一个能带几乎被电子充满, 而另一个能带则出现了带隙, 因此掺杂Ni后的二维CrSi₂表现为半金属铁磁性. 半金属铁磁材料具有较高的自旋极化率, 同时能与电阻形成良好的匹配且稳定性优良, 因此, 成为了研究的热点^[73,74]. 到目前为止, 已通过实验证实许多合金或化合物是半金属铁磁材料, 如Co₂MnSi, Fe₂CrSi等^[75-77]. 半金属铁磁体(HMF)在一个自旋通道中存在电子的金属性, 同时在另一个自旋通道中又存在绝缘性, 可产生完全的自旋极化电流, 被认为是磁性存储器及自旋电子学应用的关键候选者, 希望此次结果有助于后续的研究.
掺杂浓度为11.1%时, 掺杂元素的引入使二维CrSi₂的能带范围扩大, 说明原子间键的相互作用和原子间的重叠增强, 此时Si-3s轨道态电子和掺杂元素的d轨道态电子更易成键, 从而使得能级分裂能变大且能级形状趋于陡峭, 导致该体系的有效质量变小, 载流子迁移性质增强.
3 -->

3.1.2.态密度

为了进一步研究材料微观特性和磁性的物理机理, 需要继续计算研究体系的态密度分布情况, 本征三维及二维CrSi₂的总态密度以及分态密度曲线如图8所示.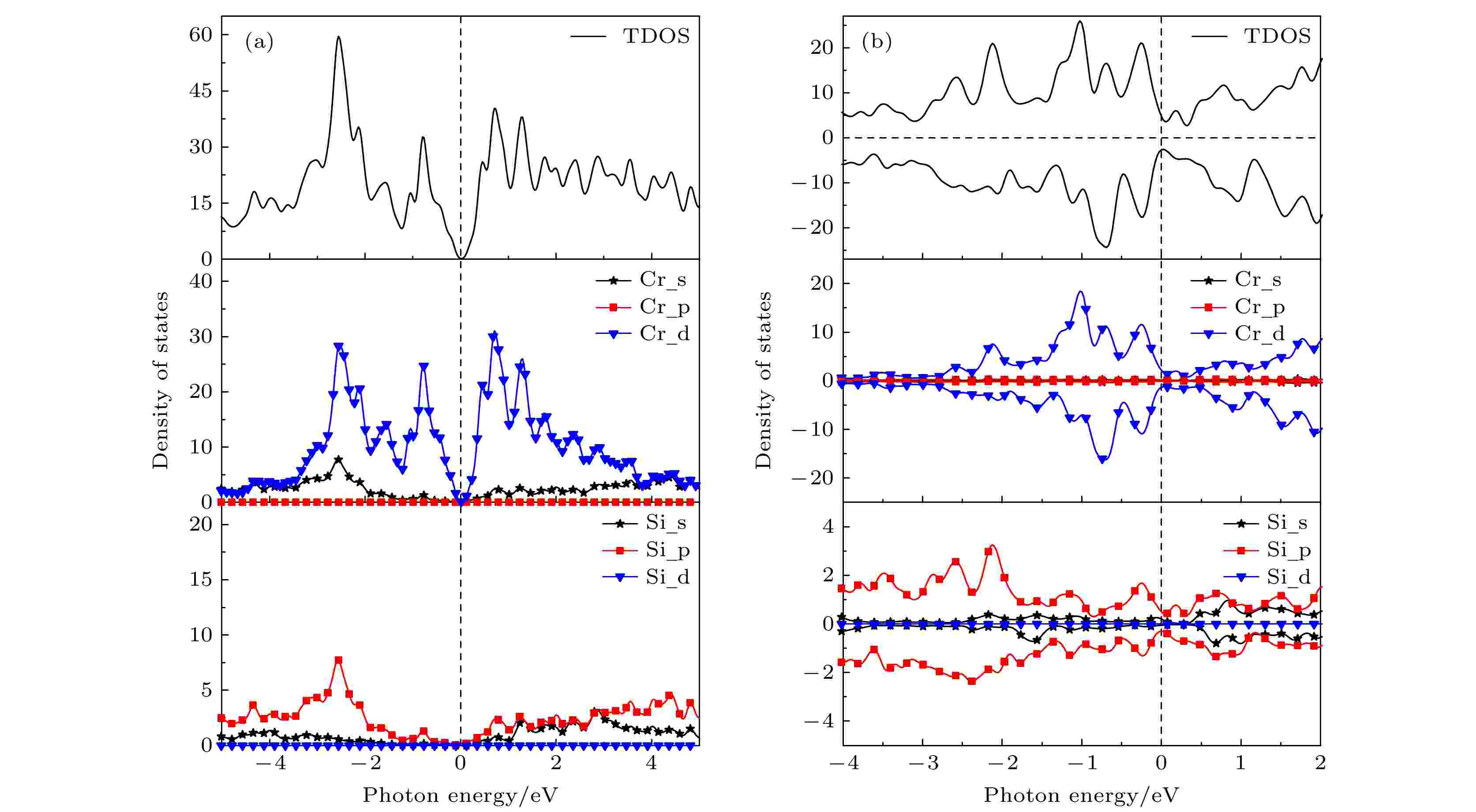
图 8 CrSi₂的态密度图　(a)三维CrSi₂; (b)二维CrSi₂
Figure8. Density of state of CrSi₂: (a) Three dimensional CrSi₂; (b) two dimensional CrSi₂.

三维CrSi₂总态密度自旋上升和自旋下降状态是完全对称的, 这里仅以自旋向上的总态密度分布表示, 如图8(a)所示.相较与此, 单层CrSi₂的态密度曲线明显具有不对称性, 展现出磁性, 可以观察到二维CrSi₂体系的磁矩主要来自于自旋向上的Cr-3d轨道态电子. CrSi₂费米能级附近的态密度主要由Cr-3d及Si-3p态轨道电子组成, 其中Cr-3d态轨道电子占据多数.
图9的电荷密度图表明, 二维CrSi₂中的Si原子已经处于完全离域化状态, 相对稳定, 而Cr原子中心处于完全局域状态, 周围被自由电子气包围. 二维CrSi₂体系中电子的移动主要受Cr的最外层电子控制, 其磁性也主要由Cr原子决定, 结合分态密度可知, 这是因为占据多数态密度的Cr(3d⁵4s¹)原子向相邻的两个Si(3s²3p²)原子转移一个4s轨道电子和一个3d轨道电子, 这时电子构型为3s²3p³的硅原子捕获一个电子, 进一步形成了稳定的电子结构, 从而具有零自旋、层内化学键能下降, 留下Cr原子电子构型为3d⁴的电子和净自旋, 因此CrSi₂材料的磁性主要由Cr决定.
图 9 二维CrSi₂的电荷密度图
Figure9. Charge density diagram of two-dimensional CrSi₂.

在3.70%和7.41%两种不同浓度下, Ti, V, Co, Ni掺杂二维CrSi₂的总态密度及分态密度分布如图10(a)—图10(h)所示. 3.70%浓度掺杂Ti的CrSi₂总态密度自旋上升和自旋下降状态是完全对称的, 除此之外, 其余掺杂体系由于总态密度上、下自旋曲线明显具有不对称性, 均呈现出磁性. 各体系态密度主要由Cr-3d, Si-3p和掺杂元素的3d轨道态电子耦合杂化而成, 自旋向上的Cr-3d态电子成为体系态密度及磁矩的主要贡献者. 同时, Cr-3d 态电子两峰分别与位于导带及价带掺杂原子的3d态电子表现出p-d杂化现象, 说明体系含有较弱的共价键. 顺磁掺杂元素Ti, V的态电子在导带贡献较多, 而铁磁Co, Ni元素的态电子主要分布在价带, 在导带贡献有限. 随着掺杂浓度的增加, 掺杂元素对体系态密度的贡献也随之增加, 同时还可看出, 铁磁性Co, Ni元素的态密度贡献相比于顺磁性Ti, V元素较多.
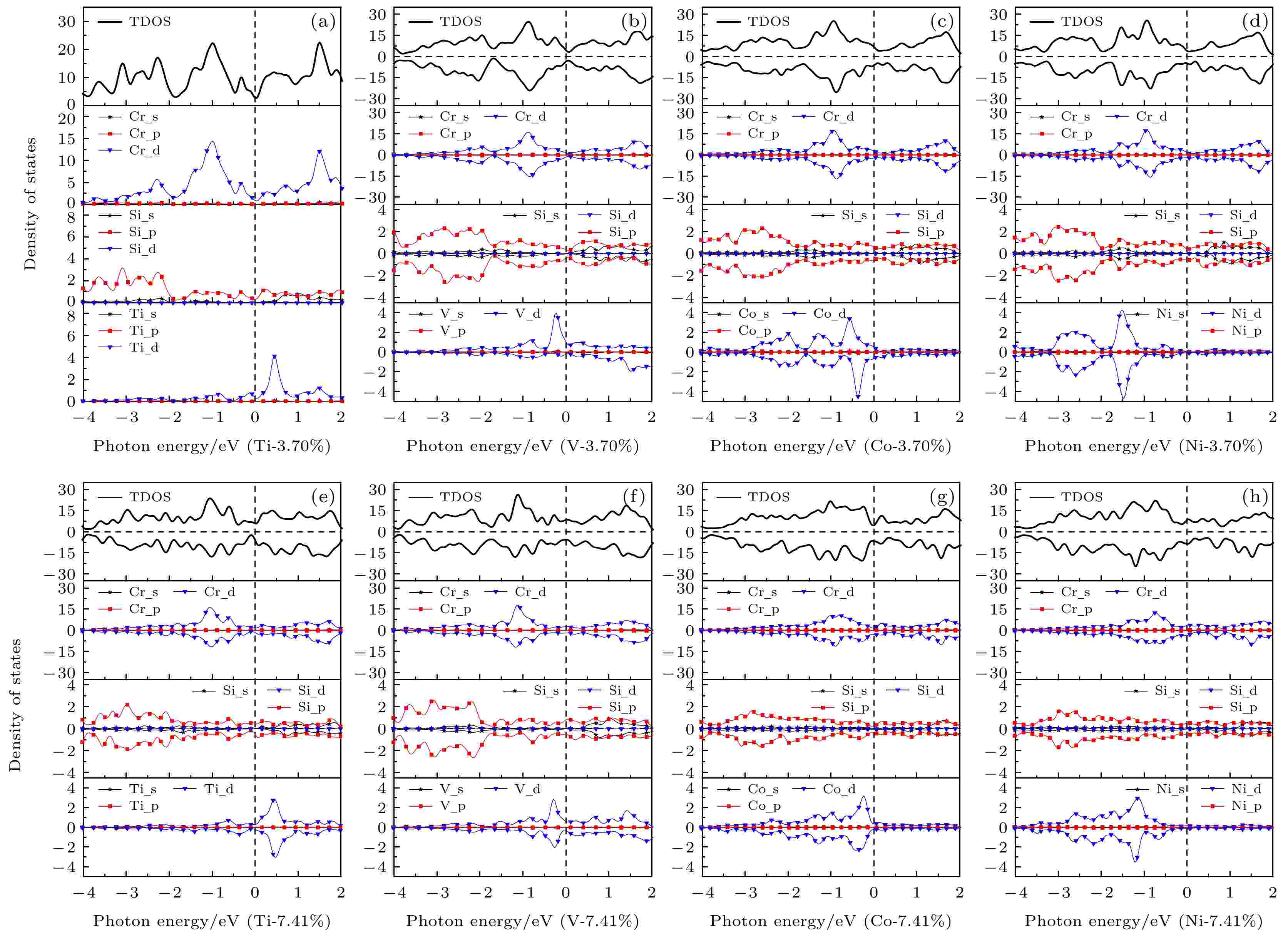图 10 不同浓度掺杂后二维CrSi₂的态密度图　(a) Ti-3.70%; (b) V-3.70%; (c) Co-3.70%; (d) Ni-3.70%; (e) Ti-7.41%; (f) V-7.41%; (g) Co-7.41%; (h) Ni-7.41%
Figure10. Density of states of two-dimensional CrSi₂ doped with different concentrations: (a) Ti-3.70%; (b) V-3.70%; (c) Co-3.70%; (d) Ni-3.70%; (e) Ti-7.41%; (f) V-7.41%; (g) Co-7.41%; (h) Ni-7.41%.

进一步分析分态密度可知, 在3.70%的掺杂浓度下, 掺杂Ti后的二维CrSi₂态密度分布主要由Cr-3d轨道以及Ti-3d轨道电子组成, Cr-3d轨道占据多数, Ti-3d轨道电子主要分布在导带. 图10(b)中掺杂V后的二维CrSi₂费米能级附近的态密度主要由Cr-3d与V-3d轨道电子组成, 而Cr-3p轨道和Si-3p轨道电子对系统的总态密度贡献有限, 但在远离费米能级的区域Si-3p轨道电子贡献变多. 掺杂Co后的CrSi₂电子结构中, 在费米能级附近的价带Co的3d态轨道电子增多, 证明在Co元素掺杂进体系之后, 核外电子变得活跃起来, 但Co对二维CrSi₂在导带部分的态密度分布几乎没有贡献, 可以看到, Co原子在体系结构稳定后处于完全离域化的状态. 由图10(d)可知, Ni掺杂的二维CrSi₂费米能级附近的态密度中Cr, Si的3p态轨道电子对系统的贡献较少, 主要由Cr-3d态轨道电子组成.
在7.41%的浓度下, 掺杂后的二维CrSi₂费米能级附近的态密度由Cr-3d轨道电子占据多数, 同时掺杂元素的3d态轨道电子成为二维CrSi₂态密度的主要贡献者. 掺杂Ti, V的二维CrSi₂在导带附近, Ti和V原子的3d态轨道电子贡献变多, Cr-3p轨道和Si-3p轨道电子对系统的总态密度贡献有限. 掺杂浓度为7.41%的二维CrSi₂的磁矩依旧主要来自自旋向上的Cr-3d态轨道电子. 图10(g)和图10(h)表明, 掺杂Co, Ni的3d态电子对二维CrSi₂分别在价带、导带的电子贡献较多, Cr-3p轨道和Si-3p轨道电子对系统的总态密度贡献有限. 与3.70 %浓度下的分布相似, 在7.41%浓度下, 铁磁元素对二维的电子贡献度降低, 这是因为在元素掺进体系后, Co和Ni原子的3d态轨道电子迅速向Cr原子周围移动, 根据洪特规则形成稳定的状态, 使得二维CrSi₂的态密度在费米能级附近的峰值减小.
2 -->

3.2.磁学性质

通过计算CrSi₂体系中的总磁矩来研究体系中的磁性, 如图11所示, 结果令人满意. 可以看出, 三维与二维CrSi₂在磁矩上有很大差异, 二维CrSi₂晶胞有明显的磁矩(3.55 μB), 每6个Cr和Si原子的局部磁矩分别为3.85 μB和–0.18 μB, 而三维CrSi₂体系中的铬和硅原子几乎没有磁矩, 这与Viet等^[54]以及Chen和Yan^[55]的结论一致.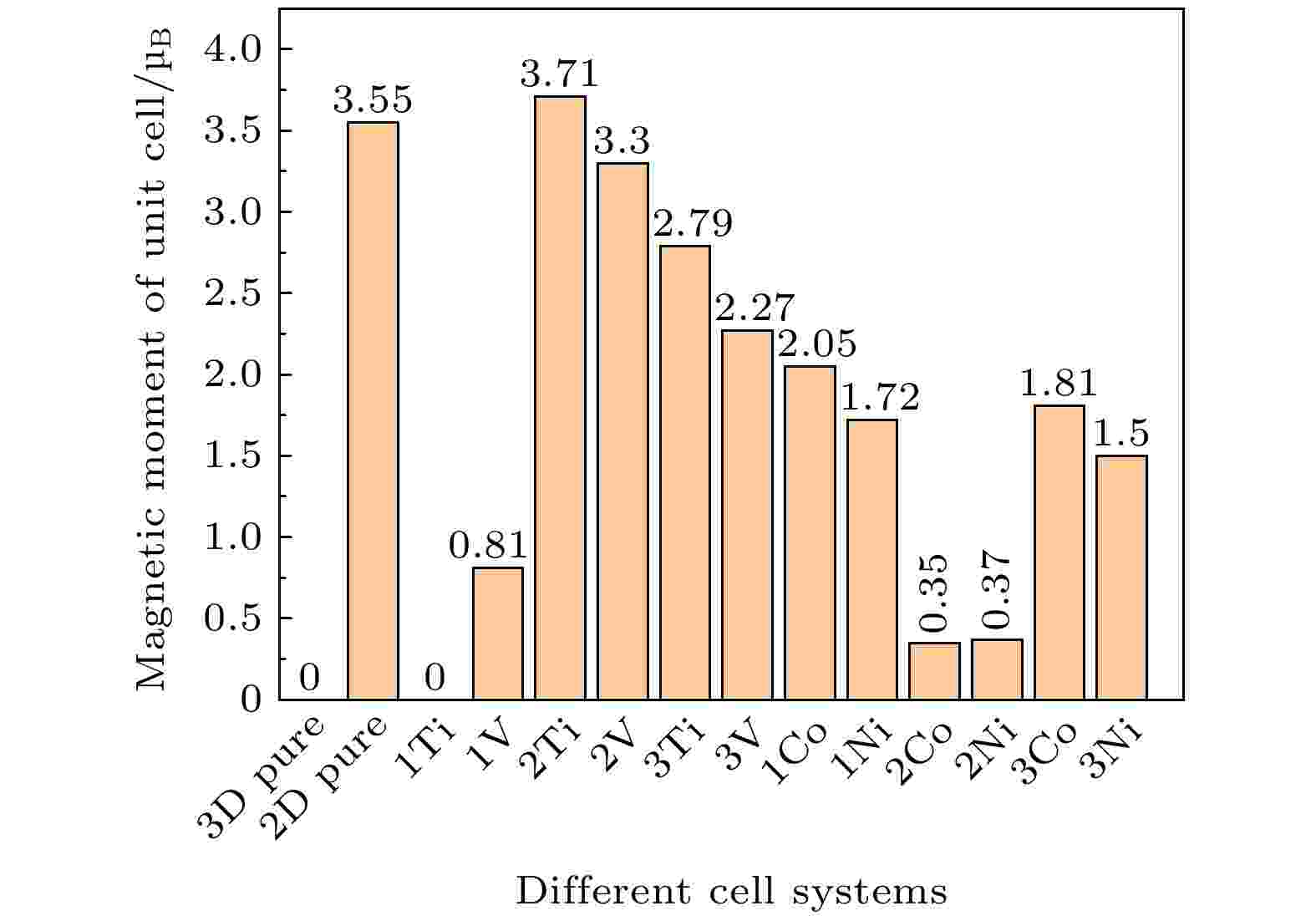
图 11 二维CrSi₂未掺杂及掺杂不同浓度的Ti, V, Co, Ni元素的磁矩
Figure11. Magnetic moments of two-dimensional CrSi₂ undoped and doped with Ti, V, Co and Ni elements of different concentrations.

在3.70%的掺杂浓度下, Ti掺杂二维CrSi₂的磁矩由本征的3.55 μB变为0 μB, 掺杂V, Co和Ni元素的磁矩分别为0.81, 2.05和1.72 μB, 掺杂后的CrSi₂磁矩均减小. 在7.41%的掺杂浓度下, 掺杂Ti元素后磁矩增大为3.71 μB, 预示着此时掺杂体系的自旋程度变强; 掺杂V元素后磁矩减小为3.30 μB, 表明V的加入削弱了Cr元素的最外层核外自旋电子数; 在该掺杂浓度下, 铁磁性Co, Ni元素对二维CrSi₂的磁影响较大, 掺杂Co元素后其磁矩变为0.35 μB, 证明二维CrSi₂自旋程度变弱; 掺杂Ni元素后, 体系磁矩变为0.37 μB, 这表明, Ni的引入削弱了Cr原子自旋向上的核外自旋电子数, 使得控制系统磁性的主要电子变为自旋向下的核外电子. 在掺杂浓度为7.41%时, 无论是掺杂Co还是Ni, 掺杂体系的磁矩均减小.
在11.1%的浓度下, 掺杂顺磁Ti, V元素后, 体系磁矩较之前浓度明显减小, 而掺杂铁磁Co, Ni元素使得二维CrSi₂磁矩增加, 但相较于本征二维CrSi₂, 该掺杂浓度下体系的磁矩减小, 表明体系自旋程度减弱, 产生磁矩的自旋向上d轨道电子贡献变小.

随着材料种类的不断丰富, 人们对材料光学性质研究的关注度逐渐提高, 通过对诸如复介电函数、折射率、吸收系数和光激发记忆光谱等性质的研究, 可以直接获得材料有关电子能带结构、杂志缺陷态及原子震动等多方面的信息, 进而理解材料的光学特征.
2

-->

4.1.复介电函数

电子跃迁的微观变化过程通过介电函数反映, 介电函数也能用以描述材料的电磁辐射响应. 图12为三维及二维CrSi₂的复介电函数, 三维CrSi₂静态介电常数ε₁(0) = 30.92, 随着光子能量的增加, 在能量到达0.95 eV处生成了一个较大的峰值40.06; 随后在能量3.51 eV处, ε₁到达第二峰; 此后开始急速下降, 对应于反射光谱的变化趋势; 在能量达到5 eV后, 三维CrSi₂的ε₁为负. 二维CrSi₂静态介电常数ε₁(0) = 27.33, 与三维CrSi₂相比其值减小, 随着能量的增加, 二维CrSi₂静态介电常数减小, 在4—8.4 eV的能量范围内, 介电函数实部为负值, 二维CrSi₂的反射谱在该能量段有一个峰值, 表明在此范围内, 光在二维CrSi₂材料中的传播较为困难, 表现出金属反射特性.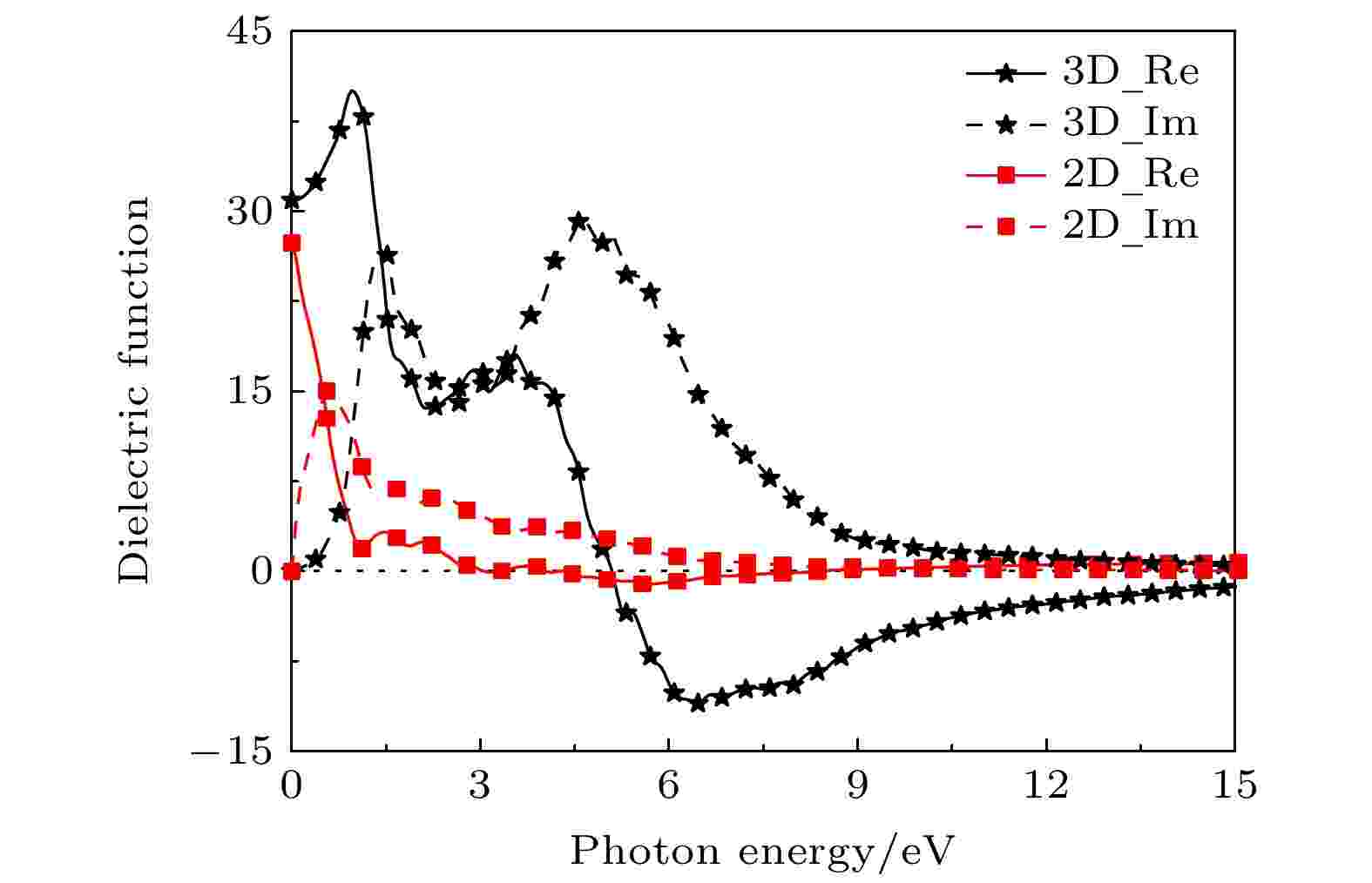
图 12 三维及二维CrSi₂的复介电函数图
Figure12. Three-dimensional and two-dimensional complex dielectric function diagrams of CrSi₂.

三维CrSi₂介电函数虚部出现了3个明显的介电峰, 分别位于1.47, 3.04与4.61 eV的能量处. 能量为1.47 eV的第一介电峰对应了来自Si原子的s轨道电子与Cr原子的d轨道电子杂化后从价带到导带的间接跃迁, 后续的两个介电峰来自价带间Si原子的p轨道电子到导带Cr原子的d轨道电子的带间跃迁. 二维CrSi₂的介电函数虚部在能量为0.56 eV时出现第一个介电峰, 由于二维CrSi₂材料呈现金属特性, 这里的吸收主要由电子从低能态向高能态的跃迁产生.
掺杂后的二维CrSi₂复介电函数如图13和图14所示, 在3.70%, 7.41%及11.1%的浓度下, Ti, V, Co, Ni掺杂二维CrSi₂的静态介电常数分别为62.36, 67.97, 66.75(Ti); 24.15, 83.83, 231.5(V); 48.34, 27.22, 371.9(Co); 39.6, 51.83, 120.43(Ni).
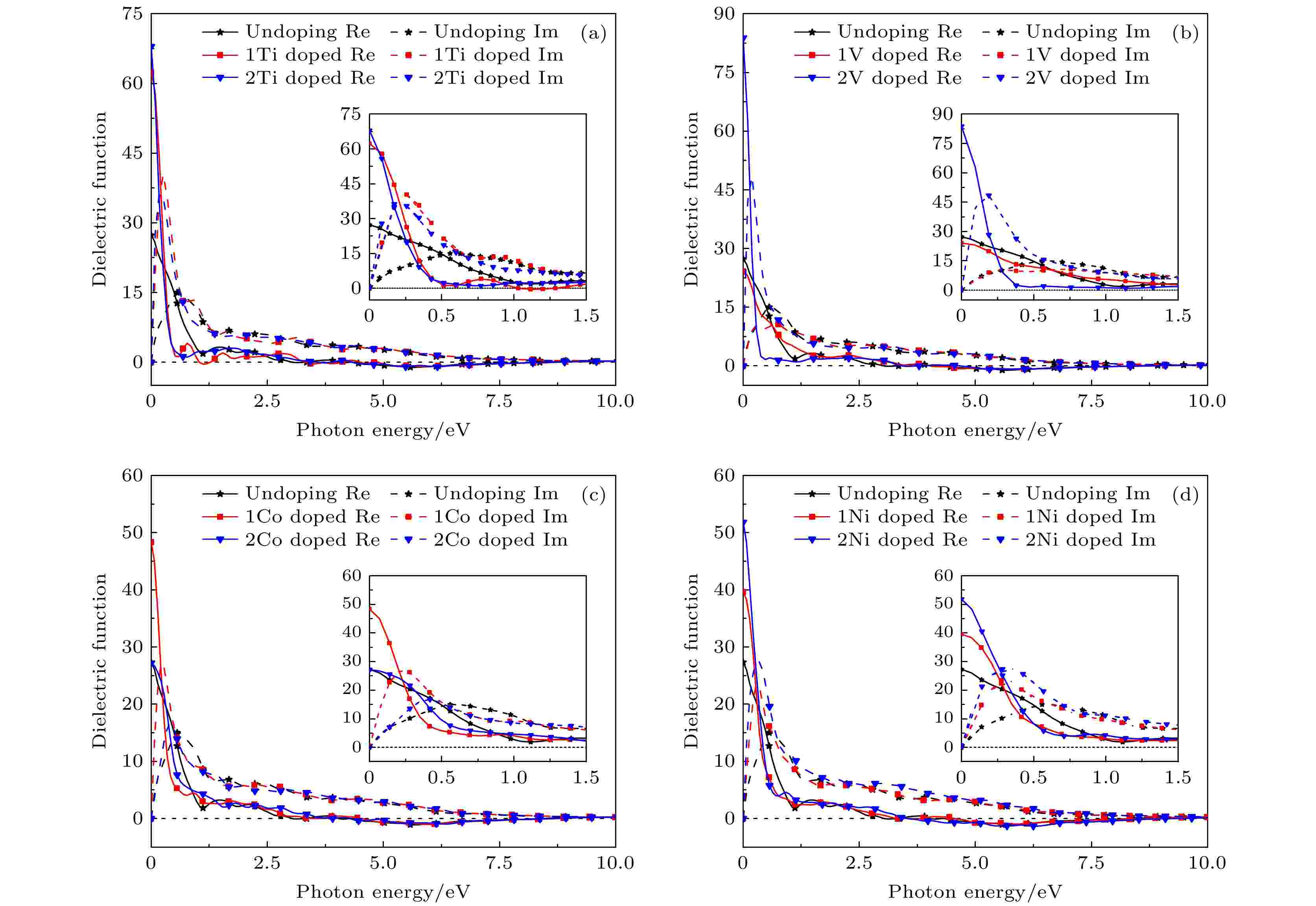图 13 3.70%及7.41%浓度下掺杂后的复介电函数图　(a) Ti; (b) V; (c) Co; (d) Ni
Figure13. Complex dielectric function diagrams of doping at 3.70% and 7.41% concentrations: (a) Ti; (b) V; (c) Co; (d) Ni.

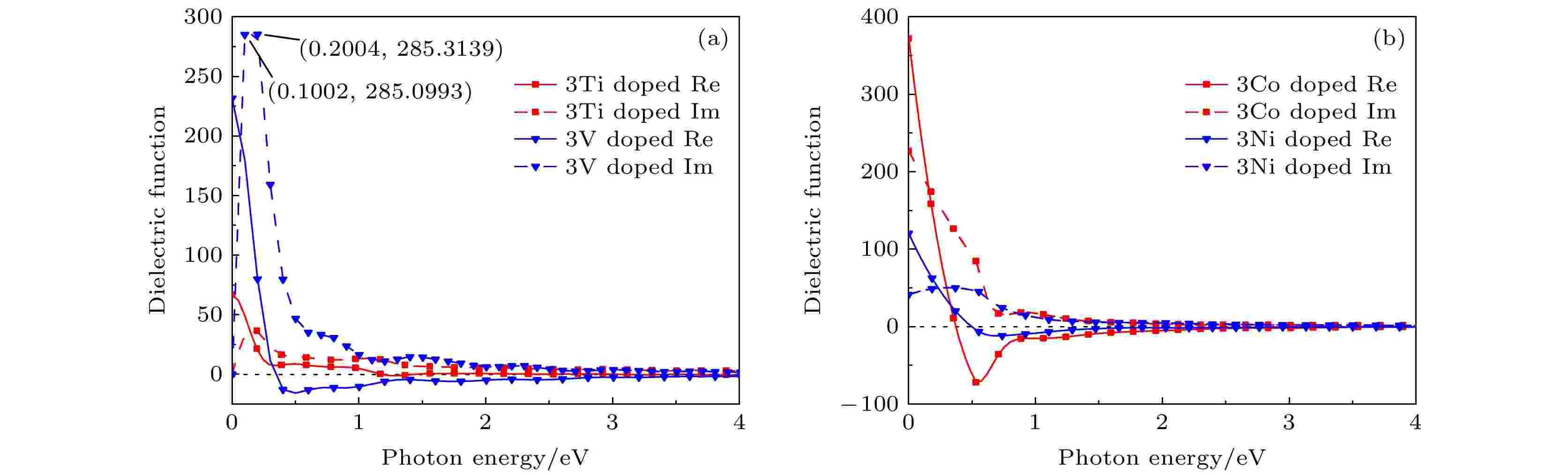图 14 11.1%浓度下掺杂后的复介电函数图　(a) Ti, V; (b) Co, Ni
Figure14. Complex dielectric function of doping at 11.1 % concentration: (a) Ti, V; (b) Co, Ni.

随着掺杂V, Ni元素浓度的提高, 二维CrSi₂的静态介电常数也相应增加, 而Ti的掺杂浓度对其静态介电常数影响较小, 其余元素的影响较大, 11.1%的掺杂浓度对二维CrSi₂体系的静态介电常数的影响较大. 相较于本征二维CrSi₂的静态介电常数ε₁(0) = 27.33, 除在3.70%浓度下掺杂V和在7.41%浓度下掺杂Co后二维CrSi₂静态介电常数数值减小, 其余掺杂体系的ε₁(0)值均增加.
对在3.70%浓度下, 掺杂Ti, V, Co, Ni后分别表现为间接半导体、稀磁半导体、金属磁体和半金属铁磁体的二维CrSi₂进一步分析可知, Ti掺杂的二维CrSi₂介电函数实部随着光子能量的增加迅速减小, 能量到达0.77 和1.54 eV时生成了4.07, 2.01的峰值, 在1.03—1.28 eV的能量范围内, 介电函数的实部为负值, 同时Ti掺杂二维CrSi₂的反射谱也在这个能量段出现一个峰值, 随后随着光子能量的增加, 介电函数的实部数值趋于0. V掺杂的二维CrSi₂静态介电常数ε₁(0) = 24.15, 随着光子能量的增加, 介电函数的实部逐渐减小为0, 期间并未出现峰值. Ti掺杂的二维CrSi₂呈现半导体性质, 所以介电函数的实部呈现多个峰值, 而V掺杂的二维CrSi₂表现为稀磁半导体的性质, 其介电函数的实部曲线变化趋势较为特殊. Co掺杂的二维CrSi₂静态介电常数ε₁(0) = 48.34, 比本征二维CrSi₂的静态介电常数大, 随着光子能量的增加, 介电函数的实部迅速减小, 在光子能量到达0.9 eV时生成了第一个峰值4.5, 随后在能量1.73 eV处生成了第二个峰值3.09, 在4.5—8.6 eV的能量范围内, 介电函数的实部表现为负值, 同时掺杂Co后二维CrSi₂的反射谱也在这个能量段出现一个峰值, 随后随着光子能量的增加, 介电函数的实部数值趋于0. Ni掺杂的二维CrSi₂静态介电函数实部在光子能量到达1.73 eV时生成了第一个峰值2.89, 在4.51—8.7 eV的能量区间介电函数的实部为负值.
介电函数虚部ε₂(ω)的变化曲线中, Ti掺杂的二维CrSi₂在图13(a)的能量范围内出现了4个明显的介电峰, 能量位置分别为0.26, 0.86, 1.63与3.09 eV, 位于能量为0.26 eV处的第一介电峰对应了来自Si原子的s轨道电子与Cr原子的d轨道电子杂化, 同时受到Ti原子的d轨道电子影响后, 从价带到导带的间接跃迁, 后续的介电峰来自价带间Ti原子的d轨道、Si原子的p轨道电子到导带Cr原子的d轨道电子的带间跃迁. V掺杂的二维CrSi₂在能量0.28 eV时出现第一个介电峰, 其电子由低能态向高能态进行跃迁. 对于Co掺杂的二维CrSi₂, ε₂(ω)出现2个明显的介电峰, 对应的能量分别为0.21与0.96 eV. 位于能量0.21 eV的第一介电峰对应了来自Si原子的s轨道电子与Cr原子的d轨道电子杂化, 同时受到Co原子的d轨道电子影响的电子移动. 后续的介电峰, 则来自价带间Co原子的d轨道、Si原子的p轨道电子到导带Cr原子的d轨道电子的移动. 对于Ni掺杂的二维CrSi₂, 在能量为0.28 eV时出现第一个介电峰, 但由于二维CrSi₂材料呈现的特殊性质, 电子也由低能态向高能态进行跃迁. 在11.1%的掺杂浓度下, 掺杂体系的介电函数迅速提高, 这是由体系表现出的金属性使得电子传播率更强导致的.
2 -->

4.2.吸收系数和反射系数

光通过固体材料时由于与电子和原子发生相互作用, 会发生光的吸收, 当光照射至固体表面时也会发生光的反射, 频率与反射系数之间的关系以反射谱表征. 在一定的理论近似下, 材料的光吸收系数可以直接计算, 但实验难以准确测量, 主要通过反射系数间接实现光吸收性质的计算与分析. 三维及二维CrSi₂的吸收谱与反射谱如图15所示, 在能量小于0.35 eV的范围, 三维CrSi₂的吸收系数为零, 此后, 其吸收系数随能量的增大而增大, 并在入射光能量E = 7.93 eV时取得最大值2.61 × 10⁶ cm^–1, 随后吸收系数随光子能量的增大逐渐减小, 并在入射光能量E = 40 eV时减少为零. 由于二维CrSi₂表现为金属性, 在低能区, 其吸收系数随着光子能量的增加而增加, 并伴有三个吸收峰, 对应的能量位置分别为1.04, 3.06及5.57 eV, 在入射光能量E = 5.57 eV时, 吸收系数取得最大值0.73 × 10⁶ cm^–1. 在0—1.18 eV的能量范围内, 二维CrSi₂的吸收系数高于三维CrSi₂, 而能量大于1.18 eV以后, 三维CrSi₂吸收系数较大. 图15表明, 本征二维CrSi₂对红外区和紫外区, 甚至在远红外和真空紫外区的光子也有很好的吸收.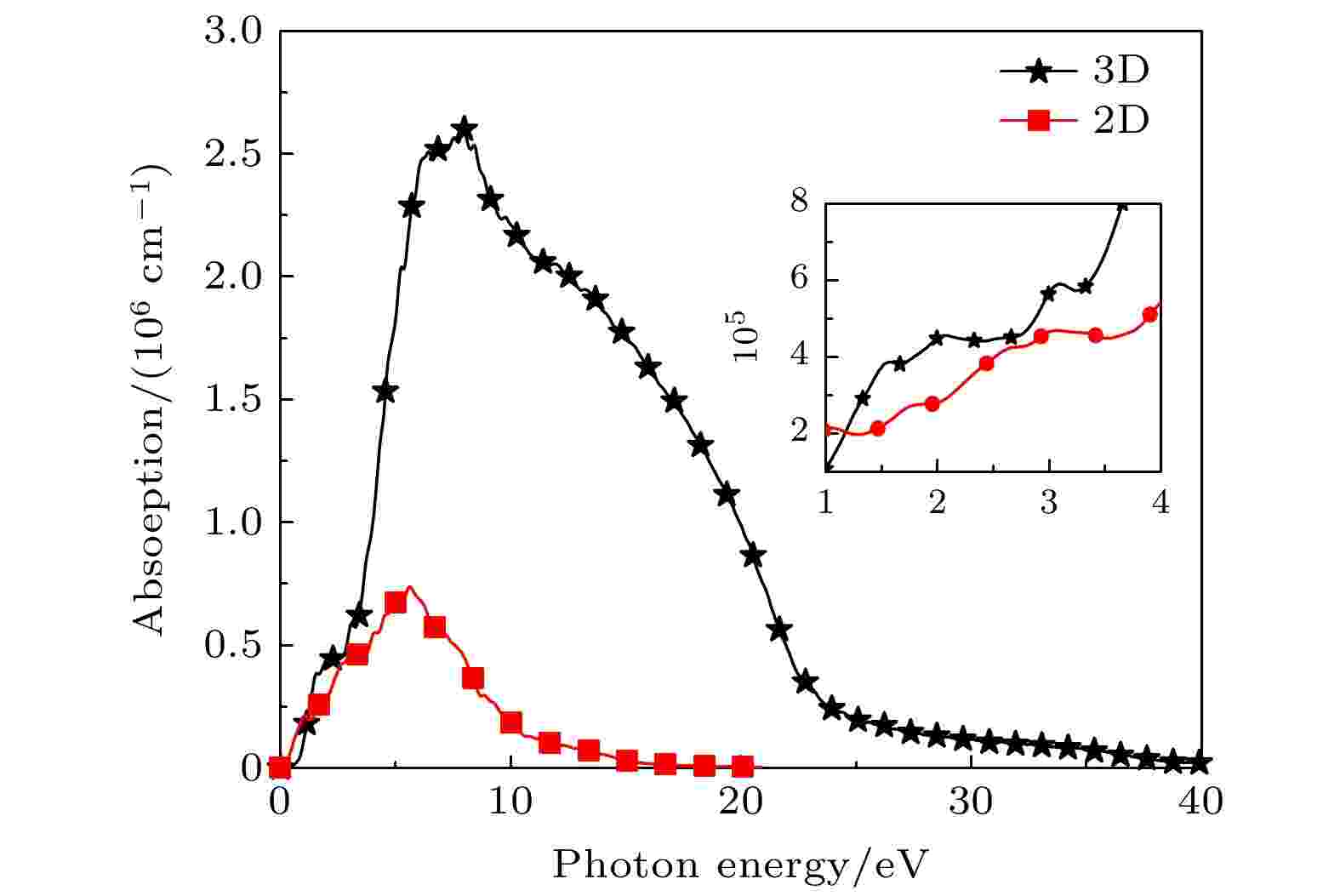
图 15 三维和二维CrSi₂的吸收系数
Figure15. Absorption coefficient of three-dimensional and two-dimensional CrSi₂.

不同掺杂浓度下对应二维CrSi₂的吸收谱如图16所示. 7.41%浓度下掺杂Ti, V, Co, Ni二维CrSi₂的吸收系数延伸到远红外区, 直接证明对应体系表现出的金属性, 同时具有自由载流子吸收, 意味着其在远红外和真空紫外探测器中有潜在的应用.
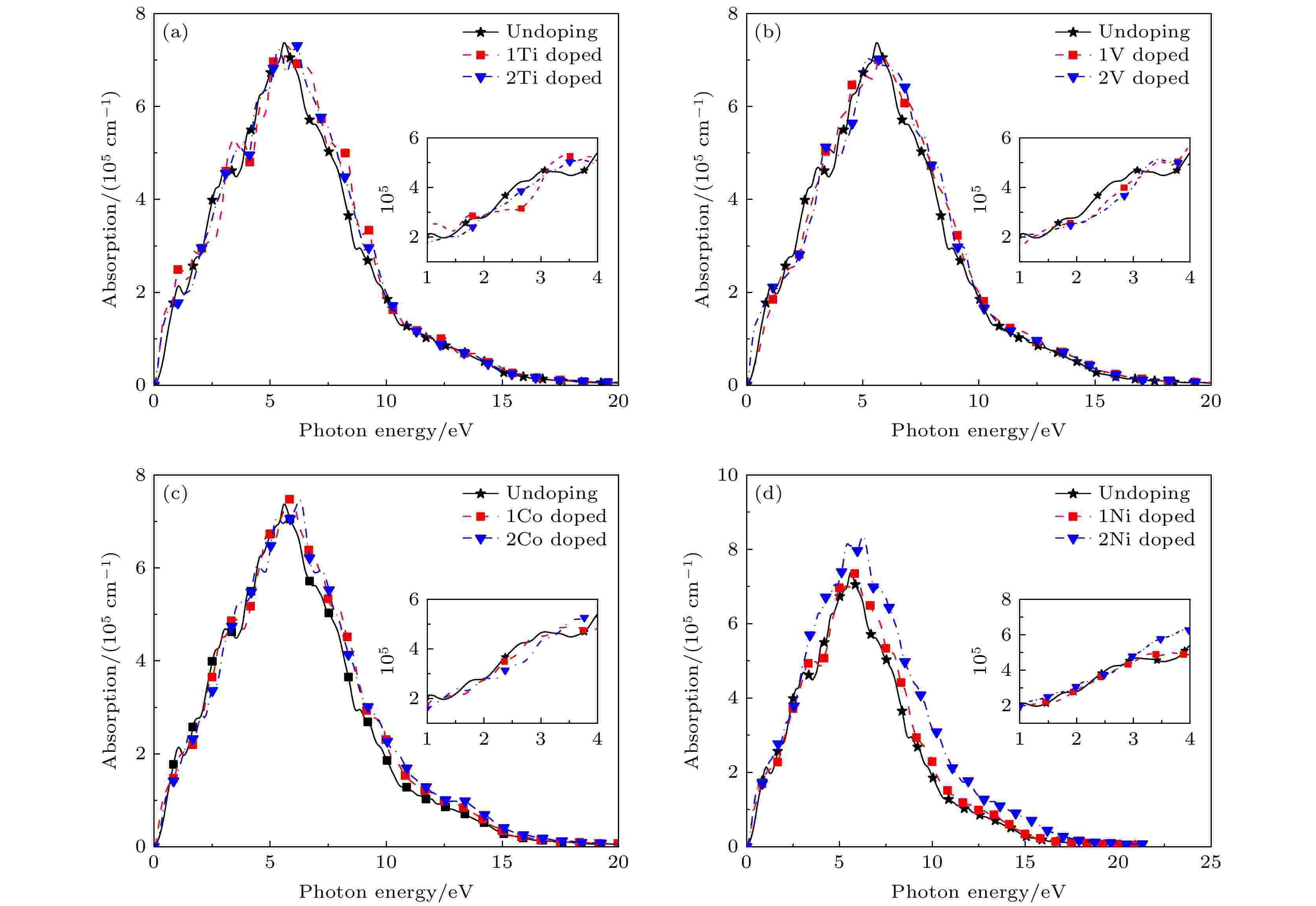图 16 3.70%及7.41%浓度下掺杂后的吸收系数　(a) Ti; (b) V; (c) Co; (d) Ni
Figure16. Absorption coefficient of doping at 3.70 % and 7.41% concentrations: (a) Ti; (b) V; (c) Co; (d) Ni.

进一步对3.70%掺杂浓度的体系分析可知, 相较于本征CrSi₂, Ti掺杂二维CrSi₂的最大吸收峰峰值增大且吸收谱蓝移, 而引入V后, 其最大吸收峰峰值减小. 掺杂Ti的二维CrSi₂在红外、可见光以及紫外区的吸收系数明显高于其本征态, 并且伴有多个吸收峰, 在入射光能量E = 5.74 eV时, 吸收系数取得最大值0.73 × 10⁶ cm^–1, 随后吸收系数随光子能量的增大逐渐减小并在入射光能量E = 20.00 eV时减小至零. 掺杂V的CrSi₂的最大吸收峰发生蓝移, 在入射光能量E = 5.77 eV时, 吸收系数取得最大值, 为0.71 × 10⁶ cm^–1, 随后吸收系数随光子能量的增大逐渐减小, 同时可以看出其在红外、可见光以及紫外的范围吸收系数小于本征二维CrSi₂.
掺杂Co, Ni的最大吸收峰峰值略有增大, 吸收谱发生蓝移. 在3.70%掺杂浓度下, 引入Co的二维CrSi₂吸收系数随能量的增大而增大, 其在红外、可见光及紫外范围的吸收系数明显高于本征CrSi₂, 并且有多个吸收峰, 在入射光能量E = 5.89 eV时, 吸收系数取得最大值0.749×10⁶ cm^–1, 随后吸收系数随光子能量的增大逐渐减小, 在入射光能量E = 20 eV时减小为零. 掺杂Ni元素在红外、可见光及紫外范围的吸收系数同样大于未掺杂的CrSi₂, 其最大吸收峰蓝移, 在入射光能量E = 5.89 eV时吸收系数取得最大值, 0.735 × 10⁶ cm^–1, 随后吸收系数随光子能量的增大逐渐减小.
图17给出了本征三维及二维CrSi₂的反射谱, 三维CrSi₂的反射谱出现多个峰值, 在能量E = 1.18 eV处到达第一峰, 这时三维CrSi₂有54.8%的反射系数, 随后在能量E = 8.55 eV时到达第二峰, 此时反射系数为77.3%, 结合前述可以得出: 三维CrSi₂对光的吸收和折射特性都较强. 本征二维CrSi₂在4—8.4 eV的能量范围内, 介电函数实部表现为负值, 对应反射谱在这个能量段出现了一个63.4%的峰值, 二维CrSi₂相较于三维CrSi₂的反射系数整体较小, 但同样在紫外区呈现出较强的反射特性, 而在红外区域反射系数较低, 这对光电子材料的应用是有帮助的.
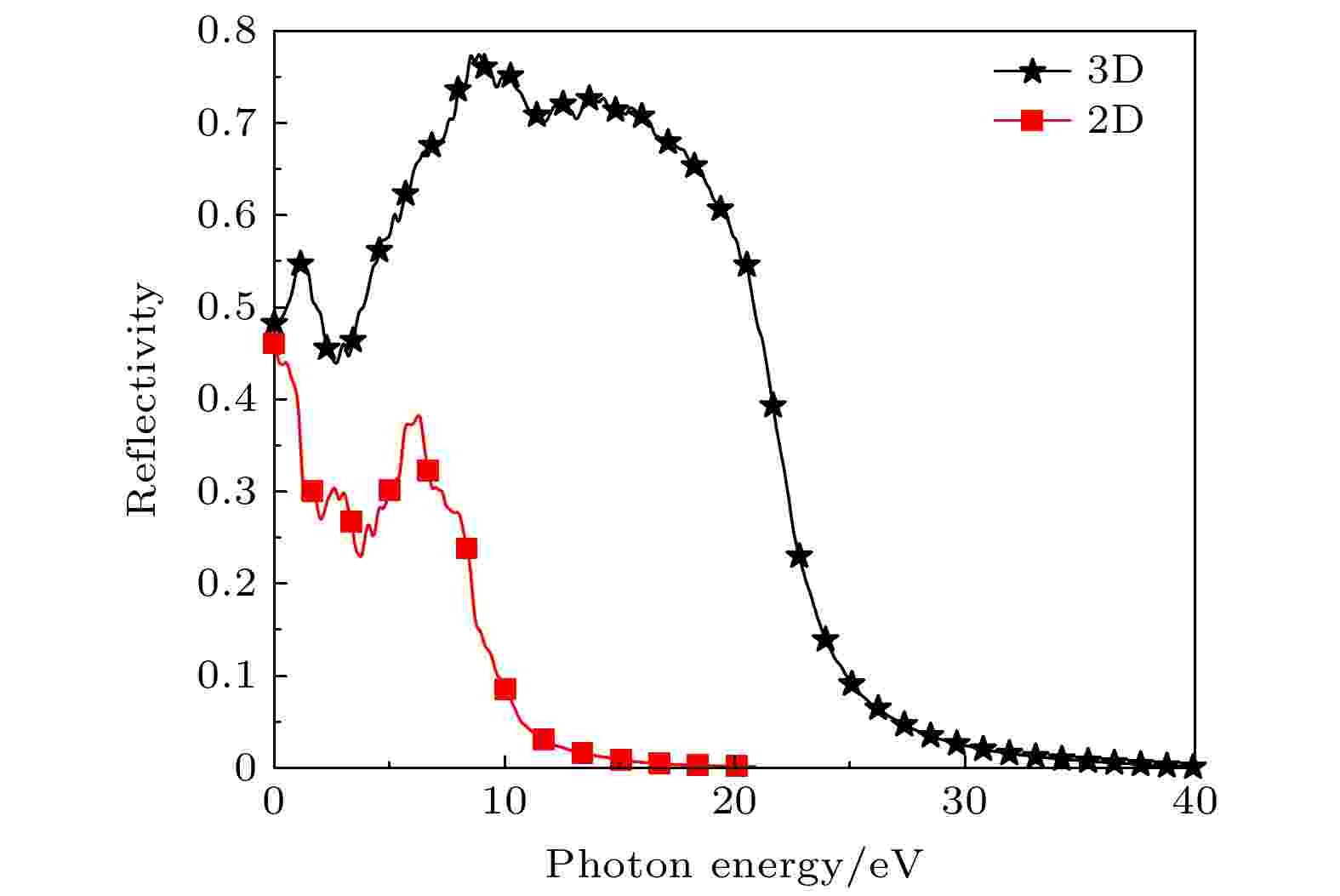图 17 三维和二维CrSi₂的反射系数
Figure17. Reflection coefficient of CrSi₂ in three and two dimensions.

掺杂后的CrSi₂反射谱如图18所示, 掺杂体系的反射谱出现了多个峰值且整体趋势与本征CrSi₂的反射谱相似. 在3.70%的浓度下, 能量为0 eV时Ti掺杂的二维CrSi₂的反射系数大幅提升, 达到了60%, 随着能量的增加, 反射系数逐渐变小, 在可见光范围内拥有将近35%的反射系数, 随后在能量E = 6.85 eV时达到最高峰, 此时拥有38%的反射系数; 掺杂V后, 材料在能量为0 eV时的反射系数降低为43.4%, 在能量变大的过程中, 反射系数逐渐变小, 在能量E = 6.14 eV时达到减小之后的最高峰, 拥有33%的反射系数; 掺杂Co后, 材料在能量为0 eV时的反射系数大幅提升至56%, 在能量变大的过程中, 反射系数逐渐变小, 在能量E = 6.1 eV时达到最高峰, 拥有37.16%的反射系数; 掺杂Ni后, 材料在能量为0 eV时的反射系数降低为52.2%, 在能量变大的过程中, 反射系数逐渐变小, 在能量E = 6.03 eV处到达第二反射峰, 拥有36%的反射系数. 以上分析说明掺杂前后的二维CrSi₂对光的吸收和反射特性都较强, 这对实现光电子材料的应用是极为有利的.
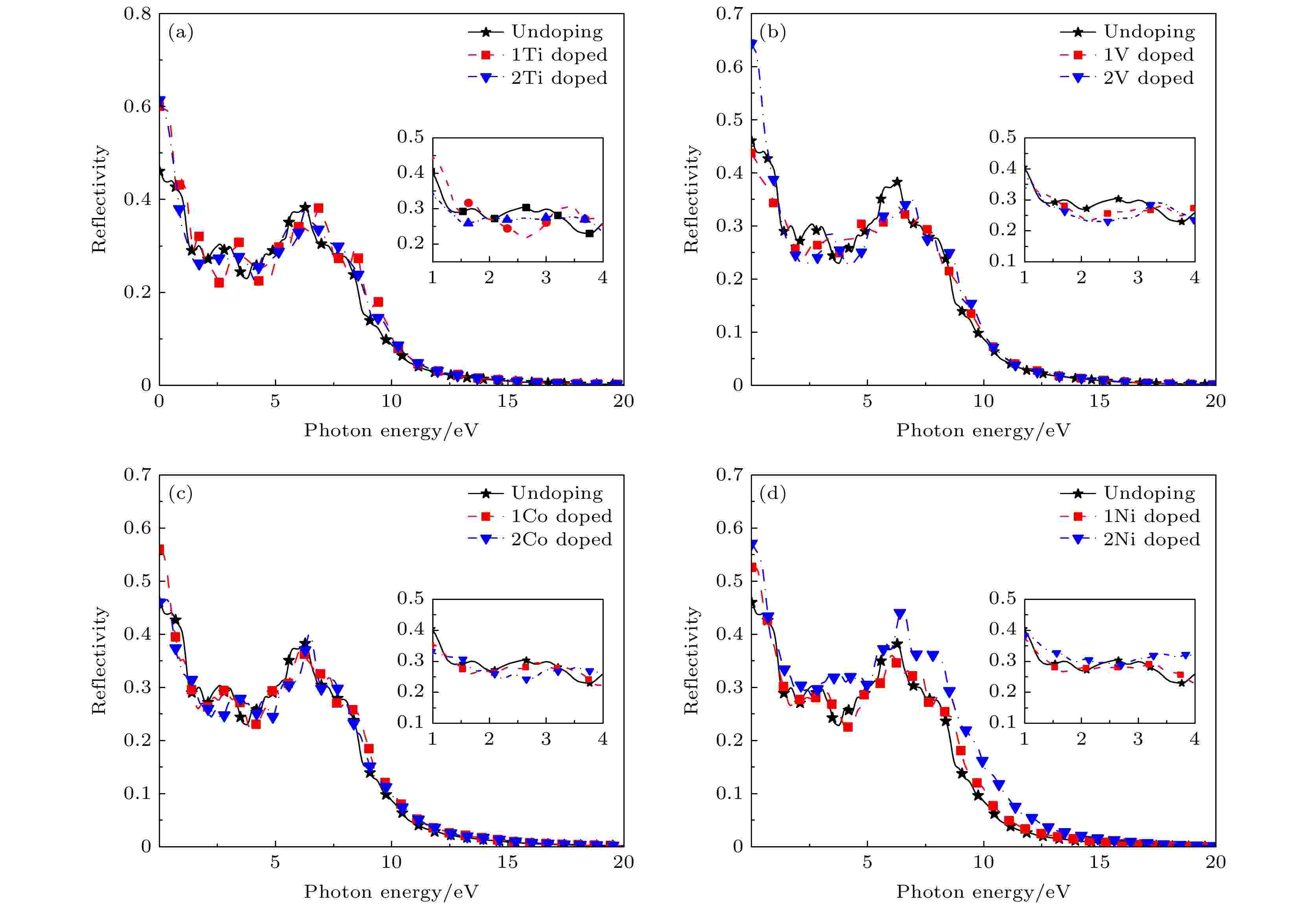图 18 3.70%及7.41%浓度下掺杂后的反射系数　(a) Ti; (b) V; (c) Co; (d) Ni
Figure18. Reflection coefficient of doping at 3.70% and 7.41% concentrations: (a) Ti; (b) V; (c) Co; (d) Ni.

2 -->

4.3.能量损失函数

图19为本征二维、三维CrSi₂的能量损失函数, 其中能量损失光谱的峰值代表了物质从金属性向介电性的过渡点. 三维、二维CrSi₂的能量损失函数分别在E = 21.75, 8.57 eV时达到峰值8, 3.02, 相较于三维CrSi₂, 切割其块体而成的二维CrSi₂的等离子体频率ω_p发生蓝移且峰值减小. 随着入射光能量的增加, 不难发现位于吸收系数和反射系数对应能量区域的能量损失谱峰值突然减小, 两种体系逐渐变为透明, 它还对应于在吸收光谱中吸收系数减小的能量范围. 当三维、二维CrSi₂的入射光能量E分别大于40和19.86 eV时, 两种体系的离子体频率ω_p为零, 此时系统在完全透明的状态下运行, 可以观察到在该能量范围内, 吸收光谱与反射光谱对应的吸收系数和反射系数也接近于零.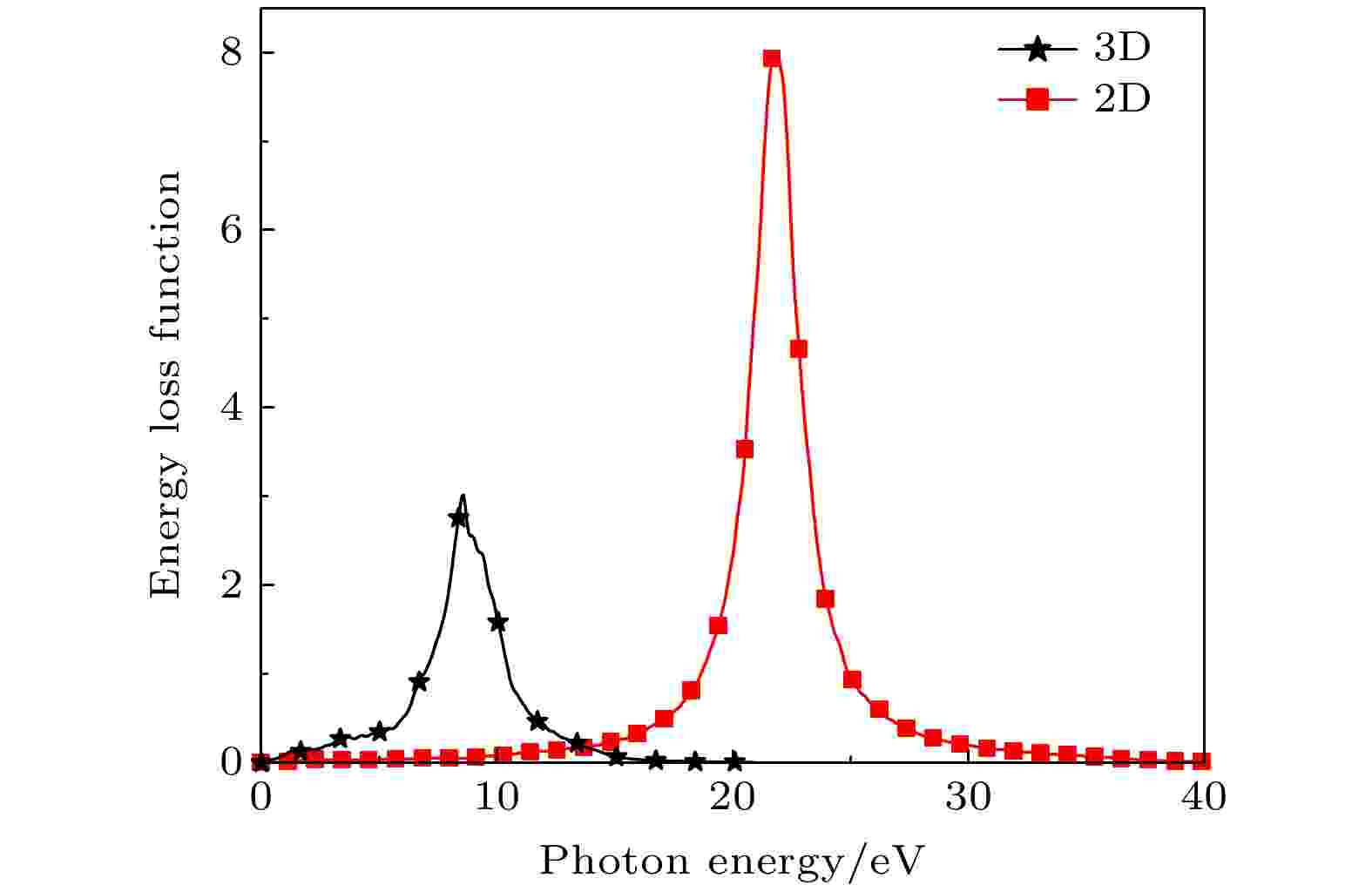
图 19 三维和二维CrSi₂的能量损失函数
Figure19. Energy loss function diagrams of three-dimensional and two-dimensional CrSi₂.

图20为掺杂后二维CrSi₂的能量损失函数曲线. Ti, V, Co及Ni以3.70 %浓度掺杂二维CrSi₂后, 得到的能量损失函数分别在能量E = 9.43, 9.18, 8.95及8.88 eV时达到峰值3.17, 2.85, 2.85及2.92, 以7.41%浓度掺杂二维CrSi₂后, 分别在E = 8.90 , 8.89, 8.78和9.8 eV达到峰值2.92, 3.05, 2.66和2.87. 由于掺杂3.70%的Ti元素后, 二维CrSi₂变为半导体, 所以ω_p的峰值大于其本征态, 而7.41%掺杂浓度时, 由于体系的金属性增强所以系统的ω_p峰值减小. 相较于本征态, 在3.70 %及7.41%掺杂浓度下, 掺杂的二维CrSi₂等离子体频率ω_p发生蓝移, 但在11.1%掺杂浓度下, 顺磁元素Ti, V掺杂体系的ω_p红移, 铁磁元素Co, Ni掺杂体系的等离子体频移动幅度较小, 保持在本征态附近.
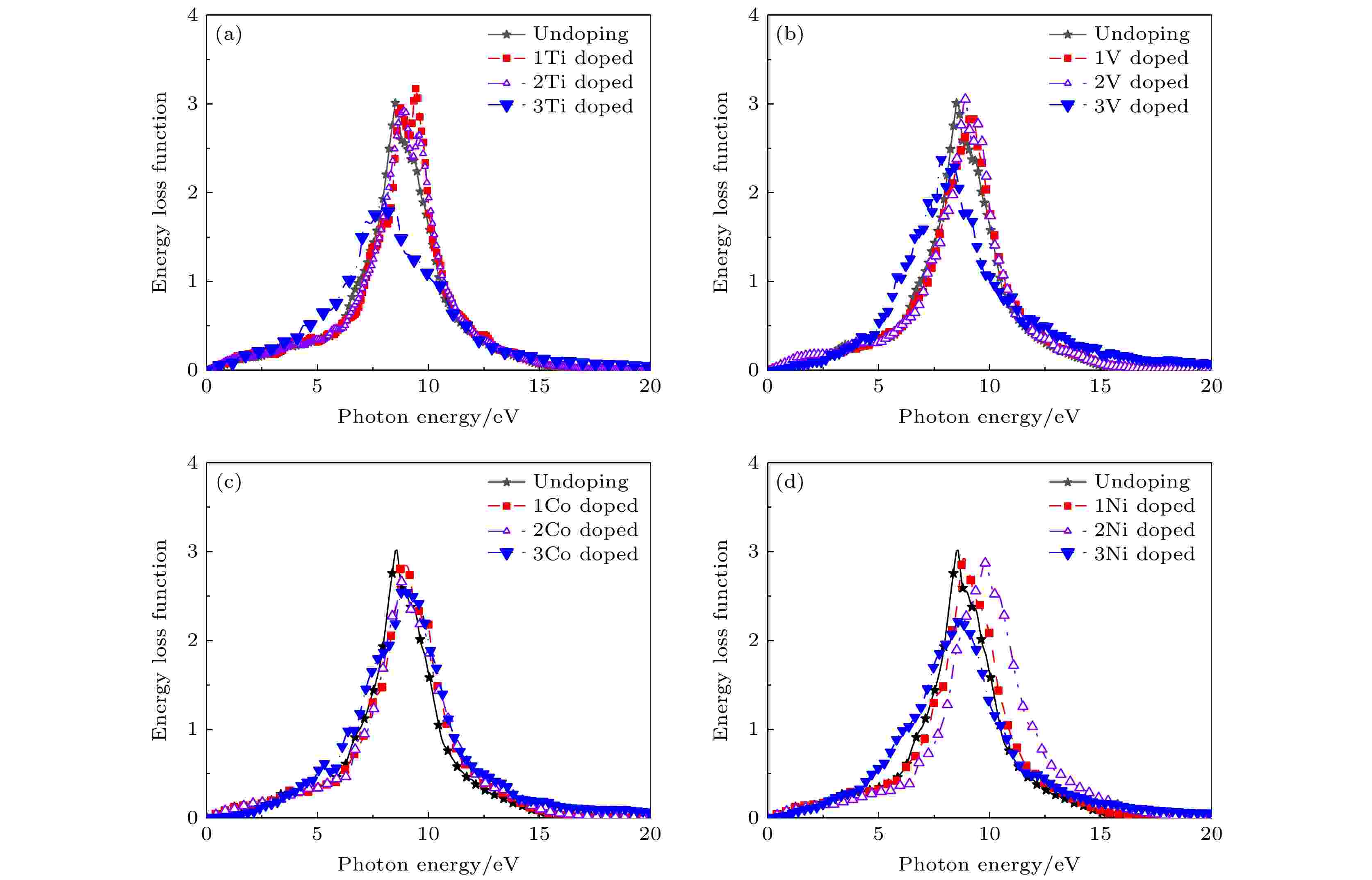图 20 3.70%及7.41%浓度下掺杂后的能量损失函数　(a) Ti; (b) V; (c) Co; (d) Ni
Figure20. Energy loss function after doping at the concentration of 3.70% and 7.41%: (a) Ti; (b) V; (c) Co; (d) Ni.

铁磁元素掺杂体系的能量损失函数峰值均减小, 其中, 浓度为11.1%的掺杂体系减小幅度最大, 这是由于在较高的掺杂浓度下体系的金属性较强导致的, 此时, 对应体系能量损失函数峰值的下降幅度最大. 可以观察到随着入射光能量的增加, 能量损失函数曲线先增加而后开始降低, 掺杂体系逐渐变为透明, 对应吸收谱中吸收系数的下降.

采用基于密度泛函理论的第一性原理赝势平面波方法对切割块体CrSi₂(001面)得到的单分子层结构进行了研究, 同时采用有着特殊3d壳层的4种过渡金属元素Ti, V, Co, Ni对单层CrSi₂材料在不同浓度下进行替位式掺杂, 计算掺杂前后的电子结构、磁学及光学性质, 主要结论如下:
三维CrSi₂是一种间接带隙值为0.355 eV的非磁性半导体, 二维CrSi₂则表现出金属性和磁性. 二维CrSi₂磁矩主要来自自旋向上的Cr-3d轨道电子, 磁矩为3.55 μB, 体系磁性令人满意, 同时其在远红外及紫外范围内的吸收系数与反射系数都很强, 表现出优异的光学性质.
在3.70%的掺杂浓度下, 掺杂后的二维CrSi₂磁矩均减小, 其中掺杂Ti元素后, 磁矩变为0 μB, 同时由本征态表现出的金属性向带隙为0.125 eV的间接半导体转变; 掺杂V后二维CrSi₂同时拥有电子电荷和自旋两种自由度, 表现出与稀磁半导体一致的特性, 有望在自旋电子器件中发挥巨大作用; 掺杂Ni后二维CrSi₂自旋向上的能带图出现0.09 eV的带隙, 自旋向下的能带图则表现为金属性, 体系呈现半金属铁磁体的特性, 其独特的电子结构是设计高效自旋滤波器的理想材料. 掺杂结果表明, 二维CrSi₂是一种充满希望的磁性材料. 在7.41%的掺杂浓度下, 掺杂体系均呈现出金属性, Ti和V掺杂的二维CrSi₂磁矩变化较小, 在该浓度下掺杂Ti元素的体系具有最大磁矩, 为3.71 μB; 掺杂Co和Ni元素后相较于本征及3.70%浓度下的掺杂体系, 磁矩减小. 在11.1%的掺杂浓度下, 体系能带范围扩大且形状趋于陡峭, 使得键的相互作用变大, 能级分裂能变大, 说明在11.1%的掺杂浓度下, 体系的有效质量变小, 载流子迁移性质变强, 又因为导带和价带均超过费米能级, 说明材料的金属性变得更强; 掺杂Ti和V后, 体系的磁矩较7.41%掺杂浓度减弱. 掺杂前后的二维CrSi₂均有着优良的光学性质, 多数体系的光学性质发生蓝移, 峰值增大, 体系在远红外范围内的吸收系数与反射系数较强, 表明在远红外和真空紫外探测器中具有潜在的应用价值.