摘要:短纤维结构对聚合物材料玻璃化转变温度及非线性力学具有非常重要的影响. 本文利用粗粒化分子动力学方法研究了碳纳米管(CNTs)含量对聚甲基丙烯酸甲酯(PMMA)玻璃化转变、扩散系数及非线性力学特性的影响. 分子动力学模拟结果显示: 短CNTs纤维的加入的确会改变PMMA体系的玻璃化转变温度, 模拟结果与实验测量结果一致, 而且随着CNTs含量的增加其对应的玻璃化转变温度也会随着增加. 进一步分析扩散特性发现, CNTs加入PMMA对于体系扩散特性的改变主要发生在玻璃化温度以上, 玻璃化温度以下结构对应的扩散系数差异非常的小. 聚合物材料在服役过程中难免要遭受应力-应变的作用, 而且其结构对应的模量和韧性成反比. 基于此, 本文通过非平衡分子动力学探究了短CNTs纤维添加PMMA复合材料的非线性力学特性. 模拟结果显示: 随着CNTs纤维的含量增加, 其对应的屈服模量也在不断的增加, 而且含有短CNTs纤维的体系还能够保持原来的韧性. 因此, 分子层面的理论研究策略可以为进一步的实验和加工提供理论指导.
关键词: 玻璃化转变温度/
非线性力学/
聚合物纳米复合材料/
扩散

English Abstract

全文HTML

--> --> -->

通过短纳米纤维增强聚合物材料的力学、热学及电学性能的研究最近几年引起了研究者广泛的关注^[1-4]. 首先, 短纤维增强聚合物复合材料不仅仅在力学性能方面得到了很大的提升, 而且短纳米纤维材料可以使聚合物力学模量提升的同时其对应的韧性特征受到很小的损失. 其次, 短纳米纤维增强的聚合物纳米复合物材料相比于连续性纤维材料更容易加工^[5], 成本更低, 更容易被市场接受. 故而, 在成本和性能之间的折衷使得短纤维聚合物复合材料成为材料领域优秀的替代品. 经过前期调研, 我们发现在不同类型的纤维中, 随着碳纳米管(CNTs)制备技术的成熟以及其优异的力学及电学性能可以为高性能聚合物基复合材料的制备及产业化提供可能^[4,6,7].
根据现有的实验, 不难发现CNTs纤维与聚合物分子复合形成的聚合物纳米材料的确可以提高其对应的力学特性^[8,9], 这其中CNTs的长度、取向和含量等参数都起着非常重要的作用. 然而, 由于当前实验表征技术在分子层面表征的困难, 实验上还不能很好地描述CNTs和聚合物之间微观相互作用机理. 如何解释其中的微观相互作用机理弥补实验上的不足, 对于CNT与聚合物复合物材料的制备至关重要. 相比于实验技术, 分子动力学(MD)模拟可以在纳米尺度揭示实验一些现象的详细信息^[10-13], 如链构象、结构堆积信息及非平衡条件下的结构与力学性质的关系等. MD模拟也有助于解释一些实验现象并且为纳米复合材料的设计开辟一条新的策略. 因此, MD模拟是理解纳米粒子增强聚合物纳米复合材料力学行为非常有利的手段.
尽管MD模拟已广泛应用于增强聚合物纳米复合材料的建模, 但对于一个全原子模型, 其模拟所需要的计算工作量完全限制了其在有限时间尺度上对分子系统的适用性. 很多时候只能通过单根CNTs与聚合物的界面相互作用来探究其对应的微观机理^[14-16], 但是对于实际聚合物纳米复合物体系, 纳米管是无规则分布在聚合物熔体中, 在某种意义上来说小的全原子体系并不能体现出材料的宏观特性. 这些缺陷也阻碍了MD模拟研究纤维含量、尺寸和取向对增强聚合物纳米复合材料力学行为的影响. 为了克服这些困难和限制, 粗粒化(CG)模型无疑是最优的选择. 当然, 基于这些问题, 文献[17-19]中针对石墨和CNTs已经发展了一系列粗粒化MD方法, 并且这些方法的可靠性也得到了进一步的验证. 目前, 基于CG模型大部分的研究主要还是在探究其结构对应的断裂行为, 或者模型可靠性方面的验证性工作, 对于聚合物纳米复合材料的热力学转变及结构和非线性力学关系的研究还非常的缺乏.
针对以上问题, 本文选取短CNTs纤维的CG结构模型和PMMA聚合物分子CG模型构成的复合材料模型为研究对象. 基于CG的分子力场来探究随机分布的短CNTs纤维增强聚合物基体的玻璃化转变行为及非线性力学行为, 并且给出不同CNTs纤维含量下PMMA玻璃化转变、扩散系数及相关拉伸和取向结构与非线性力学的关系.

本文使用了前人最近开发的CG模型. 基于CG模型, 构建了PMMA/CNTs聚合物纳米复合材料的体系. 在该模型中, 将每个甲基丙烯酸甲酯(C₅O₂H₈)单体作为如图1(a)所示的原子质量为100.12 amu的珠子, 选择珠的中心作为单体的质量中心. CG模型也用于建模(5, 5) CNT, 将5个原子环映射成原子质量为600.55 amu的CG珠子(见图1(b)). 基于以上的单体模型, 本文构建了3种体系, 分别命名为PMMA, PMMA/10CNTs和PMMA/20CNTs. 其中, PMMA体系结构每根链含有200个珠子, 体系中包含200根链(40000个珠子). PMMA/10CNTs和PMMA/20CNTs体系分别包含10根和20根CNTs纤维, 每根CNT纤维包含30个珠子, 并且CNT在最开始的时候是无规分布在PMMA熔体结构中, 图2给出了PMMA及其CNT在PMMA中的分布图.
图 1 (a) 1个PMMA聚合物链的3个单体及其由3个珠子组成的CG模型; (b) 1个(5, 5)带有10个碳原子环的CNT及其由3个珠子组成的CG模型
Figure1. (a) Three monomers of a PMMA polymer chain and its CG model made of three beads; (b) a (5, 5) CNT with 10 rings of carbon atoms and its CG model made of three beads.

图 2 PMMA及PMMA/CNTs结构示意图
Figure2. Schematic diagram of PMMA and PMMA/CNTs.

描述体系的粗粒化力场主要由非键相互作用(E_vdW)、键合(E_b)及键角(E_a)相互作用构成, 具体形式如下所示^[20]:

$ {E}_{\mathrm{v}\mathrm{d}\mathrm{W}}\left(r\right)={D}_{0}\left[{\left(\frac{{r}_{0}}{r}\right)}^{12}-2{\left(\frac{{r}_{0}}{r}\right)}^{6}\right], $

$ {E}_{\rm b}\left(d\right)=\frac{{k}_{d}}{2}{\left(d-{d}_{0}\right)}^{2}, $

$ {E}_{\rm a}\left(\theta \right)=\frac{{k}_{\theta }}{2}{\left(\theta -{\theta }_{0}\right)}^{2}, $

其中, D₀和r₀分别为与平衡井深和平衡距离相关的Lennard-Jones参数, 在计算范德瓦耳斯(vdW)相互作用时, 截断半径为1.25 nm. k_d和d₀分别为键长弹簧常数和平衡键距; k_θ和θ₀分别为键角的弹簧常数和平衡键角; 力场参数如表1所列. 本文中所有的模拟都是基于Lammps开源并行MD软件, 在宜宾学院曙光超级计算机上进行. 为了保证体系的合理性, 将所研究的体系在高温T = 650 K下进行20 ns的NPT系综时间弛豫, 压强保持1 atm (1 atm = 1.01×10⁵ Pa). 动力学弛豫和非平衡动力学过程中, 本文选取的时间步长都是10 fs.

Type of interaction	Parameters	PMMA	CNT	PMMA /CNT
Bond	kd/(kcal·mol–1·?–2)	97.3	805.15	—
	d0/?	4.05	9.45	—
Angle	kθ/(kcal·mol–1·?–2)	400	32140	—
	θ0/(o)	84.6	180	—
vdW	D0/(kcal·mol–1)	0.56	5.34	1.4
	r0/?	6.53	9.45	7.7

表1PMMA及PMMA-CNT粗粒化粒子之间相互作用力场参数
Table1.Parameters of the CG force field for PMMA and CNT beads.

2

-->

3.1.PMMA及PMMA/CNTs聚合物纳米复合材料玻璃化转变特性

玻璃化转变温度对于聚合物纳米复合材料体系的应用起着至关重要的作用. 图3中通过体系的比容变化给出了PMMA, PMMA/10CNTs及PMMA/20CNTs体系对应的玻璃化转变温度. 为了保证模拟的合理性, 降温过程中, 本文选取的降温速度为20 K/10 ns. 在玻璃化转变温度(T_g)以上或者以下, 比容基本都是趋于线性变化, 通过交叉点可以确定体系对应的玻璃化转变温度. PMMA体系对应的玻璃化转变温度点约为434 K, 与最近的实验及全原子模拟值基本相符^[16,21,22], 进一步证明本文中选取模型及方法的可靠性. 通过图3不难发现, 随着CNTs纤维含量的增加, 玻璃化转变温度随之增加, 两个体系对应的玻璃化转变温度为454 K和475 K. 玻璃化温度的提升可以进一步拓展PMMA结构体系在极端环境的使用. 根据自由体系理论, CNTs的加入, 限制了PMMA体系结构的运动能力, 这一点会在接下来作进一步阐述.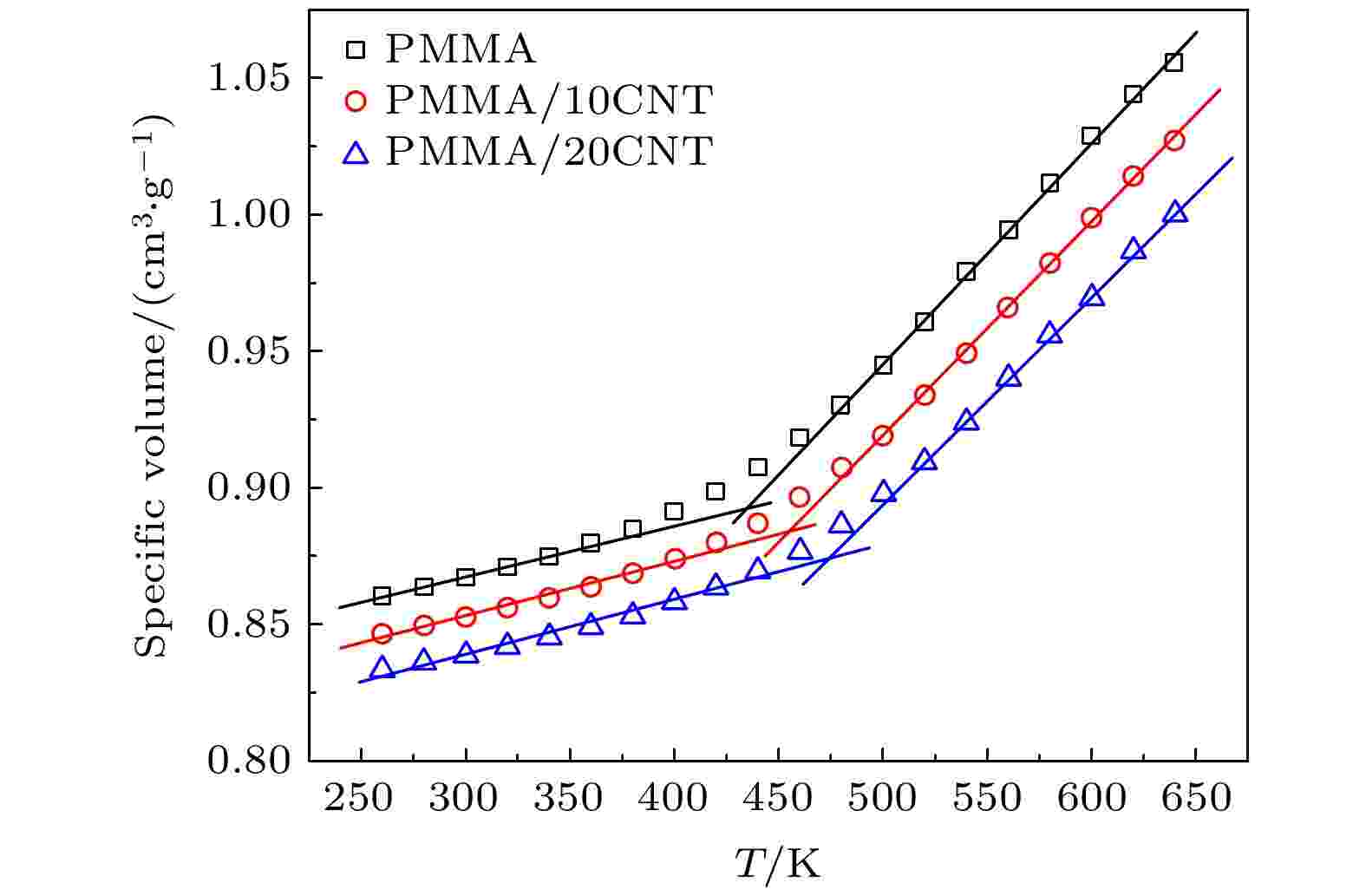
图 3 PMMA, PMMA/10CNTs及PMMA/20CNTs体系对应的比容随着温度的变化
Figure3. Specific volumes of PMMA, PMMA/10CNTs and PMMA/20CNTs under the different temperatures.

CNTs纤维加入PMMA之后, 它们之间的相互作用会直接影响PMMA的运动能力, 进而会影响其玻璃化温度的转变. 最近的实验数据也指出, 如果分子自由空间未被占据, 对应的分子的运动能力也比较强. 例如, 在玻璃化温度以下, 由于分子没有足够的自由空间, 分子就无法运动和转动. 但是目前, 针对这一点实验上很难从分子层面解释其对应的构效关系和微观相互作用机理. 为了进一步在分子层面解释清楚玻璃化温度提升的原因, 分子层面上测定PMMA及PMMA/CNTs体系的运动及松弛动力学过程就尤为重要. 基于平衡的MD方法, 给出了所建3个体系中PMMA分子链整体的均方位移(MSD), 根据MSD的变化, 计算了其对应的扩散系数. 根据爱因斯坦方程, 扩散系数与MSD的关系如下^[13]:

$ D=\underset{t\to \infty }{\mathrm{lim}}\frac{1}{6t}\langle {\left[r\left(t+{t}_{0}\right)-r\left({t}_{0}\right)\right]}^{2} \rangle , $

其中, r(t₀)是粒子的初始坐标, r(t+t₀)是粒子在时刻t的坐标. 通过MSD (图4(a), PMMA/10CNTs与PMMA/20CNTs对应的MSD图已略去)与扩散系数满足的关系(4)式, 图4(b)给出了PMMA, PMMA/10CNTs及PMMA/20CNTs体系中PMMA分子链整体运动对应的扩散系数随着温度的变化. 从图4(b)不难发现, 很明显CNTs纤维加入之后PMMA的扩散系数在不同的温度下会发生明显的降低. 而且各体系都是以玻璃化温度为转变点发生突然的增长. 这一点也印证了实验上的自由体积假说理论.
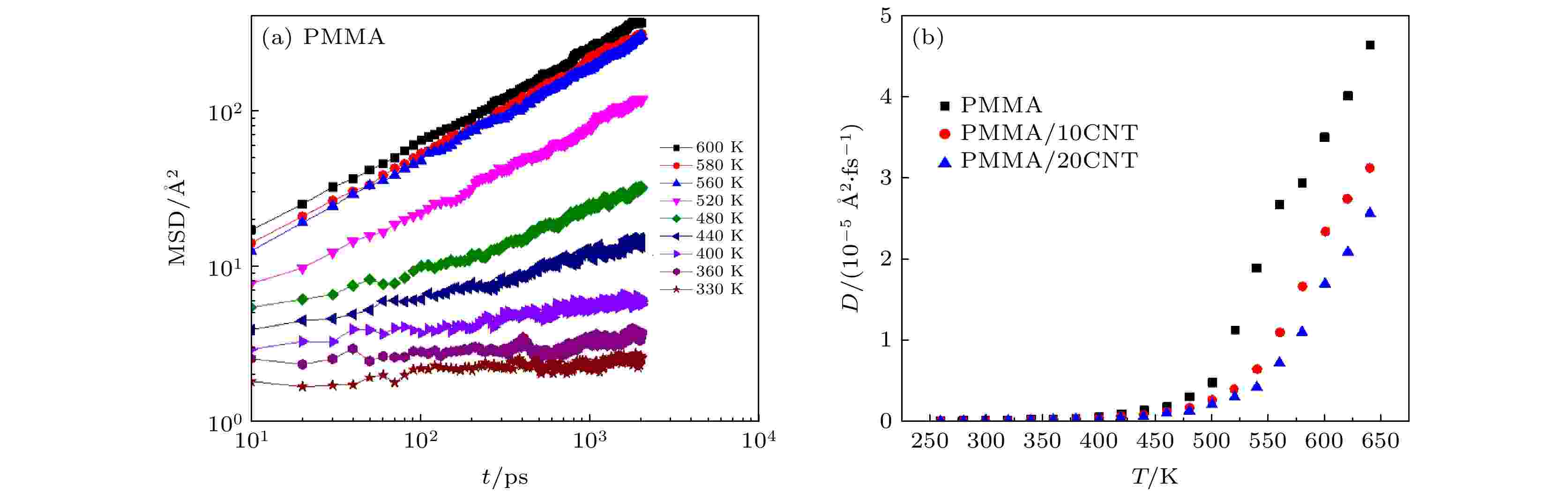图 4 (a) PMMA体系对应的MSD; (b) PMMA, PMMA/10CNTs及PMMA/20CNTs体系不同温度下对应的扩散系数
Figure4. (a) Evolution of mean square displacement (MSD) of PMMA system; (b) the diffusion coefficient of PMMA, PMMA/ 10CNTs and PMMA/20CNTs under the different temperatures.

2 -->

3.2.PMMA/CNTs聚合物纳米复合材料非线性力学特性

聚合物材料在服役过程中难免要遭受外力场的作用, 深刻认识外力作用下材料的结构和性能关系不仅具有重要的学术价值, 也是决定材料能否长期有效服役的关键因素. 聚合物纳米复合材料凝聚态结构是由大量的高分子依靠分子内和分子间的范德瓦耳斯相互作用凝聚而成, 而且材料最后的拉伸性能是这些微观结构相互作用的结果. 因此, 非常有必要探究聚合物纳米复合材料结构与其非线性力学关系. 图5(a)中, 我们施加了一个恒定的拉伸速率1×10⁹ s^–1来探究PMMA, PMMA/10CNTs及PMMA/20CNTs结构体系的应力-应变过程, 温度为室温(300 K). 随着应变的增加, 应力会经历典型的弹性形变、应力屈服、应力软化、应变硬化及断裂区. 进一步观察, 不难发现随着CNTs的含量不同, PMMA结构对应的力学性能会有很大的差别. 随着CNT的含量增加, 其对应的屈服模量也在不断的增加. 但是3个体系的断裂伸长率并没有发生太大的改变, PMMA/10CNTs相比于PMMA体系稍微有所增加, 但是随着含量的增加PMMA/20CNTs相比于PMMA就有所减小, 总体而言断裂应变的变化都不大.
图 5 PMMA, PMMA/10CNTs及PMMA/20CNTs体系在300 K下对应的应力-应变(a)、拉伸比(b)和取向参数(c)变化曲线
Figure5. Evolutions of stress-strain curves (a), stretch ratio (b) and orientational parameter (c) of PMMA, PMMA/10CNTs and PMMA/20CNTs under the temperature of 300 K.

聚合物纳米复合材料的力学特质主要由链构象对应的链结构微观拉伸比和链沿着拉伸方向的取向参数决定. 图5(b)和图5(c)分别给出了PMMA, PMMA/10CNTs及PMMA/20CNTs体系中PMMA分子链对应的链微观拉伸比和末端矢量取向参数. 采用$\lambda =({L-{L}_{0}})/{{L}_{0}}$计算链结构在宏观拉伸过程对应的微观拉伸比, 其中, L₀和L分别表示链原始末端距和受到拉伸以后的末端距, 采用公式$P=\dfrac{3}{2}\cos$θ－$\dfrac{1}{2}$计算取向参数, 其中, θ代表末端矢量与拉伸方向的夹角. 不难发现, 最开始阶段CNTs含量越多, PMMA分子拉伸比增加得越快, 这也是为什么在弹性形变区CNTs含量越高, 其结构对应的模量越高. 但在3个应变之后, PMMA/10CNTs体系对应更高的拉伸比和断裂应变. 进一步分析取向参数, 不难发现同样是PMMA/10CNTs体系中PMMA分子取向参数最大. 根据拉伸比和取向参数不难得出, 应力-应变曲线主要是分子链拉伸和取向协同作用的结果.
除此之外, 还探究了不同温度对于PMMA, PMMA/10CNTs及PMMA/20CNTs结构体系的应力-应变过程的影响. 图6(a)—(c)给出了PMMA, PMMA/10CNTs及PMMA/20CNTs体系在不同温度下对应的应力-应变曲线. 不难发现, 玻璃化温度以下3个结构体系相比于玻璃化温度以上都发生了明显的应力软化现象及应变硬化现象. 而且, 随着CNTs纤维含量的增加, 硬化和屈服现象也越发得明显. 为了进一步探究相同过冷度下, 图6(d)给出了3个体系在过冷度(ΔT = T_g – T = 135 K)下的应力-应变曲线. 不难发现, 相同过冷度下随着CNTs含量的增加, 屈服强度明显的增加. 但是PMMA/20CNTs体系的断裂应变也会随着CNTs含量的增加而减小.
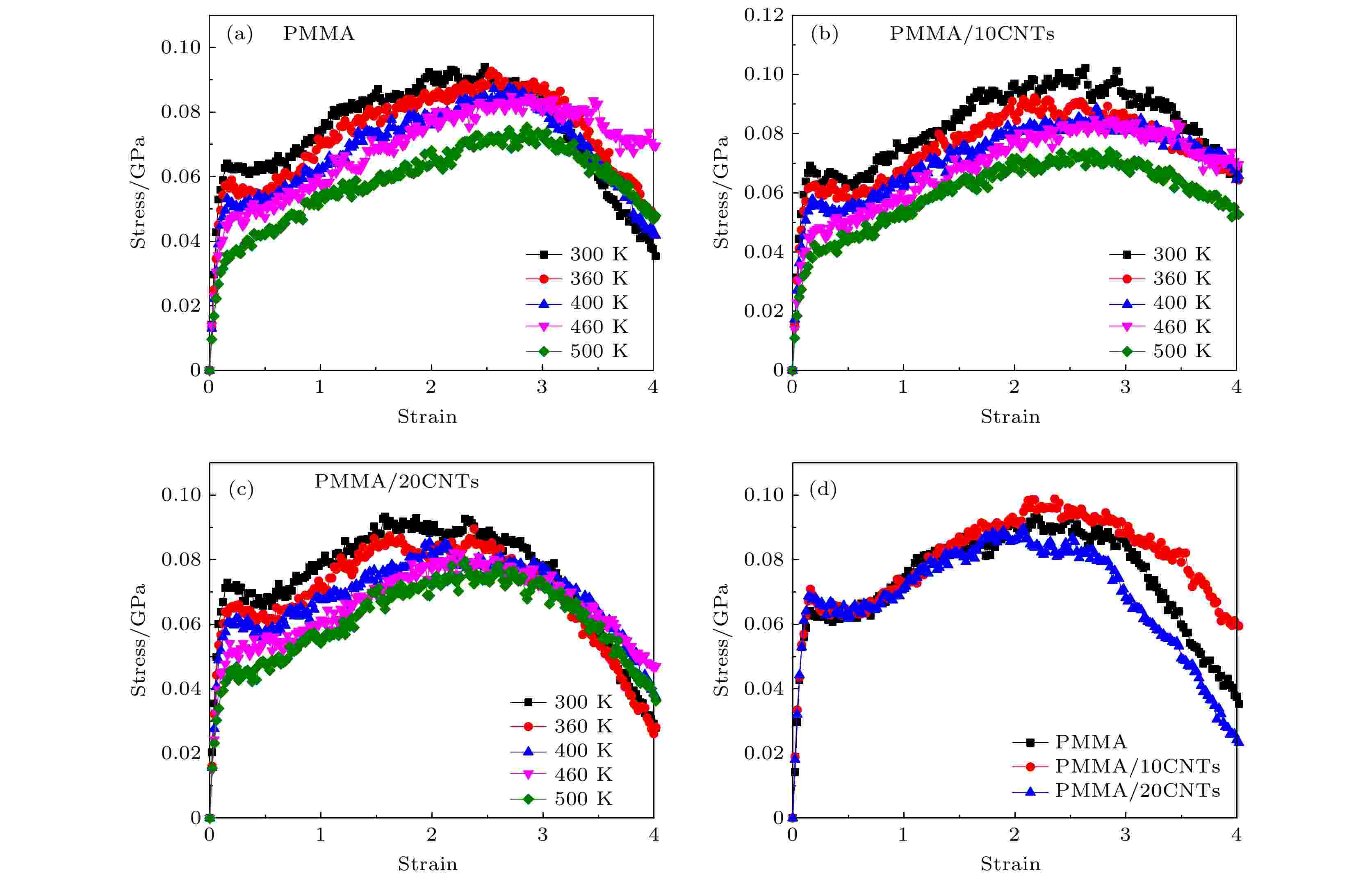图 6 PMMA (a), PMMA/10CNTs (b)及PMMA/20CNTs (c)结构体系在不同温度下对应的应力-应变曲线及在相同过冷度(ΔT= 135 K)下3个体系结构对应的应力-应变曲线(d)
Figure6. E of stress-strain curves of PMMA (a), PMMA/10CNTs (b) and PMMA/20CNTs (c) under the different temperatures and the same cooling depth (ΔT = 135 K)(d).

为了进一步说明PMMA, PMMA/10CNTs及PMMA/20CNTs结构体系在应力-应变过程的结构失效机制, 图7和图8给出了PMMA及PMMA/10CNTs结构的分子构象演化及其对应的原子维诺体积的变化图. 从局部结构维诺体积变化发现, PMMA及PMMA/10CNTs体系在屈服、软化过程及应变硬化过程并没有发生结构的断裂, 断裂发生在2次屈服软化点附近.
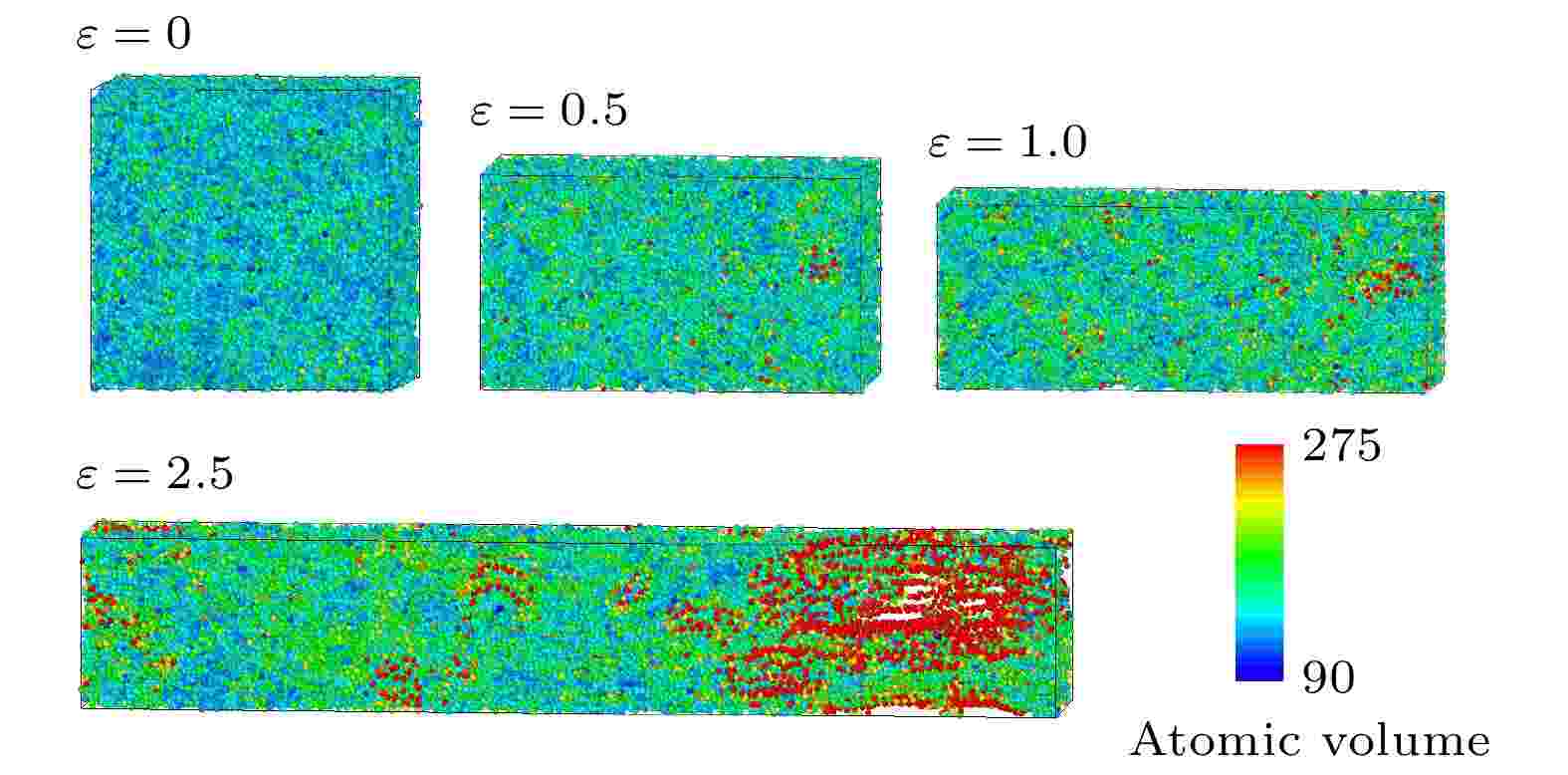图 7 PMMA体系维诺体积随着应变的变化过程
Figure7. Voronoi volume of PMMA system under the different stain.

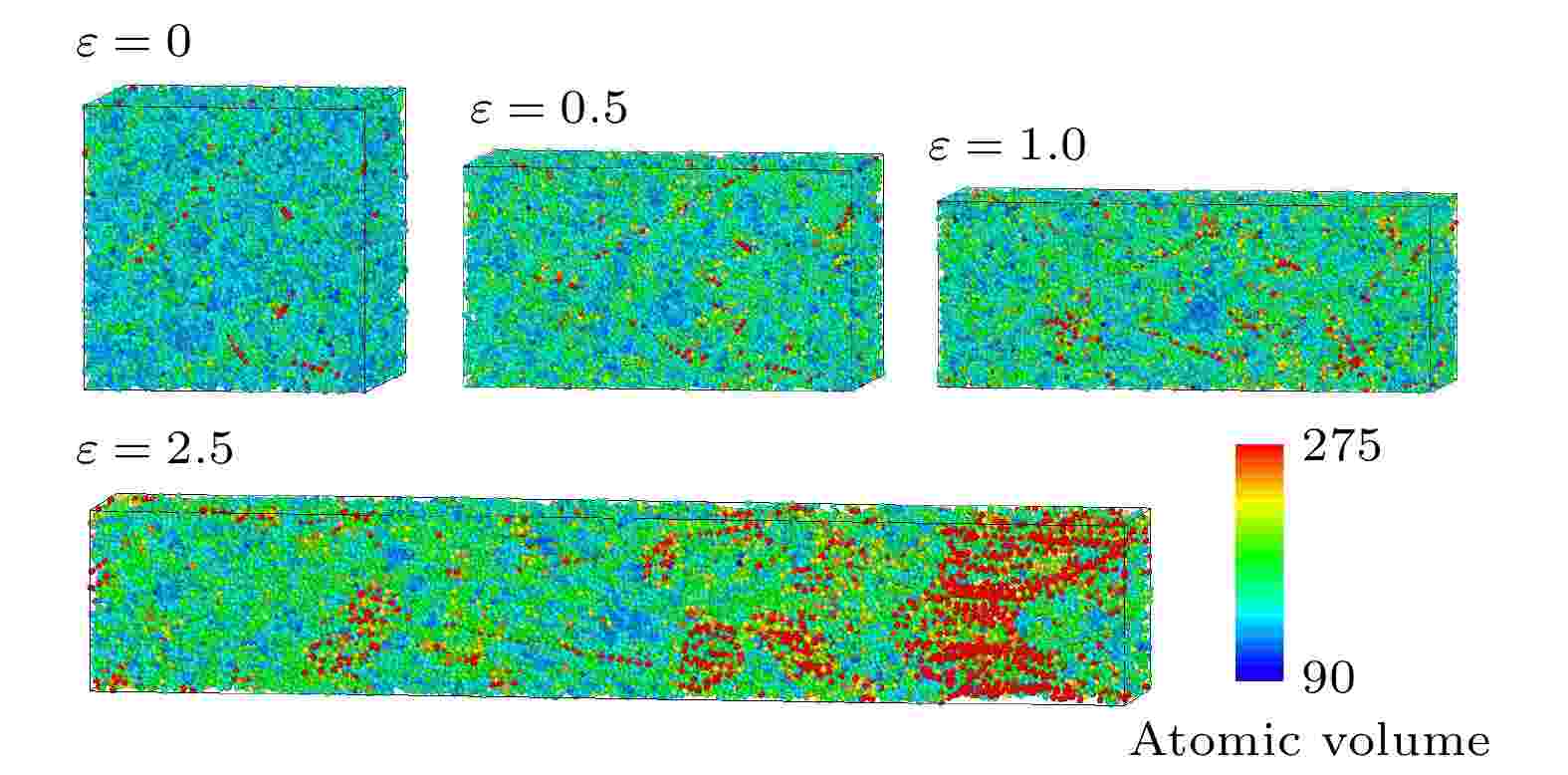图 8 PMMA/10CNTs体系维诺体积随着应变的变化过程
Figure8. Voronoi volume of PMMA/10CNTs system under the different stain.

本文通过粗粒化的MD方法对PMMA及PMMA/CNTs聚合物复合体系的玻璃化转变、扩散、黏性及非线性力学特性进行了系统研究, 具体结论如下:
1) 通过比容变化, 给出了不同温度下PMMA及PMMA/CNTs体系的特征体积, 随着CNT含量的增加引起特征体积的进一步减小(密度增加). 根据特征体系拟合出了PMMA及PMMA/CNTs体系的玻璃化转变温度, 玻璃化转变温度会随着CNTs纤维含量的增加而增加, 这些结果与实验一致.
2) 通过分析PMMA及PMMA/CNTs体系扩散特性发现, CNTs纤维加入PMMA对于体系扩散特性的改变主要发生在玻璃化温度以上. 而且PMMA, PMMA/10CNTs及PMMA/20CNTs体系扩散系数在玻璃化温度以上成指数增长.
3) 通过CNTs纤维添加PMMA复合材料的非线性力学特性分析发现, 随着CNTs纤维的含量增加, 其对应的屈服模量也在不断的增加, 但是含有CNTs的体系还能够保持原来的韧性, 这一点可以为进一步的实验和加工提供理论指导.