摘要: 相比于量子门电路模型, 基于测量的量子计算模型为实现普适量子计算提供了另一途径, 且经过近二十年的发展其内涵已得到了极大丰富. 本文对基于测量的量子计算模型的研究历史和现状进行综述. 首先简要介绍该模型的基本理论, 包括量子图态等资源态的概念和工作原理、模型的计算普适性和经典模拟方法、在相关量子信息处理领域的应用等. 接着从量子物理特性的角度概括基于测量的量子计算模型和量子多体系统之间的紧密联系, 包括量子纠缠、互文性、量子关联、对称保护拓扑序和量子物质相等作为计算资源所发挥的独特作用. 然后, 总结实现基于测量的量子计算模型的不同技术路线和实验成果. 这些理论和实验方面的进展是不断推动可扩展容错量子计算机研制的力量源泉. 最后, 对该领域未来的研究方向进行讨论和展望, 希望能启发读者进一步学习和探索相关课题.
关键词: 量子计算 /
量子纠缠 /
量子关联 /
对称保护拓扑序 English Abstract Research progress of measurement-based quantum computation Zhang Shi-Hao 1 ,Zhang Xiang-Dong 2 ,Li Lü-Zhou 1 1.Institute of Quantum Computing and Computer Theory, School of Computer Science and Engineering, Sun Yat-Sen University, Guangzhou 510006, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61772565, 62102464), the Guangdong Basic and Applied Basic Research Foundation, China (Grant No. 2020B1515020050), the Key Research and Development project of Guangdong Province, China (Grant No. 2018B030325001), and the China Postdoctoral Science Foundation (Grant Nos. 2020M683049, 2021T140761)Received Date: 15 May 2021Accepted Date: 15 June 2021Available Online: 15 August 2021Published Online: 05 November 2021Abstract: Compared with the quantum gate circuit model, the measurement-based quantum computing model provides an alternative way to realize universal quantum computation, and relevant contents have been greatly enriched after nearly two decades of research and exploration. In this article, we review the research history and status of the measurement-based quantum computing model. First, we briefly introduce the basic theories of this model, including the concept and working principles of quantum graph states as resource states, the model’s computational universality and classical simulation methods, and relevant applications in the field of quantum information processing such as designing quantum algorithms and fault-tolerant error correction schemes. Then, from the perspective of quantum physical properties, which include the specific roles of quantum entanglement, contextuality, quantum correlations, symmetry-protected topological order, and quantum phases of matter as computing resources, the close relationship between measurement-based quantum computing model and quantum many-body system is presented. For example, a type of measurement-based computing model for exploiting quantum correlations can show a quantum advantage over the classical local hidden variable models, or certain symmetry-protected topological order states enable the universal quantum computation to be conducted by using only the measurements of single-qubit Pauli operators. Next, a variety of different technical routes and experimental progress of realizing the measurement-based quantum computing model are summarized, such as photonic systems, ion traps, superconducting circuits, etc. These achievements in various physical areas lay the foundation for future scalable and fault-tolerant quantum computers. Finally, we discuss and prospect the future research directions in this field thereby inspiring readers to further study and explore the relevant subjects.Keywords: quantum computation /quantum entanglement /quantum correlations /symmetry-protected topological order 全文HTML --> --> --> 1.引 言 量子计算与量子信息是当代科学的前沿, 具有广阔的发展前景[1 ] . 在现代量子信息科学中, 有两类物理内涵丰富且实验可行的量子计算模型值得关注: 1)基于幺正演化的量子门电路模型[2 ] ; 2)基于测量的量子计算(measurement-based quantum computation, MBQC)模型[3 ,4 ] . MBQC模型在理论上和量子门电路模型等价, 都可以实现普适的量子计算. 就技术层面而言, MBQC的实现仅取决于纠缠态的制备和对量子比特的测量操作, 方便在光学和离子阱等体系中进行实验演示[5 ,6 ] . 随着量子技术的进步, MBQC已用于构建量子Toffoli门[7 ] , 演示量子算法[8 -10 ] , 展示量子纠错码[11 ] , 执行基于测量的量子网络编码[12 ] 等信息处理任务.[13 ] . 此外, 量子电路的合成与优化有经典电路作为参照, 而MBQC没有直接的经典模型对应, 因而在量子算法的设计层面需要更多巧思. 尽管在实现量子计算上存在这些挑战, 但人们发现MBQC能与其他领域的研究相结合, 如将图论、量子纠缠理论、计算复杂性、物质拓扑相、统计物理等主题联系起来, 因而逐渐成为交叉领域的研究焦点[14 ] .[15 ] 下的研究有所启示.2.MBQC的基本原理 22.1.量子计算的基础概念 2.1.量子计算的基础概念 为了便于读者更好地领会本文主旨, 在正式介绍MBQC的理论模型之前, 这里先对量子计算中的一些关键概念进行说明.$\left| {\text{0}} \right\rangle $ 和$\left| {\text{1}} \right\rangle $ 的叠加态:${c_0}$ 和${c_1}$ 称为振幅且满足归一化条件${\left| {{c_0}} \right|^2} + {\left| {{c_1}} \right|^2} = 1$ , 右矢(ket)$\left| {~} \right\rangle $ 是表示量子态的狄拉克符号. 1个qubit态可视为1个二维复向量空间中的向量, 而$\left| {\text{0}} \right\rangle $ 和$\left| {\text{1}} \right\rangle $ 构成此向量空间的正交基, 称为计算基态(computational basis state). 对于n 个qubit构成的量子系统, 其计算基态$| {x_1}{x_2} \cdots {x_n} \rangle$ 共有${2^n}$ 个, 故此系统中的任意1个量子态都可以由${2^n}$ 个振幅值确定. 因此, 用经典计算机存储1个n -qubit量子态的所有振幅信息需要指数级增长的空间. 实际上, 量子态中往往蕴含着丰富的关联和纠缠信息[16 ] , 其中2-qubit纠缠态的典型例子为4个正交Bell态:$X, Y, Z$ )和Hadamard门(H )为Z (controlled-Z , CZ)门:$(a, b)$ 表示2-qubit门的受控位和靶位分别为a 和b . 理论上[2 ] (6 )—(8 )式中的单比特旋转门和(9 )式的两比特门可以合成任意的幺正变换矩阵.$\{ {M_m}\} $ 描述, 其中下标m 表示测量1个量子态$\left| \psi \right\rangle $ 后可能得到的结果, 其发生概率为$\{ {M_m}\} $ 需满足完备性关系:$\left| \psi \right\rangle $ , (10 )式所示测量态$\left| \psi \right\rangle $ 后得到所有可能结果的概率之和为1.O 描述. O 是作用到量子态空间上的厄米算符, 具有谱分解:${P_m}$ 为O 本征空间的投影算符, m 为相应本征值. 测量量子态$\left| \psi \right\rangle $ 得到结果m 的概率为12 )式的算符$\{ {M_m}\} $ 为厄米算符, 且满足${M_m}{M_{m'}} = {\delta _{m, m'}}{M_m}$ 时, (10 )式和(11 )式可分别约化到(14 )式和(15 )式, 即为执行投影测量操作. 通常(13 )式中的投影算符${P_m}$ 可以写为$\left| {{\varphi _m}} \right\rangle \left\langle {{\varphi _m}} \right|$ 的形式, $\left| {{\varphi _m}} \right\rangle $ 称为投影测量基. 例如, 以(1 )式为测量基可对量子态做单比特局域测量, 以(2 )式和(3 )式为测量基可执行量子传态中所用Bell测量[17 ,18 ] .2.2.MBQC理论模型 -->2.2.MBQC理论模型 首先需要指出的是, 所谓基于测量的量子计算并非只能执行测量操作, 而是指计算的过程主要由测量操作序列来确定. 大部分情况下, 人们提到MBQC默认指的就是自2001年Raussendorf和Briegel[3 ,4 ] 提出的单向量子计算 (one-way quantum computation, 1WQC)模型. 但是严格来讲, MBQC也包含其他一些理论模型, 如基于隐形传态的量子计算(teleportation-based model of quantum computation, TQC)模型[19 ] , 基于量子态转移的方法[20 ,21 ] , 关联空间中的MBQC模型[22 ,23 ] 等. 下面主要对1WQC进行解释, 并简要介绍TQC.${S_1}$ 和${S_2}$ 两部分; 2)依次对${S_1}$ 部分执行适应性单qubit测量, 即该过程中的测量操作都是作用在单qubit上的, 且后一步测量操作的设置依赖于前一步的测量结果; 3)对${S_2}$ 中qubit进行泡利修正, 根据第2)步中测量${S_1}$ 的结果, 对作为输出态的${S_2}$ 部分执行(4 )式和(5 )式中的局域泡利操作X 和Z , 从而确定性地得到目标态[24 -26 ] . 如果还需进一步读取该输出态的测量结果, 那么泡利修正可直接吸收到对输出态的测量操作中[3 ,4 ] , 此时整个计算过程就只包含对资源态的适应性测量. 1WQC最常用的普适资源态为量子簇态(cluster states)和图态(graph states)[13 ,27 ,28 ] , 这里对二者进行简要介绍. 2001年Briegel和Raussendorf[27 ] 考虑在具有伊辛类型相互作用的自旋链或自旋晶格中的量子比特, 按特定哈密顿量进行演化得到态为C 为一部分量子比特形成的“簇(cluster)”, 对于一维链、二维晶格和三维晶格分别有 $T{{ = \{ 1\} }}$ , $T{{ = \{ (1, 0), \{ 0, 1\} \} }}$ 和$T{{ = \{ (1, 0, 0), \{ 0, 1, 0\}, \{ 0, 0, 1\} \} }}$ , 当$c + t \notin C$ 时$ \sigma _z^{(c + t)} = 1 $ , 这样的(16 )式称为簇态. 簇态同时具有所谓的最大连通性(maximum connectedness)和纠缠持久性(persistency of entanglement), 并经论证可用作1WQC模型的资源态[3 ] . 类似地, 量子簇态的定义被进一步推广到与图相联系的量子图态[4 ] . 首先考虑1个由N 个顶点的集合$V = \left\{ {{a_1}, {a_{\text{2}}}, \cdots, {a_N}} \right\}$ 和连接它们的边的集合E 构成的图$G = (V, E)$ . 图G 的邻接矩阵${A_G}$ 为1个N × N 矩阵, 其元素为$a \in V$ , 其近邻顶点的集合${N_a} \subset V$ 中的元素b 满足$\left\{ {a, b} \right\} \in E$ .$G = (V, E)$ , 都可以定义1个对应图态. 令每1个顶点$a \in V$ 对应一个qubit, 考虑与之相关的1个厄米算符:X 和Z 为(4 )式和(5 )式中的泡利算符. 则对于所有$a \in V$ , (18 )式可表示的N 个不同算符${\left\{ {K_G^{(a)}} \right\}_{a \in V}}$ 构成了N -qubit系统的一组对易力学量完全集, 因此它们具有一组共同本征态. 将$K_G^{(a)}$ 的本征值为1的共同本征态称为与图G 对应的图态$\left| G \right\rangle $ , 即有${\big\{ {K_G^{(a)}} \big\}_{a \in V}}$ 生成的有限阿贝尔群${S_G} = \Big\langle {{{\big\{ {K_G^{(a)}} \big\}}_{a \in V}}} \Big\rangle$ 也被称为图态$\left| G \right\rangle $ 的稳定子群(stabilizer group).$\left| G \right\rangle $ 也可以根据图的结构直接制备. 首先将所有顶点处的qubit制备为叠加态$\left| {{ + }} \right\rangle = (| 0 \rangle + $ $ \left| 1 \right\rangle ) / {\sqrt 2 }$ , 然后对所有邻接顶点$\left\{ {a, b} \right\} \in E$ 上的一对qubit执行(9 )式中的幺正操作${\text{C}}{{\text{Z}}^{(a, b)}}$ , 就可得到图态$\left| G \right\rangle $ :${|+\rangle ^V} = { \bigotimes\limits_{a \in V}}{\left| {{ + }} \right\rangle _a}$ .图1 , 其中线性簇态和马蹄形簇态均为图态特例[29 ] , 星形图态在局域幺正变换下等价于GHZ态[30 ] , 可扩展的2D方格图态用于执行普适MBQC[3 ,28 ] . 在大多数MBQC的相关研究中, 都将簇态视为定义在特定晶格结构上的图态例子[4 ,13 ,28 ,31 ] , 可按(20 )式直接制备. 下面介绍如何基于簇态确定性地执行任意单qubit旋转操作和2-qubit CNOT门.图 1 不同类型的图态 (a)线性簇态; (b)星形图态; (c)马蹄形簇态; (d)可扩展的二维方格图态Figure1. Different types of graph states: (a) A linear cluster state; (b) a star-graph state; (c) a horseshoe cluster state; (d) the scalable 2D square graph state.$| {{\psi _{{\text{out1}}}}} \rangle = H{R_z}( - \alpha )| + \rangle$ 如图2(a) , 其中H 和${R_z}( - \alpha )$ 表达式见5 )式和8 )式. 图2(b) 为相应基于测量的实现方案: 输入态$ |+\rangle |+\rangle $ 经过CZ门后, 对第1个qubit执行基$| {{ \pm _\alpha }}\rangle = (| 0 \rangle \pm {{\text{e}}^{{\text{i}}\alpha }} | 1 \rangle )/\sqrt 2$ 中的测量, 所得结果$m \in \{ 0, 1\} $ , 相应第2个qubit所处态为$(\left| + \right\rangle + {( - 1)^m}{{\text{e}}^{ - {\text{i}}\alpha }}\left| - \right\rangle )/\sqrt 2 $ . 因此为了确定性得到$\left| {{\psi _{{\text{out1}}}}} \right\rangle $ , 图2(b) 中以m 作为控制位对第2个qubit做泡利X 修正, 所得输出态为图 2 单向量子计算执行量子门操作 (a)输入态$ \left| + \right\rangle $ 经过${R_z}( - \alpha )$ 旋转和Hadamard门作用; (b)以测量纠缠态的方式等价地实现(a); (c)为(b)的扩展, 制备并测量4-qubit线性簇态以实现任意的单量子比特旋转门; (d)以4-qubit星形簇态执行CNOT门Figure2. Realization of quantum gates in the 1 WQC model: (a) Input state $ \left| + \right\rangle $ undergoes a ${R_z}( - \alpha )$ rotation and a Hadamard gate; (b) a circuit equivalent to (a) by measuring an entangled state; (c) a generalization of (b) to prepare and measure a 4-qubit linear cluster state for implementing arbitrary single-qubit rotation gates; (d) a circuit performing the CNOT gate via a star cluster state.$\left| {{\psi _{{\text{out2}}}}} \right\rangle $ 与$\left| {{\psi _{{\text{out1}}}}} \right\rangle $ 仅相差一个整体相位因子, 即图2(b) 等价实现了图2(a) .$ U = H{R_z}( - \gamma ){R_x}( - \beta ){R_z}( - \alpha ) $ . 将未经泡利X 修正的图2(b) 中线路作为基本单元串联3次, 其中各qubit的测量基分别为$\left| {{ \pm _\alpha }} \right\rangle $ , $\left| {{ \pm _\beta }} \right\rangle $ , $\left| {{ \pm _\gamma }} \right\rangle $ 并得到结果$k, l, m \in \{ 0, 1\} $ , 则qubit 4上的态为[4 ,32 ] 可知, 以上线路等价于先用3个CZ门作用到输入态$ {\left| + \right\rangle _1}{\left| + \right\rangle _2}{\left| + \right\rangle _3}{\left| + \right\rangle _4} $ , 再分别在基$\left| {{ \pm _\alpha }} \right\rangle $ , $\left| {{ \pm _\beta }} \right\rangle $ , $\left| {{ \pm _\gamma }} \right\rangle $ 中测量qubit 1, 2和3并得到qubit 4的态为(22 )式. 因此, 为了实现任意旋转门的效果$ U\left| + \right\rangle $ , 如图2(c) 所示用CZ门制备1个如图1(a) 所示的4-qubit线性簇态, 且测量结果$k, l, m$ 依次决定后续测量基的设置以及对输出态qubit 4的泡利修正操作, 即可确定性地得到$ \left| {{\psi _{{\text{out3}}}}} \right\rangle = {{\text{e}}^{ - {\text{i}}(\alpha + \beta + \gamma )/2}}U\left| + \right\rangle $ . 实际上制备所用资源簇态的方式并不唯一, 如光量子体系常用的“融合操作(fusion operation)”[30 ,33 ,34 ] . 此外, 容易验证当图2(c) 中qubit 1的输入态为任意单量子比特态$ \left| {{\psi _{{\text{in}}}}} \right\rangle $ 时, 运行此线路得到qubit 4上的输出态与$ U\left| {{\psi _{{\text{in}}}}} \right\rangle $ 等价.图1(b) 所示图态可视为六角晶格结构上的星形簇态[34 ] , 当在泡利X 基中测量其qubit 1和2并分别得到结果$m, n \in \{ 0, 1\} $ , 则剩余两个qubit 3和4所处的输出态为图2(d) 所示先制备这样的星形簇态, 再对qubit 1和2做泡利X 测量并对作为输出态的qubit 3和4做相应泡利修正$(Z_3^n \otimes Z_4^nX_4^m{{)}}$ , 可确定性实现$ \left| {{\psi _{{\text{out4}}}}} \right\rangle = {\text{CNOT}}| + \rangle | + \rangle $ . 更一般地, 可验证当图2(d) 中的输入qubit 3和2 换成任意2-qubit态$ \left| {{\psi _{in}}} \right\rangle $ 时, 则经过后续操作最终qubit 3和4所处输出态为$ \left| {{\psi _{{\text{out4}}}}} \right\rangle = {\text{CNOT}}\left| {{\psi _{{\text{in}}}}} \right\rangle $ . 类似地, 测量图1(c) 中马蹄形簇态的qubit 1和4并对qubit 2和3做泡利修正, 可以实现2-qubit CZ门[29 ] . 以上理论显示一般的输入态本身也可以由测量簇态来得到, 因此当如图1(d) 所示2D方格图态足够大时, 通过精心设计测量模式并辅以适当的泡利修正就能够确定性地实现普适量子计算[3 ] . 若量子方案需要对输出态做读取测量, 那么泡利修正操作也可以合并到测量操作中[4 ] . 相比于1WQC使用单比特测量来完成计算, 下面简要介绍另一种使用两比特测量的MBQC模型—基于传态的量子计算(TQC).[19 ] 提出使用量子传态技巧[17 ,18 ] 和单qubit操作来实现普适量子计算. 图3(a) 为量子传态的1个例子: Alice对制备好的单qubit态$U\left| \alpha \right\rangle $ 和(2 )式中Bell态$\left| {{\beta _{{\text{00}}}}} \right\rangle $ 的1个qubit执行联合Bell测量, 并将测量结果a 和b 发送给Bob. 后者对$\left| {{\beta _{{\text{00}}}}} \right\rangle $ 态的另1个qubit执行${Z^b}{X^a}$ , 即可得到态$U\left| \alpha \right\rangle $ . 实际上Alice的操作等价于在一组新基$\left\{ {({U^{\dagger} } \otimes I)\left| {{\beta _{ij}}} \right\rangle } \right\}$ ($\left| {{\beta _{ij}}} \right\rangle $ 为(2 )式和(3 )式中的Bell态)中对态$\left| \alpha \right\rangle $ 和$\left| {{\beta _{{\text{00}}}}} \right\rangle $ 的1个qubit做2-qubit测量[35 ] , 则此时对U 的实现只用到联合测量操作和泡利修正.图 3 基于传态的方案实现单量子比特门 (a)一方远程制备态$U\left| \alpha \right\rangle $ 并通过Bell测量和泡利修正传给另一方, 注意U 和Bell测量可以直接合并成新的联合测量; (b)利用制备好的资源态$(I \otimes U)\left| {{\beta _{{\text{00}}}}} \right\rangle $ 来间接执行$U\left| \alpha \right\rangle $ Figure3. Teleportation-based scheme for implementing any sing-qubit gate: (a) State $U\left| \alpha \right\rangle $ is remotely prepared at one site and teleported to another site via Bell measurement and Pauli corrections, note here U and Bell measurement can be directly combined into a new joint measurement; (b) the scheme to indirectly implement $U\left| \alpha \right\rangle $ via a prepared resource state $(I \otimes U)\left| {{\beta _{{\text{00}}}}} \right\rangle $ .U 的方式如图3(b) 所示, 将态$\left| \alpha \right\rangle $ 和资源态$(I \otimes U)\left| {{\beta _{{\text{00}}}}} \right\rangle $ 中的1个qubit做Bell测量, 并根据测量结果对另1个qubit做修正操作$\widetilde X = UX{U^{\dagger} }$ 和$\widetilde Z = UZ{U^{\dagger} }$ , 即可确定性地得到目标输出态$U\left| \alpha \right\rangle $ . 这样的传态技巧可以从单量子比特门U 推广到多量子比特门的作用, 如用CNOT门作用2-qubit态等价于制备资源态$({I^{(1)}} \otimes $ $ {\text{CNO}}{{\text{T}}^{(3, 2)}} \otimes {I^{(4)}})\left| {{\beta _{{\text{00}}}}} \right\rangle \left| {{\beta _{{\text{00}}}}} \right\rangle$ 并执行两组Bell测量和相应泡利修正[19 ] . 因此, 这种利用传态思想的计算方法的好处在于: 即便目标操作U 难以直接实现, 也可以通过制备已知的初始资源态来间接地执行U . 在Gottesman-Chuang方案的启发下, 后又发展出各种不同的TQC模型, 如Leung[35 ] 提出对任意双量子比特执行适应性2-qubit测量来完成计算.[21 ,36 ,37 ] : 二者的执行依赖于相近的基本要素和底层原理, 因此在一些具体案例中(如价键态计算模型[38 ] )具有等价性, 并能启发一些兼顾两者长处的混合计算模型[39 ,40 ] . 不同MBQC模型的计算效果与所依赖多体量子系统的物理特性有关, 将在后文第3 部分详述.2.3.MBQC的计算普适性及其经典模拟 -->2.3.MBQC的计算普适性及其经典模拟 在1WQC模型中, 对2D方格簇态执行特定模式的单qubit测量就可以实现普适量子计算. 反过来1个自然的问题是: 用于MBQC的普适资源态具有何种必要属性? 更确切地, 既然涉及有限纠缠的系统可以被经典计算机有效模拟[41 ] , 那么执行普适MBQC的资源态中需要多少纠缠? 最强的“普适性”可以自然地定义为对资源态执行单qubit操作来产生任意量子态的能力, 则此意义下的普适资源态(如2D簇态)的多种纠缠度量必然随系统尺寸呈现无界增长. 例如, 2006年Nest等[32 ] 引入熵纠缠宽度(entropic entanglement width)作为评判图态普适性的标准, 并举出对应六角晶格、三角晶格、Kagome晶格的普适资源图态例子. 相对地, 他们也揭示出n 粒子1D簇态, GHZ态, W态以及某些1D自旋系统的基态至少不满足一种纠缠度量下的最大纠缠性, 因此非普适资源[25 ] . 当普适性的概念为只要求MBQC能够有效再现量子门电路的经典输出结果时, 矩阵乘积态(matrix-product state, MPS)和投影纠缠对态(projected entangled pair state, PEPS)可以作为相应关联空间量子计算的普适资源[22 ,23 ] , 而无需具备2D簇态呈现的一些纠缠特征(如最大局域纠缠).[32 ,42 ,43 ] . 细致考虑图的拓扑结构和纠缠性质, 研究者揭示出一系列特定资源态参与的MBQC可以用张量网络方法有效模拟, 如任意两体划分的纠缠(Schmidt数)较小[44 ] 或具有对数有界的Schmidt-rank宽度情形[45 ] , 有限宽度的簇态计算[46 ] , 以及图的树宽度较小且最大度(degree)为常数的图态计算[42 ] 等. 除了图态外, 参考平面图Ising模型的严格可解性, 基于环面码(toric code)态这种量子资源的MBQC也可以有效经典模拟[47 ] . 这些围绕经典模拟的研究不仅有助于深入理解MBQC计算能力的普适性, 还能启发新的经典算法[48 ,49 ] .2.4.MBQC在量子信息领域的应用 -->2.4.MBQC在量子信息领域的应用 MBQC在量子信息处理领域具有多方面应用. 首先, 作为一种普适量子计算模型, MBQC模型已用于构建量子Toffoli门[7 ] , 演示Deutsch-Jozsa, Bernstein-Vazirani算法[8 ,9 ] 以及Grover量子搜索算法[5 ,29 ,50 ] , 执行QFT[13 ,28 ] 和量子加法器[4 ] , 求解Simon问题[10 ] , 计算非线性布尔函数[51 ,52 ] 等量子算法相关场景. 值得一提的是, 1WQC和量子电路模型在执行这些算法上是多项式时间等价的, 但前者可能在并行化方面优于后者[53 ,54 ] . 例如, 2010年Browne等[55 ] 提出QFT在1WQC模型中能以常数深度近似执行, 从而更有利于实验演示. 因此, 利用量子电路模型与MBQC模型之间的转换关系来研究电路的深度复杂性具有理论和实用意义.[56 ] 就讨论了容错1WQC方案: 可使用2D簇态模拟1D容错量子电路. 随后, Nielsen和Dawson[57 ] 也证明了当错误率低于某个阈值时, 能够实现基于簇态的可扩展容错1WQC, 并以光学量子计算中的光子损失噪声和去极化噪声为例数值研究了容错阈值[58 ] . Raussendorf等[59 ,60 ] 还进一步利用3D簇态中的2D切片来模拟一种常用的纠错码—表面码(surface code), 其中特定的测量模式可模仿拓扑量子计算中的任意子编织操作. 这样以拓扑保护的量子门实现的容错MBQC具有较高的容错阈值[61 ,62 ] , 且适合qubit和连续变量系统的实验演示[63 -65 ] .[12 ] 、盲量子计算[66 ,67 ] 、多人协作量子计算[68 ] 、量子博弈[69 ] 、量子通信[70 ] 等量子信息处理场景中. 例如, 量子网络编码技术有望提升分布式量子计算中的资源利用率, 而使用量子簇态实施纠缠交换(entanglement swapping)或基于测量的纠缠分布(entanglement distribution)时可以给电路深度[71 ] 、最终的Bell态保真度[12 ] 等方面带来改善. 又如盲量子计算是一种与MBQC模型有紧密联系的安全计算协议. 未来量子计算机可能趋向于以云计算形式提供给客户使用, 因此如何保证客户的数据和计算过程的私密性显得尤为重要. 2009年Broadbent等[66 ] 首次提出的通用盲量子计算协议中, 客户端将制备好的随机量子比特发送给服务器, 服务器将这些qubit制备为brickwork纠缠态并按客户的要求进行测量, 再将测量结果返回给客户端, 后者又根据这些测量结果确定后面量子比特的测量参数并发送给服务器. 这样双方不断交互进行直至所有量子比特都被测量, 协议完成. 此协议秉承MBQC的基本思想, 能够保证客户端的信息安全. 在物理学领域, MBQC模型可以用作研究经典自旋模型[72 ,73 ] 、量子模拟架构[74 ] 及对称保护的拓扑相[75 ] 等物理理论的工具.3.MBQC的物理内涵 特定MBQC模型的计算能力与其内在的物理属性有紧密联系, 如一类利用量子关联及非适应性测量的计算模型可展现出相对经典局域隐变量模型的量子优势[76 ] . 下面从量子纠缠、量子关联、对称保护的拓扑相等角度概述相关物理内涵.3.1.MBQC中的量子纠缠 3.1.MBQC中的量子纠缠 MBQC模型的计算能力可以追溯到其所用纠缠资源态的性质. 在2.3 节中, 已概述了纠缠和MBQC的普适资源态及经典可模拟性之间的关系. 后续围绕量子纠缠在MBQC中作用的研究包括: 一些多体纠缠量子系统的基态(如自旋${5}/{2}$ 系统[77 ] 和自旋${3}/{2}$ 系统[78 ] )可用作普适MBQC的资源态, 而某些具有两体相互作用的自旋${1}/{2}$ 无阻挫哈密尔顿(frustration-free Hamiltonian)系统则无此能力[79 ] ; 关联空间中执行“普适态制备”意义下的MBQC时, 所用资源必然会展现类似簇态的极值纠缠特征[80 ] ; 近年类比量子图态提出的超图态[81 ,82 ] , 其独特的纠缠和非局域性质导致相应MBQC在一些方面优于图态方案, 例如2016年Gachechiladze等[83 ] 揭示出超图态相比于GHZ态对于粒子损失噪声具有更强的鲁棒性.[84 ] 发现随机态等具有过多纠缠的量子态反而无益于MBQC展现量子计算加速. 同年, Bremner等[85 ] 也在抽象MBQC框架下得到了类似的结果. 实际上, 2017年Morimae[86 ] 论证了寻找适用于MBQC的资源态通常是1个困难任务.3.2.MBQC模型与量子关联 -->3.2.MBQC模型与量子关联 量子关联是量子计算、量子通信等领域的重要资源, 其具体表现如量子非局域性(quantum nonlocality)[87 ] 和量子互文性(quantum contextuality)[88 ] 可用于分析和诠释MBQC中通过测量纠缠资源态展现的计算能力.[89 ] , 并以典型的GHZ和CHSH问题作为例子, 揭示出局域实在模型的违背和纠缠资源态的计算能力之间的有趣关系, 例如3-qubit GHZ态加上线性副处理(经典异或门和非门)足以实现经典计算所用的普适与非门. 如图4 所示, 此计算模型包含两部分: 1个关联多方资源态和1个经典控制计算机, 彼此之间可以交换经典信息. 其中关联多方资源由一些个体组成, 控制计算机可为其提供k 个不同的测量设置, 每个个体经测量后得到l 个可能结果中的1个并返回控制计算机. 当设置$k = l = 2$ 时, 此框架与原始的量子one-way模型相符. 此外, 他们还从计算复杂度的角度探讨了在使用不同的资源态(如簇态, 二维图态, 计算张量网络态等)和仅包含经典CNOT操作和NOT操作的计算机时, 三种复杂度类别$ \oplus L$ , P 和BQP 之间可能的转化关系. 除了直接考察量子资源态中的关联, 2014年Hoban等[90 ] 提出利用量子方式生成的概率分布中的关联, 来构造一种MBQC的经典对应(称为“基于测量的经典计算”, MBCC), 可以展现特定量子模型的非经典计算特性, 如计算一种可能无法用传统经典计算设备有效模拟的IQP* 量子线路.图 4 利用关联的计算模型. 经典控制计算机提供k 个测量设置中的1个作为对关联多方资源态中个体的经典输入(蓝色箭头), 并且接收l 个测量结果中的1个(红色箭头)作为输出Figure4. A computational model exploiting correlations. The classical control computer provides one of k measurement settings as the classical input (blue arrows) to each of the parties in the correlated resource state and receives one of l possible measurement results (red arrows) as the output.[91 ] 提出在一般的具有线性副处理(做模2加法运算)且非自适应的MBQC (non-adaptive MBQC with linear side-processing, $ {\text{NMQ}}{{\text{C}}_ \oplus } $ )模型, 通过测量特定纠缠态得到的非局域关联结果可以实现对非线性布尔函数的确定性计算、与多方Bell不等式违背有关的概率计算等. 2013年, Raussendorf[51 ] 展示了在一些自然的假设下, 以高成功率计算1个非线性布尔函数的MBQC具有互文性. 互文MBQC中的1个有趣例子是求解离散对数问题的量子算法, 其相对经典算法能展现超多项式加速. 2017年, Oestereich和Galv?o[52 ] 进一步基于互文性MBQC发展出的非线性函数计算模型中, 实现了可靠计算所需的3-MAJ门和3输入的XNAND门. 与仅能计算线性布尔函数的局域隐变量模型或非互文隐变量模型相比, $ {\text{NMQ}}{{\text{C}}_ \oplus } $ 模型仅用少量量子资源就能展现量子优势, 且2017年Abramsky等[92 ] 提出一种互文性度量方式来量化这样的量子优势. 这是不同于某些量子霸权方案中通过不断扩展量子规模来达到量子优势的思路[93 ] , 为人们理解量子计算与经典计算之间的差异提供新颖的视角. 此外, 由于不需要用到传统适应性测量操作, $ {\text{NMQ}}{{\text{C}}_ \oplus } $ 模型对实验维持相干性的要求更低, 因而更容易在近期的实验平台上进行演示. 2021年, Demirel等[76 ] 于实验上演示了利用4光子GHZ态来计算简单的低度非线性函数.3.3.MBQC与对称保护的拓扑相 -->3.3.MBQC与对称保护的拓扑相 具有特定群对称性的量子态所呈现的多体纠缠可导致所谓的对称保护拓扑序(symmetry-protected topological order, SPTO)现象[94 -97 ] , 而SPT态可以为MBQC普适资源态的刻画提供一种新的视角. 2012年, Else等[98 ] 论证了所有属于1D自旋链SPT相的基态都具有“量子计算导线(quantum computational wires)”的统一属性, 如${Z_2} \times {Z_2}$ 旋转对称性保护的1D簇态和1D Affleck-Kennedy-Lieb-Tasaki (AKLT)态, 并能确保MBQC中恒等门的完美操作. 2015年, Miller和Miyake[99 ] 展示了${S_4}$ 对称下的1D SPT相能以任意高保真度执行单qubit门操作且能作为TQC的潜在资源, 随后2017年Raussendorf等[100 ] 将该结果推广到了执行更一般的MBQC模型.[101 ] 刻画了任意晶格上的元格态(plaquette state)呈现的非平凡SPTO, 及用作MBQC的普适资源态. 与之不同的是, 2016年Miller和Miyake[75 ] 提出将3-qubit CCZ门作用到位于Union Jack晶格中三角元胞上的qubit, 可以得到具有2D SPTO的资源态(系统具有${Z_2} \times {Z_2} \times {Z_2}$ 对称). 该工作指出具有1D SPTO的纠缠态(如传统簇态)配合任意单qubit测量可以实现普适量子计算, 而对于具有更加复杂纠缠形式的2D SPTO只需执行泡利测量就可以得到相同的结果. 基于Union Jack态实现普适MBQC的工作将凝聚态物理中SPTO的层级概念和量子计算中的所谓Clifford层级联系起来. 这样的量子计算普适性也于2018年推广到了d 维量子比特(qudit)系统的非平凡${Z_d} \times {Z_d} \times {Z_d}$ SPT态[102 ] . 除了以上运用群上同调(group cohomology)工具构建MBQC的普适资源态及SPTO分类, 最近一两年的工作系统性地研究所谓“量子物质的计算相(computational phases of quantum matter)”概念, 指出具有普适计算能力的对称保护量子相由所谓的子系统对称性保护[103 -105 ] . 在取得这些理论成果的同时, 2018年以来对SPT态的表征和基于测量的算法也出现实验演示[106 ,107 ] .4.MBQC的实验进展 除了理论进展外, 在硬件方面当前量子技术已进入NISQ时代, 光量子、离子阱、超导体系、半导体量子点等多条技术路线并行发展, 面向特定领域、特定问题的专用量子计算设备已取得了较大进步. 下面概述量子实验中对于MBQC算法的演示或相关量子原理的验证.4.1.光量子系统 4.1.光量子系统 光子具有能同时应用于量子信息处理的多自由度(极化、轨道角动量、空间模式、频率等)和退相干率低等特点, 近年来研究者围绕MBQC计算模型开展了一系列基于光学系统的实验演示, 主要包括以下几方面:[29 ] 利用后选择技术制备4光子簇态并实现1WQC中的基本要素: 单量子比特旋转门和两量子比特受控门, 并演示四元素搜索的Grover算法. 随后的光学实验扩展到利用多光子多自由度制备纠缠图态, 且运用前馈技术来克服执行测量操作时的随机误差, 从而执行确定性1WQC中的门操作[5 ,34 ,50 ,108 ,109 ] , 并演示Deutsch算法[8 ,110 ] 和Simon算法[10 ] , 量子博弈[69 ] , 盲量子计算[67 ] , 量子纠错码[111 ] , 关联空间中的MBQC模型[112 ] 等. 2019年, Reimer等[113 ] 利用光子的时间和频率自由度实验演示了基于多能级簇态的高维1WQC, 显示出相对传统二能级簇态更高的抗噪特性. 从技术上看, 1WQC模型与集成光量子芯片技术的结合有助于未来可扩展的光学量子信息处理[114 ,115 ] .[19 ] 为基础, 2001年Knill-Laflamme-Milburn (KLM) 方案[116 ] 仅用分束器、相移器、单光子源和光探测器等构成的线性光学系统就能有效实现量子计算. 具体而言, 光探测过程中潜在的非线性可以通过测量转移到量子比特上, 从而实现普适计算. 2005年, 中国科学技术大学郭光灿课题组[117 ] 利用线性光学操控、参数下转换产生的光子极化-路径纠缠以及符合测量中的后选择技术, 实现了TQC模型中关键的量子CNOT门传输. 随后, 该组又实现了传输单量子比特旋转作用于远程光子[118 ] . 2010年, 潘建伟课题组[119 ] 也发展出了基于其他光子自由度和纠缠态来实现传输量子门的实验方案及演示工作.[120 -123 ] 和东京大学Furusawa课题组[65 ,124 -126 ] 在制备连续变量光学簇态和实验演示MBQC方面积累了显著的系统性工作, 当前基于连续变量系统执行容错MBQC的挑战在于低错误率立方相位门的实现及可扩展的光学集成等方面.4.2.离子阱体系 -->4.2.离子阱体系 早在1995年Cirac和Zoller[127 ] 就提出了将离子阱系统用于量子计算的方案. 离子阱将一串离子囚禁在线性阱中, 且用其冷却到基态的两个内能级编码1个量子比特. 单比特操作可以通过激光脉冲寻址作用在相应离子上实现, 两比特的受控操作可通过用离子串的公共质心及声子协助完成, 测量离子发出的荧光光谱就实现了量子态读取. 离子阱系统在制备二维簇态上表现出良好的扩展性[128 ] , 且可在2D离子阱阵列上演示适用于容错MBQC方案的3D簇态[129 ] . 2013年Lanyon等[6 ] 制备多种不同类别的图态用于演示MBQC中的普适门操作和纠错码, 并获得较高的态保真度. 进一步地, 该课题组[130 ] 也演示了离子阱系统图态对于多方Bell不等式的违背.4.3.超导量子体系 -->4.3.超导量子体系 在超导量子系统中, 基于约瑟夫森效应构造超导约瑟夫森结作为量子比特, 通过施加电流、电场或微波控制实现相应的量子门操作. 早期MBQC相关的实验方案包括: 超导量子电路中使用“一步法”制备大规模簇态[131 ] , 与腔QED相结合的超导量子比特系统[132 -134 ] 等. 2019年, 潘建伟组在超导电路系统制备具有真多方纠缠且保真度达到70%的12量子比特簇态[135 ] , Mooney等[136 ] 也基于IBM的量子云平台制备20量子比特规模的图态并用特定的纠缠见证(entanglement witness)进行刻画, 且Albarrán-Arriagada等[137 ] 提出使用几十个量子比特执行1WQC且相比簇态更加节省资源的超导实验方案. 这些成果为未来可扩展的MBQC奠定了理论和实验基础. 目前已有一些基于超导电路的量子计算云平台问世(如IBM Q), 方便研究者们实验演示各种MBQC相关的信息处理方案, 如执行基于测量的量子网络编码[12 ] .4.4.其他方案 -->4.4.其他方案 当前, 基于其他物理体系来制备量子簇态和图态或演示MBQC模型的方案包括光学晶格囚禁冷原子体系[138 ,139 ] 、量子点[140 ,141 ] 、核磁共振(NMR)系统[142 ] 、腔量子电动力学(QED)[143 ] 等. 整体而言, 当前基于离散变量系统演示MBQC的实验规模还局限在几十个量子比特, 而连续变量系统技术上可以产生具有上百万个不可分模式的簇态[126 ] . 这些实验技术与方法的新进展为未来实现大规模MBQC提供了更多选择.5.MBQC的未来研究展望 如前文所述, MBQC将量子信息处理和凝聚态物理领域中的问题相联系, 相关研究内容至今还在不断拓展和深化. 这里对未来具有潜力的研究方向进行讨论和展望.X , Y 和Z 测量[75 ] , 或对2019年Takeuchi等[144 ] 构造的特定超图态仅用泡利X 和Z 测量都足以实现普适量子计算. 就计算鲁棒性而言, 超图态本身的一些非局域性和纠缠性质使得其对于局域实在(local realism)呈现指数增加的违背, 因而可以很好地抵抗粒子损失[83 ] . 如何基于其他类别的资源态设计抗噪且操作简便的普适MBQC也符合实际的实验需求. 此外, 2019年Gachechiladze等[145 ] 提出了一种3-一致超图态用作新型确定性MBQC的资源态, 且相关计算模型具有一些新的特征: 仅用泡利测量就可以实现普适计算; 允许并行执行所有的逻辑CCZ和SWAP门; 计算的逻辑深度等于逻辑Hadamard门的整体层数等. 因此, 有望进一步从深度复杂性和并行化计算的角度研究MBQC的优化方案.3.2 节中已介绍了MBQC模型和量子关联非经典性之间的紧密联系, 这些研究近年来启发了不少新奇的后续进展, 如2018年Mansfield和Kashefi[146 ] 提出“序列文本变换中的互文性”可能导致的计算优势, Frembs等[147 ] 展示在d 维qudit系统中, 强非局域性配合经典线性处理足以估计高度多项式函数. 因此, 值得进一步探索的问题是: 其他类型的MBQC是否也具有特定的量子关联特性? 这样的特性能否带来相对经典算法的计算优势? 傅里叶分析理论表明任意的布尔函数都具有相应的多项式表示. 因此, 进一步发展和挖掘$ {\text{NMQ}}{{\text{C}}_ \oplus } $ 以及MBQC模型的潜力, 有望构建出能计算任意非线性布尔函数且相对特定经典模型展现量子优势的新型计算模型, 并应用到依赖于Bent函数等高度非线性布尔函数的密码学[148 ] , 或需要非线性激活层的量子神经网络[149 ] 等领域. 不同量子资源态在计算特定布尔函数的同时, 所得结果又能反过来用于测试和核实该量子态在实际实验中的非经典特性, 预示着新的量子态验证方法.[103 ,104 ] . 如3.3 节所述, 考虑SPTO的概念包含了多种不同类别的态结构和物质相, 进一步探索SPTO和MBQC及量子元胞自动机(cellular automaton)这几者之间的关系, 有助于构造新型计算普适的物质相(如对称保护簇相[105 ,150 ] ), 及相应SPT态执行普适量子计算的具体例子. 在应用层面, 考虑将MBQC和拓扑纠错的思想结合起来, 能促进对噪声环境中顺利运行的可扩展量子计算设备的研制.6.总 结 MBQC计算模型及相关理论经过近二十年的发展其内涵已得到了极大丰富, 重要结果和相关文献资料繁多, 本文在选题上注重基础概念和典型案例, 希望能启发读者进一步学习和探索本文中未加详述但同样具有重要研究意义的相关课题, 如用于普适MBQC的AKLT态[151 ] , MBQC与经典自旋模型的联系[72 ] 等. 本文涵盖的主要内容如下. 











































































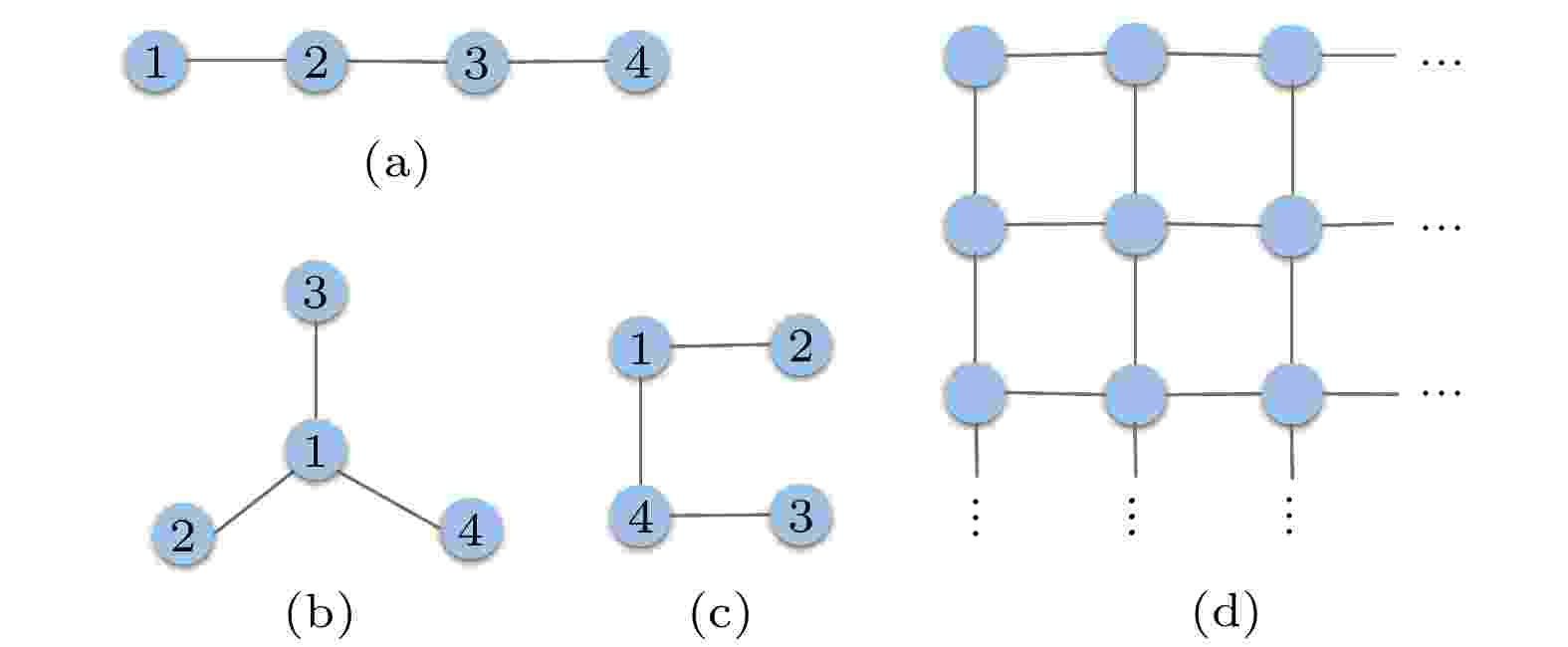 图 1 不同类型的图态 (a)线性簇态; (b)星形图态; (c)马蹄形簇态; (d)可扩展的二维方格图态
图 1 不同类型的图态 (a)线性簇态; (b)星形图态; (c)马蹄形簇态; (d)可扩展的二维方格图态






 图 2 单向量子计算执行量子门操作 (a)输入态
图 2 单向量子计算执行量子门操作 (a)输入态









































 图 3 基于传态的方案实现单量子比特门 (a)一方远程制备态
图 3 基于传态的方案实现单量子比特门 (a)一方远程制备态





















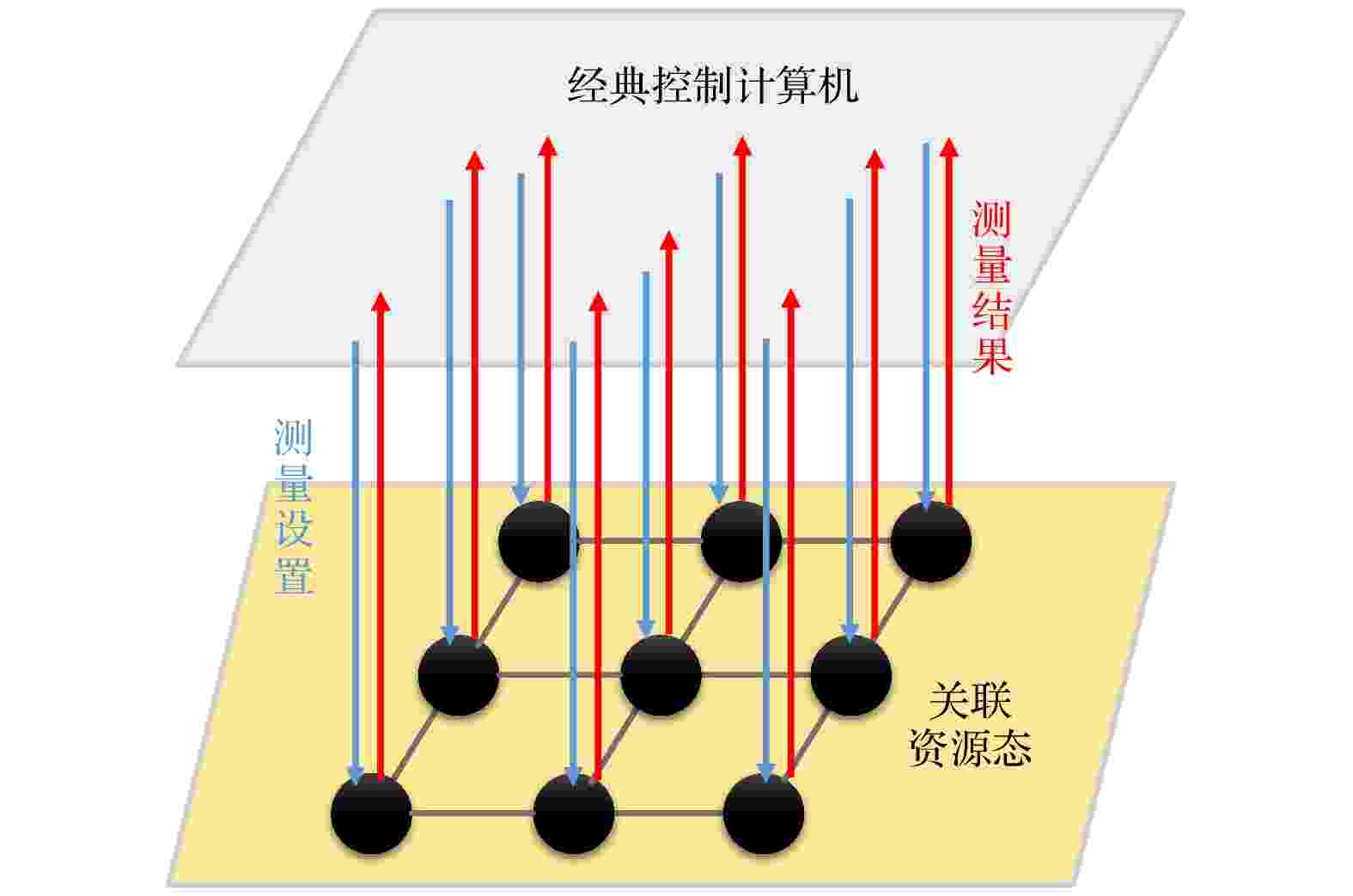 图 4 利用关联的计算模型. 经典控制计算机提供k个测量设置中的1个作为对关联多方资源态中个体的经典输入(蓝色箭头), 并且接收l个测量结果中的1个(红色箭头)作为输出
图 4 利用关联的计算模型. 经典控制计算机提供k个测量设置中的1个作为对关联多方资源态中个体的经典输入(蓝色箭头), 并且接收l个测量结果中的1个(红色箭头)作为输出













