全文HTML
--> --> -->现有的高精度绝对重力仪普遍采用自由落体法, 主要包括以角锥棱镜为下落物体的激光干涉式绝对重力仪(简称光学重力仪)[5-8]和以冷原子团为下落物体的原子干涉式绝对重力仪(简称原子重力仪)[9-13]. 前者通过激光干涉仪测量角锥棱镜在真空中自由下落的运动轨迹, 拟合求解重力加速度; 后者根据原子团在自由下落的过程中经过3次拉曼激光脉冲作用形成的原子干涉相位来计算重力加速度. 由于二者的实际测量对象是下落物体或下落原子团相对于仪器内1个参考镜(角锥棱镜或平面镜)的运动加速度, 因此参考镜自身的加速度必然耦合到测量结果中. 现有的绝对重力仪可以达到微伽(μGal, 1 μGal = 1×10–8 m/s2)量级的测量精度, 此时如果直接将参考镜放置在地面上, 地面振动引起的测量值离散度将远大于该测量精度. 因此高精度绝对重力仪必须利用隔振系统使参考镜自身的运动大幅衰减, 或利用测振仪器获得参考镜自身的运动加速度并在计算重力加速度时对其进行修正. 目前多数高精度绝对重力仪主要使用隔振系统.
影响绝对重力测量的地面振动噪声包括环境噪声和仪器自身噪声. 环境噪声与测量时间和测量点的坐标、地基及周围环境有关, 可以根据频率来粗略区分. 首先是人类活动噪声, 一般大于1 Hz, 如车辆、风机等人工振源的振动、 建筑物和树木的晃动、 仪器测试期间附近的人员走动. 其次是地球本身产生的噪声, 一般在0.1—1 Hz, 如风激振、 地震、火山等地球内部运动引起的振动, 以及周期性的地脉动. 根据美国地质调查局对分布在全球多个地震台站测量数据的分析, 地脉动噪声模型的加速度功率谱密度在周期为5和1/3 s的位置存在峰值[14]. 最后是大气运动噪声, 一般小于0.1 Hz, 如风造成的植物晃动以及气压波动, 这部分噪声变化较为缓慢, 幅值也相对较低, 对绝对重力测量的影响可以忽略[15,16]. 仪器自身噪声主要指仪器运行引起的振动. 光学重力仪中, 传动机构每次释放下落物体时, 绝对重力仪的静态质量瞬间减小, 此时地面支持力与仪器所受重力不再平衡, 等效为1个瞬时冲击, 称为自振效应; 传动机构主要由电机控制, 下落物体运动过程中电机自身的振动也会传递到地面. 原子重力仪中, 当隔振系统内有带铁磁性的金属件且仪器未使用磁屏蔽罩时, 隔振系统附近磁光阱产生的规律变化的磁场将使这些金属件及与其固定的参考镜发生受迫振动[17], 从而对测量结果产生影响. 综上, 为了配合绝对重力仪的测量精度, 隔振系统的本征频率应不高于0.1 Hz, 即本征周期在10 s以上. 地面振动包含水平分量和垂直分量, 由于绝对重力测量只依靠垂直方向的位移数据进行计算, 因此现有的隔振系统普遍为垂直隔振系统, 可以从原理上分为被动式和主动式, 其中主动式又分为一级和二级.
实际测量中, 光学重力仪内参考镜的振动全部来源于地面振动, 易通过地震计得到其具体数值并建立仿真. 其中来源于环境的地面振动噪声(主要为人类活动噪声、周期性地脉动及随机振动)的产生及持续与重力仪的测量过程是相对独立的, 即时间上不相关, 理论上不会引入恒定的系统误差. 而光学重力仪的自振效应与仪器采集下落物体运动轨迹的时间段存在固定的时间差, 即自振效应导致的地面振动对测量环节而言具有固定相位的噪声, 由此引起的隔振系统内参考镜的振动也具有固定相位. 这种参考镜振动将导致光学重力仪存在系统误差, 即影响测量准确度. 对于原子重力仪, 目前尚无完整资料给出关于参考镜振动来源及真实振动情况的定量分析, 不易建立仿真. 因此下文主要对光学重力仪进行仿真分析. 本文将从被动式、一级主动式、二级主动式这3大类垂直隔振系统的工作原理出发, 分析这些系统在自振效应、地脉动及随机振动构成的地面振动输入下对重力加速度测量值在系统误差和测值离散度两方面的影响, 为进一步提高国产光学重力仪的测量精度提供建议.
2.1.参考镜振动对重力值测量误差的影响
首先回顾误差理论的基本概念. 测量误差指的是仪器的测量值与被测量的真实值之差 [18], 正常条件下包括系统误差和随机误差[18]. 系统误差指在同一条件下测量被测量值时出现的大小和符号都保持不变的误差, 或根据一定规律随测量条件的变化而变化的误差; 随机误差指在同一条件下测量被测量值时出现的大小和符号都以不可预测的方式变化的误差[18], 一般遵循正态分布、矩形分布等分布规律. 仪器的测量精度(精确度, accuracy)指的是准确度(trueness)和精密度(precision)的综合[19], 分别由系统误差和随机误差决定[20], 如图1所示.
图 1 系统误差与随机误差Figure1. Systematic error and random error.
绝对重力测量普遍以n次测量值的均值作为最终结果, 并用均值标准差ν表征测量值离散度[21], 满足
下面考察参考镜的实际振动对重力测量值的影响. 光学重力仪利用迈克耳孙干涉仪测量下落物体的运动轨迹, 对其进行二次拟合来计算重力加速度. 设t为下落过程中的某一时刻, 以开始测量的瞬间为时间零点; s(t), N(t)分别为该时刻下落物体、参考镜相对于惯性参考系的位移; sm(t)为干涉仪实测的下落物体相对于参考镜的位移. 因此有
当参考镜位于隔振系统内时, 其真实振动是地面振动输入下该镜作为被隔振物体的振动, 可以通过以下方法评估光学重力仪中与其对应的测量误差: 1)利用地震计或加速度计测量下落物体完成1次自由下落期间的地面振动, 提取其中的典型信号作为仿真参数, 包括地脉动信号、随机振动信号和释放引起的自振脉冲信号; 2)在仿真软件中建立隔振系统的物理模型; 3)将1)中获得的典型信号作为2)中隔振系统的输入信号, 求取系统的输出信号即参考镜的振动位移信号; 4)对3)中得到的参考镜振动位移信号进行二次拟合, 该二次项系数即为参考镜振动引入的重力测量误差ΔgL.
2
2.2.垂直隔振系统的物理模型
下面介绍绝对重力测量领域中普遍使用的各类隔振系统的物理模型, 仿真时将据此搭建相应的仿真模型.被动式垂直隔振系统主要有零长弹簧结构、 欧拉压杆结构、 负刚度弹簧结构等[22-24], 其中最具代表性的是基于零长弹簧结构的Lacoste型, 以及由负刚度压杆及正刚度弹簧组成的美国Minus K公司生产的隔振系统[25]. Lacoste型系统可以实现30 s的长周期[26], 但长期稳定性较差, 负载在百克量级; Minus K型系统的周期一般为1 s附近, 但长期稳定性强, 负载达到十千克量级. 这两类系统在其平衡位置附近的等效物理模型均如图2(a)所示, 其中k1和β1分别为弹簧的刚度和阻尼, M1为参考镜及其他与之固定的结构件的总质量, zi(t)为地面振动在惯性参考系中的位移, 即系统底座的绝对位移, z1(t)为参考镜的绝对位移. 后续将分别分析这两种系统.
图 2 (a) 被动式隔振系统的物理模型; (b) 一级主动式隔振系统的物理模型; (c) 二级主动式隔振系统的物理模型Figure2. Physical models: (a) Passive vibration isolator; (b) one-stage active vibration isolator; (c) double-stage active vibration isolator
一级主动式垂直隔振系统在原子重力仪中应用较为广泛, 如美国斯坦福大学和中国科学院精密测量科学与技术创新研究院搭建的隔振系统[27,28] , 理论上也可以应用于光学重力仪. 这些系统的等效物理模型如图2(b)所示, 其中k1和β1分别为一级弹簧的刚度和阻尼, M1为一级框架的总质量, 包括参考镜和传感器及其他结构件, zi(t)和z1(t)分别为地面振动和参考镜的绝对位移, f(t)为反馈力. 系统的工作原理是: 传感器探测一级框架的绝对位移z1(t)输入至控制器, 驱动器根据控制器的输出信号向一级框架提供反馈力f(t), 使其绝对位移趋于0, 从而实现对参考镜的隔振. 下文将以中国科学院精密测量科学与技术创新研究院研制的系统[28]为典例进行仿真, 这是因为该系统与上述Minus K型被动系统具有相同的机械结构, 对比二者的仿真结果可以直观地考察反馈控制对系统性能的提升.
二级主动式垂直隔振系统主要应用于光学重力仪, 目前应用最广泛且性能最好的是美国Micro-g公司研制的“Superspring”系统[29], 清华大学等单位也研制了不同结构的同类系统[30-32]. 这些系统的等效物理模型均如图2(c)所示, 其中, k1和β1分别为一级弹簧的刚度和阻尼; M1为一级框架的总质量; k2和β2分别为二级弹簧的刚度和阻尼; M2为包括参考镜在内的二级框架的质量; zi(t), z1(t)和z2(t)分别为地面振动、一级框架和参考镜的绝对位移; Δz(t)为一级框架和二级框架之间的相对位移; f(t)为反馈力. 系统的工作原理是: 安装在一级框架和二级框架之间的位移探测模块探测二者的相对位移Δz(t)并输入至控制器, 驱动器根据控制器的输出信号向一级框架提供反馈力f(t), 使其跟踪二级框架的运动, 此时系统的闭环周期达到20 s以上, 可以等效为由1个超长弹簧与1个质量块组成的弹簧振子, 从而实现对参考镜的隔振[33].
2
2.3.隔振系统内参考镜的实际运动
光学重力仪完成一次测量的基本流程为: 1)下落物体被释放; 2)信号采集系统被触发, 开始采集干涉仪探测到的下落物体运动轨迹; 3)干涉仪信号采集结束; 4)下落物体减速、静止并被复位. 受软件控制, 信号采集的开始和停止时刻一般与下落物体被释放的时刻有固定的延时. 如前所述, 环境振动噪声与重力测量的信号采集过程在时间上不相关, 即具有随机相位, 理论上不会导致系统误差. 而以自振效应导致的地面振动脉冲为主的仪器自身噪声与信号采集过程一般有固定的时间差, 即具有固定相位. 下面忽略随机相位振动噪声的影响, 考虑地面振动仅为自振脉冲时的情况, 以此为例说明该类噪声将对重力测量引入系统误差.以脉冲信号为隔振系统的输入信号, 此时系统的输出信号即参考镜的真实运动遵循该系统自身的脉冲响应规律, 如图3所示, 其中4个瞬时t0, t1, t2和tm分别对应下落物体被释放、信号采集开始、信号采集结束以及下落物体停止.
图 3 自振脉冲输入下隔振系统内参考镜的振动Figure3. Real vibration of reference retro-reflector in a vibration isolator under the impulse caused by self-vibration effect.
从图3可以看出, 不使用隔振系统时参考镜的振动与地面的脉冲信号完全相同, 如果在t1—t2时段N(t) = 0, 则自振脉冲不会引入系统误差(但此时测值离散度往往较大). 而当参考镜位于隔振系统内时, t1—t2时段N(t)一般为系统的脉冲响应, 由此引入的重力测量误差ΔgL即为该段N(t)二次拟合时的二次项系数. 对每一次下落而言, N(t)都具有基本相同的相位及幅值, 因此ΔgL为固定的系统误差. 这种现象可以推广至其他类似的噪声源, 即任何对下落信号采集过程而言具有固定相位的振动噪声, 如传动电机的振动等, 都将对重力测量引入系统误差.
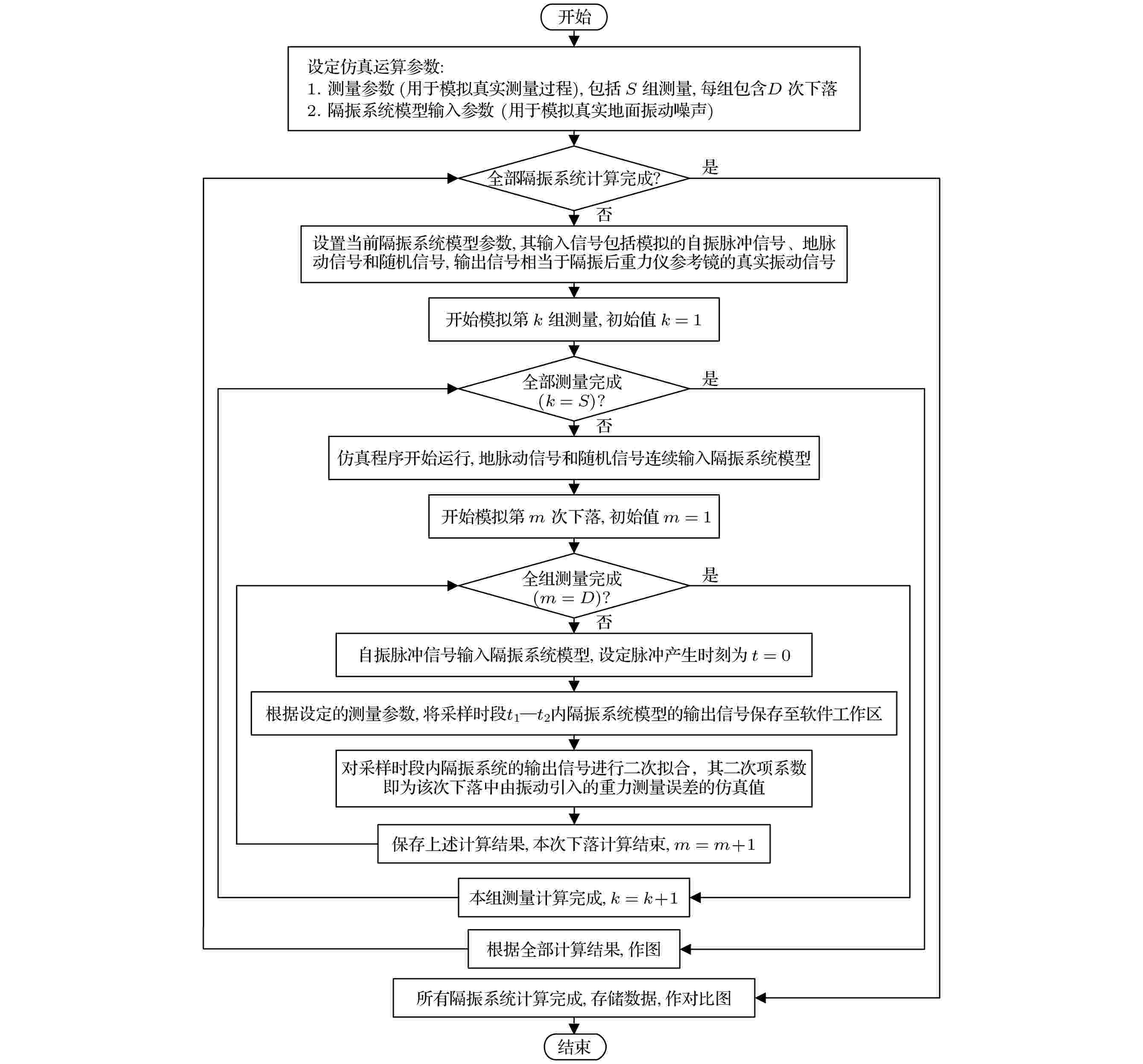图 4 仿真程序流程框图Figure4. Flow chart of the simulation program.
仿真参数汇总在表1中. 该表左侧的测量参数主要参考国产光学重力仪[7,8]. 同时, 考虑到实测要求, 该表右侧振动信号的设定以一般的非安静地面环境为主: 自振效应导致的脉冲信号幅值根据速度型地震计CMG-3ESP实测的绝对重力仪在一般地面环境中测量时的地面振动来设定[34]; 代表随机振动的高斯白噪声的功率谱密度(power spectral density, PSD)根据绝对重力仪不使用隔振时在一般地面环境的实测结果设定[34]; 地脉动用两个正弦信号模拟, 其幅值和频率主要参考美国地质调查局的研究报告[14]. 需要说明的是, 实际测试中自振效应的幅值不仅与仪器本身有关, 也与测点的地基环境有关: 当测点为中国计量科学研究院昌平院区等具有隔振地基的测点时, 自振效应产生的振动脉冲幅值很小; 当测点位于一般条件下的普通地基上时, 振动脉冲幅值则相对较大.
| 测量参数 | 数值 | 振动信号 | 参数 | 数值 |
| 单次测量中采集的 下落物体运动时长/ms | 120 | 信号1: 自振效应导致的脉冲 | 速度/(mm·s–1) | 0.1 |
| 采集电路触发时刻与下落物体释放瞬间的延时/ms | 30 | 信号2: 第1种地脉动 (正弦信号) | 幅值/nm | 5 |
| 单组测量包含的下落次数 | 100 | 信号2: 第1种地脉动 (正弦信号) | 频率/Hz | 0.2 |
| 单组测量期间相邻两次测量的时间间隔/s | 20 | 信号3: 第2种地脉动 (正弦信号) | 幅值/nm | 2 |
| 相邻两组测量的时间间隔/h | 1 | 信号3: 第2种地脉动 (正弦信号) | 频率/Hz | 3 |
| 总测量组数 | 12 | 信号4: 代表随机振动的 高斯白噪声 | PSD /(m2·Hz–1) | 2.5×10–17 |
表1仿真运算参数表
Table1.Parameters used in simulation.
4种隔振系统的仿真模型见图5, 分别是周期为0.85 s的Minus K型、周期为30 s的Lacoste型、闭环周期为66 s的一级主动式、闭环周期30 s的二级主动式. 图5(a)为各模型传递函数的伯德图, 其中黑色虚线表示地脉动的主要频带0.1—10 Hz, 红色虚线表示该频带内的两个峰值频率0.2 Hz (周期5 s)和3 Hz; 图5(b)为各模型的阶跃响应, 可以直观地反映各系统的周期. 这些隔振系统仿真模型的参数来源分别为: 1) Minus K型. 以中国计量科学研究院所购产品的实测机械结构参数为依据. 2) Lacoste型. 根据文献[26]的实验数据推算而得. 3)一级主动式. Minus K的机械结构参数同上, 拾振器参数以中国计量科学研究院所购的CMG-3ESP地震计参数为依据, 控制器(proportion integration differentiation, PID)参数根据文献[28]提供的该类型系统的性能推算而得. 4)二级主动式. 机械参数及PID控制器参数根据文献[33]提供的该类型系统的性能推算而得, 传感器参数、驱动器参数采用同一系统的实际参数[33].
图 5 4种隔振系统 (a)传递函数伯德图; (b)阶跃响应Figure5. Four vibration isolators used in simulation: (a) Bode diagrams; (b) step responses.
图5揭示了以下信息. 首先, 对同样基于Minus K型机械结构的隔振系统, 增加反馈控制使系统由被动式变为一级主动式后, 0.02—20 Hz的传递函数幅频曲线下移, 说明一级主动式系统对该频段地面振动的衰减效果提升, 提升幅度最大可达40 dB以上, 而此频段以外的超低频段和高频段的幅频曲线则保持不变. 其次, Lacoste型系统与Minus K型系统的幅频曲线形状大致相同, 但二者周期不同, 在频率特性上表现为前者的幅频曲线相当于后者左移的结果(同时阻尼比略有改变, 使得谐振峰高度有所区别), 因此Lacoste型系统对0.4 Hz以上的地面振动(涵盖地脉动的一个峰值频率3 Hz)的衰减效果比Minus K型系统更好. 此外, 被动式系统和一级主动式系统的高频衰减速度都是–20 dB/dec, 但二级主动式系统采用了两级弹簧, 高频衰减速度是–40 dB/dec, 因此虽然仿真中二级主动式系统的闭环周期是一级主动式系统的1/2(且与Lacoste型系统的周期相同), 但对于频率在0.1 Hz以上的地面振动(涵盖地脉动的两个峰值频率0.2和3 Hz)来说, 二级主动式系统的衰减效果仍优于一级主动式、Lacoste型及Minus K型系统, 这也是目前光学重力仪普遍采用Superspring来实现更高测量精度的原因[33]. 需要说明的是, 伯德图中一级主动式系统的两个谐振峰来源于地震计, 二级主动式系统的谐振峰来源于两级弹簧振子结构. 对于一级主动或二级主动式系统, 这两个谐振峰均相差3个量级左右, 因此系统的阶跃响应只会体现低频谐振频率, 而高频谐振频率不会影响系统的隔振效果. 最后, 虽然4种系统的相频曲线均有较大变化, 但后续仿真及实际测量中尚未观察到该变化对测量结果的影响, 因此本文暂不对此进行探究.
4.1.仿真运算结果
仿真运算得到的不同隔振条件下参考镜振动对光学重力仪引入的重力测量误差如表2所列, 包含12组数据, 每组100次下落. 图6(a)和图6(b)分别表示表2中输入为综合振动信号时光学重力仪的单组及12组测量误差. 表中数据以“E ± ν”的形式表示, 其中E为系统误差, 用测量误差的均值表示, ν为测量值离散度, 以测量误差的均值标准差表示, 二者均按照国际比对的惯例精确至0.1 μGal[35]. 表2中综合信号输入时的运算结果并非由其前两列数据直接相加得到, 而是由前两列信号之和为输入重新运行仿真程序所得, 以便于更准确地模拟实际情况.| 隔振类型 | 输入信号 | ||
| 自振脉冲 (信号1) | 地脉动及随机振动 (信号2—4) | 综合振动 (信号1—4) | |
| 无隔振 | 5.1 ± 15.1 | 21.0 ± 74.9 | –121.8 ± 90.4 |
| Minus K型 (被动式) | 655.8 ± 0.4 | 2.1 ± 2.0 | 658.5 ± 2.5 |
| Lacoste型 (被动式) | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
| 一级主动式 | –15.9 ± 0.0 | –0.4 ± 0.2 | –15.9 ± 0.2 |
| 二级主动式 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.0 ± 0.0 |
表2基于12组仿真数据得到的参考镜振动对光学重力仪引入的测量误差(单位: μGal)
Table2.Measurement errors introduced in laser-interferometry absolute gravimeter by the vibration of retro-reflector, obtained from 12 data sets simulated results (unit: μGal)
图 6 综合振动输入下参考镜振动对光学重力仪引入的(a)单组重力测量误差, (b) 12组重力测量误差, 图(b)中误差条为每组测值的标准差Figure6. Measurement errors of obtained from (a) one data set and (b) 12 data sets introduced in laser-interferometry absolute gravimeter by the vibration of retro-reflector under impulse, seismic noise and random noise, with the error bar in (b) indicating the standard deviation of each set.
根据图6(a), 不使用隔振时重力仪的测量误差主要分布在±5000 μGal左右, 与在一般地面环境的实测数据相符[34], 验证了表1右侧输入参数的合理性.
纵向对比表2各行, 使用隔振系统后测量值离散度ν相比无隔振时均明显减小, 这验证了各系统仿真模型的合理性. 需要注意的是, 当输入为自振脉冲时, 使用Minus K型被动式系统或一级主动式系统后, 系统误差的绝对值|E|反而大于无隔振时的|E|, 与2.3节及图3的理论分析相符. 具体来看, 相同综合振动输入下隔振效果从低到高分别为Minus K型系统、一级主动式系统(基于Minus K型系统设计)、二级主动式系统: 使用Minus K型系统时, 系统误差的绝对值|E|和测量值离散度ν分别达到0.6 mGal和2 μGal左右; 使用一级主动式系统时二者分别为16和0.2 μGal左右; 使用二级主动式系统时二者均在0.1 μGal以内(可忽略不计). 该仿真结果符合第3节给出的定性分析: 根据图5, 频率在0.1 Hz以上(涵盖地脉动频带)的输入信号对应的输出信号的幅频衰减程度由低到高分别为Minus K型系统、一级主动式系统和二级主动式系统, 这意味着同等输入下系统内参考镜的振动位移越小, 引入的系统误差和测值离散度越小.
虽然仿真结果表明Lacoste型被动式系统的隔振效果与二级主动式系统的效果相当, 但实际的Lacoste型系统易受温度等环境因素的影响及弹簧蠕变等材料特性的限制, 无法长期保持数十秒的长周期; 根据文献[6], 目前仅IMGC型绝对重力仪曾经应用该类系统进行长期重力检测, 因此下文不再提及该系统.
横向对比表2各列, 应用同一系统时, 自振脉冲将导致重力测量存在系统误差; 地脉动和随机振动一般不会导致系统误差, 表现为使用二级主动式、一级主动式、甚至Minus K型被动式系统时, 二者引起的系统误差均不大于5 μGal; 综合振动导致的系统误差与自振脉冲导致的系统误差相同.
增大用于计算的数据组数, 可以直观看出上述结果的统计收敛规律, 如图7所示, 图7中点划线对应的纵坐标等于相应输入信号下所有计算结果的均值, 表示收敛极限. 对各类型的振动输入, 随着数据量的增加, 测量值离散度ν都将不断减小; 自振脉冲输入或综合振动输入下的系统误差E相同且不会随数据量的增加而改变; 地脉动和随机信号输入下的系统误差E将收敛至0.
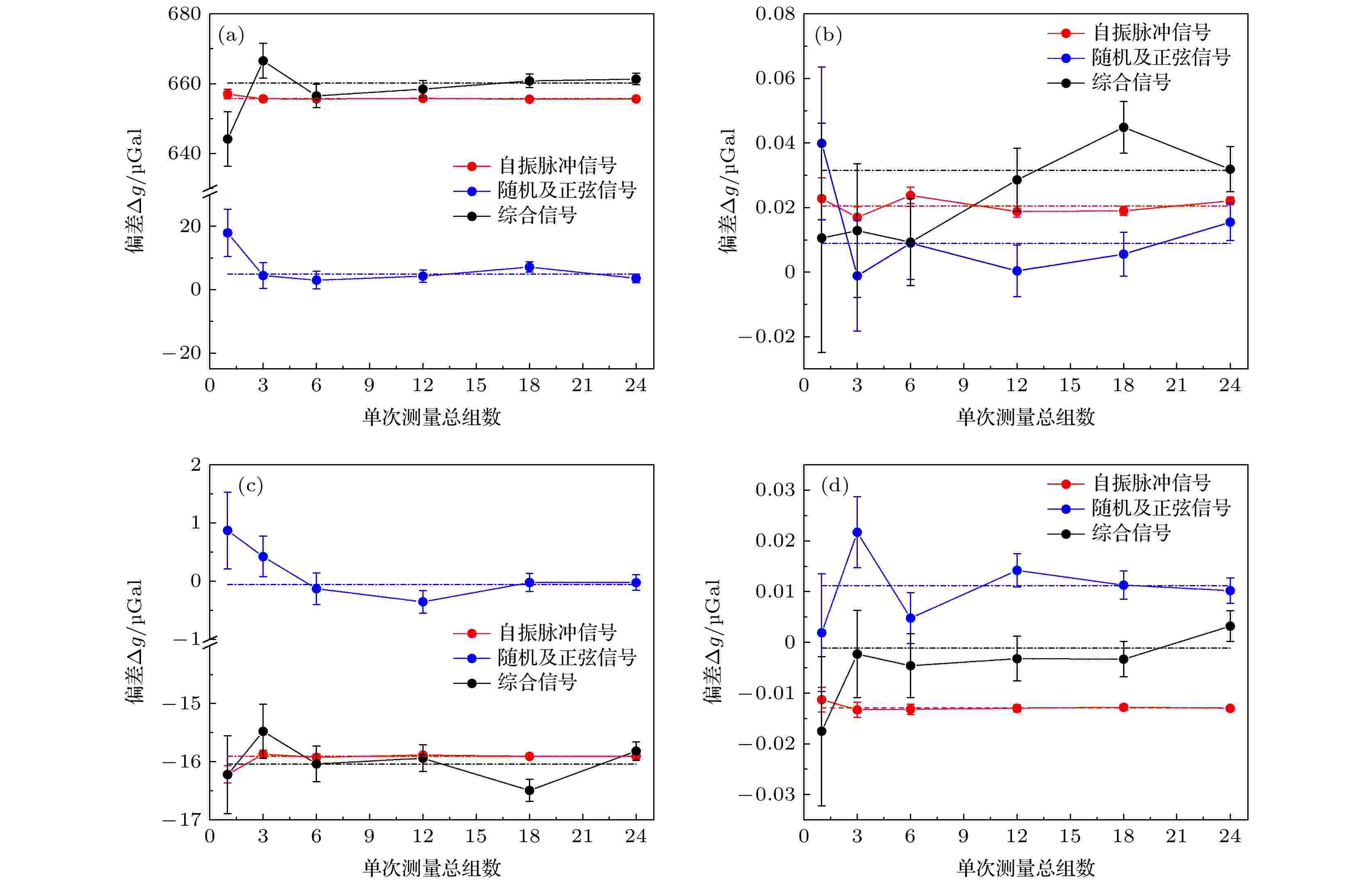图 7 参考镜振动对光学重力仪引入的测量误差随测量组数的变化 (a) Minus K型被动隔振系统; (b) Lacoste型被动隔振系统; (c) 一级主动隔振系统; (d) 二级主动隔振系统Figure7. Measurement errors introduced in laser-interferometry absolute gravimeter by the vibration of retro-reflector, varying with the numbers of data sets used in simulation: (a) Minus K passive vibration isolator; (b) Lacoste passive vibration isolator; (c) one-stage active vibration isolator; (d) double-stage active vibration isolator.
2
4.2.实验测量结果
仍以光学重力仪为例, 为了更清楚地考察一般地面环境中固定相位振动噪声对重力测量值的影响, 利用清华大学T-1型绝对重力仪[7]分别配合Minus K型被动式隔振系统和Superspring型二级主动式隔振系统进行对比实验(图8(a)和图8(b)). 无隔振时的测量在Superspring未解锁期间完成, 此时其内部的参考镜与底座固定, 相当于参考镜直接放置在地面上. 除隔振系统外, 测量时重力仪的其他硬件及软件设备均保持不变. 本次实验包含6组测量, 每组100次下落.
图 8 实验验证现场图 (a) 干涉仪下方放置Minus K型被动式系统; (b) 干涉仪下方放置Superspring二级主动式系统Figure8. Picture of absolute gravimeter with (a) Minus K passive vibration isolator or (b) Superspring double-stage active vibration isolator.
在测量过程中的一段时间内, CMG-3 ESP型地震计同步采集了重力仪下方的地面振动速度信号. 在下落物体释放瞬间, 地震计信号中出现1个脉冲, 其幅值约为0.1 mm/s, 是其他时刻信号幅值的14倍, 且持续时间不大于30 ms, 说明该脉冲同时包含自振脉冲、地脉动和随机振动, 而其他时刻的地震计信号则只包含后两者. 据此可以将自振脉冲单独识别出来, 并确认其真实幅值与表1右侧第1种自振脉冲信号的设定值相符; 而其他时刻的信号幅值及图6(a)也已表明表1右侧第2, 3种地脉动信号和第4种随机信号的设定值合理, 符合实际情况.
综上, 前述仿真运算时使用的综合信号输入参数与实测情况相符, 仿真结果可以与实测结果对比(表3). 表1同样采用“系统误差E ± 测值离散度ν”的形式表示(精确至0.1 μGal), 以A-10型绝对重力仪在该实验地点的实测值为参考值, 以根据T-1型绝对重力仪的不确定度表修正后的本实验的实测值与该参考值的偏差为系统误差.
| 隔振类型 | 结果类型 | |
| 实测结果 (综合信号) | 仿真结果 (综合信号) | |
| 无隔振 | –52.0 ± 110.0 | –40.7 ± 123.3 |
| Minus K型(被动式) | 655.2 ± 77.8 | 656.5 ± 3.3 |
| 一级主动式 | — | –16.0 ± 0.3 |
| Superspring型 二级主动式 | –6.7 ± 12.6 | 0.0 ± 0.0 |
表36组实际测量结果(单位: μGal)
Table3.Measurement results obtained from 6 data sets (unit: μGal).
纵向对比表3各行发现:首先, 无隔振时的系统误差反而小于使用Minus K型系统时的系统误差, 与2.3节的理论分析及表2的仿真结果一致, 且无隔振时测值离散度的实际值与仿真值一致, 再次验证了输入参数的合理性; 其次, 使用Minus K型系统时系统误差的实测值与仿真值基本一致, 证明此时以自振效应为主的固定相位振动噪声引入的系统误差确实高达0.5 mGal以上. 该结果不仅验证了仿真算法的合理性, 同时表明, 如果仅使用Minus K及类似的被动式隔振系统来搭建小型化绝对重力仪时, 实现毫伽量级的测量精度也存在一定困难.
另外, 当使用Minus K型被动式系统及Superspring型二级主动式系统时, 测量值离散度的实测值虽明显小于无隔振时, 但远大于各自对应的仿真值. 这主要是因为各系统的仿真模型是基于图2中完全理想的理论模型建立的, 没有考虑实际系统内存在的干扰因素, 如系统调平精度有限使得参考镜的水平扰动耦合进垂直方向, 系统中弹性元件刚度非线性、机械结构参数受温度等环境因素的影响而变化等. 后续工作中将对这些干扰因素进行深入分析, 有望更好地改进仿真模型. 虽然这些因素使得实际系统的性能具有一定的局限性, 不过绝大多数情况下Superspring等二级主动式垂直隔振系统已能够满足微伽量级的测量精度要求.
最后, 随测量组数的增加, 实测结果同样具有统计收敛规律(图9).
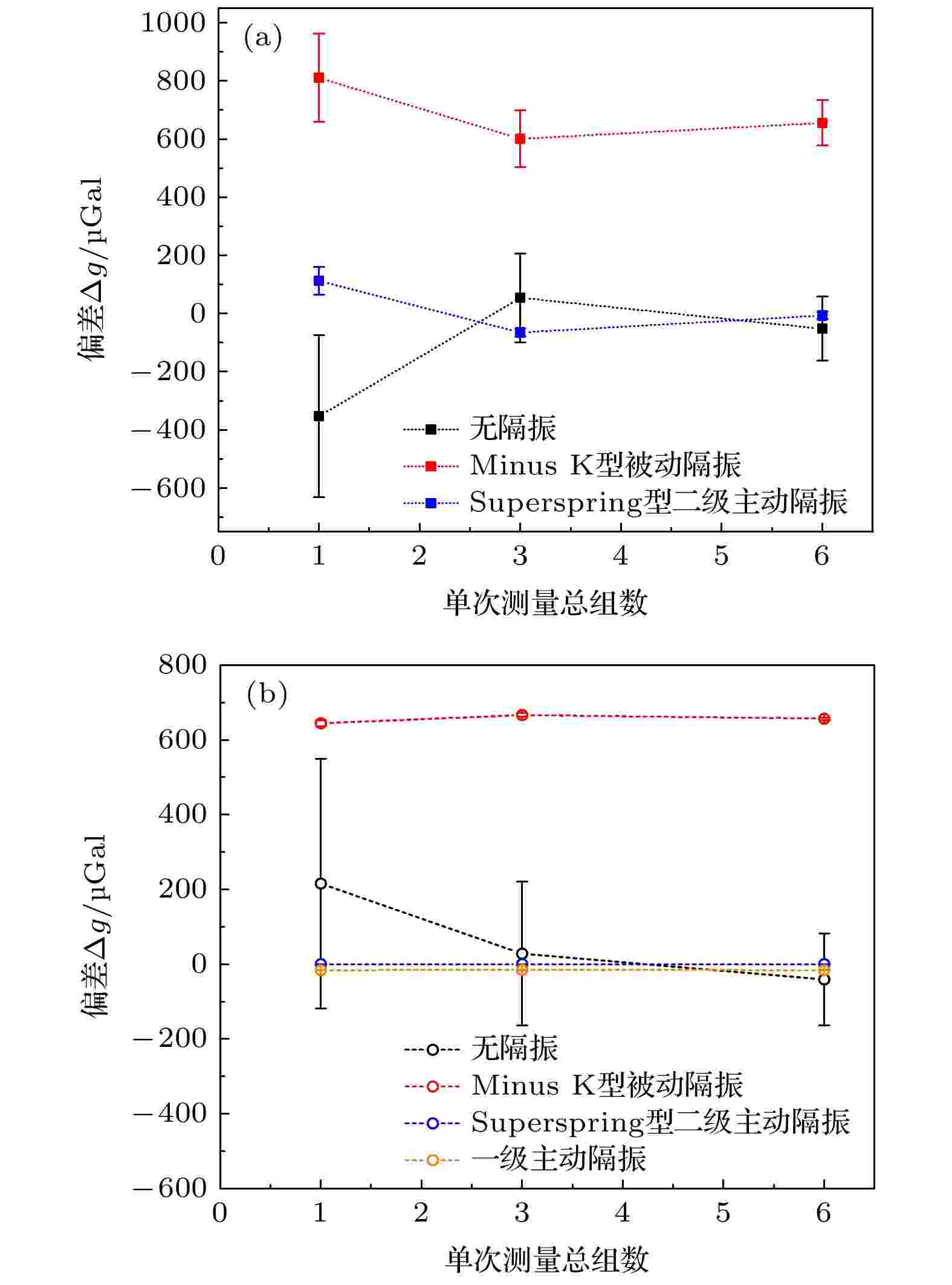图 9 实际测量结果(a)及相同振动输入下的仿真结果(b)Figure9. Measurement results (a) and simulation results (b) of g values under the same vibration input.
| 隔振类型 | 采样起点t1/ms | ||
| 34 | 35 | 36 | |
| 无隔振 | –84.6 ± 314.7 | 215.6 ± 334.0 | 154.2 ± 294.5 |
| Minus K型 (被动式) | 658.6 ± 8.1 | 660.8 ± 9.2 | 660.7 ± 7.7 |
| 一级主动式 | –16.2 ± 0.7 | –16.1 ± 0.8 | –17.3 ± 0.7 |
| 二级主动式 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.1 ± 0.0 |
表4采集过程起始时刻改变时的仿真结果(单位: μGal)
Table4.One set of simulated results with different t1 (unit: μGal).
首先, 由图3可看出, 如果信号采集过程相对于下落物体被释放时刻的时间差发生改变, 则t1—t2这段“采集窗口”将在参考镜的振动位移曲线上前后移动, 使真正影响重力计算结果的参考镜位移也发生改变. 当采集时长固定为120 ms时, 可以通过改变t1的取值来计算该问题的影响, 此时的一组(包含100次下落, 下同)仿真结果如表4所列. 目前大多数光学重力仪普遍采用电触发的方式来启动采集过程, 实际上t1的不确定度仅为0.35 ms[21]. 根据表4, 可以推测这种情况下使用各类型隔振系统时系统误差E的变化基本不会超过此时的测量离散度ν, 因此t1变化造成的影响一般情况下可以忽略. 在使用其他触发方式的光学重力仪中, 该方法同样可以用来分析t1变化或采集时长变化对重力测量误差造成的影响.
其次, 下落间隔的变化也可能对仿真结果产生影响, 比如下落间隔太短可能导致隔振系统的上一次脉冲响应尚未充分衰减时重力仪已开始下一次测量, 此时仿真结果的系统误差理论上将进一步增大. 由于实际光学重力仪的最短下落间隔为3 s[36], 可以在下落间隔分别为30, 20, 10, 7, 3 s时重新进行计算, 此时的一组仿真结果如表5所列. 从表5可以看出, 使用Minus K型被动式隔振系统时, 系统误差的绝对值|E|确实会随着下落间隔的缩短而增大; 而一级主动式和二级主动式隔振系统的隔振效果很好, 因此即使连续两次测量的脉冲响应发生叠加, 参考镜的振动幅度也足够小, 进而测量结果不会有明显变化.
| 隔振类型 | 下落间隔/s | ||||
| 30 | 20 | 10 | 7 | 3 | |
| 无隔振 | –168.0 ± 328.5 | 215.6 ± 334.0 | 176.7 ± 281.9 | 49.7 ± 322.1 | –281.3 ± 295.2 |
| Minus K型(被动式) | 658.5 ± 9.4 | 667.5 ± 8.1 | 631.2 ± 9.2 | 937.9 ± 8.7 | 1037.1 ± 8.5 |
| 一级主动式 | –16.3 ± 0.7 | –15.4 ± 0.8 | –15.7 ± 0.7 | –16.5 ± 0.8 | –16.8 ± 0.8 |
| 二级主动式 | 0.0 ± 0.0 | 0.0 ± 0.0 | 0.1 ± 0.0 | 0.1 ± 0.0 | 0.2 ± 0.0 |
表5下落间隔改变时的仿真结果(单位: μGal)
Table5.One set of simulated results with different drop interval (unit: μGal).
此外, 前述仿真运算过程中只以2个位于地脉动峰值频率的正弦函数来模拟地脉动, 但实际的地脉动包含的频率成分更为丰富, 可以通过增加仿真输入中的正弦函数来考察这种简化是否会对仿真结果产生影响. 在0.1—10 Hz这个对绝对重力测量影响最大的频段取频率值重新构建正弦函数(0.1—1 Hz按0.1 Hz的间隔取值, 在1—10 Hz按1 Hz的间隔取值), 这些正弦函数各自的幅值按照地脉动噪声功率谱密度的新高噪声模型(new high noise model, NHNM)[14]来设定. 由此得到的一组仿真结果如表6所列, 其与使用2个正弦函数模拟地脉动时的仿真结果基本一致, 再次证明与重力测量的信号采集过程在时间上不相关的环境振动噪声理论上不会导致系统误差.
| 隔振类型 | 地脉动信号 | |
| 19个正弦信号 | 2个正弦信号 | |
| 无隔振 | 226.3 ± 297.3 | 215.6 ± 334.0 |
| Minus K型(被动式) | 662.4 ± 8.3 | 644.2 ± 7.8 |
| 一级主动式 | –15.1 ± 0.8 | –16.2 ± 0.7 |
| 二级主动式 | 0.1 ± 0.0 | 0.0 ± 0.0 |
表6使用多种正弦函数模拟地脉动时的仿真结果(单位: μGal)
Table6.One set of simulated results with multiple sinusoidal signals as the seismic noise (unit: μGal)
| 隔振类型 | 结果类型 | ||
| 仿真值 (真实振动信号) | 仿真值 (设计信号) | 实测值 | |
| 无隔振 | –264.5 ± 849.3 | –513.9 ± 678.3 | 471.5 ± 676.6 |
| Minus K型 (被动式) | 646.0 ± 16.5 | 629.1 ± 18.8 | 876.7 ± 615.6 |
| 一级主动式 | –12.1 ± 2.5 | –17.9 ± 1.5 | — |
| 二级主动式 | 1.8 ± 0.1 | 0.0 ± 0.0 | –20.0 ± 62.6 |
表7以16次下落的地震计原始数据为输入时的计算结果(单位: μGal)
Table7.Results with the ground vibrations measured during 16 drops as input signal (unit: μGal).
还可以将实验期间地震计实测的地面振动数据直接作为隔振系统模型的输入来计算仿真结果. 以16次下落对应的地震计数据为例, 其结果如表7所列. 从表7可以看出, 使用隔振系统后, 以地震计原始信号为输入与以表1的设计信号为输入时的仿真计算结果基本吻合. 两种输入下仿真结果相差较大的是二级主动式系统, 这再次说明真实振动环境总比仿真设计更复杂, 即使在测量时使用了性能最好的隔振系统, 实际的重力测量系统误差E也可能达到微伽量级, 需要引起注意. 考虑测量离散度ν, 可以认为3种隔振条件下的实测结果均与仿真结果基本一致.
除上述参数外, 表1中其他仿真参数的变化也可能使计算结果改变. 研究人员可以依据实测参数值修改表1并按照图4所示的流程图自编仿真程序, 预估此时不同类型的振动噪声对重力测量结果的影响.
总体而言, 重力测量过程中相对于信号采集过程具有固定相位的振动噪声将引入无法通过统计方法消除的系统误差, 其大小与噪声的实际幅值有关. 对光学重力仪来说, 可以通过在真空腔内增加平衡下落机构以减小自振效应, 调节传动电机参数以减小电机振动等方法来减小该系统误差. 为了实现更高的测量精度, 一般应使用二级主动式隔振系统; 如受其他条件所限必须使用Minus K型或一级主动式隔振系统时, 则可以利用地震计实测上述噪声引起的地面振动, 并根据本文的仿真运算思路预测由此引入的重力测值系统误差. 具有随机相位的振动噪声不会引入系统误差, 且可以通过增加数据量来减小该类噪声引起的测量值离散度.
感谢清华大学精密仪器系的王力军教授、伍康副研究员和文艺博士提供实验设备及场地.
