摘要:利用密度泛函理论计算, 本文系统研究了δ掺杂的La:SrTiO₃超晶格结构的电子性质随掺杂维度和掺杂浓度改变而变化的规律性. 该结构通过在SrTiO₃等间距的单元层中掺入一定浓度的La来实现. 在25% La掺杂浓度下, 随着相邻掺杂层间距从1个单层增加到5个单层, 掺杂维度从三维过渡到二维, 超晶格从金属性变到绝缘体性, 并在带隙中产生局域态, 且该局域态呈现出电荷序、自旋序和轨道序. 这种金属-绝缘体转变是由于二维电子体系呈现出更强的关联性造成的. 而随着二维掺杂浓度提高到50%, 关联性降低, 体系变成金属性.
关键词: 二维掺杂/
强关联/
金属-绝缘体转变

English Abstract

全文HTML

--> --> -->

由于具有较强的电子关联性, 过渡金属氧化物经常展现出一些非凡的特性, 其晶格、电子和磁性构型与一些引人注目的物理性质存在着紧密的相关性^[1]. 这些特性通常是电子电荷、自旋和轨道自由度与晶格微妙作用的结果^[2,3]. 调控这些参数有可能产生丰富的电学性质, 有助于发展出有新特性的功能材料和器件^[4,5]. 比如, 掺杂能调控材料内部的多个自由度, 如电荷、自旋、轨道占据等, 通过掺杂改变d轨道的填充度能诱导过渡金属氧化物实现金属-绝缘体转变、反铁磁-铁磁转变、普通导体-超导体转变等^[1-3,5]. 这种调控手段和对应的性能已经在传感器、自旋电子器件、存储器等领域得到应用.
电子体系的维度也是影响材料内部电子学特性的一个重要调控参数. 随着电子体系的维度降低, 如从三维变到二维, 电子间的关联作用变强并可能起主导作用^[6]. 这可能导致电子体系呈现出整体有序性并使得体系进入非同于三维体系的新的相. 随着材料生长技术的进步, 制备二维电子体系已经比较容易实现, 如在异质界面体系或者二维掺杂体系. 最近几年在钙钛矿过渡金属氧化物界面体系的研究表明过渡金属氧化物异质结二维电子体系具备一些独特的性质^[7-21], 如金属-绝缘体转变、磁性-非磁性转变、超导等. 为了研究过渡金属氧化物电学性质随着掺杂维度和掺杂浓度改变而变化的规律, 本文利用密度泛函理论计算研究了δ掺杂(在一个单元层中掺杂La而其近邻层不掺杂)的La:SrTiO₃超晶格结构的电子性质, 通过改变掺杂层的间距可实现从三维掺杂过渡到二维掺杂, 并通过改变掺杂浓度来改变二维电子的密度. 计算结果表明, 调节这些参数可改变电子关联强度进而实现体系的金属-绝缘体转变.

计算由VASP程序包执行^[22], 其中采用PBE型广义梯度近似泛函(PBE-GGA)^[23]和投影缀加平面波方法^[24,25], 平面波截断动能为500 eV. Ti 3d轨道局域性较强, 轨道中电子的在位库伦相互作用较强, 计算中采用Dudarev的LSDA+U方法近似描述^[26]. 计算中Ti 3d轨道电子的在位库伦相互作用能分别取U=0, 2.0, 3.0, 3.5, 3.7, 4.4, 5.0 eV等数值, 将不同数值得到的基态电子态与实验测得的电子性质对比进而确定出合适的U值. 图1展示了两种超晶格原胞结构, 即[Sr_0.75La_0.25TiO₃]1|[SrTiO₃]n (n = 1, 5)(简写为[SLTO]1|[STO]n), 其中掺杂层中25%的Sr原子被La原子替代, 沿着[001]方向周期性重复, 面内周期为4 × 4. 相应地, 采用4 × 4 × 4和4 × 4 × 2的Monkhost型k点网格在布里渊区中取样. 有限温度展宽采用Gaussian方法, 其中σ = 0.1 eV. 计算中所有原子都充分弛豫, 直到受力小于0.01 eV/?.
图 1 (a) 超晶格结构面内4 × 4周期俯视图; (b) [SLTO]1|[STO]1侧视图; (c) [SLTO]1|[STO]5侧视图. 绿色球代表Sr原子, 蓝色代表La原子, 红色代表O原子, Ti原子在八面体中心
Figure1. (a) Top view of the superlattices with in-plane 4 × 4 unit cells; (b) side view of [SLTO]1|[STO]1; (c) side view of [SLTO]1|[STO]5. Green balls represent Sr atom, blue balls La atom, red balls O atom, Ti atoms are at the centre of the octahedrons.

SrTiO₃导带底部态主要由Ti 3dt_2g (dxy, dyz, dxz) 轨道构成, 掺杂La的价电子轨道5d6s能级高于SrTiO₃中的Ti 3dt_2g 轨道能级, La掺杂产生的电子全部进入Ti 3dt_2g轨道能级. 计算中Ti 3d轨道在位库伦相互作用能U为可调参数, 本文通过比较计算结果与实验结果来确定U的最佳数值. 图2展示了两种典型的U计算的结果. 如图2(a)和图2(b)所示, 在U = 2 eV情况下, 费米能级穿过导带下部, 两种结构都为金属态. 在U = 3.7 eV情况下, 如图2(c)和图2(d)所示, [SLTO]1|[STO]1仍然为金属态, 而[SLTO]1|[STO]5为绝缘态, 费米能级穿过带隙, 且在带隙里出现局域态. 计算表明当U < 3.5 eV时两种体系都是金属态, 而当U ≥ 3.5 eV时[SLTO]1|[STO]5才会展现为绝缘态基态. 实验中观察到[SLTO]1|[STO]1呈现金属性, 而[SLTO]1|[STO]5的电阻温度曲线为绝缘态且光电导检测表明带隙内存在局域态. 又考虑了50% La掺杂结果和带隙宽度等因素后, 确定在上述超晶格体系中U = 3.7 eV的计算结果与实验结果吻合最好.
图 2 分自旋总态密度图和能带图 (a1), (a2) U = 2 eV, [SLTO]1|[STO]1; (b1), (b2) U = 2 eV, [SLTO]1|[STO]5; (c1), (c2) U = 3.7 eV, [SLTO]1|[STO]1; (d1), (d2) U = 3.7 eV, [SLTO]1|[STO]5, 红色箭头所指为带隙内局域态. 图中红线为费米能级, 价带顶部设为能量零点. 态密度图中水平线上部为上自旋态密度, 下部为下自旋态密度
Figure2. Spin-polarized total densities of states and band structures: (a1), (a2) U = 2 eV, [SLTO]1|[STO]1; (b1), (b2) U = 2 eV, [SLTO]1|[STO]5; (c1), (c2) U = 3.7 eV, [SLTO]1|[STO]1; (d1), (d2) U = 3.7 eV, [SLTO]1|[STO]5, the in-gap localized states are pointed out by the red arrow. The red lines are Fermi level, the top of valence band is set to be zero.

为了澄清[SLTO]1|[STO]5带隙内局域态的性质, 图3(a)和图3(b)详细地展示了其能带结构和局域态对应的空间电荷分布. 带隙内的局域态出现在掺杂的SrO层两侧的TiO₂层内, 掺杂电子局域在Ti原子的3dt_2g轨道内, 则这部分有局域电子占据的Ti原子呈现+3价, 其他Ti原子呈现+4价. 计算表明Ti³⁺—O键长大于Ti⁴⁺—O键长, 由于外延生长限制xy面内的晶格常数, 这导致掺杂层的TiO₆八面体受到了xy面内的压缩应力, 使得原来简并的dxy, dyz, dxz三个轨道劈裂, 最终dxy轨道略高于dxz和dyz轨道, 因而电子优先占据dxz和dyz轨道. 如图3(b)所示, 在掺杂SrO层一侧掺杂电子分布在Ti dxz轨道, 而在另一侧则分布在dyz轨道. 通过对多种自旋构型的计算比较, 结果表明图3(b)所示的反铁磁自旋序具备更低的能量. 图3(c)展示了局域态所在的Ti³⁺与近邻的6个O原子的键长, 沿着y, z方向键长明显大于x方向, 这与电子占据Ti dxz和dyz轨道相吻合. 计算结果还表明Ti³⁺与近邻的O原子的键长也明显大于Ti⁴⁺与近邻的O原子的键长.
图 3 (a) [SLTO]1|[STO]5能带结构图, 其中带隙内局域态为Ti dxz和dyz轨道态. 水平红色虚线为费米能级; (b) [SLTO]1|[STO]5带隙内局域态电荷空间分布, 局域态为Ti dxz和dyz轨道态, 上下箭头代表自旋方向; (c)掺杂层局部结构和Ti³⁺O₆八面体键长, 沿着y和z方向Ti³⁺—O键较长
Figure3. (a) Band structure of [SLTO]1|[STO]5, in which the in-gap states mainly consist of Ti dxz and dyz orbitals; (b) charge distribution of the in-gap states, the charge is mainly localized at Ti dxz and dyz orbitals. The arrows represent spin directions; (c) local structure of the doped layer and bond lengths of Ti³⁺—O bonds of the Ti³⁺O₆ octehedron.

从体掺杂的角度看, [SLTO]1|[STO]5结构中La离子平均体密度为4.17%, 而[SLTO]1|[STO]1结构中La离子平均体密度为12.5%, 似乎La离子的体密度与上述金属绝缘体转变有关. 而Tokura等^[27]和Okuda等^[28]的实验结果表明在STO内La离子体掺杂密度在1.5%—92%区间内体系都呈现金属态. 由此可知, 在STO中均匀掺杂4.17%的La会导致金属态. 而δ掺杂的[SLTO]1|[STO]5超晶格结构中La离子平均体密度同为4.17%, 却呈现绝缘体性, 这意味着掺杂维度变化是导致上述金属绝缘体转变的决定因素. 图4展示了三维掺杂和二维掺杂情况下杂质离子层在空间中产生的电势分布示意图. 在[SLTO]1|[STO]1掺杂情况下, 如图4(a), 相邻的杂质离子层较近, 其吸引势相互重叠较大, 最终在空间产生较为平缓的势. 而在[SLTO]1|[STO]5掺杂情况下, 如图4(b)所示, 相邻的杂质离子层较远, 其吸引势重叠小, 最终在掺杂层形成势阱, 该势阱束缚了电子在垂直掺杂面方向的运动, 结果电子只能在掺杂层内运动. 通常, 电子系统的能量取决于电子在邻近格点间跳跃的动能和电子间排斥势能的总和, 关联性强弱大致取决于电子间排斥势能与电子动能的比值, 比值越大则关联性越强. 相比三维掺杂, 二维掺杂情况下电子在杂质离子层的势阱中运动, 在垂直方向运动受限制, 允许电子跳跃的近邻格点变少, 总动能变小, 电子运动关联性变强. 二维体系情况下, 若体系呈现金属态, 即电子可在近邻格点巡游, 则动能较低, 但存在两个电子同时占据同一个Ti原子3d轨道的几率, 由于Ti 3d轨道上存在较大的在位库伦排斥能, 这会导致较大的电子间排斥势能, 体系的总能量可能因此更高. 若体系呈现绝缘态, 带隙内局域态电子不能在近邻格点巡游, 则动能较大, 但避免了两个电子同时占据同一个Ti原子3d轨道引起的较大的在位库伦排斥能, 这降低了电子间排斥势能, 体系的总能量可能因此更低. 这意味着在同样的在位库伦排斥能情况下, 相比三维电子体系, 二维电子体系具有更小的动能, 即更强的关联性, 更容易变为绝缘态. 上述计算中得到的SrTiO₃中层状25% La掺杂导致的金属-绝缘体转变正是电子维度降低导致关联性增强的一个实例.
图 4 掺杂离子层的电势V和掺杂电荷ρ分布示意图 (a) [SLTO]1|[STO]1, 虚线代表单个掺杂层阳离子产生的吸引势, 实线代表相邻掺杂层阳离子吸引势叠加后总的吸引; (b) [SLTO]1|[STO]5
Figure4. Diagrams of electric potential V and charge distribution: (a) [SLTO]1|[STO]1, dashed lines present the potential produced by a single impurity layer, the solid lines present the total potential of all impurity layers; (b) [SLTO]1|[STO]5.

此外, 二维电子的密度也影响着体系关联性. 从平均场的角度看, 二维电子体系的电子间排斥势能正比于n^1/2(n为二维电子密度), 动能正比与n, 则电子间排斥势能与动能比值约为n^–1/2[29]. 这意味随着二维掺杂浓度的提高, 关联性会变弱, 体系有可能从绝缘态变为金属态. 实验研究^[16]和本文的计算都验证了这一点, 图5所示的态密度和能带结构表明当二维La掺杂的掺杂浓度为50%时上述超晶格结构呈现金属态.
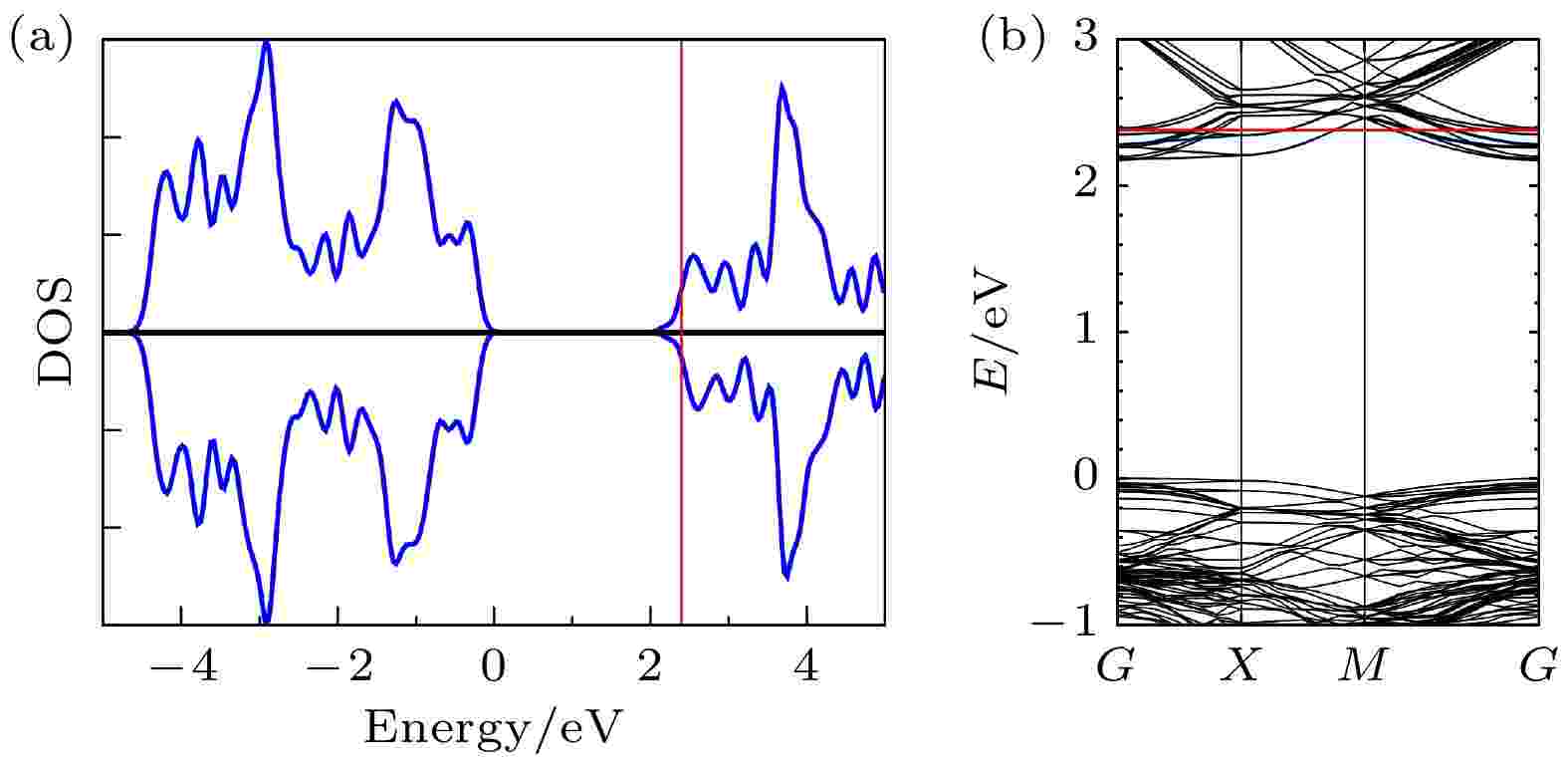图 5 50% La掺杂的[SLTO]1|[STO]5总态密度图(a)和能带结构图(b), 红线为费米能级
Figure5. Total density of states (a) and band structure (b) of [SLTO]1|[STO]5 with 50% La doping in the doping layer.

本文利用第一性原理计算研究了δ掺杂的La:SrTiO₃中掺杂维度和浓度变化引起的金属绝缘体转变. 在La掺杂浓度为25%情况下, 随着掺杂层间隔增加, 即掺杂维度从三维过渡到二维, 体系从金属态过渡到绝缘体态. 二维掺杂在SrTiO₃带隙内产生了局域态, 并且局域态呈现出一定的电荷序、反铁磁自旋序和轨道序. 分析表明, 局域态的电子是由二维体系情况下关联性增强引起的. 此外, 二维掺杂的电子密度也影响着体系的状态, 在二维La掺杂的结构中掺杂浓度为50%时, 体系又呈现金属态. 本文的研究结果加深了对于过渡金属氧化物中电子关联性与其维度和浓度关系的认识, 有助于利用维度和浓度调控过渡金属氧化物电子器件的性能.