摘要:研究并分析了一种采用三层芯结构的单模大模场面积低弯曲损耗光纤. 纤芯由纤芯高折射率层、包层低折射率层和下陷低折射率层三层结构构成. 系统地分析了三层芯光纤(three-layer-core fiber, TLF)中不同结构参数对基模模场面积及弯曲损耗的影响. 研究表明, 通过调整三层芯的结构参数, 在不牺牲截止波长的前提下, 这种TLF可以实现在增大基模有效面积(A_eff)的同时, 将弯曲损耗降到更低. 通过调整纤芯中三层芯的结构参量, A_eff可以达到100—330 μm²甚至更高. 此外, 在相同模场面积A_eff下, 三层芯光纤的弯曲损耗可以比普通阶跃型光纤(SIF)要低2—4个数量级. 分析表明这种大有效面积、低弯曲损耗三层芯单模光纤在宽带大容量传输、及大功率光纤激光器和放大器中具有重要的潜在应用价值.
关键词: 三层芯/
单模/
大模场面积/
弯曲损耗

English Abstract

全文HTML

--> --> -->

随着目前高功率大容量光纤通信传输系统的高速发展, 光纤传输容量的需求越来越受到广泛关注, 因此如何在光纤中实现单模运转、基模大模场面积(A_eff)逐渐成为研究重点^[1-3]. 针对此, 目前已提出了不少光纤结构^[4-6]. 但存在的主要问题是制造难度较大, 究其原因主要是低数值孔径NA的实现、管棒堆积拉丝技术、光子晶体光纤的六角密排结构特点.
然而A_eff和弯曲性能之间存在此消彼长的关系^[7], 光纤中产生的弯曲损耗, 使得基模A_eff的增大受到限制. 低数值孔径NA的要求不可避免地影响弯曲性能和单模截止波长^[8]. 因此, 如何在保持单模、大A_eff的同时, 提高弯曲性能是目前研究中亟待解决的问题. 然而, 目前大多数关于大模场面积光纤的研究中, 在增大有效面积的同时, 并未降低其弯曲损耗. 另外一些研究的重点是如何降低弯曲损耗^[9-11]. 然而, 他们更注重的是在模场直径(MFD)与标准单模光纤SMF(SSMF)相匹配的情况下, 如何进一步提高其弯曲性能, 对于如何增大其模场面积并未研究.
基于此, 本文提出可以采用三层芯结构, 来实现在保持单模、大模场面积A_eff的同时, 提高其弯曲性能. 三层芯光纤(three-layer-core fiber, TLF)结构的纤芯部分由三层组成, 包括纤芯折射率层、包层折射率层和下陷折射率层. 近年来曾对类似的结构进行了广泛的研究^[12-14], 然而很少有报道研究纤芯中三层芯的结构参量对光纤的光学性能的影响, 以及如何调整不同结构参量以实现在增大模场面积 A_eff的同时保持更低的弯曲损耗^[15]. 文献[15]中只分析了部分参数d₁和d₂对模场面积A_eff和弯曲损耗的影响, 且关于参数纤芯中包层低折层的厚度d₁对弯曲损耗的变化分析并不全面, 此外并未固定二阶模的截止波长λ_C. 针对此, 本文系统地研究了三层芯结构参数对TLF光学特性的影响. 详细分析了三层芯不同结构参数对截止波长λ_C、有效A_eff和弯曲性能的影响. 研究发现, 随着包层低折层的厚度的增大, 弯曲损耗存在极小值. 结果表明, 在单模截止波长λ_C保持不变的情况下, 三层芯光纤结构可以在增大有效A_eff的同时, 降低弯曲损耗. 这种光纤具有结构简单、制造方便、成本低等优点, 可适用于大功率光纤放大器和激光器、密集波分复用 DWDM 系统中, 可有效满足快速增长的数据通信需求, 特别是大数据、云计算、人工智能和其他创新技术的需求.

TLF的横截面结构及折射率分布如图1所示. 纤芯由内到外依次由纤芯高折射率层、包层低折射率层和下陷低折射率层三层结构构成. 图中的中心黑色区域代表纤芯高折射率层, 中间白色区域代表包层低折射率层, 外围灰色区域代表下陷低折射率层. 实际制造的光纤纤芯高折层可以由铒离子及铝离子的掺杂来实现, 而下陷低折层可以通过掺氟来实现. 包层低折射率层为纯石英结构, 其折射率为n_clad = 1.444. 假定纤芯高折射率层的半径为a, 纤芯高折层和包层之间的折射率差为Δ₁ = n₁ – n_clad, 其中n₁是纤芯高折层的折射率. 下陷低折层宽度为c, 包层低折层的厚度为b, 包层与下陷低折层之间的折射率差为Δ₂ = n_clad – n₂, 其中n₂为下陷低折层的折射率. 包层直径为d_clad = 125 μm, 包层折射率为n_clad = 1.444. 除非另有说明, 否则本文将单模工作波长λ固定在 1.55 μm. 为了确保单模工作在1.55 μm, 二阶模的截止波长λ_C固定在1.3 μm. 系统地分析了包层低折层和下陷低折层参数对TLF特性的影响, 为大模场面积和低弯曲损耗的光纤设计提供了参考.
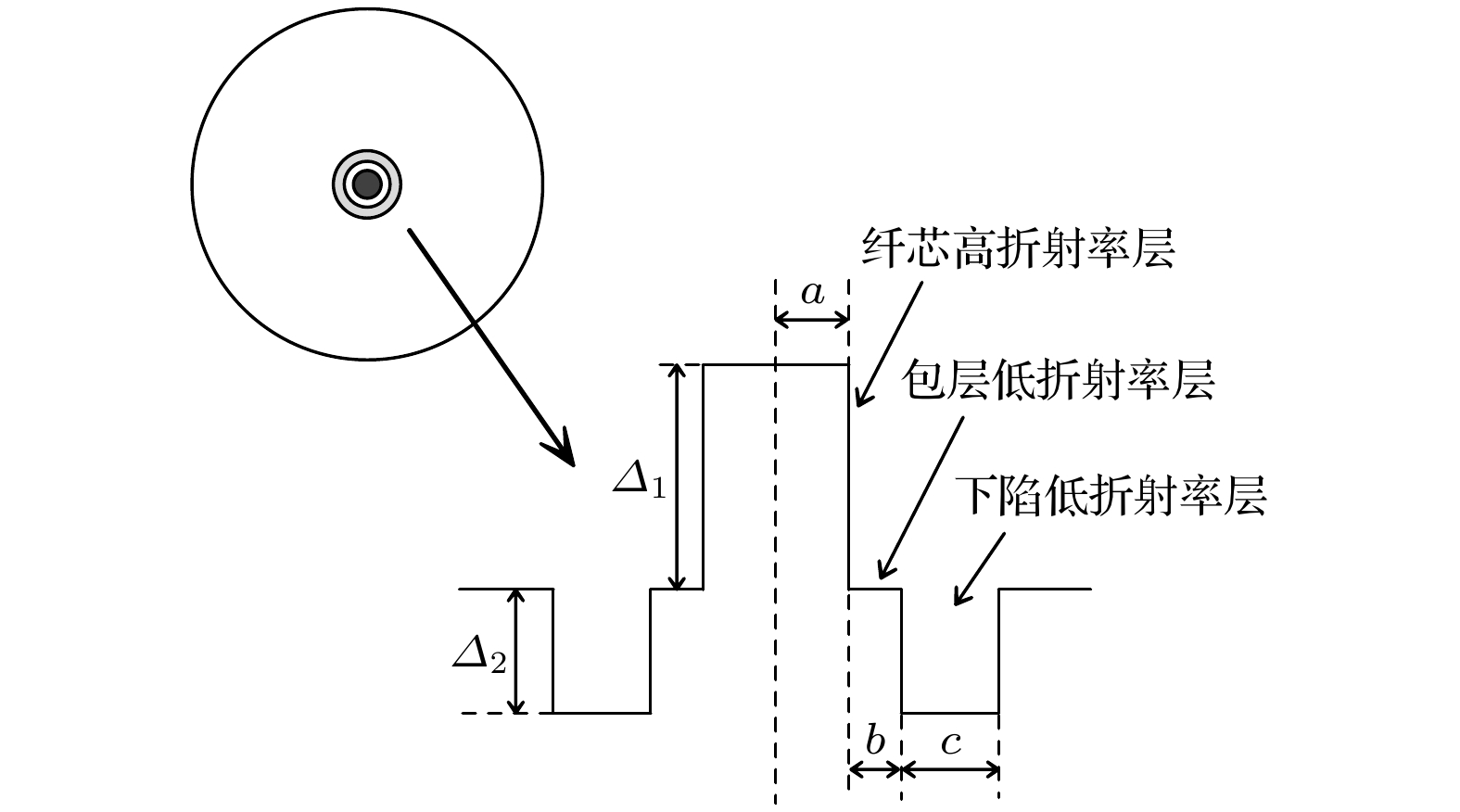图 1 TLF的横截面结构及折射率分布图
Figure1. Cross section schematic and refractive index profile of TLF structure.

在TLF中, 传输各模式的电场强度E满足亥姆霍兹方程:

$ \nabla \times ({n^{ - 2}}\nabla \times {\boldsymbol{E}}) - k_0^2{\boldsymbol{E}} = 0, $

其中, $ \boldsymbol E?=?\boldsymbol E(x,?y)?×?{\rm e}^{-{\rm j} \beta z} $, n是光纤中的横截面折射率大小, k₀是真空中的波数, β是传播常数, β = (2π/λ) × n_eff. 这里采用传输矩阵法进行求解^[16,17], 通过(1)式可以求出其特征向量和特征值, 即不同模式的电场强度E及传播常数β. 通过给定TLF的结构参量: 纤芯高折层的半径a, 纤芯高折层和包层之间的折射率差Δ₁, 包层低折层的厚度b, 下陷低折层宽度c, 包层与下陷低折层之间的折射率差Δ₂, 就能唯一确定TLF 的折射率大小, 从而确定某一特定波长λ下不同模式的电场分布E及传播常数β.
在传统光纤中, 导模的模式折射率n_eff必须满足: n_clad < n_eff < n_core, 其中n_clad和n_core分别为包层和芯层的折射率, 模式折射率低于n_clad的模式不能在该光纤中传导, 由此可以判断其截止特性^[18,19]. 理论截止波长为单模光纤中只有基模传输的最短波长, 通常定义为: 模式有效折射率n_eff随波长变化过程中等于包层折射率n_clad时对应的波长值即为该模式的截止波长. 因此, 令二阶模的模式有效折射率n_eff = n_clad, 即可反推出二阶模的截止波长λ_C. 本文给出了TLF中纤芯不同层结构参量对截止波长λ_C的影响. 假设纤芯高折层半径a = 6 μm, 纤芯高折层和包层的折射率差Δ₁ = 0.003, 图2给出了截止波长λ_C随纤芯不同层结构参数c, b和Δ₂的变化关系. 其中图2(a)—2(c)中的结构参数分别固定为: b = 3 μm, Δ₂ = 0.004; c = 6 μm, Δ₂ = 0.004; c = 6 μm, b = 3 μm. 如图2(a)中所示, 随着c的增大, 截止波长λ_C呈指数单调递减, 当c大于 4 μm 时, λ_C逐渐趋于一常数不再发生显著变化. 由图2(b)和图2(c)分别可以看出, λ_C随b的增大而逐渐增大, 随Δ₂的增大而逐渐减小. 因此, 通过改变TLF中纤芯不同层结构参数可以达到不同截止波长λ_C的要求.
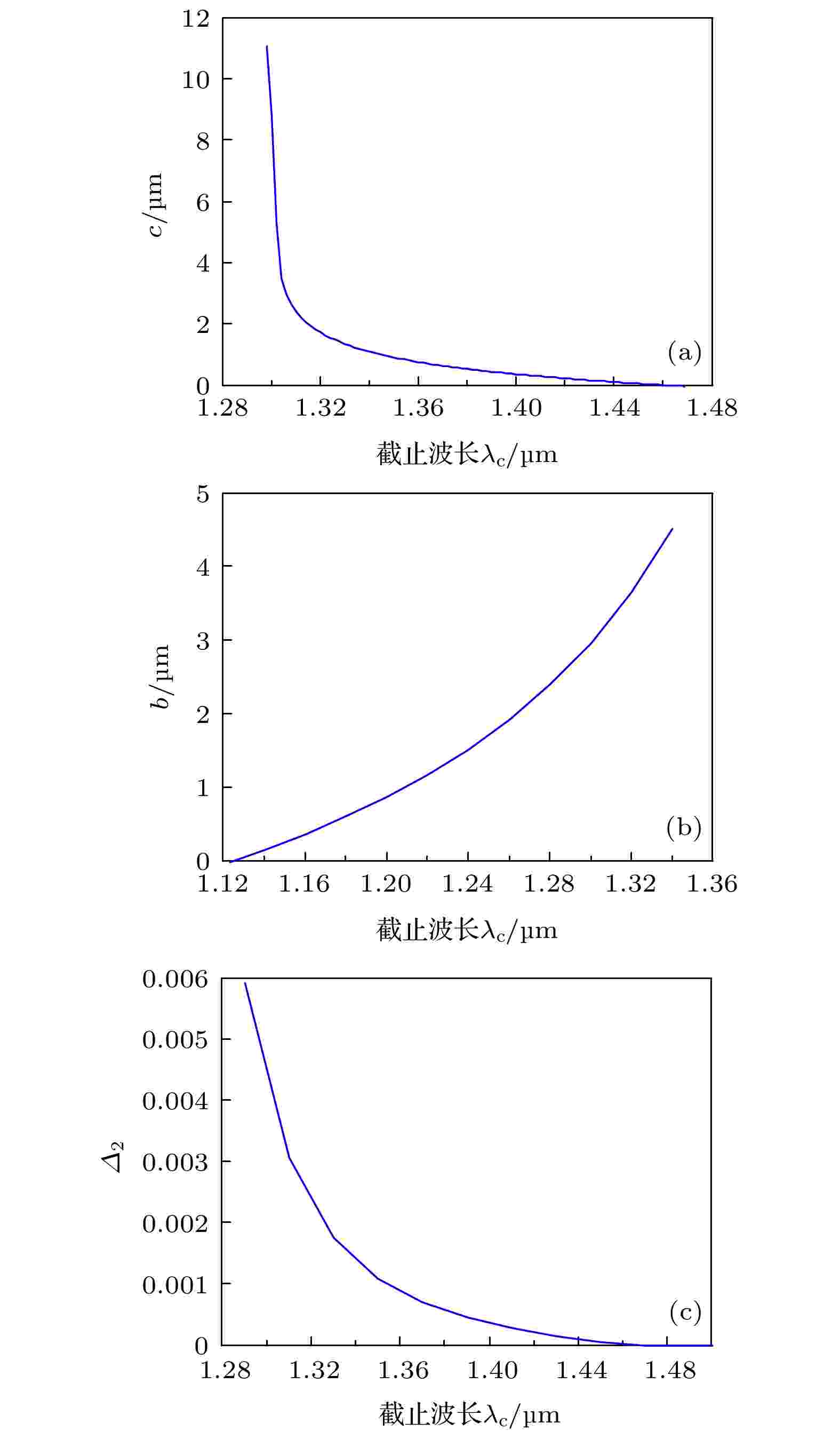图 2 截止波长λ_C随不同层结构参数　(a)c、(b) b和 (c) Δ₂的变化关系
Figure2. Cutoff wavelength λ_C as a function of the layer parameters: (a) c; (b) b; (c) Δ₂.

为了能更加完整和全面地反映满足截止波长条件下的参数区间, 本文给出了TLF纤芯中的任意两个不同结构参量对截止波长λ_C的影响. 图3分别给出了截止波长λ_C随纤芯不同层结构参数b和c, b和Δ₂, Δ₂和c的三维变化图. 其中图3(a)—图3(c)中的结构参数分别固定为: Δ₂ = 0.004, c = 6 μm, b = 3 μm. 如图中所示, 纤芯不同层结构参量c, b和Δ₂对截止波长λ_C的影响与图2中的分析结果一致, 故可以反映出截止波长λ_C随纤芯不同层结构参数的变化关系.
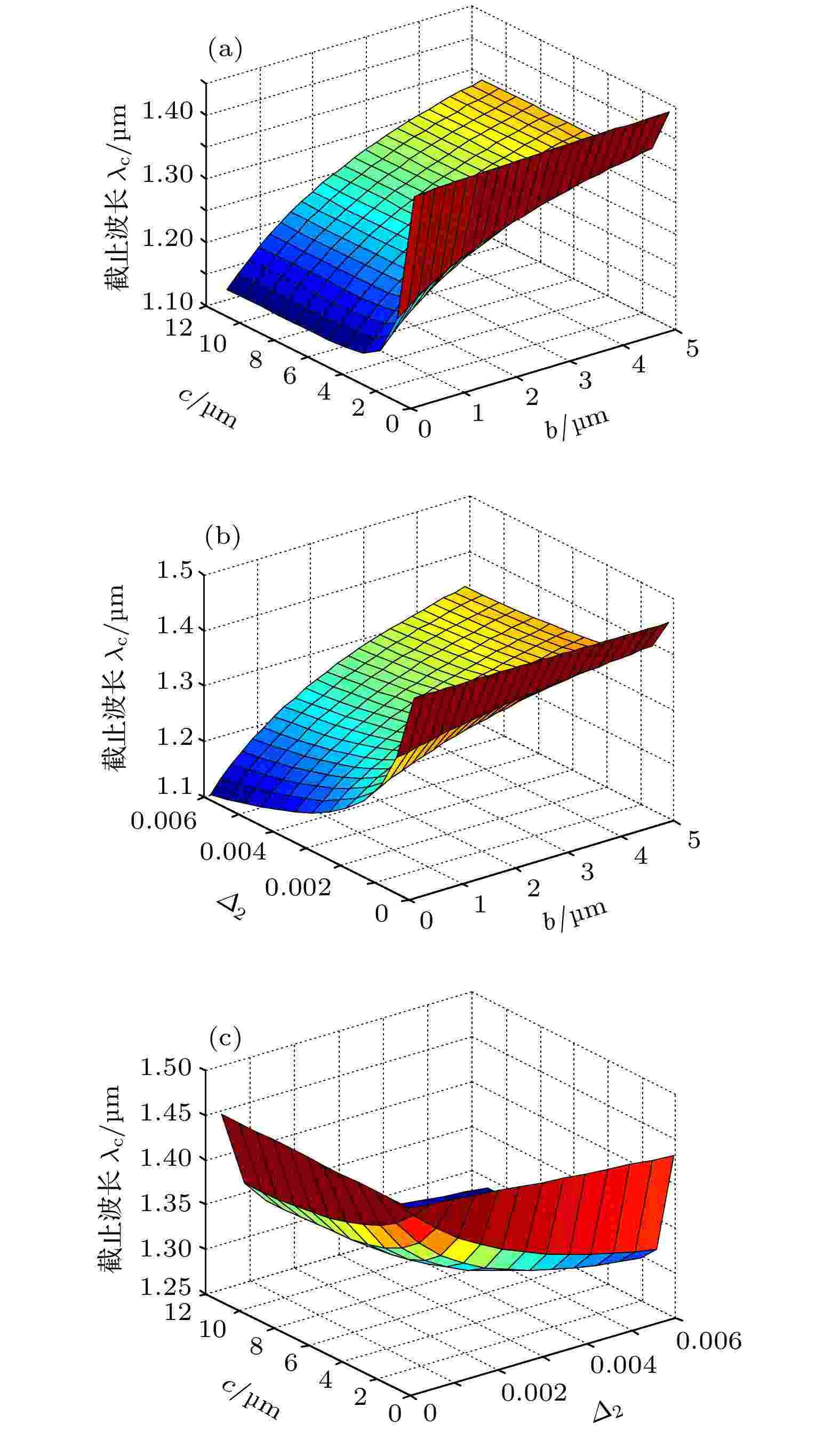图 3 截止波长λ_C随不同层结构参数　(a)b和c、(b) b和Δ₂、(c) Δ₂和c的变化关系
Figure3. Cutoff wavelength λ_C as a function of the layer parameters: (a) b and c, (b) b and Δ₂, (c) Δ₂ and c.

假设固定截止波长λ_C = 1.3 μm, 通过改变TLF中纤芯不同层结构参数可以实现较大的纤芯高折层半径a. 光纤分为有源光纤和无源光纤, 对于有源光纤如稀土掺杂光纤, 增大a有利于稀土离子的吸收, 从而提高光纤的增益性能. 对于无源光纤, 增大a有利于模场有效面积A_eff的增大, 从而增强光纤的传输性能. 图4给出了纤芯高折层半径a随纤芯不同层结构参数c, b和Δ₂的变化关系. 其中图4(a), 图4(b), 图4(c)中的结构参数分别固定为: b = 1 μm, Δ₂ = 0.004; c = 6 μm, Δ₂ = 0.004; c = 6 μm, b = 1 μm. 如图4(a)所示, 当Δ₁ = 0.0025时, 随着c从 0 增大到 6.5 μm, a可以从 5.8 μm 增大到 7.2 μm. 图4(b)和4(c)分别显示, a随b的增大而减小, 随Δ₂的增大而增大. 而在阶跃型单模光纤中, 当工作波长λ和截止波长λ_C均固定时, 纤芯半径与Δ₁成反比. 通常情况下, 在普通阶跃型光纤中, 由于制造工艺的限制, 纤芯折射率Δ₁不能过小, 即数值孔径NA不能低于0.06, 否则基模的弯曲损耗将呈指数形式递增, 光纤对弯曲效应将变得十分敏感, 因而普通阶跃型光纤的纤芯半径a存在最大极限值. 而这种TLF则可以避免这些问题, TLF中的下陷低折层可以增强对基模模场的限制能力, 防止模场扩散到包层中, 基模将被很好地限制在纤芯中. 因此, TLF可以突破NA的极限值, 在增大纤芯半径的同时保持单模运转.
图 4 纤芯高折层半径a随不同层结构参数　(a)c、(b) b和(c) Δ₂的变化曲线
Figure4. Relationship between core radius a and (a) c, (b) b, and (c) Δ₂.

在实现高功率大容量光纤通信中, 保持大传输容量的同时减小非线性效应是必不可少的, 因而增大光纤模场面积A_eff十分重要. 这种TLF结构的基模模场分布并不是近高斯型的, 因而采用Petermann I 定义的公式来计算其模场有效面积A_eff^[16,20-22]:

$ {A_{{\rm{eff}}}} = \frac{{2{\rm{\pi }}\displaystyle \int_0^\infty {{{\boldsymbol{E}}^2}{r^3}{\rm{d}}r} }}{{\displaystyle \int_0^\infty {{{\boldsymbol{E}}^2}r{\rm{d}}r} }} = \frac{{2{\rm{\pi }}\displaystyle \iint_\varOmega {{{\boldsymbol{E}}^2}({x^2} + {y^2})}{\rm{d}}x{\rm{d}}y}}{{\displaystyle \iint_\varOmega {{{\boldsymbol{E}}^2}{\rm{d}}x{\rm{d}}y}}}, $

其中, E为基模电场分布. 假设固定截止波长λ_C = 1.3 μm, 图5给出了基模有效面积A_eff随纤芯不同层结构参数c, b和Δ₂的变化关系. 其中a由截止波长λ_C来确定, 即通过改变a以达到λ_C = 1.3 μm的要求. 由图5可以看出, 随着Δ₁的减小A_eff逐渐增大, 可以达到约220 μm². A_eff随着c和Δ₂的增大而减小, 随着b的增大而增大. 因此实际制作中若想要大的A_eff, 则需选择小的c、小的Δ₂以及大的b值. 可以看出, 通过调整三层芯的结构参数, 在不牺牲截止波长λ_C的前提下, 这种三层芯光纤结构可以增大A_eff.
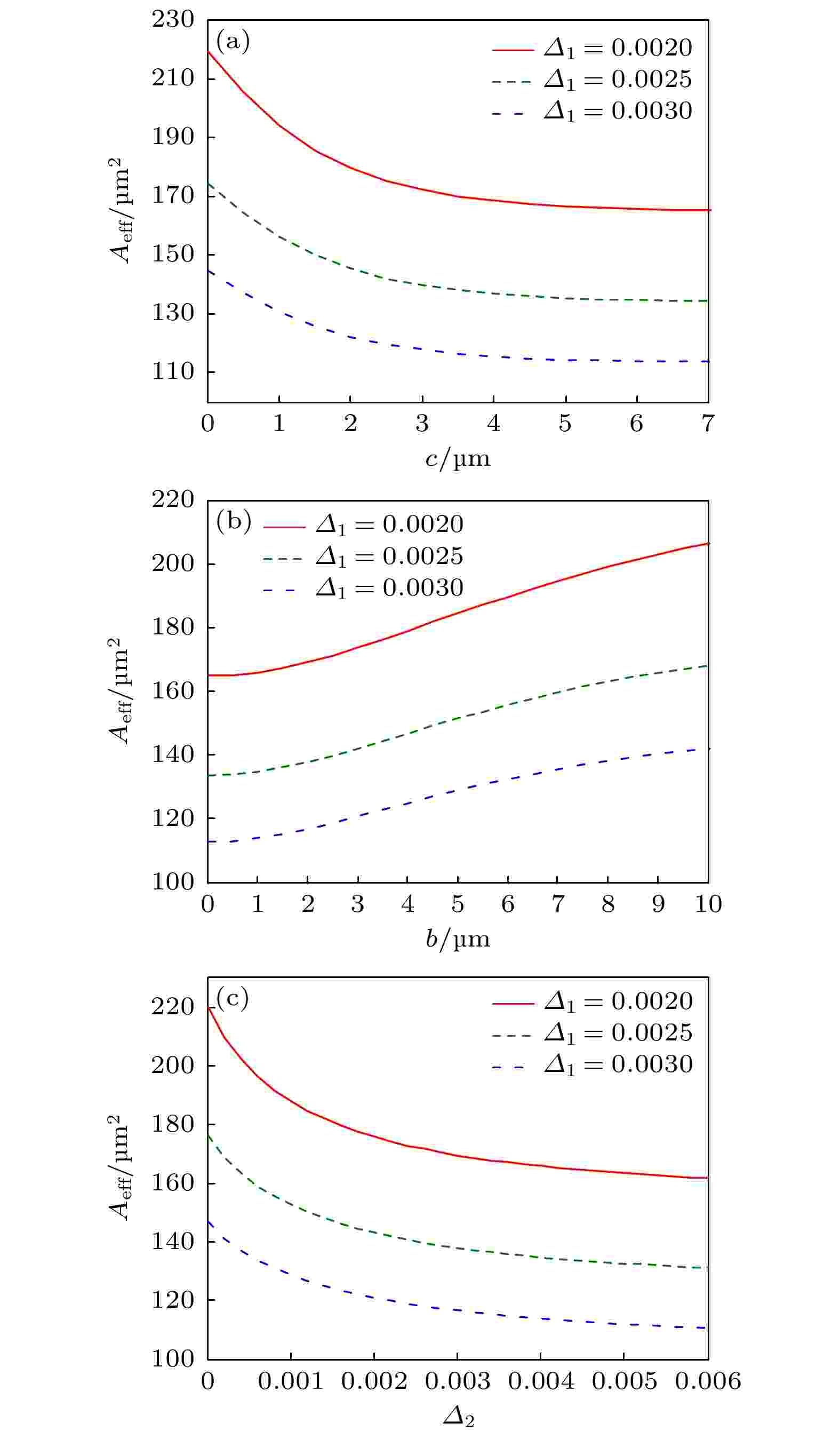图 5 A_eff随不同层结构参数　(a) c、(b) b和 (c) Δ₂的变化曲线
Figure5. Relationship between A_eff and (a) c, (b) b, and (c) Δ₂

其物理意义可以表述如下: 由于纤芯周围的下陷低折层的限制, 使得光纤基模模场不易泄漏到光纤包层区域, 光纤基模模场被很好地限制在了纤芯内部, 从而使得光纤基模的A_eff就越小. 通过改变下陷层参数大小, 可以调节模场束缚的程度. c和Δ₂越大说明纤芯中的最外层—下陷低折层越大, 下陷低折层对基模场的限制能力就越强, 因而A_eff就越小. b越大说明纤芯高折层离纤芯的最外层—下陷低折层就越远, 下陷低折层对纤芯的影响就越小, 因而A_eff就越大.
为了避免陷入局部极值, 本文给出了多维参数对应的A_eff的变化曲线, 即纤芯中的任意两个不同结构参量对A_eff的影响. 纤芯高折层和包层的折射率差Δ₁ = 0.003. 图6分别给出了基模有效面积A_eff随纤芯不同层结构参数b和c, b和Δ₂, Δ₂和c的三维变化图. 其中图6(a)—6(c)中的结构参数分别固定为: Δ₂ = 0.004, c = 6 μm, b = 3 μm. 如图中所示, 模场面积A_eff随纤芯结构参量c, b和Δ₂的变化趋势与文中图5的分析结果一致, 故可以反映出A_eff随纤芯不同层结构参数的变化关系.
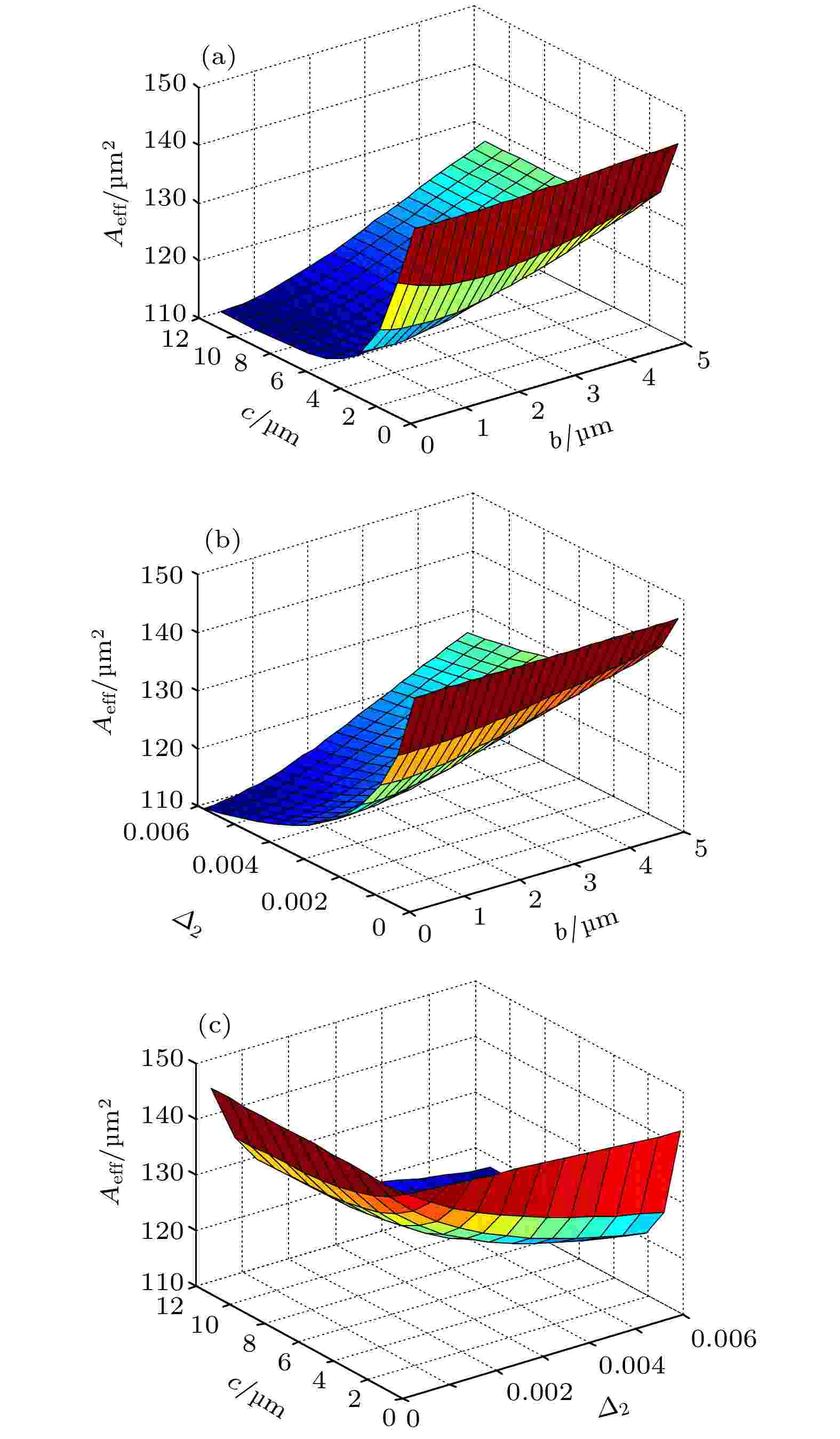图 6 A_eff随不同层结构参数　(a) b和c、(b) b和Δ₂和 (c) Δ₂和c的变化关系
Figure6. Relationship between A_eff and (a) b and c, (b)b and Δ₂, and (c) Δ₂ and c.

基模有效面积A_eff和弯曲性能之间存在此消彼长的关系, 光纤中产生的弯曲损耗, 使得A_eff的增大受到限制. 在不牺牲截止波长λ_C的前提下, 这种三层芯光纤结构可以在相同模场面积 A_eff 下, 降低光纤的弯曲损耗. 光纤弯曲时, 由于形变造成的几何结构及折射率差Δ发生变化, 从而使得传输性能受到影响. 假设光纤沿+x方向发生弯曲, 可以等效为折射率沿弯曲方向呈倾斜分布的平直光纤, 弯曲半径越小, 倾斜斜率越大. 光纤横截面的等效折射率表示为^[23]

$ {n_0}(x,y) = n(x,y)\sqrt {(1 + 2x/R)} , $

其中, n₀(x, y)是弯曲光纤的等效折射率大小, n(x, y)是平直光纤的折射率大小, x为弯曲方向, R为弯曲半径. 计算结果基于有限元方法, 通过全矢量麦克斯韦方程组, 采用商业软件Comsol Multiphysics计算得出. 除光纤结构外, 在光纤边界处采用圆形完美匹配层边界条件(PML)来模拟模型中无限域的效果, 因而模式的传播常数β成为一个复数, 实部是模式折射率, 虚部是与限制损耗有关的量. 光纤中某一模式的限制损耗α_B由β的虚部计算得出:

$ {\alpha _{\rm{B}}} = 20\lg ({\rm{e}}){\rm{Im}} (\beta ) \approx 8.686\frac{{2{\rm{\pi }}}}{\lambda }{\rm{Im}} ({n_{{\rm{eff}}}}). $

利用等效折射率模型^[9,24]及(3)式和(4)式, 当为平直光纤时, 计算结果为限制损耗. 当光纤发生弯曲时, 计算结果为弯曲损耗^[9,24].
假设固定截止波长λ_C = 1.3 μm, 图7给出了纤芯不同层结构参数c, b和Δ₂下, 弯曲损耗随不同弯曲半径R的变化关系. 其中a由λ_C来确定, 通过改变a以达到λ_C = 1.3 μm的要求. 光纤中的弹光修正因子R_eff/R = 1.28, 这里R_eff是有效弯曲半径^[25]. 工作波长固定为λ = 1.55 μm. 其中图7(a)—7(d)中的结构参数分别固定为: Δ₁ = 0.003, b = 1 μm, Δ₂ = 0.004; Δ₁ = 0.003, c = 6 μm, Δ₂ = 0.004; Δ₁ = 0.003, c = 6 μm, Δ₂ = 0.004; Δ₁ = 0.003, c = 6 μm, b = 1 μm. 从图7可以看出, 随着弯曲半径R的增大, 弯曲损耗呈指数方式逐渐降低, 之后不再变化. 如图7(a)和(d) 所示, 弯曲损耗随着c、Δ₂的增大而减小. 图7(b)中显示, 随着b的增大, 弯曲损耗先减小后增大. 这一点从图7(c)中也可以清楚地看出, 随着b的增大, 弯曲损耗首先减小, 当b超过4 μm时, 弯曲损耗逐渐增大. 值得注意的是, 弯曲损耗存在极小值, 此时的b即为设计低弯曲损耗的最佳值. 因此在实际制作中, 为了提高弯曲性能, 可以选择尽量大的c、大的Δ₂以及靠近最佳值的b值.
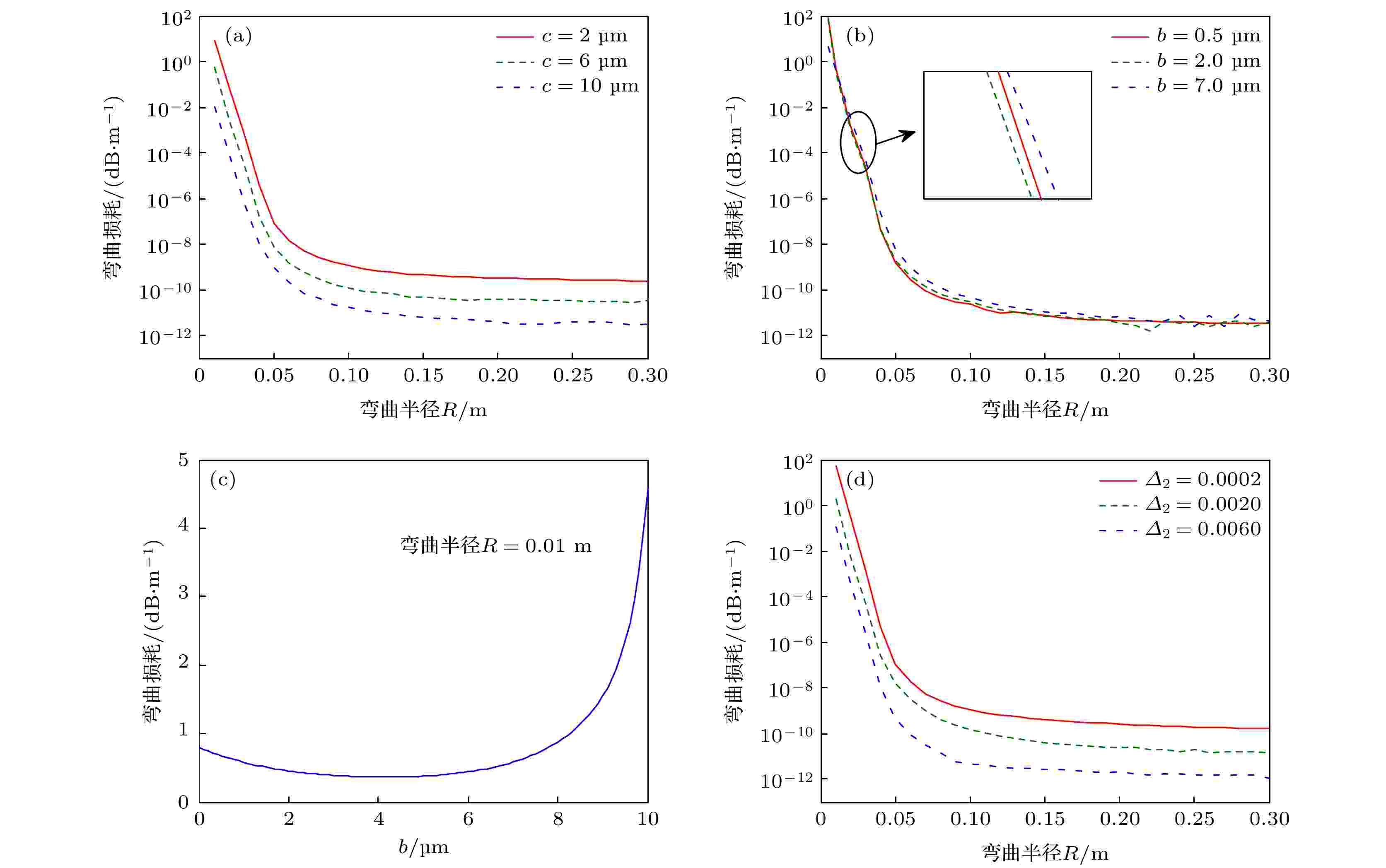图 7 不同层结构参数　(a) c、(b) b和 (d) Δ₂下弯曲损耗随弯曲半径R的变化曲线; (c)弯曲半径R = 0.01 m时弯曲损耗随b的变化曲线
Figure7. Relationship between the bending lossand (a) c, (b) b, and (d) Δ₂ at various R; (c) relationship between the bending lossand b at R = 0.01 m.

其物理意义可以表述如下: 当弯曲光纤中某处包层的折射率超过模式的等效折射率时, 该处模式的电场边缘处会引发功率泄漏, 从而导致弯曲损耗^[26,27]. 由于纤芯最外层折射率较低, 可以抑制电场边缘的有效折射率的增大, 因而这种光纤的弯曲损耗可以保持在一个较低的水平. c, Δ₂越大说明纤芯中的最外层—下陷低折层越大, 下陷低折层抑制电场边缘有效折射率的效果就越明显, 因而弯曲损耗就越低.
参数b对弯曲损耗的影响要从两个方面来讲: 一方面, 随着b的增大, 纤芯中间的包层低折层逐渐增大, 导致纤芯的等效折射率变大, 使得光功率较多的分布于纤芯中, 因而弯曲损耗变小; 另一方面, 随着b的增大, 纤芯高折层离下陷低折层就越远, 下陷低折层抑制电场边缘有效折射率的效果就越弱, 因而弯曲损耗就变大. 这两种效应给弯曲损耗带来的影响是相反的, 因而要结合起来辩证地看影响结果. 当b较小时, 下陷低折层离纤芯高折层距离较近, 此时对整个纤芯的等效折射率影响较大, 因而主要表现为弯曲损耗变小; 当b较大时, 下陷低折层离纤芯高折层距离较远, 此时对纤芯的等效折射率影响较小, 而主要表现为抑制电场边缘有效折射率的效果, 因而主要表现为弯曲损耗变大.
图8 给出了在弯曲半径R为 0.01 m 时, TLF光纤结构的A_eff与弯曲损耗之间的变化关系. 为了验证弯曲性能是否得到改善, 图中同样给出了传统普通阶跃型光纤SIF的变化关系. 这里纤芯高折层和包层的折射率差Δ₁由不同A_eff的变化确定, 纤芯高折层半径a由截止波长λ_C = 1.3 μm的大小来确定. 工作波长固定为λ = 1.55 μm. 其他结构参数固定如下: TLF1: c = 6 μm, b = 3 μm, Δ₂ = 0.004; TLF2: c = 7 μm, b = 4 μm, Δ₂ = 0.004. 从图8可以看出, 在相同A_eff下, TLF的弯曲损耗要比SIF低2—4个数量级. 如图中所示, 在R = 0.01 m、基模A_eff约为180 μm²时, SIF的弯曲损耗高达320 dB/m, 而TLF1的三层芯光纤结构的弯曲损耗很低, 约为 2.05 dB/m, 而 TLF2 的弯曲损耗可以低至 0.34 dB/m. 研究证明, 通过调整TLF中纤芯的不同层结构参数, 弯曲性能可以进一步得到改善. 综上所述, 由于下陷低折射率层的存在, TLF光纤结构可以有效改善弯曲性能和/或增大A_eff. 研究表明, 在不牺牲截止波长λ_C的前提下, TLF光纤可以实现在增大基模有效面积A_eff的同时, 将弯曲损耗降到更低.
图 8 TLF和SIF光纤结构的基模弯曲损耗随A_eff的变化曲线
Figure8. Bending loss as a function of A_eff for TLFs comparedto step-index fiber.

图9 给出了不同弯曲半径R下, TLF弯曲损耗及A_eff的变化曲线. 光纤结构参量固定为: λ_C = 1.3 μm, c = 7 μm, b = 4 μm, Δ₂ = 0.004. 工作波长λ固定为1.55 μm. 为进行对比, 图中同样给出了相同A_eff下的传统普通阶跃型光纤SIF的变化关系. 从图9可以看出, 随着弯曲半径R的增大, 弯曲损耗和A_eff以指数方式逐步降低. 在相同的R下, TLF的弯曲损耗要比SIF低的多. 当R = 0.02 m时, SIF的弯曲损耗高达约为 3930.375 dB/m, 而 TLF的弯曲损耗约为0.43 dB/m. 当R增大到0.14 m时, SIF的弯曲损耗约为1.2 × 10^–4 dB/m, 而TLF的弯曲损耗低至3.7 × 10^–6 dB/m. 当R > 0.2 m时, 弯曲损耗基本不再变化. 总体上TLF的弯曲损耗比SIF要低2—4个数量级.
图 9 不同弯曲半径R下　(a)弯曲损耗、(b) A_eff的变化曲线
Figure9. Relationship between (a) bending loss, (b) effective area A_eff and bending radius. R.

从图9(b)可以看出, 当弯曲半径R > 0.2 m 时, TLF 的A_eff与SIF基本一致. 但当R较小时, 如R < 0.2 m时, SIF的A_eff模场形变量要比TLF大的多. 当R = 0.02 m时, SIF的A_eff增大至 4302.63 μm², 比平直状态增大了约3996.44 μm², 由此可以看出SIF的模场变形和增大问题更为严重. 而当R = 0.02 m时, TLF的A_eff约为371.32 μm², 比平直状态增大了约65.17 μm², 二者处于同一数量级水平. 说明TLF的模场形变量比SIF有着明显的降低, 可以满足大与低弯曲损耗的实际应用需求.
为了讨论TLF结构的限制损耗特性, 这里固定光纤结构参数为: TLF1: λ_C = 1.3 μm, a = 10.36 μm, Δ₁ = 0.0011, c = 7 μm, b = 4 μm, Δ₂ = 0.004; TLF2: λ_C = 1.3 μm, a = 8.74 μm, Δ₁ = 0.00155, c = 6 μm, b = 3 μm, Δ₂ = 0.004. 图10给出了不同工作波长λ下, TLF的基模限制损耗的变化关系. 从图10可以看出, 随着λ的不断增大, 基 模的限制损耗逐渐增大. 在1.2 μm < λ < 1.65 μm时, 基模的限制损耗总体上低于10^–5 dB/m水平. 在λ = 1.55 μm时, TLF1的限制损耗约为2.81 × 10^–7 dB/m, 而TLF2的限制损耗约为 3.14 × 10^–8 dB/m. 综上所述, 这种单模、大、低弯曲损耗三层芯光纤在大容量、高功率光纤通信系统中具有潜在的实际应用价值.
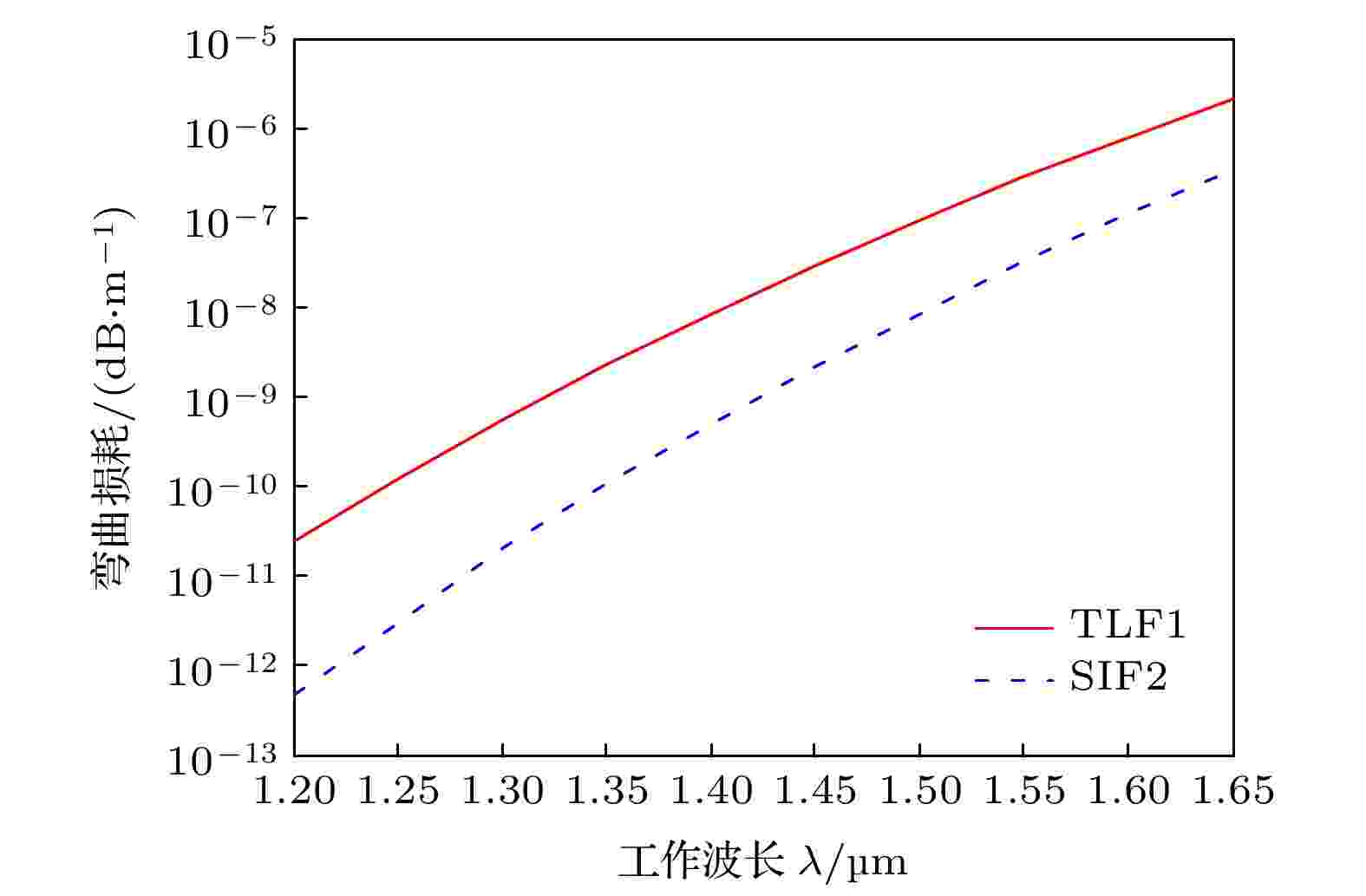图 10 TLF基模的限制损耗随波长的变化曲线
Figure10. Transmission loss of fundamentalmode for TLFs.

本文系统的研究并分析了如何采用三层芯结构光纤, 来实现在保持单模、大A_eff的同时, 提高其弯曲性能. 分析了不同层结构参数对TLF性能的影响, 为大和低弯曲损耗光纤的设计提供了指导意义. 详细分析了纤芯不同层结构参数对截止波长、和弯曲性能的影响. 通过调整纤芯中三层芯的结构参量, A_eff可以达到100—330 μm²甚至更高. 此外, TLF光纤结构可以有效改善弯曲性能, 在相同的A_eff下, TLF的弯曲损耗比SIF要低2—4个数量级. 研究表明, 在不牺牲截止波长的前提下, TLF光纤可以实现在增大基模有效面积A_eff的同时, 将弯曲损耗降到更低. 这种光纤制作简单, 可以采用传统的MCVD法. 分析表明这种单模、大、低弯曲损耗三层芯光纤在宽带大容量传输、及大功率光纤激光器和放大器中具有重要的潜在应用价值.