摘要:毛细管放电型脉冲等离子体推力器在微纳卫星在轨机动应用中具备良好的发展前景. 本文系统研究了单次放电能量5 J条件下, 不同毛细管腔体尺寸参数对推力器能量沉积特性、烧蚀特性、输出推力参数和等离子体羽流参数的影响规律. 实验结果表明, 增大毛细管腔体内径会显著降低放电电流密度, 减小沉积能量和等效功率; 增大腔体长度有助于提升能量传递效率. 腔体结构尺寸变化影响单位面积沉积能量和管壁温度, 进而改变烧蚀特性. 当毛细管内径从1 mm增加至3 mm时烧蚀质量显著下降, 随着腔体内径的进一步增大, 等效烧蚀质量近似不变; 烧蚀质量随毛细管长度的增加持续增大, 但单位面积烧蚀质量不断下降. 推力器元冲量取决于烧蚀质量与其等效速度, 烧蚀特性的差异进一步影响腔体内等离子体密度和等效压强, 影响等离子体电热加速过程. 毛细管腔体内径和长度的不断增加, 使得加速过程滞后于放电和烧蚀过程, 作用于加速过程的电弧沉积能量比例降低, 降低推力器等离子体喷射速度, 元冲量减小, 比冲降低, 总体效率下降. 结合总体效率传递模型分析, 毛细管内径对推力器效率的影响主要体现在能量传递效率方面, 毛细管长度变化主要影响等离子体电热加速效率, 优化推力器总体效率需要从能量沉积效率和加速效率两方面入手.
关键词: 脉冲等离子体推力器/
毛细管放电/
腔体结构/
等离子体加速

English Abstract

全文HTML

--> --> -->

微纳卫星具有研发成本低、扩展能力强、发射方式灵活等优点, 在低轨宽带卫星通信系统、气象观测、空间科学实验等领域展现出巨大的应用价值, 近年来得到迅猛发展^[1-3]. 搭载微型电推进系统能够显著地增强微纳卫星在轨机动能力, 实现卫星高精度位置保持、姿态调整和轨道控制, 对未来高功能密度卫星执行组网编队等复杂任务, 保持长期在轨自主运行具有重要意义^[4]. 然而, 由于卫星体积、重量和总体功率的制约, 微型电推进系统面临着苛刻的参数要求, 如何利用有限系统储能高效地产生特定需求的输出参数成为微型电推进技术研究的关键问题^[5].
毛细管放电型脉冲等离子体推力器(capillary discharge based pulsed plasma thruster, CDPPT)采用固体聚四氟乙烯工质, 无需储供机构, 采用脉冲工作模式, 系统简单紧凑、可靠性高, 在微纳卫星应用中具有显著优势^[6,7]. CDPPT 单次放电能量通常在焦耳量级, 通过脉冲放电在毛细管腔体中产生初始电弧, 烧蚀并电离工质产生等离子体, 在电热电磁加速作用下向外喷射产生推力, 其输出元冲量可精细调节(μN·s 量级), 契合微纳卫星姿轨控制需求, 发展前景广阔^[8,9]. 随着微纳卫星任务场景的拓展, 要求推力器具备高比冲、高效率参数输出和较大范围元冲量调节的能力. 然而目前, CDPPT 比冲参数仍有待提高、输出效率较低, 这制约了其进一步应用, 迫切需要进行性能参数优化. 由于CDPPT工质供给和加速过程耦合机制复杂, 且腔体内部等离子体无法直接进行诊断, 人们尚未掌握设计参数对等离子体形成、加速过程的影响机制, 给参数优化带来挑战.
CDPPT在工作过程中, 烧蚀、电离和电热加速都发生在毛细管腔体内, 因此腔体结构参数的选择对推力器的工作过程和性能产生着重要的影响. 为进一步提升推力器比冲和总体效率, 国内外****从实验和仿真两个方面对毛细管推力器工作过程和输出参数开展了优化研究. 仿真方面, 国内外****深入研究了烧蚀模型^[10,11]、等离子体演化过程等^[12], 目前可较为准确地获得烧蚀质量流量和等离子体参数分布^[13,14], 但对元冲量和比冲参数计算方法和能量传递过程鲜有涉及. 目前, 实验方面的主要研究方法为利用微冲量测量系统, 对推力器输出力学参数进行直接测量获得变化规律. Aoyagi等^[15]分析了不同毛细管腔体长径比下, 元冲量的变化规律并结合任务需求进行了参数筛选. Hiroki 和Hirokazu^[16]测量了不同放电能量下推力器比冲、效率参数, 发现输出参数与放电能量成正相关. 斯图加特大学Matthias等^[17]研究了放电能量在3 J 量级时不同电压和电容参数组合方式下, 等效单次烧蚀质量和元冲量变化规律. 由于推力器性能参数表征过程涉及真空实验、微冲量测量和烧蚀质量测量等多个步骤, 过程繁琐, 现有研究多是在单一条件下获得的参数变化趋势, 尚未阐明腔体结构设计参数对等离子体产生和加速过程的影响机制, 也未掌握结构参数与输出比冲效率参数间的相互关联. 本文建立毛细管型脉冲等离子体推力器实验平台, 利用电学、微冲量测量及发射光谱等手段研究了毛细管腔体结构参数对推力器输出参数影响规律及内在物理机制, 建立推力器输出效率的能量传递分析模型, 深入分析不同腔体结构参数对推力器放电特性和输出参数的影响规律, 为推力器结构参数优化提供理论依据.

2

-->

2.1.推力器结构

毛细管脉冲等离子体推力器结构示意图如图1所示. CDPPT整体结构主要包括五部分: 半导体火花塞、阴极喷嘴、阳极基座、绝缘护套和工质. 工质采用聚四氟乙烯(polytetrafluoroethylene, PTFE)材料, 加工为中空圆柱型毛细管腔体结构. 阳极与阴极喷嘴采用黄铜材料, 具有较好的抗电弧烧蚀性能. 尼龙绝缘护套用于连接阴极和阳极, 同时对PTFE工质腔体进行固定, 实现腔体与阴极喷嘴的同轴布置. 半导体火花塞采用SiC材料, 中间安装钨棒作为触发电极. 推力器工作时, 通过外部触发电路在触发电极与阴极间施加高压触发脉冲, 使SiC沿面闪络, 释放初始带电粒子, 诱发毛细管腔体内部主放电的形成. 火花塞触发电路放电电压1 kV, 单次放电能量50 mJ, 具有良好的稳定性. 主电容通过铜皮连接阴极与阳极, 电路采用紧凑化布局, 尽可能减小回路等效阻抗, 提高能量传递效率^[18].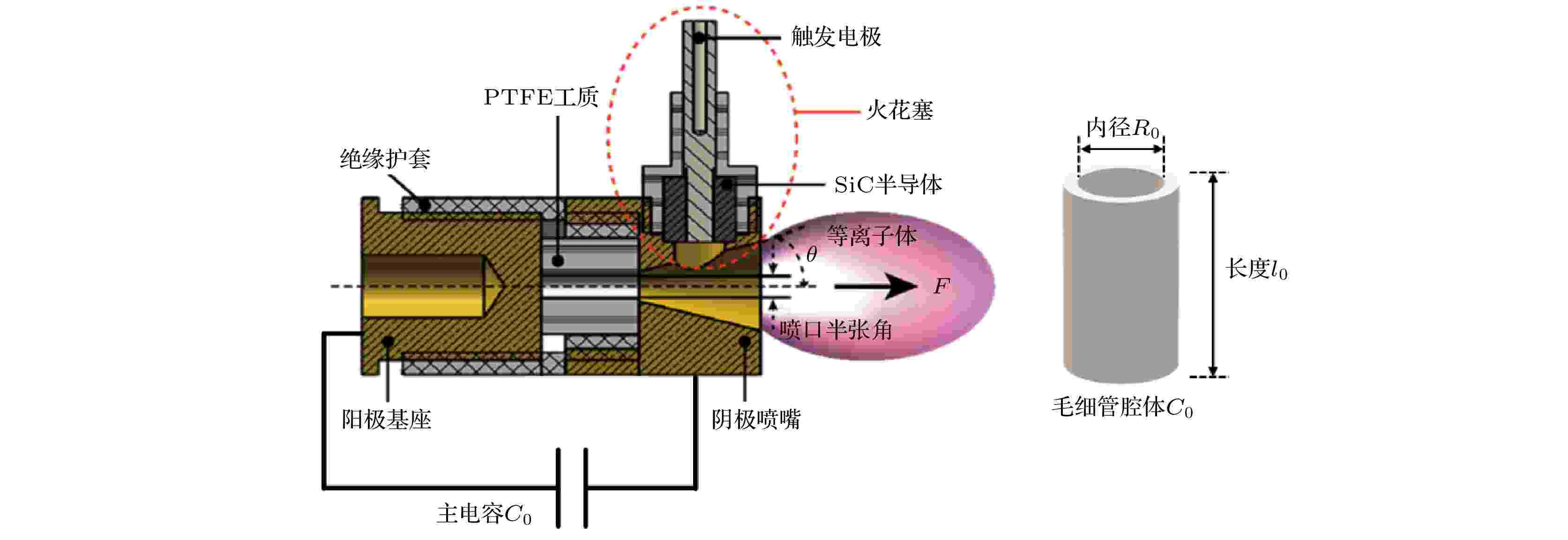
图 1 毛细管推力器结构示意图
Figure1. The schematic of CDPPT structure.

实验中, 毛细管腔体结构尺寸, 主电容容值及电压参数配置如表1所列. 实验中, 为减小参数测量误差, 对于同一物理量, 每个毛细管结构尺寸下重复测量5次取平均值.

参数	取值
主电容容值 C0/μF	2.5
充电电压 U0/kV	2
毛细管长度 l0/mm	14, 16, 18, 20, 25, 30, 35, 40
毛细管内径 R0/mm	1, 3, 5, 7, 9

表1毛细管推力器工作参数与结构参数
Table1.Operation parameters and structural parameters of CDPPT.

2 -->

2.2.实验平台

毛细管型脉冲等离子体推力器工作特性研究平台如图2所示. 主要包括真空系统、电源系统、电学诊断、光谱诊断和微推力测量系统. 推力器工作时, 利用真空泵组将真空腔内抽至一定气压(≤ 5 × 10^–3 Pa). 利用高压直流电源将主电容充电至2 kV, 此时对应CDPPT单次放电能量为5 J. 推力器放电电压和电流波形通过电压探头(Lecory PPS 6 kV, 400 MHz)和罗氏线圈(Pearson 4997, 15 MHz)测量, 同时利用示波器(Tektronix DPO7054C)进行数据采集, 后期分析中, 利用 Matlab对测量系统采集电压电流波形信号进行数据处理和计算.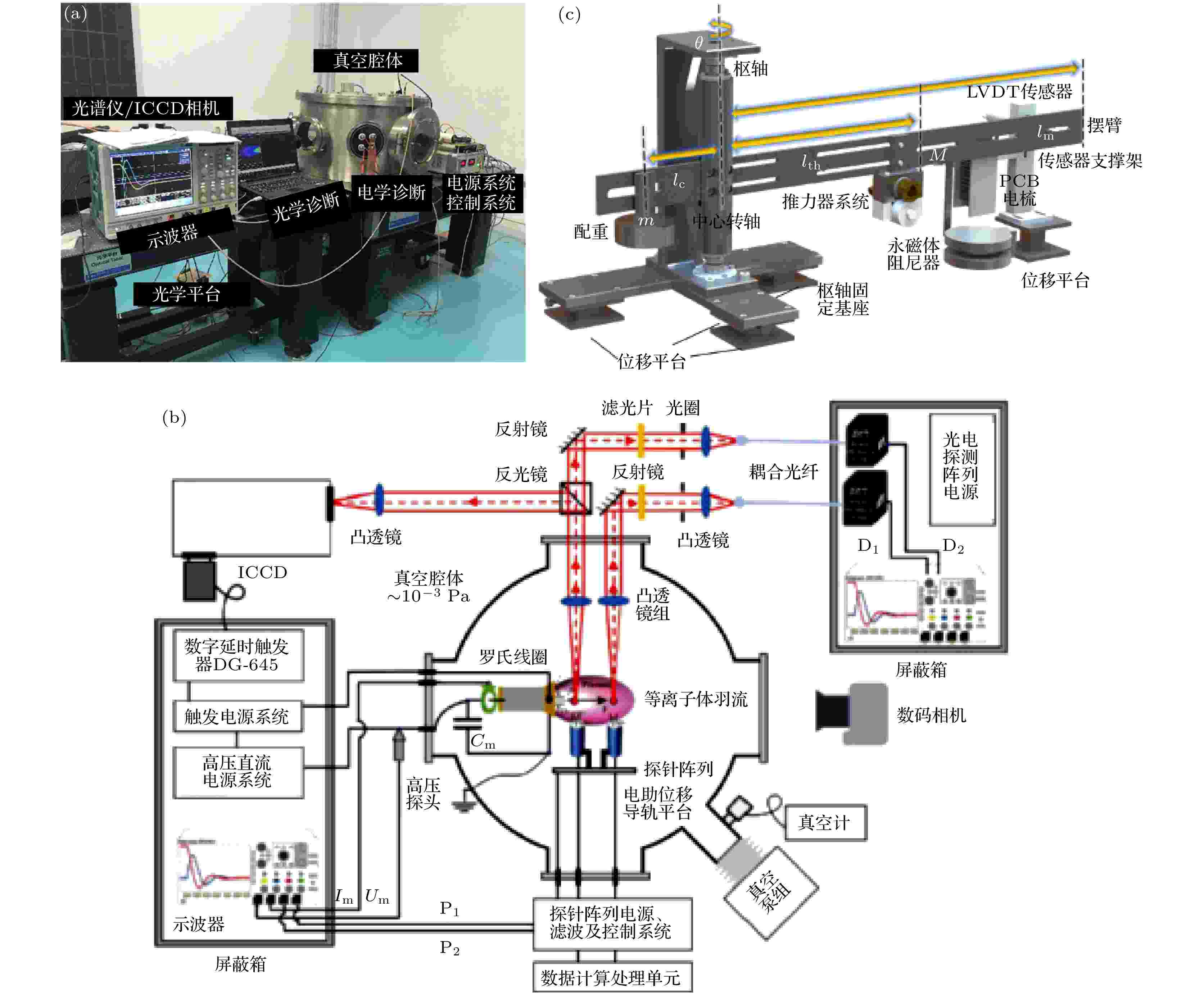
图 2 实验平台　(a) 实物图; (b) 示意图; (c) 微推力测量扭摆
Figure2. Experimental platform: (a) Photo; (b) schematic diagram of the system; (c) thrust balance.

实验中, 利用光谱仪(Shamshock 750i)和ICCD相机(Andor iStar)采集并记录CDPPT工作过程中不同时刻的等离子体发射光谱. 推力器放电过程中, 放电电弧不断烧蚀毛细管腔壁材料, 烧蚀材料进入腔体与电弧等离子体不断碰撞, 迅速进行能量传递, 通常可以认为放电腔体内等离子体满足局部热平衡条件. 此外, 根据实测光谱结果, 辐射光谱谱线均为孤立的线状谱线, 未检测到自吸收谱线等, 等离子体羽流满足光学薄条件. 因此通常情况下, 对应于波长λ_ji和λ_kl的两条谱线, 可以利用(1)式, 根据原子发射光谱的谱线强度进行计算获得电子温度^[19,20],

$ \frac{{{I}_{j}}_{i}}{{{I}_{kl}}}=\frac{{{\lambda }_{kl}}{{A}_{ji}}{{g}_{j}}}{{{\lambda }_{ji}}{{A}_{kl}}{{g}_{k}}}\exp \left( \frac{{{E}_{k}}-{{E}_{j}}}{kTe} \right). $

利用该方法计算时, 一般要求选择能级差较大且辐射强度适中的谱线, 然而, 利用不同谱线计算时, 其计算结果通常有较大偏差, 为了改善该方法, 对(1)式两端同时取对数可得

$ \ln \left(\frac{{\varepsilon {\lambda _{ul}}}}{{{A_{ul}}{g_u}}}\right) = - \frac{{{E_u}}}{{{k_{\rm{B}}}{T_{{\rm{e}}x}}}} + \ln \left(\frac{{hcFp{C_j}}}{{4\pi {Z_j}{k_B}{T_{{\rm{e}}x}}}}\right) . $

以该式左侧项为纵坐标, 利用上能级能量E_u作为横坐标, 将多条谱线对应数据带入计算, 并绘制在坐标系中, 对这些计算结果进行线性拟合, 由此可以确定对应的电子温度. 利用该方法进行计算时, 同时考虑了多条谱线数据, 能够提高计算精度. 对于推力器羽流等离子体电子密度的计算可采用Stark 展宽法. 等离子体发射谱线的展宽由自然展宽、Doppler 展宽和Stark 展宽等因素共同决定, 其表达式为^[21]

$ \Delta {\lambda _{\rm{m}}} = \sqrt {\Delta {\lambda _{\rm{s}}^2} + \Delta {\lambda _{\rm{d}}^2} + \Delta {\lambda _{\rm{I}}^2}} , $

其中λ_m, λ_s, λ_d, λ_I分别为光谱仪测量谱线展宽、Stark效应展宽、Doppler效应展宽以及光谱仪展宽. 对于毛细管放电产生的等离子体而言, 其电子温度通常在5 eV以下, 此时Doppler展宽效应较小, 可会略其对谱线展宽的影响. 对于Stark展宽, 计算公式如(4)式所示^[22]:

$ \begin{split}\Delta {\lambda _s} =\;& 2 \Big[1 + 1.75 \times {10^{ - 4}} n_{\rm e} ^{1/4}\alpha \\& \times \big(1- 0.068 n_{\rm e}^{1/6}T_{\rm e}^{-1/2}\big)\Big] \times {10^{ - 16}}\omega {n_{\rm{e}}} ,\end{split} $

式中, ω为Stark展宽因子; α为离子展宽因子, 根据光谱仪测量典型光谱谱线, 通过Voigt函数曲线进行拟合获得光谱展宽, 再利用(3)式和(4)式即可计算得到等离子体密度.
毛细管推力器单次元冲量在数十至数百μN·s量级, 其推力脉宽约为毫秒量级, 目前尚无商业传感器可满足灵敏度和频带要求. 实验中, 采用自研微推力测量扭摆进行测量, 如图2(c)所示. 微推力测量扭摆的基本原理为, CDPPT工作时产生的推力作用在扭摆摆臂上, 扭摆系统在推力器作用下的运动方程可以用二阶系统的零状态冲击响应表示, 通过精密位移传感器测量摆臂位移进而求解推力器输出元冲量. 微推力测量扭摆在测量前利用静电梳标定装置进行标定, 微冲量测量系统最小分辨率可达0.5 μN·s, 不确定度低于1%, 且多次重复实验线性度良好, 满足CDPPT输出元冲量测量需求^[23,24].

CDPPT工作时, 放电等效电路示意图如图3所示. 其中, R_c和L_c分别为储能电容寄生电阻和寄生电感, R_c1, R_c2和L_c1, L_c2分别为电极及放电回路连接线的等效串联电阻和电感, R_p对应等离子体电弧通道等效电阻, L_p对应电弧通道等效电感.
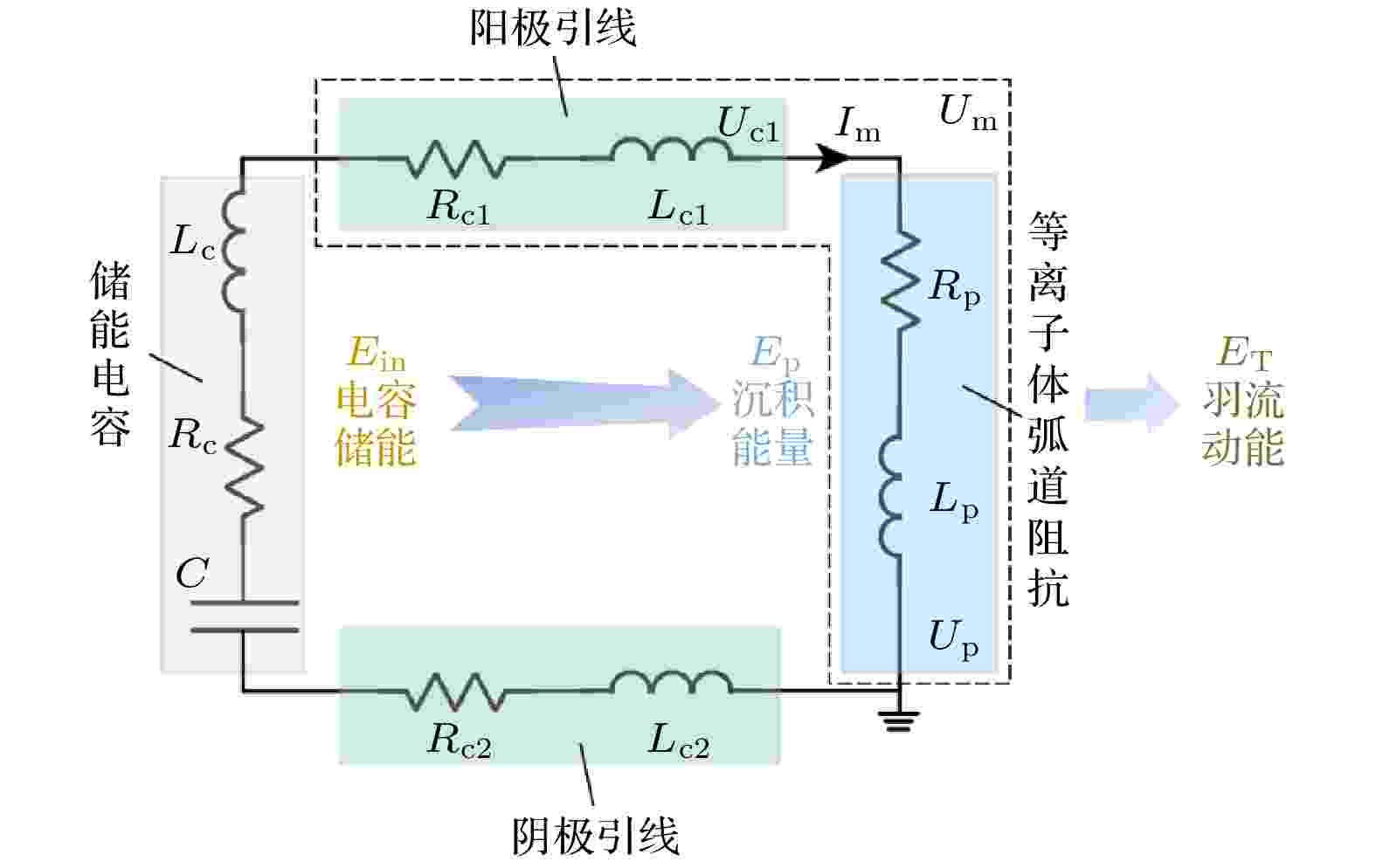图 3 推力器放电等效电路及能量传递路径
Figure3. The equivalent circuit of CDPPT discharge circuit and energy transfer path.

将推力器放电回路等效为RLC二阶电路, 由基尔霍夫电压定律可得等离子体电弧通道电压分量U_p为

$ {U_p}(t) = {U_{\rm{m}}}(t) - {L_{{\rm{c}}1}}\frac{{d{I_{\rm{m}}}(t)}}{{dt}} - {R_{{\rm{c}}1}}{I_{\rm{m}}}(t) . $

对于CDPPT而言, 放电过程中腔体约束放电等离子体电弧通道, 其截面近似为常数, 因此等离子体通道电感变化引起的电压变化可忽略不计, 等离子体通道阻性电压分量U_R可表示为

$ {U_{\rm{R}}}(t) = {U_{\rm{p}}}(t) - {L_{\rm{P}}}\frac{{{\rm{d}}{I_{\rm{m}}}(t)}}{{{\rm{d}}t}} . $

在此基础上可获得CDPPT电弧通道等效功率P_R,

$ {P_{\rm{R}}}\left( t \right) = {U_{\rm{R}}}\left( t \right) \times {I_{\rm{M}}}\left( t \right) . $

等离子体电弧通道沉积能量为

$ {E_{\rm{p}}} = \int_0^{{t_{\rm{p}}}} {{P_{\rm{R}}}(t){\rm{d}}t} . $

通过测量CDPPT放电主电压和主电流波形, 结合(5)式—(8)式可得到等离子体弧道沉积能量. 由于高压探头测量电压信号中包含引线电阻和电感分量, 在计算推力器弧道等效阻抗和沉积能量时, 需排除引线部分阻抗的影响, 利用手持式精密电桥(TH2822C)对引线阻抗进行测量, 可获得测量回路中包含的引线电阻R₀为8.5 mΩ, 引线电感L₀为15.9 nH. 估算等离子体阻抗时需要除去外回路电感的影响, 为了获得主电容等效电感参数, 实验前向主电容充电, 将阴极和阳极短接, 利用短路电流法估算放电回路参数, 不同容值主电容对应电感值计算结果如表2所列.

主电容值/μF	0.5	1.0	1.5	2.0	2.5
Lc + L0/nH	97.13	89.02	86.32	84.97	84.16

表2不同容值下等效放电回路参数
Table2.Equivalent circuit parameters of CDPPT with different capacitance.

此外在放电过程中, 等离子体等效电阻为时变电阻, 而瞬时沉积功率变化则反映了弧道阻抗焦耳热功率. 为了便于比较不同电路参数、结构参数下, 推力器等效阻抗的变化情况, 本文从能量沉积角度建立等效稳态阻抗表达式:

$ {R_{\rm{P}}} = {E_{\rm{P}}}\bigg/\int_0^{{t_{\rm{p}}}} {{I_{\rm{m}}}} {(t)^2}{\rm{d}}t . $

图3同时给出了CDPPT工作过程中存在的能量传递路径, 推力器工作时总体能量效率传递过程可用(9)式表示

$ {E_{\rm{T}}} = {E_{\rm{p}}} \cdot {\eta _{{\rm{acc}}}} = {E_{{\rm{in}}}} \cdot {\eta _{{\rm{acc}}}} \cdot {\eta _{{\rm{trans}}}} = {E_{{\rm{in}}}} \cdot {\eta _{\rm{o}}} , $

式中η_acc表示等离子体加速效率; η_trans表示能量传递效率; η_o表示推力器总体效率. 对于脉冲等离子体推力器而言, 总体效率又可用(10)式进行计算:

$ {\eta _{\rm{o}}} = \frac{{{E_{{\rm{plume}}}}}}{{{E_{{\rm{in}}}}}} = \frac{{1/2\Delta m{{\overline v }^2}}}{{{E_{{\rm{in}}}}}} = \frac{{{{(\Delta m\overline v )}^2}}}{{2\Delta m{E_{{\rm{in}}}}}} = \frac{{{I_{{\rm{bit}}}}^2}}{{2\Delta m{E_{{\rm{in}}}}}} , $

I_bit为推力器单次输出元冲量, 可利用微推力测量扭摆精确测量; Δm为等效平均单次烧蚀质量, 实验中, 利用微量天平测量推力器工作1000次前后质量变化获得.

2

-->

4.1.不同结构参数下CDPPT放电特性

当放电能量一定时, 毛细管推力器的结构尺寸参数(包括毛细管内径和长度)将会影响单位体积内能量密度, 使得烧蚀产物粒子密度和电离度等产生变化, 改变电弧通道特性进而影响推力器输出参数. 图4给出了不同毛细管内径下, 推力器放电电压波形、放电电流波形、弧道阻性分量功率和沉积能量曲线. 其中, 毛细管长度为16 mm, 内径分别为1, 3, 5, 7 mm和9 mm, 主电容容值2.5 μF, 充电电压2 kV, 单次放电能量5 J.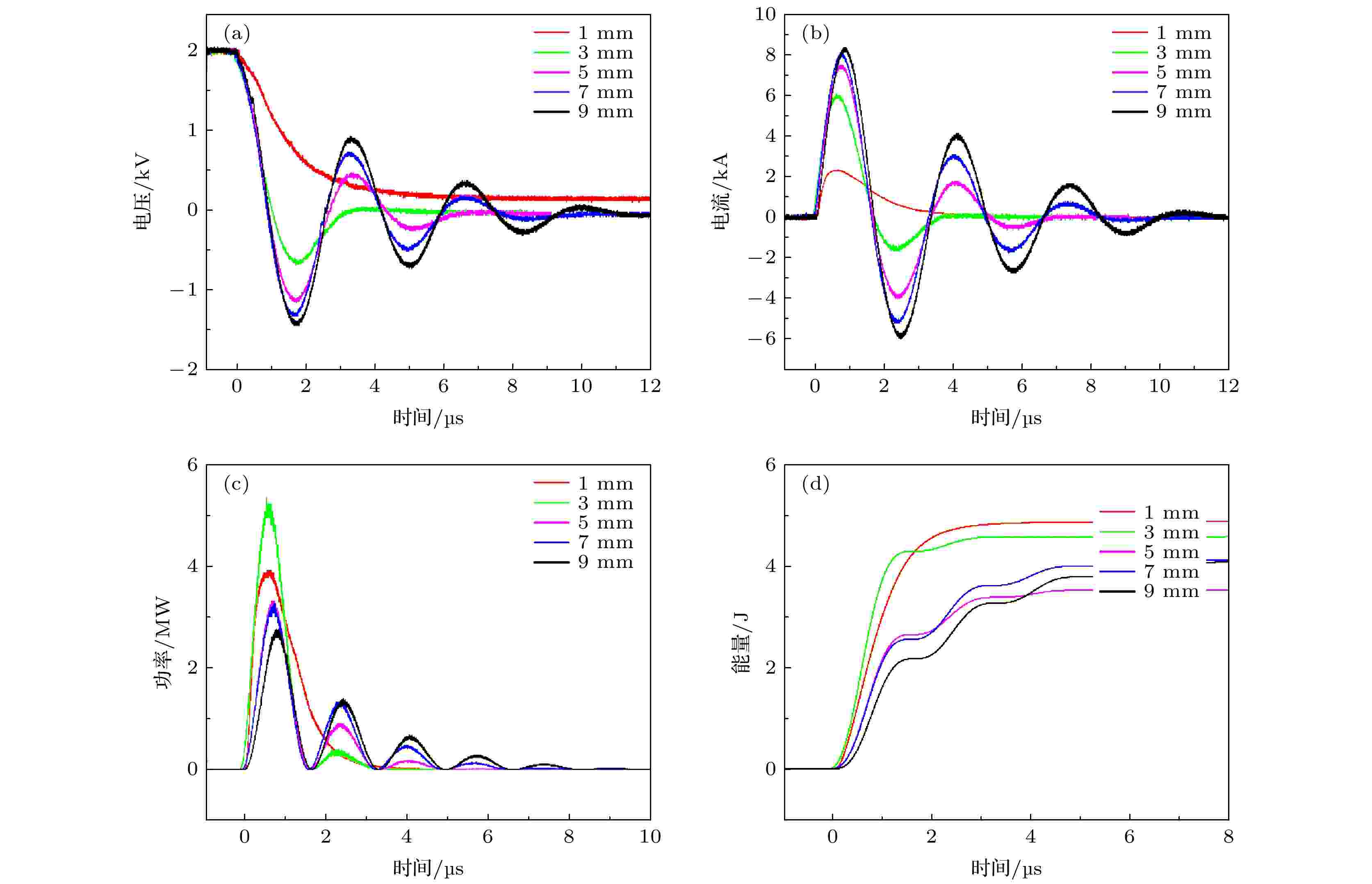
图 4 不同内径下　(a) 电压波形; (b) 电流波形; (c) 阻性功率; (d) 沉积能量
Figure4. The discharge characteristics of CDPPT with different cavity diameter: (a) Voltage waveform; (b) current waveform; (c) arc resistance power; (d) deposited energy.

从图4(a)和图4(b)可以看出, 当毛细管内径为1 mm时, 放电电流呈现过阻尼特性. 随着毛细管内径的增加, 放电电流波形逐渐转变为欠阻尼振荡, 且放电电流幅值不断增大, 放电周期略微减小. 与此同时, 放电持续时间也随着电流振荡的加剧不断增加. 当毛细管内径为1 mm时, 可以看到放电电压波形并未归零, 即储能电容能量未完全释放, 而在实验中也观察到熄弧现象. 该现象产生的主要原因在于: 1) 毛细管内径过小时, 电弧将对管壁剧烈烧蚀, 所产生的烧蚀产物进入放电通道内, 使得腔体内压力急剧增加, 不利于电弧维持; 2) 弧道等效阻抗较大, 放电时间常数增大, 放电电流峰值降低, 不利于电弧发展; 3) 由于烧蚀产物剧烈增加, 低温蒸汽层将在电弧通道周围积累并向内扩散, 使得电弧更易中断^[10]. 图4(c)显示了弧道等效功率变化曲线, 随着毛细管内径从3 mm增加至5 mm, 功率峰值从4.84 MW降低至2.15 MW. 与之对应, 在图4(d)中沉积能量曲线中, 当毛细管内径从1 mm增加至3 mm时, 出现了快速沉积阶段对应的平台特征. 当毛细管内径继续增大时, 沉积能量台阶数量增加且沉积能量速率不断减小, 快速沉积能量阶段沉积能量也不断下降. 表3给出了不同内径下等效放电回路参数. 当毛细管内径从1 mm增加至3 mm时, 其弧道等效电阻由(703.10 ± 15.43) mΩ迅速减小至(143.70 ± 0.53) mΩ. 随着内径继续增加, 其等效电阻最终降低至(39.38 ± 0.18) mΩ. 利用毛细管内径求得其截面积, 可以获得等效电阻率变化趋势. 随着毛细管内径的增加, 弧道等效电阻率呈现减小趋势, 从186.4 Ω/m 变化至32.12 Ω/m. 这是由于随着毛细管内径的增加, 腔体内表面积增加, 使得烧蚀质量降低, 粒子密度减小, 且由于放电腔体的增大, 粒子间相互碰撞概率降低, 致使电子可以保持相对较高能量, 提高了电导率, 加之腔体截面的增加, 使得宏观上弧道电阻增大.

毛细管内径/mm	初始储能/J	主电流幅值/A	弧道电阻/mΩ	弧道电感/nH
1	5.06	2379 ± 38.20	703.10 ± 15.43	49.98 ± 2.38
3	5.00	6116 ± 8.94	143.70 ± 0.53	35.50 ± 3.08
5	5.18 ± 0.01	7568 ± 17.89	58.72 ± 0.13	28.19 ± 1.92
7	5.05 ± 0.01	8148 ± 26.83	49.74 ± 0.70	27.75 ± 2.05
9	5.08 ± 0.01	8400	39.38 ± 0.18	21.53 ± 2.94

表3不同内径下等效放电回路参数
Table3.Equivalent circuit parameters of CDPPT with different cavity diameter.

由图4所示电流波形和沉积能量波形可以看到, 当放电腔体内径较大时, 放电电流出现振荡, 沉积能量曲线出现多个平台. 对于毛细管推力器而言, 由于腔体内压力与电弧状态关系密切, 等离子体能量沉积和内能增加主要出现在第一个电流过零点之前, 通常将此部分称为快速能量沉积阶段^[14]. 图5所示为沉积能量和能量传递效率的变化曲线. 在相同的单次放电能量下, 随着放电电流的增加, 外回路中能量损失增大, 因此, 当毛细管内径从1 mm增加至9 mm时, 其能量沉积效率由95.61%降低至63.71%. 由于弧道阻抗的降低, 使得弧道沉积能量由4.84 J降低至3.23 J. 此外, 毛细管内径的增大也将会降低腔体内压强, 不利于等离子体在腔体内热膨胀加速, 使得等离子体喷射速度下降.
图 5 不同内径下沉积能量及沉积能量效率
Figure5. The deposited energy and efficiency of CDPPT with different cavity diameter.

图6所示为不同毛细管长度时, 推力器放电电压、放电电流、弧道功率和沉积能量曲线的变化规律. 其中毛细管长度分别为14, 16, 18, 20, 25, 30, 35 和40 mm, 毛细管内径为5 mm, 主电容容值2.5 μF, 充电电压2 kV, 单次放电能量5 J. 随着毛细管长度的增加, 放电电流幅值逐渐减小, 从7.9 kA降低为5.7 kA. 毛细管长度的增加使得放电回路阻尼系数增大, 放电波形振荡减弱, 放电持续时间缩短. 弧道等效功率峰值随毛细管长度增加呈增大趋势, 这是由于毛细管腔体长度的增加增大了弧道等效阻抗, 尽管放电电流幅值在一定程度上有所下降, 但弧道沉积能量增大. 相对应地, 当毛细管腔体长度增大后, 能量沉积上升速率增大, 快速能量沉积阶段沉积能量较大.
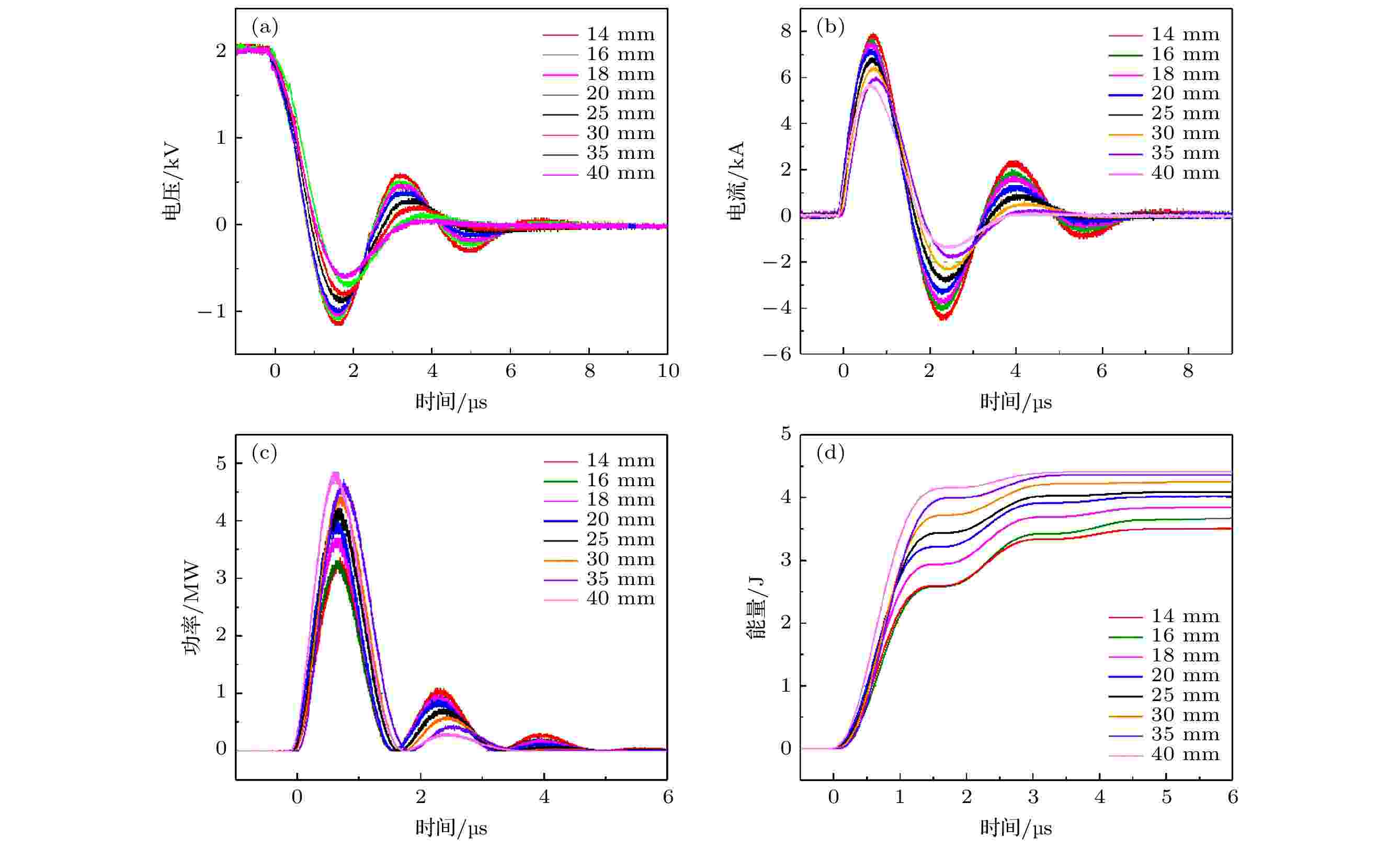图 6 不同长度下　(a) 电压波形; (b) 电流波形; (c) 阻性功率; (d)沉积能量
Figure6. The discharge characteristics of CDPPT with different cavity length: (a) Voltage waveform; (b) current waveform; (c) arc resistance power; (d) deposited energy.

表4给出了不同毛细管长度下放电回路参数. 当毛细管长度从14 mm增加至40 mm时, 弧道等效电阻从(53.00 ± 0.07) mΩ增加至(148.86 ± 0.73) mΩ, 弧道等效电感从(14.14 ± 0.46) nH增加至(36.24 ± 1.89) nH.

毛细管长度/mm	初始储能/J	主电流幅值/A	弧道电阻/mΩ	弧道电感/nH
14	5.16 ± 0.01	7944 ± 35.78	53.00 ± 0.07	14.14 ± 0.46
16	5.11 ± 0.03	7640	56.47 ± 0.36	19.36 ± 1.69
18	5.07 ± 0.01	7544 ± 35.78	66.20 ± 0.45	22.25 ± 2.12
20	5.16 ± 0.06	7256 ± 35.78	77.56 ± 0.40	22.32 ± 0.22
25	5.05	6872 ± 43.82	90.66 ± 0.81	22.74 ± 3.12
30	5.09	6436 ± 21.91	107.34 ± 0.19	25.67 ± 2.12
35	5.17 ± 0.01	6004 ± 21.91	129.86 ± 0.34	34.27 ± 2.84
40	5.10 ± 0.08	5684 ± 21.91	148.86 ± 0.73	36.24 ± 1.89

表4不同长度下等效放电回路参数
Table4.Equivalent circuit parameters of CDPPT with different cavity length.

图7显示了毛细管长度变化时, 沉积能量变化及能量转移效率的变化规律. 放电全过程中弧道沉积能量由14 mm时的3.69 J增大至40 mm时的4.41 J, 相应地, 能量沉积效率由71.43%提高至86.55%. 这意味着放电通道的延长将有效约束电弧通道发展时的热沉积过程, 提高了等离子体焦耳热的转换效率.
图 7 不同内径下沉积能量及沉积能量效率
Figure7. The deposited energy and efficiency of CDPPT with different cavity length.

综合而言, 结构参数对于毛细管放电特性有较大影响, 随着毛细管内径增大, 长度减小, 等效沉积能量、弧道等效功率均出现较大变化. 毛细管内径的改变会显著地降低放电电流密度, 从而导致沉积能量和等效功率的改变. 因此, 在毛细管推力器工作中, 需要关注因管壁烧蚀造成腔体内径增大对推力器输出参数的影响.
2 -->

4.2.不同结构参数下等效平均单次烧蚀质量

图8(a)为不同内径时推力器烧蚀质量变化规律. 毛细管腔体长度为16 mm, 内径分别为1, 3, 5, 7 和9 mm, 主电容容值2.5 μF, 充电电压2 kV, 单次放电能量为5 J. 当毛细管内径从1 mm增大到3 mm时, 由于电流密度减小, 电弧对腔壁辐射功率密度降低, 电弧对毛细管管壁的烧蚀作用迅速减弱, 平均单次烧蚀质量从(146.48 ± 0.33) μg降低至(67.40 ± 0.29) μg. 当进一步增大腔体内径时, 烧蚀质量基本不变. 为了进一步分析腔体内表面对烧蚀质量的影响, 定义单位面积烧蚀质量, 可利用(12)式进行计算: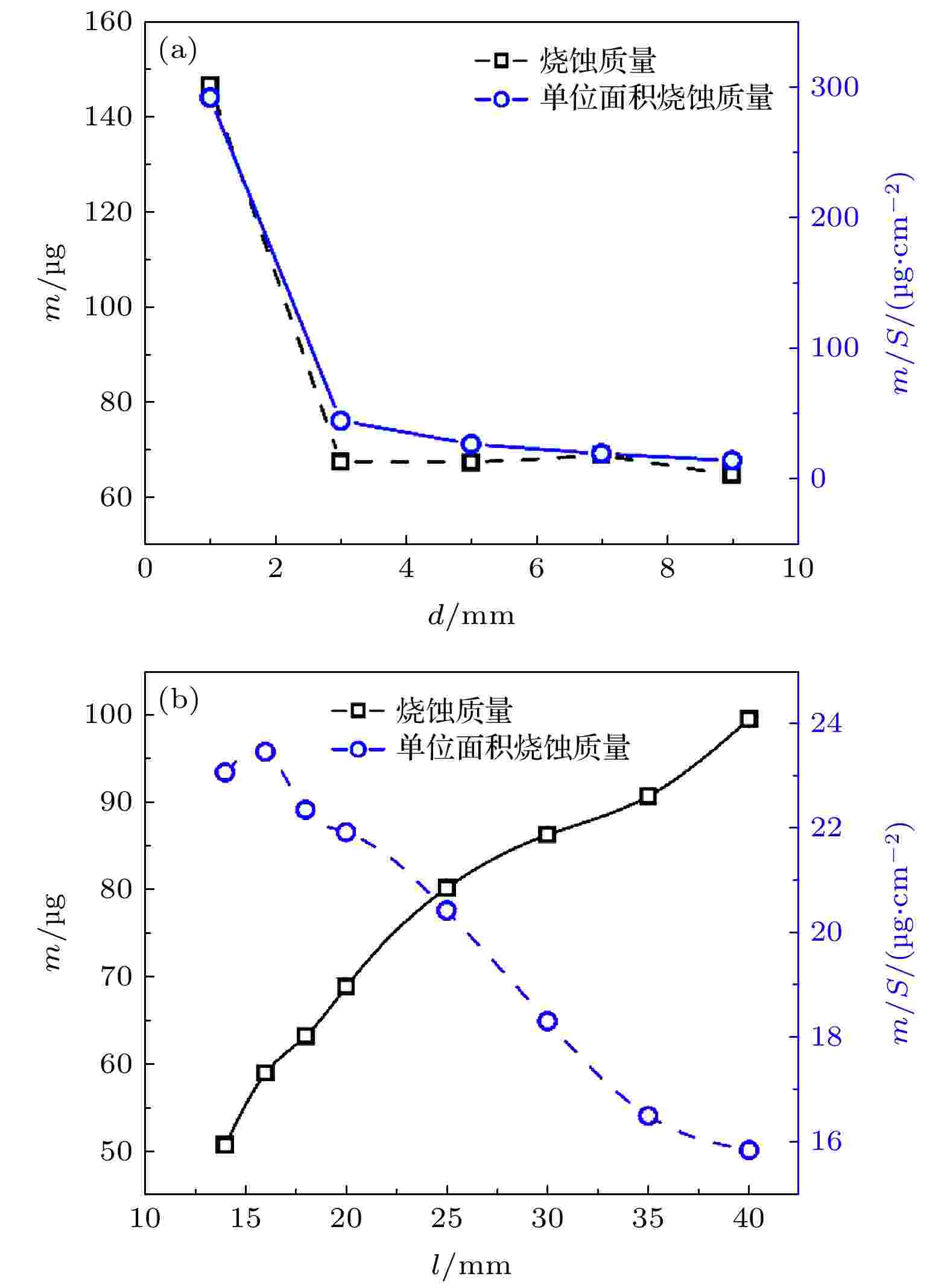
图 8 烧蚀质量与单位面积烧蚀质量　(a) 不同内径; (b) 不同长度
Figure8. The ablation mass per shot and ablation mass per unit surface of CDPPT: (a) With different cavity diameter; (b) with different cavity length.

$ \dfrac m S = \dfrac m {2{\rm{π }}rl } , $

其中r为腔体内径; l为腔体长度. 对于单位面积烧蚀质量而言, 可以看到, 随着腔体内径的增大不断减小. 特别地, 当内径从1 mm增加至3 mm时, 单位面积烧蚀质量从(291.56 ± 0.33) μg/cm²降低至44.72 μg/cm². 图8(b)显示了不同毛细管腔体长度下平均单次烧蚀质量的变化曲线. 毛细管长度分别为14, 16, 18, 20, 25, 30, 35 和40 mm, 内径为5 mm. 由图8(b)可以看到, 随着腔体长度的增加, 平均单次烧蚀质量从(50.78 ± 0.34) μg增大至(99.66 ± 0.34) μg, 单位面积烧蚀质量从(23.09 ± 0.34) μg/cm²减小至(15.86 ± 0.34) μg/cm².
CDPPT烧蚀特性可利用动力学烧蚀模型进行分析. 动力学烧蚀模型是由Keidar等^[10]和Zaghloul^[11]提出并完善地用于描述电弧等离子体对聚合物材料的烧蚀过程的数值计算模型. 在动力学烧蚀模型中, 把工质壁面与等离子体区域之间的非平衡过渡层划分为三个区域, 利用动力学理论, 获取工质壁面、努森层与非平衡动力学层边界以及非平衡动力学层与等离子体区域边界的粒子分布联系, 最终获得烧蚀速率表达式. 烧蚀速率的影响因素主要包括管壁温度、腔体等离子体温度和密度. 根据仿真和实验结果所获得的等离子体温度和密度值代入动力学烧蚀模型进行计算发现, 对于单次放电能量在10 J以下量级的毛细管放电而言, 腔体内等离子体参数所在量级区间变化对烧蚀质量流率的影响较小^[13,14]. 随着毛细管长度的增加, 尽管回路能量传递效率增加, 但腔壁单位面积上分配辐射能量减小, 致使管壁温度降低, 烧蚀速率减小, 烧蚀质量降低. 与改变毛细管腔体长度相比, 当腔体内径较小时, 平均烧蚀质量对内径变化更加敏感. 对于推力器而言, 由于工作过程中腔体材料不断消耗, 内径增大会改变推力器单次烧蚀质量, 不利于推力器保持稳定的输出参数. 综合来看, 腔体尺寸变化对烧蚀质量的影响在于, 增大腔体面积使得电弧与管壁接触面积增加, 有利于烧蚀质量的增大; 但于此同时, 弧道沉积能量和等离子体加速过程也将受到影响, 使得等离子体喷射速度变化, 进而影响单位时间内从腔体喷射烧蚀产物质量^[25].
2 -->

4.3.结构参数对输出推力参数的影响

图9给出了不同内径和长度时毛细管推力器输出元冲量、单次等效烧蚀质量、比冲和效率参数的变化规律. 实验中, 毛细管长度为16 mm, 内径分别为1, 3, 5, 7和9 mm. 从图9的实验结果可以看到, 当毛细管内径从3 mm增加至9 mm时, 输出元冲量从(350.80 ± 7.50) μN·s降低至(173.90 ± 13.30) μN·s. 毛细管内径在此范围内变化时, 平均单次烧蚀质量近似保持不变, 基本维持在60 μg左右. 当毛细管内径从1 mm增加至3 mm时, 元冲量近似不变, 但单次平均烧蚀质量迅速从(146.48 ± 0.34) μg减小至(67.4 ± 0.29) μg. 由于烧蚀质量的迅速减小, 使得比冲参数从(241.09 ± 5.11) s增加至(531.10 ± 9.07) s, 总体效率从8.17%增加至18.26%. 当毛细管内径继续增加时, 由于元冲量不断下降, 单次烧蚀质量近似保持不变, 使得计算所得比冲参数随着毛细管内径增加从(531.10 ± 9.07) s降低至(274.35 ± 20.04) s, 总体效率从18.26%下降至4.68%. 根据放电特性实验结果可知, 随着毛细管内径增大, 等离子体等效阻抗减小, 放电电流峰值不断增加, 但弧道沉积能量不断减小. 毛细管内径的增加, 使得腔体内等离子体的热膨胀加速作用减弱, 因而推力器输出元冲量不断下降. 实验中发现, 当毛细管内径为1 mm时, 推力器工作过程中甚至出现熄弧现象. 电容中存储能量未完全释放, 实际单次放电能量较小, 使得输出元冲量与腔体内径3 mm时元冲量较为接近. 内径从1 mm增加至3 mm时, 放电波形从过阻尼振荡转变为欠阻尼振荡. 当毛细管内径进一步增加时, 放电腔体内表面积增大, 有利于增大烧蚀质量. 但与此同时, 由于弧道沉积能量的降低, 烧蚀质量逐渐减小.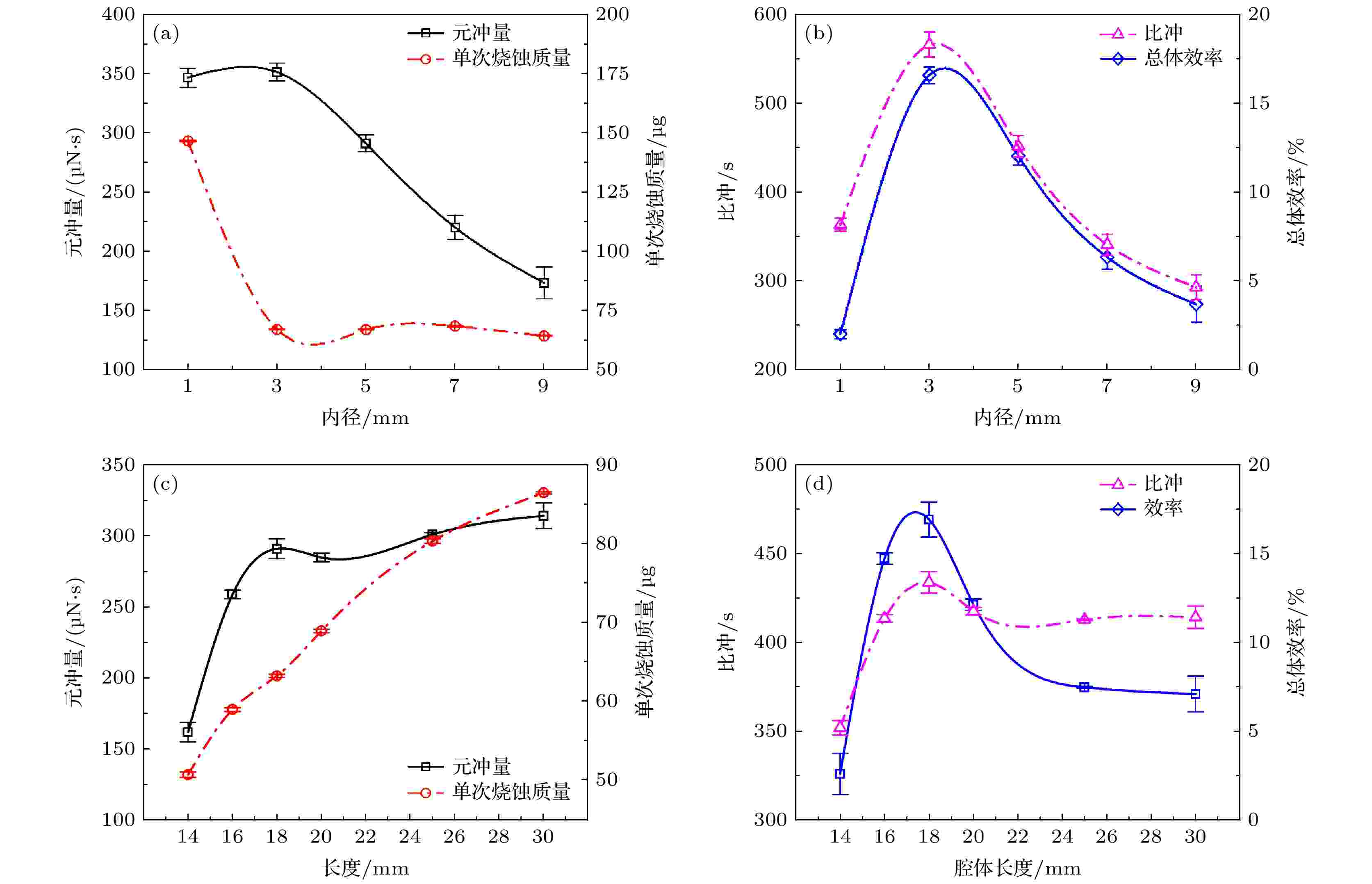
图 9 不同内径下(a) 元冲量, (b) 比冲与效率; 不同长度下 (c) 元冲量, (d) 比冲与效率
Figure9. The impulse bit (a), specific impulse and efficiency (b) of CDPPT with different cavity length; impulse bit (c), specific impulse and efficiency (d) of CDPPT with different cavity diameter.

图9(c)和图9(d)为改变放电腔体长度时, 毛细管型推力器输出元冲量, 单次烧蚀质量, 比冲和总体效率的变化趋势. 毛细管内径为5 mm, 长度变化范围为14至30 mm. 由图9(c)所示实验结果可见, 随着毛细管长度的增大, 推力器输出元冲量先增大后保持在一定范围内波动. 平均单次烧蚀质量随着毛细管长度的增加持续增大. 随着腔体长度的增大, 等离子体在腔体中受到电热加速作用的距离增大, 腔体出口处等离子体喷射速度将会提高, 因而比冲和效率随着腔体长度的增加迅速上升. 当长度为18 mm时, 比冲为468.96 s, 效率为13.36%, 均到达最大值. 随着腔体长度进一步增大, 腔体对等离子体加速的黏滞阻力增强, 等离子体的喷射速度难以继续提高, 因此元冲量呈现饱和趋势. 由于单次烧蚀质量持续增大, 推力器比冲和效率不断下降. 当毛细管腔体长度增加时, 等离子体密度和腔体内压强将增加, 但等离子体温度和速度将随之减小, 变化趋势与之相反. 综合不同条件下实验结果, 推力器原理样机在毛细管长度为16 mm, 内径3 mm达到较优性能参数, 可输出元冲量为350.79 μN·s, 比冲为531.10 s, 总体效率为18.26%.
2 -->

4.4.结构参数对推力器等离子体羽流参数的影响

图10为不同毛细管内径时, 推力器羽流等离子体电子温度和密度的变化曲线. 其中主电容容值2.5 μF, 充电电压2.0 kV, 单次放电能量5 J, 毛细管长度为16 mm. 从图10可以看到, 毛细管内径为1 mm时, 羽流等离子体温度明显小于其他内径时等离子体温度. 尽管较小内径时, 电弧通道内沉积能量较高, 但此时烧蚀质量显著增加, 使得放电腔体内粒子密度增大, 频繁的粒子碰撞使电子温度下降. 当毛细管内径从3 mm增加至5 mm时, 等离子体温度峰值较为接近, 但由于弧道沉积能量的逐渐减小, 使等离子体温度峰值表现出略微下降的趋势.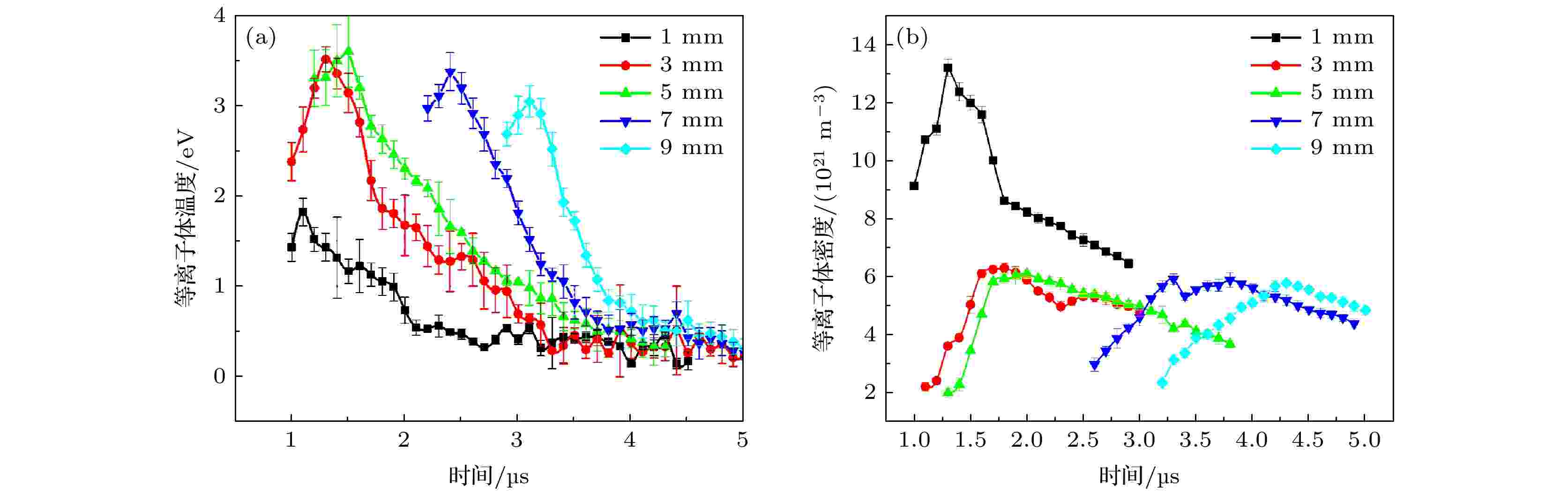
图 10 不同内径下羽流等离子体　(a) 等离子体温度; (b) 等离子体密度
Figure10. Theplasma temperature (a) and plasma density (b) of CDPPT plasma plume with different cavity diameter.

毛细管内径的增加, 显著降低了放电腔体对等离子体热膨胀的加速效果, 在相同时刻下, 较大的放电腔体内对应压强较低, 因此等离子体喷射所需压强梯度累计时间延长, 等离子体羽流出现时间增大. 毛细管内径为1 mm时, 烧蚀质量最大, 且较小的腔体体积进一步增加了等离子体密度, 使其远高于其他内径对应等离子体密度. 当毛细管内径从3 mm增加至5 mm时, 等离子体密度峰值较为接近约为6 × 10²¹ m^–3, 但峰值出现时刻逐渐推迟. 当毛细管内径为1和3 mm时, 等离子体密度存在二次增长时刻, 这意味着二次羽流建立过程的存在. 随着放电腔体的增大, 等离子体密度变化曲线更加连续, 二次羽流建立过程消失.
根据不同内径下等离子体温度和密度的变化曲线规律分析可知, 增大毛细管腔体内径主要影响了等离子体电热加速过程. 毛细管腔体内径的增加, 将使得加速过程滞后于放电和烧蚀过程, 电弧沉积能量作用于加速过程的比例降低, 使得推力器等离子体喷射速度下降, 元冲量减小, 比冲降低, 总体效率下降.
图11为不同毛细管长度时, 推力器羽流等离子体电子温度和密度的变化曲线. 其中主电容容值2.5 μF, 充电电压2.0 kV, 单次放电能量5 J, 毛细管内径为5 mm. 随着毛细管长度的增加, 等离子体羽流电子温度峰值呈现下降趋势. 由于工质腔体内部表面积与腔体长度成正比, 增大腔体长度时使得工质与电弧接触面积增大, 烧蚀质量增加. 然而, 一定程度上增大的腔体容积减弱了热膨胀效果, 使得电子温度峰值时刻逐渐滞后. 从图11中可以看到, 电子温度变化曲线仅在羽流起始过程存在差异, 随着放电过程的进行, 弧道阻性分量电功率差距逐渐减小, 等离子体温度较为接近.
图 11 不同长度下羽流等离子体　(a) 等离子体温度; (b) 等离子体密度
Figure11. The plasma temperature (a) and plasma density (b) of CDPPT plasma plume with different cavity length.

图11(b)显示了等离子体密度的变化趋势, 可以看到, 毛细管长度的增加对等离子体密度的影响主要包括两个方面. 首先, 增加放电腔体的长度可以在一定程度上增大等离子体密度峰值, 这也对应了逐渐增大的烧蚀质量. 由于等离子体喷射需要足够的压力梯度, 腔体长度的增加推迟了密度峰值出现的时刻. 其次, 随着腔体长度的增加, 等离子体密度到达峰值后衰减速率减慢, 对应ICCD图像可以发现, 当采用较长毛细管腔体时, 等离子体羽流可持续更长时间, 且其喷射过程更为稳定, 不再存在二次建立过程.
结合不同毛细管长度对等离子体参数的影响规律分析可知, 增大放电腔体长度可以提高烧蚀质量, 延长推力器推力持续时间, 增加推力器输出元冲量. 然而, 由于持续产生推力过程中, 较长放电腔体内压力梯度建立所需时间更长, 使得等离子体加速效率降低, 在一定程度上降低等离子体喷射速度, 不利于比冲和总体效率的提高.

毛细管推力器工作时, 电容器储存电能量转化为等离子体弧道内能, 进一步转化为等离子体的喷射动能. 当推力器放电起始后, 由于回路传输线阻抗的存在, 其焦耳热将产生传输损耗. 随着放电电流的逐渐增大, 弧道沉积能量增大, 等离子体温度升高. 毛细管管壁在热辐射的作用下, 温度逐渐升高, 烧蚀过程建立. 推力器工作时, 部分能量将以光辐射形式耗散, 因此放电腔体外部可观察到较为强烈发光. 此外, 由于腔体压强的增大, 部分烧蚀产物回流至工质管壁, 无法对等离子体喷射过程产生贡献. 研究表明, 放电阶段的能量损耗中, 辐射损耗与烧蚀粒子回流损耗相比可近似忽略^[14]. 在推力器工作过程中, 由于烧蚀过程所消耗的能量无法直接测量, 需要进行估算. 烧蚀过程消耗能量与材料分解和相变所需能量有关, 可用(13)式表示^[26,27]

$ {E_{{\rm{ablation}}}} = {E_{\rm{d}}} + {E_{\rm{f}}} , $

式中, E_ablation 为单位工质烧蚀所需能量; E_d 为工质分解耗能; E_f 为工质相变耗能. 结合材料热重分析特性, E_ablation主要取决于材料物性参数. 以PTFE为例, E_ablation约为1.5 × 10⁶ J/kg. 当放电能量为6.25 J时, 单次烧蚀质量约为100 μg, 烧蚀过程消耗能量约为0.15 J, 约占单次放电能量的2.4%. 可见, 在推力器工作过程中, 用于加热管壁的能量消耗较小, 绝大部分注入能量用于工质电离、加热和加速阶段. 尽管烧蚀过程消耗能量较小, 但是其决定了等离子体产生与腔体内部压力等状态参数及匹配状态, 影响了电热加速过程. 随着管壁烧蚀不断持续, 腔体内压力的增大, 等离子体在压强梯度作用下向喷口处加速运动. 在电热加速过程中, 由于黏滞阻力的存在, 将会使等离子体损失部分动能. 此外, 当毛细管腔体喷射等离子体进入喷嘴后, 在理想条件下, 等离子体将产生绝热膨胀, 使其内能逐渐转化为动能继续产生加速效果. 然而实际情况中, 由于等离子体在喷嘴滞留时间较短, 其内能无法充分释放, 将产生冻结流损耗^[28,29], 不利于推力器总体效率的提高.
由图12(a)可以看到, 当放电电压增加时, 能量传递效率略有下降, 但基本维持在较小范围内波动, 推力器总体效率主要受等离子体加速效率的制约. 当放电电压从1 kV增加至2 kV时, 随着放电能量的增加, 腔体内压强不断增大, 等离子体电热加速效果增强, 使得推力器推力效率不断提高. 然而, 由于放电腔体中压强的提高, 烧蚀过程中产生的粒子回流比例也不断增大, 制约了推力效率随放电能量的进一步提高. 增大毛细管管径时, 能量传递效率显著降低, 导致推力器总体效率明显下降. 对于推力效率而言, 随着内径的增加, 在压强梯度和黏滞阻力的相互制约下, 推力效率呈现先增大后减小的变化趋势. 内径变化时, 能量传递效率和推力效率的变化共同制约了推力器能量传递效率的变化. 图12(b)为腔体长度对效率的影响规律. 放电腔体长度的增加使得弧道等效阻抗增加, 有利于提高能量传递效率. 等离子体在放电腔体中进行加速时, 随着作用距离的增大, 将具有更大的出口速度, 因此当毛细管内径从14 mm增加至18 mm时, 加速效率不断提高. 当进一步增加放电腔体长度时, 由于单位面积烧蚀质量的减小和粘滞阻力的增大, 等离子体加速效率将不断减小. 结合实验结果来看, 改变腔体长度时, 推力器总体效率主要受加速效率的制约.
图 12 推力器能量效率　(a) 不同长度; (b) 不同内径
Figure12. The CDPPT thrust efficiency and transfer efficiency with different (a) cavity length and (b) different cavity diameter.

以上分析表明, 提高推力器总体效率需要从能量沉积效率和加速效率两方面入手. 能量传递效率主要取决于弧道等效阻抗与外回路阻抗比值, 推力器应进行紧凑化设计较小回路阻抗. 减小充电电压, 增大放电腔体长度, 减小内径均有利于提高能量传递效率. 烧蚀粒子回流损耗与烧蚀过程有关, 放电能量的增加会提高加速效率, 但增大的腔体压强会增大烧蚀产物回流, 这在一定程度上制约了推力器加速效率的上限. 较小的电流幅值下, 对应较低的等离子体温度, 能够降低辐射损耗, 其主要受限于放电电压. 此外, 为了降低冻结流损耗, 还需要对喷嘴的结构进行优化设计.

本文系统开展了不同腔体结构参数下推力器放电特性、烧蚀特性、推力特性和等离子体羽流参数的变化规律研究. 实验表明, 减小毛细管腔体内径、增大腔体长度, 使等离子体等效电阻增大, 有利于提升弧道沉积能量, 提升能量传递效率; 但腔体内径1 mm时, 会出现熄弧, 电容储能无法完全释放. 腔体内径从1 mm增加至3 mm时, 平均等效单次烧蚀质量显著减小, 进一步增大腔体直径烧蚀质量维持基本不变; 腔体内径增加, 烧蚀质量增大, 但单位面积烧蚀质量降低. 毛细管推力器总体效率受回路能量传递效率和加速效率的共同制约. 增大腔体内径显著降低能量传递效率, 增大腔体长度主要影响推力器加速效率. 综合不同腔体结构参数下输出结果, 推力器原理样机在单次放电能量5 J, 毛细管长度为16 mm, 内径3 mm达到较优性能参数, 可输出元冲量350.79 μN·s, 比冲531.10 s, 总体效率为18.26%. 下一步工作将进一步完善等离子体羽流诊断方法, 从羽流粒子组分和速度分布角度, 分析推力器能量耦合传递对推力器工作特性的影响机制.