摘要:测试质量是空间引力波测量的核心传感器, 宇宙线高能粒子能够穿透航天器屏蔽对其造成电荷注入, 进而产生库仑力和洛伦兹力噪声对引力波科学探测造成严重影响. 本文采用蒙特卡洛仿真方法, 探究了不同宇宙线高能粒子对测试质量的充电过程和机制. 研究结果表明, 在同一能谱下随着截止能量的降低充电速率逐步增大, 充电速率变化约为9%; 太阳活动极小年时测试质量的充电速率为39.5 +e/s, 其中贡献最大的质子占比约为83.16%, 太阳活动极大年时测试质量的充电速率约为12.5 +e/s, 1989年最恶劣的太阳高能粒子事件造成测试质量的充电速率约为120700 +e/s; 在太阳活动极小年时, 银河宇宙线各成分的充电速率取决于各成分的初级粒子在测试质量中的沉积, 其中初级粒子贡献占测试质量总充电速率的73%; 太阳活动极小年时, 质子的充电贡献主要来自能量为0.1—1 GeV的区间, 占比约为65%. 研究结果可用于评估测试质量在轨充电规律, 为电荷管理的设计和在轨工作提供依据.
关键词: 引力波/
测试质量/
宇宙线/
GEANT4

English Abstract

全文HTML

--> --> -->

引力波是爱因斯坦广义相对论中非常重要的一个预言, 探测空间引力波不仅是对爱因斯坦广义相对论直接精确的检验, 也对物理学和天文学等基础学科未来的发展有着十分重大的作用和意义^[1,2]. 实现空间引力波探测的核心设备是测试质量, 测试质量位于航天器的望远镜筒内. 航天器在深空环境中航行时, 空间环境中的宇宙线高能粒子能够穿透航天器屏蔽入射到测试质量, 导致测试质量带电. 带电后的测试质量在电极库仑力或者磁场洛伦兹力的干扰下, 产生加速度噪声对引力波科学探测造成严重影响. 欧洲和美国的研究人员利用蒙特卡洛模拟仿真工具GEANT (geometry and tracking)对LISA(laser interferometer space antenna)测试质量的充电速率进行了仿真模拟评估^[3-8], 由于其考虑的几何模型、银河宇宙射线(galactic cosmic rays, GCR)通量和截断能量的不同, 计算得到太阳活动极小年时GCR对测试质量的充电速率为11–52 +e/s. 利用另一款蒙特卡洛仿真软件FLUKA(Fluktuierende Kaskade)对LISA简化几何模型的充电模拟也有很大的进展^[9], 得到太阳活动极小年能量0.1—1000 GeV宇宙线质子的充电速率为37 +e/s(截断能量为1 keV). 国内的研究者主要是针对单航天器激光天文动力学空间计划(astrodynamical space test of relativity using optical devices, ASTROD)利用GEANT4开展测试质量的充电机制模拟, 仿真模拟了太阳活动极小年时高能宇宙射线入射简化等效几何和相对复杂完整几何模型中的充电速率^[10,11], 得到太阳活动极小年时充电速率为24.2 +e/s和33.3 +e/s(截断能量为250 eV). Grimani等^[12]和Wass等^[13]针对LISA Pathfinder, 利用相同的简化模型仿真模拟的充电速率为38.2 +e/s和43.7 +e/s, 在轨充电速率为TM1: 22.9 +e/s; TM2: 24.5 +e/s^[14]. 虽然国内外的研究者对测试质量的充电速率已经开展了较多的研究, 但是对于不同截断能量阈值对充电速率影响、不同宇宙线的充电能力和初、次级粒子充电速率占比、同一粒子不同能量段的充电贡献等方面的研究尚不完善.
本文依据LISA航天器建立几何模型, 仿真采用CREME96模型计算得到的GCR能谱, 利用粒子传输仿真工具GEANT4进行模拟. 为了揭示宇宙线不同种类、不同能量粒子对测试质量的充电机制与规律. 对不同截断长度下测试质量充电影响进行评估. 针对测试质量在太阳活动极小年、太阳活动极大年时能量大于100 MeV/n的质子、氦核(³He和⁴He)和C, N, O等粒子进行充电模拟, 对1989年太阳高能粒子(solar energetic particle, SEP)事件也进行了充电模拟. 太阳极小年时对宇宙线各粒子的初、次级粒子充电率贡献以及质子在不同能量段的充电率贡献进行仿真模拟.

2

-->

2.1.几何建模

针对引力波探测中测试质量的充电机制与规律进行仿真模拟, 对LISA的复杂航天器结构模型进行简化^[15]. LISA航天器整体模型和惯性传感器模型如图1所示.
图 1 LISA航天器模型　(a)整体模型; (b)惯性传感器模型
Figure1. LISA spacecraft model: (a) Overall model; (b) inertial sensor model.

本文简化的等效航天器模型如图2所示, 模型包括: 测试质量(test mass, TM), 为边长46 mm的立方体; 钼电极(Mo), 为内边长74 mm、外边长为86 mm的立方体壳层; 钛室(Ti), 为内半径长75 mm、外半径长80 mm的球壳层; 碳外壳(C)(航天器其它结构如电池、望远镜筒和支架等), 为内半径长80 mm、外半径长100 mm的球壳层; 测试质量(TM)与钼电极(Mo)之间和钼电极(Mo)与钛室(Ti)之间的区域均为真空, 具体航天器几何尺寸和材料如表1所列. 在本文的模拟中, 真空的密度为1.0 × 10^–25 g/cm³, 设置宇宙线粒子是从一个半径为120 mm的球面上各项同性均匀地入射到整个航天器模型.
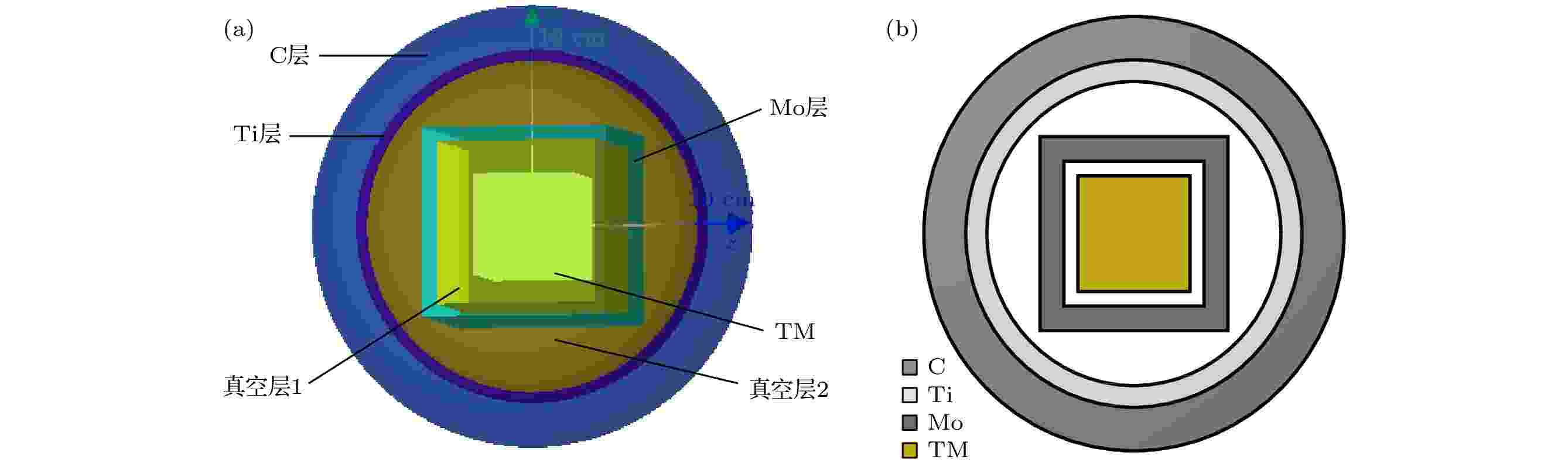图 2 本文航天器模型图　(a) geant4模型图; (b)模型平面示意图
Figure2. The spacecraft model diagram in this paper: (a) Geant4 model diagram; (b) schematic diagram of the model plane.

名称	组成成分	密度/(g·cm–3)	尺寸	厚度/mm
测试质量	Au(70%); Pt(30%)	19.837	46 mm立方体	—
钼电极	Mo	10.28	74—86 mm立方体壳层	6
钛室	Ti	4.54	75—80 mm球壳层	5
碳外壳	C	2.10	80—100 mm球壳层	20

表1航天器几何尺寸和材料构成
Table1.Spacecraft geometric dimensions and material composition.

2 -->

2.2.辐射环境

引力波探测航天器在类地球轨道绕太阳飞行^[16], 将受到GCR和SEP的轰击, 导致测试质量带电. GCR能谱随太阳周期的变化强度会有所不同, 在太阳极小年GCR的通量最高. 在太阳极小年, GCR能谱组成为: 大约90%的质子、8%的氦核(³He和⁴He), 1%的重核和1%的电子. 本文主要考虑太阳极小年通量相对较大的质子、氦核(³He和⁴He)和C, N, O等粒子和太阳极大年质子、氦核(³He和⁴He)以及对于典型的1989年SEP峰值能谱进行充电机制仿真分析.
利用CREME96模型计算得到太阳活动极大、太阳活动极小年距太阳1AU处各粒子的能谱如图3所示, 1989年9月29日的SEP峰值能谱通量如图4所示. 由于只有大于100 MeV/n的粒子才能穿透航天器测试质量外围的屏蔽, 故只考虑能量大于100 MeV/n的粒子. CREME96模型计算得到的宇宙线能谱数据没有区分³He和⁴He, 需要对宇宙线He能谱进行参数化. 针对³He/⁴He比例C的测量试验已经获得比较准确细致的结果^[17-20], 表2和表3中展示了太阳活动极大年参数C(M)、太阳活动极小年参数C(m)的值^[21], 根据公式由³⁺⁴He的通量可以分别得到³He和⁴He的通量^[22,23]:
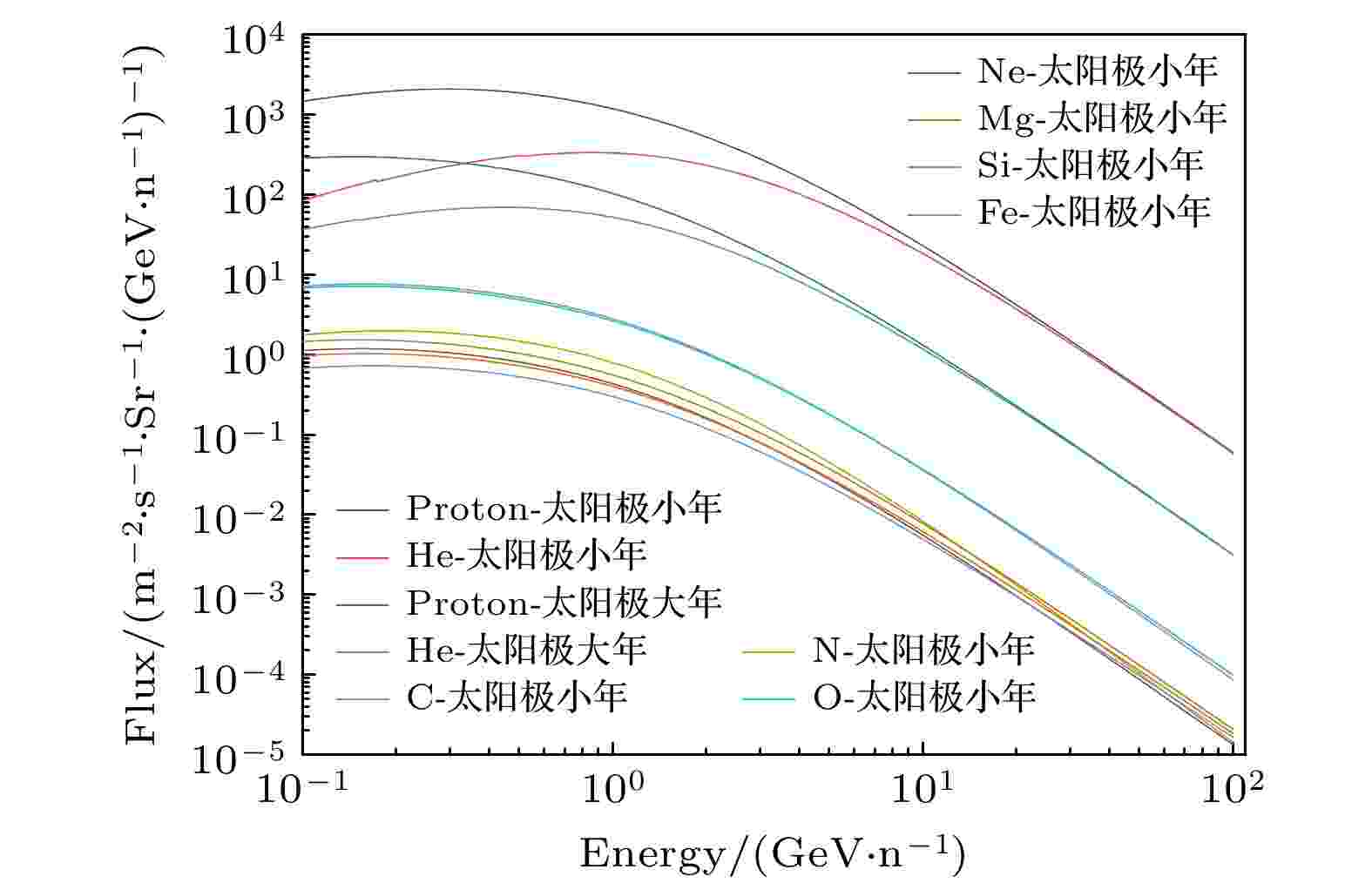图 3 1 AU处GCR各粒子微分能谱
Figure3. Differential energy spectra of each element of GCR at 1 AU.

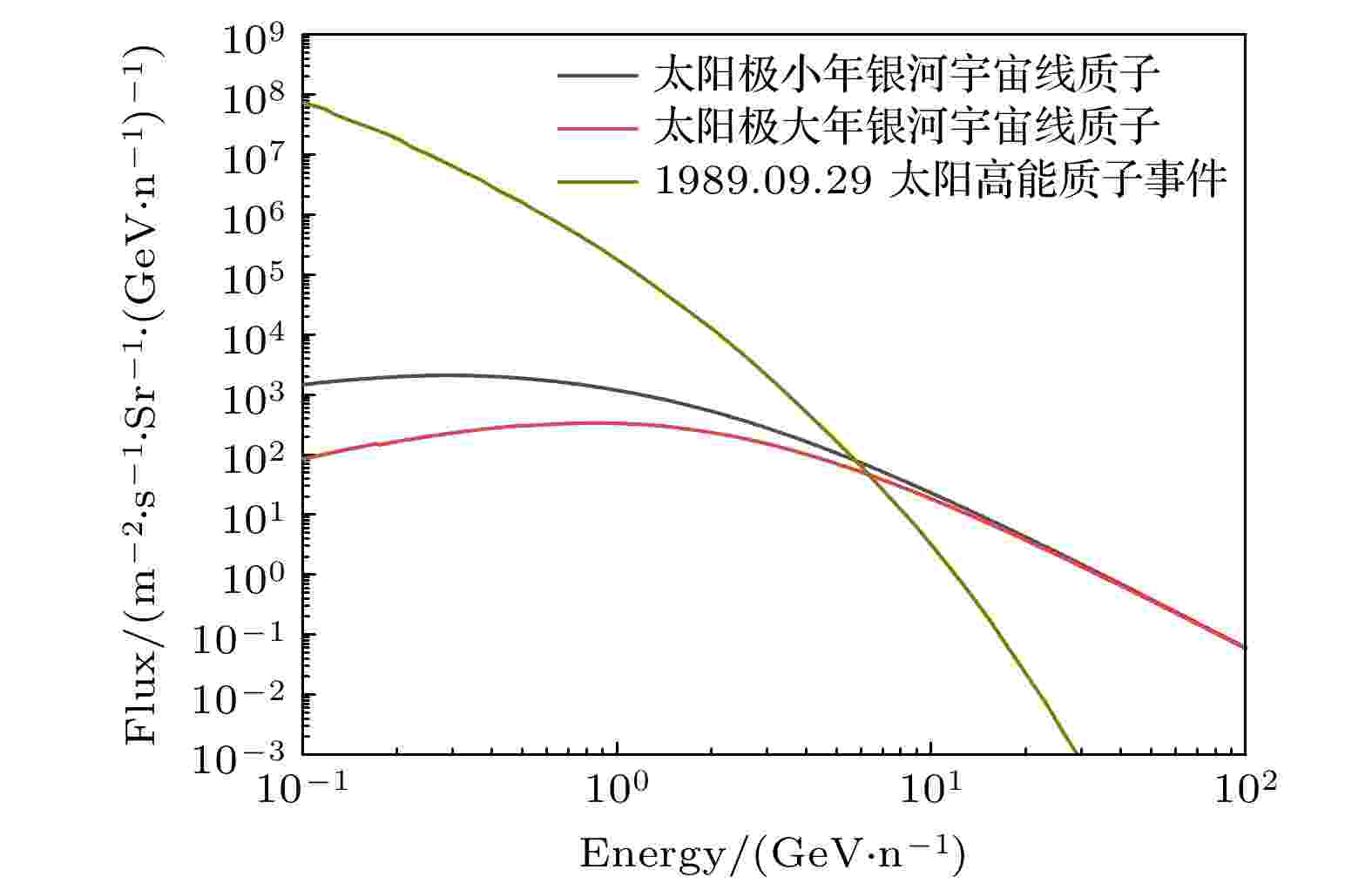图 4 1AU处1989年SEP微分能谱
Figure4. 1989 SEP differential energy spectra at 1AU.

E/(GeV·n–1)	0.10 ≤ E ≤ 0.36	0.36 ≤ E ≤ 1.00	1.00 ≤ E ≤ 1.40	E > 1.40
C(m)	0.335 × E0.569	0.187	0.187 × E0.491	0.22

表2太阳极小年³He/⁴He的参数化比例C(m)
Table2.The parameterized ratio C(m) of ³He/⁴He in solar minimum.

E/(GeV·n–1)	0.10 ≤ E ≤ 0.30	0.30 ≤ E ≤ 0.80	0.80 ≤ E ≤ 2.50	E > 2.50
C(M)	0.239 × E0.538	0.125	0.140 × E0.496	0.22

表3太阳极大年³He/⁴He的参数化比例C(M)
Table3.The parameterized ratio C(M) of ³He/⁴He during solar maximum.

$ F(^3{\rm{He}}) = C/(1 + C)F({}^{3 + 4}{\rm{He}}) , \tag{1a}$

$ F({}^4{\rm{He}}) = 1/(1 + C)F({}^{3 + 4}{\rm{He}}) , \tag{1b}$

其中C为³He与⁴He的比例; F的单位为m^–2·s^–1·Sr^–1·(GeV/n)^–1.
根据表2和表3太阳活动极大、极小年的参数化³He/⁴He比例C, 代入³He和⁴He的通量计算公式(1a)式和(1b)式中, 结合由CREME96模型计算得到的³⁺⁴He的通量, 计算得到太阳活动极大、太阳活动极小年³He和⁴He的通量, 如图5所示.
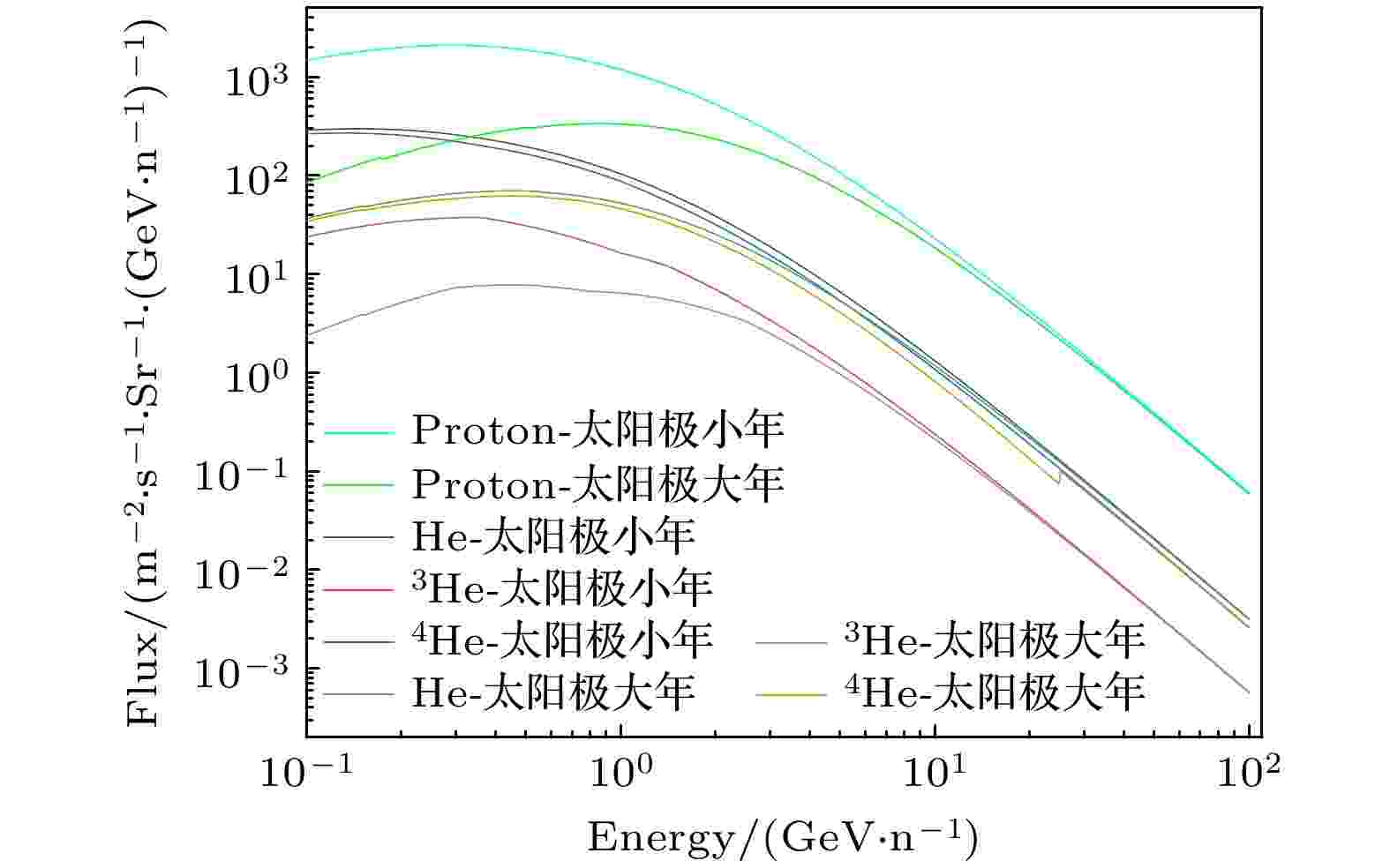图 5 宇宙线Proton和He(³He和⁴He)微分能谱
Figure5. Differential energy spectra of cosmic rays Proton and He (³He and ⁴He).

2 -->

2.3.物理模型

GCR和SEP的高能性和强子性意味着入射到航天器中会与航天器材料发生复杂的物理过程, 并产生大量次级带电粒子. 将这些次级带电粒子追踪到尽可能低的能量, 就能更加准确的模拟测试质量的充电过程. 本文利用GEANT4模拟包含从数百eV到TeV能量范围的物理模型, 并且对每个粒子和它产生的所有次级粒子进行全程跟踪. 不同种类和能量的粒子与相应物理过程紧密联系, 考虑的物理过程为: 低能电磁过程、强子过程、衰变过程和光核过程, 随着粒子能量的增高与其对应的物理过程也不断变化. 对于低能电磁过程, GEANT4默认电磁过程次级粒子(e^–, e⁺, γ)产生最低阈值为250 eV(对应的截断长度约为50 nm), 低于这个能量的粒子将不再进行跟踪.

2

-->

3.1.GEANT4不同截断长度的充电模拟

在GEANT4中, 电磁过程产生次级粒子的最低阈值为250 eV. 本文利用太阳活动极小年质子能谱对不同截断长度下的测试质量充电率进行模拟计算, 当50万质子入射航天器模型, 分别得到截断长度为1 mm, 100 μm, 10 μm, 1 μm, 100 nm和50 nm时的充电速率, 如图6所示.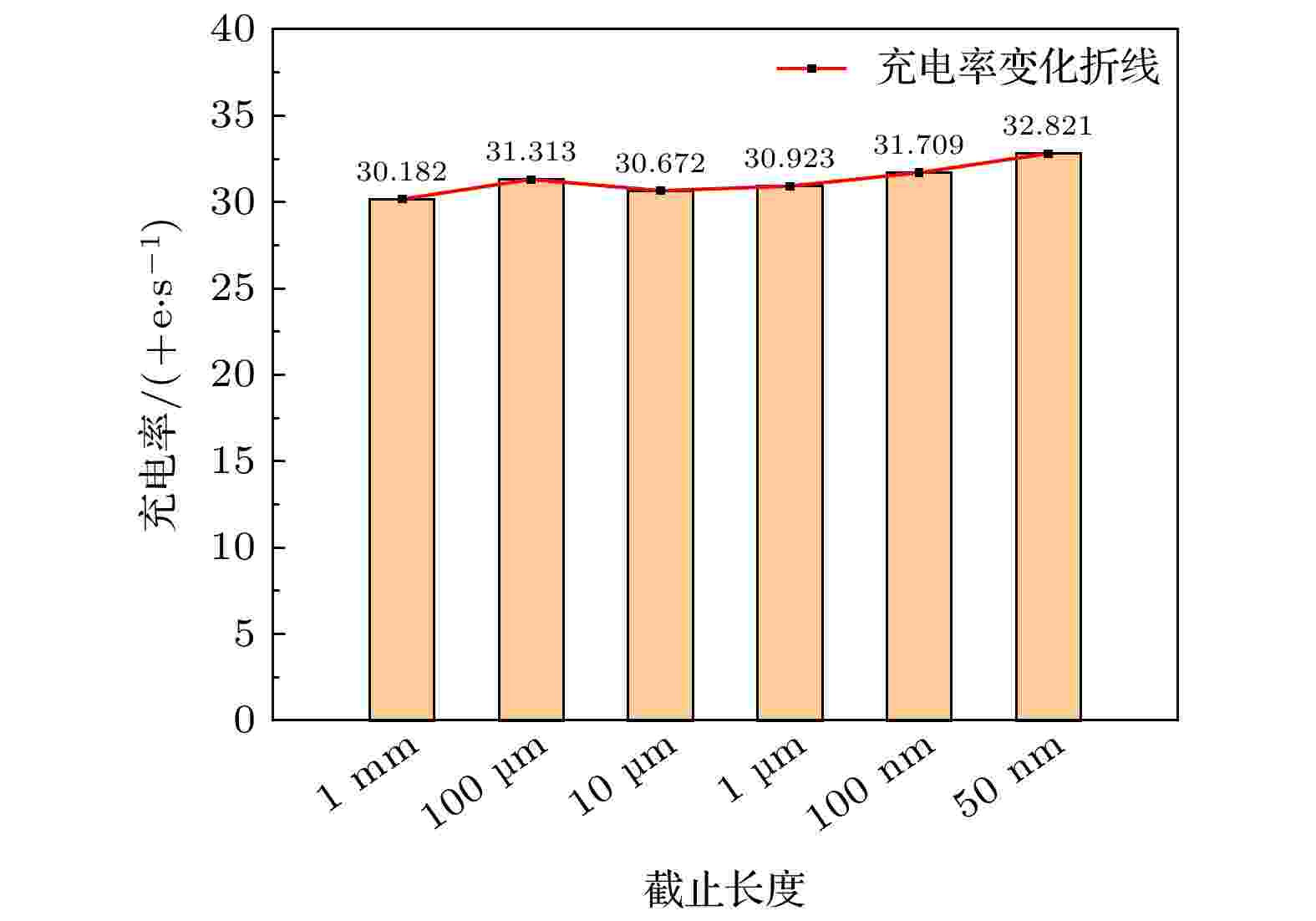
图 6 不同截断长度的充电速率
Figure6. Charging rate with different cut-off lengths.

如图6所示, 不同截断长度对太阳活动极小年质子的充电速率会产生影响, 总体来说, 截断长度越低(次级粒子产生的能量阈值越低)模拟得到的充电速率会越高. 在截断长度为50 nm时充电速率最大, 为32.821 +e/s. 随着截断长度的减小, 截断长度从1 mm减小到50 nm充电率增长了8.74%. 表明截断长度的变化不会显著的影响测试质量的充电速率.
2 -->

3.2.太阳活动极大、极小年GCR和SEP的充电模拟

在太阳活动极小年下, 仿真模拟的宇宙线Proton, ³He, ⁴He, C, N, O, Ne, Mg, Si和Fe粒子的参数如表4所列, 获得这些粒子入射到航天器后造成测试质量的充电速率如图7所示. 因为C, N和O等重离子在银河宇宙线总的通量占比仅为1%, 与Proton, ³He和⁴He相比可以忽略, 导致各重离子入射航天器得到测试充电率非常小, 所以在太阳极大年将不考虑重离子的贡献, 仅考虑Proton, ³He和⁴He对充电率的贡献. 在太阳活动极大年下, 仿真模拟的宇宙线Proton, ³He和⁴He粒子的参数如表5所列, 获得这些粒子入射到航天器后造成测试质量的充电率分布如图7所示.

粒子种类	粒子数目/个	暴露时间/s	积分通量/(cm–2·s–1)
Proton	700000	353.65	4.375
3He	100000	3563.35	0.062
4He	120000	806.26	0.329
C	100000	21052.63	0.0105
N	100000	77561.47	0.00285
O	100000	22128.79	0.00999
Ne	10000	13644.98	0.00162
Mg	10000	10476.25	0.00211
Si	10000	14542.70	0.00152
Fe	10000	19562.20	0.00113

表4太阳极小年宇宙线主要粒子仿真参数
Table4.The main particle simulation parameters of cosmic rays during solar minimum.

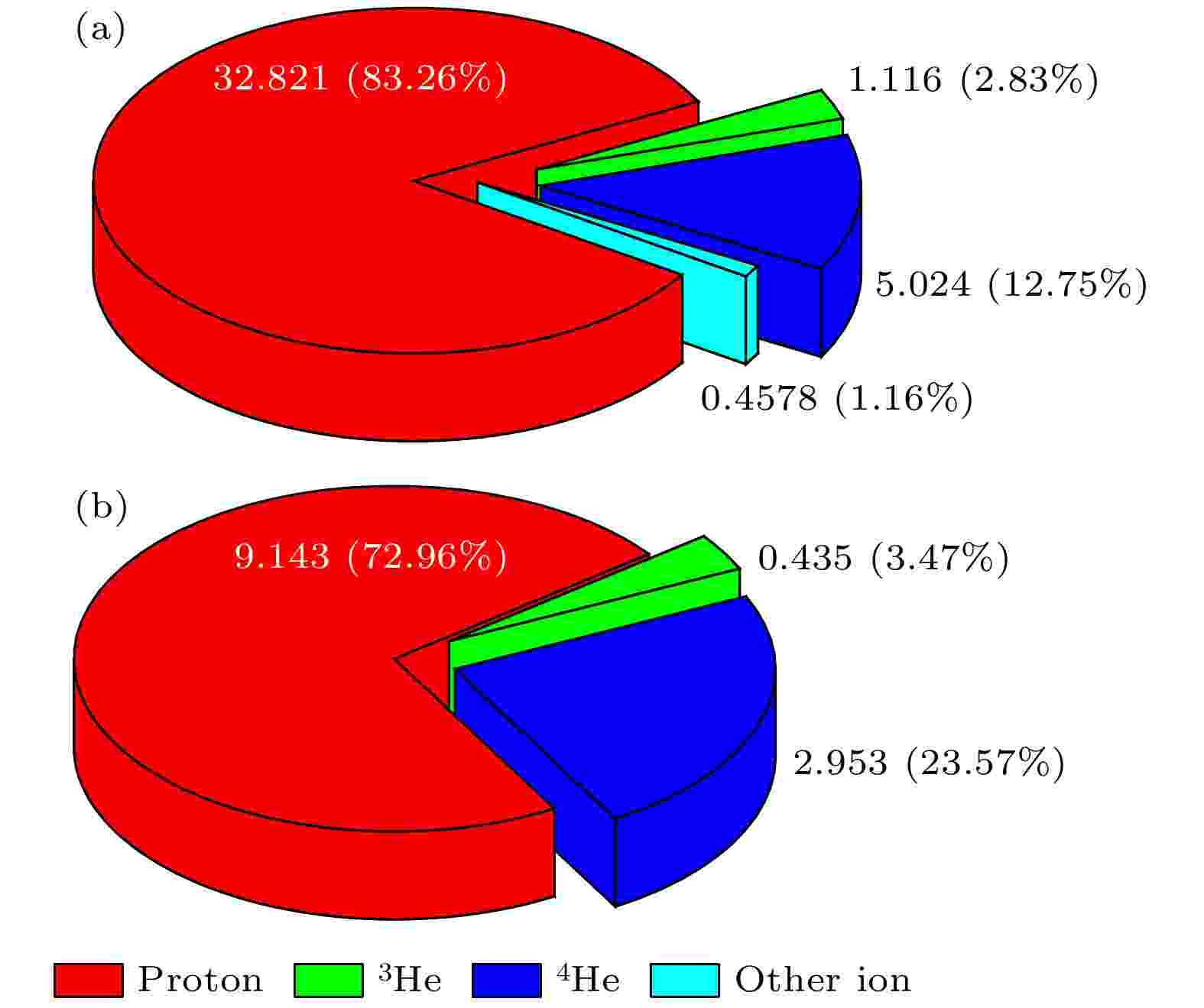图 7 宇宙线各粒子的充电率　(a) 太阳活动极小年; (b) 太阳活动极大年
Figure7. The charging rate of each particle of cosmic rays: (a) Solar minimum year; (b) solar maximum year.

粒子种类	粒子数目/个	暴露时间/s	积分通量/(cm–2·s–1)
Proton	700000	353.65	4.375
3He	100000	3563.35	0.062
4He	120000	806.26	0.329

表5太阳极大年宇宙线主要粒子仿真参数
Table5.The main particle simulation parameters of cosmic rays during solar maximum.

如图7所示, 在太阳活动极小年银河宇宙线各粒子入射的总充电速率为39.469 +e/s: 入射Proton的充电速率为32.821 +e/s; 入射³He的充电速率为1.166 +e/s; 入射⁴He的充电速率为5.024 +e/s; 入射其它重离子的充电速率为0.458 +e/s. 其中质子充电率占比83.16%; ³He的充电率占比为2.95%; ⁴He的充电率占比为12.73%; 其它重离子的充电率占比为1.16%. 在太阳活动极小年, Proton的充电速率贡献占主导地位, 质子和⁴He的充电速率贡献占总充电速率的95.89%, 其他重离子的贡献仅占充电率的1.16%, 可以忽略.
在太阳活动极大年银河宇宙线各主要贡献粒子入射的总充电速率为12.531 +e/s: 入射Proton的充电速率为9.143 +e/s; 入射³He的充电速率为0.435 +e/s; 入射⁴He的充电速率为2.953 +e/s. 太阳活动极大年的总充电率为太阳极小年(GCR最恶劣情况)的三分之一. 其中质子充电率占比72.96%; ³He的充电率占比为3.47%; ⁴He的充电率占比为23.57%. 可以看到, 太阳活动极大年质子的充电率贡献占比最大, 质子和⁴He的充电速率贡献占总充电速率的96.53%.
1989年9月29日SEP峰值能谱模拟仿真参数如表6所列, 模拟了能量范围为0.1—30 GeV的太阳质子. 仿真得到在1989年9月29日的太阳爆发极端环境下的充电速率为120700 +e/s, 是太阳活动极小年时充电率的3000多倍. 对于零星发生的SEP事件, 对航天器造成极大的充电风险, 极短的时间内就会达到引力波探测能忍受的最大加速度噪声.

粒子种类	粒子数目/个	暴露时间/s	积分通量/(cm–2·s–1)
Proton	500000	0.150	7385.53

表61989年9月29日太阳高能粒子事件仿真参数
Table6.Simulation parameters of the SEP event on September 29, 1989.

2 -->

3.3.太阳活动极小年GCR初、次级粒子贡献和充电能力模拟

在太阳活动极小年, 计算了银河宇宙线各粒子入射航天器产生的初、次级粒子造成的测试质量充电速率, 如表7所列. 宇宙线各粒子的初级粒子充电速率比例都占总充电率的60%以上(除通量过小的Fe). 对于充电率贡献最大的质子和⁴He, 初级粒子充电率占比分别为67.07%和100%. 所有宇宙线的初级粒子充电率占比为72.86%, 表明测试质量充电速率的主要贡献来源于初级粒子直接沉积在测试质量中.

粒子 种类	初级粒子充电 率/(+e·s–1)	次级粒子充电 率/(+e·s–1)	初级粒子 充电率占比
Proton	22.016	10.805	67.07%
3He	1.196	–0.029	100%
4He	5.125	–0.100	100%
C	0.182	0.023	88.78%
N	0.042	0.009	82.35%
O	0.123	0.020	86.01%
Ne	0.0132	0.0026	83.54%
Mg	0.0137	0.0064	68.16%
Si	0.0087	0.0058	60%
Fe	0	0.0084	0%

表7宇宙线初、次级粒子造成的充电率
Table7.Charge rate caused by primary and secondary particles of cosmic rays.

如图8所示, 在太阳活动极小年, 模拟计算得到宇宙线各粒子的充电能力. 值得注意的是, 在初级宇宙线中占比为8%的He(³He和⁴He), 贡献了总充电率为15.68%; 在初级宇宙线中占比为1%的重粒子, 贡献了总充电率的1.16%. 针对ASTROD I也有类似的结果^[11]. 这是由于银河宇宙线入射航天器测试质量的充电能力不同(各粒子的电离能力和射程的不同), ⁴He充电能力约为质子的2倍, 重粒子的充电能力基本都大于质子的充电能力.
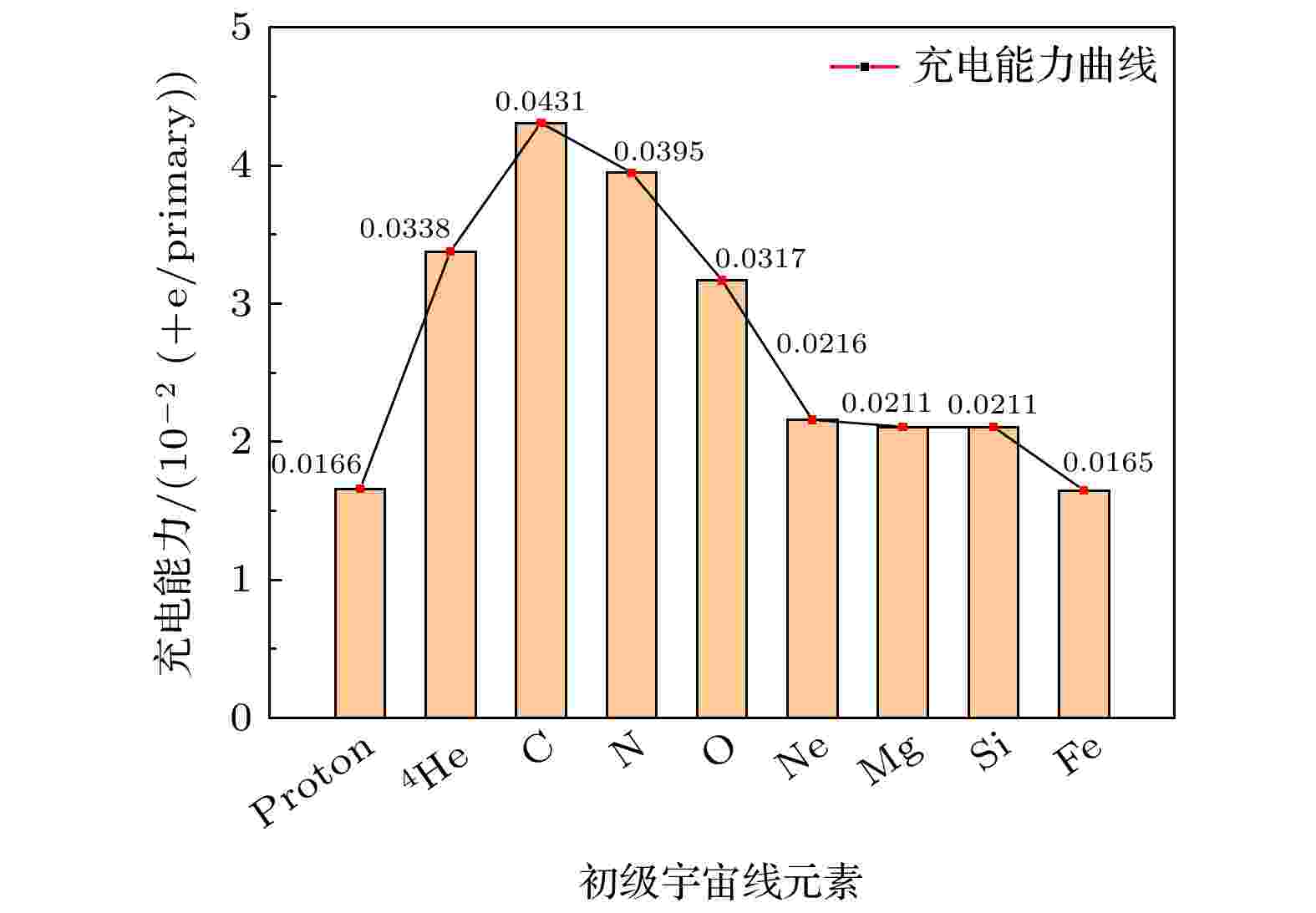图 8 宇宙线各粒子的充电能力
Figure8. The charging ability of each particle of the cosmic ray

2 -->

3.4.太阳活动极小年GCR质子不同能量段的充电模拟

在太阳活动极小年, 仿真模拟从0.1—100 GeV范围内不同能量的银河宇宙线质子各向同性入射到航天器模型, 对于每个单能点仿真模拟10000个事例(其它条件与能谱仿真时保持相同), 得到了不同能量质子的充电能力(单个粒子入射造成的测试质量净充电个数). 如图9所示, 能量为200 MeV时充电能力有峰值0.0498 +e/primary, 在高能部分(大于10 GeV)充电能力迅速增大为另一个峰值0.2077 +e/primary.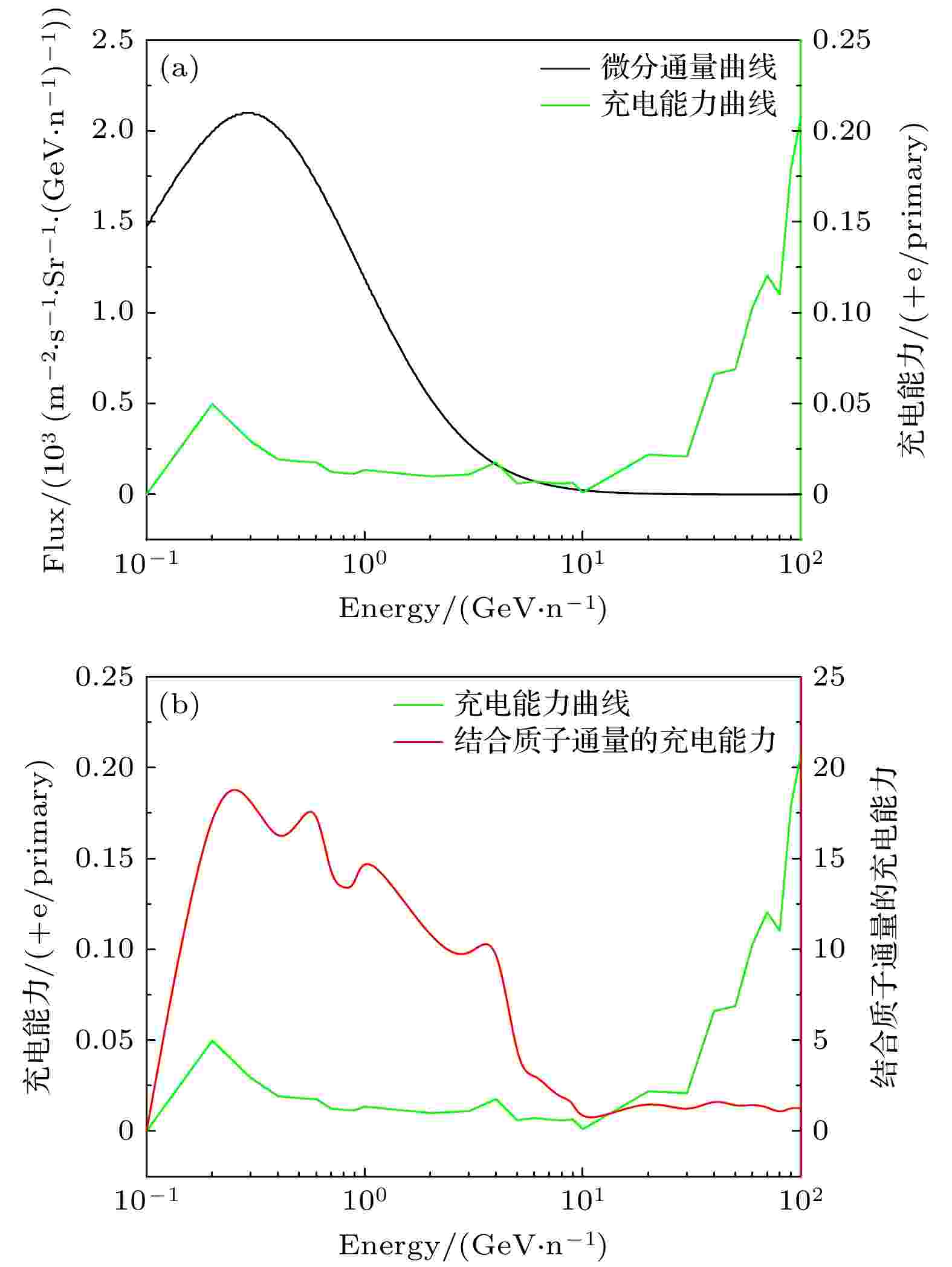
图 9 太阳活动极小充电能力　(a) 不同能量充电能力和质子通量; (b) 充电能力和结合质子通量的总充电比例
Figure9. Solar minimum charging capacity: (a) Different energy charging capacity and proton flux; (b) charging capacity and total charge ratio of combined proton flux.

结合太阳活动极小年时入射的质子能谱, 可以得到对于太阳极小年不同能量的初级宇宙线质子对测试质量充电的贡献. 设仿真模拟的粒子数为N₀, 测试质量的净充电个数为N, 充电能力为C_A, 充电率为C_R, 各能量点质子的微分通量为F, 各向同性粒子出射的半径为R.

$ {C_{\rm{A}}} = N/{N_0} , \tag{2a}$

$ {C_{\rm{R}}} = \frac{N}{{{N_0}/\pi {R^2} \cdot F}} .\tag{2b} $

由(2a)式和(2b)式可到:

$ {C_{\rm{R}}} = {C_{\rm{A}}} \times {\rm{π }}{R^2} \cdot E \cdot F , $

其中E为质子的能量, 单位为GeV.
由(2a)式和(2b)式得到(3)式, 可以反应不同能量下的充电率贡献. 结合质子能谱的初级宇宙线质子对测试质量充电的贡献如图9所示, 充电能力峰值的高能部分由于能谱通量远低于低能部分, 导致最终的充电率贡献很低. 计算可以得到, 在能量区间0.1—10 GeV内, 对测试质量充电的占比约为94%. 在能量区间0.1—1 GeV, 对测试质量充电的占比约为65%. 仿真结果可为在轨粒子探测器的设计提供依据.

本文使用Geant4全面仿真了引力波探测航天器在距太阳1 AU处受到宇宙线高能粒子的轰击导致测试质量充电的规律. 本文的仿真计算考虑了更为全面的初级和次级粒子、更低的能量阈值, 与LISA探路者飞行试验结果相吻合, 可为后续引力波探测任务中在轨电荷实时监测、预报和管理提供重要依据. Grimani 等^[12]利用Fluka仿真模拟了参数化的太阳极大、极小年质子和氦核能谱注入LISA探路者相对复杂几何模型中的充电率, 得到太阳极大年充电率为15.13 +e/s, 太阳极小年充电率为38.2 +e/s. 该结果与本文的研究结果高度一致, 但是由于Fluka软件的最低截断能量为1 keV和Grimani 等^[12]使用的能谱为参数化能谱, 进而会造成一定的误差. Araújo 等^[15]利用Geant4仿真模拟了LISA模型在太阳极大、极小年测试质量的充电率, 但此工作中没有考虑到e⁺在测试质量中的沉积, 最终得到太阳极大年充电率为23.7 +e/s, 太阳极小年充电率为49.9 +e/s, 而本文全面地考虑3—20号元素、proton, ³He, ⁴He, e^–, e⁺、氘、氚和正负π介子, 更综合地分析了测试质量的充电情况. 空间验证试验结果也证明了本文仿真模拟的正确性, LISA探路者作为LISA的验证计划于2015年发射, 已经得到其上搭载的2个测试质量的充电率, TM1和TM2的充电率分别为22.9 +e/s和24.5 +e/s^[14], 此次的测量是在太阳极小前3—4年, 测试质量的充电率在本文仿真的预期范围内12.531—39.469 +e/s. 在此基础上, 本文进一步研究分析了典型SEP充电率、太阳活动极小年银河宇宙线的初级粒子充电率占比以及太阳活动极小年银河宇宙线质子在不同能量区间的充电率贡献. 研究表明典型SEP峰值能谱通量下的充电速率为120700 +e/s, 认为零星发生的SEP事件对航天器造成极大的充电风险, 太阳活动极小年银河宇宙线的初级粒子充电率占比最大, 针对太阳活动极小年测试质量总充电贡献占比最大的银河宇宙线质子, 其低能部分充电率贡献较大.
本文仿真方法更切合实际地模拟分析了宇宙线高能粒子对测试质量的充电率, 更进一步研究了太阳极小年各银河宇宙线粒子的充电率贡献以及对银河宇宙线质子在不同能量区间的贡献. 此项工作可以讨论由于测试质量充电而引起的加速度噪声和它的频谱分析, 以及对未来引力波探测计划中粒子探测器的粒子探测种类和能量区间提供一些启示, 最终设置合理的放电方案对引力波探测的航天器进行电荷控制, 以降低由于测试质量充电所引起的噪声. 本文的研究结果可为未来中国引力波探测计划测试质量的加速度噪声预测、粒子探测器的设计和放电方案提供理论依据.

本文研究了高能宇宙线粒子对测试质量的充电机制, 建立了等效航天器模型来仿真空间引力波探测中的航天器的结构与材料. 通过GEANT4对航天器在太阳活动极大、太阳活动极小年银河宇宙线各粒子和SEP的轰击下测试质量充电过程的仿真模拟, 可以得出以下结论:
1) 在同一能谱不同截断能量下, 随着截断长度的降低充电速率逐步增大, 截断长度从1 mm减小到50 nm充电率增长了8.74%. 在本文几何模型、物理过程和能谱设置条件下, 截断长度的变化不会显著的影响测试质量的充电速率;
2) 太阳活动极小年时的总充电速率为39.469 +e/s, 除Proton, ³He和⁴He之外, 其他重粒子对充电率的贡献仅为1.16%; 太阳活动极大年的总充电速率为12.531 +e/s, 为太阳活动极小年的三分之一; 1989年9月29日SEP峰值能谱通量下的充电速率为120700 +e/s, 零星发生的SEP事件对航天器造成极大的充电风险;
3) 太阳活动极小年时, 银河宇宙线的初级粒子充电率占比为72.86%, 其中充电率贡献最大的是质子和⁴He, 初级粒子充电率占比分别为67.07%和100%, 表明测试质量充电速率的主要贡献来源于初级粒子直接沉积在测试质量中;
4) 太阳活动极小年时Proton在总充电贡献中占比最大, 为83.16%, He的总充电率贡献为15.68%, 是初级宇宙线中He通量占比的2倍, 其他重离子对测试质量的充电率贡献不大;
5) 太阳活动极小年时, 宇宙线质子低能部分充电率贡献最大, 在能量区间0.1—1 GeV的充电率贡献约占总充电率贡献的65%, 在能量区间0.1—10 GeV内, 对测试质量充电率的占比约为94%.
感谢国家科技基础条件平台-国家空间科学数据中心(https://www.nssdc.ac.cn)对本文空间环境数据的支持.