摘要:材料内部缺陷对复合材料的拉伸断裂性质有着极其重要的影响. 纤维束模型是研究材料拉伸断裂性质常用的理论模型, 已有含缺陷纤维束模型的工作表明, 在纤维束模型中引入单纤维缺陷后, 缺陷对模型拉伸断裂性质产生了显著影响. 为研究实际材料内部存在的不同尺寸及损伤程度的缺陷, 本文引入缺陷的空间尺寸、缺陷程度和缺陷内部纤维损伤程度分布等影响因素, 构建了含团簇状缺陷的扩展纤维束模型. 在最近邻应力再分配下, 通过数值模拟分析了缺陷个数α、缺陷尺寸上限β和缺陷内部纤维缺陷程度的线性、指数和常数函数分布形式对复合材料断裂过程的影响. 分析发现, 由于缺陷空间分布存在的重叠竞争机制, 在缺陷尺寸上限β较大时, 缺陷个数对系统负载能力的影响具有饱和的趋势. 而由于缺陷中心纤维的缺陷程度正比于缺陷尺寸, 因此随着缺陷尺寸上限β的增加, 其对模型负载能力的影响越来越显著. 缺陷内部纤维缺陷程度的空间分布函数对以上规律没有产生实质影响, 仅改变了各断裂性质的具体取值. 本文的模拟分析结果对提高复合材料的力学性能具有一定的理论意义.
关键词: 纤维束模型/
缺陷/
本构关系/
雪崩尺寸

English Abstract

全文HTML

--> --> -->

材料在受到过度负载作用时, 会发生由微观裂纹到宏观断裂的不可逆演化过程. 在各种工程领域, 经常发生起源于微裂纹或终结于裂纹扩展的灾难性断裂事故, 如地震引起的地质构造开裂或建筑垮塌, 工程结构受到反复负载或者碰撞而损坏, 压力管道的裂纹或机械构件的断裂等. 这些损坏或断裂给生产生活带来巨大损失^[1], 因此研究材料断裂过程中的断裂力学性质具有十分重要的理论和实践意义^[2]. 研究材料宏观断裂的微观机制有助于掌握断裂的临界现象, 进而避免或者减少材料断裂造成的危害^[3,4], 甚至可以对材料的宏观断裂现象进行预测^[5]. 材料本身或材料在制备过程中都会存在不同程度的杂质和缺陷, 导致实际非均匀材料的微观结构属于一种无序系统^[6-8]. 由于无序系统的复杂性, 目前没有确定的微分方程可以描述和解决无序材料断裂中复杂的动力学过程. 所以研究无序材料的微观断裂机制需要依赖于一些基于统计的格点模型^[9], 纤维束模型是研究无序材料拉伸断裂机制的常用统计模型. 虽然纤维束模型相对比较简单, 但是却能够模拟材料的微观断裂机制, 模拟结果也可以和实际拉伸实验进行比较^[10-12]. 近年有针对PET纤维束的准静态和动态拉伸断裂实验的研究, 通过与实验结果对比, 发现准静态拉伸断裂实验得到的本构曲线与纤维束模型的模拟结果比较符合^[13].
经典纤维束模型用来模拟线弹性纤维在准静态加载条件下的脆性断裂过程^[6], 纤维的断裂阈值满足具体的概率分布函数和累计分布函数, 关系如下^[14,15]:

$ P(x) = \int_0^x p (u){\text{d}}u, $

当纤维承受的负载超过阈值后, 这根纤维发生断裂, 不再承受任何力, 释放的负载再分配给其他未断纤维. 根据负载再分配方式的不同, 纤维束模型可分为平均应力再分配模型 (GLS)、最近邻应力再分配模型(LLS)和一般的局域应力再分配模型. 平均应力再分配模型可以看成是考虑了长程作用的平均场模型, 可以应用平均场理论得到精确的解析结果, 而最近邻应力再分配模型则考虑了短程相互作用, 纤维断裂后负载只会分配给最近邻的纤维^[16-19], 最近邻应力再分配模型难以得到解析结果^[19,20], 主要依赖于数值模拟方法进行处理.
为了更好地模拟不同材料的拉伸断裂过程, 在经典纤维束模型的基础上, 又构建了大量的扩展纤维束模型. 经典纤维束模型的每根纤维本身是脆性断裂, 即纤维达到阈值后立即断裂. 而在连续损伤模型中, 当纤维承担的应力在达到损伤阈值后, 纤维并不会直接断裂而是先受到损伤, 此时受损伤纤维的杨氏模量会衰减^[21,22]. 在连续损伤模型中损伤次数和阈值分布是影响非脆性断裂过程及其断裂性质的主要因素^[23]. 为了模拟高聚物等纤维强化复合材料的动态力学行为而构建的黏弹性纤维束模型可以研究蠕变断裂行为. 黏弹性纤维束模型中最重要的断裂性质就是蠕变寿命的统计^[24,25]. 近年来有些研究者通过改变阈值分布指数和阈值上限值这两个无序参数控制系统的无序程度, 分布指数越大阈值无序度越低, 阈值上限值越高无序程度越高^[17,26,27]. 这类模型实质是通过控制阈值分布改变系统无序性, 系统无序程度的变化导致断裂性质发生极大的改变. 另外还有针对高维度纤维束模型的研究, 在最近邻应力再分配的基础上分别对1—8维的模型进行了模拟计算, 结果发现随着维数增加, 最近邻应力再分配模型逐渐渡越到平均应力再分配模型^[28,29].
在研究材料断裂的微观机制时发现, 实际材料的拉伸强度常比应用连续性理论得到的理论结果小得多, 出现这一现象的主要原因是材料的微观结构中广泛存在的缺陷结构. 缺陷对材料的力学性质和断裂过程具有复杂影响, 缺陷不仅具有随机性, 而且种类繁多, 常见的缺陷包括空洞、空隙、杂质、位错和微裂纹等. 近年有些工作利用实验方法和有限元方法研究材料微观结构中的缺陷对材料断裂的影响, 这些随机分布的微观缺陷结构对复合材料的力学性能和断裂过程造成显著的影响^[30,31]. 缺陷影响了材料断裂过程中裂纹微观的成核过程和前沿的传播性质, 进而影响材料的可靠性, 制约了材料的负载能力. 因此, 有必要从理论上研究缺陷对材料拉伸断裂性质的影响^[32,33]. 理论上研究缺陷的影响, 首先需要构建能够描述缺陷的统计模型. 纤维束模型可以很好地描述无序材料的拉伸断裂性质, 但没有考虑到缺陷对拉伸断裂性质的影响. 在以往的工作中, 我们在经典纤维束模型的基础上, 初步构建了考虑单尺寸缺陷的含缺陷纤维束模型, 并应用数值模拟的方法分析了缺陷对纤维束模型拉伸断裂性质的影响^[34,35]. 本文将在此基础上, 构建更加符合实际材料结构的含缺陷纤维束模型, 进一步深入研究缺陷对材料拉伸断裂性质的影响.

在已有研究单尺寸缺陷的简单含缺陷纤维束模型^[34,35]中, 仅考虑了随机分布的单根纤维的缺陷, 没有考虑缺陷尺寸这一重要因素的影响. 除了纤维束模型, 弹簧网络模型中也有相似的缺陷算法, 缺陷密度是弹簧网络模型中最重要的影响因素^[36]. 仅仅考虑单一尺寸缺陷的密度和缺陷程度还不足以描述实际材料的缺陷性质. 为了更好地分析缺陷对材料拉伸断裂过程的影响, 本文构建更加符合实际的含缺陷纤维束模型. 纵向上, 同一根纤维可能出现多处缺陷, 计算时取最大程度的缺陷值为这根纤维的缺陷; 横向上, 考虑缺陷聚集在一起形成团簇状结构. 此模型在考虑缺陷空间分布的基础上, 引入随机缺陷尺寸变量, 同时考虑缺陷程度的空间衰减因素, 假设缺陷程度按照一定的函数关系随着缺陷尺寸变化.
在模拟过程中, 首先构建经典纤维束模型, 假设纤维阈值最初满足均匀分布, 其概率密度为

$ p(x) = \left\{ {\begin{aligned}& {1,}\qquad{{\text{ }}0 \leqslant x \leqslant 1,} \\ & {0,}\qquad{{\text{ }}x > 1,} \end{aligned}} \right. $

对应的累积分布函数为

$ P(x) = \left\{ {\begin{aligned}& {x,}\qquad{{\text{ }}0 \leqslant x \leqslant 1,} \\ &{1,}\qquad{{\text{ }}x > 1,} \end{aligned}} \right. $

然后, 在此基础上, 引入团簇状缺陷的描述方法^[37]. 首先假设纤维束中有α个大小不同的缺陷, 缺陷的中心位置在纤维束中满足均匀分布, 再根据缺陷尺寸确定缺陷的边界范围. 缺陷尺寸可以采用固定值或满足一定的概率分布, 本文选定缺陷尺寸在[0, β]之间满足均匀分布, 并假设缺陷同纤维束一样满足周期性边界条件. 第i个缺陷的缺陷尺寸记为β_i, 其中心纤维的缺陷程度定义为${C_i}$,

$ {C_i} = \frac{{{\beta _i}}}{\gamma }, $

其中$\gamma > \beta $是决定中心缺陷程度的控制变量. 如图1所示, 以缺陷中心为坐标零点建立直角坐标系. 在缺陷内部不同纤维的缺陷程度与其位置之间满足一定的函数关系, 本文首先采用了简单的线性衰减函数关系. 如图1所示, 假设第i个缺陷内部, 以缺陷中心为计数基准, 第$j~(j \leqslant {\beta _i}/2)$根纤维的初始阈值记为${x_j}$, 引入缺陷后其断裂阈值$x_j^*$表示为
图 1 一维纤维束模型的团簇状缺陷程度示意图
Figure1. Schematic diagram of cluster defect degree for one-dimensional fiber bundle model. The Cartesian coordinate system is established with defect center as its coordinate zero.

$ x_j^* = {x_j}\left[ {1 - \left( {{C_i} - \frac{{{C_i}}}{{{\beta _i}/2}}j} \right)} \right]. $

对一维排列的纤维束来说, 缺陷中心纤维的缺陷程度最大, 向左右两边逐渐呈线性衰减. 不同尺寸的缺陷, 其中心纤维的缺陷程度与该缺陷的尺寸呈正比, 缺陷尺寸越大, 中心纤维缺陷程度越高. 因为考虑了不同尺寸的缺陷, 所以会出现同一根纤维可能同时处于多个缺陷之中. 由于模型假设了在多个缺陷重合的情况下, 取最大的缺陷程度作为这根纤维的实际缺陷. 因此, 在多个缺陷出现空间重叠现象时, 纤维束系统会出现一个大尺寸缺陷边缘处的缺陷程度与小尺寸缺陷中心位置缺陷程度的竞争, 也就是说大尺寸缺陷不能完全覆盖其他缺陷. 图2为团簇状缺陷模型示意图, 以3个缺陷为例, 同一根纤维可能多次受到团簇状缺陷的影响, 缺陷满足周期性边界条件.
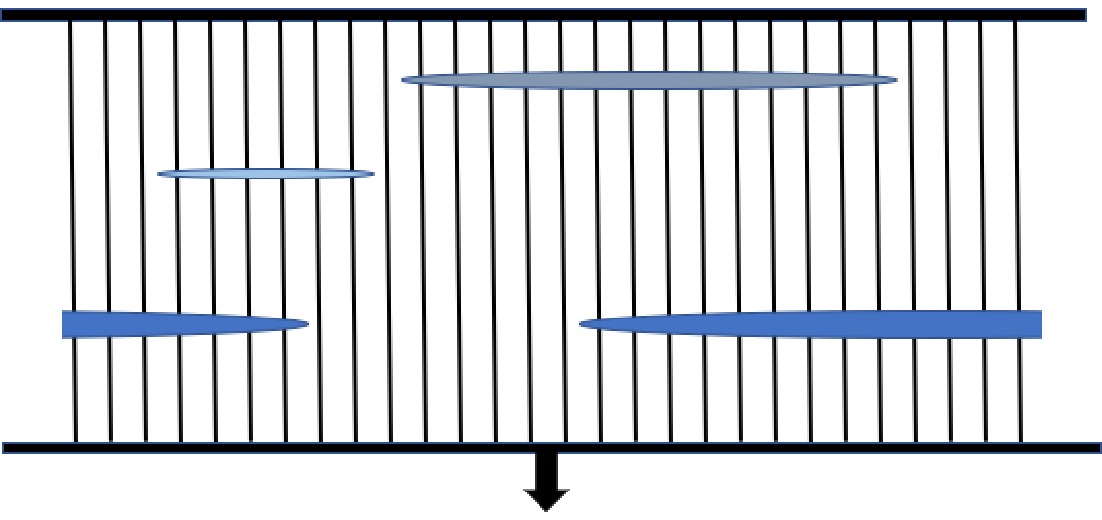图 2 一维纤维束模型的团簇状缺陷模型示意图, 其中包含3个缺陷, 缺陷和纤维束都采用周期性边界条件
Figure2. Schematic diagram of the clustered defect model of the one-dimensional fiber bundle model, which contains 3 defects, both the defect and the fiber bundle adopt periodic boundary conditions.

在以上构建的含缺陷的纤维束模型中, 假设纤维束被准静态地拉伸直至完全断裂. 一根纤维断裂后, 所承担的应力需要在其他未断裂的纤维中进行重新分配. 由于缺陷对整个纤维束来说是局域的, 直接影响了纤维之间的局域相互作用, 因此, 本模型的应力再分配机制采用最近邻应力再分配. 根据上述模型构建方法可知, 该模型最重要的参数是缺陷个数α以及缺陷尺寸上限β. 接下来, 应用数值模拟方法分别分析缺陷个数α以及缺陷尺寸上限β对模型拉伸断裂性质的影响. 在模拟中, 纤维束尺寸取100000根纤维, 以下分析的结果是不少于5000次模拟结果的系综平均.

缺陷个数α表示了纤维束中缺陷的多少, 为了单独分析缺陷个数α对模型拉伸断裂性质的影响, 首先固定缺陷尺寸上限β的值. 在本模型中, 考虑到系统的尺寸以及实际材料出现缺陷的情况. 一般情况下, 缺陷尺寸相比系统的尺寸来说要小得多, 因此β不应太大; 另外, 在以往的研究中, 我们已经分析了β = 1的极限情况, 当β太小时, 模型趋向于β = 1时的极限情况, 团簇状缺陷结构不明显, 因此, β取值也不应太小. 在以下的模拟中, 首先固定β = 150, $\gamma = 200$, 考虑缺陷个数α在50—3200之间变化, 分析缺陷个数α对断裂性质的影响.
图3给出了模型在拉伸断裂过程中本构曲线与缺陷个数α的关系, 横坐标$\varepsilon $表示应变, 纵坐标$\sigma $表示应力, 其中缺陷尺寸上限β固定为150. 从图3可以看出, 虽然模型中每一根纤维都具有脆性断裂性质, 但整体上本构曲线在断裂阶段还是表现出一定的非脆性断裂性质. 由于模型中各纤维的断裂阈值分布存在着涨落, 使得每次模拟得到的临界应变和临界应力也存在涨落, 在最后模拟结果中, 进行系综平均后就呈现出一定的非脆性断裂性质, 在达到临界应力之后, 应力并没有立即降为0. 不同缺陷个数α下的本构曲线在临界断裂前基本上是重合的, 在接近临界断裂时稍有变化. 对拉伸断裂过程的应力应变关系来说, 初始阶段的本构曲线主要由断裂阈值较小的纤维的阈值分布决定, 而缺陷对纤维束中纤维断裂阈值中较小阈值的分布影响较小. 由于在不同的缺陷个数取值下, 纤维断裂阈值分布中较小阈值的分布均近似符合均匀分布, 因此, 缺陷个数取值对模型拉伸断裂的本构曲线初始阶段几乎没有产生影响. 缺陷个数α对纤维束断裂力学性质的影响不是线性的, 在缺陷个数α较小时, 对本构关系的影响比较明显; 而当缺陷个数α取值较大时, 对本构关系的影响反而较小, 接下来定量分析缺陷个数α对临界应力大小的影响.
图 3 不同缺陷个数α下系统的本构关系, α在50—3200的范围内变化, 图中$\varepsilon $表示应变, $\sigma $表示应力
Figure3. Constitutive curves of the system under different number of defects α, α varies from 50 to 3200. In the figure, $\varepsilon $ represents strain and $\sigma $ represents stress.

图4为临界应力σ_c与缺陷个数α的关系曲线, 其中缺陷尺寸上限β为固定值150. 从图中不难发现, 临界应力随着缺陷个数的增加单调地减小, 当缺陷个数比较小时临界应力随缺陷个数的变化比较明显, 而当缺陷个数增加到相对较大数值时, 临界应力的减小则缓慢得多. 值得注意的是, 模拟中采用了相对较大的缺陷尺寸, 也就是说即使在缺陷数目比较少的情况下, 大尺寸缺陷的出现仍然会对临界应力造成较大的影响. 而且由于缺陷数目比较小, 缺陷的空间分布比较分散, 缺陷之间重叠的情况很少. 因而纵向上不同缺陷程度的竞争作用不强, 此时少数的大尺寸缺陷会对系统的力学性质产生较大的影响. 而当缺陷数目增加到较大值的时候, 缺陷之间将出现较多的重叠, 纵向上缺陷程度的竞争变得激烈, 使得最终缺陷纤维根数和缺陷数目不成正比, 因此对系统力学性质的影响趋于平缓. 为了进一步说明这一点, 减小缺陷尺寸, 将缺陷尺寸上限设定为β = 40, 模拟结果如图4插图所示. 这样在保持缺陷个数的变化区间不变的情况下, 由于缺陷的尺寸较小, 缺陷的重叠可以忽略不计, 也就是纵向上缺陷程度的竞争现象不明显, 此时缺陷纤维的根数和缺陷数目近似呈线性关系, 表现在模拟结果上就是临界应力与缺陷数目之间近似呈线性关系. 以上模拟结果也说明, 减小缺陷尺寸使得模型从团簇状缺陷向非团簇状孤立缺陷转变, 在接下来的分析中将根据最大雪崩尺寸和负载加载步数的变化情况讨论团簇状缺陷模型和非团簇状缺陷模型的区别.
图 4 临界应力随缺陷个数α的变化关系, 插图为β = 40时临界应力随着缺陷个数α的变化关系, 此时临界应力接近于线性变化
Figure4. Relationship between critical stress and the number of defects α. In the inset, the relationship between critical stress and the number of defects α with β = 40 is shown, at this time, the critical stress changes linearly with α.

在团簇状缺陷模型中, 最大雪崩尺寸${\varDelta _{\text{m}}}$和负载加载步数step随着缺陷个数α呈现相反的变化关系. 如图5所示, 缺陷个数从50个逐渐增加到3200个, 最大雪崩尺寸和负载加载步数均呈非单调变化, 在缺陷个数为400附近, 最大雪崩尺寸和负载加载步数都出现了极值. 当缺陷个数从50增加到400时, 最大雪崩尺寸逐渐增加, 相应的负载加载步数逐渐减少, 系统更容易在经历少数大尺寸雪崩后发生宏观断裂. 而当缺陷个数由400继续增加时, 最大雪崩尺寸开始减少, 而负载加载步数则开始增加, 此时, 系统具有更强的韧性, 在拉伸过程中更不容易发生脆性断裂. 缺陷个数等于400是一个极值点, 此时, 系统具有最小的负载加载步数, 同时最大雪崩尺寸取最大值, 说明此时系统最接近于脆性断裂. 而当缺陷个数大于400时, 随着缺陷个数增加, 虽然临界应力单调减小, 但是减小的速度降低了. 另一方面, 负载加载步数反而增加了, 说明系统虽然能够承担的负载有所下降, 却具有更强的韧性. 需要注意的是, 以上结果只是在β = 150条件下模拟得到的, 对应了缺陷尺寸比较大的情形. 为了详细分析极值出现的条件, 又针对不同β值进行了数值模拟. 如图6所示, 模拟得到了不同β取值下, 最大雪崩尺寸和负载加载步数随缺陷个数的变化关系, 其中图6(a)—图6(d)分别对应β = 120, 90, 70, 60.
图 5 最大雪崩尺寸${\varDelta _{\text{m}}}$和负载加载步数step随着缺陷个数α的变化, 在α = 400处最大雪崩尺寸和负载加载步数均出现极值
Figure5. The maximum avalanche size (${\varDelta _{\text{m}}}$) and the step number of load increase (step) vary with the number of defects. The maximum avalanche size and the step number of load increase reach the extreme value at α = 400.

图 6 不同β取值下的最大雪崩尺寸和负载加载步数极值的出现情况　(a) β = 120; (b) β = 90; (c) β = 70; (d) β = 60. 当β取值较大时最大雪崩和加载步数与缺陷个数α存在类似二次函数的关系
Figure6. The extreme values of the maximum avalanche size and the step number of load increase with different β: (a) β = 120; (b) β = 90; (c) β = 70; (d) β = 60. When the value of β is large, there is a similar quadratic function between the maximum avalanche, the step number of load increase and the number of defects α.

在不同的β取值下, 最大雪崩尺寸和负载加载步数随着缺陷个数的变化规律存在明显差异. 当β = 120时, 最大雪崩尺寸和负载加载步的极值点出现在α = 800处. 当β = 90时, 最大雪崩尺寸和负载加载步数的极值点出现在α = 1200处. 而当β降到70时, 最大雪崩尺寸和负载加载步数的极值点增加到α = 2300. 可以发现, 随着缺陷尺寸上限β的降低, 最大雪崩尺寸和负载加载步数出现极值点对应的缺陷个数α的值逐渐增大. 在β = 60时, 增大α的变化范围, 进一步模拟发现, 此时极值点出现在α = 3200附近. 不难发现, 当系统的缺陷尺寸较大时, 最大雪崩尺寸和负载加载步数的极值出现在缺陷个数较小时, 随着缺陷尺寸的降低, 这一极值出现在更大的缺陷数目处, 当缺陷尺寸足够小时, 极值逐渐消失. 这就说明, 在不同的缺陷尺寸上限β取值下, 模型中缺陷可以表现出不同的性质, 当β较大时, 模型缺陷可以看成团簇状缺陷, 而当β取值较小时, 则表现出非团簇状缺陷的性质. 虽然缺陷尺寸不同, 但是在极值点之前, 最大雪崩尺寸和负载加载步数的变化性质相似, 也就是说如果缺陷个数被限制在一定范围内, 团簇状缺陷模型也会过渡为非团簇状缺陷模型.
由于模拟采用了应力控制型拉伸方式, 在拉伸断裂过程中会产生一系列雪崩, 雪崩尺寸是反映雪崩过程的主要参量, 而雪崩尺寸分布则能够很好地描述模型在断裂过程中的统计性质. 图7为不同缺陷个数取值下雪崩尺寸分布的统计结果, 为了更好地展示雪崩尺寸分布的统计性质, 图中使用了双对数坐标. 与平均应力再分配的模型不同, 一般情况下, 最近邻应力再分配下, 由于存在着显著的局域相互作用, 雪崩尺寸分布一般不满足简单的幂律分布. 从本文模拟结果可以看出, 和其他最邻近应力再分配下的纤维束模型类似, 整体上雪崩尺寸并不满足简单的幂律分布. 但是在雪崩尺寸较小时, 其分布还是能比较好地满足以下形式的幂律分布:
图 7 缺陷个数α不同取值下的雪崩尺寸分布
Figure7. The avalanche size distribution under different values of the number of defects α.

$ D(\varDelta ) \sim {\varDelta ^{ - \delta }}, $

其中$\varDelta $为负载每次准静态加载所引起的雪崩尺寸, 即每次加载后纤维的断裂数. 从图7可以看出, 在缺陷个数为100和800时, 对于较小尺寸的雪崩, 其雪崩尺寸分布的幂律指数满足δ = 6.5和δ = 5.9. 以上统计结果显示, 缺陷个数对模型拉伸断裂过程统计性质的影响较小, 只小幅度地影响了较小尺寸雪崩尺寸的幂律分布指数.

对于含缺陷的材料来说, 其中的缺陷尺寸也是影响其力学性质的重要参量. 通过以上的分析发现, 缺陷尺寸上限β影响了模型中的缺陷状态. 接下来, 为了详细分析缺陷尺寸上限β对模型断裂性质的影响, 假设缺陷个数α取固定值. 在以上的讨论中发现, 如果缺陷个数太小的话, 缺陷之间的相互作用不明显, 团簇状缺陷模型会过渡为非团簇状缺陷模型. 为了使缺陷尺寸上限β对系统的影响较明显, 在以下的模拟中, 固定缺陷个数α = 800, 模拟缺陷尺寸上限β在20—180之间变化时系统的拉伸断裂性质.
图8为缺陷尺寸上限对本构关系影响的模拟结果. 可以看出, 由于系统的涨落导致系综平均以后的模拟结果中, 本构曲线呈现出一定的非脆性断裂性质. 在系统达到临界值之后, 应力并没有立即降为0, 但是对于模型的每一次模拟结果来说, 缺陷或涨落的存在不会影响模型的脆性断裂性质. 在拉伸的初始阶段, 不同缺陷尺寸上限的本构曲线几乎完全重合, 说明缺陷尺寸对纤维束中较弱纤维的强度分布没有产生明显影响, 主要影响了较大强度纤维的强度分布. 随着缺陷尺寸的增加, 系统的临界应力和临界应变单调减小. 不难看出, 随着缺陷尺寸上限的增加, 本构曲线差距越来越大. 这也说明, 对于尺寸较小的孤立缺陷, 缺陷之间的空间重叠可以忽略, 此时材料拉伸断裂性质的主要影响因素是缺陷个数, 缺陷尺寸的影响较小. 而当缺陷尺寸较大时, 缺陷之间的空间重叠概率较大, 相互作用较强, 因此缺陷尺寸对材料拉伸断裂性质的影响较大.
图 8 不同缺陷尺寸上限β下模型的本构关系曲线
Figure8. The constitutive curves of the model with different maximum defect sizes.

图9为临界应力σ_c与缺陷尺寸上限β的关系, 可以清晰地看出, 小尺寸缺陷对临界应力的影响并不明显, 随着缺陷尺寸的增加, 临界应力迅速减小. 当缺陷尺寸上限足够大时, 临界应力随着缺陷尺寸上限的增加近似呈线性减小. 临界应力的变化也说明, 较小尺寸的孤立缺陷, 其尺寸对模型拉伸断裂性质的影响是非常有限的; 而对较大尺寸的团簇状缺陷, 缺陷之间的空间重叠引起的竞争作用使得系统容易受到缺陷尺寸的影响. 因为缺陷尺寸决定团簇状缺陷中心的缺陷程度, 导致团簇状缺陷模型的断裂性质更容易受到缺陷尺寸的影响.
图 9 不同缺陷尺寸上限β下的临界应力, β值在20—560之间变化
Figure9. The critical stress at different maximum defect sizes β varying from 20 to 560.

改变缺陷尺寸上限β, 最大雪崩尺寸和负载加载步数随缺陷尺寸上限β的变化规律如图10所示. 随着缺陷尺寸上限β的增加, 最大雪崩尺寸先缓慢增加后快速增长, 而负载加载步数则相应减小. 这说明缺陷尺寸上限β增加后, 模型更容易在较小的负载加载步数后, 出现较大尺寸的雪崩, 说明此时模型整体上更加体现出脆性断裂性质. 随着缺陷尺寸上限β的增加, 最大雪崩尺寸和负载加载步数都没有出现饱和的趋势. 这是因为此模型中, 增加缺陷尺寸相应增大了团簇状缺陷中心的缺陷程度, 缺陷尺寸和中心缺陷程度的增加单调地加速了系统的整体断裂过程. 在保持缺陷中心缺陷程度和团簇状缺陷尺寸关系不变的情况下, 增加缺陷尺寸和增加缺陷中心缺陷程度是同步的. 而且在团簇状缺陷内部, 不同纤维的缺陷程度与其空间位置之间满足较简单的线性关系. 当然, 不同纤维的缺陷程度与其空间位置之间的函数关系对纤维束拉伸断裂性质也会产生一定的影响.
图 10 不同缺陷尺寸上限β下的最大雪崩尺寸和负载加载步数, β值在20—180之间变化
Figure10. The maximum avalanche size and the step number of load increase at different maximum defect sizes β varying from 20 to 180.

图11为系统的临界应力随着缺陷数目和缺陷尺寸变化的三维空间相图, 可以看出, 系统的临界应力对缺陷尺寸很敏感, 当缺陷尺寸较大时, 临界应力变化很快, 只有当缺陷尺寸减少到足够小时, 其对临界应力的影响才比较小. 同时, 在缺陷尺寸较小时, 缺陷个数对临界应力的影响也较小, 只有当缺陷尺寸较大且缺陷个数较少时, 缺陷个数对临界应力的影响才比较显著. 相比较而言, 缺陷尺寸上限比缺陷个数对模型断裂强度的影响更大. 这说明控制系统中缺陷的尺寸处于较小范围内, 才能使系统拉伸断裂的临界应力相对稳定.
图 11 系统的临界应力随着缺陷数目以及尺寸变化的三维空间相图, 其中缺陷数目在50—1200之间变化, 缺陷尺寸在20—180之间变化
Figure11. Phase diagram of critical stress that varies with the number and size of defects, where the number of defects varies from 50 to 1200 and the size of defects varies from 20 to 180.

为了分析团簇状缺陷内部不同纤维缺陷程度的空间分布对纤维束拉伸断裂性质的影响, 接下来在线性关系的基础上, 引入不同纤维缺陷程度随空间的指数分布和常数缺陷两种分布形式. 缺陷程度随着空间位置满足指数变化时, 第i个缺陷中第j根 (从缺陷中心开始计算) 纤维的断裂阈值表示为

$ x_j^* = {x_j}\big[ {1 - \big( {{C_i} - q_i^j} \big)} \big], $

其中${C_i}$表示第i个缺陷中心纤维的缺陷程度, ${x_j}$表示其中第j根纤维的初始断裂阈值, ${q_i} = {C_i}^{2/{\beta _i}}$. 而常数缺陷程度分布的纤维缺陷程度都固定为C_i, 常数缺陷程度分布的缺陷纤维断裂阈值则表示为

$ x_j^* = {x_j}{C_i}. $

固定缺陷尺寸上限和缺陷个数的情况下, 缺陷程度空间衰减方式分别为线性、指数和常数函数时, 临界应力随着中心缺陷程度的变化如图12所示. 在三种空间衰减方式下, 临界应力随着中心缺陷程度的减小均单调增加. 同时也能发现, 不同的缺陷程度空间衰减方式下, 临界应力随中心缺陷程度都有类似的变化规律. 但是空间衰减方式采用指数函数和常数函数的模型其临界应力的变化曲线很接近, 说明不但变化规律一致, 具体的临界应力数值也足够地近似, 而采用线性衰减方式的模型其临界应力会显著大于另外两种形式. 在三种空间衰减方式下, 临界应力随着中心缺陷程度的减小逐渐出现饱和的趋势, 当缺陷中心的缺陷程度足够小时, 即使缺陷个数和尺寸很大也不会对系统造成显著的影响. 类似的规律也出现在最大雪崩尺寸和负载加载步数随中心缺陷程度的变化关系中. 如图13所示, 最大雪崩尺寸随着中心缺陷程度的减少而减小, 而负载加载步数则正好相反. 这说明减少中心缺陷程度, 断裂过程中的负载加载步数增加, 延缓了宏观断裂发生的进程. 而相应地两次负载加载之间所能够断裂的纤维根数, 也就是雪崩尺寸减小了, 同时最大雪崩尺寸也变小了, 说明系统的断裂进程相应延缓了. 在三种空间衰减方式下, 最大雪崩尺寸和负载加载步数随着中心缺陷程度的减小逐渐出现饱和的趋势, 当缺陷中心的缺陷程度足够小时系统受缺陷的影响很小. 中心缺陷程度和缺陷尺寸之间都是单调的变化关系, 因此, 中心缺陷程度和缺陷尺寸上限对断裂性质具有类似的影响关系.
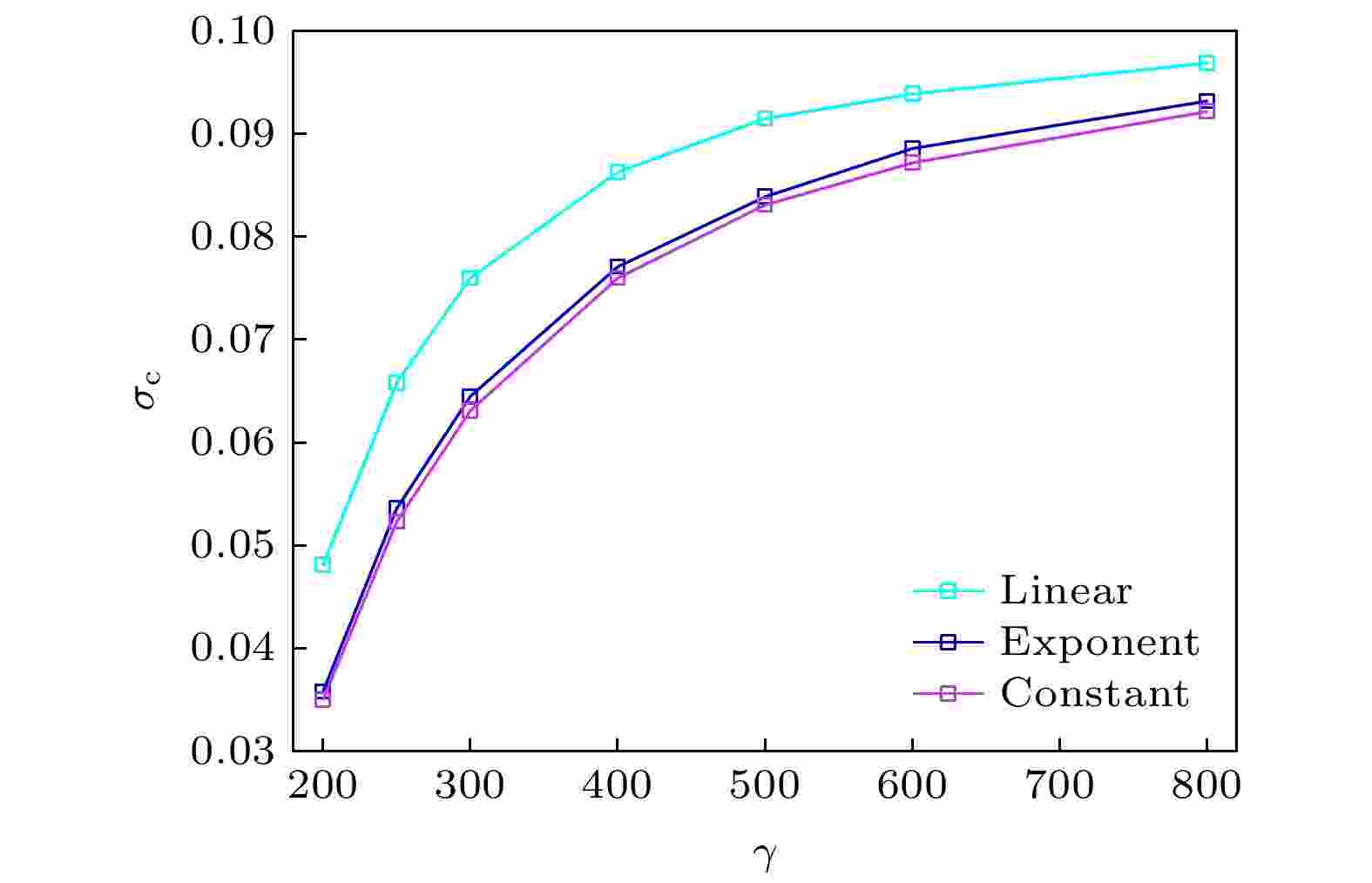图 12 缺陷程度空间衰减方式分别为线性、指数和常数函数情况下的中心缺陷程度对临界应力的影响, 缺陷个数为800, 缺陷尺寸上限为150
Figure12. The influence of the degree of central defect on the critical stress when the spatial attenuation modes of the defect degree are linear, exponential and constant functions. The number of defects is 800, and the maximum defect size is 150.

图 13 缺陷程度空间衰减方式分别为线性、指数和常数函数情况下, 最大雪崩尺寸和负载加载步数随中心缺陷程度的变化. 缺陷个数为800, 缺陷尺寸上限为150
Figure13. The maximum avalanche size and the step number of load increase vary with the degree of the central defect when the spatial attenuation modes of the defect degree are linear, exponential and constant functions. The number of defects is 800, and the maximum defect size is 150.

本文在已有含缺陷纤维束模型的基础上, 考虑到缺陷的尺寸大小和内部纤维的不同空间衰减形式, 构建了含团簇状缺陷的纤维束模型. 此模型中的缺陷尺寸大小和位置分布均采用均匀分布, 团簇状缺陷中心纤维的缺陷程度最大, 且随着缺陷尺寸的增加而增大. 模型先假设了每个团簇内部纤维的缺陷程度从中心向外呈线性衰减, 后又引入了指数衰减和常数缺陷程度两种空间衰减形式. 在本团簇状缺陷的纤维束模型中, 最主要的两个影响因素就是缺陷个数α和缺陷尺寸上限β. 应用数值模拟的方法, 分析了该模型在最近邻应力再分配下, 进行准静态负载加载时的拉伸断裂性质, 主要分析了缺陷个数和缺陷尺寸上限对断裂的宏观力学性质和断裂统计性质的影响, 这包括本构曲线、临界应力、负载加载步数、最大雪崩尺寸和雪崩尺寸分布.
在保持缺陷尺寸上限β不变的情况下, 改变缺陷个数α的大小, 通过数值模拟发现, 临界应力和临界应变都会随着缺陷个数α的增加而减小. 当缺陷尺寸上限比较大的时候, 即使缺陷个数很少, 但依然会对宏观和微观断裂过程造成比较大的影响. 原因是缺陷虽然个数少, 但是尺寸足够大, 纤维的缺陷程度也足够大, 但不同缺陷之间的重叠竞争不明显. 随着缺陷个数α的增加, 不同缺陷间的重叠竞争也越发激烈, 但是对断裂过程的影响却相对α较小时减缓了, 这说明不同缺陷间的竞争机制会减缓系统整体缺陷程度随缺陷个数的变化. 虽然缺陷个数的增加会强化缺陷间的竞争作用, 从而减缓系统整体缺陷程度的增加, 但是当缺陷个数较小, 即竞争机制不强时, 增大缺陷个数依然会加速系统的断裂, 因此最大雪崩尺寸和负载加载步数随着α的变化必然会出现极值. 进一步分析极值出现的条件发现, 随着β值的增加极值对应的α值不断减小, 这说明增加缺陷尺寸在一定程度上也会增加缺陷间的竞争.
在固定缺陷个数的取值, 改变缺陷尺寸上限β时, 模拟发现, 而当缺陷尺寸上限比较小时, 其对断裂过程影响并不大; 而随着缺陷尺寸上限的增加, 其对模型断裂过程的影响越来越显著. 原因是当缺陷尺寸比较小的时候, 相应缺陷程度也较小, 即使缺陷数目很多, 但是对整个系统断裂性质的影响并不大. 而随着缺陷尺寸上限的增加, 由于大尺寸缺陷的引入, 出现了缺陷间的重叠竞争作用, 因此, 随着缺陷尺寸的增加断裂进程加快. 对于缺陷中纤维的缺陷程度, 除了假设缺陷中心纤维的缺陷程度随着缺陷尺寸线性变化, 且缺陷内部不同纤维的缺陷程度也随位置呈线性衰减外, 为了分析缺陷内部纤维的缺陷分布对系统断裂性质的影响, 又引入了指数衰减和常数缺陷两种空间衰减形式. 通过数值模拟分析了三种空间衰减形式下中心纤维缺陷程度对断裂性质的影响. 结果表明, 缺陷尺寸、中心纤维缺陷程度以及缺陷内部的缺陷程度空间衰减方式都会对材料的承受负载能力和韧性产生影响.
无论是缺陷个数还是缺陷尺寸上限对临界应力的影响都是单调的. 增加缺陷个数α和缺陷尺寸上限β, 临界应力都会单调减小, 即纤维束系统强度逐渐减小. 但是值得注意的是, 在β取值较大时, α对σ_c的影响逐渐平缓, 而β对σ_c的影响逐渐加强. 这是因为团簇状缺陷模型的缺陷程度随缺陷尺寸的增大单调增加, 因而增加缺陷尺寸时既增加了系统缺陷纤维的比例, 又增加了缺陷纤维整体的缺陷程度, 所以对系统断裂强度的影响越来越大. 而增大缺陷个数并不直接影响纤维的缺陷程度, 反而由于重叠竞争机制减缓系统缺陷纤维比例的增加. 总之, 本文的模拟结果表明, 材料中的缺陷尺寸和个数均会对材料拉伸力学性质产生显著的影响. 而当大尺寸的缺陷存在时, 即使缺陷个数较少, 也会显著降低材料的承载性能. 本文的模拟结果对复合材料的设计、制备和加工过程中优化设计方案和加工工艺、改善制备方法具有一定的理论意义. 文中考虑了空间对称缺陷, 但实际的缺陷可能包含更复杂的非对称形态, 在后续研究中将分析这种复杂的含非对称缺陷的纤维束模型.