摘要:基于傅里叶导热定律, 两种具有不同热导率温度依赖特性的材料组合而成的两段式组合材料可以实现热整流效应. 本文提出在体材料上均匀布置多孔结构, 通过多孔结构孔隙率调整材料的热导率参数, 进而强化热整流效应. 基于有限元方法和有效介质理论, 计算并分析了温差和孔隙率等参数对体材料热整流系数的影响. 计算结果表明, 温差较大时, 孔隙率对对体材料热整流系数的影响较为明显. 在热导率随温度升高而增大的材料中布置多孔结构, 一般会降低系统的热整流系数; 若在热导率随温度升高而减小的材料中布置多孔结构, 则存在一个最佳的孔隙率, 相对于无多孔结构的系统, 其热整流系数可以提高2—3倍. 本文研究结果为体材料热整流系数的调控提供了新的思路.
关键词: 热整流/
热导率/
多孔结构/
有效介质理论

English Abstract

全文HTML

--> --> -->

热整流是一种热流量大小依赖于温度梯度方向的热量传递现象(或者系统在一个方向上的传热能力明显强于相反方向的传热能力)^[1,2]. 热整流效应为控制热量传递提供了新的思路, 可应用于节能、热防护及能源管理^[3,4]等方面. 此外, 热整流的可能应用还包括废热回收^[5]、热二极管、热三极管和热逻辑门^[6,7], 以及通过使用热桥式整流器利用地球表面温度的周期振荡驱动热机实现清洁能源的收集^[8]. 2021年中国两会上, “碳达峰”、“碳中和”首次被写入政府工作报告, 倍受关注. 为应对气候变化, 绿色低碳发展被列为中国重点任务之一. Henry等^[9]提出在外界高温时使建筑墙体隔热, 而在外界低温时使墙体导热可使建筑节能7${\text{%}}$— 42${\text{%}}$, 从而有效地实现低碳发展和降低温室气体的排放, 其核心内容就是建筑材料在不同方向上的可变传热特性.
早期, 关于热整流现象的研究主要集中于宏观体材料^[10-12], 相应的热整流原理包括界面处的热势垒^[11]、界面处的表面热应变^[12]等. 近十几年来, 关于纳米系统中热整流效应的研究逐渐得到广泛的关注^[13-17], 其主要的热整流机理为声子输运的不对称性^[3,18]. 但是, 考虑到热整流现象的实际应用, 仍然有必要开展关于宏观体材料中热整流现象的研究. 基于傅里叶导热定律, Hoff^[19]提出一种利用体材料热导率随温度变化的不同来实现热整流的机制: 一种材料的热导率随温度升高而降低, 另一种材料的热导率则随温度升高而增加, 将两种材料组合为两段式系统, 在热流方向相反时会产生不同的等效热阻, 从而实现热整流. 基于此原理, ****们深入地研究了体材料中基于热导率温度依赖特性的热整流效应^[20-27]. 研究表明, 体材料实现热整流的必要条件是材料热导率为温度或空间函数^[21], 其热整流效应随着热导率温度依赖参数的差异增大而明显增强(正反方向热流密度的最大比值约为10)^[8]. 两段式材料之间的界面热阻也是影响其热整流效应的重要因素. 有研究表明, 界面热阻具有一定的温度依赖性, 基于界面热阻的不对称性也可实现热整流效应^[28,29]. 即使对于恒定的界面热阻, 通过调整界面热阻的大小也可实现热整流系数的最优化^[23,24]. 此外, 文献中也报道了其他的体材料热整流模型^[30-33], 诸如相变式热整流器^[30]、利用材料的热膨胀率不同设计的基于形变的热整流器^[31]、辐射式热整流器^[32-33]以及基于行波式时空调制的非互易性热输^[34]等.
虽然已有大量关于体材料热整流效应的研究, 但其热整流系数相对较低, 因此开展关于体材料热整流效应的研究, 实现强化或者调控热整流效应, 仍然十分必要. 采用多孔结构调控材料属性是常用且有效的方法, 已有大量文献研究了多孔介质的有效电导率和孔隙率的关系^[35-39]. 基于有效介质理论(effective medium approximation, EMA)可以计算得到周期填充复合材料的非线性电导率^[39]. 近期, 有效介质理论被推广到周期填充复合材料的热导率计算, 实现了材料热导率的调控^[40]. 对材料热导率的调控是在体材料热整流系统中强化热整流效应的关键, 因此本文采用多孔结构调节体材料的热导率, 基于有效介质理论计算热整流系数与孔隙率之间的变化关系, 验证了此方法的可行性, 并实现了体材料系统热整流效应的强化.

在研究两段式体材料热整流时, 已有诸多热导率模型被采用, 例如κ(T) = κ₀[1+μ(T–T_ref)]^[22]以及更简单的κ(T) = AT+B^[27]模型, 其中μ, A和B为待定参数. 文献[8]中, Dames总结了部分常见材料的热导率随温度的变化趋势, 并提出了幂指数模型. 此外, 文献[41]总结了69种金属及270余组合金的热导率, 其热导率在一定范围内均与温度呈现幂指数变化. 因此本文将采用更具有普遍意义的幂指数模型, 即

$ \kappa = {\kappa _0}{\left( { {T}/{{{T_{{\text{ref}}}}}}} \right)^\alpha }, $

式中, T_ref为参考温度, α为热导率温度依赖参数(幂指数), 通常–3.5 < α < +5.4^[8] , κ₀为材料的热导率参数.
考虑两种不同材料 1 和 2 连接而成的两段式组合材料, 如图1所示. 材料1和2的热导率温度依赖参数分别为α₁和α₂, 其组合简记为(α₁, α₂). 材料1的热导率随温度的升高而升高(α₁ > 0), 材料2的热导率随温度的升高而降低(α₂ < 0), 当系统左侧与高温热源T_H接触, 右侧与低温热源T_L接触时, 系统中两段材料的热导率均较大, 此时系统整体导热性能较好; 交换热源温度后, 系统左侧与低温热源接触, 右侧与高温热源接触时, 系统中两段材料的热导率均较小, 此时系统整体导热性能较差. 通常采用热整流系数γ表征热整流效应的强弱,
图 1 两段式复合体材料热整流系统示意图
Figure1. Schematic diagram of the two-segment thermal rectifier.

$ \gamma {\text{ = }}\left| { {{{j_ + }}}/{{{j_ - }}}} \right| - 1, $

式中, |j₊| > | j_–|, j₊表示正向模式下的热流量, j_–表示反向模式下的热流量. 当γ = 0时, 系统中不存在热整流效应, γ越大表示热整流效应越强. 采用无量纲温差|Δ|表示高低热源的差异, 其中${{{T}}_{\text{H}}\;=\;{T}}_{\text{0}} $$ {(1+}\Delta /\text{2}\text{)}$, ${{{T}}_{\text{L}}\;=\;{T}}_{\text{0}} {(1-}\Delta /\text{2}\text{)}$, T₀ = T_ref.
建立如图1所示的计算模型, 两段材料的尺寸均为长150 mm, 宽100 mm. 为方便计算, 取参考温度T_ref = 200 K, 幂指数组合取(α_1, α₂) = (+3, –3), 热导率参数取单位热导率, 即κ₀₁ = κ₀₂ =1 W?m^–1·K^–1. 基于有限元方法(finite element method, FEM)可以计算得到通过系统的热流量和热整流系数. 图2给出了在不同温差下, 上述热整流器在正反模式下的热流和热整流系数. 可以看出, 正温差下的热流明显大于反向温差的下的热流, 且该差异性随着温差的增加而增大, 热整流系数不断上升(如图2中插图所示). 图3显示了正反模式下热整流器内部的温度分布及局域热导率分布, 其中|Δ| = 1.5. 可以看出, 正向模式下左侧材料的局域热导率远小于右侧材料, 但相较于反向模式, 两段材料的热导率均较大, 因此可以出现明显的热整流现象. 此外, 正向模式中, 由于左段材料的热阻相对较大(热导率较小)而右段材料的热阻相对较小(热导率较大), 左段材料内的温度分布在靠近界面处出现急剧下降, 局域热导率明显降低, 导热能力下降, 不利于实现较高的热整流系数.
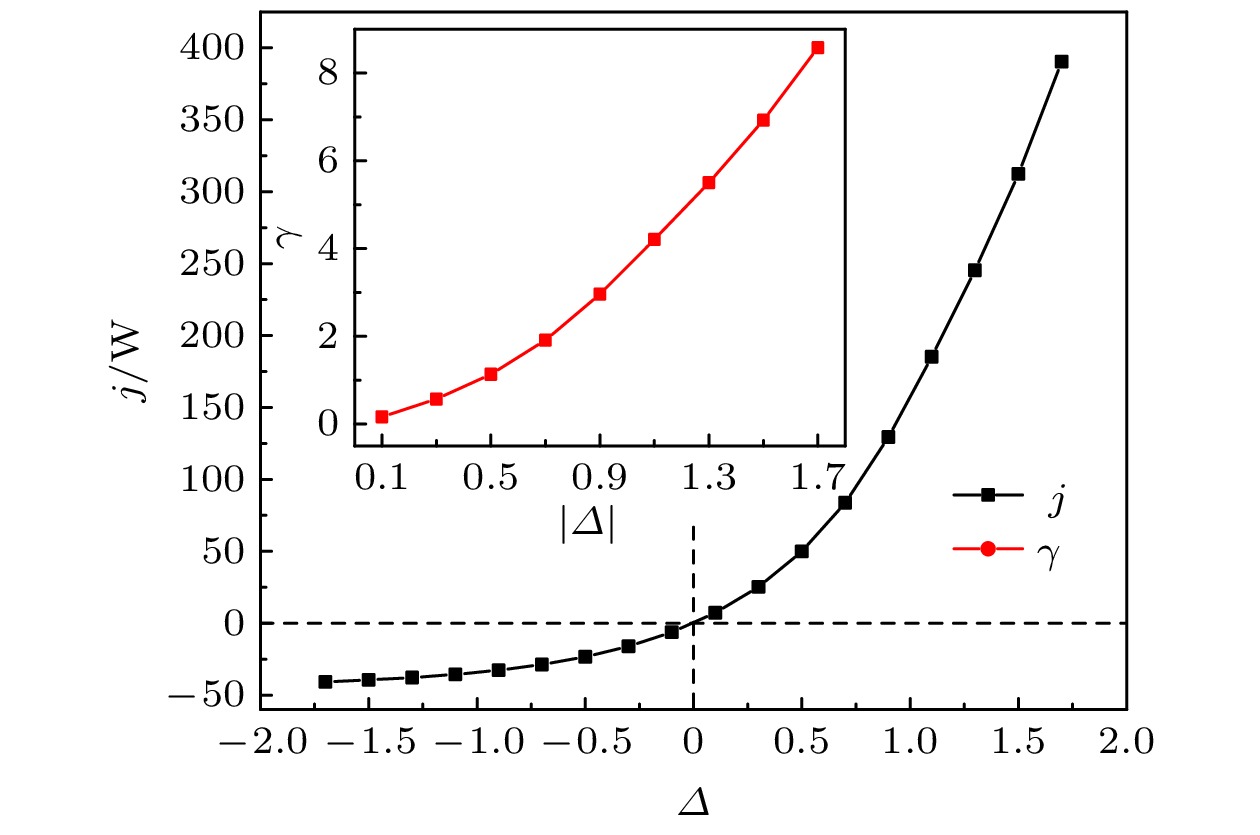图 2 (α_1, α₂)=(+3, –3)时, 正反热流量及热整流系数随无量纲温差的变化趋势
Figure2. For the case of (α_1, α₂)=(+3, –3), the heat flux and thermal rectification ratio versus the dimensionless temperature difference.

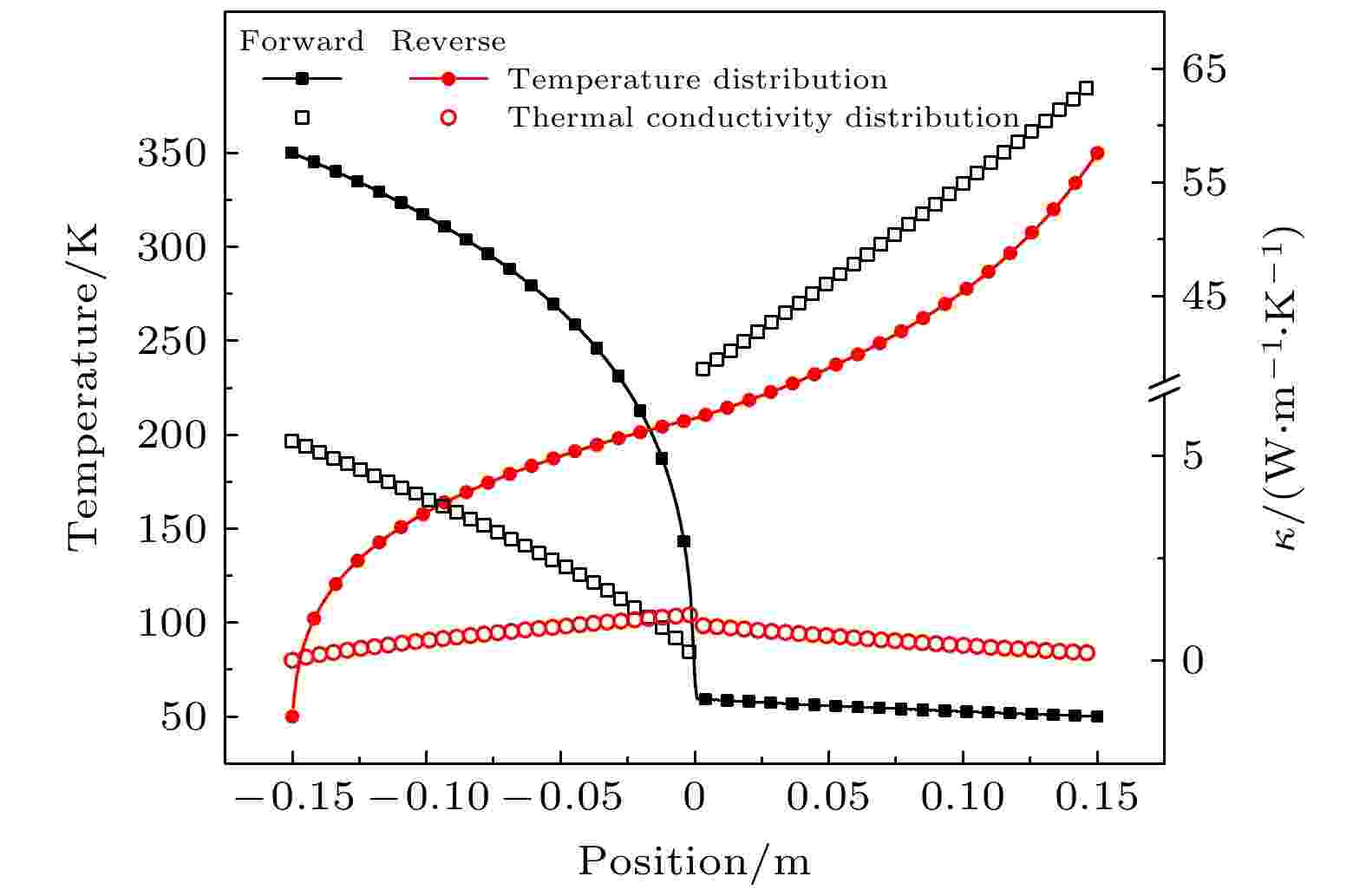图 3 |Δ| = 1.5时, 正反模式下热整流器内部的温度分布和局域热导率分布
Figure3. For the case of |Δ| = 1.5, temperature and local thermal conductivity distribution under forward and reverse cases.

在材料内部按照周期排列打孔可以形成多孔结构, 通过改变打孔的尺寸可以实现材料热导率的调控^[40], 从而有可能调节系统的热整流效应. 材料1和材料2的热导率温度依赖参数组合取为(α₁, α₂) = (3, –3), 分别在材料1(如图4(a)所示)或者材料2上均匀布置15×10个半径r = a的多孔结构, 孔隙率为f. 在无量纲温差为|Δ| = 1.5时, 图4(b)给出了热整流系数和正反方向热流量随材料1或材料2孔隙率的变化趋势. 图中, 虚线左侧表示在材料1上加工多孔结构, 虚线右侧表示在材料2上加工多孔结构.
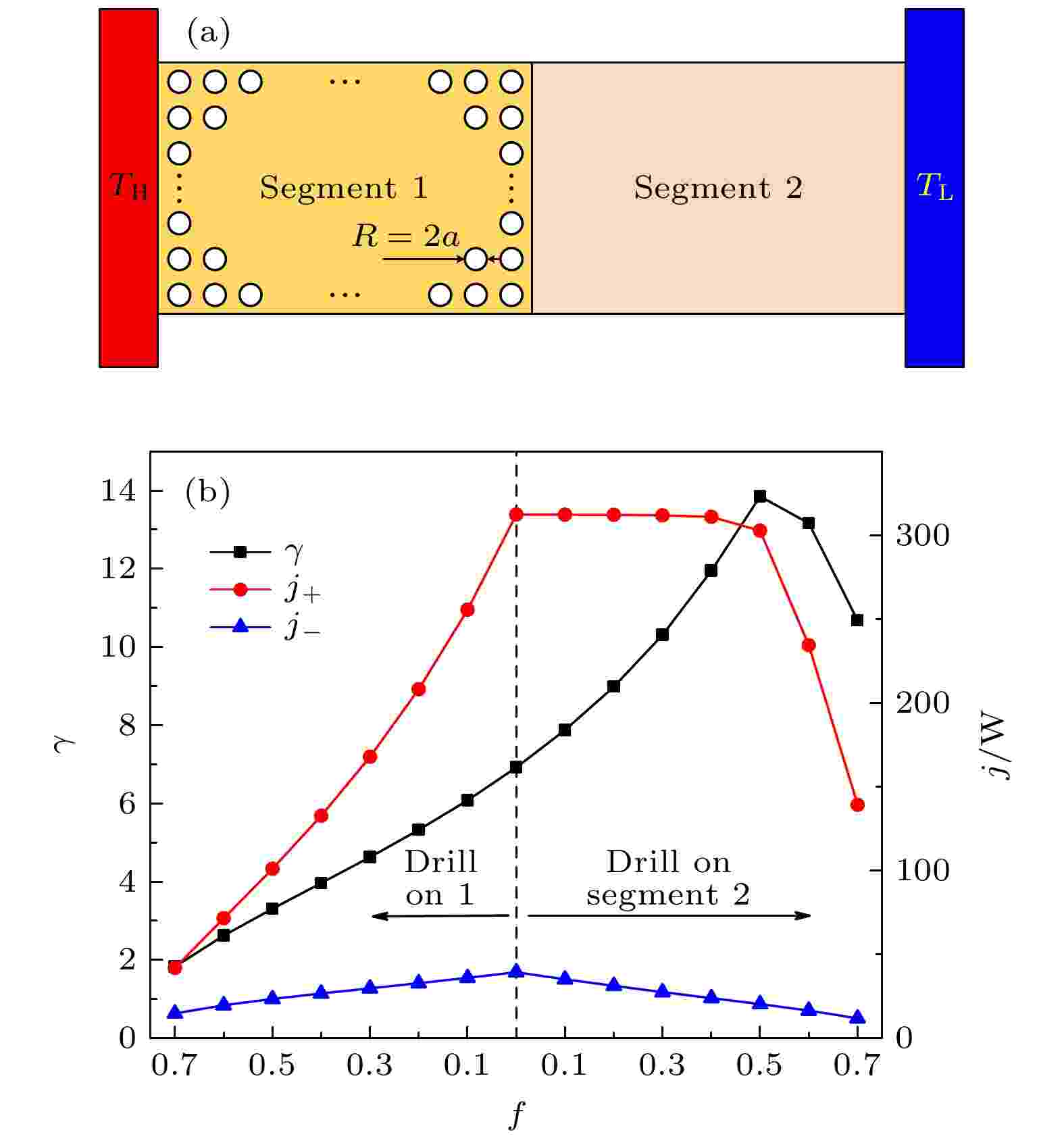图 4 (a) 材料1中的多孔结构; (b) 热整流系数(左)及正反热流(右)随材料1或材料2孔隙率f的变化趋势
Figure4. (a) Schematic diagram of the porous structure of the thermal rectifier (drill on segment 1); (b) thermal rectification ratio (left) and heat flux (right) versus porosity.

在材料1上加工多孔结构时, 等效于降低了左段材料的热导率. 如图3所示, 正向导热时左段材料为主要热阻, 因而多孔结构使得正向传热衰减较为明显; 而反向导热时左右段材料的热阻分布较为均匀(见图3), 材料1中的多孔结构使得热流量降低, 系统整体的热整流系数随孔隙率的增大而逐渐减小. 当在材料2上加工多孔结构时, 等效于降低了材料2的热导率. 正向导热时右段材料的热阻较小, 因而较低的孔隙率(孔隙率小于0.5)对系统的正向导热性能影响不大, 正向热流量几乎不变, 而反向热流量逐渐减小; 当孔隙率超过0.5时, 导致材料2的热阻明显降低, 并逐渐成为系统的主要热阻, 正向热流量随着孔隙率增大而明显下降, 因此系统的热整流系数明显下降. 由此可见, 通过在材料2上加工多孔结构可以调节系统的热整流效应. 对于上述选定的参数而言, 在材料2上加工孔隙率为0.5的多孔结构时可使热整流现象得到最优化, 其最大热整流系数比未打孔时提高了2倍多.
图5给出了材料2孔隙率分别为f₂ = 0(无多孔结构)和f₂ = 0.5时, 正反模式下两段材料的局域热阻分布. 正向模式下, 无多孔结构时材料1靠近界面处的热阻非常大(见图5(a)), 这是由于界面处的温度较低(见图3); 随着孔隙率逐渐增大, 多孔结构降低了材料2的导热能力, 材料2的热阻增大, 但其热阻对系统整体热阻的贡献仍然较小, 在f < 0.5时, 系统的正向热流量几乎不变(见图3). 反向模式下, 如图5(b)所示, 材料1和2的热阻相差不多, 多孔结构不仅降低了材料2的导热能力, 系统整体的热阻也明显上升. 因此, 正反向导热能力差异明显, 热整流系数提高. 在f = 0.5时, 材料2的热阻与材料1相当, 如图5(b)所示. 因此, 在f > 0.5时, 正向热流量明显降低, 系统的热整流系数明显降低.
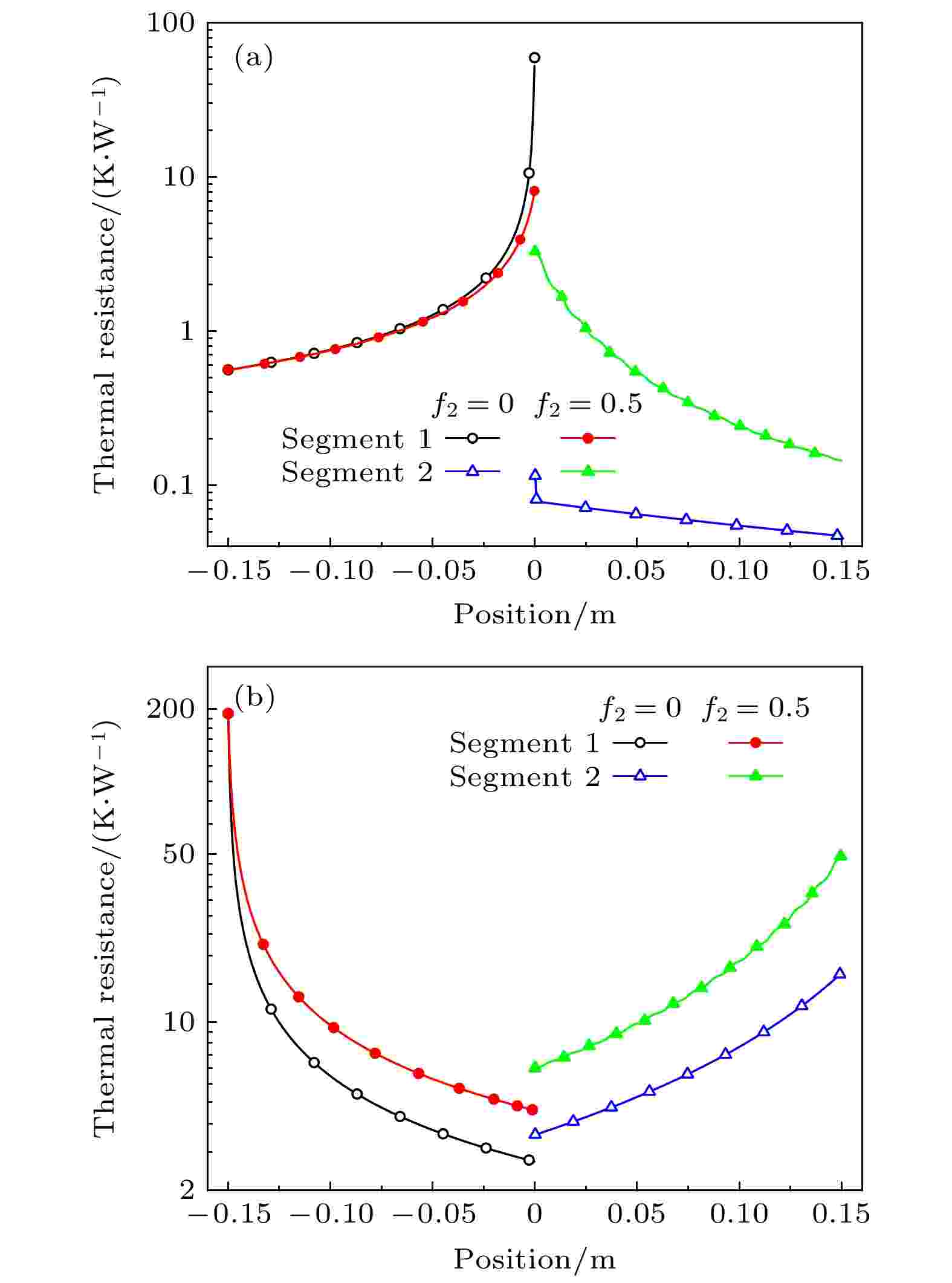图 5 两段式体材料热整流器内的热阻分布　(a) 正向模式; (b) 反向模式
Figure5. Local thermal resistance distribution in two-segment thermal rectifier: (a) Forward case; (b) reverse case.

图6显示了不同温差下热整流系数随孔隙率的变化趋势, 其中(α₁, α₂) = (3, –3). 可以看出, 当无量纲温差较小时(|Δ| = 0.5), 热整流系数随孔隙率几乎不变, 但随着温差的增大, 最大热整流系数所对应的孔隙率也逐渐增大, 当温差较大时(|Δ| = 1.7), 热整流系随材料2孔隙率的增加而不断增加, 且当f₂ = 0.7时, 与无孔结构相比热整流系数提升至原来的约3.5倍. 这是因为更大的温差使正反模式下的热导率存在更大的差异性, 因此热整流系数增加, 且在正向模式下两段材料在热阻上存在更大的差异, 因此对应的最佳孔隙率也逐渐增大. 图7显示了改变热导率温度依赖参数组合时热整流系数随孔隙率的变化趋势, 系统无量纲温差取|Δ| = 1.5. 图7(a)中改变了正负幂指数的大小, 图7(b)则在保持幂指数之差的绝对值不变的情况下, 改变了幂指数组合. 可以看出, 材料1和2的幂指数绝对值相等时, 孔隙率对热整流系数的影响随幂指数的增加而增大, 但最佳热整流系数均出现在曲线右侧(即在热导率随温度升高而降低的材料2上加工多孔结构). 当正负幂指数差值的绝对值一定时, 正幂指数较大则多孔结构对热整流系数影响较小, 仅在材料1孔隙率较小时有利于提升热整流系数; 但多孔结构对热整流系数的影响会随负幂指数的增加而增加; 当负幂指数较大时, 调整孔隙率可大幅提升热整流系数, 且在约f₂ = 0.6时, 整流系数提升至原来的2倍以上. 这是因为当材料幂指数的绝对值相同时, 正反温差下, 负幂指数材料的热导率变化更明显(例如α = +3时, κ_{(Δ = 1.5)} = 5.36 W?m^–1·K^–1, κ_{(Δ = –1.5)} = 0.02 W?m^–1·K^–1, 而当α = –3时, κ_{(Δ = 1.5)} = 0.19 W?m^–1·K^–1, κ_{(Δ = –1.5)} = 64 W?m^–1·K^–1), 因此负幂指数越大则越有利于增加正反温差下热流的不对称性, 实现更高的热整流系数, 同时对应的最佳空隙率也随之增加.
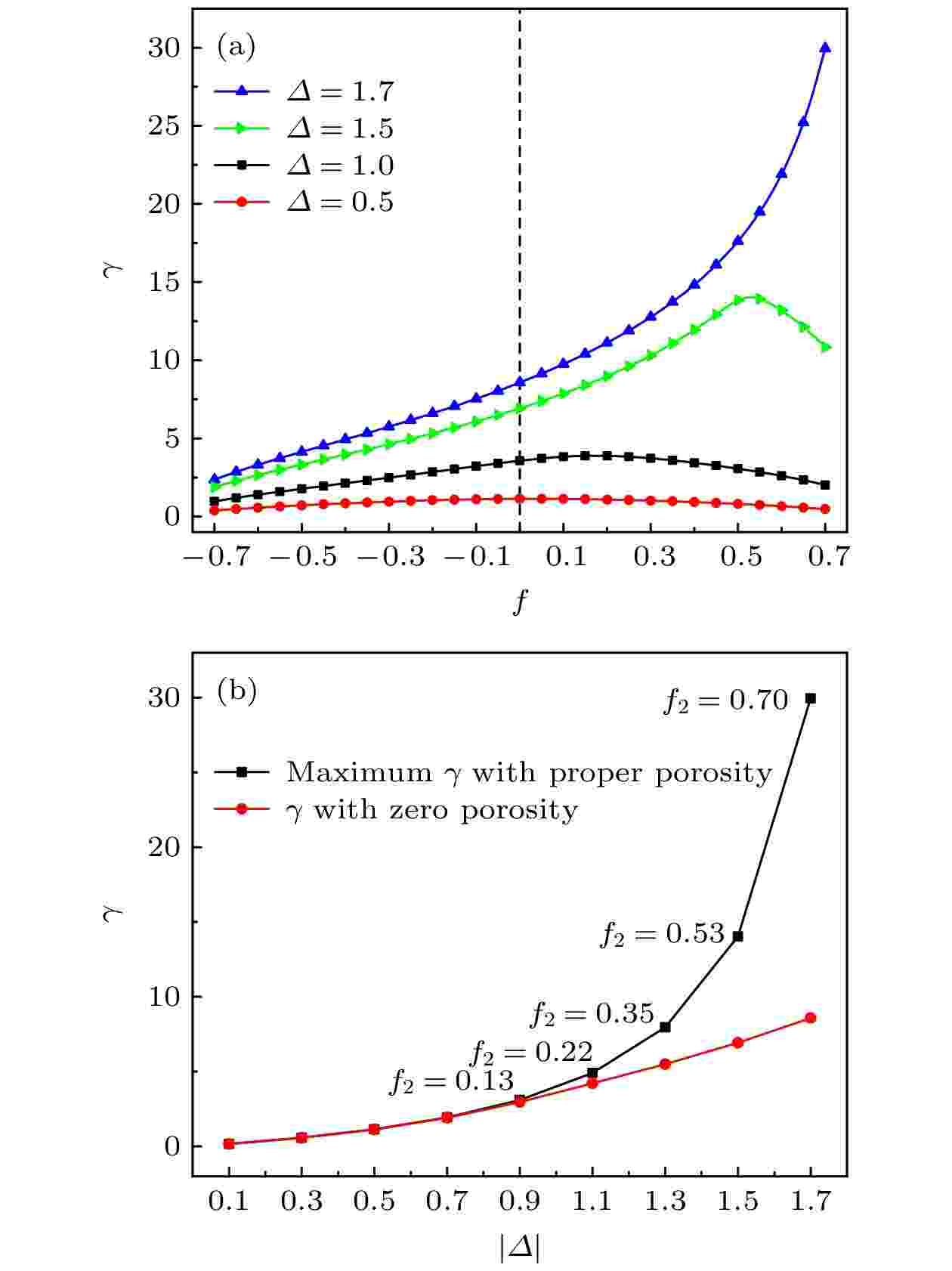图 6 (α₁, α₂) = (+3, –3)时, (a) 不同温差下热整流系数随孔隙率的变化趋势, (b) 不同温差下无孔热整流系数和有孔最佳热整流系数及对应孔隙率
Figure6. For the case of (α₁, α₂) = (+3, –3), (a) thermal rectification ratio versus porosity under different dimensionless temperature differences, (b) thermal rectification ratio without porous structure and the optimal thermal rectification ratio under different dimensionless temperature differences.

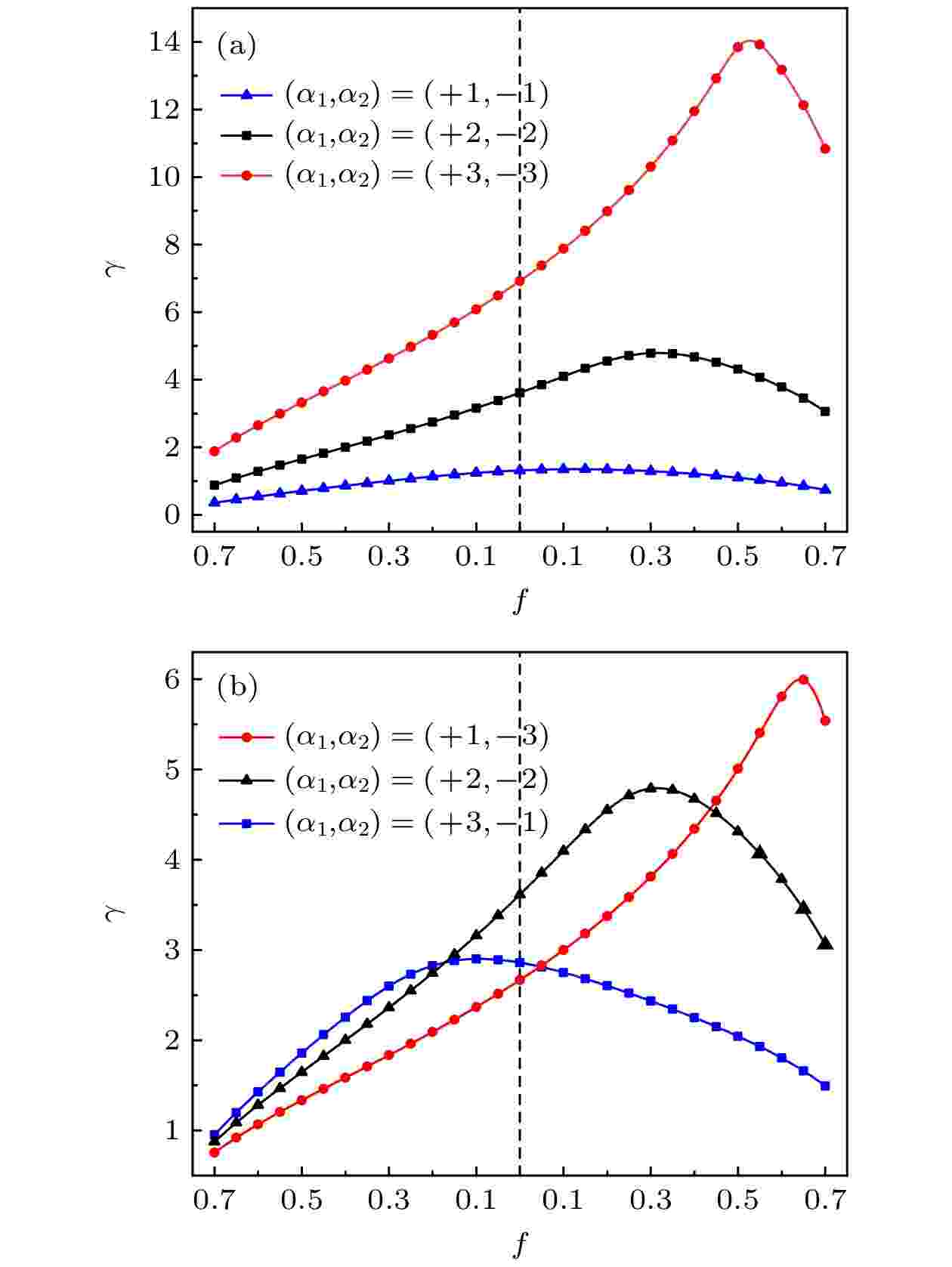图 7 |Δ| = 1.5时, (a) 改变幂指数大小和 (b) 改变幂指数组合时, 热整流系数随孔隙率的变化趋势
Figure7. For the case of |Δ| = 1.5, thermal rectification ratio versus porosity under (a) different magnitude of the power exponent and (b) different combination of power exponent.

此外, 对于上述含有多孔结构的热整流系统, 孔隙内的热辐射也是影响其内部传热的重要因素^[33]. 由玻尔兹曼四次方定律可知, 其热辐射强度与材料的发射率成正比, 图8给出了不同孔隙率下, 发射率分别为ε = 0 (不考虑热辐射)和ε = 1时, 热辐射对系统热整流系数的影响. 当在材料1上布置多孔结构时, 辐射效应会略微提升热整流系数, 而在材料2上布置多孔结构时, 辐射效应则小幅降低了热整流系数. 当在材料1上布置多孔结构时, 正向模式下多孔结构距离高温热源较近而反向模式下距离低温热源较近, 因此, 正向模式中热辐射效应对热流的影响大于反向模式, 从而增强了正反热流的不对称性; 另一方面, 孔隙中的热辐射效应等效于增强了材料1的导热能力, 而正向模式下材料1的导热能力弱于材料2, 因此热整流系数仅得到了较微弱的提升. 当在材料2上布置多孔结构时, 反向模式下的多孔结构离高温热源较近, 因此热辐射对反向热流的提升大于正向模式, 热整流系数出现一定程度的降低.
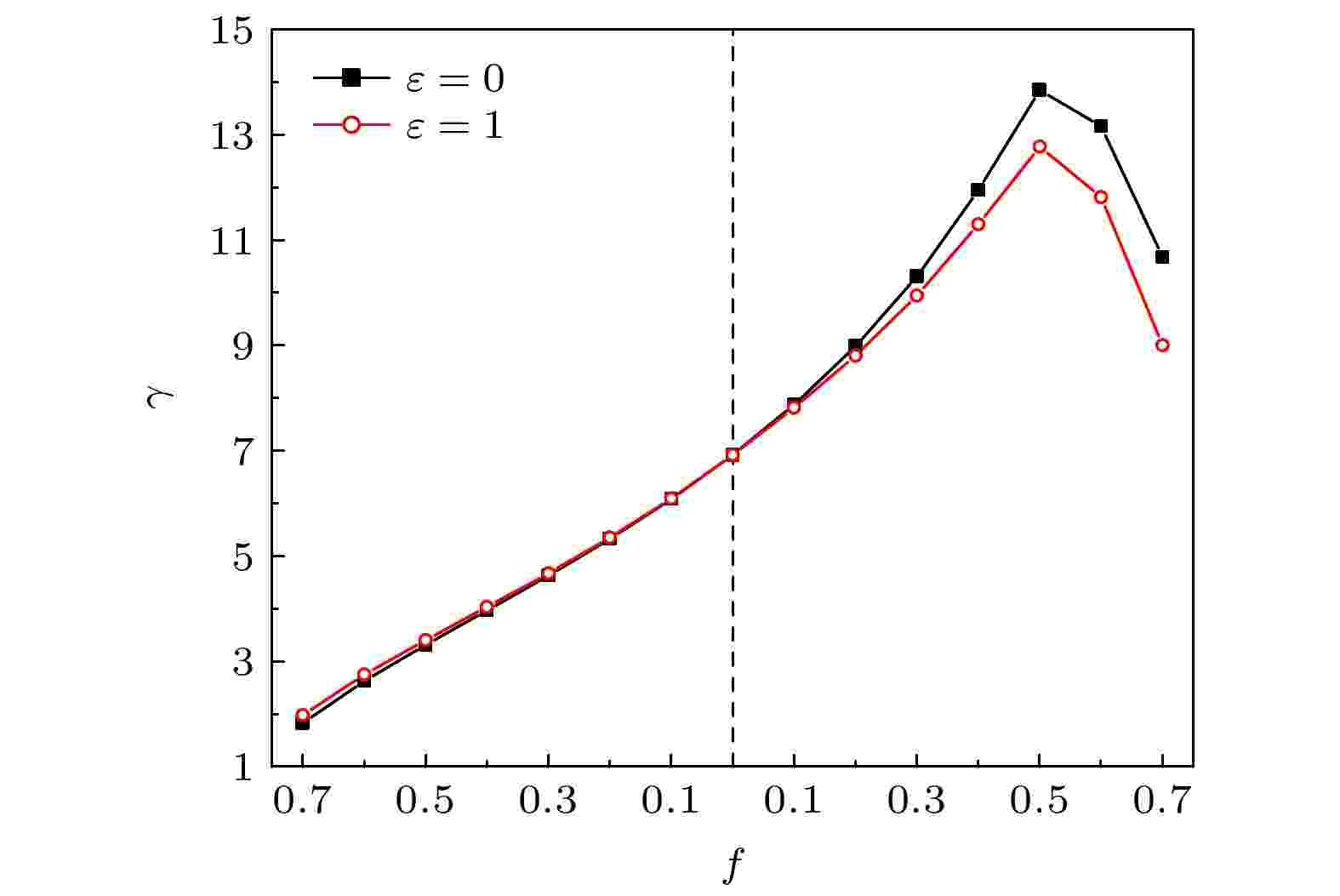图 8 |Δ| = 1.5时, 不同孔隙率下, 热辐射对热整流系数的影响
Figure8. For the case of |Δ| = 1.5, thermal rectification ratio versus porosity under ε = 0 and ε = 1.

为进一步验证上述采用多孔结构提高系统热整流系数的方法, 本文选取锌和铍镁合金组合而成的两段式组合材料进行计算. 材料1采用铍镁合金(元素质量含量为: 铍, 98%; 镁, 2%), 材料2采用充分退火的金属锌(纯度大于99.999%). 在10—100 K范围内, 二者的热导率可分别近似表示为^[41]:

$ {\kappa _{{\rm Zn} }} = 208{\left( {\frac{T}{{50}}} \right)^{ - 1.75}}\left( {\rm {W} \cdot {{\text{m}}^{ - 1}} \cdot {{K} ^{ - 1}}} \right)\text{, } $

$ {\kappa _{\rm {Be} {\text{\& }}Mg Alloy}} = 132 {\left( {\frac{T}{{50}}} \right)^{}}\left({\rm {W} \cdot {{\text{m}}^{ - 1}} \cdot {{K} ^{ - 1}}} \right). $

图9给出了无量纲温差|Δ| = 1.5时, 热整流系数和正反热流随孔隙率的变化趋势. 可以看出, 此系统中热整流系数的变化趋势与图4基本一致. 计算结果表明, 在金属锌(材料2)中打孔可以使系统的热整流系数得到提升. 由于金属锌的幂指数绝对值大于铍镁合金的幂指数绝对值, 因此最佳孔隙率右移(约为f₂ = 0.5). 其最大热整流系数相对于未打孔的情况提高了65%.
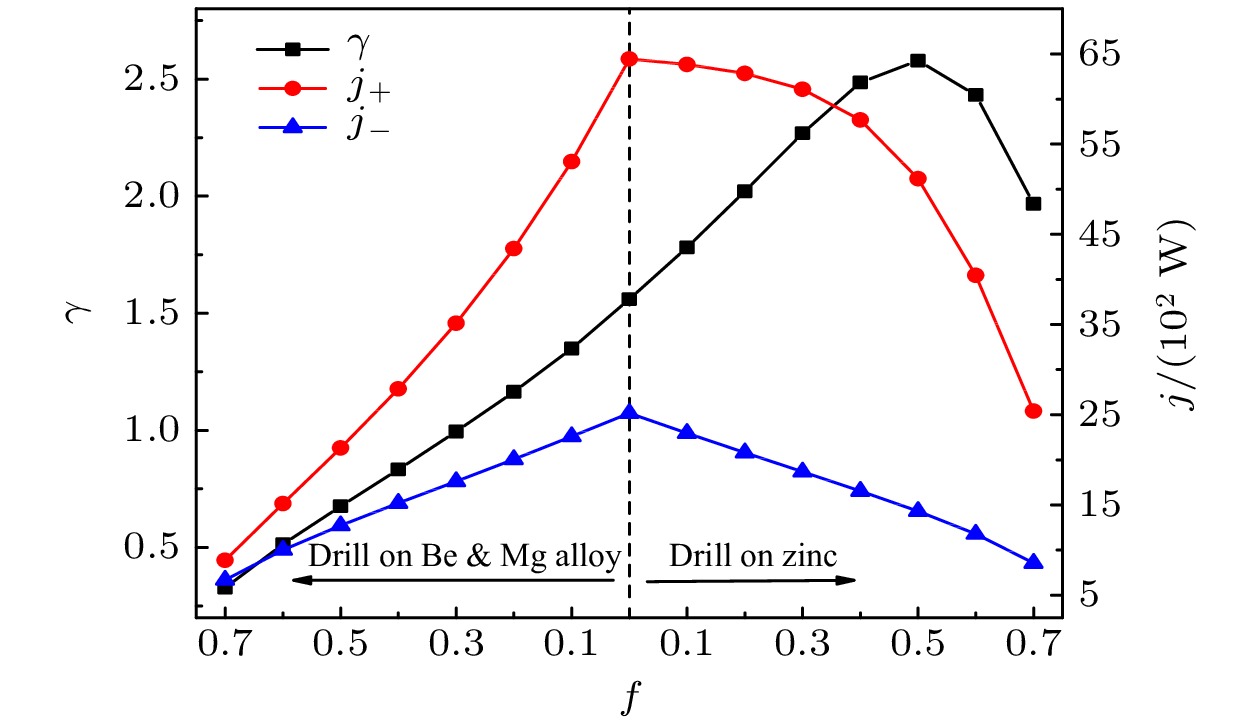图 9 热整流系数(左)及正反热流(右)随铍镁合金或金属锌孔隙率f的变化趋势
Figure9. Thermal rectification ratio (left) and heat flux (right) versus porosity in a Be & Mg alloy-Zn two-segment system.

2

-->

4.1.多孔模型及有效介质理论

本文参考Rayleigh法对多孔介质有效热导率进行求解^[39]. 图10中, 模型尺寸与热整流系统中的一段材料相同, 即长为150 mm, 宽为100 mm, 介质热导率为κ_h, 上面均匀分布10 × 15个半径r = a的多孔结构, 孔隙率为f. 左侧为高温热源, 右侧为低温热源, 温度梯度为G₀, 介质内存在由左向右的热流, (5)式为该模型中的导热控制方程: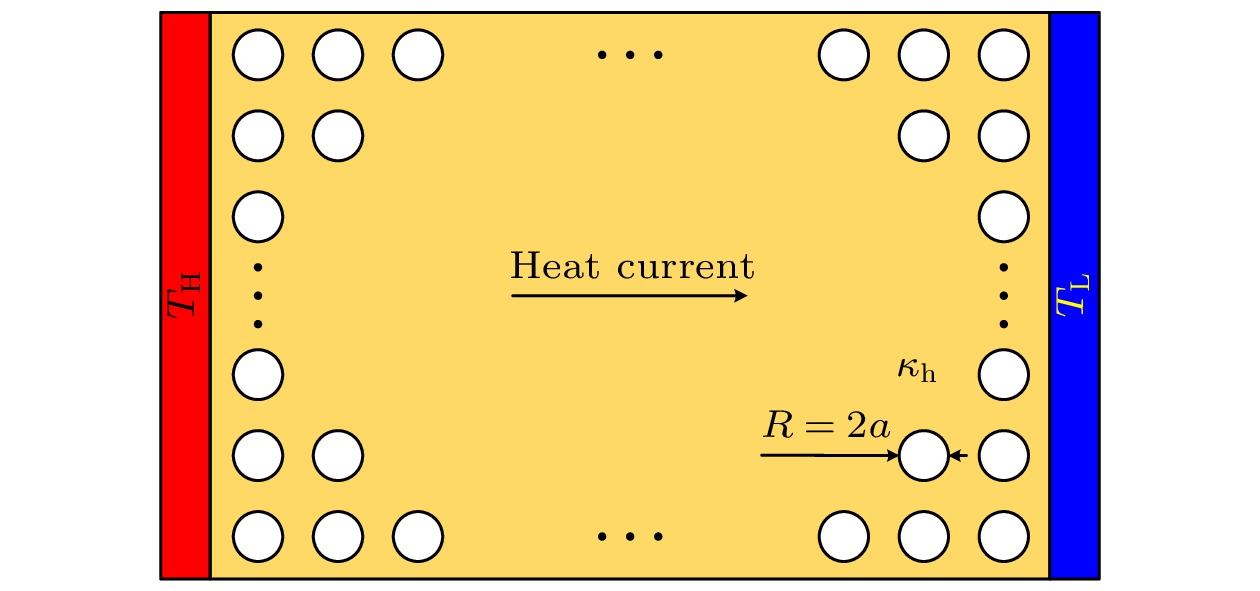
图 10 多孔介质模型示意图(均匀分布10 × 15个圆形孔)
Figure10. Schematic diagram of porous media (10 × 15 circular holes are uniformly distributed).

$ \nabla \cdot \left( {\kappa \nabla T} \right) = - Q , $

式中, $ \nabla $为拉普拉斯算子, Q为该介质中的内热源, T为介质内温度. 当无内热源时, (5)式在极坐标系下的通解为^[40]

$ \begin{split} T =\;& \left( {{A_0} + {B_0}{\text{ln}}\rho } \right)\left( {{\mu _0} + {\nu _0}\theta } \right) \\ & + \sum\limits_{m = 1}^\infty \left( {{A_m}{\rho ^m} + {B_m}{\rho ^{ - m}}} \right)\\ & \times \left[ {{\mu _m}{\text{sin}}\left( {m\theta } \right) + {\nu _m}\cos (m\theta )} \right]. \end{split} $

由于介质中的多孔结构可以视为周期性分布, 因此首先随机挑选其中一个孔洞结构, 并将极坐标系原点(用来描述单个孔周围的温度)和直角坐标系(用来描述每个孔洞单元的位置)原点置于该孔圆心处, 设温度梯度方向沿x轴方向, 通解中B₀和v₀为0, 多孔介质的温度分布

$ \begin{split}& T\left(\rho ,\theta \right)=\\\;&{A}_{00}+\displaystyle \sum _{m=1}^{\infty }{\rho }^{m}\big[{A}_{0m}^{1}\sin (m\theta ) +{A}_{0m}^{2}\cos (m\theta )\big]+ \\& \displaystyle \sum _{m=1}^{\infty }{\rho }^{-m}\big[{B}_{0m}^{1}\sin(m\theta ) + {B}_{0m}^{2}\cos (m\theta )\big],~~ \rho \geqslant a. \end{split} $

参考电磁场中的叠加原理(任一支路的电势可以看成电路中每一个单独电源独立工作于电路时, 在该支路产生的电势的代数和), 针对(7)式的温度场, 同样可以由叠加原理得到多孔介质内的温度,

$ \begin{split}\;& T=-{G}_{0}x + \\& \displaystyle \sum _{i=1}^{\infty }\displaystyle \sum _{m=1}^{\infty }{\rho }_{i}^{-m}\big[{B}_{0m}^{2}\cos(m{\theta }_{\text{i}})+{B}_{0m}^{1}\sin(m{\theta }_{\text{i}})\big]+ \\& \displaystyle \sum _{m=1}^{\infty }{\rho }^{-m}\big[{B}_{0m}^{1}\sin(m\theta ) + {B}_{0m}^{2}\cos (m\theta )\big] ,~ \rho \geqslant a.\end{split} $

既然(7)式和(8)式均表示多孔介质内的温度分布情况, 因此这两个等式必然相等. 两式中的第三项相同, 因此两式前两项之和也必然相等, 于是可得到

$ \begin{split} & {A_{00}} + \sum\limits_{m = 1}^\infty {{\rho ^m}\left[ {A_{0m}^2\cos (m\theta ) + A_{0m}^1\sin (m\theta )} \right]} = - {G_0}x \\ \;& + \sum\limits_{i = 1}^\infty {\sum\limits_{m = 1}^\infty {{\rho ^{-m}}\left[ {B_{0m}^2\cos (m{\theta _{\text{i}}}) + B_{0m}^1\sin (m{\theta _{\rm{i}}})} \right]} }. \\[-12pt]\end{split} $

多孔介质中的孔壁可近似为绝热边界条件

$ {\kappa _{\text{h}}}{\left. {\frac{{\partial T}}{{\partial \rho }}} \right|_{\rho = \varOmega }} = 0\text{, } $

式中Ω表示孔洞的边界. 参考文献[39, 40]的方法, 将(9)式左右两侧对x求导, 并结合(10)式可得:

$ \begin{split} &\sum\limits_{m = 1}^\infty \frac{{m!\rho _0^{m - n}}}{{\left( {m - n} \right)!{a^{2m}}}}\left[\right. B_{0m}^1\sin \left( {\left( {m - n} \right){\theta _0}} \right) \\ &+ B_{0m}^2\cos \left( {\left( {m - n} \right){\theta _0}} \right)\left. \right] \\ & - \sum\limits_{m = 1}^\infty {{\left( { - 1} \right)}^n} \frac{{\left( {m + n - 1} \right)!}}{{\left( {m - 1} \right)!}}\left[\right. B_{0m}^1W_{m + n}^1\left( Q \right) \\&+ B_{0m}^2W_{m + n}^2\left( Q \right) \left.\right] = - {G_0}{\delta _{1,n}}\,, \hfill \\ \end{split} $

式中,

$ {\delta }_{1,n}=\Bigg\{\begin{aligned}&1, ~~~~n=1, \\ &0, ~~~~n\ne 1, \end{aligned} $

$ W_l^1\left( Q \right) = \sum\limits_{i = 1}^\infty {\rho _i^{ - l}\sin \left( {l{\theta _i}} \right)} \text{, } $

$ W_l^2\left( Q \right) = \sum\limits_{i = 1}^\infty {\rho _i^{ - l}\cos \left( {l{\theta _i}} \right)} \text{, } $

$ {\rho _i} = \sqrt {{{\left( {{x_0} - u} \right)}^2} - {{\left( {{y_0} - v} \right)}^2}} \text{, } $

$ \cos \left( {{\theta _i}} \right) = {{{x_0} - u}}/{{{\rho _i}}}. $

(11)式中, 由于温度梯度方向沿x方向, $B^1_{0m}$和$ B^2_{0m} $ (m为偶数时)可消去, 因此为简化求解, 仅保留m = 1项,

$ B_{01}^2 = - \dfrac{{{G_0}}}{{\left( { {1}/{{{a^2}}} - 29.4{a^6}} \right)}}. $

同样, 基于有效介质理论可得:

$ {\kappa _{\text{e}}}{\text{ = }}{\kappa _{\text{h}}}\left( {1 - \frac{{\left\langle {{\nabla _x}{T_0}} \right\rangle }}{{{{\left\langle {{\nabla _x}{T_0}} \right\rangle }_i}}}} \right), $

式中,

$ \begin{gathered} \left\langle {{\nabla _x}{T_0}} \right\rangle {\text{ = }} - {\text{2}}{G_0}, \hfill \\ {\left\langle {{\nabla _x}{T_0}} \right\rangle _i}{\text{ = }}\frac{2}{{{a^2}}}B_{01}^2f. \hfill \\ \end{gathered} $

结合(12)式和(13)式, 可得图10所示多孔介质有效热导率为

$ \dfrac{{{\kappa _{\text{e}}}}}{{{\kappa _{\text{h}}}}} = \dfrac{{ - {{\text{π }}^4} + {{\text{π }}^4}f + 29.407{f^4}}}{{ - {{\text{π }}^4} - {{\text{π }}^4}f + 29.407{f^4}}}. $

保持介质热导率的参考温度T_ref = 200 K, 介质热导率参数κ₀ = 1 W?m^–1·K^–1, 无量纲温差|Δ| = 1.5. 图11(a)给出了多孔介质热导率参数随孔隙率的变化. 可以看出, 多孔介质的热导率参数随孔隙率的增加而逐渐降低, 这是因为多孔结构增加了额外的热阻, 孔隙率越大则热阻越大. 由圆形与方形的面积比为π/4 = 0.785可知, 图10所示圆形多孔介质的最大孔隙率为0.785 (孔洞结构互相相切). 图11(b)给出了不同材料热导率幂指数下, (14)式计算结果与有限元模拟所得热流与孔隙率的变化关系, 可以看出, 二者吻合很好. 当孔隙率较低时(f < 0.7), EMA法获得的多孔介质热导率几乎与有限元模拟解几乎完全吻合, 当孔隙率较高时(f = 0.7), EMA法热导率与有限元模拟稍有偏差. 越接近最大孔隙率, 误差越大. 因此, 本文中, 孔隙率计算范围取0 < f < 0.75.
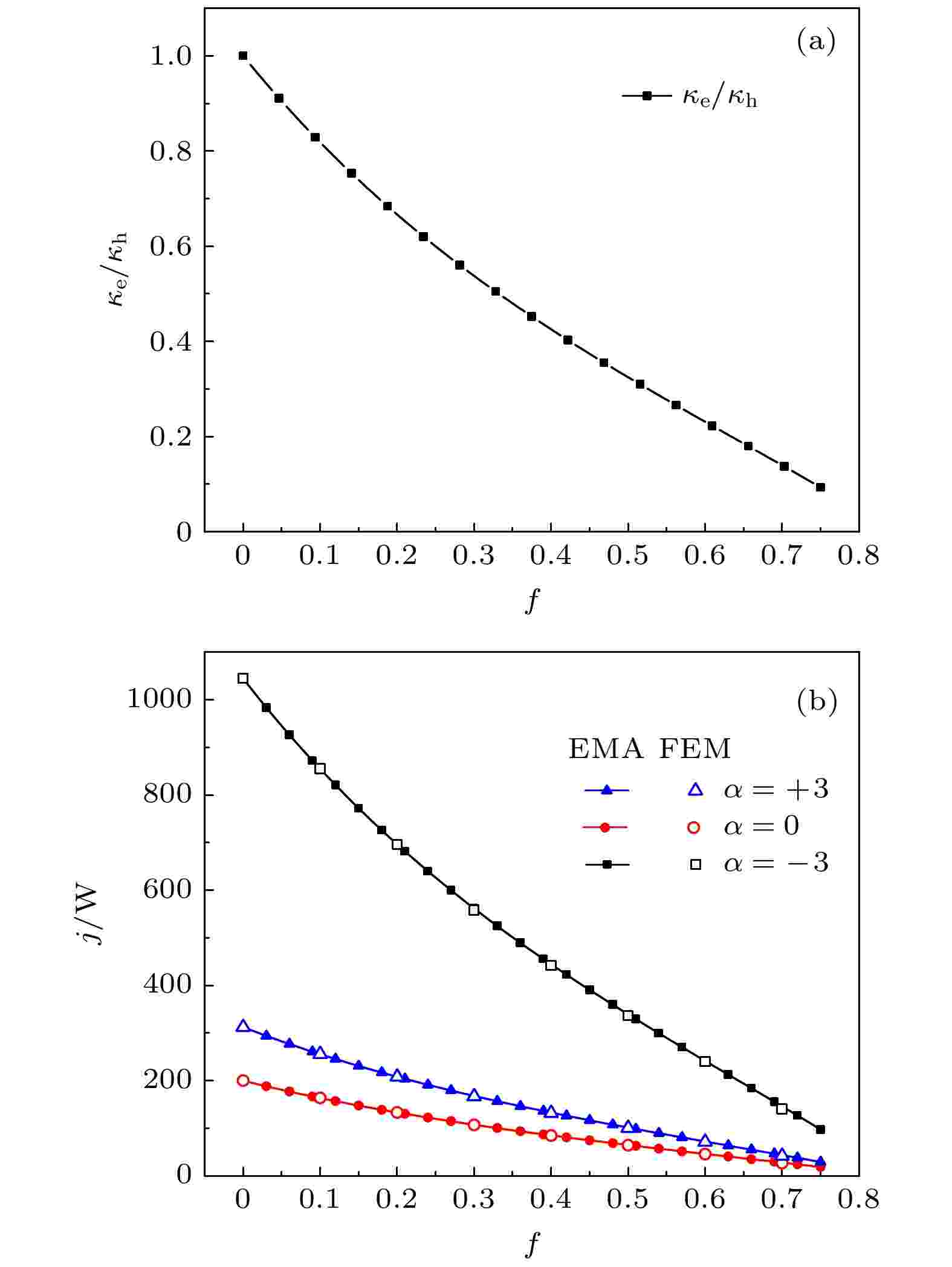图 11 (a) 多孔介质有效热导率随孔隙率的变化关系; (b) |Δ| = 1.5时, EMA与FEM计算所得热流与孔隙率的变化关系
Figure11. (a) The relationship between the effective thermal conductivity of the porous medium and the porosity; (b) the comparison of the heat flux calculated by EMA and FEM for the case of |Δ| = 1.5.

2 -->

4.2.多孔结构热整流模型

在材料上加工多孔结构并不能改变材料热导率随温度变化的特性, 而是等效于降低了材料的热导率参数κ₀, 此时两段材料的热导率参数可表示为孔隙率的函数κ₁(f₁)和κ₂(f₂), 基于傅里叶定律, 正反模式下的热流可分别表示为: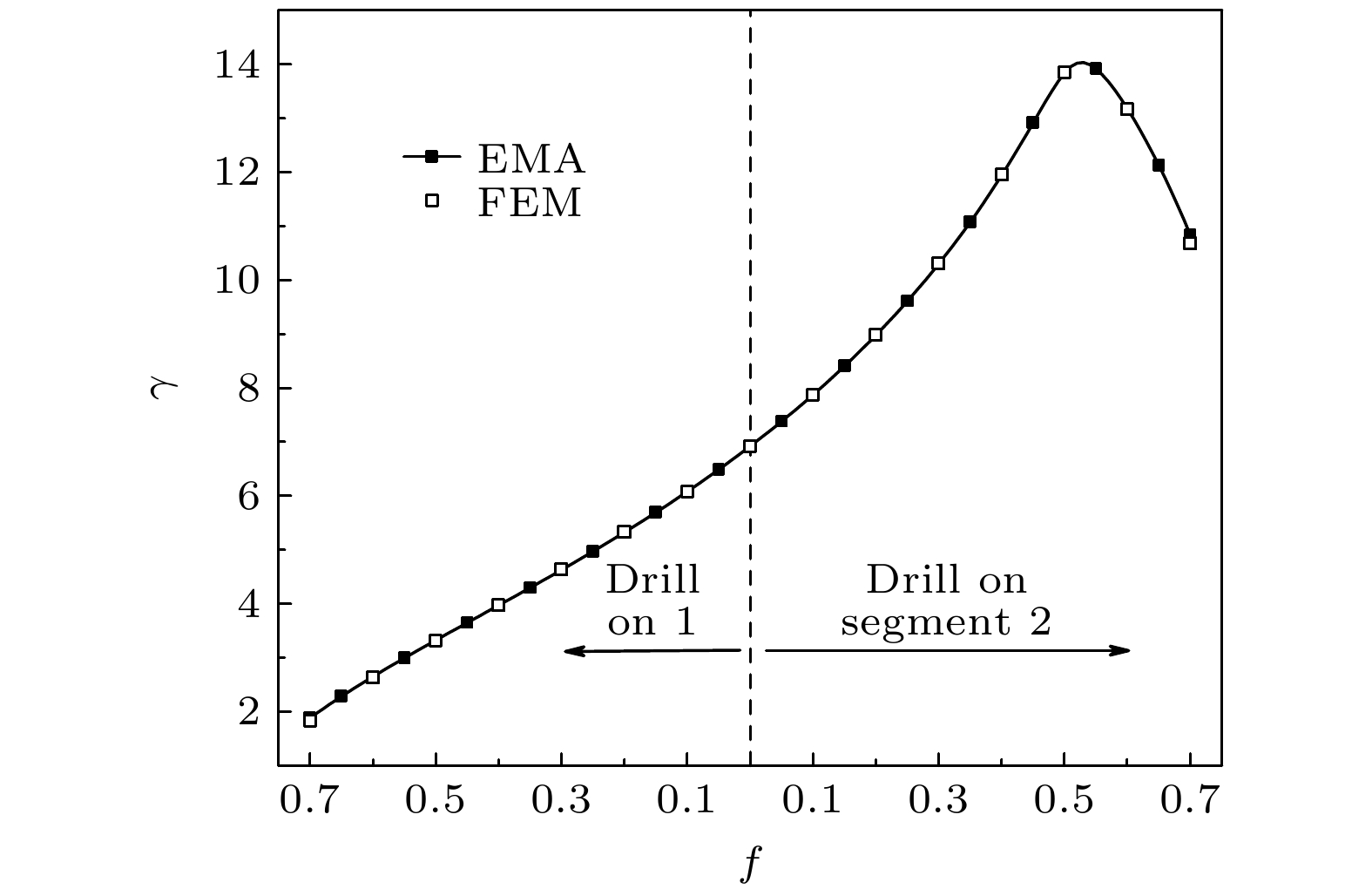

$\begin{split} {j_ + } =\;& {\int_{{T_{{int} + }}}^{{T_{H} }} {{\kappa _1}\left( {{f_1}} \right)\left( {\frac{T}{{{T_{{\text{ref}}}}}}} \right)} ^{{\alpha _1}}}{\text{d}}t\\ =\;& {\int_{{T_{L} }}^{{T_{i} }_{nt + }} {{\kappa _2}\left( {{f_2}} \right)\left( {\frac{T}{{{T_{{\text{ref}}}}}}} \right)} ^{{\alpha _2}}}{\text{d}}t, \end{split}$

$\begin{split} {j_ - } =\;& {\int_{{T_{L} }}^{{T_{i} }_{nt - }} {{\kappa _1}\left( {{f_1}} \right)\left( {\frac{T}{{{T_{{\text{ref}}}}}}} \right)} ^{{\alpha _1}}}{\rm{d}}t\\ =\;& {\int_{{T_{{int} - }}}^{{T_{H} }} {{\kappa _2}\left( {{f_2}} \right)\left( {\frac{T}{{{T_{{\text{ref}}}}}}} \right)} ^{{\alpha _2}}}{\text{d}}t . \end{split}$

由(15)式和(16)式可分别获得正反传热模式下界面处的温度和热流量, 进而计算出系统的热整流系数, 其结果如图12所示. 可以看出有效介质理论的计算结果与有限元方法的结果基本完全一致.
图 12 |Δ| = 1.5时, EMA与FEM计算所得热整流系数随材料1或材料2孔隙率的变化趋势
Figure12. Comparison of the thermal rectification ratio calculated by EMA and FEM for the case of |Δ| = 1.5.

如前所述, 在材料1或者2中加工多孔结构等效于降低了材料的热导率参数κ₀. 为方便对比分析, 考虑材料的热导率参数变化对热整流系数的影响. 设材料1与材料2均未布置多孔结构, 二者的热导率参数比值为κ₀₁/κ₀₂ = β. 图13给出了热导率温度依赖参数取(α₁, α₂) = (3, –3)和温差|Δ| = 1.5时, 热整流系数γ随热导率参数比值β的变化趋势.
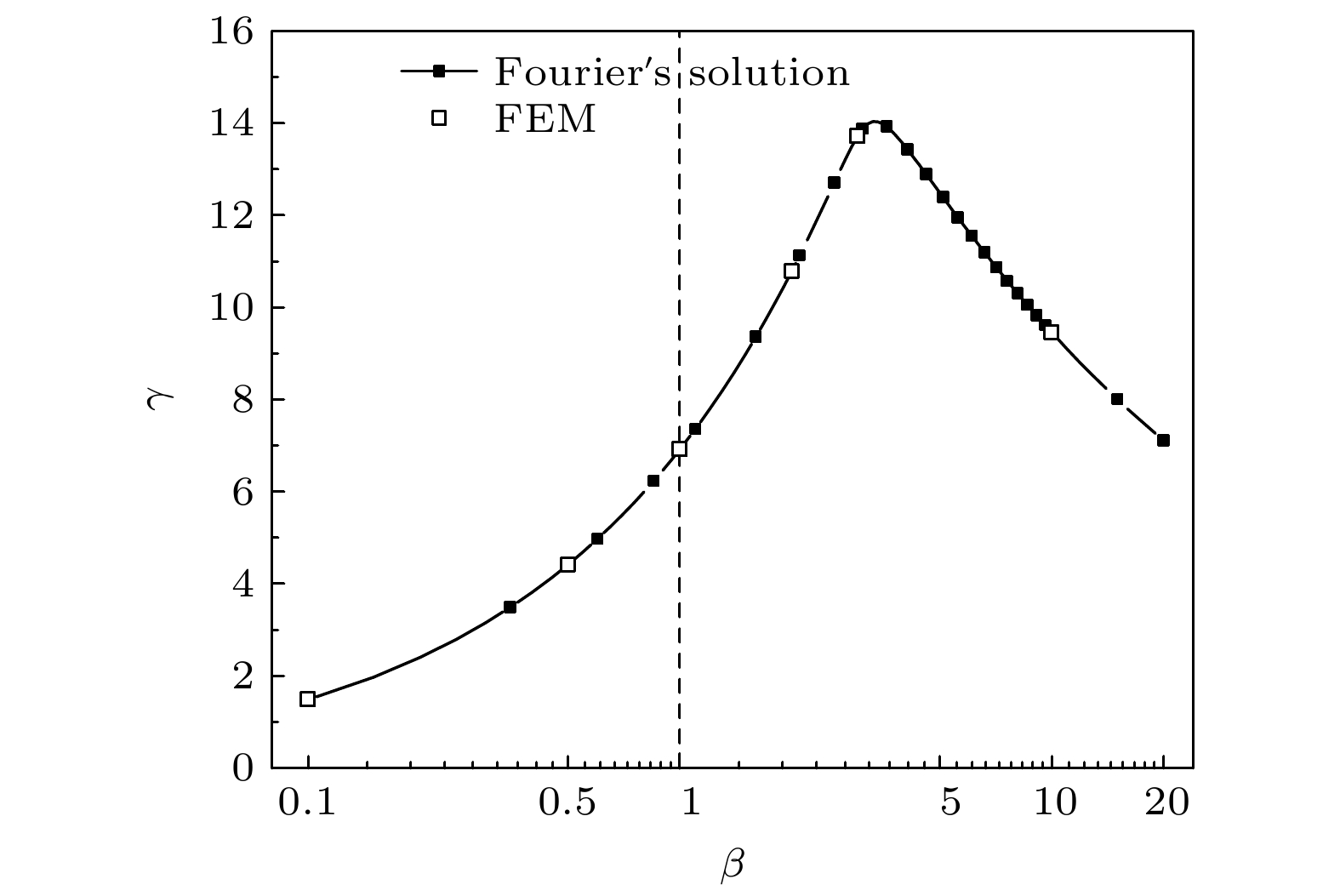图 13 热整流系数随热导率参数比值的变化趋势
Figure13. Thermal rectification ratio versus thermal conductivity parameter ratio.

当β < 1时, 材料1的热导率相对较小, 类似于图4中虚线左侧的情况(在材料1上加工多孔结构), 降低β值等效于增大材料1的孔隙率, 热整流系数逐渐降低. 当β > 1时, 材料2的热导率相对较小, 类似于图4中虚线右侧的情况(在材料2上加工多孔结构), 增大β值等效于增大材料2的孔隙率, 热整流效率逐渐增大并达到一个极大值, 然后逐渐降低. 可以看出, 图13和图4的变化趋势完全类似, 验证了利用多孔结构调节系统热整流效应的可行性.
根据上述分析, 两种材料的热导率参数比值对体材料热整流现象有很大的影响, 合适的β值能够明显提升系统的热整流系数. 但是, 通常自然界中很难找到一组热导率参数比值处于最佳状态的体材料, 大大限制了体材料热整流系数的提升. 因此, 本文提出在体材料上均匀布置多孔结构, 通过多孔结构调整材料的热导率参数, 最终达到热整流系数的最优化.

在热导率温度依赖特性不同的两种材料组合而成的两段式材料中, 可以实现热整流效应. 本文提出通过布置多孔结构来提高系统热整流系数的方法. 分别利用有限元法和有效介质理论计算了系统的热整流系数, 二者结果基本一致. 计算表明, 温差较小时, 孔隙率对热整流系数的影响较小; 当温差较大时, 布置多孔结构可以实现热整流效应的调控. 在热导率随温度升高而增大的材料中布置多孔结构, 会降低系统的热整流系数; 在热导率随温度升高而减小的材料中布置多孔结构, 可以实现热整流效应的强化; 孔隙率较小时正向热流量基本保持不变, 反向模式热流量减小, 热整流系数增大; 孔隙率较大时正反向热流量都减小, 热整流系数降低. 因而存在一个最佳的孔隙率, 相对于无多孔结构的系统, 热整流系数可以提高2—3倍.