摘要: 由大量耦合相振子组成的Kuramoto模型是研究各种自持续振荡系统同步相变和集体动力学的重要模型. 近些年, 高阶耦合Kuramoto模型引起了广泛的研究兴趣, 尤其高阶耦合结构在模拟编码和信息存储的动力学方面起到重要作用. 为了研究高阶耦合的影响, 本文通过考虑频率与耦合之间的关联对高阶耦合的Kuramoto模型进行了推广, 所得到的模型出现了一些新颖的动力学现象, 包括多集团态(多团簇态)、双稳态、爆炸性同步以及振荡态. 对无序态的线性稳定分析得到表征系统由无序向同步转变的临界耦合强度, 利用自洽方法分析得到系统的多团簇态, 并进一步在等效低维子空间中对多团簇态进行线性稳定性分析得到稳定的多团簇态解以及去同步相变点. 对理论分析结果的讨论总结了系统由迟滞到振荡态的转变. 此外, 本文强调结合表征系统不对称性的Kuramoto序参量和表征系统多团簇态的Daido序参量可以对系统宏观动力学给出完整的描述. 通过本文的研究可以进一步加深对高阶耦合相振子系统中耦合异质性以及爆炸性同步的理解.
关键词: 耦合相振子 /
同步 /
相变 /
多集团态 English Abstract Collective dynamics of higher-order coupled phase oscillators Cai Zong-Kai 1,2 ,Xu Can 1,2 ,Zheng Zhi-Gang 1,2 1.College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11875135), the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11905068), the Scientific and Technological Foundation of Quanzhou, China (Grant No. 2018C085R), and the Scientific Research Funds of Huaqiao University, China (Grant No. ZQN-810)Received Date: 29 June 2021Accepted Date: 29 July 2021Available Online: 15 August 2021Published Online: 20 November 2021Abstract: The Kuramoto model consisting of large ensembles of coupled phase oscillators serves as an illustrative paradigm for studying the synchronization transitions and collective behaviors in various self-sustained systems. In recent years, the research of the high-order coupled phase oscillators has attracted extensive interest for the high-order coupled structure playing an essential role in modeling the dynamics of code and data storage. By studying the effects of high-order coupling, we extend the Kuramoto model of high-order structure by considering the correlations between frequency and coupling, which reflects the intrinsic properties of heterogeneity of interactions between oscillators. Several novel dynamic phenomena occur in the model, including clustering, extensive multistability, explosive synchronization and oscillatory state. The universal form of the critical coupling strength characterizing the transition from disorder to order is obtained via an analysis of the stability of the incoherent state. Furthermore, we present the self-consistent approach and find the multi-cluster with their expressions of order parameters. The stability analysis of multi-cluster is performed in the subspace getting stability condition together with the stable solutions of order parameters. The discussion of all the results summarizes the mechanism of the transition from hysteresis to oscillatory states. In addition, we emphasize that the combination of the Kuramoto order parameter capturing the asymmetry of the system and the Daido order parameter representing the clustering can give a complete description of the macroscopic dynamics of the system. The research of this paper can improve the understanding of the effects of the heterogeneity among populations and the explosive synchronization occurring in higher-order coupled phase oscillators.Keywords: coupled phase oscillators /synchronization /phase transition /multi-cluster 全文HTML --> --> --> 1.引 言 同步涌现是耦合非线性系统中的一个显著现象, 对这种自组织行为的研究涵盖了物理学、工程学、生物学以及社会系统等多个学科领域. 典型的例子包括超导中的耦合约瑟夫森结、电力网络、心脏起搏器、大脑中的神经元放电以及观众现场掌声的形成等[1 -4 ] . 探索通往同步的道路并揭示这种集体行为背后的内在机制具有重要的现实意义, 也为理解复杂系统宏观动力学提供理论依据[5 -7 ] .[8 ] , 该模型于1975年被正式提出. Kuramoto模型由具有随机固有自然频率的相振子系统组成, 并且振子间通过相差的正弦函数进行全局耦合. Kuramoto模型由弱耦合极限环振子通过快慢时间尺度分离绝热地消去系统的振幅效应而得到, 在这一框架下, 系统从无序到有序的同步转变可以被看作是一种典型的非平衡相变. 经典的Kuramoto模型指出系统从无序态到同步态的转变呈现出一系列连续相变, 相应地, 刻画系统同步程度的序参量经历了一个从零到非零的超临界分岔, 这一同步转变特性与统计力学中的二级相变十分类似[9 -11 ] .[12 -17 ] , 即系统的耦合函数包含了相差的二阶乃至更高阶简谐项, 这类高阶耦合相振子模型被统称为Kuramoto–Daido模型, 这类模型与现实中的许多物理系统密切相关[18 -22 ] . 最近研究表明, 作为Kuramoto耦合相振子模型的一种重要推广, 当耦合函数引入高阶结构时, 相较于单纯的一阶耦合, 系统会产生一系列新颖的动力学现象[23 -29 ] , 例如多集团态、广泛多稳态、一系列爆炸性去同步转变等[30 -35 ] . 此外, 全局高阶耦合相振子系统中涌现出一系列非平庸动力学特性可以用来有效地模拟编码和数据存储, 也为揭示人脑中结构与功能的关联提供了重要的理论启示. 以往对高阶耦合相振子的研究集中在振子间为均匀的耦合方式, 而现实中个体间的相互作用往往是异质性且非对称的, 例如社交中人与人之间的交流受到个体性格差异的影响、大脑中神经元连接的不对称性以及电力网络中节点间耦合存在差异等. 由此本文主要考虑异质性且非对称的耦合, 耦合异质性的引入也使得系统的宏观动力学行为和发生的相变过程完全不同(相比于均匀耦合系统中出现的连续的二级相变), 除了多集团态、广泛多稳态, 系统还将出现由表征系统一级相变的迟滞现象向振荡态的转变, 此外系统中表现出的爆炸式同步相变与现实中一些突发性现象具有高度相似性, 对爆炸式同步的研究具有重要的现实意义.2 节引入高阶耦合的动力学模型, 并展示了该动力学模型的数值模拟结果; 第3 节进行理论分析, 包括通过无序态的稳定分析得到依赖于频率分布参数的临界耦合强度, 利用自洽分析得到了系统的多团簇态解, 以及对多团簇态的稳定性分析得到稳定的多团簇态解, 并结合各分析结果讨论系统相变机制的转变; 最后, 在第4 节对全文内容进行概括总结, 并对高阶耦合的研究进行展望.2.理论模型及数值模拟 22.1.理论模型 2.1.理论模型 首先, 考虑将经典Kuramoto模型推广到一般的高阶耦合相振子模型, 其动力学演化方程如下:$``\cdot "$ 表示对时间的导数, $ \theta_i(t) $ 表示第$ i $ 个振子在$ t $ 时刻的相位, $ \omega_i $ 是振子$ i $ 的固有自然频率, 一般取自一个给定的概率分布函数$ g(\omega) $ . $ K_{ij} $ 代表第$ i $ 个振子和第$ j $ 个振子间的耦合强度, 并且耦合强度大于$ 0 $ 表示振子间的相互吸引. 与振子间的相互作用为均匀耦合的经典Kuramoto模型相比, 该模型中的耦合强度是异质性且非对称的, 即$ K_{ij}\neq K_{ji} $ , 由此更能反映实际耦合的非对称的本质[36 ,37 ] , 这也与大脑中的神经元连接的不对称性一致.$ K_{ij} = K|w_i| $ , 且$ K > 0 $ [38 -47 ] , 这种耦合称为内耦合, 即在耦合系统中通过建立耦合强度与振子本身固有频率的关联而赋予振子间耦合的异质性, 在这样的框架下, 耦合的异质性源自振子本身的固有特性. 频率权重模型通常被用来揭示耦合相振子系统通往同步过程中发生的一级相变[48 -53 ] , 但是这些研究工作仅仅考虑相差的一次简谐函数. 本文主要研究高阶耦合相振子系统在自然频率的分布为双峰对称情形下的动力学特性.$ Z_k(t) $ 是宏观变量, 对应于复平面单位圆上$ N $ 个振子$ \{{\rm e}^{{\rm i}k\theta}\} $ 的质心. $ R_k(t) $ 和$ \varTheta_k(t) $ 分别是复序参量$ Z_k(t) $ 的幅值和幅角. $ Z_1(t) $ 是Kuramoto序参量, 而$ Z_2(t) $ 则被称作Daido序参量. 从下文将会发现, 这两个序参量的组合可以很好地描述方程(1 )的宏观动力学. 这组序参量可以被解释为由振子群产生的集体节律, 特别地, $ Z_2(t) $ 可以衡量振子间的同步程度以及集团态的形成, 而$ Z_1(t) $ 则反映系统的不对称度, 尤其当所有振子同步到两个不同的团簇上时. 显然, 当系统在单位圆上的不同位置出现多个同步团簇时, $ Z_2(t) $ 可以更好地刻画系统的同步程度, 而$ Z_1(t) $ 则表示团簇间的大小差异, 即两个团簇的不对称程度. 具体而言, $ R_1 = 0 $ 表明两个同步团簇完全对称, 幅角相差$ \pi $ , 而当$ R_1 = 1 $ 时, 意味着整个系统表现为一个巨大的振子团簇, 说明了系统达到完全同步.2 )式定义的序参量方程可以将方程(3 )改写成平均场的形式:$ R_2 $ 和$ \varTheta_2 $ 耦合, 而与其他所有振子似乎解耦了, 且对每一个振子而言, 与平均场的有效作用强度为$ KR_2 |\omega_i| $ .2.2.数值模拟结果 -->2.2.数值模拟结果 接下来, 通过展示方程(3 )的数值模拟结果来直观地了解该系统所表现出的新颖的动力学现象. 以$ N = 50000 $ 个振子数, 利用四阶Runge-Kutta方法对方程(3 )进行数值模拟, 自然频率分别服从双峰洛伦兹分布$ \varDelta = 0.1 $ 观察不同$ \omega_0 $ 情形下系统随耦合强度的改变(增加或减小)所表现出的同步相变过程, 而对于均匀分布直接固定$ \gamma = 1 $ 观察其同步相变过程, 并且在持续增大耦合强度$ K $ 时选取任意的相位初始条件$ \theta_i(0) $ , 而在持续减小耦合强度$ K $ 的过程中, 以不同概率$ \alpha $ 和$ 1-\alpha $ 分别选取相位初始条件为$ \theta_i(0) = 0 $ 和$ \theta_i(0) = \pi $ .图1 给出了自然频率服从双峰洛伦兹情形下序参量$ R_2 $ 和$ R_1 $ 对应不同初始条件和频率分布参数下随耦合强度$ K $ 的相变图. 其中, 双峰洛伦兹分布的半宽$ \varDelta $ 固定为$ 0.10 $ , 中心频率$ \omega_0 $ 取值分别为$ 0.08 $ (图1(a) ), $ 0.12 $ (图1(b) ), $ 0.30 $ (图1(c) ), 和$ 0.40 $ (图1(d) ). $ \alpha $ 分别取$ 1.00 $ (粉), $ 0.90 $ (青), $ 0.80 $ (蓝), $ 0.70 $ (绿), $ 0.60 $ (红). 图1 中的正三角形表示序参量随耦合强度增大方向的点, 而倒三角形表示序参量随耦合强度减小方向的点. 当$ \omega_0 $ 相对较小时, 从图1(a1) 和图1(b1) 可以看出Daido序参量$ R_2 $ 随耦合强度$ K $ 的变化经历了一级相变, 即当$ K $ 从小往大增加时, 在临界耦合$ K_{\rm f} $ 处二阶序参量$ R_2 $ 发生由无序态($ R_2 = 0 $ )到同步态($ R_2 > 0 $ )的不连续跳变. 而当耦合强度$ K $ 由大减小的过程中, $ R_2 $ 从同步态($ R_2\approx0.71 $ )到无序态($ R_2\approx0 $ )的去同步转变也是以不连续跳变的形式, 并且去同步临界耦合强度为$ K_{\rm b}\approx2 < K_{\rm f} $ . 区间$ K_{\rm b} < K < K_{\rm f} $ 称为迟滞区, 意味着系统存在双稳态(无序态与同步态的共存). 相比于Daido序参量$ R_2 $ 而言, Kuramoto序参量$ R_1 $ 的相变更加复杂(图1(a2) 和图1(b2) ). 当耦合强度足够大($K > K_{\rm b}$ ), $ R_1 $ 表现为依赖于不对称度参数$ \alpha $ 的同步态(亦即依赖于初始条件), 并且随着耦合强度逐渐减小, 每一支解都在相同的临界耦合强度$ K = K_{\rm b}\approx2 $ 经历一系列不连续的去同步转变. 值得注意, 序参量$ R_2 $ 和$ R_1 $ 拥有相同的去同步耦合强度$ K_{\rm b} $ , 而$ K_{\rm f} $ 随着$ \omega_0 $ 的增大而减小, 进而迟滞区随着$ \omega_0 $ 增大而缩小.图 1 序参量$ R_2 $ 和$ R_1 $ 随耦合强度$ K $ 的相变图. $ g(\omega) $ 为双峰洛伦兹分布, 且$ \varDelta = 0.10 $ , $ \omega_0 $ 分别取(a)$ 0.08 $ , (b)$ 0.12 $ , (c)$ 0.30 $ , (d)$ 0.40 $ . 其中正三角形$ \vartriangle $ 表示耦合强度$ K $ 增大的方向, 倒三角形$ \triangledown $ 表示耦合强度$ K $ 减小的方向. (a2)?(d2)中$ R1 $ 的相变曲线自上往下$ \alpha $ 分别取$ 1.00 $ (粉, 方形), $ 0.90 $ (青, 圆形), $ 0.80 $ (蓝, 菱形), $ 0.70 $ (绿, 左三角), $ 0.60 $ (红, 右三角)Figure1. Phase transition diagram of order parameters $ R_ 2 $ and $ R_1 $ with the coupling strength $ K $ . $ g(\omega) $ is bimodal Lorentz distribution with $ \varDelta = 0.10 $ , and $ \omega_ 0 = $ $ 0.08 $ (a), $ 0.12 $ (b), $ 0.30 $ (c), $ 0.40 $ (d), respectively. The regular triangle $ \vartriangle $ indicates the direction of the increase of coupling strength $ K $ and the inverted triangle $ \triangledown $ indicates the direction of the decrease of coupling strength $ K $ . In (a2)?(d2), phase transition of $ R_1 $ with $ \alpha = $ $ 1.00 $ (pink, square), $ 0.90 $ (cyan, circle), $ 0.80 $ (blue, diamond), $ 0.70 $ (green, left triangle) and $ 0.60 $ (red, right triangle) from top to bottom, respectively.$ \omega_0 $ 较大时(图1(c) 和图1(d) ), 宏观序参量$ R_2 $ 和$ R_1 $ 的动力学现象与之前的图1(a) 和图1(b) 又截然不同. 首先, 随着耦合强度的增大或减小时, 序参量$ R_2 $ 并不存在迟滞现象, 并且在减小和增大$ K $ 的过程中$ R_2 $ 的相变是对称的. 具体而言, 系统的无序态$ R_2 = 0 $ 在$ K_{\rm f} < 2 $ 处失稳, 对于同步态而言, $ R_2 $ 在$ K_{\rm b}\approx2 $ 处发生不连续跳变, 在区间$ K_{\rm f} < $ $ K < K_{\rm b} $ 存在非定态. 对于$ R_1 $ 而言, 其同步态依赖于不对称度参数$ \alpha $ , 且$ R_1 $ 在$K_{\rm b}$ 处的不连续跳变更为明显. 为了探究在$ K_{\rm f} < K < K_{\rm b} $ 区间序参量的具体宏观表现, 在图1(c) 和图1(d) 中选取耦合强度$ K = 1.6 $ ($ K_{\rm f} < 1.6 < K_{\rm b} $ ), 将$ R_2 $ 和$ R_1 $ 随时间$ t $ 演化的过程展示出来(如图2 所示).图 2 耦合强度$ K = 1.6 $ 时序参量$ R_2 $ 和$ R_1 $ 随时间$ t $ 的演化. $ g(\omega) $ 为双峰洛伦兹分布, 且$\varDelta = 0.1$ , $ \omega_0 $ 分别取(a), (b)$ 0.30 $ , (c), (d)$ 0.40 $ . (b), (d)中$ R_1(t) $ 曲线自上往下$ \alpha $ 分别取$ 1.0 $ (粉, 实线), $ 0.9 $ (青, 划线), $ 0.8 $ (蓝, 点线), $ 0.7 $ (绿, 点划线), $ 0.6 $ (红, 双点划线)Figure2. Evolution of the order parameters $ R_ 2 $ and $ R_1 $ with time $ t $ at coupling strength $ K = 1.60 $ . $ g(\omega) $ is bimodal Lorentz distribution with $ \varDelta = 0.10 $ , and $ \omega_0 = $ $ 0.30 $ ((a), (b)), $ 0.40 $ ((c), (d)), respectively. The evolution of $ R_ 1(t) $ with $ \alpha = $ $ 1.00 $ (pink, solid line), $ 0.90 $ (cyan, dash line), $ 0.80 $ (blue, dot line), $ 0.70 $ (green, dash dot line), $ 0.60 $ (red, dash dots line) from top to bottom, respectively.图2 可以清晰地看到序参量$ R_2 $ 和$ R_1 $ 随时间是周期振荡的, 并且振荡的最低点都是$ 0 $ , 于是, 在此将系统的宏观序参量$ R_2 $ 和$ R_1 $ 随时间$ t $ 表现出周期振荡的行为称为振荡态. 同样, 对于$ R_1 $ 而言, 其随时间振荡的幅度依赖于不对称度参数$ \alpha $ . 为了进一步考察自然频率分布对系统宏观动力学的影响, 图3 展示了自然频率服从半宽为$ 1 $ 的均匀分布, 其情形与图1(c) 、图1(d) 和图2 类似. 系统无迟滞存在, 宏观序参量$ R_2 $ 和$ R_1 $ 在相变过程中呈现出振荡态, 同时, $ R_1 $ 的同步态和振荡态也依赖于不对称度参数$ \alpha $ .图 3 $ g(\omega) $ 为均匀分布, $ \gamma = 1.0 $ (a), (b)序参量$ R_2 $ 和$ R_1 $ 随耦合强度$ K $ 的相变图. 其中相变曲线自上往下$ \alpha $ 分别取$ 1.00 $ (粉, 方形), $ 0.90 $ (青, 圆形), $ 0.80 $ (蓝, 菱形), $ 0.70 $ (绿, 左三角), $ 0.60 $ (红, 右三角). (c), (d)耦合强度$ K = 1.90 $ 时序参量$ R_2 $ 和$ R_1 $ 随时间$ t $ 的演化. 图中$ R_1 $ 曲线自上往下$ \alpha $ 分别取$ 1.0 $ (粉, 实线), $ 0.9 $ (青, 划线), $ 0.8 $ (蓝, 点线), $ 0.7 $ (绿, 点划线), $ 0.6 $ (红, 双点划线)Figure3. $ g(\omega) $ is uniform distribution with $ \gamma = 1.0 $ (a), (b) Phase transition diagram of order parameters $ R_ 2 $ and $ R_1 $ with the coupling strength $ K $ . Phase transition of $ R_1 $ with $ \alpha = $ $ 1.00 $ (pink, square), $ 0.90 $ (cyan, circle), $ 0.80 $ (blue, diamond), $ 0.70 $ (green, left triangle) and $ 0.60 $ (red, right triangle) from top to bottom, respectively. (c), (d) Evolution of the order parameters $ R_ 2 $ and $ R_1 $ with time $ t $ at coupling strength $ K = 1.90 $ . The curve of $ R_ 1 $ with $ \alpha = $ $ 1.00 $ (pink, solid line), $ 0.90 $ (cyan, dash line), $ 0.80 $ (blue, dot line), $ 0.70 $ (green, dash dot line), $ 0.60 $ (red, dash dots line) from top to bottom, respectively.3.理论分析 23.1.无序态稳定性分析 3.1.无序态稳定性分析 考虑热力学极限情况下($ N\rightarrow \infty $ ), 系统的状态可以用概率密度分布函数$ \rho(\theta, \omega, t) $ 来描述. 其中, $ \rho(\theta, \omega, t){\rm d}\theta {\rm d}\omega $ 表示在$ t $ 时刻介于区间$ \omega\in(\omega, \omega+{\rm d}\omega) $ 和$ \theta\in(\theta, \theta+{\rm d}\theta) $ 内振子的比例. 此外, $ \rho(\theta, \omega, t) $ 是关于相位$ \theta $ 周期为$ 2\pi $ 的函数, 并且满足归一化条件$ N $ 趋于无穷时, 系统的振子数守恒, 故分布函数$ \rho(\theta, \omega, t) $ 满足以下连续性方程:$ v(\theta, \omega, t) $ 为2 )式定义的宏观序参量$ Z_k $ 在连续极限的情况下写成积分的形式为$ K $ 增加由无序向同步转变的临界耦合强度$ K_{\rm f} $ . $ \rho_0(\theta, \omega, t) = 1/2\pi $ 表示系统的无序态, 对应于连续性方程(6 )的平庸解. 相应地, 序参量$ Z_k = 0 $ , 所有振子以自然频率绕单位圆运动.$ \rho(\theta, \omega, t) $ 在平庸解$ \rho_0 $ 附近考虑一个小的扰动$ \varepsilon $ 是扰动幅值, 且$ 0 < \varepsilon\ll 1 $ , $ \nu(\theta, \omega, t) $ 是关于相位$ \theta $ 周期为$ 2\pi $ 的扰动函数. 由(5 )式的归一化条件可以得到$ \nu(\theta, \omega, t) $ 对$ \theta $ 的均值为$ 0 $ , 即$ v(\theta, \omega, t) $ 可写成如下形式:$ \bar{Z_2'} $ 为$ Z_2' $ 的复共轭. 将(9 )式、(11 )式和(12 )式代入连续性方程(6 ), 并忽略$ \varepsilon $ 的高阶项, 得到关于扰动函数$ \nu(\theta, \omega, t) $ 的线性演化方程为$ \nu(\theta, \omega, t) $ 是关于$ \theta $ 周期为$ 2\pi $ 的函数, 可以将$ \nu(\theta, \omega, t) $ 对$ \theta $ 进行傅里叶级数展开:$ \nu_n(\omega, t) $ 为傅里叶展开系数, 由于$ \nu(\theta, \omega, t) $ 是实函数, 故而$ \nu_0(\omega, t) = 0 $ 且$ \nu_n(\omega, t) = \bar{\nu}_{-n}(\omega, t) $ . 将(14 )式代入(11 )式得到关于Daido序参量的简洁形式:15 )式右边定义了积分算符$ \hat {g} $ .15 )式右边可以发现, 仅$ \nu(\theta, \omega, t) $ 傅里叶级数展开的二次简谐项对非平庸线性化振幅方程有作用, 这与方程(3 )定义的高阶耦合有关. 将(14 )式代入方程(13 )可以直观地得到这一结论, 即16 )右边定义一个线性算符, 即17 )式右边第一项为乘积算子, 其相应的本征值为$ \lambda = -2 {\rm i}\omega $ , 而右边第二项$ K|\omega|\hat g $ 可以看作是扰动算子作用在第一项上. 文献[54 ,55 ]指出线性算子的本征谱在微扰作用下保持不变, 且文献[56 ]表明$ \mathcal L $ 的连续谱就是乘积算子的本征值, 即$\sigma_{\rm c}(\mathcal L) = \{ \lambda = $ $ -2 {\rm i}\omega, \; \omega \in \mathrm {support}(g) \}$ . 与传统的Kuramoto模型及其推广模型一样, $ \mathcal L $ 的连续谱是纯虚的, 并不会诱导高阶耦合相振子系统的无序态线性失稳.$ \mathcal L $ 的离散谱. 对于$\lambda \in \mathbb C \; \backslash \; \sigma_{\rm c}(\mathcal L)$ , 令17 )式和(18 )式, 得$ \hat g $ 作用于(19 )式左右两边, 并利用积分算符的定义得到关于$ \lambda $ 的本征方程:$ \lambda $ 的实部决定了无序态的稳定性. 对于(20 )式, 很容易验证如果$ \lambda $ 存在, 那么其实部一定非负, 因此, 表征系统无序态失稳的临界耦合强度$ K_{\rm f} $ 通过取极限$ \mathrm{Re}(\lambda)\to 0^+ $ 和 $ \mathrm {Im}(\lambda) \to \varOmega_{\rm c} $ 可求得. 令$\lambda = $ $ x+{\rm i}y$ , 那么本征方程(20 )在极限条件下可分别写成实部和虚部两个等式, 即$ \mathrm{P.V.} $ 表示对$ \omega $ 沿实轴的主值积分. 最终可以确定临界耦合强度$K_{\rm f}$ 的一般形式$ \varOmega_{\rm c} $ 由平衡方程(22 )确定. 如, 对于单位半宽的单峰洛伦兹分布, 其$ \varOmega_{\rm c} = \pm2 $ , 相应地, $ K_{\rm f} = 4 $ . 对于$ \omega \in [-1, 1] $ 的均匀分布, 其$ \varOmega_{\rm c} = \sqrt{2} $ , $ K_{\rm f}\approx1.80 $ . 而本文主要考虑的双峰洛伦兹分布, 其临界频率为$ \varDelta = 0.1 $ , 如果$ \omega_0 = 0.08 $ , 那么$ K_{\rm f}\approx 3.12 $ (图1(a1) ), 同样地, $ \omega_0 = 0.12 $ , $ K_{\rm f}\approx 2.56 $ (图1(b1) ), $ \omega_0 = 0.30 $ , $ K_{\rm f}\approx 1.26 $ (图1(c1) ), $ \omega_0 = 0.40 $ , $ K_{\rm f}\approx $ $ 0.97 $ (图1(d1) ). 通过改变不同的中心频率$ \omega_0 $ , 可得到不同的临界耦合强度$ K_{\rm f} $ , 并且表征无序态失稳的临界耦合强度$ K_{\rm f} $ 与表征同步态去同步的临界耦合强度的大小关系, 可产生完全不同的宏观相变过程(图1(a1) 、图1(b1) 与图2(c1) 、图1(d1) )与微观动力学现象.$ K < K_{\rm f} $ , 本征值不存在, 表明无序态在微扰的作用下处于中性稳定. 而当$ K > K_{\rm f} $ , 本征值存在且实部大于$ 0 $ , 意味着无序态失稳. 在临界点$ K = K_{\rm f} $ , 本征值虚部非$ 0 $ , 即$ \varOmega_{\rm c}\neq 0 $ , 说明在$ K = K_{\rm f} $ 处发生Hopf分岔, 系统出现了不连续爆炸性同步相变[57 ] .3.2.自洽方法 -->3.2.自洽方法 为了更好地理解系统动力学分岔以及同步相变机制, 接下来利用自洽方法分析系统长时间演化的宏观动力学特性. 自洽方法最核心的思想就是假定系统在长时间的演化之后处于定态, 即$ R_k(t) $ 为随时间不变的定值, 且$ \varTheta_k(t) $ 均匀旋转. 由于方程(3 )满足旋转不变性和反演对称性, 在旋转框架下选取适当的初始条件可以令$ \varTheta(t) = 0 $ , 故而$ Z_k = $ $ R_k $ . 此时平均场方程为$ KR_2 $ 的幅值大小, 系统会表现出两种不同的宏观动力学行为. 当$ KR_2 > 1 $ 时, 所有振子都会被锁住, 与自然频率大小无关, 并且锁相相位满足$ \theta_i^* $ 或$ \theta_i^*+\pi $ , 这两个不动点对应于振子形成的团簇. 因此, 锁相情形下对应的分布函数可写成$ \delta(\cdot) $ 表示Dirac函数, 参数$ \alpha $ 是反映两个团簇间的不对度. 当$ KR_2 < 1时 $ , 所有振子处于漂移的状态, 并在单位圆上非均匀地运动, 此时的相位分布为$\langle \cdot \rangle$ 表示所有振子取平均. 在连续极限的情况下, 按照(8 )式关于序参量的定义以及系统的对称性, 可以计算得到关于二阶序参量的一个简洁形式:$ K $ 和$ R_2 $ , (36 )式有解必须满足$ K\geqslant2 $ . 结合序参量$ R_1 $ 的定义和$ R_2 $ 的表达式, 求得$ R_1 $ 关于耦合强度$ K $ 和不对称度参数$ \alpha $ 的表达式为37 )式可以看出, 序参量$ R_1 $ 是取决于不对称度参数$ \alpha $ 的广泛多稳态, 而由序参量$ R_2 $ 的表达式(36 )式可知, $ R_2 $ 只与耦合强度有关, 并不依赖于不对称度参数$ \alpha $ . 对于足够大的耦合强度$ K $ , 序参量$ R_2 $ 有两支解, 且其中一支是稳定的, 另一支是不稳定的, 下文将证明其中$ R_2^+ $ 是稳定的, $ R_2^- $ 是不稳定的. 在耦合强度$ K $ 由大逐渐减小的过程中, 序参量$ R_1 $ 和$ R_2 $ 的每一支解都会在相同的临界耦合强度$ K_{\rm b} = 2 $ 处消失, 表明系统在此处发生爆炸性去同步转变, 至于去同步之后系统会处于无序态还是振荡态取决于振子自然频率分布的中心频率.3.3.多团簇态稳定性分析 -->3.3.多团簇态稳定性分析 3.2 节基于自洽方程得到了多团簇态的一般形式, 但是其稳定性特性仍然是模糊的, 使得对系统集体动力学的理解不够深刻. 这一节将解决多集团态的稳定性问题, 具体而言, 就是对各个团簇进行线性稳定性分析.27 )式可以看出, 锁相时所有振子被锁在4个团簇, 分别为 $ \theta_{\rm p}^* $ , $ \theta_{\rm n}^* $ , $ \theta_{\rm p}^*+\pi $ 和$ \theta_{\rm n}^*+\pi $ , 换句话说, 对于$ N $ 维的的系统方程(3 ), 最终演化到一个$ 4 $ 维的子流形. 在这样的低维子空间中, 系统的演化方程退化到一个相对简洁的形式:$ \omega > 0 $ 为团簇$ \theta_{\rm p} $ 的自然频率. 接着, 引入相差$ \varphi = \theta_{\rm p}-\theta_{\rm n} $ , 那么可以得到相差$ \varphi $ 的演化方程$ K > 2 $ 时, (40 )式存在两个不动点, 即40 )式进行线性稳定性分析, 可以很容易得到稳定的条件为$ \cos(2\varphi) > 0 $ . 并且, 注意到$\cos(2\varphi) > 0$ 等价于$ K > 2 $ 时, $ R_k^\pm $ 存在, 且只有$ R_K^+ $ 这支解是稳定的, 对应于图1 中的同步部分, 而解$ R_K^- $ 是不稳定的.3.4.一级相变与振荡态 -->3.4.一级相变与振荡态 从3.3 节的多团簇态的稳定性分析可以得到, 在耦合强度$ K > K_{\rm b} = 2 $ 时, 多团簇态的解$ R_K^+ $ 存在且稳定. 又由3.1 节无序态的稳定性分析得到, 无序态的失稳点$ K_{\rm f} $ 的一般表达式((23 )式), 与自然频率分布函数的中心频率$ \omega_0 $ 和半宽$ \varDelta $ 有关, 若固定$ \varDelta $ 为常数不变, 那么表征无序态失稳的临界耦合强度$ K_{\rm f} $ 将随着$ \omega_0 $ 增大而减小. 当$ \omega_0 $ 较小时, 使得$ K_{\rm f} > $ $ K_{\rm b} $ , 就会出现迟滞现象(图2(a) 和图2(b) ), 具体而言, 当耦合强度从小往大增加时, 无序态将在$K_{\rm f} > K_{\rm b} = $ $ 2$ 处失稳, 所有振子发生同步, 且临界点处的序参量$ R_K^+ > 0 $ , 可由(36 )式和(37 )式及(43 )式求得, 分别为$ R_K $ 在临界点由$ R_K = 0 $ 直接向$ R_K > 0 $ 发生跳变, 表现为不连续相变(一级相变), 即爆炸式同步. 同样地, 当耦合强度由大往小减时, 多团簇态将在$ K_{\rm b} = 2 $ 处去同步, 且$ 0 $ 跳到$ 0 $ , 表现为爆炸式去同步, 值得注意, 耦合强度在$ K_{\rm b} < K < K_{\rm f} $ , 系统存在双稳态, 即无序态与多团簇态共存. 而当$ \omega_0 $ 较大时, 使得$ K_{\rm f} < K_{\rm b} $ , 无序态在$ K_{\rm f} < 2 $ 处失稳, 多团簇态在$ K > 2 $ 时稳定, 那么在$ K_{\rm f} < K < 2 $ 区间内, 序参量$ R_K $ 为非定态, 此时$ R_K $ 表现为随时间周期变化的振荡态(图1(c) , 图1(d) 和图2 ), 且对于$ R_1 $ 而言, 其振荡的幅值与初始条件有关, 即表现为依赖于不对称度参数$ \alpha $ 的广泛多振荡态(图2(b) 和图2(d) ). 当自然频率分布为均匀分布, 且半宽$ \gamma = 1 $ 时, 求得$K_{\rm f} = $ $ 4\sqrt2/\pi\approx1.8 < K_{\rm b} = 2$ , 相变过程中也会有振荡态的出现, 具体为序参量$ R_K $ 随时间为周期振荡(图3 ). 由于$ R_2 $ 和$ R_1 $ 随耦合强度的相变图中取的是$ R_2 $ 和$ R_1 $ 长时间演化之后的时间平均, 对于振荡态而言, 平均时间足够大, 求的是$ R_2 $ 和$ R_1 $ 的周期平均, 且周期振荡的最低值是$ 0 $ , 于是在$ K_{\rm b} $ 处会有不连续的宏观相变.4.结 论 综上, 本文探讨了耦合强度与频率关联的高阶耦合相振子的动力学. 由数值模拟与理论分析得出, 在自然频率服从双峰分布的情形下, 随着自然频率分布的中心频率的增加, 系统将由ASDT向Os转变. 具体而言, 首先, 利用无序态线性稳定性分析得到了系统发生同步的临界耦合强度, 再通过自洽分析得到系统的多团簇态及其一般表达式, 并对多团簇态进行线性稳定性分析得到其稳定解. 当频率分布的中心频率较小时, 系统由无序向同步转变的临界耦合强度大于多团簇态的去同步点, 将存在无序态与多团簇态共存的双稳态, 此时系统表现为ASDT. 当增大自然频率分布的中心频率, 系统无序态失稳的临界耦合强度小于多团簇态的去同步点, 此时, 迟滞消失且在无序态失稳点与多团簇态去同步点之间存在非定态解, 即Os. 值得注意, 本文指出二阶序参量可以很好地描述系统多团簇态的形成, 而一阶序参量则反映系统的不对称性. 
















































































































































































 图 1 序参量
图 1 序参量













































































































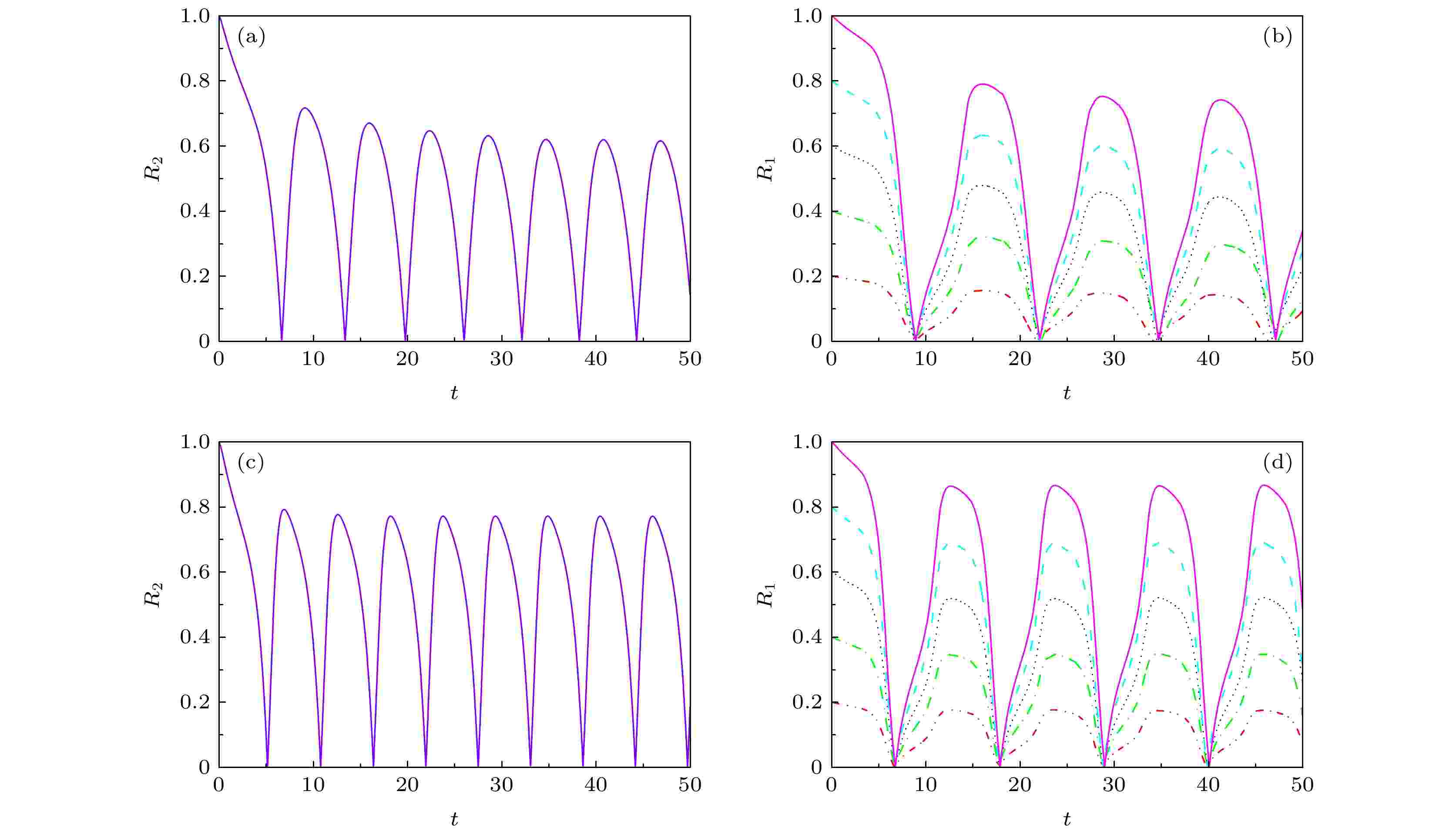 图 2 耦合强度
图 2 耦合强度








































































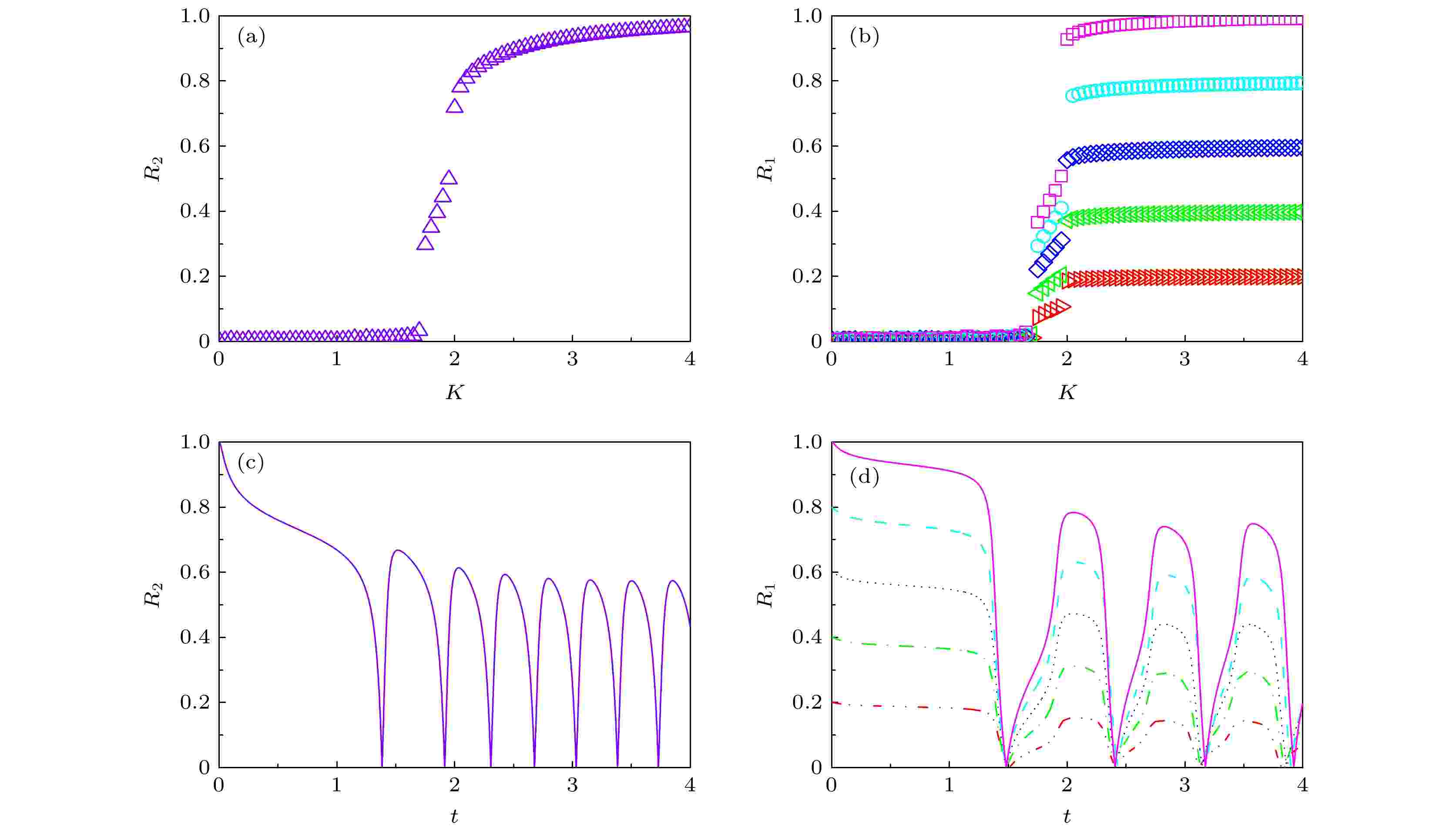 图 3
图 3 




















































































































































































































































































































































