摘要: 利用多重尺度法解析地研究了窄脉冲探测光激发下半导体三量子点分子系统中高阶效应对光孤子稳定性的影响. 结果表明, 由标准非线性薛定谔方程所描述的光孤子在传播的过程中会出现较大衰减, 而由高阶非线性薛定谔方程所描述的光孤子却有着较为良好的稳定性. 此外, 数值模拟光孤子间的相互作用发现, 由标准非线性薛定谔方程所描述的两光孤子碰撞后其振幅迅速衰减并辐射出较为严重色散波, 而由高阶非线性薛定谔方程所描述的两光孤子碰撞后其形状几乎不发生任何变化. 这主要是由于当入射的探测光脉冲足够窄时, 系统须采用高阶方程来描述, 其物理原因是方程中的高阶效应, 包括非瞬时效应和三阶色散效应不能被忽略或当作微扰处理. 这种稳定的光孤子对于将来的光信息处理和传输技术有着潜在的应用价值.
关键词: 隧穿诱导透明 /
光孤子 /
半导体量子点分子 English Abstract Stability of optical soliton in symmetrical three-quantum-dot system under high-order effects Ren Bo 1,2 ,She Yan-Chao 2 ,Xu Xiao-Feng 2 ,Ye Fu-Qiu 1 1.School of Physics and Mechatronics Engineering, Jishou University, Jishou 416000, China Fund Project: Project supported by the the National Nature Science Foundation of China (Grant Nos. 12064038, 12165008), the NSF of Guizhou Province Education Department, China (Grant Nos. KY[2019]179, KY[2017]315, ZK[2021]034), the Outstanding Young Science and Technology Talents of Guizhou Pronice, China (Grant No. [2019]5673), and the NSF of Tongren Science and Technology Bureau, China (Grant No. [2020]77).Received Date: 19 May 2021Accepted Date: 19 June 2021Available Online: 15 August 2021Published Online: 20 November 2021Abstract: The influence of high-order effects on the stability of the optical soliton in a semiconductor three-quantum-dot molecular system under the excitation of narrow pulse probe light is analyzed analytically by using the multi-scale method. The results show that optical soliton described by the standard nonlinear Schr?dinger equation will have a large attenuation in the propagation process, while the optical soliton described by the high-order nonlinear Schr?dinger equation has relatively good stability. In addition, numerical simulations of the interaction between optical solitons show that the amplitudes of the two optical solitons described by the standard nonlinear Schr?dinger equation attenuate rapidly after the collisions and radiation of more serious dispersion waves, while the shapes of the two optical solitons described by the high-order nonlinear Schr?dinger equation hardly changes after the collision. This is mainly because when the incident probe light pulse is narrow enough, the system must be described by a higher-order equation. The physical reason is that the higher-order effects in the equation, including non-instantaneous effects and third-order dispersion effects, cannot be ignored or treated as perturbations. This kind of stable optical soliton has potential application value for future optical information processing and transmission technology.Keywords: tunneling induced transparency /optical solitons /semiconductor quantum dot molecules 全文HTML --> --> --> 1.引 言 随着半导体技术的兴起, 作为半导体量子局限材料的半导体量子阱、量子点(semiconductor quantum dot, SQD)在非线性光学等领域已成为了研究的热点之一[1 -3 ] . 这是由于半导体量子阱、量子点具有着类似超冷原子的分立能级结构, 且在实际应用中有着易于集成、易于调控, 以及较大的非线性参数等优良特性[4 ,5 ] . 此外, 在量子阱、量子点介质中产生保真度高、抗干扰能力强的光孤子[6 -9 ] 也被人们在量子通信和量子调控等领域广泛地关注[10 -12 ] . 如, Yang 等[13 ] 在单个量子点中通过双激子相干成匹配慢光孤子对, 发现孤子间碰撞的作用力是吸引还是排斥是由孤子间的相位差来控制的; Mahmoudi等[14 ] 在半导体双量子点(Double Quantum Dots, DQD)系统中, 证实了点间隧穿耦合强度能够对控制光的群速度进行有效调控, 并在非相干泵浦场的间接激发下, 利用吸收双态到增益双态的转换实现了光脉冲的无吸收超光速传播; She等[15 ] 在研究DQD分子系统中时间光孤子的形成时发现, 调节控制场强度可以实现亮、暗光孤子的转换; Hao等[16 ] 通过对半导体双量子阱系统中光孤子的传播性质进行研究, 得到了弱场激发下的以超慢群速度传播的暗光孤子.[17 -22 ] . 如, Huang等[23 ,24 ] 在超冷原子和量子阱系统中发现, 当脉冲宽度较窄时, 系统的三阶色散、非瞬时效应是十分显著的, 此时, 这些参量不能被当作微扰处理; 2016年, Mani等[25 ] 研究了高阶非线性效应对于脉冲宽度为1 ps内孤子脉冲偏移的影响, 结果表明, 负三阶色散能够有效抑制相邻孤子脉冲之间的碰撞; 2017年, Liu等[26 ] 在研究变系数耦合HNLS方程中孤子的相互作用时发现, 两个孤子的速度与三阶色散系数有关, 高阶效应会影响高比特率孤子脉冲的传输等.2.理论模型及其麦克斯韦-薛定谔方程组 根据现有的实验条件, 利用分子束外延法和原子层刻蚀法可构建如图1 所示的对称TQD分子模型[27 -30 ] . 该模型在中心频率为$ {\omega _{\text{p}}} $ 的窄脉冲弱探测场激发下, 在QD1内可形成电子空穴对的状态, 即激子态$ \left| 4 \right\rangle $ , 同时通过外加偏置电压的作用, QD1导带中的电子将通过隧穿薄势垒耦合效应被限制在QD1与QD2, QD3的导带间[29 ,31 ] 分别形成间接激子态$ \left| 2 \right\rangle $ 、$ \left| 3 \right\rangle $ . 而对于能级$ \left| 1 \right\rangle $ 则是体系的基态. TQD系统的哈密顿量可表示为(假设$ \hbar = 1 $ )图 1 (a) TQD有效激子能级示意图; (b)相应能级结构图. ${{\varGamma} }_{m1}(m=2, 3, 4)$ 表示退相干通道, $ {\omega _{4 n}}(n = 1, 2, 3) $ 表示能级差, ${\varDelta _{\text{p}}} = {\omega _{\text{p}}} - {\omega _{{\text{41}}}}$ 为探测场与能级差$ {\omega _{{\text{41}}}} $ 的频率失谐量.Figure1. (a) Energy level diagram of TQD effective exciton; (b) corresponding energy level structure diagram.${\varGamma }_{m1} $ $ (m=2, 3, 4)$ represents the decoherent channel, ${\omega _{4 n}}\left(\right.n = $ $ 1, 2, 3\left.\right)$ represents the energy level difference, ${\varDelta _{\text{p}}} = {\omega _{\text{p}}} - $ $ {\omega _{{\text{41}}}}$ is the frequency detuning between the probe laser field and the energy level difference.${\varOmega _{\text{p}}} = {{{p_{{\text{41}}}}{\varepsilon _{\text{p}}}} \mathord{\left/ {\vphantom {{{p_{{\text{41}}}}{\varepsilon _{\text{p}}}} \hbar }} \right. } \hbar }$ 是探测场的半拉比频率, ${T_{{\text{e1}}}} = $ $ {{{p_{42}}{\varepsilon _{\text{p}}}} \mathord{\left/ {\vphantom {{{p_{42}}{\varepsilon _{\text{p}}}} \hbar }} \right. } \hbar }$ , $ {T_{{\text{e}}2}} = {{{p_{43}}{\varepsilon _{\text{p}}}} \mathord{\left/ {\vphantom {{{p_{43}}{\varepsilon _{\text{p}}}} \hbar }} \right. } \hbar } $ 描述的是QD1与QD2(QD3)之间的隧穿耦合强度, $ {p_{4 i}}(i = 1, 2, 3) $ 表示能级$ \left| i \right\rangle $ 和$ \left| {\text{4}} \right\rangle $ 的电偶极跃迁矩阵元. 系统的光场形式可表${{{\boldsymbol{E}}}}(r, t) = {{\boldsymbol{e}}_{\text{p}}}{\varepsilon _{\text{p}}}{\text{exp[i(}}{{\boldsymbol{k}}_{\text{p}}}z - {\omega _{\text{p}}}t{\text{)]}} + {\rm{E.c}}$ , 其中${{\boldsymbol{e}}_{\text{p}}}$ , $ {\varepsilon _{\text{p}}} $ 及${{{k}}_{\text{p}}}$ 分别为极化方向、探测光场的包络及波矢, $\rm E.c$ 表示探测光场的复共轭项. 在相互作用绘景下, 考虑旋转波近似和电偶极近似以及慢变包络近似[4 ,5 ,11 ,15 ] , 描述探测光场与TQD系统相互作用的麦克斯韦-薛定谔方程组(麦克斯韦-布洛赫方程组已在 附录A 中给出)可表示为:${d_{2, 3}} = {\varDelta _{2, 3}} + {\text{i}}{\varGamma _{2, 3}}$ , ${d_4} = {\varDelta _{\text{p}}} + {\text{i}}{\varGamma_4}$ , ${\varDelta }_{2, 3} = {\varDelta }_{\text{p}}+ $ $ {\omega }_{42, 43}$ , ${\varGamma _m} = {{{\varGamma _{m1}}} \mathord{\left/ {\vphantom {{{\varGamma _{m1}}} {2 + \gamma _{\text{m}}^{\varphi }(m = 2, 3, 4)}}} \right. } {2 + \gamma _{\text{m}}^{\varphi }~(m = 2, 3, 4)}}$ , ${\varGamma _{m1}}$ 是能级$ \left| m \right\rangle $ 与能级$ \left| {\text{1}} \right\rangle $ 之间的弛豫衰减率, $ \gamma _m^{{\varphi }} $ 描述的是$ \left| m \right\rangle $ 的纯相移衰减率, ${\kappa }_{\text{14}}=({N}_{\text{a}}{\omega }_{\text{p}}{\left|{p}_{14}\right|}^{2})/(2 {\epsilon }_{0}\hslash c)$ 为传播常数, $ {N_{\text{a}}} $ 为原子数密度.3.多重尺度法及其HNLS方程 一般来说, 方程(2 )是不可积的, 无法直接得到其解析解, 因此采用标准多重尺度法[32 -36 ] 将几率幅和探测光的半拉比频率进行渐进展开$ \varepsilon $ 是一个微小参量, 刻画的是基态粒子布局的偏离, 并且假定几率幅${a}_{j}^{(n)}~~(j = 2, 3, 4; n= 1, 2, $ $ 3, 4)$ 和半拉比频率$\varOmega _p^{{(}n{)}}$ 都是不同尺度的时间变量${t_n} = {\varepsilon ^n}t~~(n =$ $ \text{0}, \text{1}) $ 和空间变量${z_n} = {\varepsilon ^n}z~~(n = 0, 1, 2, $ $ 3)$ , $ {x_n} = \varepsilon x $ , $ {y_n} = \varepsilon y $ 的函数, 将方程(3 )代入方程(2 ), 麦克斯韦-薛定谔方程组可变换为$\varOmega _{\text{p}}^{(n)} = F {\rm exp(i} \theta )$ , 其中$\theta = K(\omega )z - $ $ \omega t,$ $ F $ 为时空慢变量$ {t_1} $ , ${z_n}~~(n = 1, 2, 3)$ 及$ {x_1} $ , $ {y_1} $ 待定包络函数.$ n = 1 $ 时, 系统的线性色散关系可表示为$D = (\omega + {d_4}) (\omega + {d_2} )(\omega + {d_3} ) - T_{{\text{e}}1}^2 (\omega + {d_3} ) - $ $ T_{{\text{e2}}}^{2} (\omega + {d_2})$ , ${D_{\text{c}}} = (\omega + {d_2} )(\omega + {d_3} )$ 可以对$K(\omega )$ 围绕其中心频率${\omega _{\text{p}}}$ 做泰勒级数展开, 有${K_0} = \varphi + {{{\text{i}}\alpha }/ 2}$ , 其中实部$\varPhi$ 表示探测光穿过单位长度介质后获得的相位, $ \alpha $ 表示探测光强的线性吸收系数; ${K_1} = \dfrac{\partial K(\omega)}{\partial \omega} \bigg|_{\omega = 0}$ 与群速度有关, 其关系为${V_{\text{g}}} = {\text{Re}} \dfrac{1}{K_1}$ , ${K_2} = \dfrac{\partial ^2 K(\omega )}{\partial \omega ^2} \bigg|_{\omega = 0}$ 描述的是探测光场的群速度色散效应. ${K_3} = \dfrac{\partial^3 K(\omega )}{ \partial \omega^3} \bigg|_{\omega = 0}$ 描述了系统的三阶色散效应.$ n = 2 $ 时, 由二阶可解条件可得$ n = 3 $ 时, 由三阶可解条件得$\bar \alpha = {\varepsilon ^{\text{2}}}\alpha = {\text{2}}{\varepsilon ^{\text{2}}}{\rm Im} \left[ {K(\omega )} \right]$ , $ \alpha $ 刻画了介质对探测光的吸收,$ n = 4 $ 时, 由四阶可解条件得7 )—(9 )我们可以得到$\tau = t - z/V_{\rm{g}}$ , 且在求解过程中已定义${\varOmega _{\text{p}}} \approx $ $ \varOmega _{\text{p}}^{{\text{(1)}}} = \varepsilon F{\text{exp(i}}{K_0}z{)} = U{\text{exp(i}}{K_0}z{)}$ . 一般来说, 高阶非线性方程(10 )往往是不可积的, 因为它具有复系数. 然而, 通过考虑量子点实验参数[37 ,38 ] : ${\kappa _{14}} = $ $ 3.4 \times {10^{{{ 2}}}}\;{{\rm meV}} \cdot \text{μm}^{ - 1}$ , ${\varGamma _4} = 0.054\;{\text{meV}}$ , ${\varGamma_2} = {\varGamma _3} = $ $ {10^{ - 3}}{\varGamma _4}$ , ${T_{{\text{e1}}}} = {T_{{\text{e2}}}} = 0.7{\varGamma _{\text{4}}}$ , ${\omega _{{\text{42}}}} = - {\omega _{43}} = 0.5{\varGamma _4}$ , $ c = 3 \times {10^{10}}\;{\text{cm}} \cdot {{\text{s}}^{ - 1}} $ , ${\varDelta _{\text{p}}} = - 8\;{\text{meV}}$ . 我们发现该方程系数的实部可以远远大于其对应的虚部, 如图2 所示, 这是由于在隧穿诱导透明的机制下, 系统的共振吸收被大大抑制的结果. 因此, 方程(10 )可变换为图 2 方程(10 )相关系数虚部与实部的比值随${{{\varDelta _{\text{p}}}}/{{\varGamma _4}}}$ 的变化关系 (a)$ {{{K_{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{2 i}}}}} {{K_{2{\text{r}}}}}}} \right. } {{K_{2{\text{r}}}}}} $ ; (b)$ {{{K_{{\text{3 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{3 i}}}}} {{K_{{\text{3 r}}}}}}} \right. } {{K_{{\text{3 r}}}}}} $ ; (c)$ {{{W_{\text{i}}}} \mathord{\left/ {\vphantom {{{W_{\text{i}}}} {{W_{\text{r}}}}}} \right. } {{W_{\text{r}}}}} $ ; (d)$ {{{\beta _{{\text{1 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{1 i}}}}} {{\beta _{{\text{1 r}}}}}}} \right. } {{\beta _{{\text{1 r}}}}}} $ ; (e)$ {{{\beta _{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{2 i}}}}} {{\beta _{{\text{2 r}}}}}}} \right. } {{\beta _{{\text{2 r}}}}}} $ Figure2. The ratio of the imaginary part and the real part of the correlation coefficient of equation (10 ) as a function of ${{{\varDelta _{\text{p}}}} \mathord{\left/ {\vphantom {{{\Delta _{\text{p}}}} {{\Gamma _4}}}} \right. } {{\varGamma _4}}}$ : (a)$ {{{K_{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{2 i}}}}} {{K_{2{\text{r}}}}}}} \right. } {{K_{2{\text{r}}}}}} $ ; (b)$ {{{K_{{\text{3 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{3 i}}}}} {{K_{{\text{3 r}}}}}}} \right. } {{K_{{\text{3 r}}}}}} $ ; (c)$ {{{W_{\text{i}}}} \mathord{\left/ {\vphantom {{{W_{\text{i}}}} {{W_{\text{r}}}}}} \right. } {{W_{\text{r}}}}} $ ; (d)$ {{{\beta _{{\text{1 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{1 i}}}}} {{\beta _{{\text{1 r}}}}}}} \right. } {{\beta _{{\text{1 r}}}}}} $ ; (e)$ {{{\beta _{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{2 i}}}}} {{\beta _{{\text{2 r}}}}}}} \right. } {{\beta _{{\text{2 r}}}}}} $ .11 )写成无量纲的形式, 引入无量纲化的参数: $ \tau = {\tau _0}\sigma $ , $ z = - 2{L_{\text{D}}}s $ , $ U = {U_0}u $ , $ (x, y) = {R_ \bot }(x', y') $ , 其中${L_{\text{D}}} = {{\tau _0^2}/ {{K_{{\text{2 r}}}}}}$ 为色散长度, 刻画的是系统的色散效应起作用所需的有效距离. $ {L_{{\text{NL}}}} $ 为非线性长度, 刻画的是系统的非线性效应起作用所需的有效距离, $ {\tau _0} $ 表示探测光的特征脉冲长度. 当$ {L_{{\text{NL}}}} = {L_{\text{D}}} $ 时, 系统中的色散效应与非线性效应达到平衡从而形成时间光孤子. 由平衡条件可得${U_0} = ({1/{{\tau _0}}})\sqrt {{{{K_{{\text{2 r}}}}}/ {{W_{\text{r}}}}}}$ , 表示其探测光的特征拉比频率. 另外, ${g_j} = {{2{L_{\text{D}}}}/{{L_j}}}$ $(j = 0, 1, 2, 3, $ $ 4, 5)$ , ${L_0} = $ $ {1 / {{K_{1{\text{r}}}}}}$ 表示系统的线性吸收长度, ${L_1} = $ $ {\tau _0^3{W_{\text{r}}}}/ {{(}{\beta _{{\text{1 r}}}}{K_{{\text{2 r}}}}{)}}$ 为系统的非线性色散长度, ${L_2} = $ $ - \tau _0^3 {W_{\text{r}}}/ ({\beta _{{\text{2 r}}}} {K_{{\text{2 r}}}})$ 为系统的非线性折射率延迟长度, ${L_3} = {6\tau _0^3} / {{K_{3{\text{r}}}}}$ 为系统的三阶色散长度, ${L_4} = {{{\tau _0}}/ {{K_{{\text{1r}}}}}}$ 为系统的导数吸收长度, ${L_5} = {2{\omega _{\rm{p}}}R_ \bot ^2} / c$ 为系统的衍射长度. 即${g_j} \ll 1$ 时, 方程(12 )可简化为SNLS方程, 另外, 当$ {L_0} $ , $ {L_4} $ , $ {L_5} $ 远远大于$ {L_{\text{D}}} $ , 忽略正比于$ {g_0} $ , $ {g_4} $ , $ {g_5} $ 的项[24 ] 时, 方程(12 )可表示成HNLS方程, 于是有$ {K_{{\text{2 r}}}}{W_{\text{r}}} > 0 $ 时, SNLS方程的基阶亮孤子解[24 ] 可表示为$\varOmega \ne {1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}$ , $\beta - 2\varOmega + 3{\varOmega ^2} > 0$ 时, HNLS方程的基阶亮孤子解[24 ] 可表示为$ {V}_{\text{g}}^{\text{H}}=1/{V}_{\text{g}}-\beta {\tau }_{0}/(\text{2}{L}_{\text{D}}{g}_{3}) $ 为光孤子的传播速度, $ {c_1} = {{{g_1}} \mathord{\left/ {\vphantom {{{g_1}} {(2{g_3})}}} \right. } {(2{g_3})}} $ , $ {c_{\text{2}}} = {{{g_{\text{2}}}} \mathord{\left/ {\vphantom {{{g_{\text{2}}}} {(2{g_3})}}} \right. } {(2{g_3})}} $ , $\varOmega = $ $ (3{c}_{1}+2{c}_{2}-3)/\left[6({c}_{1}+{c}_{2})\right]$ , $ \beta $ 为实的自由参数, 与光孤子的传播速度有关.4.孤子稳定性分析 为了检验孤子的稳定性, 在图3 中分别以方程(14 )和(15 )作为初始条件, 对方程(2 )进行了数值模拟. 图中实线、虚线、点虚线分别表示初态以及演化1个单位长度和2个单位长度时的数值结果. 从图3(a) 中可以看出, 当孤子演化到1单位长度时, 其幅值迅速减小, 宽度有所增加, 并且在孤子前沿也辐射出了小振幅色散波; 随着演化距离逐渐增大到2个单位长度, 对应的孤子幅值和宽度也分别出现了进一步的减小和增加, 同时色散波的辐射也越来越严重. 这表明孤子在传播的过程出现了较为严重的衰减失真. 反观图3(b) : 随着孤子的逐渐演化, 除孤子幅值发生轻微减小外, 整体看来, 孤子的形状几乎不发生明显变化, 这表明孤子能够稳定传播. 对比图3(a) 、图3(b) 可以得知, 当探测光的脉冲宽度较窄时, 使用HNLS方程的基阶孤子解得到的演化结果较前者更为稳定.图 3 (a)方程(14 )作为初始条件的数值演化结果; (b)方程(15 )作为初始条件的数值演化结果. 波形给出的演化距离为1个单位长度(虚线)和2个单位长度(点虚线), 取$ {\tau _0} = 5 \times {10^{ - 13}}\;{\text{s}} $ , $ \beta = 0.5 $ , $\varPhi = {\text{0}}$ , 其他参数与图2 相同Figure3. (a) Numerical evolution result using equation (14 ) as the initial condition; (b) numerical evolution result using equation (15 ) as the initial condition. The evolution distance given by the soliton waveform is 1 unit length (dotted line) and 2 unit lengths (dotted dotted line), and the parameters used are $ {\tau _0} = 5 \times {10^{ - 13}}\;{\text{s}} $ , $ \beta = 0.5 $ , $\varPhi = {\text{0}}$ , other parameters used are the same as Fig. 2 16a )、(16b )作为初始条件对方程(2 )进行了孤子间碰撞的数值模拟分析(见图4 ).图 4 相邻孤子间的相互作用 (a)方程(16a )作为初始条件的数值演化结果; (b)方程(16b )作为初始条件的数值演化结果. 除$ {\theta _1} = {\theta _2} = 0 $ 外, 其他参数与图2 相同Figure4. Interaction between adjacent optical solitons: (a) Numerical evolution result using equation (16a ) as the initial condition; (b) numerical evolution result using equation (16b ) as the initial condition. Except for $ {\theta _1} = {\theta _2} = 0 $ , the other parameters are the same as in Fig. 2 图4(a) 和图4(b) 可以发现, 由SNLS方程所描述的光孤子碰撞后, 其振幅呈现出快速地减小, 对应的孤子宽度也逐渐增加, 并且随着孤子的逐渐演化, 在其两侧和中间也会辐射出较为明显的色散波, 从而导致光孤子碰撞后出现较大程度衰减失真, 这主要是由于系统的高阶效应所导致的. 与此相反, 由HNLS方程所描述的光孤子碰撞后其振幅及形状几乎没有发生任何变化, 这进一步说明在该系统中当脉冲宽度较窄时考虑高阶效应所得到的光孤子具有更好的稳定性.2e )是否满足慢变包络近似条件: ${{\partial {\varOmega _{\text{p}}}} \mathord{\left/ {\vphantom {{\partial {\varOmega _{\text{p}}}} {\partial z \ll {k_{\text{p}}}\varOmega {}_{\text{p}}}}} \right. } {\partial z \ll {k_{\text{p}}}\varOmega {}_{\text{p}}}}$ 、${\partial {\varOmega _{\text{p}}}} \mathord{\left/ {\vphantom {{\partial {\varOmega _{\text{p}}}} {\partial t \ll {\varOmega _{\text{p}}}\varOmega {}_{\text{p}}}}} \right. } \partial t \ll {\omega _{\text{p}}} $ $ \varOmega {}_{\text{p}}$ , 即${\lambda _{\text{p}}} \ll {V_{_{\text{g}}}}{\tau _0}$ , ${\omega _{\text{p}}}{\tau _0} \gg 1$ . 在上面所给的量子点参数条件下, 孤子的群速度为$ {V_{\text{g}}} = 6 \times {10^{ - 2}}c $ , ${\tau _0} = $ $ 5 \times {10^{ - 13}}\;{\text{s}}$ , 探测场的中心角频率为${\omega _{\text{p}}} = 2.43 \times $ $ {10^{15}}\;{\text{rad}} \cdot {{\text{s}}^{ - 1}}$ , 对应的波长${\lambda _{{\rm p}}} = 0.78\;\text{μm}$ , 有${V_{{g}}}{\tau _0} = $ $ 9\;\text{μm}$ , $ {\omega _{\text{p}}}{\tau _0} = 1.215 \times {10^3} $ , 因此该系统能够有效地满足慢变包络近似的条件. 此外, 通过上面参数可得孤子的空间长度${L_{{{\rm sol}}}} = {V_{{\rm g}}}{\tau _0} = 9\;\text{μm}$ , 系统的色散长度${L_{\rm{D}}} = {L_{\rm {{NL}}}} = 0.33\;\text{μm}$ , 以及系统的线性吸收长度${L_0} = 35.7\;\text{μm}$ . 可以看出, 该系统的线性吸收长度是远远大于其色散长度的, 这就保证了孤子能够稳定的保形传播. 并且, 根据现有量子点制备条件[13 ] , 对于该系统的配置而言, 由于拥有一个相对较长的传播距离(约为毫米量级). 因此, 能够很好地保证其色散长度和空间长度是远远小于该长度, 以便于观察光孤子形成与传播.5.结 论 基于以上分析, 本文从四能级TQD系统的麦克斯韦-薛定谔方程组出发, 运用标准多重尺度法解析得到了描述该系统的HNLS方程以及SNLS方程, 并给出了其对应的基阶孤子解. 通过数值计算, 发现该系统中由HNLS方程所描述的光孤子具有更好的稳定性, 尤其当入射探测光脉冲较窄时系统内光孤子的传播须采用HNLS方程描述. 其物理原因是方程中的高阶效应, 包括非瞬时克尔效应和三阶色散效应等将会导致脉冲在时间和光谱上产生不对称展宽及脉冲的红移增加, 从而不能被忽略或当作微扰处理. 最后, 为了进一步验证形成的光孤子的稳定性, 分别数值模拟了这两种孤子的各自碰撞特性, 模拟结果进一步表明由HNLS方程所描述的光孤子具有更好地稳定性. 这种稳定的光孤子对于将来的光信息处理和传输技术有着潜在的应用价值.附 录.A 麦克斯韦-布洛赫方程组:$ {\rho _{ij}} = \rho _{ji}^* $ $ (i, j = 1, 2, 3, 4) $ 为密度矩阵元. 





 图 1 (a) TQD有效激子能级示意图; (b)相应能级结构图.
图 1 (a) TQD有效激子能级示意图; (b)相应能级结构图. 



















































































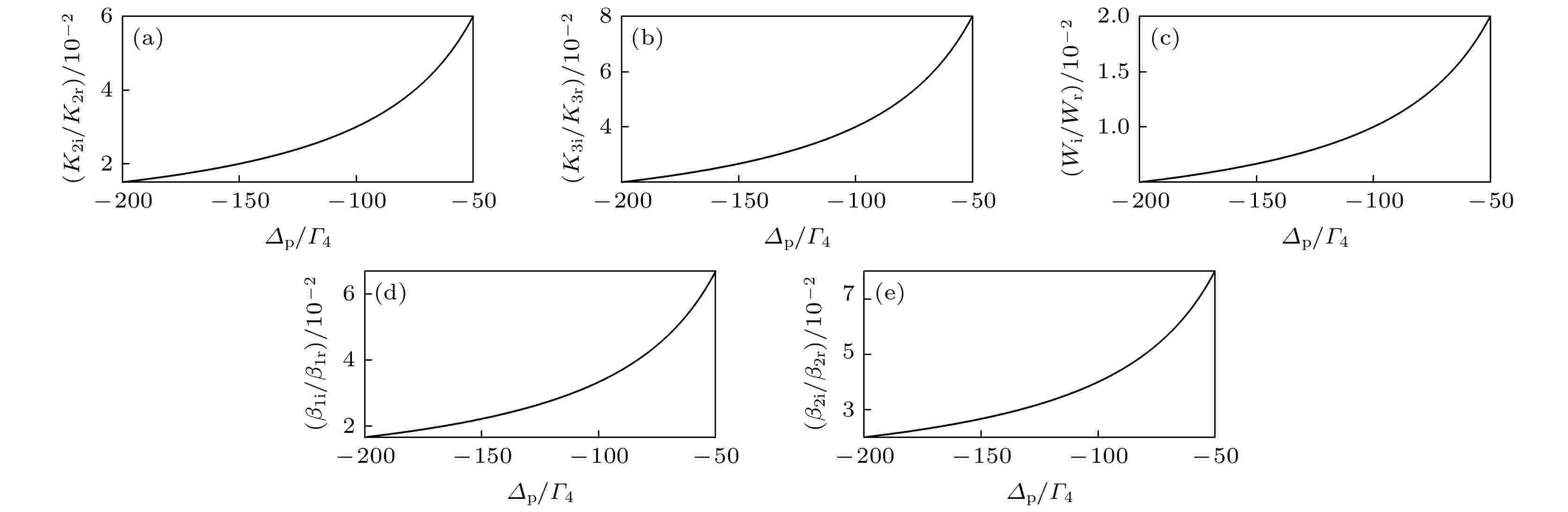 图 2 方程(10)相关系数虚部与实部的比值随
图 2 方程(10)相关系数虚部与实部的比值随

















































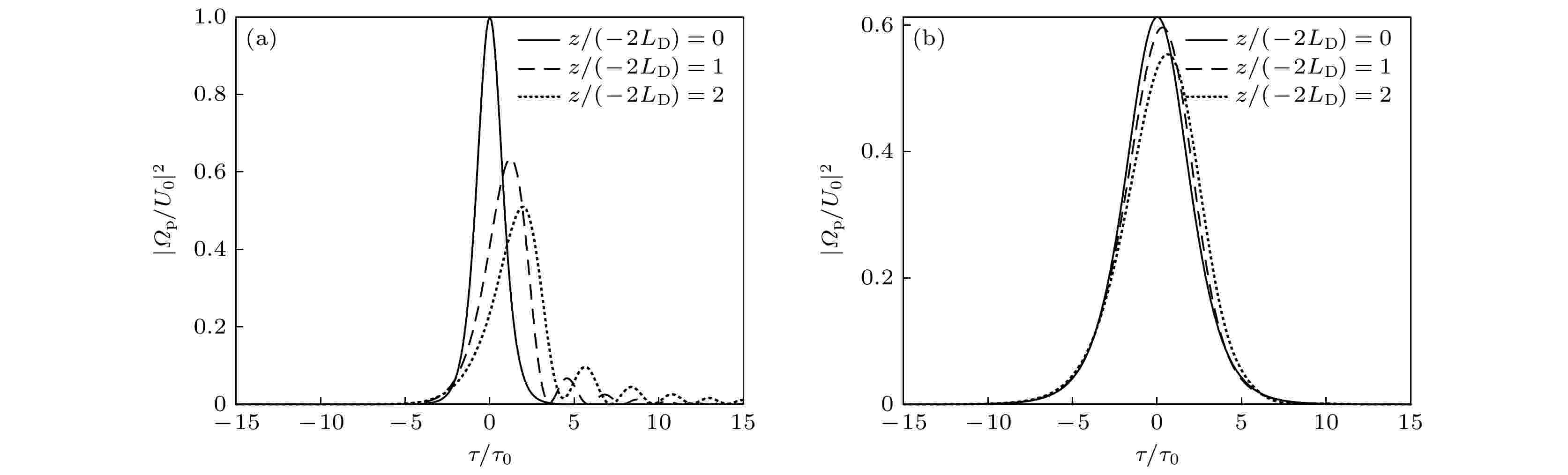 图 3 (a)方程(14)作为初始条件的数值演化结果; (b)方程(15)作为初始条件的数值演化结果. 波形给出的演化距离为1个单位长度(虚线)和2个单位长度(点虚线), 取
图 3 (a)方程(14)作为初始条件的数值演化结果; (b)方程(15)作为初始条件的数值演化结果. 波形给出的演化距离为1个单位长度(虚线)和2个单位长度(点虚线), 取





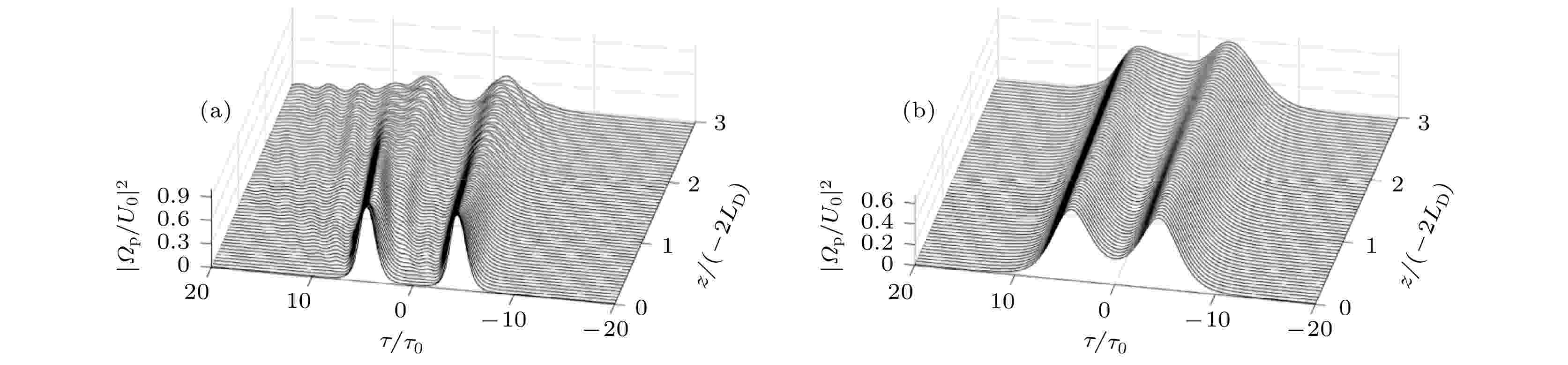 图 4 相邻孤子间的相互作用 (a)方程(16a)作为初始条件的数值演化结果; (b)方程(16b)作为初始条件的数值演化结果. 除
图 4 相邻孤子间的相互作用 (a)方程(16a)作为初始条件的数值演化结果; (b)方程(16b)作为初始条件的数值演化结果. 除




















