摘要:晶界的结构对氮化硅陶瓷材料的物理和化学性能、特别是高温力学性能有重要影响. 本文利用基于电子背散射衍射技术、体视学及统计学的五参数分析法研究了国产和国外产热等静压烧结的商用氮化硅轴承球样品的晶界特征分布. 结果表明, 两个样品的晶界取向差分布均在约180°处出现异常, 相关晶界占总晶界的比例明显高于随机分布, 其取向差主要包括[0 1 –1 0]/180°和[–1 2 –1 0]/180°, 分别对应Σ2和Σ3晶界. 两个样品中的Σ2晶界的界面匹配基本一致, 均以{0 0 0 1}/{0 0 0 1}基面/基面匹配为主, 但二者Σ3晶界的界面匹配存在很大差异, 表现为国产样品以{–1 2 –1 0}/{–1 2 –1 0}柱面匹配为主, 而国外产样品以{1 0 –1 0}/{1 0 –1 0}柱面匹配为主; 具有{–1 2 –1 0}/{–1 2 –1 0}, {0 0 0 1}/{0 0 0 1}和{1 0 –1 0}/{1 0 –1 0}三种界面匹配特征的晶界, 其面重合点密度分别为2.45 /nm², 7.95 /nm²和9.10 /nm², 晶界的结构有序度依次升高. 分析指出, 具有{1 0 –1 0}/{1 0 –1 0}界面匹配特征的Σ3晶界以及具有{0 0 0 1}/{0 0 0 1}界面匹配特征的Σ2晶界是氮化硅陶瓷材料中的一类特殊晶界.
关键词: 氮化硅陶瓷/
电子背散射衍射/
晶界特征分布/
晶界界面匹配

English Abstract

全文HTML

--> --> -->

氮化硅作为一种先进陶瓷材料, 具有耐磨、耐蚀、自润滑和优异的高温力学性能, 广泛用作超高温结构材料、散热功能材料和耐磨耐蚀材料. 例如, 涡轮机热导体、燃气轮机叶片、轴承和电解铝设备关键部件等^[1-3]. 然而, 随着现代装备制造业的快速和高质量发展, 人们对氮化硅陶瓷材料性能提出了更高要求, 如新一代涡轮发动机向高流量比、高推重比和高转速方向发展, 要求氮化硅陶瓷具有更高的高温蠕变开裂抗力和高周疲劳开裂抗力^[4]; 当代电解铝行业为了实现节能降耗, 要求其关键部件材料氮化硅陶瓷具有更高的耐受特殊介质和特殊气氛的腐蚀抗力^[5]. 因此, 如何进一步提升高温力学性能、高周疲劳性能和特殊环境下的腐蚀性能, 是氮化硅陶瓷材料研究领域亟待解决的共性关键问题.
有研究表明, 氮化硅陶瓷的高温蠕变开裂和高周疲劳开裂, 以及特殊环境中的腐蚀破坏均与留存在材料晶界处的烧结助剂密切相关^[6-8]. 这是因为, 相比于氮化硅基体, 烧结助剂是玻璃相, 没有固定熔点, 随温度升高存在连续软化行为, 且在高温受力条件下会引起氮化硅晶粒沿晶界滑动, 导致蠕变开裂问题; 其次, 烧结助剂的强度远不及氮化硅基体, 且塑韧性很差, 高转速条件下的高周疲劳裂纹往往萌生于烧结助剂处; 再者, 烧结助剂的耐蚀性不及氮化硅基体, 在特殊环境下的腐蚀优先产生于烧结助剂, 进而沿烧结助剂发展为沿晶界腐蚀开裂, 即晶界腐蚀开裂. 针对上述问题, 人们主要从三个方面对氮化硅陶瓷的性能进行改进: 1) 通过优化烧结助剂的组成和配比来改变晶界玻璃相的构成, 以提高其耐熔度, 进而改善氮化硅陶瓷的高温力学性能^[9,10]. 但是, 这种方法会导致液相的形成温度偏高, 不利于材料的致密化, 同时提高烧结温度也增加了成本, 因此, 这种方法的应用受到一定限制. 2) 晶界玻璃相的晶化处理^[11,12]. 烧结后的氮化硅陶瓷再经过一定时间的热处理, 使晶界玻璃相转变为高熔点的结晶相, 以减少或消除残余玻璃相来改善氮化硅陶瓷材料的高温力学性能和耐蚀性能. 但高熔点结晶相的热膨胀系数往往与氮化硅基体的热膨胀系数不匹配, 在高温条件下容易在高熔点结晶相或氮化硅基体生成裂纹. 3) 形成Sialon 单相固溶体陶瓷, 避免晶界玻璃相^[13,14]. 这需要特定的氮化物相作为烧结助剂, 但是, 其他元素进入氮化硅基体形成的多元相, 其平衡规律很复杂, 此类多元固溶体的制备很难控制, 且制备出来的材料断裂韧性不高, 很难满足实际需求.
可见, 上述几种方法均是针对晶界处的烧结助剂而采取的对策, 并不能从根本上显著改善氮化硅陶瓷材料的高温力学性能、高周疲劳性能和特殊环境下的腐蚀性能. 考虑到晶界是Si₃N₄陶瓷材料的一个基本结构单元, 对材料微观组织结构和性能起着至关重要的作用. 那么以氮化硅晶界本身的结构和特性研究为切入点, 通过设计和控制晶界特征分布(grain boundary character distribution, GBCD)将有可能从根本上显著提升氮化硅陶瓷材料的高温力学性能、高周疲劳性能和特殊环境下的腐蚀性能. 这便是“晶界工程”(grain boundary engineering, GBE)的研究思想, 意指在多晶材料中引入高比例的特殊晶界来有效阻断一般晶界的网络连通性, 从总体上显著改善材料与晶界相关的多种性能^[15,16]. 这类特殊晶界是指那些原子排列有序度高、能量低且结构稳定的一类晶界. 目前, GBE已在奥氏体不锈钢^[17]、铅钙合金^[18]、黄铜^[19]和镍基超合金^[20]等多种金属材料中得到广泛研究和应用, 使这些材料的晶界腐蚀抗力得到了显著提升.
显然, 尽快开展氮化硅晶界本身结构与特性的研究, 掌握其特殊晶界的基本特征, 通过GBE技术引入高比例的特殊晶界, 将有望从根本上显著改善氮化硅材料的高温力学性能、高周疲劳性能和特殊环境下的腐蚀性能, 从而满足现代装备制造业对氮化硅这一先进陶瓷材料的性能要求. 因此, 本文将利用电子背散射衍射(electron backscatter diffraction, EBSD)技术^[21]并结合五参数分析法(five parameter analysis, FPA) ^[22], 首先对比研究国产和国外产热等静压(hot isostatic pressing, HIP)烧结的商用氮化硅陶瓷轴承球的显微组织, 重点是晶界特征分布, 主要包括晶界取向差分布、晶界面分布和晶界界面匹配(grain boundary inter-connection, GBIC) ^[23], 以掌握两种氮化硅陶瓷轴承球的晶界结构特征, 为氮化硅陶瓷材料GBE研究及应用奠定理论基础, 提供实验依据.

选用国产和国外产两种商业级HIP氮化硅陶瓷轴承球作为研究对象, 并分别命名为样品E (sample E)和样品F (sample F). 首先利用金刚石线切割机从轴承球中切出厚度为0.5 mm 的片状样品, 再采用Leica EM TXP精研一体机对其表面进行研磨, 磨布粒度由粗至细(9 μm—2 μm—0.5 μm). 然后, 依次使用粒度分别为0.05 和0.02 μm的SiO₂悬浮抛光液(国产标乐公司产)对研磨后的样品进行机械抛光. 最后, 利用Leica EM TIC 3X三离子束抛光机对样品进行电压递减三步骤离子抛光, 即5 kV/45 min, 4.5 kV/45 min和4 kV/90 min. 为避免荷电效应, 经离子抛光的样品再经Leica EM ACE200真空镀膜仪镀碳2—6 nm后才可进行EBSD测试. 为观察两个样品的晶粒形貌, 经机械抛光后的样品进行50 ℃水浴氢氟酸(HF)腐蚀240 min, 超声清洗干燥后待用.
将上述制备好的样品置入配有Oxford Aztec附件的美国FEI公司产Nova nano 450热场发射扫描电子显微镜(field emission scanning electron microscopy, FE-SEM)中进行EBSD测试, 测试参数为: 加速电压为15 kV, 束斑尺寸为5.5, 步长为0.05 μm, 测试区域为8 μm×8 μm. 为保证结果具有统计代表性, 每个样品均测试多个区域, 采集到的Si₃N₄/Si₃N₄晶界数量均超过50000条. 对测得的EBSD原始数据进行处理, 得到全欧拉角显微组织图、Si₃N₄/Si₃N₄晶界网络图、取向成像显微图(orientation imaging microscopy, OIM)和取向分布函数图(orientation distribution function, ODF). 对OIM图做进一步数据处理, 重点是提取晶界迹线的相关信息, 主要包括晶界迹线的长度、晶界迹线所关联的两相邻晶粒之间的取向差以及晶界迹线在两晶粒晶体学空间中的取向, 等等. 在此基础上, 对所提取的Si₃N₄/Si₃N₄晶界(β-Si₃N₄晶胞参数为a = b=0.76 nm, c = 0.29 nm, c/a = 0.38; 空间群P63/m, 176^[24])按照其取向差(轴角对)特征进行过滤, 即先进行以旋转轴为特征的轴过滤(偏差为±5°), 再对轴过滤后的晶界进行以旋转角为特征的角度过滤(偏差为±2.5°), 这样就可以把全部Si₃N₄/Si₃N₄晶界分成若干组, 且每组晶界具有各自固定的取向差特征.
为了更加准确地掌握Si₃N₄/Si₃N₄晶界结构特征, 对比分析两种氮化硅陶瓷轴承球产品的差异, 利用Rohrer^[22]基于体视学原理的FPA方法对上述过滤出来的每组晶界的晶界面分布进行统计分析, 给出晶界面分布的FPA图(即晶界面法线方向在(0 0 0 1)上的极射赤面投影). 通过比对FPA图中的取向强点(本文只关注最强点和次强点), 结合晶体学有关理论进行分析后, 便可以确定每组晶界的GBIC特征, 即晶界结构的本征参量. 最后利用近重位点阵理论(near coincidence site, NCS) ^[25], 考虑Si₃N₄晶体具体结构及N原子和Si原子在各晶面内的标准分布, 确定具有特定界面匹配特征晶界的面重合点密度(planar coincident site density, PCSD) ^[26], 即面重合原子密度. 确定晶界GBIC的详细过程可参考Wang等近年来公开发表的相关工作^[23,27,28].

2

-->

3.1.显微组织及取向差分布

图1给出样品E和F的EBSD全欧拉角显微组织. 通过对比图1(a)和图1(c)与图1(b)和图1(d)可以看到, 样品E的长棒状β-Si₃N₄晶粒较少, 而样品F的β-Si₃N₄晶粒多呈细棒状. 同时, 还可以看到, 样品E的组织较为粗大, 晶粒尺寸分布不够均匀, 且长径比较小; 而样品F的组织较为细小, 晶粒尺寸分布比较均匀, 长径比也较大. 图2给出的两个样品的SEM晶粒组织与图1是一致的. 图3给出样品E和F的OIM(图3(a)和图3(b))及其Si₃N₄/Si₃N₄晶界网络图(图3(c)和图3(d)). 从图3可以看到, 尽管两个样品的晶粒尺寸有一定差异, 但其烧结助剂(玻璃相)(图3(a)和图3(b))中的白色区域以及图3(c)和图3(d)中的线条断开部分)含量及空间分布是相近的. 当然, 从OIM图中也可以看到两个样品中的晶粒取向分布均匀(各种颜色分布均匀), 没有存在明显的宏观织构, 这与图4中的ODF结果是吻合的, 符合氮化硅陶瓷轴承球的热等静压烧结工艺. 图5给出了样品E和F的晶界取向差分布. 从图5可以看出, 虽然晶界取向差分布差异不大, 整体上满足随机分布, 但是, 取向差角度大约为180°的晶界占总晶界的比例显著高于随机分布, 并且这一比例在两个样品中存在一定差异, 其中样品E的约为5.4% (图5(a)中A+B+C之和), 而样品 F的约为3.6% (图5(b)中A+B+C之和). 为了深入探讨这一现象, 需要对所有晶界按其取向差特征(轴角对)进行过滤分析, 并重点针对取向差角度为180°的晶界. 首先, 按晶界取向差旋转轴的不同对所有晶界进行轴过滤. 这些旋转轴按其密勒指数由低到高分别为[0 0 0 1], [0 1 –1 0], [–1 2 –1 0]和[–1 5 –4 0]等共19个, 轴偏差设定为±5°, 过滤出来的晶界占总晶界的比例约为52%. 然后, 对上述轴过滤出来的晶界进行归一化处理, 发现这些晶界的旋转轴主要为[–1 2 –1 0], [0 1 –1 0], [2 1 –3 0], [1 2 –3 0], [–1 5 –4 0]和[5 –1 –4 0], 以这6个晶轴为旋转轴的晶界占到上述轴过滤出来的晶界的近70%, 这一比例在两个样品中的差异很小(图6). 在轴过滤基础上, 进一步按晶界取向差旋转角的不同进行角过滤后, 发现取向差角度为180°晶界的63%是旋转轴为[0 1 –1 0]和[–1 2 –1 0]的晶界(图7), 即取向差为[0 1 –1 0]/180°和[–1 2 –1 0]/180°的晶界. 下文将主要针对这两类晶界展开分析.
图 1 电子背散射衍射(EBSD)全欧拉角去噪前(a)和(b)及去噪后(c)和(d)显微组织 (a), (c)样品E; (b), (d) 样品F
Figure1. All Euler microstructures before (a) and (b) and after (c) and (d) noise reduction, obtained by electron backscatter diffraction (EBSD): (a), (c) Sample E; (b), (d) sample F.

图 2 经50 ℃氢氟酸(HF)浸泡240 min后样品E(a)和F(b)的二次电子显微组织(SEM)
Figure2. The secondary electron microscopy (SEM) of sample E (a) and F (b) after soaking in hydrofluoric acid at 50 ℃ for 240 min.

图 3 取向成像显微图(a)和(b)及Si₃N₄/ Si₃N₄晶界网络(c)和(d) (a), (c) 样品E; (b)和(d) 样品F
Figure3. Orientation imaging microscopy (OIM) (a) and (b), and Si₃N₄/Si₃N₄ grain boundary networks (c) and (d): (a), (c) Sample E; (b), (d) sample F.

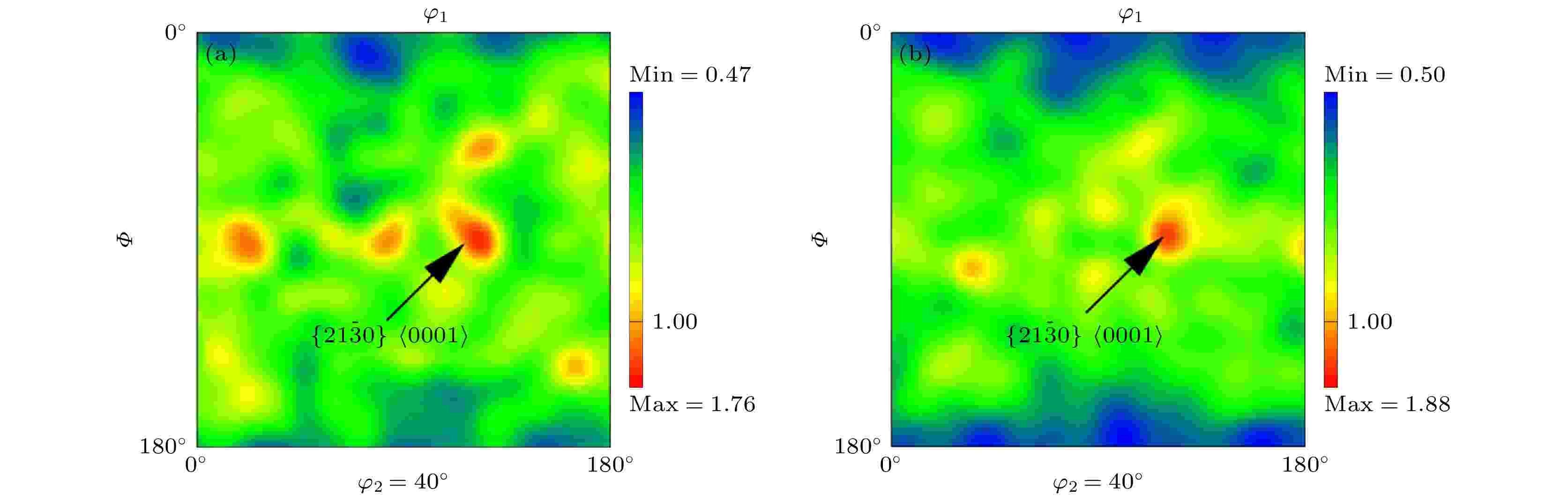图 4 φ₂ = 40°截面的取向分布函数图　(a) 样品E; (b) 样品F
Figure4. φ₂ = 40° section of orientation distribution function (ODF): (a) Sample E; (b) sample F.

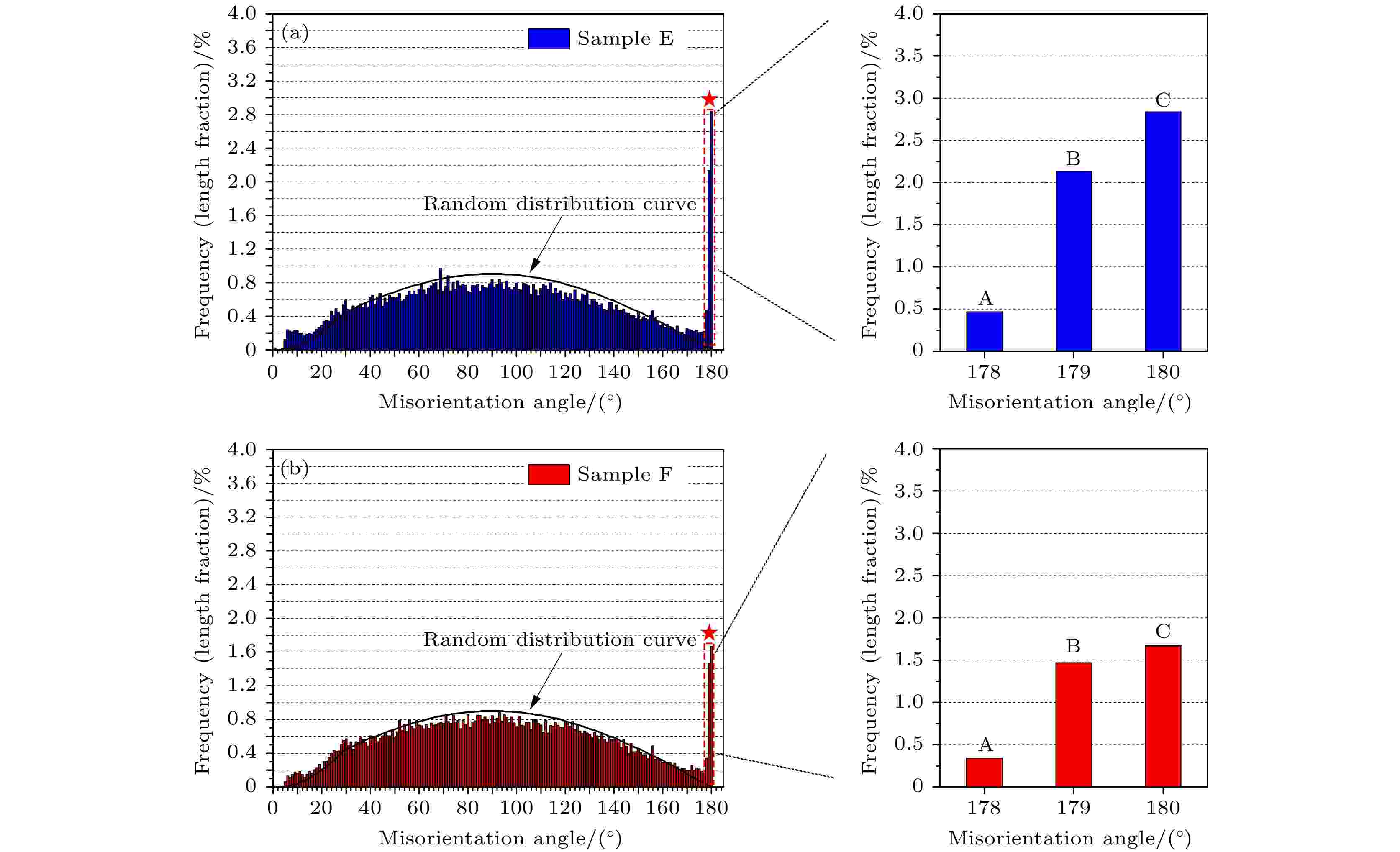图 5 Si₃N₄/Si₃N₄晶界取向差分布图　(a) 样品E; (b) 样品F
Figure5. Misorientation distributions of Si₃N₄/Si₃N₄ grain boundaries of sample E (a) and F (b).

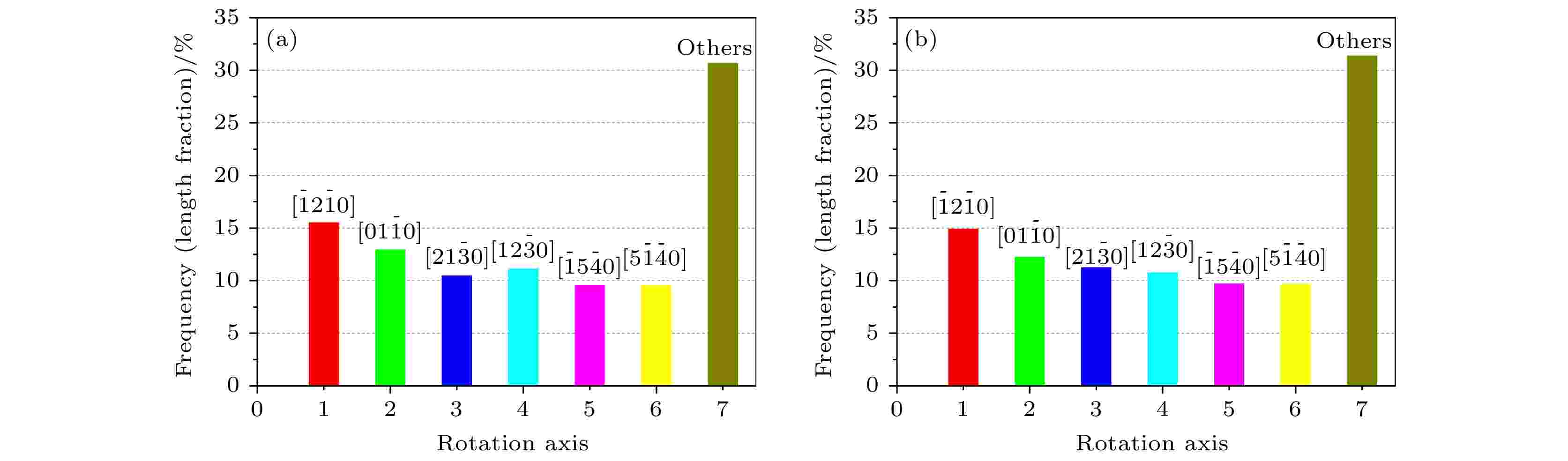图 6 Si₃N₄/ Si₃N₄晶界随旋转轴分布　(a) 样品E; (b) 样品F
Figure6. The frequencies of the gain boundaries with varied rotation axis in sample E (a) and F(b).

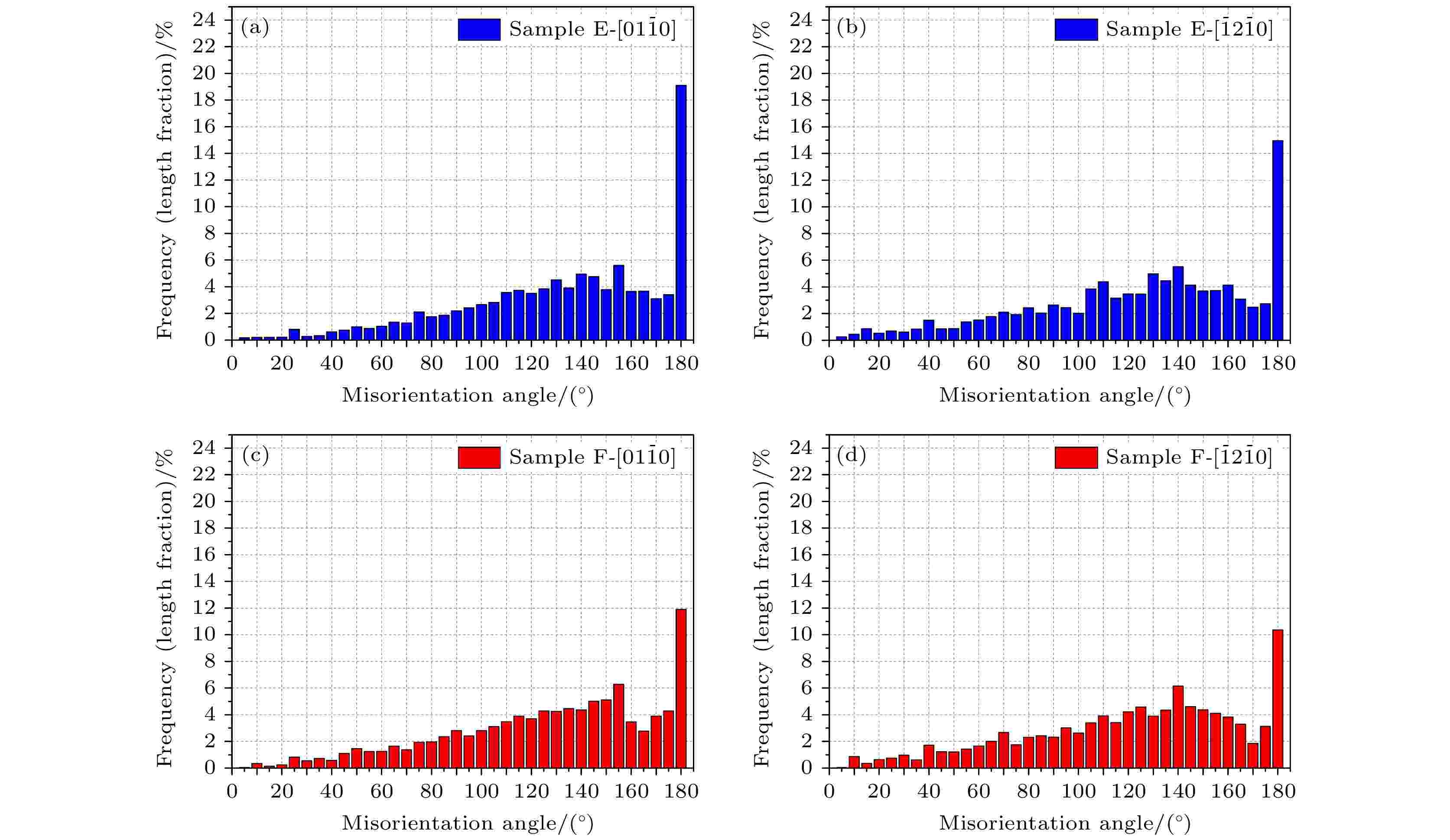图 7 以[0 1 –1 0]((a)和(c))及[–1 2 –1 0] ((b)和(d))为旋转轴的Si₃N₄/Si₃N₄晶界取向差分布 (a), (b) 样品E; (c), (d) 样品F
Figure7. Misorientation distributions of Si₃N₄/Si₃N₄ grain boundaries possessing rotation axis [0 1 –1 0] (a) and (c) and [–1 2 –1 0] (b) and (d): (a), (b) Sample E; (c), (d) sample F.

取向差为[0 1 –1 0] /180°和[–1 2 –1 0]/180°的晶界是由相邻晶粒分别绕共同的[0 1 –1 0]和[–1 2 –1 0]晶轴旋转180°形成的晶界. 从晶体学考虑, β-Si₃N₄属于复式密排六方结构, 虽然其布拉菲点阵仍为简单六方, 但约化到每个阵点上的基元实为2个方向性不同的Si₃N₄分子, 每个晶胞内含有14个原子, 即6个硅原子和8个氮原子. 氮化硅的这种特定结构使其相对于其他简单六方晶胞(如Mg和Zr等六方金属材料晶胞)少了一种对称操作, 因此不能用简单的重位点阵来研究β-Si₃N₄特定取向差的点阵重合度. 类比重位点阵的定义以及将容忍偏差值设定为0.1a (a为晶胞参数), 用原子重合占比Q值的倒数反映β-Si₃N₄特定取向差的点阵重合度, 称类Σ值. 对于[0 1 –1 0]/180°取向差, 2个N1等价氮原子以及6个等价硅原子的重合度均为1.0, 6个N2等价氮原子完全不重合, 单胞内共有14个原子, 其Q值 = (2 + 6)/14 = 4/7 ≈ 0.57, 其类Σ值 = 2(图8); 对于[–1 2 –1 0]/180°取向差, 单胞内2个N1等价氮原子重合度均为0.5, 6个等价硅原子完全不重合, 6个N2等价氮原子重合度均为0.6, 单胞内共有14个原子, 其Q值 = (2 × 0.5 + 6 × 0.6)/14 = 2.3/7 ≈ 0.33, 其类Σ值 = 3 (图9). 因此, 参照重位点阵理论^[29], 具有[0 1 –1 0]/180°和[–1 2 –1 0]/180°这两种取向差的晶界均属于低Σ值晶界, 分别为Σ2和Σ3晶界. 显然, 这只是基于取向差三参数^[30]确定的晶界特征, 还不足以解释[0 1 –1 0]/180°和[–1 2 –1 0]/180°晶界比例显著偏高这一现象. 下文将从晶界面分布和晶界界面匹配(GBIC)两方面做进一步分析.
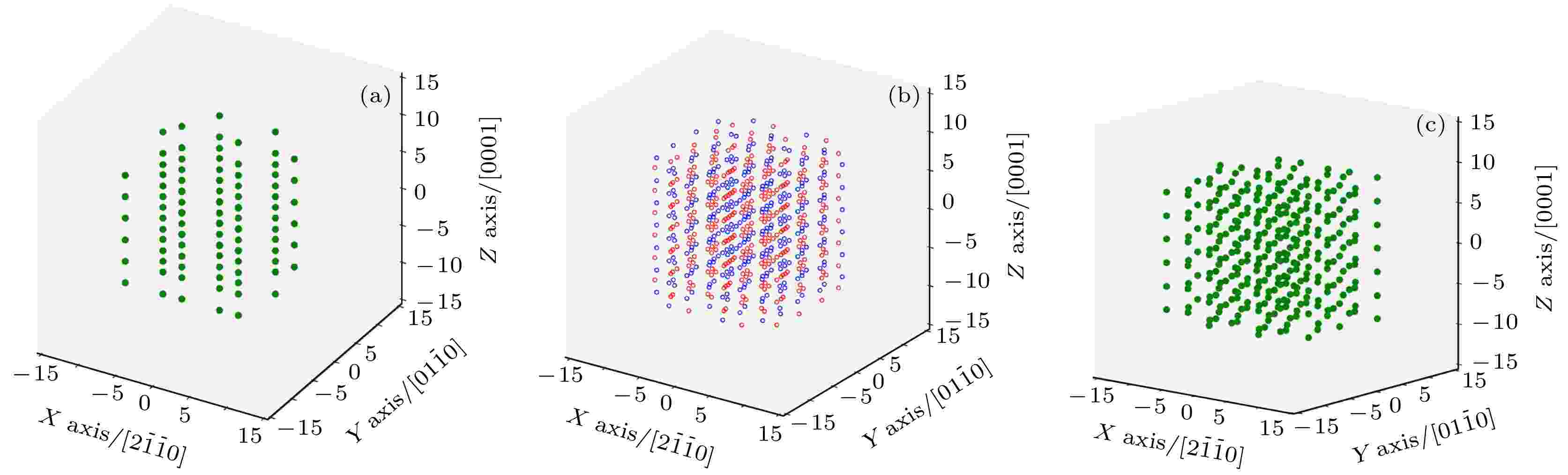图 8 两Si₃N₄晶粒呈[0 1 –1 0]/180°(Σ2)取向差关系对应的重合原子示意图　(a) 2个等价N1原子重合图; (b) 6个等价N2原子重合图; (c) 6个等价Si原子重合图. 其中蓝色圆圈和红色圆圈分别代表旋转前后的原子, 绿色圆点代表重合原子. 每个示意图均包含为50个Si₃N₄晶胞
Figure8. Schematic illustrations for the coincident atoms when two Si₃N₄ crystals have a misorientation of [0 1 –1 0]/180°(Σ2): (a) Two identical N1 atoms; (b) 6 identical N2 atoms; (c) 6 identical Si atoms. Blue and red circles stand for the atoms before and after rotation, respectively. Green dots represent the coincident atoms. Each plot contains 50 unit cells of Si₃N₄.

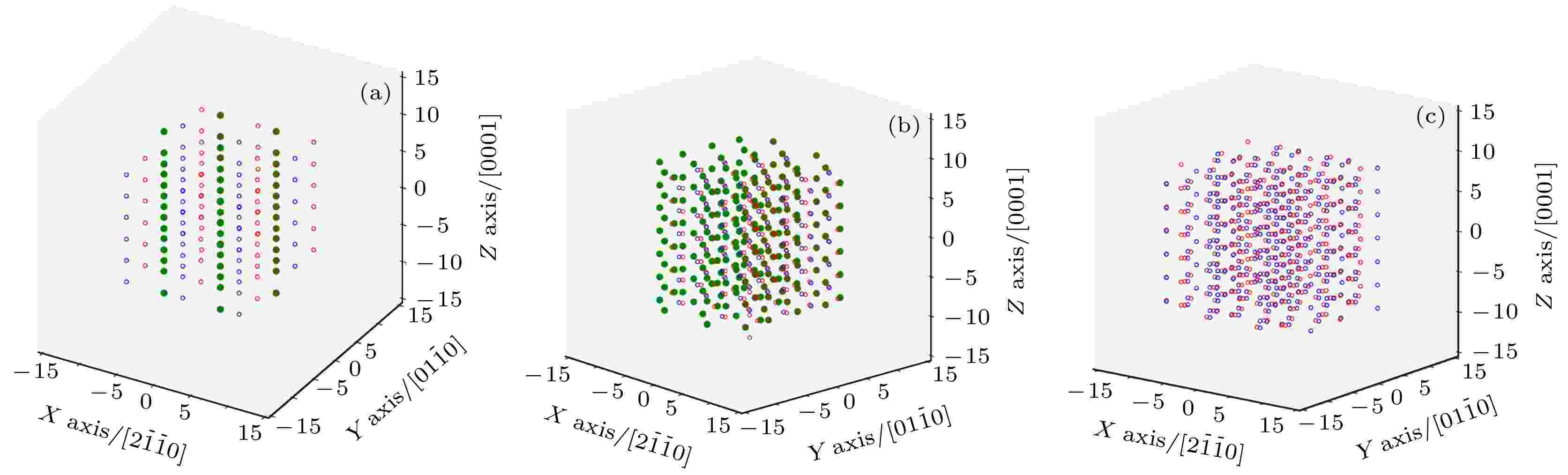图 9 两Si₃N₄晶粒呈[–1 2 –1 0]/180°(Σ3)取向差关系对应的重合原子示意图　(a) 2个等价N1原子重合图; (b) 6个等价N2原子重合图; (c) 6个等价Si原子重合图. 其中蓝色圆圈和红色圆圈分别代表旋转前后的原子, 绿色圆点代表重合原子. 每个示意图均包含为50个Si₃N₄晶胞
Figure9. Schematic illustrations for the coincident atoms when two Si₃N₄ crystals have a misorientation of [–1 2 –1 0]/180°(Σ3): (a) Two identical N1 atoms; (b) 6 identical N2 atoms; (c) 6 identical Si atoms. Blue and red circles stand for the atoms before and after rotation, respectively. Green dots represent the coincident atoms. Each plot contains 50 unit cells of Si₃N₄.

2 -->

3.2.晶界面分布

图10给出两个样品的[0 1 –1 0]/180°(Σ2)和[–1 2 –1 0]/180°(Σ3)晶界的晶界面分布FPA图. 从图10容易看出, 两个样品的Σ2晶界的晶界面分布十分接近(图10(a)和图10(b)), 均在(0 0 0 1)和(–2 1 1 2)及其等同晶面上出现强分布. 有所不同的是, 样品E还在(–2 2 0 1)及其等同晶面上存在强分布. 上述晶面中, 除(–2 2 0 1)及其等同晶面与(0 0 0 1)基面的夹角略大外, 其余晶面均与(0 0 0 1)基面夹角很小. 因此, 可以认为两个样品的Σ2晶界的晶界面以(0 0 0 1)基面分布为主. 这种分布在同为六方结构的碳化钨(WC)硬质合金中也曾被观察到^[31]. 相反, 两个样品的Σ3晶界的晶界面分布差异很大(图10(c)和图10(d)). 样品E的Σ3晶界的晶界面在(–1 2 –1 0)柱面及其等同晶面出现强分布, 在(–5 3 2 1)和(2 3 –5 –1)锥面以及这些晶面的等同晶面出现次强分布; 而样品F的Σ3晶界的晶界面则在(–1 0 1 0)柱面及其等同晶面出现强分布, 在(–8 1 7 1)和(7 1 –8 –1)锥面以及这些晶面的等同晶面出现次强分布. 也就是说, 样品E和样品F的Σ3晶界的晶界面分别以(–1 2 –1 0)和(–1 0 1 0)柱面及其等同晶面分布为主, 这一点可以从图11给出两个样品各自的全部晶界的晶界面(全谱晶界面)分布FPA图加以理解. 由图11可以看出, 两个样品各自的全部晶界的晶界面均集中分布在六方晶胞的柱面上, 即{h k m 0} (其中m = – (h + k)). 造成这种分布的主要原因是, 在HIP烧结过程中, 晶粒沿(0 0 0 1)基面法线方向生长的激活能显著低于沿(1 0 –1 0)柱面法线方向生长的激活能, β-Si₃N₄易于沿六方晶胞的[0 0 0 1]方向上生长形成长棒状, 棒的侧面刚好都是柱面^[32]. 这与样品E和F两个样品Σ3晶界的晶界面出现柱面分布密切相关. 由于FPA方法是把每个晶界所关联的两个晶界面{h₁ k₁ m₁ l₁}和{h₂ k₂ m₂ l₂}作为互不相干的独立参量进行晶界面分布统计, 因此晶界面分布结果也不能给出晶界结构特征, 仍然不能解释[0 1 –1 0]/180°(Σ2)和[–1 2 –1 0 ]/180°(Σ3)晶界比例显著偏高这一现象.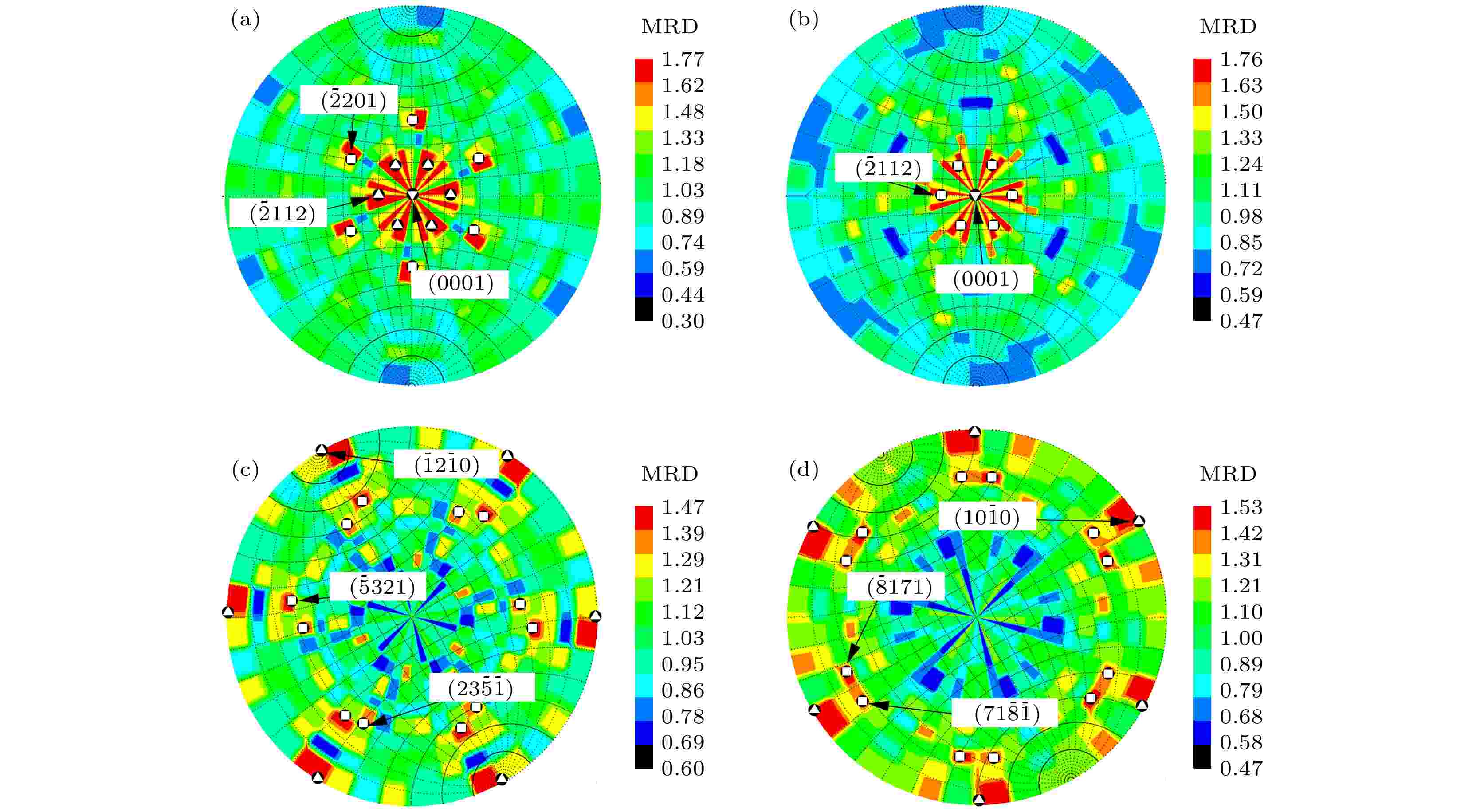
图 10 样品E((a)和(c))和F((b)和(d))[0 1 –1 0]/180°((a)和(b))以及[–1 2 –1 0]/180°((c)和(d))晶界的晶界面分布FPA图(投影在(0 0 0 1)内) (a)和(b)中的, 和 为分布强点等同位置; (c)和(d)中的 和 分别为分布强点和次强点等同位置
Figure10. (0 0 0 1) projections of grain boundary plane distributions of [0 1 –1 0]/180°((a) and (b))and [–1 2 –1 0]/180°((c) and (d)) grain boundaries in sample E ((a) and (c)) and sample F ((b) and(d)). , and in Figure (a) and (b) stand for the identical positions of the strongest distribution, while and in Figure (c) and (d) represent the identical positions of the strongest and the second strongest distribution, respectively.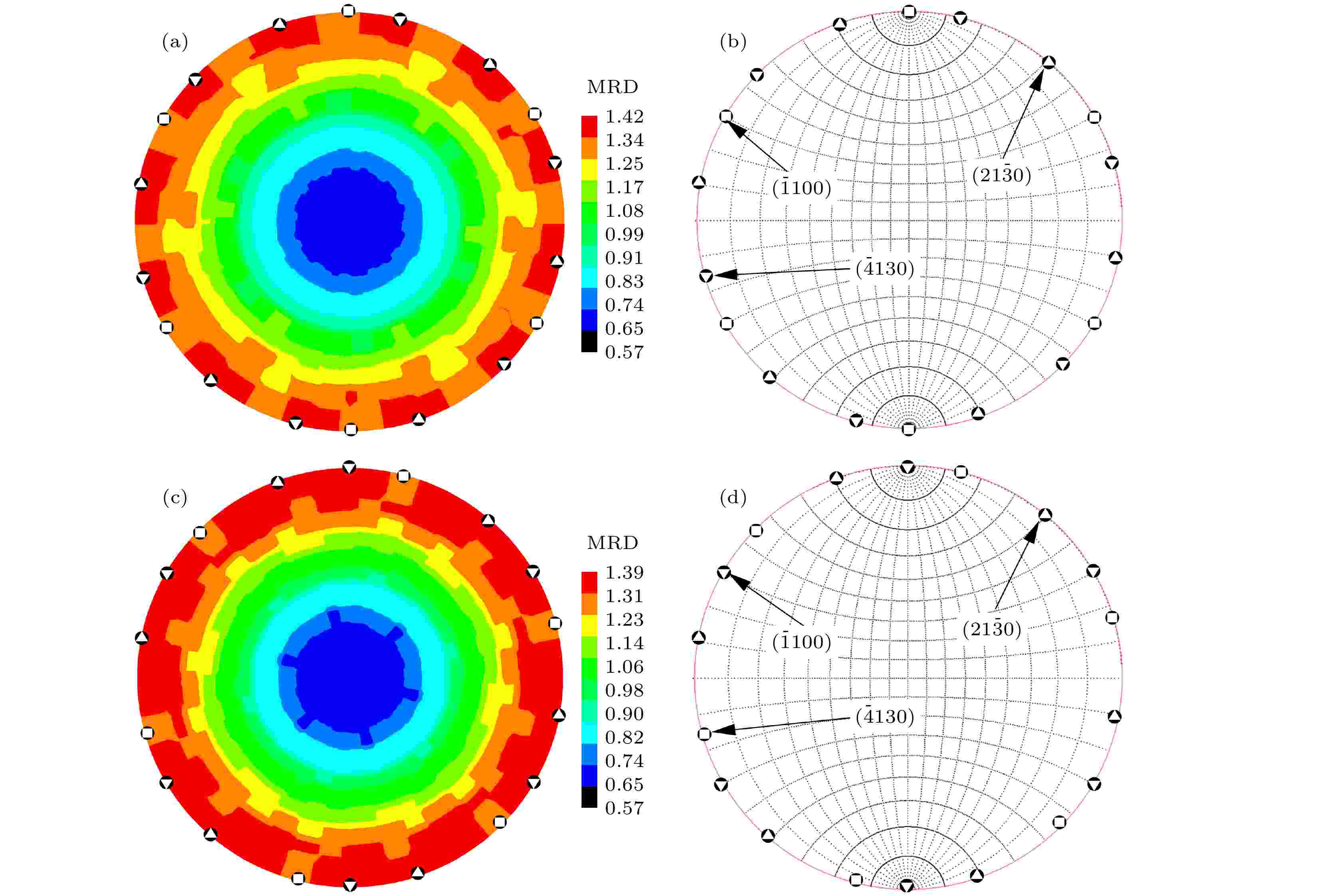

图 11 样品E((a)和(b))和F((c)和(d))各自的Si₃N₄/ Si₃N₄全部晶界的晶界面分布FPA图((a)和(c))及其分布强点和次强点位置示意图((b)和(d))(投影在(0 0 0 1)内). , 为分布最强点等同位置, 为分布次强点等同位置
Figure11. (0 0 0 1) projections of grain boundary plane distributions of all grain boundaries insample E ((a) and (b)) and F ((c) and (d)). and stand for the identical positions of the strongest distributions, while represents the identical positions of the second strongest distribution.

2 -->

3.3.晶界界面匹配(GBIC)

基于图10的实测结果, 图12给出两个样品的[0 1 –1 0]/180°(Σ2)和[–1 2 –1 0 ]/180°(Σ3)晶界的晶界面分布强点和次强点位置示意图, 同时也给出Σ2和Σ3晶界的晶体学旋转操作示意图. 例如对于样品E的Σ2晶界(图12(a)), 晶界面分布强点(–2 2 0 1)绕[0 1 –1 0]转动128°到达边缘M点, 继续绕该轴转动52°到达(2 0 –2 –1). 也就是说, 当(–2 2 0 1)绕[0 1 –1 0]连续转动180°后(Σ2操作)到达(2 0 –2 –1), 该点也是分布强点. 据此, 可以确定样品E的Σ2晶界中存在(–2 2 0 1)/(2 0 –2 –1) GBIC. 容易理解, 若选择[0 1 –1 0]的等同晶轴做相同操作, 可以得到与(–2 2 0 1)/(2 0 –2 –1)等同的GBIC, 其关联的晶面都是与(–2 2 0 1)或(2 0 –2 –1)等同的晶面, 均是分布强点(图10(a)和图12(a)). 此类GBIC可以用一般表达式(或等同表达式){–2 2 0 1}/{–2 2 0 1}表示. 以此类推, 样品E的Σ2晶界中还存在{–2 1 1 2}/{–2 1 1 2}和{0 0 0 1}/{0 0 0 1}两种GBIC, 这两种GBIC也在样品F的Σ2晶界中存在(图12(b)); 样品E的Σ3晶界中存在{–1 2 –1 0}/{–1 2 –1 0}和{–5 3 2 1}/{2 3 –5 –1}两种GBIC(图12(c)); 样品F的Σ3晶界中存在{1 0 –1 0}/{1 0 –1 0}和{–8 1 7 1}/{7 1 –8 –1}两种GBIC(图12(d)). 进一步考察N原子和Si原子在各晶面内的标准分布, 发现上述7种GBIC的面重位点密度PCSD差异很大, PCSD值由大到小对应的GBIC分别为{1 0 –1 0}/{1 0 –1 0}、{0 0 0 1}/{0 0 0 1}、{–2 1 1 2}/{–2 1 1 2}、{–1 2 –1 0}/{–1 2 –1 0}、{–8 1 7 1}/{7 1 –8 –1}、{–2 2 0 1}/{–2 2 0 1}和{–5 3 2 1}/{2 3 –5 –1}, 其PCSD值分别为9.10/nm², 7.95/nm², 3.50/nm², 2.45/nm², 1.63/nm², 1.49/nm²和0.93/nm² (表1所列). 容易理解, 在只考虑晶体学几何因素的条件下, PCSD值越大, 晶界处单位面积上重合的原子数越多, 即晶界处被晶界两侧两个晶粒所共用的原子数越多, 意味着晶界的原子结构有序度越高, 晶界能量越低、结构越稳定^[23,28,31]. 样品E和F的Σ2或Σ3晶界中存在高PCSD值的具有{0 0 0 1}/{0 0 0 1}或{–1 2 –1 0}/{–1 2 –1 0}和{1 0 –1 0}/{1 0 –1 0}界面匹配特征的晶界应具备低能和稳定的结构特征, 这是两个样品中[0 1 –1 0]/180°(Σ2)和[–1 2 –1 0 ]/180°(Σ3)晶界比例显著高于随机分布的根本原因.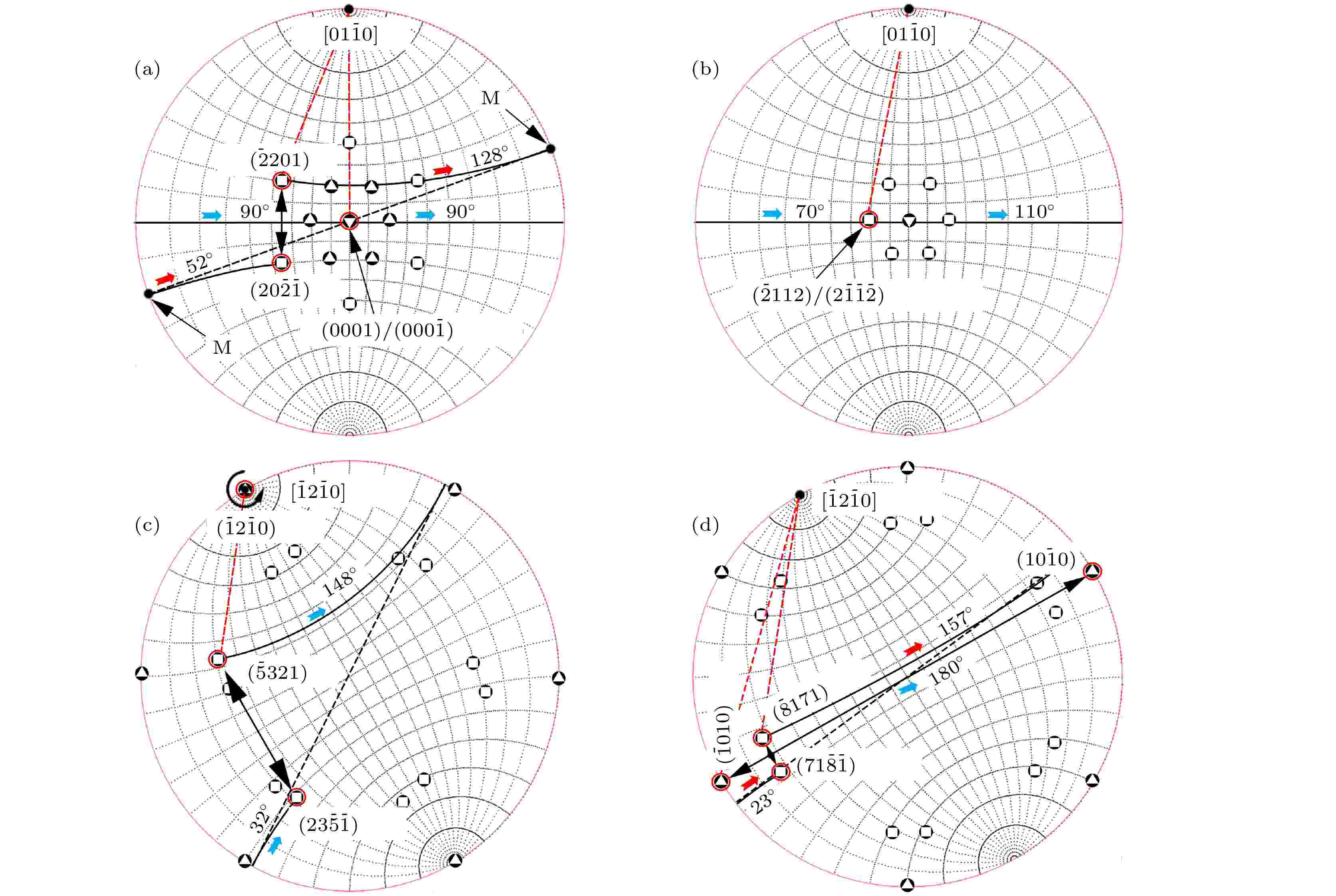
图 12 对应于图10的样品E((a)和(c))和F((b)和(d))[0 1 –1 0]/180°((a)和(b))以及[–1 2 –1 0]/180°((c)和(d))晶界的晶界面分布示意图(投影在(0 0 0 1)内)
Figure12. Schematic illustrations of grain boundary plane distributions of [0 1 –1 0]/180° ((a) and (b)) and [–1 2 –1 0]/180° ((c) and (d)) grain boundaries in sample E ((a) and (c)) and F ((b) and (d)).

Sample E				Sample F
Misorientation (u v t w/θ)	GBICs	PCSD /(/nm2)		Misorientation (u v t w/θ)	GBICs	PCSD /(/nm2)
[0 1 –1 0]/180°	{–2 2 0 1}/{–2 2 0 1}	1.49		[0 1 –1 0]/180°	{–2 1 1 2}/{–2 1 1 2}	3.5
(Σ2)	{–2 1 1 2}/{–2 1 1 2}	3.5		(Σ2)	{0 0 0 1}/{0 0 0 1}	7.95
	{0 0 0 1}/{0 0 0 1}	7.95
[–1 2 –1 0]/180°	{–5 3 2 1}/{2 3 –5 –1}	0.93		[–1 2 –1 0]/180°	{–8 1 7 1}/{7 1 –8 –1}	1.63
(Σ3)	{–1 2 –1 0}/{–1 2 –1 0}	2.45		(Σ3)	{1 0 –1 0}/{1 0 –1 0}	9.1

表1样品E和F中[0 1 –1 0]/180°和[–1 2 –1 0]/180°晶界的GBIC及对应的PCSD值
Table1.The GBICs and PCSD values of [0 1 –1 0]/180° and [–1 2 –1 0]/180° grain boundaries observed in sample E and F

基于氮化硅陶瓷晶体结构基本特征, 可以认为PCSD值大于5.0 /nm²的晶界是一种有序度高且缺陷(包括晶界自由体积和位错等)密度低的晶界, 烧结助剂(玻璃相)难以或很少在此类晶界处聚集; 提高此类晶界的比例, 则可以从根本上提升氮化硅陶瓷材料的高温力学性能和晶界腐蚀抗力. 因此, 可以把具有{0 0 0 1}/{0 0 0 1}和{1 0 –1 0}/{1 0 –1 0}界面匹配特征的晶界称为氮化硅陶瓷材料中的特殊晶界(奇异晶界或近奇异晶界^[23]). 对比国产(样品E)和国外产(样品F)陶瓷轴承球, 虽然两个样品中均存在具有{0 0 0 1}/{0 0 0 1}界面匹配特征的特殊晶界(Σ2晶界), 但国外产样品中却存在具有{1 0 –1 0}/{1 0 –1 0}界面匹配特征的特殊晶界(Σ3晶界), 其PCSD值远高于国产样品中存在的具有{–1 2 –1 0}/{–1 2 –1 0}界面匹配特征的同为Σ3晶界的PCSD值. 也就是说国外产样品中的Σ3晶界是典型的特殊晶界, 而国产样品中的Σ3晶界并非特殊晶界. 这可能与国外产样品所采用的特定的原料状态、烧结助剂种类和配方以及HIP烧结技术路线有关, 是一个值得进一步深入研究的问题.

本文利用电子背散射衍射技术和基于体视学及统计学的五参数分析法研究了国产和国外产热等静压烧结商用氮化硅轴承球样品的晶界特征分布, 主要结论如下:
1) 两个样品的晶界取向差分布均在约180°处出现异常, 相关晶界占总晶界的比例明显高于随机分布, 其取向差主要包括[0 1 –1 0]/180°和[–1 2 –1 0]/180°, 分别对应Σ2和Σ3晶界;
2) 两个样品中的Σ2晶界的界面匹配基本一致, 均以{0 0 0 1}/{0 0 0 1}基面/基面匹配为主, 但二者Σ3晶界的界面匹配存在很大差异, 表现为国产样品以{–1 2 –1 0}/{–1 2 –1 0}柱面匹配为主, 而国外产样品以{1 0 –1 0}/{1 0 –1 0}柱面匹配为主;
3) 具有{1 0 –1 0}/{1 0 –1 0}界面匹配特征的Σ3晶界以及具有{0 0 0 1}/{0 0 0 1}界面匹配特征的Σ2晶界是氮化硅陶瓷材料中的一类特殊晶界.