摘要: 非厄米拓扑系统的拓扑不变量可以由定义在双正交基下的局域拓扑指标刻画. 不同于厄米体系, 非厄米局域拓扑指标在动力学过程中的传播和演化目前还未见文献讨论. 本文研究非厄米拓扑体系局域拓扑指标的动力学特性, 重点关注淬火过程中, 局域拓扑指标由边界向体内的传播. 结果表明, 当淬火前后的体系拓扑性质不同时, 系统中存在局域拓扑指标的流动, 其流速与体系群速度相关, 但具体形式与相应厄米体系不同. 以3个具体模型为例, 通过数值计算说明了这一结论. 其中, 对于特定具有非厄米趋肤效应的模型, 可以发现局域拓扑指标的流速上限与广义布里渊区中的群速度直接相关. 但这一关系在其他非厄米模型中则需要修正, 其更普适的形式有待进一步研究. 本文的结果揭示了非厄米体系中局域拓扑指标传播的复杂性, 是进一步理解非厄米局域拓扑指标动力学行为的基础.
关键词: 非厄米拓扑 /
淬火动力学 /
开放体系 English Abstract Dynamics of non-Hermitian local topological marker Sun Kong-Hao Yi Wei CAS Key Laboratory of Quantum Information, University of Science and Technology of China, Hefei 230026, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11974331)Received Date: 26 August 2021Accepted Date: 15 September 2021Available Online: 12 October 2021Published Online: 05 December 2021Abstract: Topological invariants of non-Hermitian topological systems can be captured by local topological markers defined on the biorthogonal basis. However, unlike the scenario of Hermitian systems, the dynamics of non-Hermitian local topological marker has not yet received much attention so far. Here in this work, we study the dynamic features of local topological markers in non-Hermitian topological systems. In particular, we focus on the propagation of non-Hermitian topological markers in quench dynamics. We find that for the dynamics with topologically distinct pre- and post-quench Hamiltonians, a flow of local topological markers emerges in the bulk, with its propagation speed related to the maximum group velocity. Taking three different non-Hermitian topological models for example, we numerically calculate the propagation speed, and demonstrate that a simple universal relation between the propagation speed and group velocity does not exist, which is unlike the scenarios in previously studied Hermitian systems. Our results reveal the complexity of the local-topological-marker dynamics in non-Hermitian settings, and would stimulate further study on the matter. Keywords: non-Hermitian topology /quench dynamics /open systems 全文HTML --> --> --> 1.引 言 非厄米拓扑体系是近年来凝聚态及量子模拟领域的研究热点之一[1 -6 ] . 非厄米拓扑模型脱胎于开放系统[7 ,8 ] , 其性质与封闭系统厄米模型多有不同. 其中尤为典型的例子是具有非厄米趋肤效应的拓扑模型[9 -21 ] . 在开边界条件下, 该类体系的本征态波函数局域在边界上, 并在实空间呈能态依赖的指数分布; 同时体系本征能谱在复平面上的分布受边界条件影响. 与此对应, 在具有非厄米趋肤效应的拓扑体系中, 传统的体边对应关系失效—定义于周期边界布里渊区上的拓扑不变量不再能准确预测开边界下的拓扑边缘态. 为解释这一现象, 非布洛赫能带论应运而生[9 ,10 ,14 ] . 根据该理论, 非厄米拓扑系统在开边界条件下的性质应由计入了非厄米趋肤效应的广义布里渊区决定, 而在广义布里渊区上定义的非布洛赫拓扑不变量则保证了体边对应关系在非厄米系统中仍然成立. 目前, 非厄米趋肤效应及非厄米能带论在一系列经典或量子的人工拓扑体系中被相继观测证实[22 -25 ] . 同时, 研究者发现, 非布洛赫能带论及广义布里渊区也在非布洛赫宇称-时间对称性及非布洛赫淬火动力学等方面有重要应用[26 -30 ] .[31 ,32 ] , 而后者可以通过动力学过程中的可观测量在实验上进行观测[30 ] . 对局域拓扑指标的研究起源于厄米拓扑体系[33 -36 ] . 在这些模型中, 虽然体系具有能带拓扑及拓扑保护的边缘态等全局特性, 定义在体态上的局域拓扑指标却是量子化的, 能反映体系的全局拓扑特性, 并在拓扑相变附近呈现特定的标度行为. 更进一步, 文献[34 ]通过对厄米体系淬火动力学的研究, 发现了动力学过程中局域拓扑指标在体系内部的传播规律. 例如, 当体系从拓扑非平庸的初态出发, 由拓扑平庸的哈密顿量驱动进行时间演化时, 初始体系内部量子化的局域拓扑指标在一定时间后会受到始于边界的局域拓扑指标流影响, 在某弛豫时间$ t^\ast $ 后明显偏离量子化取值. 通过对该弛豫时间$ t^\ast $ 进行分析, 研究者发现局域拓扑指标在淬火过程中的传播速度与体系群速度相关. 这揭示了局域拓扑指标在厄米拓扑体系非平衡动力学过程中的普适行为, 具有重要意义. 与此对应, 非厄密拓扑体系的局域拓扑指标是否具有类似的行为, 还未见研究报道.${\boldsymbol{H}}^{\rm i}$ 的本征态, 在末态哈密顿量${\boldsymbol{H}}^{\rm f}$ 的驱动下做时间演化. 一般而言, ${\boldsymbol{H}}^{\rm i}$ 和${\boldsymbol{H}}^{\rm f}$ 参数不同, 且处于不同拓扑相区. 以几个具体的非厄米拓扑模型为例, 计算了淬火动力学演化过程中, 非厄米局域拓扑指标的演化, 并通过拟合确定了局域拓扑指标从边界向体系内部传播的速度. 对于本文考察的具有非厄米趋肤效应的模型, 可以发现该传播速度与定义在广义布里渊区中的群速度相关, 而与定义于一般布里渊区的群速度无关. 然而, 对于一般性的非厄米模型, 该结论并不普遍成立. 一般说来, 在非厄米体系中局域拓扑指标的传播速度与群速度相关, 但二者之间的关系是否普适则需要进一步研究.2.非厄米局域拓扑指标 为说明非厄米局域拓扑指标的特性, 考虑二维正方晶格上的非厄米哈密顿量$\bar{{\boldsymbol{c}}}_{{{{\boldsymbol{R}}}}} = (c_{{{{\boldsymbol{R}}}}, \uparrow}, c_{{{{\boldsymbol{R}}}}, \downarrow})^{\rm T}$ , $c_{{{{\boldsymbol{R}}}}, \sigma}$ ($ \sigma = \uparrow, \downarrow $ )为格点$\boldsymbol{R}= x \boldsymbol{e}_x+y\boldsymbol{e}_y$ 上具有相应自旋的费米子湮灭算符, ${\boldsymbol{\sigma}}_{j}$ ($ j = x, y, z $ )为泡利矩阵, $ t_1 $ 为近邻跃迁率, $ m $ 为格点上的塞曼场, $ \gamma_x $ 及$ \gamma_y $ 为非厄米系数, $ {{{{\boldsymbol{e}}}}}_x $ 和$ {{{{\boldsymbol{e}}}}}_y $ 为对应方向的单位格点矢量.$ \gamma_{x, y}\neq 0 $ 时, 上述模型具有非厄米趋肤效应—开边界条件下, 系统所有体态均指数局域在边界附近. 非厄米趋肤效应的直接后果是, 体系在开边界下的拓扑性质, 尤其是与边缘态相关的拓扑性质, 须通过非布洛赫能带论在广义布里渊区上计算. 对于(1 )式的模型, 该计算可以进一步简化, 因其在开边界下, 可以通过相似变换得到厄米的Qi-Wu-Zhang模型[37 ,38 ] . 具体而言, 该相似变换在实空间写作$ S\left(x, y\right) = \text{exp}\left(\gamma_x x+\gamma_y y\right) $ , 而在准动量空间该变换等价于$ {{{\boldsymbol{k}}}}\rightarrow\tilde{{{\boldsymbol{k}}}}+{\rm i}\tilde{{{\boldsymbol{k}}}}^{\prime} $ , $\tilde{{{\boldsymbol{k}}}}^{\prime} = $ $ \left(\right.-\gamma_x, - \gamma_y\left.\right)$ [10 ] . 可以认为这一变换形式上是用广义布里渊区中的准动量$ \tilde{{{\boldsymbol{k}}}}+{\rm i}\tilde{{{\boldsymbol{k}}}}^{\prime} $ 取代周期边界下布里渊区中的准动量$ {{\boldsymbol{k}}} $ . 相应的非布洛赫哈密顿量写作$\widetilde{{\boldsymbol{H}}} (\tilde{{{\boldsymbol{k}}}} )$ 的本征谱即为开边界下体系的能谱. 在此基础上, 体系的非布洛赫拓扑数可以由非布洛赫哈密顿量的左右本征矢得到:$ \alpha $ 为能带指标. 对于$\text{Re}(\tilde{E}_{\alpha}) < 0$ 的能带, 计算可得在$ m > 2 t_1 $ 时非布洛赫陈数$ C = 0 $ , $ m < 2 t_1 $ 时$ C = -1 $ .$ A_{\rm{c}} $ 是实空间中单位晶胞的面积, $ \hat{P} $ 是下能带的投影算符, $ \hat{Q} = \hat{1} - \hat{P} $ . 此处, 设非厄米体系的下能带为$\text{Re}(E_{\alpha}) < 0$ 的部分, 则$\hat{P} = \displaystyle\sum\limits_{{\rm Re}(E_\alpha) < 0} \left|\psi^{\rm R}_\alpha\right\rangle\left\langle\psi^{\rm L}_\alpha\right|$ , 其中$ \left|\psi^{\rm {L, R}}_\alpha\right\rangle $ 为开边界下$ H $ 的左右本征矢, 即${\boldsymbol{H}}\left|\psi^{\rm R}_\alpha\right\rangle = E_\alpha\left|\psi^{\rm R}_\alpha\right\rangle$ , $\left\langle\psi^{\rm L}_\alpha\right|{\boldsymbol{H}} = \left\langle\psi^{\rm L}_\alpha\right|E_\alpha$ . 利用局域拓扑指标可以从实空间出发研究体系的拓扑性质, 尤其是那些不具有平移对称性的系统. 而在非厄米系统中, 定义在双正交基下的局域拓扑指标可以准确反映体系的非厄米拓扑性质, 不论体系是否具有非厄米趋肤效应. 这是因为投影算符$ \hat{P} $ 和$ \hat{Q} $ 中的本征左矢与右矢, 已经包含了体态的拓扑及趋肤信息. 与厄米拓扑系统的局域拓扑指标类似, 非厄米局域拓扑指标可以表征系统在拓扑相变点附近的临界行为. 如图1 所示, 对于尺寸为$ L\times L $ 的体系(其中$ L $ 为$ x $ 或者$ y $ 方向的格点数), 其中格点处的非厄米局域拓扑指标在拓扑相变附近, 满足$(m-m_{\rm c})L^{\tfrac{1}{\nu}}$ 的普适标度律, 其中$ m_{\rm c} = 2 t_1 $ 为相变点, $ \nu = 1.12(6)\approx 1 $ . 这样的普适临界行为与相关厄米拓扑体系的相变临界行为一致[34 ] , 是讨论非厄米局域拓扑指标动力学行为的基础.图 1 非厄米局域拓扑指标的标度行为. 系统中心的非厄米局域拓扑指标随着$m$ 的变化遵循$(m-m_{\rm c})L^{\tfrac{1}{\nu}}$ 的标度行为. 在$L$ 分别取$15, 17, 19, 21, 23, 25, 27$ 等值时(对应于图中不同颜色的曲线), 所有曲线经变换后遵循同一函数形式, 经拟合得到$\nu\approx 1.1259$ . 在本文的数值计算中, 取$t_1=1$ , $\gamma_x=\gamma_y=0.3$ Figure1. Scaling behavior of the non-Hermitian local topological marker near the topological phase transition. The numerically calculated local topological markers for different system sizes ($L=15, 17, 19, 21, 23, 25, 27$ ) collapse to the same curve, with the functional form $(m-m_{\rm c})L^{\tfrac{1}{\nu}}$ and $\nu\approx 1.12(6)$ . For all calculations, we take $t_1=1$ , $\gamma_x= $ $ \gamma_y=0.3$ 3.非厄米局域拓扑指标的动力学行为 考虑(1 )式哈密顿量的淬火过程中, 非厄米局域拓扑指标的动力学行为. 设初始时刻体系由哈密顿量$ {\boldsymbol{H}}_{\rm i}\left(t_1, m\right) $ 描述, 且其下能带被完全占据. 在此后的时间演化中, 哈密顿量变为$ {\boldsymbol{H}}_{\rm f}\left(t^{\prime}_1, m^{\prime}\right) $ , 则相应投影算符$ \hat{P} $ 和$ \hat{Q} $ 均随时演化, 从而导致非厄米局域拓扑指标的演化. 对于厄米拓扑体系, 研究者发现, 当初末哈密顿量拓扑性质不同时, 具有开放边界的体系在淬火过程中会出现局域拓扑指标的流动, 其流速与群速度相关[34 ] . 这里我们关心的第一个问题是, 在具有非厄米趋肤效应的非厄米拓扑体系中, 是否有类似的结论.图2 所示, 数值计算了$ L = 23 $ 的开边界二维晶格体系中, 各格点的非厄米局域拓扑指标在不同时刻的行为. 选择的初始哈密顿量处于拓扑非平庸区间($ C = -1 $ ), 末态哈密顿量处于拓扑平庸区间($ C = 0 $ ). 在$ t = 0 $ 时刻, 局域拓扑指标$ C $ 在体系中心取$ -1 $ , 而在边界上取正值, 这是因为局域拓扑指标对格点求和应该始终得$ 0 $ . 而在$ t > 0 $ 时刻, 局域拓扑指标开始从边界向体内流动(见图2(a) ), 系统中心处的局域拓扑指标会在某个特征时间$ t^\ast $ 后明显偏离其量子化取值. 由$ t^* $ 与系统尺寸的线性关系, 可以定义并计算局域拓扑指标的的传播速度. 在具体数值计算中, 取时间演化的步长为$ 0.02 $ (这里时间单位为$ 1/t_1 $ ), 定义$ t^\ast $ 为体系中心处局域拓扑指标对时间的差分首次超过阈值的时间. 数值上, 取阈值为$ 10^{-3} $ . 在得到不同系统尺寸下的$ t^\ast $ 后, 通过线性拟合, 得到局域拓扑指标的传播速度$ v_{\text{lcm}} $ . 由图2(b) 可以看出, 在该模型下, 非厄米局域拓扑指标的传播速度与广义布里渊区下得到的$\left|\tilde{v}_{1 x} (\tilde{{{{\boldsymbol{k}}}}} )-\tilde{v}_{2 x} (\tilde{{{{\boldsymbol{k}}}}} )\right|$ 最大值相符(黄线), 而与周期边界下布里渊区里计算的群速度(红星)不同. 这里广义布里渊区上的群速度$ \tilde{v}_{ix} $ ($ i = 1, 2 $ )定义为$\tilde v_{ix} = \text{Re} (\partial\tilde{E}_i(\tilde{{{{\boldsymbol{k}}}}})/\partial \tilde{k}_x)$ . 相应地, 一般布里渊区上的群速度定义为$v_{ix} = \text{Re} (\partial E_i ({{{\boldsymbol{k}}}})/\partial k_x)$ . 这似乎意味着只需要利用非布洛赫能带论便可解释及预言非厄米拓扑体系淬火过程中局域拓扑指标流的动力学演化.图 2 非厄米局域拓扑指标的传播速度 (a) 淬火过程中系统中心格点处的非厄米局域拓扑指标的时间演化. 系统尺寸为$L=23$ , 取开边界. 初始时${\boldsymbol{H}}\left(t_1=1,\; m=1\right)$ 处于拓扑非平庸相, 淬火后${\boldsymbol{H}}\left(t^{\prime}_1=1,\; m^{\prime}=6\right)$ 处于拓扑平庸相, 淬火前后$\gamma_x=\gamma_y=0.3$ . 这里只考虑$x$ 方向的动力学演化, $y$ 方向的演化有类似性质. (b) 非厄米局域拓扑指标的传播速度随末态哈密顿量参数$t^{\prime}_1$ 的变化. 淬火参数与图(a)相同. 分别数值模拟了体系大小为$L=11, 15, 19, 23, 27$ 时的淬火过程, 并通过线性拟合$t^\ast$ 与$L$ 的关系, 数值得到了局域拓扑指标的传播速度Figure2. Dynamics of the non-Hermitian local topological marker. (a) Spatial distribution (along the $x$ -direction) of the non-Hermitian local topological marker at different times of the quench dynamics. The parameters are: $L=23$ , ${\boldsymbol{H}}_{\rm i}(t_1=1, \;m=1)$ , ${\boldsymbol{H}}_{\rm f}(t'_1=1, \;m'=6)$ , $\gamma_x=\gamma_y=0.3$ .(b) Propagation speed of the local topological marker as a function of $t'_1$ . Other parameters are the same as those in panel (a).4.其他非厄米拓扑系统的局域拓扑指标流 为验证上述结论的普适性, 本节考察其他非厄米拓扑模型的淬火过程. 首先考虑如下具有非厄米趋肤效应的非厄米Qi-Wu-Zhang模型:$ t_j $ 为体系参数. 如前所述, 在开边界下, 该体系的所有本征态会指数局域在边界附近, 体系在开边界下的拓扑效应因此需要在广义布里渊区上计算. 为此, 本文先通过体系本征方程和边界条件确定广义布里渊区. 参照文献[10 , 14 ], 定义$ \beta_j = {\rm e}^{{\rm i}\tilde{k}_j-\tilde{k}'_j} $ ($ j = x, y $ ), 并在本征方程$\det{\left[{\boldsymbol{H}}\left({{{\boldsymbol{k}}}}\right)-E\right]} = 0$ 中做代换$ {\rm e}^{{\rm i}k_j}\rightarrow\beta_j $ , 得到关于$ \beta_j $ 的方程:6 )式关于$ \beta_x $ 和$ \beta_y $ 均有4个解, 按绝对值大小排序, 记为$ |\beta^ { (1 )}_x |\leqslant |\beta^{ (2 )}_x |\leqslant |\beta^{ (3 )}_x |\leqslant $ $ |\beta^{ (4 )}_x |$ 及$ |\beta^ { (1 )}_{y} |\leqslant |\beta^{ (2 )}_{y} |\leqslant |\beta^{ (3 )}_y |\leqslant |\beta^{ (4 )}_y |$ . 广义布里渊区对应于满足条件$ |\beta^{ (2 )}_x | = |\beta^{ (3 )}_x | $ 和$ |\beta^{ (2 )}_y | = |\beta^{ (3 )}_y | $ 的解.$ {{{\boldsymbol{k}}}}\rightarrow \tilde{{{\boldsymbol{k}}}}+{\rm i}\tilde{{{\boldsymbol{k}}}}^{\prime} $ 得到.图3 所示. 有趣的是, 在此系统中, 定义在广义布里渊区上的$\max\left|\right.\tilde{v}_{1 x} (\tilde{{{{\boldsymbol{k}}}}} )- \tilde{v}_{2 x} (\tilde{{{{\boldsymbol{k}}}}} )\left.\right|$ 与定义在一般布里渊区的$\max \left|\right.v_{1 x}\left({{{\boldsymbol{k}}}}\right)- v_{2 x}\left({{{\boldsymbol{k}}}}\right)\left.\right|$ 几乎相同. 但局域拓扑指标的传播速度要明显大于这两个速度, 且在取$ \gamma_x = \gamma_y = \gamma $ 时, 数值上近似于$ {\rm e}^{\gamma}\max{\left|v_{1 x}\left({{{\boldsymbol{k}}}}\right)-v_{2 x}\left({{{\boldsymbol{k}}}}\right)\right|} $ .图 3 模型(5 )的非厄米局域拓扑指标的传播速度随$t^{\prime}_1$ 的变化. 初始时, $t_x=t_y=1, m=1$ ; 淬火后, $t^{\prime}_x=t^{\prime}_y=t^{\prime}_1, $ $ m^{\prime}=6$ . 淬火前后$\gamma_x= \gamma_y=\gamma=0.35$ Figure3. Propagation speed of the non-Hermitian local topological marker for Hamiltonian (5 ). We fix $\gamma_x=\gamma_y=\gamma=0.35$ , and the pre- and post-quench parameters are $t_x=t_y=1, $ $ \; m=1$ and $t^{\prime}_x=t^{\prime}_y=t^{\prime}_1, \; m^{\prime}=6$ , respectively.8 )不具有非厄米趋肤效应. 如图4 所示, 在该模型淬火过程中, 局域拓扑指标的传播速度要大于定义在一般布里渊区的群速度. 但不同于模型(5 )的指数加速, 数值上看, 局域拓扑指标传播速度与$\max\left|\right.v_{1 x}\left({{{\boldsymbol{k}}}}\right)- $ $ v_{2 x}\left({{{\boldsymbol{k}}}}\right)\left.\right|$ 相比, 相差一个常数.图 4 模型(8 )的非厄米局域拓扑指标的传播速度随$t^{\prime}_1$ 的变化. 初始时, $t_x=t_y=1, m=1$ ; 淬火后, $t^{\prime}_x=t^{\prime}_y=t^{\prime}_1, $ $ m^{\prime}=6$ . 淬火前后$\gamma=0.3$ Figure4. Propagation speed of the non-Hermitian local topological marker for Hamiltonian (8 ). We fix $\gamma=0.3$ , and the pre- and post-quench parameters are $t_x=t_y=1, m=1$ and $t^{\prime}_x=t^{\prime}_y=t^{\prime}_1, m^{\prime}=6$ , respectively.5.总结与展望 本文研究了非厄米拓扑模型中非厄米局域拓扑指标的性质. 首先刻画了非厄米局域拓扑指标在非厄米拓扑相变附近的临界行为, 数值确定了其临界系数. 然后考察了3个不同非厄米拓扑模型的动力学淬火过程, 计算了非厄米局域拓扑指标的传播速度. 与厄米拓扑体系类似, 当淬火前后的体系拓扑性质不同时, 系统的淬火过程中存在局域拓扑指标的流动. 发现局域拓扑指标的传播速度与体系群速度相关, 但其关系并不普适. 具体而言, 对于本文考察的3个模型, 局域拓扑指标的传播速度或与定义于广义布里渊区上的群速度直接相关, 或与群速度差一个指数因子, 或差一常数. 本文的结果揭示了非厄米体系中局域拓扑指标传播的复杂性, 为进一步理解非厄米局域拓扑指标的动力学行为打下了基础. 

























































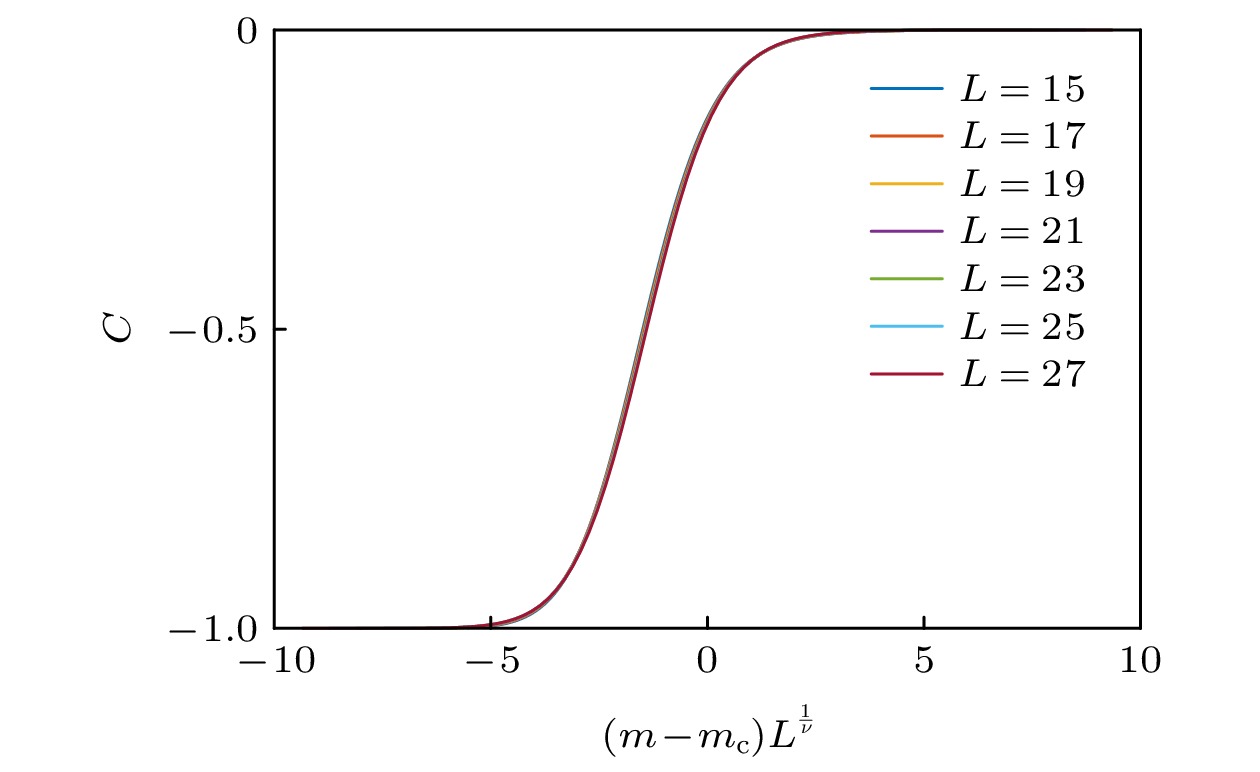 图 1 非厄米局域拓扑指标的标度行为. 系统中心的非厄米局域拓扑指标随着
图 1 非厄米局域拓扑指标的标度行为. 系统中心的非厄米局域拓扑指标随着











































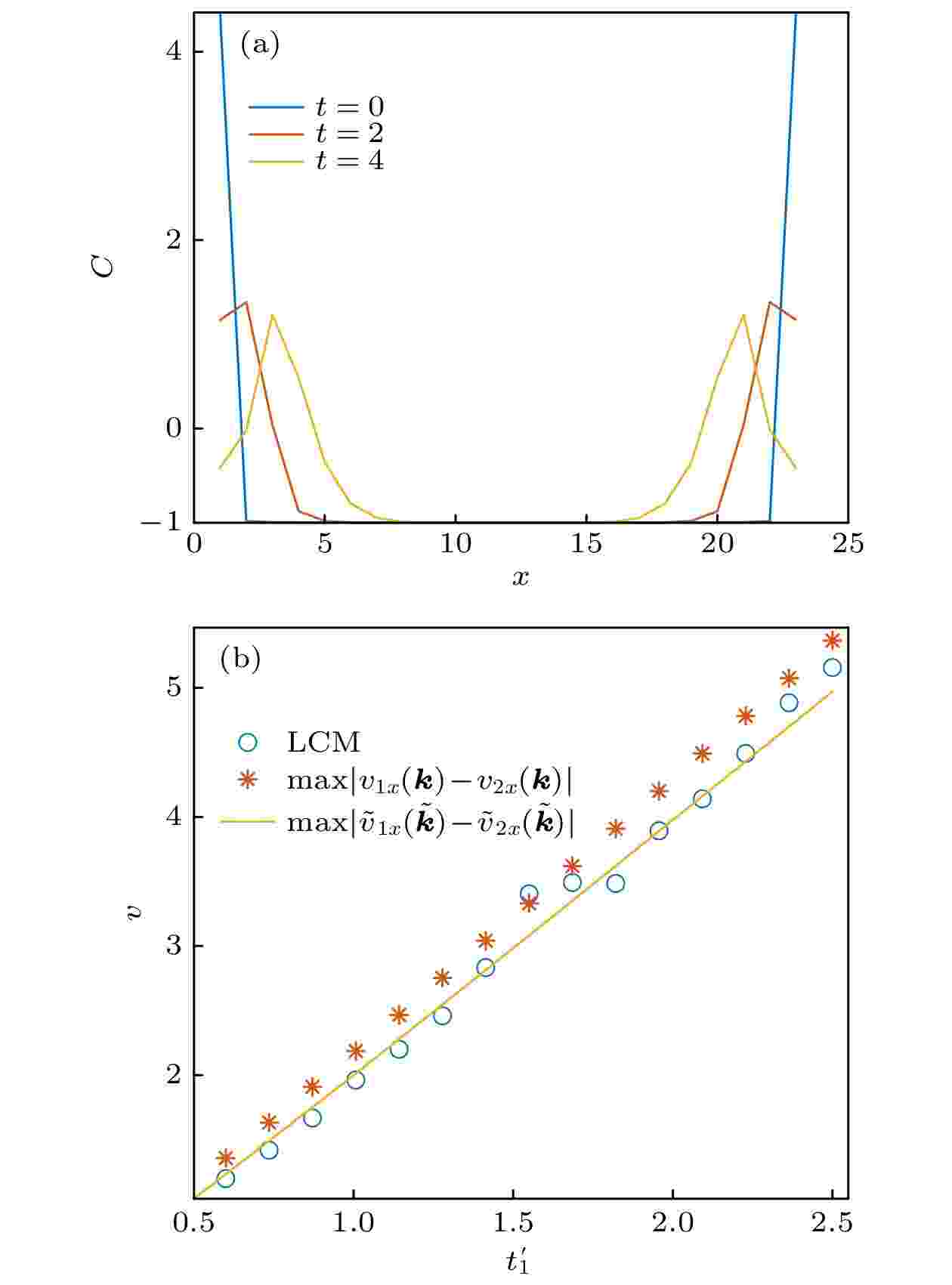 图 2 非厄米局域拓扑指标的传播速度 (a) 淬火过程中系统中心格点处的非厄米局域拓扑指标的时间演化. 系统尺寸为
图 2 非厄米局域拓扑指标的传播速度 (a) 淬火过程中系统中心格点处的非厄米局域拓扑指标的时间演化. 系统尺寸为

































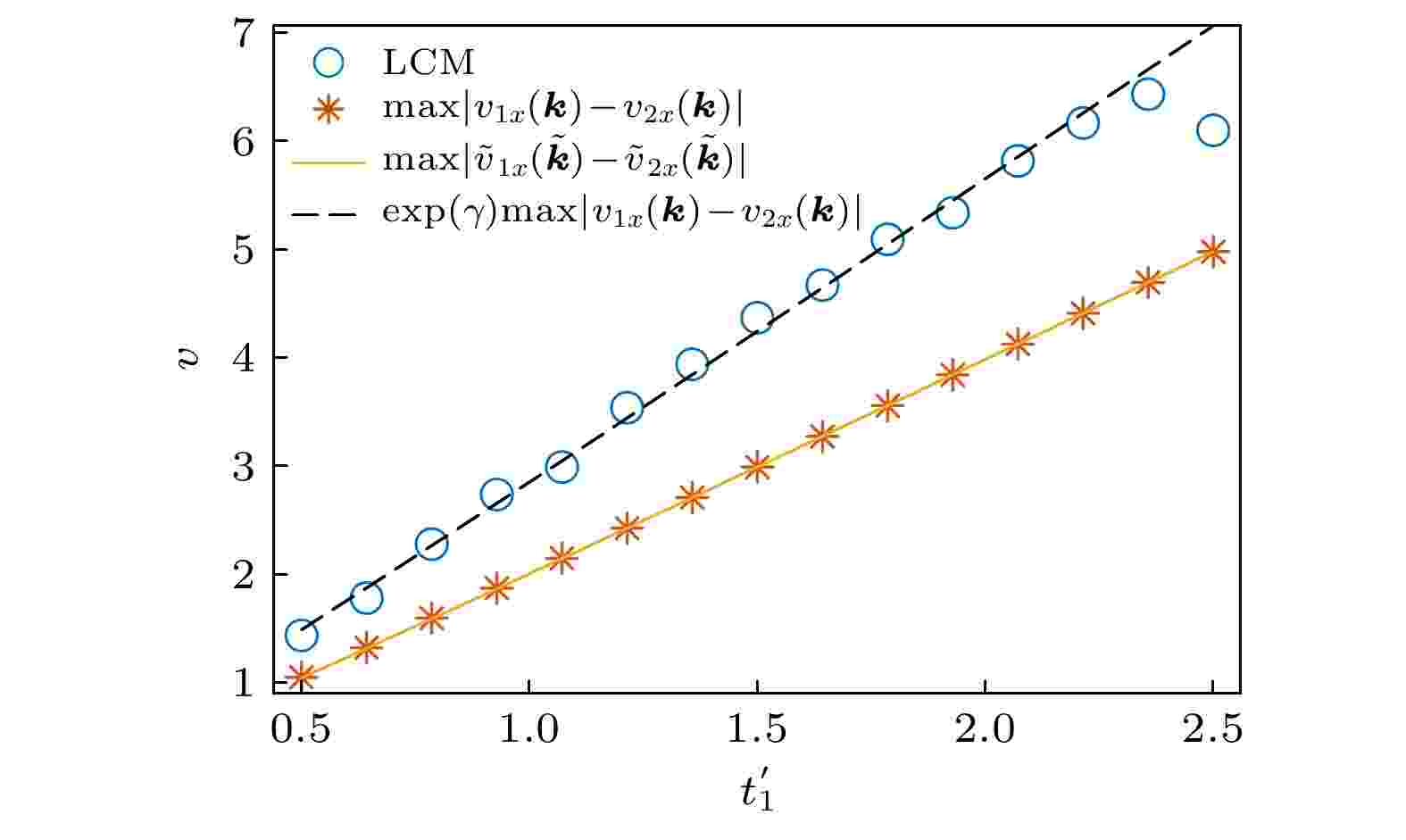 图 3 模型(5)的非厄米局域拓扑指标的传播速度随
图 3 模型(5)的非厄米局域拓扑指标的传播速度随










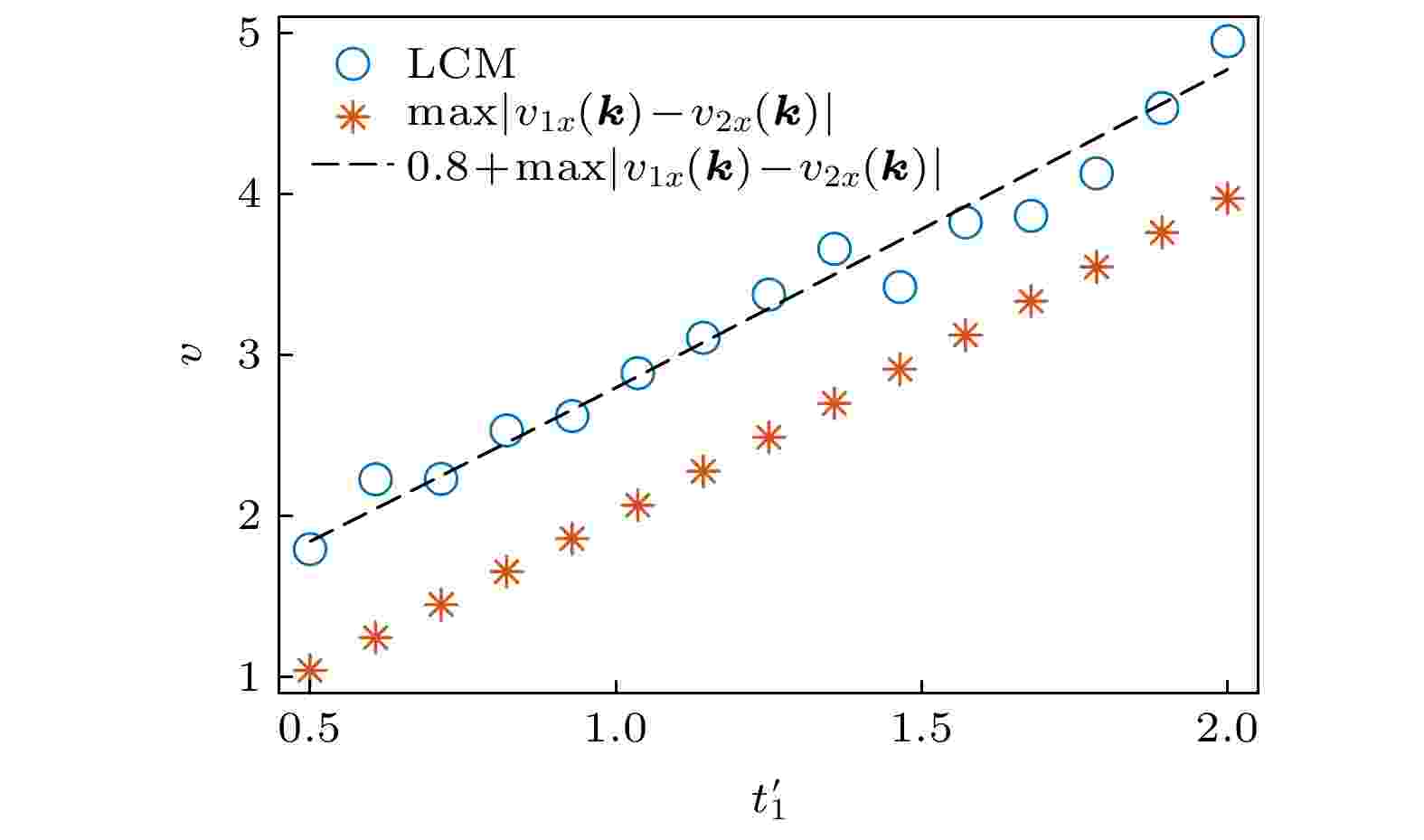 图 4 模型(8)的非厄米局域拓扑指标的传播速度随
图 4 模型(8)的非厄米局域拓扑指标的传播速度随







