摘要: 近年来, 图像加密技术备受关注. 随着人们对通信隐私及网络安全重视程度的提高, 对信息加密技术的要求更加严格, 图像作为信息的载体之一, 因携带信息的有效性和生动性而受到重视. 本文提出一种基于DNA编码与交替量子随机行走的彩色图像加密算法. 量子随机行走作为出色的密码学工具参与算法流程中各个部分, DNA编码作为核心加密方式完成算法. 本文详细描述加密、解密流程, 并对所提出算法进行仿真实验验证与结果分析. 仿真阶段设计模拟密钥参数, 编码进行彩色图像加密、解密实验, 并进行了相关分析. 实验结果表明, 本文提出的彩色图像加密算法能够进行安全有效的彩色图像加密, 且相关分析表示其加密后图像直方图平稳、像素相关性系数趋近于0、密钥空间
${2^{ 128}} $ , 三通道信息熵达到7.997以上, 能够抵御统计攻击、穷举攻击等攻击手段. 此外, DNA编码除新颖的编码及运算方式之外还有其独特的生物学特性, 为密码学的研究提供了新的思路与方向.
关键词: 量子信息 /
量子随机行走 /
图像加密 /
DNA编码 English Abstract Color image encryption algorithm based on DNA code and alternating quantum random walk Wang Yi-Nuo 1 ,Song Zhao-Yang 2 ,Ma Yu-Lin 2 ,Hua Nan 2 ,Ma Hong-Yang 1 1.School of Science, Qingdao University of Technology, Qingdao 266520, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11975132, 61772295), the Natural Science Foundation of Shandong Province, China (Grant No. ZR2019YQ01), and the Higher Educational Science and Technology Program of Shandong Province, China(Grant No. J18KZ012).Received Date: 05 July 2021Accepted Date: 04 August 2021Available Online: 20 August 2021Published Online: 05 December 2021Abstract: In recent years, image encryption technology has attracted much attention. As people pay more attention to communication privacy and network security, the requirements for information encryption technology are more stringent. As one of the information carriers, images are valuable for carrying the effectiveness and vividness of the information. This paper proposes a color image encryption algorithm based on DNA encoding and alternating quantum random walk. Quantum random walk is an excellent cryptographic tool that participates in all parts of the algorithm process, and DNA encoding is used as the core encryption method to complete the algorithm. This article describes the encryption and decryption process in detail, and conducts simulation experiments to verify and analyze the results of the proposed algorithm. In the simulation stage, we design the simulation key parameters, encode the color image encryption and decryption experiments, and carry out related analysis. The experimental results show that the color image encryption algorithm proposed in this paper can perform safe and effective color image encryption. The correlation analysis shows that the image histogram after encryption is stable, the pixel correlation coefficient approaches 0, and the key space is ${2^{ 128 }} $ , the three-channel information entropy reaches more than 7.997, which can resist statistical attacks, brute force attacks and other attack methods. In addition, DNA coding has unique biological characteristics in addition to the novel coding and calculation methods, which provide new ideas and directions for cryptographic research.Keywords: quantum information /quantum random walk /image encryption /DNA coding 全文HTML --> --> --> 1.引 言 通信领域与计算机网络技术飞速发展, 人们生活、工作越来越依赖于此的当下, 信息传递的安全性问题成为了被社会各界广泛关注的焦点. 由于互联网是一个开放与共享的社区, 这在一定程度上方便了信息交互, 同时使得信息安全性保障成为亟待解决的难题. 信息又分多个种类, 其中图像信息因其生动形象的特性被人们广泛应用. 本文正式基于上述事实提出的基于量子随机行走与DNA编码技术结合的彩色图像加密算法, 以期提高图像信息传递安全性.[1 -5 ] 及相关应用在通信[6 -11 ] 等各领域[12 -16 ] 受到关注, 在图像处理中更是得到重视[17 -20 ] . 其运算速度[21 ,22 ] 、安全性[23 ,24 ] 等方面相较于经典算法具有显著优势. 量子随机行走作为量子算法的重要工具参与算法流程各个步骤. 1993年, 以色列物理学家Aharonov等[25 ] 提出量子随机行走为经典随机行走在量子力学中的对应概念. 随着研究的推进, 其概念被细分为连续时间量子随机行走和离散时间量子随机行走, 二者分别为1998年美国MIT的Farhi和日本东北大学的Gutmann[26 ] 提出, 2001年加拿大滑铁卢大学的Watrous[27 ] 由经典随机行走直接量子化得到的. 其中, 离散时间量子随机行走因具有混沌动力学行为而被应用于量子及经典密码学系统中[28 -32 ] . 滑铁卢大学的Chris和Zhan[33 ] 在2019年以组合方法构建的3个离散时间量子行走模型为我们提供了研究思路; Abd-El-Atty等[34 ] 2021年研究发表的基于量子随机行走的光学图像加密算法为本文提供了研究方向及重要参考. 本文研究以离散时间交替量子随机行走构建的随机概率分布矩阵作为加密工具, 多次参与图像加密过程的彩色图像加密算法.[35 ] 进行了世界上第一个DNA计算实验并在《科学》杂志上发表了相关成果, 这一成果揭示了DNA分子除其稳定的遗传特性外还具有计算能力, 自此开辟了一个新的信息时代. 随着研究的深入, 新的以DNA为信息载体的密码学领域应运而生. 2000年, Leier等[36 ] 基于DNA双链设计了两种密码学方法; 2003年, Chen[37 ] 提出了基于碳纳米管的消息转换和DNA的分子密码学系统; 2005年, Chang等[38 ] 提出了3种基于DNA的并行减法器, 正式验证了两个大质数的乘积能够被分解; 2007年, Lu等[39 ] 通过将现代DNA生物技术微阵列应用于密码技术, 设计出对称密钥密码系统; 在Lu等研究成果的基础上, 2010年, Lai等[40 ] 进一步提出了一种非对称加密和签名密码系统DNA-PKC; 2012年, Wei等[41 ] 提出基于DNA序列操作和超混沌系统的彩色图像加密算法; 2017年, Niu等[42 ] 提出基于超混沌映射和核苷酸序列数据库的图像加密算法. 通过前人对DNA密码学[43 -45 ] 的研究以及其在图像加密方面[46 -48 ] 的应用, 已构建了基本的DNA密码学逻辑结构, 为本文的研究提供了基础.2 节介绍背景知识以及描述为完成提出算法进行的相关工作; 算法的具体实现过程在第3 节进行详细描述, 包括了加密以及解密步骤; 随后在第4 节中附上了仿真结果, 对提出的算法进行了性能分析.2.相关工作 22.1.量子随机行走 2.1.量子随机行走 量子随机行走包括连续时间量子随机行走和离散时间量子随机行走两个部分, 本文提出的工作以离散时间量子随机行走为工具进行开展. 离散时间量子随机行走主要包含4个要素: 行走者、行走者携带的硬币、硬币抛掷方式以及行走规则. 本文应用离散时间交替量子随机行走(如图1 所示).图 1 双方向格点上交替量子随机行走Figure1. Alternating quantum random walking on the bidirectional grid.$ {H_{\rm{w}}} $ 和硬币空间$ {H_{\rm{c}}} $ 二者共同构成量子随机行走体系的希尔伯特空间${\boldsymbol{H}} = {{\boldsymbol{H}}_{\rm{w}}} \otimes {{\boldsymbol{H}}_{\rm{c}}}$ . 在量子随机行走过程中, 每一步的行走选择相同的硬币抛掷算符$ \hat {\boldsymbol{C}} $ :$\theta = {\pi }/{4}$ 时,${{\boldsymbol{S}}_{\rm{i}}}$ 规定:$\left| x \right\rangle \left({x \in \mathbb Z} \right)$ 为构成行走者位置空间的基矢; 两个基矢$ \left| c \right\rangle \left({c = 0, 1} \right) $ 线性组合构成硬币空间. (3 )式可以描述为: 当硬币态为$ \left| 0 \right\rangle $ 时, 操控行走者右移一个单位; 当硬币态为$ \left| 1 \right\rangle $ 时, 操控行走者左移一个单位.x , y 两个方向上交替进行行走, 则整个量子随机行走过程中的行走算符$ \hat {\boldsymbol{U}} $ 可描述为$ {\hat {\boldsymbol{S}}_y} $ 为量子随机行走在y 轴各点移动的位移算符:$ {N} $ 表示位移算符在y 轴上移动的格点数. $ {\hat {\boldsymbol{S}}_x} $ 为量子随机行走在x 轴各点行走的位移算符, 其描述与$ {\hat {\boldsymbol{S}}_y} $ 相同.$ \left({{{\rm{0}}_x},\;{{\rm{0}}_y}} \right) $ , 硬币处于叠加态${{\boldsymbol{H}}_{\rm{c}}} = \cos \alpha \left| 0 \right\rangle + \sin \alpha \left| 1 \right\rangle$ , 则初始时刻系统状态为T 步后系统状态为$ \left({{x_x},\;{y_y}} \right) $ 的概率为2.2.DNA编码 -->2.2.DNA编码 在过去的研究中, 专家****们已经构建了一套基本的DNA编码结构. 从生物模型出发, DNA序列由以下4个核酸碱基组成: A (腺嘌呤), G (鸟嘌呤), C (胞嘧啶), T (胸腺嘧啶). 其中, A与T互补, C与G互补. 将以上的限制写入编码规则, 分别用2位二进制数对每个核酸碱基进行编码得到8种符合生物模型规则的编码方案, 如表1 所列.1 2 3 4 5 6 7 8 A 00 00 01 01 10 10 11 11 G 01 10 00 11 00 11 01 10 C 10 01 11 00 11 00 10 01 T 11 11 10 10 01 01 00 00 注: 满足DNA的生物学特性A-T互补、G-C互补.
表1 8种DNA编码方案Table1. Eight DNA coding schemes.表1 所述DNA编码规则对彩色图像进行编码. 首先将彩色图像拆分为R, G, B 3个色彩通道, 随即将每个通道编码为一个二进制矩阵, 对于单个通道的8位二进制矩阵可用4位DNA序列对其矩阵各数据进行编码. 例如: 红色通道第一位像素值为157, 将其转换为二进制序列得到10011101; 对此二进制序列使用表1 中方案1进行编码则可得到长度为4的DNA序列——CGTG. 而对应相同的二进制序列可以选择不同的方案进行加密, 如对应上述二进制序列, 选择方案5对其进行编码则得到的DNA序列为ATGT. 而在解码时, 若选择加密方案对DNA序列进行解码则会得到原二进制数据, 例如对方案1生成的DNA序列CGTG使用方案1进行解密则可得到10011101, 为原始二进制序列; 而当使用方案1外的任意方案, 例如使用方案4对其解码, 此时对DNA序列CGTG进行解码得到的二进制序列为00111011与原二进制不同. 因此无法确定加密以及解密的DNA编码方案, 就无法得知原始二进制序列, 这是使用DNA编码加密的手段之一.表2 所列.3.算法提出 本文提出的加密算法主要由以下几部分组成: 1)通过改变参数($N $ , $ T $ , $ \alpha $ (硬币算符初态参数)、$ \beta $ (硬币算符抛掷参数))的大小控制交替量子随机行走产生与所需加密图像对应的随机概率分布矩阵; 2)通过将量子随机行走与DNA编码以及DNA运算相结合的方式完成对原图像的置乱加密; 3)异或操作完成进一步加密. 下面展示具体算法.3.1.加密过程 3.1.加密过程 第一步: 将彩色图像(m , n , 3)拆分为3个彩色通道矩阵: R m , n ), G m , n ), B m , n ), 并将R, G, B 3通道矩阵分别转换为二进制矩阵$ {{\boldsymbol{R}}_{{1}}} $ , $ {{\boldsymbol{G}}_{{1}}} $ , $ {{\boldsymbol{B}}_{{1}}} $ , 然后执行DNA编码规则中的$ a $ 方案($a \in $ $ \mathbb Z, (1, 8)$ )对3个二进制矩阵进行编码, 得到3个大小为(m , n × 4)的矩阵.算法1 图片三通道矩阵进行DNA编码输入 图片DNA编码规则输出 经过DNA编码后的图片三通道矩阵function DNAcodingforImg (${\rm{image}}$ )${\rm{img}}\_B$ img_G ${\rm{img}}\_R \gets {\rm{image}}[0, :0] $ ${\rm{image}} [0, :1] \ {\rm{image}}[0, :2]$ $A=00, \; T=01, \;C=10,\; D=11$ for $i=1$ to $n$ do ${\rm{temp}} \gets {\rm{img}}\_B\_G\_R [i]$ ${\rm{temp:Binary system}}\gets {\rm{Decimal}} $ $ {\rm{ system}}$ ${\rm{temp(ATGC)}}\gets {\rm{temp}}({\rm{Binary }} {\rm{system}})$ end for ${\rm{newImage}}\gets{\rm{ img}}\_B$ img_G ${\rm{img}}\_R$ return ${\rm{newImage}}$ end function $ {{{N}}_1} $ , $ {T_1} $ , $ \alpha $ , $ \beta $ )生成随机概率分布矩阵$ {\boldsymbol{P}} $ (称作密钥矩阵), 并将其调整为加密图像的大小得到$ {{\boldsymbol{P}}_{\bf{1}}} $ :$ {{\boldsymbol{P}}_{\bf{1}}} $ 中各元素按照$k = $ $ {\rm{fix}}\left({{\mathop{\rm Re}\nolimits} {{\boldsymbol{P}}_1} \times {{10}^{12}}} \right)\boldsymbolod 256$ 转换为0—255之间的十进制整数, 进而转换为8位二进制矩阵$ {{\boldsymbol{P}}_{\bf{2}}} $ .算法2 生成量子随机行走概率矩阵输入 量子随机行走概率矩阵的关键参数 DNA编码规则输出 经过DNA编码后的量子随机行走概率矩阵function DNAcodingforQW ($N, T, \alpha, \beta $ )${\rm{coin}}0 \gets [1, 0]$ ${\rm{coin}}1 \gets [0, 1]$ ${\rm{Cosbeta}} \gets {\rm{cos}}(\alpha)$ ${\rm{Sinbeta}} \gets {\rm{sin}}(\beta)$ ${\rm{ posn}}0_x, {\rm{posn}}0_y = {\rm{zeros}}(P)$ ${\rm{posn}}0_x[N], {\rm{posn}}0_y[N]= 1$ ${\rm{ QW Pmatrix}} \gets{\rm{ Cosbeta}}, {\rm{Sinbeta}}$ for $i=1$ to $n$ do ${\rm{temp}} \gets{\rm{ QWPmatrix}} [i]$ ${\rm{temp:Binary system}}\gets {\rm{Decimal}} $ $ {\rm{system}}$ ${\rm{temp(ATGC)}}\gets {\rm{temp}}({\rm{Binary sy}}\text{-} $ $ {\rm{stem}})$ end for return ${\rm{ QWPmatrix}}$ end function V W V $ {{\boldsymbol{P}}_{{1}}} $ 元素形成索引; 利用索引向量W $ {{\boldsymbol{R}}_{{1}}} $ , $ {{\boldsymbol{G}}_{{1}}} $ , $ {{\boldsymbol{B}}_{{1}}} $ 的置乱重排生成(m , n × 4)的矩阵$ {{\boldsymbol{R}}_{{2}}} $ , $ {{\boldsymbol{G}}_{{2}}} $ , $ {{\boldsymbol{B}}_{{2}}} $ .算法3 图像时域置乱输入 量子随机行走概率矩阵 newImage输出 时域置乱后的图像function Matrixscrambling (QWPmatrix,image)QWP matrixafterArgsort ← QWPmmtrix. argsort()${\rm{newImage}} ={\rm{ zeros}}({\boldsymbol{P}})$ for $i=1$ to $n$ do ${\rm{temp }}\gets {\rm{QWPmatrixafterArgsort}}[i]$ i ] = image[temp]end for return ${\rm{newImage}}$ end function $ {{\boldsymbol{P}}_{{2}}} $ 使用与矩阵$ {{\boldsymbol{R}}_{{1}}} $ , $ {{\boldsymbol{G}}_{{1}}} $ , $ {{\boldsymbol{B}}_{{1}}} $ 相同的DNA编码方案$ a $ 进行编码, 得到矩阵$ {{\boldsymbol{P}}_{{3}}} $ , 随后使矩阵$ {{\boldsymbol{R}}_{{2}}} $ , $ {{\boldsymbol{G}}_{{2}}} $ , $ {{\boldsymbol{B}}_{{2}}} $ 分别与矩阵$ {{\boldsymbol{P}}_{{3}}} $ 进行方案$ a $ 的加法, 得到矩阵$ {{\boldsymbol{R}}_{{3}}} $ , $ {{\boldsymbol{G}}_{{3}}} $ , $ {{\boldsymbol{B}}_{{3}}} $ , 即:$ b $ ($b \in Z, (1, 8), $ $ b \ne a$ )对矩阵$ {{\boldsymbol{R}}_{{3}}} $ , $ {{\boldsymbol{G}}_{{3}}} $ , $ {{\boldsymbol{B}}_{{3}}} $ 进行解码操作, 得到3个二进制矩阵: $ {{\boldsymbol{R}}_{{4}}} $ , $ {{\boldsymbol{G}}_{{4}}} $ , $ {{\boldsymbol{B}}_{{4}}} $ .算法4 QWPmatrix与newImage的DNA加法输入 QWPmatrix newImage输出 经过DNA加法处理后的矩阵function DNAaddtion (${\rm{QWPmatrix}}, $ $ {\rm{image}}$ )${\rm{newImage}} ={\rm{ zeros}}({\boldsymbol{P}})$ for $i=1$ to $n$ do ${\rm{temp}} \gets {\rm{QWPmatrixafterArgsort}}[i]$ i ] = image[temp]end for return ${\rm{afterDNAaddtionImage}}$ end function $ {{\boldsymbol{R}}_{{4}}} $ ,$ {{\boldsymbol{G}}_{{4}}} $ ,$ {{\boldsymbol{B}}_{{4}}} $ 分别与$ {{\boldsymbol{P}}_{{2}}} $ 中对应元素进行按位异或运算得到矩阵$ {{\boldsymbol{R}}_{{5}}} $ , $ {{\boldsymbol{G}}_{{5}}} $ , $ {{\boldsymbol{B}}_{{5}}} $ , 将三通道加密完成后的矩阵$ {{\boldsymbol{R}}_{{5}}} $ , $ {{\boldsymbol{G}}_{{5}}} $ , $ {{\boldsymbol{B}}_{{5}}} $ 组合获得加密后的彩色图像$ {E} $ .图2 .图 2 算法流程图Figure2. Algorithm flowchart3.2.解密过程 -->3.2.解密过程 解密过程可视作加密过程的逆过程, 其步骤可简述为以下4步.$ {\boldsymbol{P}'} $ , 随后对$ {\boldsymbol{P}'} $ 元素进行降序排列生成向量 $ {{\boldsymbol{V}}'} $ , 因参数相同, 所以有$ {{\boldsymbol{V}}'}{{ = {\boldsymbol{V}}}} $ , $ {{\boldsymbol{P}}'}{{ = {\boldsymbol{P}}}} $ ; 使用向量$ \boldsymbol {W}' $ 对向量$ \boldsymbol {V}' $ 中的元素进行检索索引;E 拆分为3个色彩通道矩阵: $ {\boldsymbol{R}'} $ , $ {\boldsymbol{G}'} $ , $ {\boldsymbol{B}'} $ , 并进一步转换为8位二进制矩阵$ {\boldsymbol{R}'_{{1}}} $ , $ {\boldsymbol{G}'_{{1}}} $ , $ {\boldsymbol{B}'_{{1}}} $ ; 同时将$ {\boldsymbol{P}'} $ 中各元素转换为0—255之间的十进制整数, 随后转换为8位二进制数, 获得的矩阵$ {\boldsymbol{K}'} $ 进行按位异或运算得到矩阵$ {\boldsymbol{R}'_{{2}}} $ , $ {\boldsymbol{G}'_{{2}}} $ , $ {\boldsymbol{B}'_{{2}}} $ ;$ b $ ($b \in Z, (1, 8), {{b}} \ne {{ a}}$ 与加密中相同)对矩阵$ {\boldsymbol{R}'_{{2}}} $ , $ {\boldsymbol{G}'_{{2}}} $ , $ {\boldsymbol{B}'_{{2}}} $ 进行编码操作得到3个DNA矩阵$ {\boldsymbol{R}'_{{3}}} $ , $ {\boldsymbol{G}'_{{3}}} $ , $ {\boldsymbol{B}'_{{3}}} $ ; 执行DNA编码规则中的$ a $ 方案($ a \in Z, (1, 8) $ 与加密中相同)对矩阵$ {\boldsymbol{P}'} $ 进行DNA编码, 获得矩阵$ {\boldsymbol{P}'_{{1}}} $ ; 执行加密方案中DNA加法方案对应的减法方案, 按照以下式子进行运算得到矩阵$ {\boldsymbol{R}'_{{4}}} $ , $ {\boldsymbol{G}'_{{4}}} $ , $ {\boldsymbol{B}'_{{4}}} $ :$ {\boldsymbol{R}'_{{4}}} $ , $ {\boldsymbol{G}'_{{4}}} $ , $ {\boldsymbol{B}'_{{4}}} $ 根据向量$ \boldsymbol {W}' $ 反置乱重排得到矩阵$ {\boldsymbol{R}'_{{5}}} $ , $ {\boldsymbol{G}'_{5}} $ , $ {\boldsymbol{B}'_{{5}}} $ , 三通道组合获得原始彩色图像, 解密完成.4.仿真结果与分析 为验证所提算法的有效性与安全性, 本文进行算法实验仿真, 对像素大小290 × 290的3张彩色图片进行算法所述的加密以及解密操作, 效果见图3 , 并对加密前后图像进行像素相关性分析、直方图分析、密钥空间等安全性分析.图 3 加密算法仿真效果图Figure3. Encryption algorithm simulation renderings.4.1.实验仿真 4.1.实验仿真 为验证本文所提方法的有效性, 进行了相关仿真实验. 实验应用了如下3个290 × 290像素的彩色图像, 在量子漫步部分选取${N} = 500 $ , $ \alpha = \dfrac{\pi }{2} $ , $ \beta = \dfrac{\pi }{3} $ 在DNA加密与加法计算部分选用了表1 中编号1的编码方式与编号3的解码方式, 进行表2 和表3 所示的运算. 仿真结果与具体分析如下. + A G C T A A G C T G G C T A C C T A G T T A G C
表2 DNA编码方案1对应的加法方案1Table2. Addition plan 1 corresponding to DNA coding plan 1. – A G C T A A G C T G T A G C C C T A G T G C T A
表3 DNA编码方案1对应的减法方案1Table3. DNA coding scheme 1 corresponding to subtraction scheme 1.表2 和表3 可以看出, 相同DNA编码对应的加、减法结果是唯一对应的, 因此可以利用其加减规则对图像进行加密.4.2.相关分析 -->4.2.相关分析 相关分析首先采用相邻像素的相关性系数$ C_{AB} $ 来分析原始图像与加密图像间的差异. 原始图像中相邻位置的像素具有很强的相关性, 而加密后图像相邻像素间应接近于零.A 和B 分别表示相邻像素的值, $ {{{\mathop{\rm cov}}({A, B})}} $ 为A 和B 的协方差, $ \sqrt {D\left(A \right)} $ 和$ \sqrt {D\left(B \right)} $ 为A 和B 的方差. 这里对实验仿真中3组原始图像与解密图像分别进行水平、垂直、对角方向上的像素相关性分析, 结果如图4 —图6 所示, 具体数据结果见表4 .图 4 Lena图像加密前后相关性分析Figure4. Correlation analysis of images before and after Lena encryption.图 6 小猫图像加密前后相关性分析Figure6. Correlation analysis of images before and after cat encryption. 图像 方向 数值 原始图像 加密图像 Lena 水平 0.9275 0.0017 垂直 0.9603 –0.0005 对角 0.8941 0.0007 小猫 水平 0.9429 0.0026 垂直 0.9377 0.0009 对角 0.9097 –0.0012 蛋糕 水平 0.9229 0.0076 垂直 0.9056 0.0017 对角 0.8647 0.0017
表4 像素相关性分析数据Table4. Pixel correlation analysis data.图4(a) —图4(c) 分别为Lena原始图像在水平、垂直、对角方向上的相关性分析, 图4(d) —图4(f) 为Lena加密后图像对应的水平、垂直、对角方向上相关性分析得到的图像. 可以清晰地看出原始图像与加密后图像在像素相关性上的差别, 证明了所提算法的有效性.图 5 蛋糕图像加密前后相关性分析Figure5. Correlation analysis of images before and after cake encryption.表5 给出本文提出的算法与文献[42 ,49 ,50 ]提出算法的三方向相关性数据对比 算法 通道 平均相关性 本文 Red 水平: 0.0040 Green 垂直: 0.0010 Blue 对角: 0.0012 文献[42 ] Red 水平: 0.0042 Green 垂直: 0.0033 Blue 对角: 0.0024 文献[49 ] Red 水平: 0.0025 Green 垂直: 0.0010 Blue 对角: 0.0022 文献[50 ] Red 水平: 0.0012 Green 垂直: 0.0011 Blue 对角: 0.0032
表5 相关性分析数据对比Table5. Correlation analysis data comparison.表6 . 图像 通道 NPCR UACI Lena Red 99.6040% 33.4005% Green 99.6195% 33.2311% Blue 99.5826% 33.5902% 小猫 Red 99.6326% 33.6785% Green 99.6124% 33.4455% Blue 99.6147% 33.5784% 蛋糕 Red 99.6124% 33.4461% Green 99.6528% 33.5315% Blue 99.7004% 33.4499%
表6 密钥敏感性分析数据Table6. Key sensitivity analysis data.表7 给出本文与文献[42 , 49 , 50 ]的NPCR, UACI数据对比. 算法 NPCR平均 UACI平均 本文 99.6257% 33.4835% 文献[42 ] 99.5506% 33.4055% 文献[49 ] 99.6554% 33.4675% 文献[50 ] 99.6150% 33.3900%
表7 NPCR, UACI数据对比Table7. Comparison of NPCR and UACI data.图7(a) —图7(c) 为原始图像的R, G, B 3个通道的直方图, 图7(d) —图7(f) 对应的为加密图像的直方图. 可以看出左侧原始图像统计数据中3个通道各有一些值较为集中, 而右侧加密图像部分直方图数据较为均匀, 这表明想要对加密后图像进行统计攻击将会十分艰难.图 7 Lena图像加密前后三通道直方图分析Figure7. Analysis of R, G, B three-channel histogram before and after lena image encryption.$ {10^{ - 16}} $ 时, 密钥空间可以达到$ {2^{ 128}} $ . 目前计算机计算能力决定, 当密钥空间达到$ {2^{ 128}} $ 时算法可以抵御任何形式的暴力攻击, 因此算法具有较好的抵御穷举攻击等攻击手段的能力.5.结 论 本文进行了量子漫步与图像加密结合的相关研究并进行了有效实验, 证实所提出的基于量子随机行走的彩色图像加密方案有效且切实可行, 表明将量子相关理论技术引入经典图像处理中具有广阔的应用前景; 此外将DNA编码应用于加密方案中更是为图像加密技术前景提供了一种可能. 在此次加密方案中, 量子随机行走生成的随机概率分布矩阵作为重要工具参与加密过程, 在之后的研究中希望能够更大程度地应用, 发挥其优势作用. 此外DNA编码所具备的重要生物特性也具有更加深度的应用意义.  图 1 双方向格点上交替量子随机行走
图 1 双方向格点上交替量子随机行走


































































































































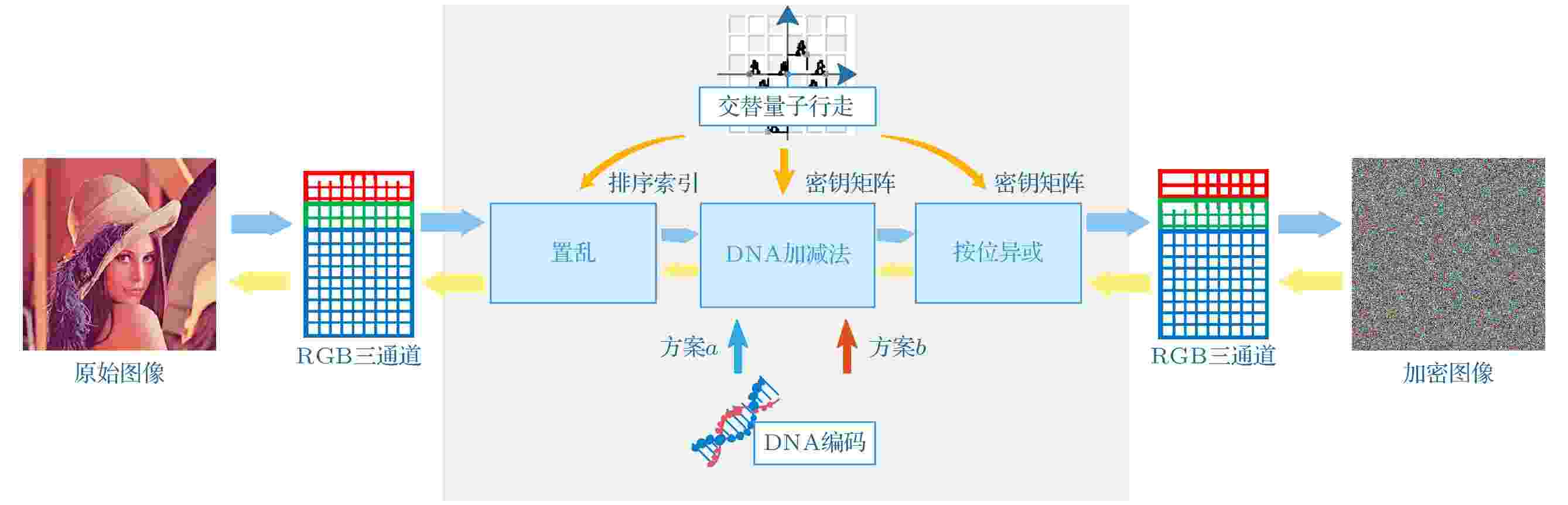 图 2 算法流程图
图 2 算法流程图









































 图 3 加密算法仿真效果图
图 3 加密算法仿真效果图






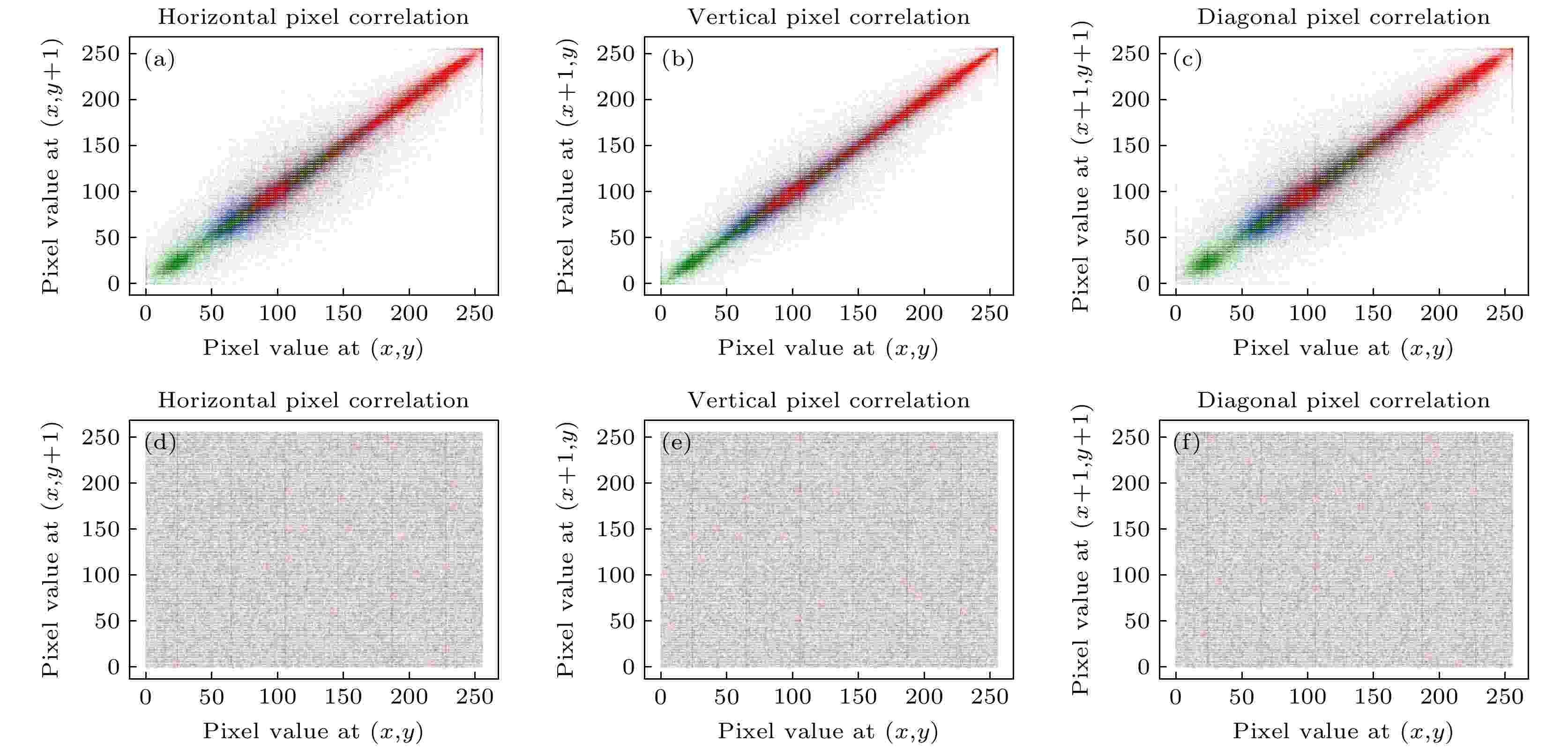 图 4 Lena图像加密前后相关性分析
图 4 Lena图像加密前后相关性分析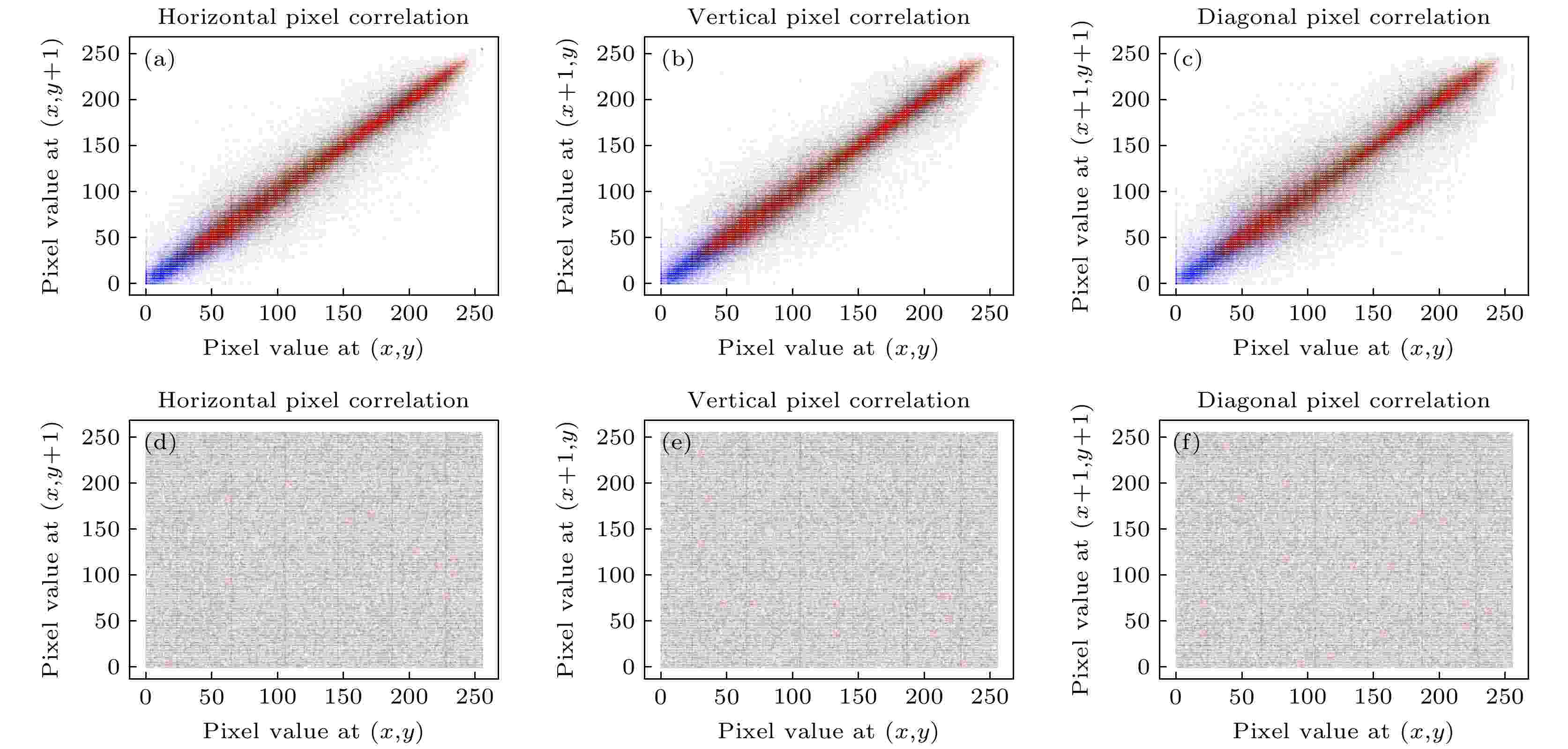 图 6 小猫图像加密前后相关性分析
图 6 小猫图像加密前后相关性分析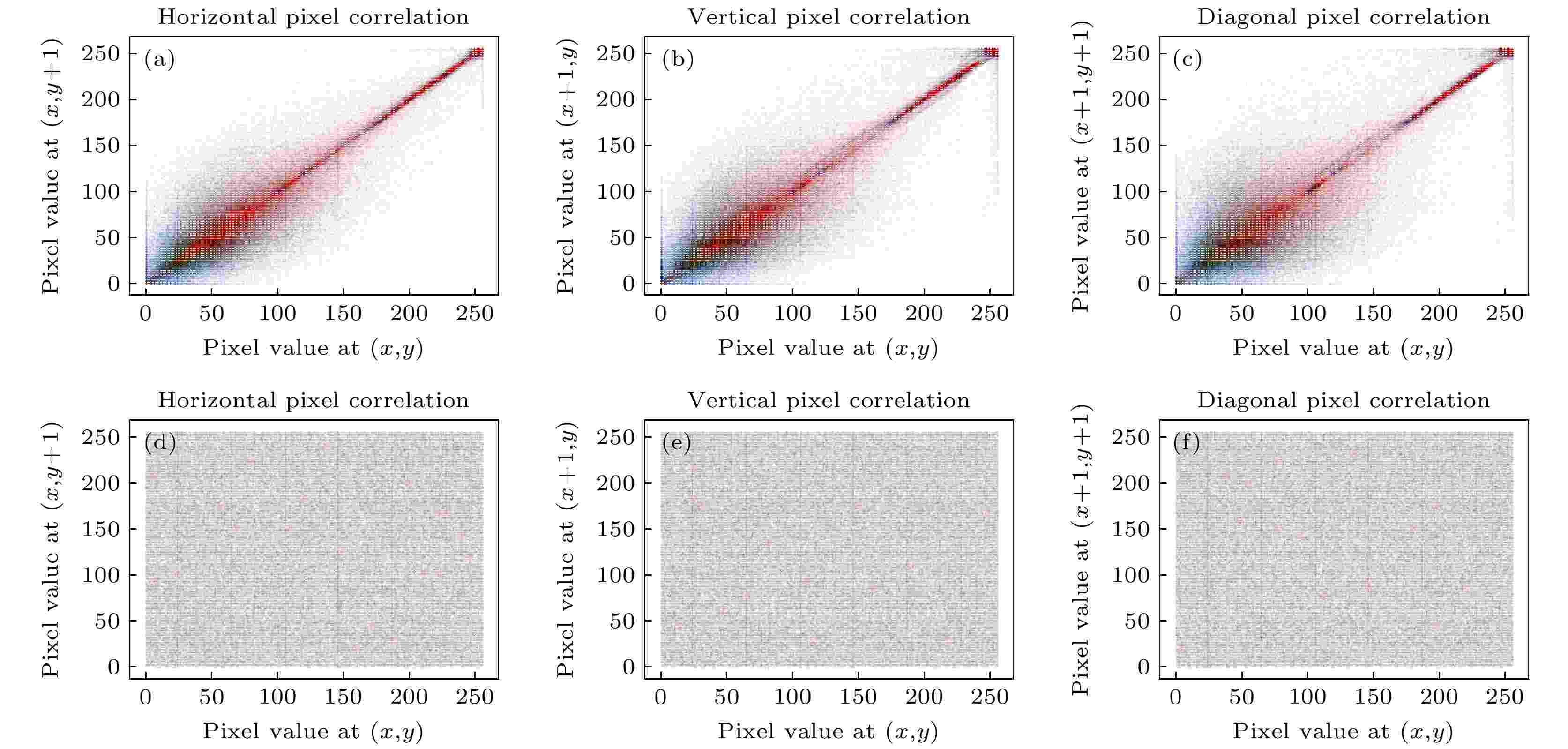 图 5 蛋糕图像加密前后相关性分析
图 5 蛋糕图像加密前后相关性分析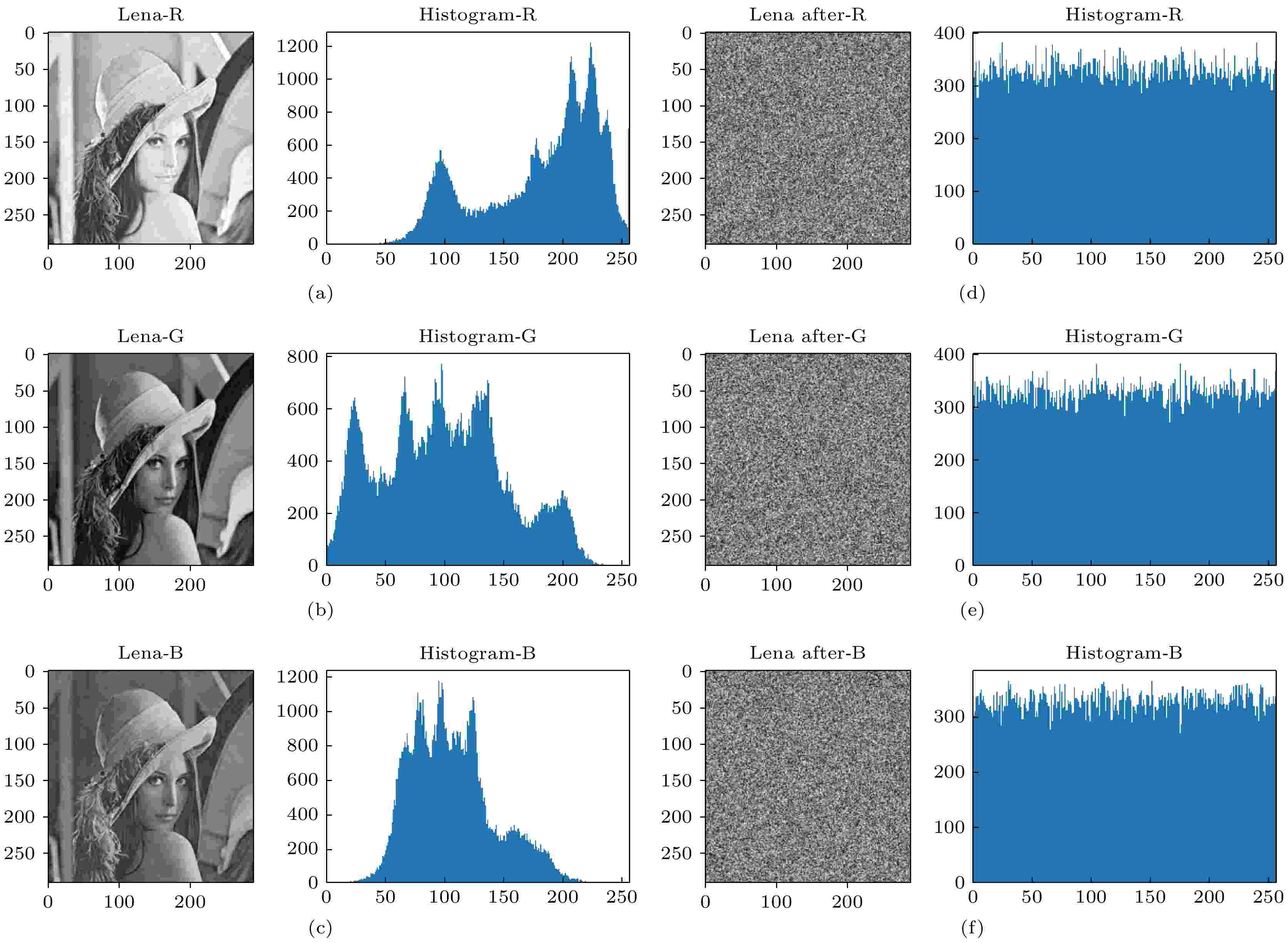 图 7 Lena图像加密前后三通道直方图分析
图 7 Lena图像加密前后三通道直方图分析






